图形的相似单元测试卷含答案
九年级上册数学单元测试卷-第1章 图形的相似-青岛版(含答案)
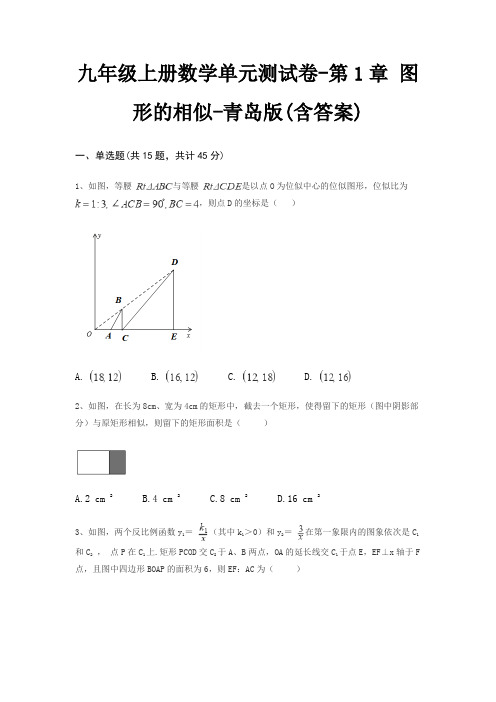
九年级上册数学单元测试卷-第1章图形的相似-青岛版(含答案)一、单选题(共15题,共计45分)1、如图,等腰与等腰是以点O为位似中心的位似图形,位似比为,则点D的坐标是()A. B. C. D.2、如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是()A.2 cm 2B.4 cm 2C.8 cm 2D.16 cm 23、如图,两个反比例函数y1=(其中k1>0)和y2=在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F 点,且图中四边形BOAP的面积为6,则EF:AC为()A. :1B.2:C.2:1D.29:144、如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=8,则S△A′B′C′=()A.18B.12C.32D.165、已知:如图,在△ABC中,∠ADE=∠C,则下列等式成立的是()A. B. C. D.6、如图,在中,,为上一点,连接,将沿翻折,点恰好落在上的点处,连.若,,则的长度为()A. B. C. D.7、如图,与相交于点,.若,则为()A. B. C. D.8、如图,矩形ABCD的对角线AC、BD交于点O,OE⊥BD交BC于E.若AB=6,BC=8,则△BOE的周长为()A.12B.C.15D.9、如图所示,在矩形ABCD中,AB=,BC=2,对角线AC,BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是()A. B. C.1 D.1.510、如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有()A.1对B.2对C.3对D.4对11、如图,铁道口的栏道木短臂长1米,长臂长16米,当短臂下降0.5米时,长臂的端点升高()米A.11.25B.6. 6C.8D.10.512、在▱ABCD中,E为BD上一点,在连结AE并延长交BC于F点,且BD=4BE,△BEF的面积为1,则▱ABCD的面积为()A.12B.24C.13D.2613、已知,,,则与的面积之比为()A. B. C. D.14、如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则DE:BC的值为()A. B. C.D.15、在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,如果△ABC的周长是16,面积是12,那么△DEF的周长、面积依次为()A.8,3B.8,6C.4,3D.4,6二、填空题(共10题,共计30分)16、如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB=________m.17、如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,﹣1),则点B的坐标是________.18、如图,在中,于点,于点,为边的中点,连接,则下列结论:①,②,③为等边三角形,④当时,.请将符合题意结论的序号填在横线上________.19、已知的周长为1,连接其三边中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,以此类推,则第2019个三角形周长为________.20、在△ABC中,E是AB上一点,AE=2,BE=3,AC=4,在AC上取一点D,使△ADE与△ABC相似,则AD的长为________.21、如图,在平面直角坐标系中,△OAB的边OB在x轴的正半轴上,AO=AB,M是边AB的中点,经过点M的反比例函数y= (k>0,x>0)的图象与边OA交于点C,则的值为________ 。
相似单元测试题及答案

相似单元测试题及答案一、选择题(每题2分,共10分)1. 下列哪项不是相似图形的特点?A. 形状相同B. 面积相等C. 大小相同D. 角度相同2. 相似比的定义是什么?A. 两个图形对应边长的比B. 两个图形对应角的比C. 两个图形对应面积的比D. 两个图形对应周长的比3. 若两个三角形相似,它们的对应角相等,对应边成比例,那么它们的对应高也成比例吗?A. 是B. 否4. 相似图形的面积比与边长比的平方相等,这是根据什么定理得出的?A. 相似定理B. 勾股定理C. 毕达哥拉斯定理D. 面积比定理5. 两个相似多边形的对应边数必须相等吗?A. 是B. 否二、填空题(每题2分,共10分)6. 如果两个三角形的相似比是2:3,那么它们的对应边长之比是________。
7. 相似图形的周长比等于它们的________。
8. 两个相似圆的面积比是25:36,那么它们的半径比是________。
9. 根据相似图形的性质,如果两个图形相似,那么它们的对应角________。
10. 在相似三角形中,如果一个三角形的边长是另一个三角形边长的1.5倍,那么它们的面积比是________。
三、简答题(每题5分,共10分)11. 解释为什么相似三角形的对应角相等。
12. 描述如何判断两个多边形是否相似。
四、计算题(每题10分,共20分)13. 已知三角形ABC与三角形DEF相似,且AB:DE = 2:3,求三角形ABC的面积与三角形DEF的面积之比。
14. 如果一个矩形的长是另一个矩形长的1.5倍,宽是另一个矩形宽的0.8倍,求这两个矩形的面积比。
五、论述题(每题15分,共15分)15. 论述相似图形在建筑设计中的应用及其重要性。
答案:一、选择题1. B2. A3. A4. D5. A二、填空题6. 2:37. 相似比8. 5:69. 相等10. 2.25:1三、简答题11. 相似三角形的对应角相等,因为相似三角形的定义就是它们的对应角相等,这是相似三角形的基本性质之一。
图形的相似单元测试【含答案】

DC B A 图形的相似 单元测试(时间:60分钟,共100分)一、选择题(每小传统3分,共30分) 1.下列语句正确的是 ( )A .在△ABC 和△A′B′C′中,∠B=∠B′=90°,∠A=30°,∠C′=60°, 则△ABC 和△A′B′C′不相似B .在△ABC 和△A′B′C′中,AB=5,BC=7,AC=8,A′C′=16,B′C′=14,A′B ′=10,则△ABC ∽△A′B′C′C .两个全等三角形不一定相似D .所有的菱形都相似2.如图所示,△ABC ∽△ADE ,AE=30cm ,EC=15cm ,BC=60cm ,则DE 的长为 ( ) A .40cm B .50cm C .45cm D .35cm 3.如图所示,能保证△ACD ∽△ABC 的条件是 ( ) A .AB:BC=AC:CD B .CD:AD=BC:AC C .CD 2=AD .DC D .AC 2=AB .AD 4.如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为 ( ) A .9:4 B .2:3 C .3:2 D .81:16 5.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,如图 所示给出的四个图案中,符合图示胶滚图案的是 ( )6.语句:“①所有度数相等的角都相似;②所有边长相等的菱形都相似;③所有的正方形都相似;④所有的圆都相似”中准确的有 ( )A .4句B .3句C .2句D .1句 7.下列语句中不正确的是 ( )A .求两条线段的比值,必需采用相同的长度单位B .求两条线段的比值,只需采用相同的长度单位,与选用何种长度单位无关C .两个相似三角形中,任意两组边对应成比例D .不相似的两个三角形中,也有可能两组边对应成比例 8.下列各组图形有可能不相似的是 ( ) A .各有一个角是50°的两个等腰三角形 B .各有一个角是100°的两个等腰三角形 C .各有一个角是50°的两个直角三角形 D .两个等腰直角三角形9.一个多边形的边长分别为2,3,4,5,6,另一个多边形和这个多边形相似,其最短边长为6,则最长边长为( )A .12B .18C .24D .301250800xy ╯ ╮ 650 536╭α ╰ ╯ 803 10. 已知cba b a c a c b +=+=+=k ,则k=( ) A .2 B .-1 C .2或-1 D .0二、填空题(每小题3分,共24分)11.如果一个三角形的面积扩大9倍,那么它的边长扩大_____________倍.12.如图所示,有一块呈三角形的草坪,其一边长为20m ,在这个草坪的图纸上,若这条边的长为5cm ,其他两边的长都是3.5cm ,则该草坪其他两边的实际长度为______________.13.如图所示的两个三角形是相似的x=_________,m=___________,n=____________.x2a 55︒m ︒45︒103a n ︒80︒45︒14. 已知如图,两个矩形相似, 则x= ,y= ,α= .15. 在相同时刻的物高与影长成比例,如果一古塔在地面上影长为50m ,同时,高为1.5m 的测竿的影长为2.5m ,那么,古塔的高是___米.16.如图中的两个矩形相似,则x=___________.17. 请把下列各组图形是否相似的结论写在下面的括号里.18.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是 .三、解答题(19小题6分,其余各小题8分,共46分) 19.把上下对应的相似图形用线连起来20.如图所示,写出多边形ABCDEF 各个顶点的坐标,并画出多边形ABCDEF 关于y 轴的轴对称图形,它们相应的对称点的坐标有什么变化?-3 -2 -1 32 1 O -1 -212 3 xy21.学生会举办一个校园摄影艺术展览会,小华和小刚准备将矩形的作品四周镶上一圈等宽的纸边,如图所示.两人在设计时发生了争执:小华要使内外两个矩形相似,感到这样视觉效果较好;小刚试了几次不能办到,表示这是不可能的.小红和小莉了解情况后,小红说这一要求只有当矩形是黄金矩形时才能做到,小莉则坚持只有当矩形是正方形时才能做到.请你动手试一试,说一说你的看法.222.以下列正方形网络的交点为顶点,分别画出两个相似比不为1的相似三角形,使它们:(1)都是直角三角形;(2)都是锐角三角形;(3)都是钝角三角形.23.如果一个图形经过分割,能成为若干个与自身相似的图形,我们称它为“能相似分割的图形”,如图所示的等腰三角形和矩形就是能相似分割的图形. (1)你能否再各举出一个 “能相似分割”的三角形和四边形?(2)一般的三角形是否“能相似分割的图形”?如果是的话给出一种分割方案,否则说明原因.24.我们通常用到的一种复印纸,整张称为A 1纸,对折一分为二裁开成为A 2纸,再一分为二成为A 3纸,…,它们都是相似的矩形.求这种纸的长与宽的比值(精确到千分位).参考答案1.B ;对应边成比例 2.A ;根据对应边成比例 3.D ;比例性质 4.C ;相似形的性质 5.C ;图形的相似 6.B ;②③④ 7.C ;注意对应 8.A ;不符合对应关系 9. 由相似多边形对应边成比例,设最长边为x .∴x662 ,∴2x=36,x=18.答案:B 10.C .2或-1二、11.3倍 12.14m 13.20314.根据相似形的性质,得x=2.5,y=1.5,α=900;⑵x=22.5. 15.在相同时刻的物高与影长成比例,设古塔的高为xm ,则505.25.1x=,解得x=30(m ) 16.已知两个矩形相似,根据相似形的性质,有x201530=,∴30x =15×20,解得x =10;又152030=x ,∴x =22.5 17. ①相似,②不相似,③不相似,④相似,⑤不相似,⑥不相似 18. 由左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),不难发现左右眼睛之间的距离2个单位;平移后的图形右图中左眼的坐标是(3,4),则右图案中右眼的坐标的纵坐标不变,横坐标为3+2=5,即右图案中右眼的坐标是(5,3). 三、19.相似形连线如(1)-(a ),(2)-(d),(3)-(g)20.提示:A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3),A′(2,0),B′(0, 3),C′(-3,-3),D′(-4,0),E′(-3,3),F′(0,3).21.只有正方形才能做到,设矩形的一边为a ,另一边为b ,等宽的纸边宽为c ,按小华的要求,应有cb ca b a 22--=,化简得a=b . 22.作图如下23.例如直角三角形,一组底角是60°、三边相等的等腰梯形. 三角形都是“能相似分割的图形”(提示:顺次连结三角形三边中点,将三角形分成的四个三角形都和原三角形相似)24. 1.414(提示:设 A 1纸的长为a ,观为b ,由A 1,A 2纸的长余观对应成比例,得a:b=b:21a )。
湘教版九年级上册数学《第3章图形的相似》单元测试题含答案
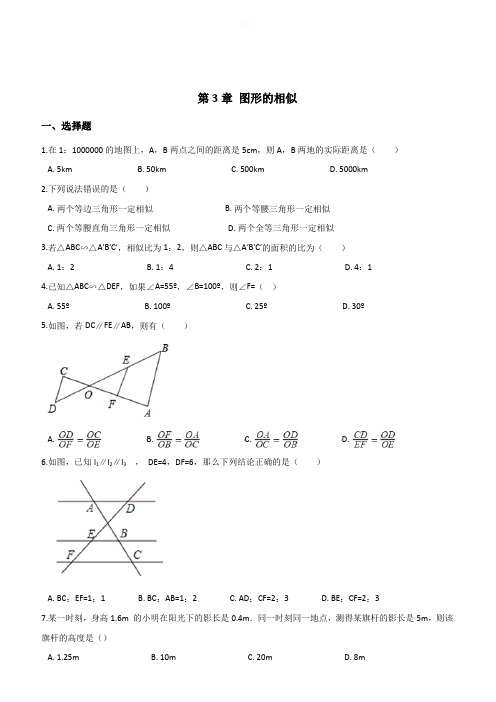
第3章图形的相似一、选择题1.在1:1000000的地图上,A,B两点之间的距离是5cm,则A,B两地的实际距离是()A. 5kmB. 50kmC. 500kmD. 5000km2.下列说法错误的是()A. 两个等边三角形一定相似B. 两个等腰三角形一定相似C. 两个等腰直角三角形一定相似D. 两个全等三角形一定相似3.若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为()A. 1:2B. 1:4C. 2:1D. 4:14.已知△ABC∽△DEF,如果∠A=55º,∠B=100º,则∠F=()A. 55ºB. 100ºC. 25ºD. 30º5.如图,若DC∥FE∥AB,则有()A. B. C. D.6.如图,已知l1∥l2∥l3,DE=4,DF=6,那么下列结论正确的是()A. BC:EF=1:1B. BC:AB=1:2C. AD:CF=2:3D. BE:CF=2:37.某一时刻,身高1.6m 的小明在阳光下的影长是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度是()A. 1.25mB. 10mC. 20mD. 8m8.如图,已知D、E分别是△ABC的AB、AC边上的点,DE∥BC,且S四边形DBCE=8S△ADE.那么AE:AC的值为()A. 1:8B. 1:4C. 1:3D. 1:99.如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A ,BC=3,AC=6,则CD的长为()A. 1B. 2C.D.10.如图,在▱ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于()A. 1:2B. 1:3C. 2:3D. 以上都不正确二、填空题11.若线段a,b,c,d成比例,其中a=3cm,b=6cm,c=2cm,则d=________ .12.如果两个相似三角形的相似比是1:3,那么这两个三角形面积的比是________.13.已知实数a,b,c满足a+b+c=10,且,则的值是________14.如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则=________ .15.如图,四边形ABCD与四边形EFGH位似,位似中心点是O,= ,则=________ .16.已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).①画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是________ ;②以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1________ ,点C2的坐标是________ ;③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________ .17.如图,已知D ,E分别是△ABC的边BC和AC上的点,AE=2,CE=3,要使DE∥AB ,那么BC:CD应等于________.18.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么=________ .19.如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=________米.20.一个等腰直角三角形和一个正方形如图摆放,被分割成了5个部分.①,②,③这三块的面积比依次为1:4:41,那么④,⑤这两块的面积比是________三、解答题21.如图,在△ABC中,点D在边AB上,满足且∠ACD=∠ABC,若AC=2,AD=1,求DB的长.22.如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,△ABE与△DEF相似吗?为什么?23.如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.24.已知:如图,.(1)求证:;(2)当时,求证:EC BC.25.在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.(1)感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;(3)应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为________.参考答案一、选择题B B BCD B C C C C二、填空题11.4cm12.1:913.14.15..16.(2,﹣2);;(1,0);(2a﹣3,2b﹣4)17.18.19.2.520.9:14三、解答题21.解∵∠ACD=∠ABC,∠BAC=∠CAD,∴△ADC∽△ACB.∴. ∵AC=2,AD=1,∴.∴DB=AB-AD=3.22.解:△ABE与△DEF相似.理由如下:∵四边形ABCD为正方形,∴∠A=∠D=90°,AB=AD=CD,设AB=AD=CD=4a,∵E为边AD的中点,CF=3FD,∴AE=DE=2a,DF=a,∴=2,=2,∴而∠A=∠D,∴△ABE∽△DEF.23.解:∵△PCD是等边三角形,∴∠PCD=60°,∴∠ACP=120°,∵△ACP∽△PDB,∴∠APC=∠B,又∠A=∠A,∴△ACP∽△ABP,∴∠APB=∠ACP=120°24.证明:(1)∵∴△ABC∽△DEF∴,(2)∵BAC=DAE∴BAD=CAE又∵∴∴△ABD∽△ACE∴ABD=ACE∵BAC=90°∴ABD+ACD=90°∴ACE+ACD=90°即EC BC.25.(1)证明:感知:如图①,∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠DAE+∠DEA=90°,∵EF⊥AE,∴∠AEF=90°,∴∠DEA+∠FEC=90°,∴∠DAE=∠FEC,∵DE=1,CD=4,∴CE=3,∵AD=3,∴AD=CE,∴△ADE≌△ECF(ASA)(2)探究:如图②,∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠DPE+∠DEP=90°,∵EF⊥PE,∴∠PEF=90°,∴∠DEP+∠FEC=90°,∴∠DPE=∠FEC,∴△PDE∽△ECF(3)2。
相似图形单元测试题(含答案)
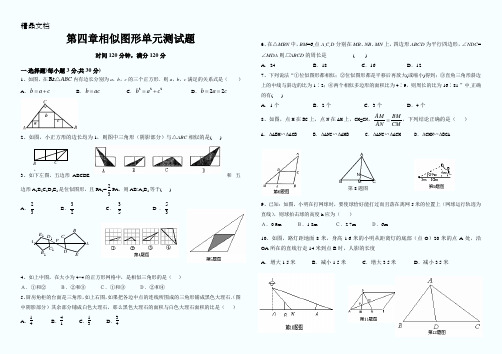
第四章相似图形单元测试题时间120分钟,满分120分一.选择题(每小题3分,共30分)1、如图,在Rt ABC △内有边长分别为a ,b ,c 的三个正方形.则a ,b ,c 满足的关系式是( )A .b a c =+B .b ac =C .222b ac =+ D .22b a c ==2、如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC 相似的是( )3、如下左图,五边形ABCDE和五边形A 1B 1C 1D 1E 1是位似图形,且PA 1=32PA ,则AB ׃A 1B 1等于( ) A .32 B .23 C . 53 D .354、如上中图,在大小为4×4的正方形网格中,是相似三角形的是( ).A.①和② B.②和③ C.①和③ D.②和④5、厨房角柜的台面是三角形,如上右图,如果把各边中点的连线所围成的三角形铺成黑色大理石.(图中阴影部分)其余部分铺成白色大理石,那么黑色大理石的面积与白色大理石面积的比是( )A .14B .41C .13D .346、在△MBN 中,BM =6,点A ,C,D 分别在MB 、NB 、MN 上,四边形ABCD 为平行四边形,∠NDC =∠MDA 则□ABCD 的周长是( )A .24B .18C .16D .127、下列说法“①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1∶2;④两个相似多边形的面积比为4∶9,则周长的比为16∶81.”中,正确的有()A .1个B .2个C .3个D .4个8、如图,点M 在BC 上,点N 在AM 上,CM=CN ,CMBMAN AM =,下列结论正确的是( ) A .∆ABM ∽∆ACB B .∆ANC ∽∆AMB C .∆ANC ∽∆ACM D .∆CMN ∽∆BCA9、已知:如图,小明在打网球时,要使球恰好能打过而且落在离网5米的位置上(网球运行轨迹为直线),则球拍击球的高度h 应为( ).A.0.9m B.1.8m C.2.7m D.6m10、如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O )20米的点A 处,沿OA 所在的直线行走14米到点B 时,人影的长度A .增大1.5米B .减小1.5米C .增大3.5米D .减小3.5米BA C第8题图ABCN ME 1D1C 1B 1A 1BDACEP二、填空题:(30分)11、如图,在平行四边形ABCD 中,M 、N 为AB 的三等分点,DM 、DN 分别交AC 于P 、Q 两点,则AP :PQ :QC= .12、如图,将①∠BAD = ∠C ;②∠ADB = ∠CAB ; ③BC BD AB ⋅=2;④DBABAD CA =;⑤DA AC BA BC =; ⑥ACDABA BC =中的一个作为条件,另一个作为结论,组成一个真命题,则条件是__________,结论是_______.(注:填序号)13、如图,Rt ∆ABC 中,AC ⊥BC ,CD ⊥AB 于D ,AC=8,BC=6,则AD=_________。
第23章 图形的相似单元测试卷(基础卷)(解析版)

1第23章图形的相似单元测试卷(基础卷)学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列四条线段中,不能成比例的是( )A .a=3)b=6)c=2)d=4B .a=1)b= 263C .a=4)b=6)c=5)d=10D .a=2)b= 5153【答案】C【解析】试题解析:∵3264=,故选项A 中的线段成比例; 22=6223=B 中的线段成比例;∵46510=,故选项C 中的线段不成比例; 2555=2325515=,故选项D 中的线段成比例;故选C)2.下列说法正确的是( )A .矩形都是相似图形;B .菱形都是相似图形C .各边对应成比例的多边形是相似多边形;D .等边三角形都是相似三角形【答案】D【解析】试题分析:根据相似多边形的判定法则可以得出所有的等边三角形都是相似三角形.2考点:相似多边形的判定3.点P 是线段AB 的黄金分割点,且AP PB >,下列命题:()()()()2221AB AP PB 2AP PB AB 3BP AP AB 4AP:AB PB:AP =⋅=⋅=⋅=,中正确的有( ) A .1个B .2个C .3个D .4个 【答案】B【解析】【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值512叫做黄金比. 【详解】∵点P 是线段AB 的黄金分割点,且AP)PB)∴根据线段黄金分割的定义得:AP 2)PB•AB)AP)AB)PB)AP)∴只有②④正确.故选B)【点睛】本题主要考查了理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键.本题同时考查了乘积形式和比例形式的转化,难度适中.4.如图,下列条件使△ACD ∽△ABC 成立的是) )3A .AC AB CD BC = B .CD BC AD AC = C .AC 2)AD·AB D .CD 2)AD·BD【答案】C【解析】试题分析:本题主要考查的就是三角形相似的判定,本题根据有一个角相等,且对应角的两边对应成比例,则两个三角形相似可以得出答案.根据题意可得∠A 为公共角,则要使三角形相似则必须满足AC AB =AD AC. 点晴:本题主要考查的就是三角形相似的判定定理,在有一个角相等的情况下,必须是角的两边对应成比例,如果不是角的两边对应成比例,则这两个三角形不相似;相似还可以利用有两个角对应相等的两个三角形全等.5.如图,在平面直角坐标系中,已知点A (―3,6)、B (―9,一3),以原点O 为位似中心,相似比为,把∠ABO 缩小,则点A 的对应点A′的坐标是( )A .(―1,2)B .(―9,18)C .(―9,18)或(9,―18)4D .(―1,2)或(1,―2)【答案】D【解析】【分析】【详解】试题分析:方法一:))ABO 和)A′B′O 关于原点位似,)) ABO))A′B′O 且OA'OA =13 .)A E AD=0E 0D =13.)A′E =13AD =2,OE =13OD =1.)A′(-1,2).同理可得A′′(1,―2). 方法二:)点A (―3,6)且相似比为13,)点A 的对应点A′的坐标是(―3×13,6×13),)A′(-1,2). )点A′′和点A′(-1,2)关于原点O 对称,)A′′(1,―2).故答案选D.考点:位似变换.6.如图,在△ABC 中,AB =6,AC =10,点D ,E ,F 分别是AB ,BC ,AC 的中点,则四边形ADEF 的周长为().5A .16B .12C .10D .8【答案】A【解析】【分析】 根据三角形的中位线定理,判断出四边形ADEF 平行四边形,根据平行四边形的性质求出ADEF 的周长即可.【详解】解:∵点D ,E ,F 分别是AB ,BC ,AC 的中点,∴DE ∥AC ,EF ∥AB ,DE=12AC=5,EF=12AB=3, ∴四边形ADEF 是平行四边形,∴AD=EF ,DE=AF ,∴四边形ADEF 的周长为2(DE+EF )=16,故选A .【点睛】本题考查了三角形中位线定理,利用中位线定理判断出四边形ADEF 为平行四边形是解题的关键. 7.课间操时,小华、小军和小刚的位置如图所示,如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以表示为( )A.(5,4)B.(4,5)C.(3,4)D.(4,3)【答案】D【解析】【分析】根据已知两点的坐标确定平面直角坐标系,然后确定其它各点的坐标即可解答.【详解】如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,如图所示就是以小华为原点的平面直角坐标系的第一象限,所以小刚的位置为(4,3).故选D.67【点睛】本题利用平面直角坐标系表示点的位置,关键是由已知条件正确确定坐标轴的位置.8.如图,锐角△ABC 的高CD 和BE 相交于点O ,图中与△ODB 相似的三角形有( )A .1个B .2个C .3个D .4个【答案】C【解析】试题解析:∵∠BDO =∠BEA =90°)∠DBO =∠EBA )∴△BDO ∽△BEA )∵∠BOD =∠COE )∠BDO =∠CEO =90°)∴△BDO ∽△CEO )∵∠CEO =∠CDA =90°)∠ECO =∠DCA )∴△CEO ∽△CDA )∴△BDO ∽△BEA ∽△CEO ∽△CDA )故选C)89.如图,已知DAB CAE ∠=∠,那么添加下列一个条件后,仍然无法判定....A ABC DE ∽△△的是( )A .AB BC AD DE = B .AB AC AD AE = C .B D ∠∠= D .C AED ∠=∠【答案】A【解析】【分析】先根据∠DAB =∠CAE 得出∠DAE =∠BAC ,再由相似三角形的判定定理对各选项进行逐一判定即可.【详解】∵∠DAB =∠CAE ,∴∠DAE =∠BAC .A .∵AB BC AD DE=,∠B 与∠D 的大小无法判定,∴无法判定△ABC ∽△ADE ,故本选项正确; B .∵AB AC AD AE =,∴△ABC ∽△ADE ,故本选项错误; C .∵∠B =∠D ,∴△ABC ∽△ADE ,故本选项错误;D .∵∠C =∠AED ,∴△ABC ∽△ADE ,故本选项错误.故选A .【点睛】本题考查了相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.10.如图,在)ABC 中,点D 是AB 边上的一点,若)ACD=)B)AD=1)AC=2))ACD 的面积为1,则)ABC9 的面积为( )A .1B .2C .3D .4【答案】D【解析】【分析】由∠ACD=∠B 结合公共角∠A=∠A ,即可证出△ACD ∽△ABC ,根据相似三角形的性质可得出214ACD ABC S AD S AC ⎛⎫== ⎪⎝⎭, 结合△ADC的面积为1,即可求出△ABC 的面积.【详解】 ∵∠ACD=∠B)∠A=∠A)∴△ACD ∽△ABC)214ACD ABC S AD S AC ⎛⎫∴== ⎪⎝⎭,∴S △ABC =4)故选D)【点睛】考查相似三角形的判定与性质,掌握相似三角形的判定方法是解题的关键.11.如图,若D 、E 分别为△ABC 中AB 、AC边上的点,且∠AED=∠B,AD=3,AC=6,DB=5,则AE 的长度为()10A.94 B .52 C .185 D .4【答案】D【解析】【分析】根据相似三角形的判定首先证出△ADE ))ACB ,然后根据相似三角形的性质得出AE AB =AD AC ,从而求出AE 的长度.【详解】解:∵∠A =)A ))AED =)B )))ADE ))ACB ))AE AB =AD AC) 又∵AD =3)AC =6)DB =5))AB =AD +DB =8))AE =8×3÷6=4)故选D)【点睛】本题主要考查了相似三角形的判定及性质.有两角对应相等的两个三角形相似.相似三角形的三边对应成比例.12.如图,在▱ABCD 中,AC )BD 相交于点O ,点E 是OA 的中点,连接BE 并延长交AD 于点F ,已知S △AEF =4,11则下列结论:①12AFFD =)②S △BCE =36)③S △ABE =12)④△AEF )△ACD ,其中一定正确的是( )A .①②③④B .①④C .②③④D .①②③【答案】D【解析】【详解】∵在▱ABCD 中,AO =12AC )∵点E 是OA 的中点,∴AE =13CE )∵AD ∥BC ) ∴△AFE ∽△CBE ) ∴AFAE BC CE ==13)∵AD =BC )∴AF =13AD )∴12AFFD =;故①正确;∵S △AEF =4) AEF BCE SS =)AF BC)2=19)12 ∴S △BCE =36;故②正确;∵EF AEBE CE = =13) ∴AEF ABE S S =13)∴S △ABE =12,故③正确;∵BF 不平行于CD )∴△AEF 与△ADC 只有一个角相等,∴△AEF 与△ACD 不一定相似,故④错误,故选D)二、填空题13.若34y x =,则x yx +=______【答案】74【解析】【分析】可设x=4k ,根据已知条件得到y=3k ,再代入计算即可得到正确结论.【详解】解:∵ 34yx =, ∴y=3k ,x=4k ; 代入x yx +=4k 3k 7=4k 4+故答案为7413【点睛】本题考查了比例的性质的应用,主要考查学生的计算能力,题目比较好,难度不大.14.已知△ABC ∽△DEF ,若△ABC 与△DEF 的相似比为2)3,则△ABC 与△DEF 对应边上的中线的比为________)【答案】2)3【解析】试题分析:根据相似三角形对应边上的中线之比等于相似比可得:∠ABC 与∠DEF 对应边上的中线的比为2:3. 考点:相似三角形的应用.15.如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O )20米的A 处,则小明的影子AM 长为 米.【答案】5. 【解析】根据题意,易得∠MBA∠∠MCO ,根据相似三角形的性质可知AB AM OC OA AM =+,即1.6AM 820AM=+,解得AM=5. ∠小明的影长为5米.16.如图,正∠ABC 的边长为2,以BC 边上的高1AB 为边作正11AB C ∆,∠ABC 与11AB C ∆公共部分的面积记为1S ;再以正11AB C ∆边11B C 上的高2AB 为边作22AB C ∆,11AB C ∆与22AB C ∆公共部分的面积记为14 2S ;......,以此类推,则n S = .(用含n 的式子表示). 33)4n【解析】【分析】【详解】因为)ABC 是边长为2的等边三角形,1AB 是高,所以1AB 31112111333(3)22A B C S S ∆=== 同理:2332AB ==,22222113393()224232A B C S S ∆==⨯=......32()n n AB =⨯,11121133332()()224n n n n n n A B C S S ---∆⎡⎤==⨯⨯⨯=⎢⎥⎣⎦.三、解答题1517.如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A (-2,4),B (4,4),C(6,0).(1)△ABC 的面积是 .(2)请以原点O 为位似中心,画出△A'B'C',使它与△ABC 的相似比为1:2,变换后点A 、B 的对应点分别为点A'、B',点B'在第一象限;(3)若P (a,b)为线段BC 上的任一点,则变换后点P 的对应点P' 的坐标为 .【答案】(1)12;(2)作图见详解;(3)11(,)22a b . 【解析】【分析】 (1)先以AB 为底,计算三角形的高,利用面积公式即可求出△ABC 的面积;(2)根据题意利用位似中心相关方法,画出△A'B'C',使它与△ABC 的相似比为1:2即可;(3)根据(2)的作图,利用相似比为1:2,直接观察即可得到答案.【详解】解:(1)由△ABC 的顶点坐标分别为A (-2,4),B (4,4),C(6,0),可知底AB=6,高为4,所以△ABC 的面积为12;16(2);(3)根据相似比为1:2,可知P 11(,)22a b . 【点睛】 本题主要考查作图-位似变换,解题的关键是掌握位似变换的定义和性质,并据此得出变换后的对应点. 18.如图,在△ABC 中,AB=AC ,点P)D 分别是BC)AC 边上的点,且∠APD=∠B,)1)求证:AC•CD=CP•BP))2)若AB=10)BC=12,当PD ∥AB 时,求BP 的长.【答案】(1)证明见解析;(2)253. 【解析】)2)易证∠APD=∠B=∠C ,从而可证到△ABP ∽△PCD ,即可得到BP AB CD CP,即AB•CD=CP•BP ,由AB=AC 即可得到AC•CD=CP•BP) )2)由PD ∥AB 可得∠APD=∠BAP ,即可得到∠BAP=∠C ,从而可证到△BAP ∽△BCA ,然后运用相似三角形的性质即可求出BP 的长.解:(1)∵AB=AC)∴∠B=∠C)∵∠APD=∠B)∴∠APD=∠B=∠C)17∵∠APC=∠BAP+∠B)∠APC=∠APD+∠DPC)∴∠BAP=∠DPC) ∴△ABP ∽△PCD)∴BP AB CD CP=) ∴AB•CD=CP•BP)∵AB=AC)∴AC•CD=CP•BP))2)∵PD ∥AB)∴∠APD=∠BAP)∵∠APD=∠C)∴∠BAP=∠C)∵∠B=∠B) ∴△BAP ∽△BCA)∴BA BP BC BA =) ∵AB=10)BC=12)∴101210BP =) ∴BP=253) “点睛”本题主要考查了相似三角形的判定与性质、等腰三角形的性质、平行线的性质、三角形外角的性质等知识,把证明AC•CD=CP•BP 转化为证明AB•CD=CP•BP 是解决第(1)小题的关键,证到∠BAP=∠C 进而得到△BAP ∽△BCA 是解决第(2)小题的关键.19.如图,△ABC 中,AB =8厘米,AC =16厘米,点P 从A 出发,以每秒2厘米的速度向B 运动,点Q 从C18同时出发,以每秒3厘米的速度向A 运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t )⑴用含t 的代数式表示:AP = )AQ = )⑵当以A )P )Q 为顶点的三角形与△ABC 相似时,求运动时间是多少?【答案】)1)AP=2t)AQ=16)3t))2)运动时间为167秒或4秒. 【解析】【分析】)1)根据路程=速度⨯时间,即可表示出AP)AQ 的长度.)2)此题应分两种情况讨论.(1)当△APQ ∽△ABC 时;(2)当△APQ ∽△ACB 时.利用相似三角形的性质求解即可.【详解】)1)AP=2t)AQ=16)3t) )2)∵∠PAQ=∠BAC)∴当AP AQ AB AC =时,△APQ ∽△ABC ,即2163816t t -=,解得167t =; 当AP AQ AC AB =时,△APQ ∽△ACB ,即2163168t t -=,解得t=4)∴运动时间为167秒或4秒.19【点睛】考查相似三角形的判定与性质,掌握相似三角形的判定定理与性质定理是解题的关键.注意不要漏解. 20.如图,O 为正方形ABCD 对角线的交点,E 为AB 边上一点,F 为BC 边上一点,△EBF 的周长等于BC 的长.)1)若AB=12)BE=3,求EF 的长;)2)求∠EOF 的度数;)3)若5OF ,求AE CF的值.【答案】(1)EF =5))2))EOF=45°))3)54AE CF =) 【解析】【分析】)1)设BF=x ,则FC=12-x ,根据△EBF 的周长等于BC 的长得出EF=9-x)Rt)BEF 中利用勾股定理求出x 的值即可得;)2)在FC 上截取FM=FE ,连接OM .首先证明∠EOM=90°,再证明△OFE))OFM)SSS )即可解决问题;)3)证明∠FOC=)AEO ,结合∠EAO=)OCF=45°可证△AOE))CFO 得5OE AE AO OF CO CF ===,推出55,由AO=CO ,可得5554CF)进20 而求解)【详解】(1)设BF=x ,则FC=BC ﹣BF=12﹣x ,∠BE=3,且BE +BF+EF=BC ,∠EF=9﹣x ,在Rt ∠BEF 中,由BE 2+BF 2=EF 2可得32+x 2=(9﹣x )2, 解得:x=4,则EF=9﹣x=5;(2)如图,在FC 上截取FM=FE ,连接OM ,∠C △EBF 的周长=BE+EF+BF=BC ,则BE +EF+BF=BF+FM+MC , ∠BE=MC ,∠O 为正方形中心,∠OB=OC ,∠OBE=∠OCM=45°,在∠OBE 和∠OCM 中,∠OB OCOBE OCM BE CM=⎧⎪∠=∠⎨⎪=⎩,21 ∠∠OBE∠∠OCM ,∠∠EOB=∠MOC ,OE=OM ,∠∠EOB+∠BOM=∠MOC+∠BOM ,即∠EOM=∠BOC=90°,在∠OFE 与∠OFM 中,∠OE OMOF OF EF MF=⎧⎪=⎨⎪=⎩, ∠∠OFE∠∠OFM (SSS ), ∠∠EOF=∠MOF=12∠EO M=45°.(3)证明:由(2)可知:∠EOF=45°,∠∠AOE+∠FOC=135°,∠∠EAO=45°,∠∠AOE+∠AEO=135°,∠∠FOC=∠AEO ,∠∠EAO=∠OCF=45°,∠∠AOE∠∠CFO .∠52OEAE AO OF CO CF ===,5,5,∠AO=CO ,225554CF , ∠AE CF =54. 【点睛】本题考查了正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题) 21.(问题情境)如图1)Rt ABC 中,90ACB ∠=)CD AB ⊥,我们可以利用ABC 与ACD 相似证明2AC AD AB =⋅,这个结论我们称之为射影定理,试证明这个定理;(结论运用)如图2,正方形ABCD 的边长为6,点O 是对角线AC )BD 的交点,点E 在CD 上,过点C 作CF BE ⊥,垂足为F ,连接OF ))1)试利用射影定理证明BOF BED ∽))2)若2DE CE =,求OF 的长.【答案】问题情境:证明见解析;结论运用:()1证明见解析;(2)655) 【解析】【分析】问题情境:通过证明Rt △ACD ∽Rt △ABC 得到AC )AB =AD )AC )然后利用比例性质即可得到AC 2=AD•AB ) 结论运用:23(1)根据射影定理得BC 2=BO •BD )BC 2=BF •BE )则BO •BD =BF •BE )即BO BE =BF BD)加上∠OBF =∠EBD )于是可根据相似三角形的判定得到△BOF ∽△BED ) )2)先计算出DE =4)CE =2)BE 10)OB 2)再利用(1)中结论△BOF ∽△BED 得到OF DE =BO BE )即4OF 32210)然后利用比例性质求OF )【详解】解:如图1)∵CD ⊥AB )∴∠ADC =90°)而∠CAD =∠BAC )∴Rt △ACD ∽Rt △ABC )∴AC )AB =AD )AC )∴AC 2=AD •AB ))1)如图2)∵四边形ABCD 为正方形)∴OC ⊥BO )∠BCD =90°)∴BC 2=BO •BD )∵CF ⊥BE )∴BC 2=BF •BE )∴BO •BD =BF •BE )即BOBE =BFBD )而∠OBF =∠EBD )∴△BOF ∽△BED )24)2)∵BC =CD =6)而DE =CE )∴DE =4)CE =2)在Rt △BCE 中)BE 2226+10.在Rt △OBC 中)OB =22BC 2) ∵△BOF ∽△BED )∴OF DE =BO BE )即4OF 32210) ∴OF =55)【点睛】本题考查了射影定理)直角三角形中)斜边上的高是两直角边在斜边上射影的比例中项)每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.也考查了相似三角形的判定与性质和正方形的性质) 22.如图, AM 是 ABC ∆ 的中线, D 是线段 AM 上一点(不与点 A 重合). //DE AB 交 AC 于点 F , //CE AM,连结 AE .25(1)如图1,当点D 与M 重合时,求证:四边形ABDE 是平行四边形(2)如图2,当点D 不与M 重合时,(1)中的结论还成立吗?请说明理由.(3)如图3,延长BD 交AC 于点H ,若BH AC ⊥,且BH AM =.①求CAM ∠的度数;②当3FH =4DM =时,求 DH 的长.【答案】(1)证明见解析(2)成立,理由见解析;(35【解析】试题分析:(1)只要证明AE=BM)AE ∥BM 即可解决问题;)2)成立.如图2中,过点M 作MG ∥DE 交CE 于G .由四边形DMGE 是平行四边形,推出ED=GM ,且ED ∥GM ,由(1)可知AB=GM)AB ∥GM ,可知AB ∥DE)AB=DE ,即可推出四边形ABDE 是平行四边形;)3)①如图3中,取线段HC 的中点I ,连接MI ,只要证明MI=12AM)MI ⊥AC ,即可解决问题; ②设DH=x ,则3,推出AM=4+2x)BH=4+2x ,由四边形ABDE 是平行四边形,推出DF ∥AB ,推出HF HD HA HB =3423x x x=+,解方程即可;试题解析:(1)证明:如图1中,26∵DE ∥AB)∴∠EDC=∠ABM)∵CE ∥AM)∴∠ECD=∠ADB)∵AM 是△ABC 的中线,且D 与M 重合, ∴BD=DC)∴△ABD ≌△EDC)∴AB=ED)∵AB ∥ED)∴四边形ABDE 是平行四边形. )2)结论:成立.理由如下:如图2中,过点M 作MG∥DE 交CE 于G)27 ∴四边形DMGE 是平行四边形, ∴ED=GM ,且ED ∥GM)由(1)可知AB=GM)AB ∥GM) ∴AB ∥DE)AB=DE)∴四边形ABDE 是平行四边形. )3)①如图3中,取线段HC 的中点I ,连接MI)∵BM=MC)∴MI 是△BHC 的中位线,∴∥BH)MI=12BH)∵BH ⊥AC ,且BH=AM)∴MI=12AM)MI ⊥AC)∴∠CAM=30°)②设DH=x ,则3∴BH=4+2x)∵四边形ABDE是平行四边形,∴DF∥AB)∴HF HDHA HB=)3423xxx=+)解得515,∴528。
2024-2025北师大九年级数学(上)第四章图形的相似单元测试卷(含答案)
第四章测试卷(时间:100分钟 满分:120分)一、选择题(每小题3分,共30分,)题号12345678910答案B C A D B C C C A C1.下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )2.在比例尺为1:500000的交通地图上,玉林到灵山的长度约为 23.6cm ,则它的实际长度约为( )A.0.118km B.1.18km C.118km D.1180km3.如图,以A ,B ,C 为顶点的三角形与以D ,E ,F 为顶点的三角形相似,则这两个三角形的相似比为( )A.2:1B.3:1C.4:3D.3:24.在△ABC 中,D 是AB 中点,E 是AC 中点,若△ADE 的面积是3,则△ABC 的面积是 ( )A.3 B.6 C.9 D.125.如图,在△ABC 中,点D 在AB 边上,过点 D 作DE ∥BC 交AC 于点E,DF ∥AC 交BC 于F,若AE:DF=2:3,则BF:BC 的值是 ( )A. 23 B. 35 C. 12D. 256.如图,在四边形ABCD 中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC 和△BAC 相似的是 ( )A.∠DAC=∠ABC B. AC 是∠BCD 的平分线 C.AC²=BC ⋅CD D.ADAB =DCAC7. 若△ABC 的各 边都分别扩大到原来的 2 倍,得到△A ₁B ₁C ₁,下列结论正确的是 ( )A.△ABC 与△A ₁B ₁C ₁的对应角不相等 B.△ABC 与△A ₁B ₁C ₁不一定相似C.△ABC 与△A ₁B ₁C ₁的相似比为1:2 D.△ABC 与△A ₁B ₁C ₁的相似比为2:18.如图,点 E 是▱ABCD 的边 BC 延长线上的一点,AE 和CD 交于点G ,AC 是▱ABCD 的对角线,则图中相似三角形共有 ( )A.2 对B.3 对C.4 对D.5 对9.如图,已知E(-4,2),F(--2,--2),以O 为位似中心,把△EFO 缩小到原来的 12,则点E 的对应点的坐标为( )A.(2,一1)或(-2,1)B.(8,一4)或(一8,4)C.(2,-1)D.(8,-4)10.如图,在正方形 ABCD 中,点 E 、F 分别在边AD 和CD 上,AF ⊥BE,垂足为G,若 AEED =2,则 AGGF 的值为( )A. 45B. 56C.67D.78二、填空题(每小题3分,共15分)11.若△ABC ∽△A'B'C',且相似比为3:5,已知△ABC 的周长为21,则△A'B'C'的周长为 .12.如图是一架梯子的示意图,其中 AA₁‖BB₁‖CC₁‖DD₁,且AB=BC=CD.为使其更稳固,在A ,D ₁间加绑一条安全绳( 线段AD ₁),量得 AE=0.4m,则 AD₁= m13.如图,阳光通过窗口照到室内,在地上留下3m 宽的亮区.已知亮区一边到窗下的墙角的距离CE=7m ,窗口高AB=1.8m,那么窗口底边离地面的高BC 等于 m.14.如图,已知每个小方格的边长均为1,则△ABC 与△CDE 的面积比为 .15.如图,在正方形ABCD 中,E 是BC 的中点,F 是CD 上一点,且 CF =14CD,下列结论:①∠BAE=30°,②△ABE ∽△ECF,③AE ⊥EF,④△ADF ∽△ECF.其中正确的结论是 (填序号).三、解答题(本大题8个小题,共75 分)16.(8分)根据下列条件,判断△ABC 与△A'B'C'是否相似,并说明理由. AB =3,BC =4,AC =5,A 'B '=12,B 'C '=16,C 'A '=2017.(9分)如图,D 是△ABC 的边AC 上的一点,连接BD,已知∠ABD=∠C,BC=6,BD=4,如果△ABD 的面积为4,求△BC D 的面积.18.(9分)在平面直角坐标系中,△ABC 的三个顶点的坐标分别是 A(1,3),B(4,1),C(1,1).(1)画出△ABC 关于x 轴成轴对称的△A ₁B ₁C ₁;(2)画出△ABC 以点O 为位似中心,相似比为 1:2的△A ₂B ₂C ₂.19.(9分)如图,四边形ABCD 是菱形,AF ⊥BC 交BD 于E,交 BC 于F.求证: AD 2=12DE ⋅DB.20.(10分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一颗大树,将其底部作为点 A,在他们所在的岸边选择了 B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB 的延长线上选择点 D 竖起标杆DE,使得点 E 与点C、A共线.已知:CB⊥AD,ED⊥AD,测得 BC=1m,DE=1.5m,BD=8.5m,测量示意图如图所示.请根据相关测量信息,求河宽 AB.21.(10分)如图,E是平行四边形ABCD的边 DA 延长线上一点,连结 EC 交AB 于 P.(1)写出图中的三对相似三角形(不添加辅助线);(2)请在你所写的相似三角形中选一对,说明相似的理由.22.(10分)阅读与计算:请阅读以下材料,并完成相应的问题.角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则ABAC =BDCD.下面是这个定理的部分证明过程.证明:如图2,过点C作CE∥DA,交 BA的延长线于点 E⋯任务:(1)请按照上面的证明思路,写出该证明过程的剩余部分;(2)如图3,在△ABC中,AD是角平分线,AB=5cm ,AC=4 cm,BC=7 cm.求 BD的长.23.(10分)在矩形 ABCD中,点 E 是对角线AC 上一动点,连接 DE,过点 E 作EF⊥DE 交AB 于点 F.(1)如图1,当DE=DA时,求证:AF=EF;(2)如图2,点E 在运动过程中,DEEF的值是否发生变化?请说明理由.第四章测试卷答案一、选择题1、B2、C3、A4、D5、B6、C7、C8、C9、A 10、C 二、填空题11、35 12、1.2m 13、2.4m 14、4:1 15、②③三、解答题16、解:相似,理由: ∵AB A 'B '=312=14,BC B 'C '=416=14,AC A 'C '=520=14,∴ABA 'B'=BCB 'C '=ACA 'C ',∴ABC ∽A 'B 'C '.17、解:∵∠ABD=∠C,又∠A=∠A,∴△ABD ∽△ACB,S ABD S ACB=(BD CB )2=(46)2=49,18、解:如图所示19、证明:连接AC 交 BD 于点O,∵四边形ABCD 为菱形,∴AC ⊥BD,BO=OD,∵AE ⊥AD,∴△AOD ∽△EAD, ∴AD OD=ED AD,∴A D 2=ED ⋅OD,即 A D 2=12DE ⋅DB.20、解:∵CB ⊥AD,ED ⊥AD, ∴∠CBA =∠EDA =90°.∵∠CAB=∠EAD, ∴ABCOADE,∴AB AD=BC DE,∴AB AB +8.5=11.5,∴AB =17,.∴河宽为17m.21、解:(1)△EAP ∽△CBP,△AEP ∽△DEC,△BCP ∽△DEC.(2)选. △EAPO △CBP,理由如下:在▱ABCD 中AD ∥BC,∴∠EAP=∠B.又∵∠APE=∠BPC,∴△EAP ∽△CBP.22、解:(1)证明:如图2,过点C作CE∥DA,交BA的延长线于点E, ∵CEDA,∴BDCD =BAEA,∠CAD=∠ACE,∠BAD=∠E,∵AD平分∠BAC,∴∠BAD=∠CAD, ∠ACE=∠E,∴AE=AC,∴ABAC =BDCD;(2)∵AD是角平分线, ∴ABAC =BDCD,AB=5 cm,AC=4 cm,BC=7 cm, C.54=BD7−BD,解得BD=359cm.23、解:(1)证明:如图,连接 DF,在矩形ABCD 中,∠DAF=90°,又∵DE⊥EF,∴∠DEF=90°,∵AD=DE,DF=DF,∴Rt△DAF≌Rt△DEF(HL),∴AF=EF;(2)DEEF 的值不变.如图,过点E作EM⊥AD于点M,过点E 作EN⊥AB 于点 N,∵EM∥CD,EN∥BC,∴EMCD =AEAC,ENBC=AEAC,∴EMEN=CDBC,∵∠DEF=∠MEN=90°,∴∠DEM=∠FEN,又·∴∠DME=∠ENF=90°,∴△DME⊗△FNE,∴DEEF =EMEN,∴DEEF=CDBC,∵CD 与BC 的长度不变, ∴DEFF的长度不变.。
第1章 图形的相似数学九年级上册-单元测试卷-青岛版(含答案)
第1章图形的相似数学九年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、下列各组图形必相似的是()A.任意两个等腰三角形B.有两边对应成比例,且有一个角对应相等的两三角形C.两边为4和5的直角三角形与两边为8和10的直角三角形 D.两边及其中一边上的中线对应成比例的两三角形2、两个相似五边形,一组对应边的长分别为3cm和4.5cm,如果它们的面积之和是78cm2,则较大的五边形面积是()cm2.A.44.8B.52C.54D.423、如图,P为反比例函数y= (k>0)在第一象限内图象上的一点,过点P分别作x 轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A,B.若∠AOB=135°,则k的值是()A.2B.4C.6D.84、如图,已知正方形ABCD的边长为1,M是AB的中点,则图中阴影部分的面积是()A. B. C. D.5、如图,△ABC中,∠BAC=90°,AD⊥BC于D,若AB=2,BC=3,则CD的长是( )A. B. C. D.6、下列说法正确的是()A.相似多边形都是位似多边形B.有一个角是100°的两个等腰三角形一定相似C.两边对应成比例,且有一个角对应相等的两个三角形一定相似 D.所有的菱形都相似7、如图,正方形BODC的顶点C的坐标是(3,3),以原点O为位似中心,将正方形BODC 缩小后得到正方形B'ODC',点C的对应点C'的坐标为(﹣1,﹣1),那么点D的对应点D'的坐标为()A.(﹣1,0)B.(0,﹣1)C.(1,0)D.(0,1)8、如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB=,则此三角形移动的距离AA′是()A. B. C.1 D.9、如图,在中,点D,E分别为AB,AC边上的点,且,CD、BE相较于点O,连接AO并延长交DE于点G,交BC边于点F,则下列结论中一定正确的是A. B. C. D.10、下列命题是真命题的是()A.两直线平行,同位角相等B.相似三角形的面积比等于相似比C.菱形的对角线相等D.相等的两个角是对顶角11、如图,在菱形ABCD中,点E是BC的中点,DE与AC交于点F,若AB=6,∠B=60°,则AF的长为()A.3B.3.5C.3D.412、如图,已知O是坐标原点,△OBC与△ODE是以0点为位似中心的位似图形,且△OBC 与△ODE的相似比为1:2,如果△OBC内部一点M的坐标为(x,y),则M在△ODE中的对应点M′的坐标为()A.(﹣x,﹣y)B.(﹣2x,﹣2y)C.(﹣2x,2y)D.(2x,﹣2y)13、如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是()A.AF=CFB.∠DCF=∠DFCC.图中与△AEF相似的三角形共有5个D.tan∠CAD=14、如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是()A. B. C. D.15、如图,在四边形中,,连接,以为直径的圆交于点.若,则的长为()A. B. C. D.二、填空题(共10题,共计30分)16、如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4 ,AC=5,AD=4,则⊙O的直径AE=________.17、如图,已知小鱼同学的身高(CD)是1.6米,她与树(AB)在同一时刻的影子长分别为DE=2米,BE=5米,那么树的高度AB=________米.18、如图,正方形ABCD中,点E是对角线BD上的一点,BE=BC,过点E作EF⊥AB,EG⊥BC,垂足分别为点F,G,则正方形FBGE与正方形ABCD的相似比为________.19、如图,在中,是中线,F是上的点,,的延长线交于点E,则________.20、如图,在等边中,,点在上,且,点是上一动点,连结,将线段绕点逆时针旋转得到线段.要使点恰好落在上,则的长是________21、如图,正方形ABCD 中,边AB=6 ,点E 在边BC 上,且BE=2 ,点F 为边CD 上的一个动点,以 EF为直角边作直角三角形,,且,点G在直线 EF的左上方,连接BG ,当点F 在边 CD上运动时,的周长的最小值为________.22、如图,在中,,,点是边上一点(点不与点,重合),将沿翻折,点的对应点是,交于点,若,则的长为________.23、如图,平面直角坐标系中,矩形ABOC的边BO,CO分别在x轴,y轴上,A点的坐标为(﹣8,6),点P在矩形ABOC的内部,点E在BO边上,满足△PBE∽△CBO,当△APC是等腰三角形时,P点坐标为________.24、如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,如果AB=12,BC=9,AC=6,四边形BCED的周长为21,那么DE的长为________.25、如图,已知直线l:y=﹣x+4分别与x轴、y轴交于点A,B,双曲线(k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=________.三、解答题(共5题,共计25分)26、如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,请确定点O的位置,如果OC=3.6cm,OF=2.4cm,求它们的相似比.27、已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.(1)若BD是AC边上的中线,如图1,求的值;(2)若BD是∠ABC的角平分线,如图2,求的值.28、如图,某校数学兴趣小组利用自制的直角三角形硬纸板来测量操场旗杆的高度,他们通过调整测量位置,使斜边与地面保持平行,并使边与旗杆顶点在同一直线上,已知,,目测点到地面的距离,到旗杆的水平距离,求旗杆的高度.29、如图,在中,点D在边上,,求证:.30、如图,以O为位似中心,在网格内作出四边形ABCD的位似图形,使新图形与原图形的相似比为2:1,并以O为原点,写出新图形各点的坐标.参考答案一、单选题(共15题,共计45分)1、D2、C3、D4、D5、D6、B7、A8、A9、C10、A11、D12、B13、D14、C15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、30、。
图形的相似单元测试(含答案)
图形的相似单元测试一、选择题1、【基础题】在比例尺为1:5000的地图上,量得甲,乙两地的距离为25 cm ,则甲、乙两地的实际距离是 ( ) A. 1250千米 B. 125千米 C. 12.5千米 D. 1.25千米2、【基础题】已知135=ab ,则ba b a +-的值是( ) ★ A. 32 B. 23 C. 49 D. 943、【基础题】如右图,在△ABC 中,看DE ∥BC ,12AD BD =,DE =4 cm ,则BC 的长为 ( ) A .8 cm B .12 cm C .11 cm D .10 cm4、【基础题】如右图,DE 是ΔABC 的中位线,则ΔADE 与ΔABC 的面积之比是( ) A .1:1B .1:2C .1:3D .1:45、【基础题】如下图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC 相似的是( ) ★★★6、【基础题】下列结论不正确的是( ) ★ A. 所有的矩形都相似 B. 所有的正方形都相似 C. 所有的等腰直角三角形都相似 D. 所有的正八边形都相似7、【基础题】下列说法中正确的是( ) ★A. 位似图形可以通过平移而相互得到;B. 位似图形的对应边平行且相等C. 位似图形的位似中心不只有一个D. 位似中心到对应点的距离之比都相等8、【综合题Ⅰ】如右上图,ABCD 是正方形,E 是CD 的中点,P 是BC 边上的一点,下列条件中,不能推出△ABP 与△ECP 相似的是( ) ★★★A. ∠APB =∠EPC ;B. ∠APE =90°C. P 是BC 的中点D. BP ︰BC =2︰3 9、【综合题Ⅱ】如右上图,Rt △ABC 中,AB ⊥AC ,AB =3, AC =4,P 是BC 边上一点,作PE ⊥AB 于E ,PD ⊥AC 于D ,设BP =x ,则PD+PE =( ) A.35x + B. 45x -C.72D.21212525x x -10、【综合题Ⅲ】如图,在Rt ABC △内有边长分别为a ,b ,c 的三个正方形.则a 、b 、c 满足的关系式是( )AB CA. b a c =+B. b ac =C. 222b a c =+D. 22b a c == 二、填空题11、【基础题】在同一时刻,高为1.5m 的标杆的影长为2.5m ,一古塔在地面上影长为50m ,那么古塔的高为 .12、【基础题】两个相似三角形面积比是9∶25,其中一个三角形的周长为36cm ,则另一个三角形的周长是 . 13、【综合题Ⅰ】如左下图,在△ABC 中,AB =5,D 、E 分别是边AC 和AB 上的点,且∠ADE =∠B ,DE =2,那么AD·BC = .14、【基础题】如右上图,在△ABC 和△DEF 中,G 、H 分别是边BC 和EF 的中点,已知AB =2DE ,AC =2DF ,∠BAC =∠EDF . 那么AG :DH = ,△ABC 与△DEF 的面积比是 .15、【基础题】把一个三角形改做成和它相似的三角形,如果面积缩小到原来的21倍,边长应缩小到原来的____倍. 16、【综合Ⅱ】如左下图在Rt △ABC 中, ∠ACB =90°,CD ⊥AB 于D ,若AD =1,BD =4,则CD = .17、【基础题】如右上图,一人拿着一支厘米小尺,站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上12厘米的长度恰好遮住电线杆,已知手臂长约60厘米,则电线杆的高为 .18、【基础题】已知一本书的宽与长之比为黄金比,且这本书的长是20 cm ,则它的宽为_____cm.(结果保留根号) 19、【综合Ⅲ】顶角为36°的等腰三角形称为黄金三角形,如图,在△ABC 中,AB =AC =1,∠A =36°,BD 是三角形ABC 的角平分线,那么AD =__ 20、【提高题】如图,点1234A A A A ,,,在射线OA 上,点123B B B ,,在射线OB 上,且112233A B A B A B ∥∥,213243A B A B A B ∥∥.若212A B B △、323A B B △的面积分别为1、4,则图中三个阴影三角形面积之和为 .(第20题图)OA 1 A 2A 3A 4 AB B 1 B 2 B 3 14三、解答题21、【基础题】(2008无锡)如图,已知点E 是矩形ABCD 的边CD 上一点,BF ⊥AE 于点F ,求证△ABF ∽△EAD .22、【综合Ⅰ】如图27-106所示,已知E 为ABCD 的边CD 延长线上的一点,连接BE 交AC 于O ,交AD 于F .求证BO 2=OF ·OE .23、如图,在平面直角坐标系中,已知OA=12 cm ,OB=6 cm ,点P 从O 点开始沿OA 边向点A 以1cm/s 的速度移动,点Q 从点B 开始沿BO 边向点O 以1cm/s 的速度移动,如果P 、Q 同时出发,用t (单位:秒) 表示移动的时间(06t ≤≤),那么: (1)当t 为何值时, △POQ 与△AOB 相似?(2)设△POQ 的面积为y ,求y 关于t 的函数解析式。
图形相似单元测试题及答案
图形相似单元测试题及答案# 图形相似单元测试题及答案一、选择题1. 两个图形相似的条件是什么?A. 面积相等B. 周长相等C. 对应角相等,对应边成比例D. 形状相同答案:C2. 如果两个三角形的对应边长比为2:3,那么它们的面积比是多少?A. 2:3B. 4:9C. 3:2D. 9:4答案:B3. 在相似图形中,对应角的大小关系是什么?A. 相等B. 互为补角C. 互为余角D. 不确定答案:A二、填空题4. 如果一个图形放大到原来的两倍,则其面积变为原来的________倍。
答案:45. 相似三角形的判定定理包括SSS(边边边)、SAS(边角边)、_______。
答案:AAA(角角角)三、简答题6. 请解释什么是相似比,并给出一个例子。
答案:相似比是指两个相似图形对应边长的比值。
例如,如果三角形ABC与三角形DEF相似,且AB:DE=2:3,那么2:3就是它们的相似比。
7. 描述如何判断两个多边形是否相似。
答案:要判断两个多边形是否相似,需要满足以下条件:对应角相等,且对应边成比例。
如果一个多边形的每个角和每条边都与另一个多边形的相应角和边成相同的比例,那么这两个多边形就是相似的。
四、计算题8. 已知三角形ABC与三角形DEF相似,AB=6cm,DE=9cm,BC=8cm,求EF的长度。
答案:由于三角形ABC与三角形DEF相似,根据相似比,我们有AB:DE = BC:EF。
将已知数值代入,得到6:9 = 8:EF。
解这个比例,我们得到EF = (8 * 9) / 6 = 12cm。
结束语本单元测试题涵盖了图形相似的基本概念、判定方法和实际应用。
通过这些题目的练习,可以帮助学生加深对图形相似概念的理解和应用能力。
希望同学们能够认真完成这些题目,并在解答过程中发现问题、解决问题,从而提高自己的数学素养。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章《图形的相似》单元测试卷一、选择题: 1.(2015?东营)若34yx=,则x yx+的值为……………………………………………()A.1;B.47; C.54; D .74;2. 已知线段a、b、c,其中c是a、b的比例中项,若a=9cm,b=4cm,则线段c长………()A.18cm; B.5cm; C.6cm; D.±6cm;3. 已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是………………()A.252-;B.25-; C.251-; D.52-;4. (2015?荆州)如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是()A.∠ABP=∠C;B.∠APB=∠ABC;C.AP ABAB AC=; D.AB ACBP CB=;5. (2016?临夏州)如果两个相似三角形的面积比是1:4,那么它们的周长比是………()A.1:16; B.1:4; C.1:6; D.1:2;6. (2015?恩施州)如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为……()A.4; B.7; C.3; D.12;8. 如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于()A.1; B.2; C.3; D.4;10.如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为……()A.2; B.或; C.或; D.2或或;二、填空题:11. 如果在比例尺为1:1?000?000的地图上,A、B两地的图上距离是厘米,那么A、B两地的实际距离是? 千米.12.如图,已知:123////l l l,AB=6,DE=5,EF=7.5,则AC= .13. 如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是.第4题图第8题图第12题图第10题图第6题图第7题图14. 如图,点G 是△ABC 的重心,GH ⊥BC ,垂足为点H ,若GH =3,则点A 到BC 的距离为 . 15. 如图,小明同学用自制的直角三角形纸板DEF 测量树的高度AB ,他调整自己的位置,设法使斜边DF 保持水平,并且边DE 与点B 在同一直线上.已知纸板的两条直角边DE =40cm ,EF =20cm ,测得边DF 离地面的高度AC =1.5m ,CD =8m ,则树高AB = .16. 如图,已知△ABC 中,D 为边AC 上一点,P 为边AB 上一点,AB =12,AC =8,AD =6,当AP 的长度为 时,△ADP和△ABC 相似.17.如图,双曲线k y x =经过Rt △BOC 斜边上的点A ,且满足23AO AB =,与BC 交于点D ,21BOD S =V ,求k =? . 18.(2016?安徽)如图,在矩形纸片ABCD 中,AB =6,BC =10,点E 在CD 上,将△BCE 沿BE 折叠,点C 恰落在边AD 上的点F 处;点G 在AF 上,将△ABG 沿BG 折叠,点A 恰落在线段BF 上的点H 处,有下列结论:①∠EBG =45°;②△DEF ∽△ABG ;③32ABG FGH S S =V V ;④AG +DF =FG .其中正确的是 .(把所有正确结论的序号都选上)三、解答题: 19.如图,在矩形ABCD 中,AB =4,BC =6,M 是BC 的中点,DE ⊥AM 于点E .(1)求证:△ADE ∽△MAB ;(2)求DE 的长.20.如图,在△ABC 中,DE ∥BC ,EF ∥AB ,若ADE S V =4cm 2,EFC S V =9cm 2,求ABC S V .21. 如图,△ABC 中,CD 是边AB 上的高,且AD CD CD BD=.(1)求证:△ACD ∽△CBD ;(2)求∠ACB 的大小.第18题图第17题图 第16题图26.如图,在平行四边形ABCD 中,对角线AC 、BD 交于点O .M 为AD 中点,连接CM 交BD 于点N ,且ON =1.(1)求BD 的长;(2)若△DCN 的面积为2,求四边形ABNM 的面积.如图,在平面直角坐标系中,点C (-3,0),点A 、B 分别在x 轴,y 轴的正半轴上,且满足0132=-+-OA OB .(1)求点A 、B 坐标。
(2)若点P 从点C 出发,以每秒1个单位的速度沿射线CB 运动,连接AP 。
设△ABP 面积为S ,点P 的运动时间为t 秒,求S 与t 的函数关系式,并写出自变量的取值范围。
(3)在(2)的条件下,是否存在点P ,使以点A 、B 、P 为顶点的三角形与△AOB 相似?若存在,请直接写出点P 的坐标;若不存在,请说明理由。
13.如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒.(1) 求直线AB 的解析式;⑵当t 为何值时,△APQ 与△AOB 相似;⑶当t 为何值时,△APQ 的面积为个平方单位?26.如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.(1)求BD的长;(2)若△DCN的面积为2,求四边形ABNM的面积.27.(2015?宜昌)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,A D.(1)求证:△DOB∽△ACB;(2)若AD平分∠CAB,求线段BD的长;(3)当△AB′D为等腰三角形时,求线段BD的长.28. (本题满分10分)(2016?青岛)已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点0.点P从点A出发,沿方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:(1)当t为何值时,△AOP是等腰三角形?(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;(3)在运动过程中,是否存在某一时刻t,使S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;(4)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.参考答案一、选择题:;;;;;;;;;;二、填空题:;;13.(9,0);;15.5.5;或9;;18.①③④;三、解答题:19.(1)略;(2);;21.(1)略;(2)90°;22.(1)略;(2)2A (-2,-2);23.4.2;24.43; 25.(1)4;(2)(3,0);(3)①当∠ABE =90°时,∵B 是AC 的中点,∴EB 垂直平分AC ,EA =EC =3x +,由勾股定理得222AD DE AE +=,即()()222413x x ++=+,解得2x =.∴E (-2,0); ②当∠BAE =90°时,ABE >∠ACD ,故△EBA 与△ACD 不可能相似.26.(1)6;(2)5;27. (1)证明:∵DO ⊥AB ,∴∠DOB =∠DOA =90°,∴∠DOB =∠ACB =90°,又∵∠B =∠B ,∴△DOB ∽△ACB ;(2)解:∵∠ACB =90°,∴AB ==10,∵AD 平分∠CAB ,DC ⊥AC ,DO ⊥AB ,∴DC =DO ,在Rt △ACD 和Rt △AOD 中,AD =AD ,DC =DO ,∴Rt △ACD ≌Rt △AOD (HL ),∴AC =AO =6,设BD =x ,则DC =DO =8-x ,OB =AB -AO =4,在Rt △BOD 中,根据勾股定理得:222DO OB BD +=,即()22284x x -+=,解得:x =5,∴BD 的长为5; (3)解:∵点B ′与点B 关于直线DO 对称,∴∠B =∠OB ′D ,BO =B ′O ,BD =B ′D ,∵∠B 为锐角,∴∠OB ′D 也为锐角,∴∠AB ′D 为钝角,∴当△AB ′D 为等腰三角形时,AB ′=DB ′,∵△DOB ∽△ACB ,∴84105OB BC BD AB ===, 设BD =5x ,则AB ′=DB ′=5x ,BO =B ′O =4x , ∵AB ′+B ′O +BO =AB ,∴5x +4x +4x =10,解得:1013x =,∴BD =5013.28. 解:(1)∵在矩形ABCD 中,AB =6cm ,BC =8cm ,∴AC =10,①当AP =PO =t ,如图1,过P 作PM ⊥AO ,∴AM =12AO =52,∵∠PMA =∠ADC =90°,∠PAM =∠CAD ,∴△APM ∽△ADC , ∴AP AM AC AD =,∴AP =t =258,②当AP =AO =t =5,∴当t 为258或5时,△AOP 是等腰三角形; (2)作EH ⊥AC 于H ,QM ⊥AC 于M ,DN ⊥AC 于N ,交QF 于G ,在△APO 与△CEO 中,∠PAO =∠ECO ,AO =OC ,∠AOP =∠COE ,∴△AOP ≌△COE ,∴CE =AP =t ,∵△CEH ∽△ABC ,∴EH CE AB AC =,∴EH =35t ,∵DN =245AD CD AC =g , ∵QM ∥DN ,∴△CQM ∽△CDN ,∴QM CQ DN CD =,即62465QM t -=, ∴QM =2445t -,∴DG =242444555t t --=,∵FQ ∥AC ,∴△DFQ ∽△DOC ,∴FQ DG OC DN =,∴FQ =56t , ∴S 五边形OECQF =S △OEC +S 四边形OCQF =213152441355122526532t t t t t -⎛⎫⨯⨯++=-++ ⎪⎝⎭g , ∴S 与t 的函数关系式为S =2131232t t -++; (3)存在,∵S △ACD =12×6×8=24, ∴S 五边形OECQF :S △ACD =2131232t t ⎛⎫-++ ⎪⎝⎭:24=9:16,解得t =3,或t =32, ∴t =3或32时,S 五边形S 五边形OECQF :S △ACD =9:16; (4)如图3,过D 作DM ⊥AC 于M ,DN ⊥AC 于N ,∵∠POD =∠COD ,∴DM =DN =245,∴ON =OM75=, ∵OP ?DM =3PD ,∴OP =558t -,∴PM =18558t -,∵222PD PM DM =+, ∴()222185248585t t ⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭, 解得:t ≈15(不合题意,舍去),t =11239, ∴当t =11239时,OD 平分∠COP .。
