几种特殊四面体的判定及其性质
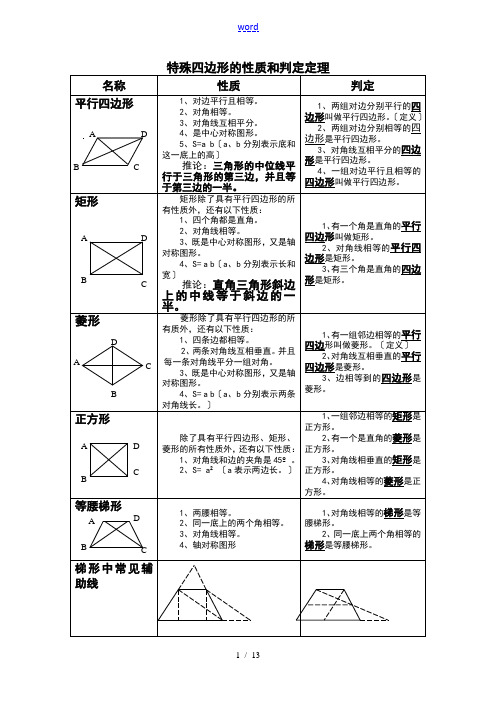
特殊的四边形地性质和判定定理
例1 如图,E、F分别为正方形ABCD的边BC、CD上的一点,AM⊥EF,垂足为M,假如AM=AB,求证:EF=BE+CF例2 :如图,正方形ABCD中,延长AD到E,使DE=AD,再延长DE到F,使DF=BD,连接BF 交CD于Q,交CE于P。
求证PD=PQ在正方形中ABCD ∠ADB=∠DBC=∠BDC=45º DF=BD ∴∠DBF=∠DFB∠ADB=∠DBF+∠F ===>∠DBF=∠º===>∠QBC=45-∠º===>∠DQP=∠BQC=90-∠ºDE=AD=DC DCE=45º∠EPF=∠BPC=180-∠PBC-∠BCD-∠º=∠F ∴EP=EF∵DF=BD=EC EP=EF ∴PC(EC-EP)=DE(DF-EF)=DC 又∵∠DCP=45º∴∠QDP=(180-∠º=∠DQP ∴PD=PQ例3 如图,在◇ABCD中,∠ABC=75°,AF⊥BC于F,AF交BD于E,假如DE=2AB,求∠AED例4 如图,在梯形ABCD中,AB∥CD,以AC、AD为边作◇ACED,DC的延长线交BE于F,求证:EF=FB证明如下列图,连接AE交DC于O.∵四边形ACED是平行四边形.∴O是AE的中点.∵在梯形ABCD中,DC∥AB,在△EAB中,OF∥AB,又∵O是AE的中点,∴F是EB的中点,∴EF=BF.例5 如图,以△ABC的AB、AC为边向形外做正方形ABDE和正方形ACFG,AM是△ABC的中线,连接EG。
求证EG=2AM延长BA至点H ,使得BA=AH对三角形EAG和三角形HAC,因为EA=AH,AG=AC ,角EAG=90+角HAG=角HAC,所以两三角形全等,得EG=CH又因为M是BC的中点,所以AM是三角形HBC的中位线,得CH=2*AM所以得AM=二分之一EG多边形一、选择题1.〔某某〕如图,D 是△ABC 内一点,BD ⊥CD ,AD =6,BD =4,CD =3,E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点,如此四边形EFGH 的周长是〔 〕A .7B .9C .10D .112. 〔某某威海〕在□ABCD 中,点E 为AD 的中点,连接BE ,交AC 于点F ,如此AF :CF =〔 〕A .1:2B .1:3C .2:3D .2:53. 〔某某某某〕四边形ABCD 中,对角线AC 、BD 相交于点O ,给出如下四组条件:①AB ∥CD ,AD ∥BC ;②AB =CD ,AD =BC ;③AO =CO ,BO =DO ;④AB ∥CD ,AD =BC .其中一定能判定这个四边形是平行四边形的条件有A .1组B .2组C .3组D .4组 4. 〔某某市潼南〕如图,在平行四边形 ABCD 中(AB ≠BC),直线EF 经过其对角线的交点O,且分别交AD 、BC 于点M 、 N ,交BA 、DC 的延长线于点E 、F ,如下结论: ①AO=BO ;②OE=OF ; ③△EAM ∽△EBN ; ④△EAO ≌△O ,其中正确的答案是A. ①②B. ②③C. ②④D.③④ 5. 〔某某某某,〕正八边形的每个内角为〔 〕A .120°B .135°C .140°D .144°6. 〔某某省,8,3分〕如图,在五边形ABCDE 中,∠BAE=120°, ∠B=∠E=90°,AB=BC ,AE=DE ,在BC ,DE 上分别找一点M,N ,使得△AMN 的周长最小时,如此∠AMN+∠ANM 的度数为〔 〕A. 100° B .110° C. 120° D. 130°7. 〔某某省某某〕如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH 〔不重叠无缝隙〕.假如①②③④四个平行四边形面积的和为14cm 2,四边形ABCD 面积是11cm 2,9题图ABCEM N O如此①②③④四个平行四边形周长的总和为〔 〕 〔A 〕48cm 〔B 〕36cm 〔C 〕24cm〔D 〕18cm8. 〔某某某某〕图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为根本单位,可以拼成一个形状一样但尺寸更大的图形〔如图2〕,依此规律继续拼下去〔如图3〕,……,如此第n 个图形的周长是(A )2n〔B 〕4n〔C 〕12n + 〔D 〕22n +9. 〔某某某某〕如图,边长为6的大正方形中有两个小正方形,假如两个小正方形的面积分别为S 1,S 2,如此S 1+S 2的值为10. 〔某某某某〕在矩形ABCD 中,有一个菱形B F D E (点E ,F 分别在线段AB ,CD 上),记它们的面积分别 为ABCD BFDE S S 和.现给出如下命题:〔 〕 ①假如232ABCD BFDE S S +=,如此3tan EDF ∠=.②假如2,DE BD EF =•如此2DF AD =.如此:A .①是真命题,②是真命题B .①是真命题,②是假命题C .①是假命题,②是真命题D ,①是假命题,②是假命题11. 〔某某某某〕如图,在矩形ABCD 中,对角线AC ,BD 交于点O .∠AOB = 60°,AC =16,〔第10题〕FABCDH EG①②③④⑤图1图2图3……… A 1A A 2 A 3 BB 1 B 2B 3 CC 2 C 1 C 3DD 2D 1D 3第10题图如此图中长度为8的线段有( ) A .2条B .4条C .5条D .6条12. 〔某某聊城,7,3分〕一个菱形的周长是20cm ,两条对角线的比是4∶3,如此这个菱形的面积是〔 〕 A .12cm2B . 24cm 2C . 48cm 2D . 96cm 213. 〔某某江津, 10,4分〕如图,四边形ABCD 中,AC=a,BD=b,且AC ⊥BD,顺次连接四边形ABCD 各边中点,得到四边形A 1B 1C 1D 1,再顺次连接四边形A 1B 1C 1D 1各边中点,得到四边形A 2B 2C 2D 2……,如此进展下去,得到四边形A n B n D n .如下结论正确的有( ) ①四边形A 2B 2C 2D 2是矩形; ②四边形A 4B 4C 4D 4是菱形; ③四边形A 5B 5C 5D 5的周长4b a +; ④四边形A n B n D n 的面积是12+n abA.①②B.②③C.②③④D.①②③④14. 〔某某某某9,3分〕如图〔5〕,在正方形ABCD 中,E 、F 分别是边BC 、CD 的中点,AE 交BF 于点H ,CG ∥AE 交BF 于点G 。
特殊四面体及其性质1

AB DCO S 1 S 2S 3 S 4 第十讲:特殊四面体及其性质一.四面体性质1.四面体的射影定理:如果设四面体ABCD 的顶点A 在平面BCD 上的射影为O ,△ABC 的面积为S 1,△ADC 的面积为S 2,△BCD 的面积为S 3,△ABD 的面积为S 4,二面角A-BC-D 为θ1-3,二面角A-DC-B 为θ2-3,二面角A-BD-C 为θ3-4,二面角C-AB-D 为θ1-4,二面角C-AD-B 为θ2-4,二面角B-AC-D 为θ1-2,则S 1 = S 2cosθ1-2 + S 3cosθ1-3 + S 4cosθ1-4 S 2 = S 1cosθ1-2 + S 3co sθ2-3 + S 4cosθ2-4 S 3 = S 1cosθ1-3 + S 2cosθ2-3 + S 4cosθ3-4S 4 = S 1cosθ1-4 + S 2cosθ2-4 + S 3cosθ3-4 2.性质2(类似余弦定理) S 12 = S 22 + S 32 +S 42- 2S 2S 3 cosθ2-3 - 2S 2S 4 cosθ2-4 - 2S 3S 4 cosθ3-4S 22 = S 12 + S 32 +S 42- 2S 1S 3 cosθ1-3 - 2S 1S 4 cosθ1-4 - 2S 3S 4 cosθ3-4 S 32 = S 12 + S 22 +S 42- 2S 1S 2 cosθ1-2 - 2S 1S 4 cosθ1-4 - 2S 2S 4 cosθ2-4S 42 = S 12 + S 22 +S 32- 2S 1S 2 cosθ1-2 - 2S 1S 3 cosθ1-3 - 2S 2S 3 cosθ2-3特别地,当cosθ1-2 = cosθ1-4 = cosθ2-4 = 0,即二面角C-AB-D 、 C-AD-B 、B-AC-D 均为直二面角(也就是AB 、AC 、BC 两两垂直)时,有S 32 = S 12+ S 22 +S 42,证明:S 32= S 3S 1c osθ1-3 + S 3S 2cosθ2-3 + S 3S 4cosθ3-4= S 1 S 3cosθ1-3 + S 2 S 3cosθ2-3 + S 3 S 4cosθ3-4 = S 1(S 1 - S 2cosθ1-2 + S 4cosθ1-4)+S 2(S 2 - S 1cosθ1-2 + S 4cosθ2-4)+S 4(S 4 - S 1cosθ1-4 + S 2cosθ2-4)= S 12 + S 22 +S 42- 2S 1S 2 cosθ1-2 - 2S 1S 4 co sθ1-4 - 2S 2S 4 cosθ2-4 3. 任意四面体都有内切球及外接球。
第二十三章特殊四面体的性质及应用

第二十三章 特殊四面体的性质及应用【基础知识】特殊四面体包括垂心四面体(四条高线交于一点的四面体),直角四面体(有一个三面焦是直三面角的四面体,或过同一顶点的三条棱互相垂直的四面体),拟腰四面体(两对对棱相等的四面体),等面四面体(三对对棱相等的四面体),正四面体(六条棱长相等的四面体)等.特殊四面体除了具有一般四面体的性质外,还具有各自独特的性质. 1.垂心四面体性质1垂心四面体的对棱互相垂直.反之亦然.事实上,若四面体ABCD 为垂心四面体,垂心为H ,则AH ,BH 均与CD 垂直,从而AB CD ⊥. 同理,AC BD ⊥,AD BC ⊥.反之,由AB CD ⊥,过AB 作CD 的垂面交CD 于E ,设H 为ABE △的垂心,则AH BE ⊥,AH CD ⊥,所以AH 是面BCD 的垂线.同样,BH 是面ACD 的垂线,四面体ABCD 的每两条高交于一点,每三条高不共面,所以四条高必交于同一点.于是H 为四面体的垂心,即四面体为垂心四面体. 性质2垂心四面体的高过底面的垂心,反之亦然. 事实上,由性质1,设顶点A 在底面BCD 上的射影为F ,由于AB CD ⊥,所以AB 的射影BF CD ⊥.同样CF BD ⊥,即F 为BCD △的垂心.性质3垂心四面体对棱的平方和相等.反之亦然.事实上,由性质2,知A 在面BCD 上的射影F 为BCD △的垂心.设BF 交CD 于E ,则 22222222AC AD CF DF CE DE BC BD --==-=-,即有2222AC BD AD BC +=+. 同理,2222AC BD AB CD +=+.性质4垂心四面体连接对棱中点的线段相等.反之亦然. 事实上,由性质3,设E ,F 分别为AB ,CD 的中点,则()22222222222114222EF AF BF AB AC AD CD BC BD CD AB =+-=+-++--()222222AC BD BC AD AB CD =+=+=+.即证.反之,考察过对棱的相互平行的六个平面构成的平行六面体,六面体的棱长恰好等于连结四面体对棱中点的线段,因此,六面体的棱均相等,各面为菱形,菱形对角线(即四面体的对棱)互相垂直. 由于从性质1⇒性质2⇒性质3⇒性质4⇒性质1,从而性质2,3,4的反之亦然. 上述性质中的反之亦然,其实也是垂心四面体的四条判定定理.由性质4的证明中可知有 性质5垂心四面体的外接平行六面体(四面体的棱为平行六面体的侧面对角线)各面是菱形. 性质6平行于四面体任一组对棱的平面截其余四条棱的截口面为矩形. 性质7垂心四面体对棱之公垂线共点于垂心.性质8垂心四面体的外心、重心、垂心共线,且外心到重心的距离等于重心到垂心的距离. 2.直角四面体直角四面体有如下判定定理和性质:判定定理对棱都垂直且有一个面角为直角的四面体是直角四面体.事实上,在四面体ABCD 中,若90DAC ∠=︒,则由AD BC ⊥,知AC ⊥面ABC ,从而AD AB ⊥,即90DAB ∠=︒.又由AB CD ⊥,知AB ⊥面ACD ,有90BAC ∠=︒.即证. 推论1两组对棱垂直且有一个面角为直角的四面体是直角四面体.推论2四面体一顶点到对面的射影是该面的垂心,且该顶点的三面角的面角中有一个为直角,那么这个四面体是直角四面体.显然,上述判定定理及推论的逆命题也是直角四面体的性质.为了方便讨论直角四面体的一系列性质引进一些记号:设直角四面体PABC 的直三面角是三面角P ABC -,其体积为V ,棱PA a =,PB b =,PC c =.顶点x 所时的面的面积记为x S ;以棱y 为二面角棱的二面角大小记为y θ;四面体PABC 的内切球、外接球的半径分别记为x r .由于直角四面体是垂心四面体,因此,可得 性质1直角四面体具有垂心四面体的所有性质.性质2三对对棱中点的连线共点(设为G ,且此点称为四面体的重心)且互相平分;三对对棱中点的性质3不含直角的侧面三角形是锐角三角形,且这每一个面角的正切值等于这个面的面积的2倍与该面角所对的棱长平方之比;这每一面角的余弦值等于与此面共顶点的另两个面角余弦值之积. 性质4(1)cos cos cos P A BC B AC C AB S S S S θθθ=⋅+⋅+⋅; (2)cos A P BC S S θ=⋅,cos B P AC S S θ=⋅,cos C P AB S S θ=⋅; (3)222cos cos cos 1BC AC AB θθθ++=;(4)34AB BC AC θθθπ<++<π. 下面只给出(4)式的证明思路: 由(3)式有222cos cos cos cos cos cos cos 0BC AC AB AB AC AB AC θθθθθθθ---⋅+>==()(). 又cos cos 0AB AC θθ->,则cos cos 0AB AC θθ+<,故2AB AC θθπ<+.同理还有两式,相加即证(4)式左端.又()()cos cos AB AC AB AC θθθθ⎡⎤π++=-+⎣⎦,在[]0,π内余弦函数递减,有cos[]cos[]cos AB AC AB AC AB AC θθθθθθπ-+π--<-()=()(),即有()22cos cos BC AB AC θθθ⎡⎤>π-+⎣⎦,由此 即证得(4)式右端.由性质4(3)及幂平均、算术一几何平均值不等式,我们有推论(1)cos cos cos AB BC AC θθθ++(2)cos cos cos AB BC AC θθθ⋅⋅ (3)cos cos cos cos cos cos 1AB BC BC AC AB AC θθθθθθ⋅+⋅+⋅≤;(4)sin sin sin AB BC AC θθθ++;(5)sin sin sin AB BC AC θθθ⋅⋅; (6)sin sin sin sin sin sin 2AB BC BC AC AB AC θθθθθθ⋅+⋅+⋅≤.性质5含直角的侧面面积是它在不含直角的侧面上的射影面积与这不含直角的侧面面积的比例中项.性质62222P A B C S S S B =++.性质7二面角大小为θ(90θ≠︒)的两侧面中,含直角的侧面面积S 与不含直角的侧面面积P S 之比为cos θ.特别地,60θ=︒时,12P S S =∶∶;45θ=︒时,2P S S ∶;30θ=︒时,2P S S =∶;θ=P S S =∶ 性质P ABBCACS ==.性质916V abc ==性质10设S 为直角四面体的全面积,L 为6条棱长的乘积,则SL ≥. 性质11直角四面体的四顶点与其所对侧面重心的四条连线共点,共点于三对对棱中点连线的交点.亦即七线共点于直角四面体重心.性质12直角四面体的四顶点与其所对的侧面垂心的四条连线共点,共点于其直三面角顶点P ,此点为直角四面体的垂心.由此也可知直角四面体是垂心四面体.性质13非直三面角体的三顶点与其所对的侧面外心的三条连线共点,共点于不含直角的侧面三角形的重心.性质14过含直角的侧面三角形的外心,且与该侧面垂直的三直线共点,共点于直角四面体的外心. 性质15设A m 、B m 、C m 、P m 分别为直角四面体四顶点与所对面的重心的连线长(或称四面体的4条中线长),则()222222243A B C P m m m m a b c +++=++. 分析如图23-1,设1G 为侧面ABC △的重心,设1PG E α∠=.由三角线中线长公式,有()22214PE b c =+,()2222144AE a b c =++.又 图23-1ABEPG 1()2222222211222222cos 2cos 333333P P P P P PE PA AE m AE m AE m AE m m AE αα⎡⎤⎡⎤⎛⎫⎛⎫+=+-⋅⋅⋅+++⋅⋅⋅=+⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦由此即有()222219P m a b c =++.类似可求()2222199A m a b c =++,()2222199B m a b c =++,()2222199C m a b c =++,由此即获结论. 性质16R =,且与对棱中点的连线长相等;外接球的球心是分别过直三面角的三条棱与其所对棱中点的三个平面的公共点.性质17()2AB C P A B C P S S S S abcr S S S S a b c ++-==+++++;内切球的球心是其棱不共顶点的三个二面角平分面的公共点. 性质18()2AB C P P A B C P S S S S abcr S S S S a b c+++==++-++; ()2AP B C A B C P A S S S S abcr S S S S b c a +--==++-+-; ()2BP A C B A C P B S S S S abcr S S S S a c b+--==++-+-; ()2CP A B C A B P C S S S S abcr S S S S a b c+--==++-+-. 旁切球的球心是其相切侧面与另三个延展切面所成二面角平分面(其中只须其棱不共顶点的三个二面角的平分面即可)的公共点. 证明思路只推证A r ,其余类似推证.作外切于侧面PBC 的旁切球的外切三棱台B C P BCP '''-,得新四面体AB C P ''',如图23-2.图23-2A'由()22C A B P AB C P A S S S S aS S S S a r ====''''+及()()()3313123A B C P ABCD AB C P A A A B C P r S S S S V a V a r r S S S S '''''''+++=='++++. 并注意到性质6、性质17,即可推证A r 的关系式. 推论1r 最小,P r 最大,且11112A B C P r r r r r+++=或 2A B C PA B C A B P A C P B C P r r r r r r r r r r r r r r r r r⋅⋅⋅⋅⋅+⋅⋅+⋅⋅+⋅⋅=推论2()32P V abc r r a b c a b c ⋅==++++或1111P A B C r r S S S =++⋅.推论3记()1122A B C P S S S S S S '==+++,则()()()()2222233333A AB BC C P P V S r S S r S S r S S r S S r '''''==-⋅=-⋅=-⋅=-⋅.推论4记四顶点到所对面的距离为A h 、B h 、C h 、P h ,则11111A B C P h h h h r +++=;11111A B C P Ph h h h r ++-=. (*)还有类似(*)式的三式.此略. 推论5令l 为四面体六条棱长之和,()12A B C P S S S S S '=+++,则)2l ≤;2S ';(39V r +≥;32V . 性质19设am S 、bm S 、cm S 是分别过棱PA 及BC 的中点,过棱PB 及AC 的中点,过棱PC 及AB 的中点的截面面积,则am Sbm Scm S ,且222212am bm cm PS S S S ++=. 性质20设maS '、mb S ',mc S '是分别过棱BC 及PA 的中点,过棱AC 及PB 的中点,过棱AB 及PC 的中点的截面面积,则maS '=mb S '=mc S '222232ma mb mc P S S S S '''++=. 性质21设ad S 、bd S 、cd S 分别为过棱PA 与BC 垂直、过棱PB 与AC 垂直、过棱PC 与AB 垂直的截面面积,则/ad B C S S S =⋅bd A C S S S =⋅,cd A B S S S =⋅ 2222221111112ad bd cd AB C S S S S S S ⎛⎫++=++ ⎪⎝⎭. 性质22设at S 、bt S 、ct S 分别为过棱PA 及BPC ∠的平分线,过棱PB 及APC ∠的平分线,过棱PC 与APB ∠的平分线的截面面积,则B C at B C S S S S ⋅=+,A C bt A C S S S S ⋅=+,A Bct A BS S S S ⋅=+,且111111a t b t c t AB CS S S SSS⎫++=++⎪⎭. 性质23在直角四面体中,(1)斜面上任一点与直角顶点的连线和三条直角棱所成角的余弦的平方和等于1; (2)斜面上任一点与直角顶点的连线和三个直角面所成的角的余弦的平方和等于2; (3)斜面上每一条棱与三条直角棱所成角的余弦的平方和等于1; (4)斜面上每一条棱与三个直角面所成的角的余弦的平方和等于2; (5)三条直角棱与斜面所成角的余弦的平方和等于2;(6)三条直角棱的平方的倒数和等于直角顶点到斜面的距离的平方的倒数. 性质24直角四面体的外接平行六面体,(1)当四面体的六条棱均成为平行六面体的侧面对角线时,平行六面体是菱形六面体; (2)当四面体的直三面角的三条棱成为平行六面体的棱,其余三条棱成为平行六面体的侧面对角线时,平行六面体是长方体. 3.直棱四面体三条相连棱形成三边直角折线(即空间直角四边形)的四面体,称为直棱四面体. 显然,直棱四面体每个面都是直角三角形,若令1ADC β∠=,2ADB β∠=,3BDC β∠=, 则(1)123cos cos cos βββ⋅=; (2)321sin sin sin sin sin CD AD βββθθ==; (3)3sin cos sin ADCDθβθ=; (4)1tan tan sec AD CD θθβ⋅=.直角四面体和直棱四面体,都可以看作从长方体上截下的一部分,在部分多面体过程中,在棱、锥、台的计算中,它们经常出现.由于它有多方面的垂直关系和比较多的等量关系,有人称之为基本四面体.它们可以看作直角三角形在空间的自然推广,是工具性的四面体. 4.等腰四面体从某一顶点出发的三条棱(称为腰)相等的四面体称为等腰四面体,这一顶点称为腰顶点. 性质1等腰四面体的腰顶点在所对的面的射影为该面的外心.反之亦然. 性质2等腰四面体的腰顶点出发的三条棱与该点所对的面成等角.反之亦然. 性质3等腰四面体的底面为正三角形时,则该四面体为垂心四面体.性质4等腰四面体的底面为正三角形,且其边长为腰的压时,则该四面体是等腰直角四面体. 5.拟腰四面体两组对棱分别相等的四面体称为拟腰四面体.性质1两对对棱分别相等的四面体的充要条件是它的棱均成为侧面对角线的外接平行六面体为直平行六面体.证明设四面体ABCD 的外接平行六面体为1111ACB D AC BD -,AD BC =,AC BD =⇔侧面11A DD A 与侧面11CB BC 为全等矩形,侧面11A CC A 与侧面11DB BD 为全等矩形1111ACB D AC BD -为直平行六面体. 推论1两对对棱分别相等的四面体的充要条件是另一对对棱中点的连接线段垂直于此二棱.推论2两对对棱分别相等的四面体的充要条件是这两对对棱中点的连接线段均与第三对对棱中点的连接线段垂直.推论3两对对棱分别相等的四面体的充要条件是四面体在平行于这两对对棱中的每一对对棱的每一个平面上的射影为矩形.性质2两对对棱分别相等的四面体的充要条件是两侧面面积相等,且另两侧面面积也相等,或四侧面分成等面积的两组.证明此定理即为:在四面体ABCD 中,AD BC =,ACD BCD AC BD S S =⇔=△△,ABC ABD S S =△△. 必要性(⇒):显然.充分性(⇐):如图23-3,作四面体ABCD 的外接平行六面体1111ACB D AC BD -.此时A 、B 到底面11A CB D 的距离1AH 、2BH 相等,作AE CD ⊥于E ,BF CD ⊥于F ,连1H E ,2H F .图23-321则由ACD BCD S S =△△,有A E B F=,从而12AEH BFH ∠∠=,即二面角1A CD A --等于二面角1B CD B --,此时二面角A CD B --的平分面α垂直于底面11A CB D ,也就垂直于面11AC BD ,且面α交AB 于其中点1O .又可证A 、B 两点到此平分面α的距离相等. 设此平分面α交AB 于1O ,则1O 为上底面中心.同理,由ABC ABD S S =△△,有二面角C AB D --的平分面β也垂直于两底面,也交CD 于其中点2O .此时12O O αβ=∩且垂直于两底面,故平行六面体1111ACB D AC BD -为直平面六面体.由性质1即证得了充分性.性质3两对对棱分别相等的四面体的充要条件是另一对对棱每条棱所张的二个面角分别相等.证明此性质即为:在四面体ABCD 中,AD BC =,AC BD CAD CBD =⇔∠=∠,ACB ADB ∠=∠. 必要性(⇒):显然. 充分性(⇐):如图23-3,作四面体ABCD 的外接平行六面体1111ACB D AC BD -.由题设CAD CBD ∠=∠,又A 、B 、C 、D 四点共球O ,则ACD △和BCD △所在的平面截球O 的截面圆是等圆.而A 、B 两点到面11A CB D 的距离相等,则过CD 及AB 中点1O 的截面圆必是球O 的大圆.从而1O 、O 及CD 的中点2O 在过CD 的球O 的大圆面内.同理,1O 、O 、2O 也在过棱AB 的球O 的大圆面内.故1O 、O 、2O 三点共线于这两个大圆面的交线上.又1OO AB ⊥,2OO CD ⊥,则111OO A B ⊥,211OO C D ⊥,从而12O O 垂直于平行六面体的两底面11A CB D 、11AC BD ,故知此平行六面体为直平行六面体,由性质1,充分性获证.此性质的充分性也可以这样证:设CAD CBD α∠=∠=,ACB ADB β∠=∠=,令AC a =,AD b =,BC c =,BD d =,CD x =,AB y =.对ADC △和BDC △应用余弦定理可得()()()22222222cos a b x c d y ab cd x bc ad ac bd ab cd α+-+-==⇒-=--.① 同理,得()()()2ad bc y cd ab ac bd ---=.②由①、②可知,若0ab cd -=,则0ad bc a c -=⇒=,b d =.因此论断获证.若0ab cd -≠,则0ad bc -≠,0ac bd -≠,于是由①、②推得()222x y ac bd =-⇒或xy bd ac +=,或0xy ac by +-=.③由托勒密定理及③式,可知A 、B 、C 、D 四点共圆,与题设矛盾.因此充分性获证. 性质4两对对棱分别相等的四面体的充要条件是其外心(外接球球心)在另一对对棱中点的连线上(重心亦在此连线上). 必要性(⇒):设在四面体ABCD 中,AD BC =,AC BD =,作四面体ABCD 的外接平行六面体如图23-3.由性质1,即知此平行六面体为直平行六面体,从而上、下底面中心1O 、2O 的连线既是AB 、CD 中点的连线,又是AB 、CD 的公垂线,亦即既是AB 的中垂线,又是CD 的中垂线,因而四面体ABCD 的外心在12O O 上.充分性(⇐):由题设,四面体的外心在一对对棱AB 、CD 的中点1O '、2O '的连线上,则12O O ''是AB 、CD 的中垂线,从而12O O '':垂直于四面体ABCD 的外接平行六面体1111ACB D AC BD -的两底面,故此外接平行六面体是直平行六面体.由性质1,充分性获证. 性质5两对对棱分别相等的四面体的充要条件是其内心(内切球球心)在另一对对棱中点的连线上(重心亦在此连线上). 证明必要性(⇒):设在四面体ABCD 中,AD BC =,AC BD =.作四面体ABCD 的外接平行六面体如图23-3,则此平行六面体为直平行六面体,故11A DC B CD S S =△△.又AD C BD C S S =△△,则二面角1A DC A --等于二面角1B DC B --.而上、下底面中心1O 、2O 所在直线与DC 两相交线所在对角面垂直于两底面,即知此对角面平分二面角A DC B --.同理,12O O 与AB 所在对角面也平分二面角C ABD --.故四面体内心I 在12O O 上.充分性(⇐):设四面体ABCD 的内心I 在12O O 上,则1O 到面ACD 、BCD 的距离相等,从而A 到面BCD 的距离与B 到面ACD 的距离相等(都等于点1O 到这两个面的距离的两倍).由13V Sh =得BCD ACD S S =△△.同理ABD ABC S S =△△.由性质2即证.性质6四面体有两对对棱相等的充要条件是,以这两对对棱为棱的二面角,分别相等.证明在四面体ABCD 中,AD BC =,AC BD =的充要条件是二面角B AD C --等于二面角D BC A --,二面角B AC D --等于二面角A BD C --.必要性(⇒):设AD θ、BC θ分别表示二面角B AD C --、二面角D BC A --的平面角的大小,由AD BC =、AC BD =,有DAC DBC △≌△,ABC BAD △≌△,如图23-4.图23-4H GI DABCEFMN于是DAC DBC ∠=∠,BAC ABD ∠=∠,BAD ABC ∠∠=.由三面角余弦公式(如cos cos cos cos sin sin AD BAC BAD DACBAD DACθ∠-∠⋅∠=∠⋅∠)或三面角全等定理,有AD BC θθ=,即二面角B AD C --等于二面角D BC A --.同理,可证二面角B AC D --等于二面角A BD C --. 充分性(⇐):记I 为四面体ABCD 的内心,从I 向各侧面引垂线,垂足为E 、F 、G 、H ,如图23-4,设过IE 、IF 的平面交AC 于M ,过IG 、IH 的平面交BD 于N ,则EMF ∠,GNH ∠分别为二面角B AC D --、二面角A BD C --的平面角,由题设有EMF GNH ∠=∠. 在Rt IMF △和Rt ING △中,IF IG =,1122IMF EMF GNH ING ∠=∠=∠=∠,从而IM IN =.故I 在对棱AC 、BD 的公垂线段的中垂面α内.同理,I 又在对棱AD 、BC 的公垂线段的中垂面β内,故I 在α与β的交线上.作四面体ABCD 的外接平行六面体如图23-3,知α与β的交线就是平行六面体上、下底面中心1O 、2O 的连线.由性质5即证得充分性.性质7两对对棱分别相等,则四面体的内切球切侧面于第三对对棱的中垂线上. 证明此性质即为:在四面体ABCD 中,若AD BC =,AC BD =,则四面体ABCD 的内切球I 切ACD △、BCD △于CD 的中垂线上,切ACB △、ADB △于AB 的中垂线上.如图23-5,由性质6的充分性证明中可推知12O M O N =,①其中1O 、2O 为球I 切侧面ACD △、BCD △的切点,M 、N 为I 在棱AC 、BD 上的射影.图23-5O 1O 2DABCEFMNI设过1IO 、2IO 的平面交CD 于E ,连1O E 、2O E ,则由球的切线长定理,知12O E O E =.②又由ACD BDC △≌△有MCE NDE ∠∠=,而1O E CD ⊥,2O E CD ⊥,则M 、C 、E 、1O 共圆,E 、D 、N 、2O 共圆.故12MOE EO N ∠=∠.③由①、②、③知ME EN =,从而12sin sin ME ENO C O D MCE EDN===∠∠,∴12Rt Rt CO E DO E CE ED ⇒=△≌△. 故1O E ,2O E 均是CD 的中垂线段.同理,球I 切侧面ACB △,ADB △于AB 的中垂线上. 6.等面四面体我们称三组对棱分别相等的四面体为等面四面体.为了讨论问题的方便,先引进一些记号:等腰四面体ABCD 中,设BC AD a ==,AC BD b -=,AB CD c ==;设()12p a b c =++,()222212k a b c =++;以BC 、BD 、CD 为棱的两侧面所成二面角的大小依次为α、β、γ;四面体的体积记为V ,其内切、外接球半径分别记为r 、R ;顶点x 所对的面的面积记为x S ;外切于顶点x 所对的面,且与其余侧面的延展面相切的旁切球的半径记为x r . 性质1等面四面体对棱所成角的余弦值可表示为()222cos ,b c a a a -=,()222,cos b c a b b -=,()222cos ,a b c c c -=.性质2等面四面体中,对棱中点的连线共点(此点为四面体的重心),且互相平分;连结对棱中点的每一线段均垂直于此二棱,或者说,当四面体绕这样的线段旋转180︒则与本身重合;连结对棱中点的三线段彼此互相垂直.且后两个结论的逆命题也是成立的.推论四面体为等面四面体的充要条件是三对对棱的公垂线两两相互垂直.性质3设a d 、b d 、c d 分别为等面四面体对棱中点连线的长,则a d =,b d =,c d =性质4四面体为等面四面体的充要条件是四面体各面为全等的三角形. 性质5等面四面体所有的面角均为锐角,或者说各侧面是锐角三角形.(见本章练习题A 第7题) 性质6四面体为等面四面体的充要条件是过四面体的每一顶点的三条棱长的m (m ∈R 且0m ≠)次方之和相等.分析只证充分性:令BC a =,AC b =,AB c =,AD x =,BD y =,CD z =,由m m m m m m m m m m m m b c x c a y a b z x y z ++=++=++=++,即推得a x =,b y =,c z =.推论四面体为等面四面体的充要条件是四面体的每一顶点的三条棱长之和相等.性质7四面体为等面四面体的充要条件是四面体各侧面三角形边长的m (m 为非零实数)次方之和相等.推论四面体为等面四面体的充要条件是四面体各侧面三角形的周长相等.性质8四面体为等面四面体的充要条件是四面体各侧面三角形的三条中线长的平方和相等. 性质9四面体为等面四面体的充要条件是四面体每一顶点处的三个面角之和为180︒.性质10四面体为等面四面体的充要条件是过每对对棱的二面角相等(即三对二面角分别相等).性质11cos cos cos 1αβγ++=.性质1222sin sin sin 3x S a b cVαβγ===(其中x 可表示A 、B 、C 、D ,后面亦同). 性质13()()()22222222222224cos cos cos 222xa k ab k bc k c S αβγ---===. 性质14在等面四面体ABCD 中,A B C D S S S S ==== 性质15四面体为等面四面体的充分必要条件是各面的面积相等.分析四面体的各二面角的大小分别用α、β、γ、α'、β'、γ'表示,如图23-6.图23-6β'γ'α'γβαDOAB由cos cos cos D C B A S S S S αβγ⋅+⋅+⋅=及D C B A S S S S ===有cos cos cos 1αβγ++=.同理,有cos cos cos 1γβα''++=,cos cos cos 1αβγ''++=,cos cos cos 1βαγ''++=. 由上推出,cos cos αα'=,cos cos ββ'=,cos cos γγ'=,而0α<,β,γ,α',β',γ'<π,所以αα'=,ββ'=,γγ'=,由此即证. 性质16等面四面体的体积V =()222212k a b c =++. 分析作四面体ABCD 的外接平行六面体,使四面体的棱成为平行六面体的侧面对角线,如图23-7.由四面体对棱相等,可证得平行六面体侧面均为矩形,即为长方体,于是列方程组求得长方体共顶点的图23-7DABC性质17记等面四面体共顶点的三个面角分别为1θ、2θ、3θ,则V =分析如图23-8,设1B D Cθ∠=,2ADC θ∠=,3ADB θ∠=.又设A 点在面BCD 内的射影为E ,作A H C D⊥于H ,连EH ,则AHE γ∠=.由12B S CD AH =⋅,有2B AH S c =⋅,则2sin sin B AE AH S cγγ=⋅=⋅⋅.图23-8γabc D ABCEH注意到31212cos cos cos cos sin sin θθθγθθ-⋅=⋅,有1233A A B V S AE S S c=⋅=⋅123θθθ++=π及()222123123121cos cos cos 2cos cos cos cos θθθθθθθθ---+⋅⋅=-+()()()212312123cos cos cos cos cos θθθθθθθθ⋅--+++-⋅=⎡⎤⎣⎦1234cos cos cos θθθ⋅⋅,11sin 2A S bc θ=⋅,21sin 2B S ac θ=⋅,由此即证.性质18等面四面体的体积为 222222sin sin sin 333x x x V S S S c b a γβα=⋅=⋅=⋅;或43x V S r =⋅. 性质1912R k ==. 性质20r =性质21四面体为等面四面体的充要条件是四面体的外心(外接球球心)与重心重合(见本章例13证明部分).或者,四面体各顶点和外心的连线与对面的交点为该面的重心.性质22四面体为等面四面体的充要条件是四面体的外心与内心(内切球球心)重合.(见本章例12) 性质23四面体为等面四面体的充要条件是四面体的内心与重心重合.或者,各顶点和内心的连线与对面的交点为该面的重心.推论若四面体的外心、内心、重心中任意两个相重合,则第三个也必和它们重合. 性质24在等面四面体中,2A B C D r r r r r =====.(提示:设顶点x 到所对面的距离为x h ,则可证2x x x h rr h r⋅=-,由此即推得)性质25四面体为等面四面体的充要条件是四面体的四条高长之和等于内切球半径的16倍(即16A B C D h h h h r +++=).分析充分性:由以3x x Vh S =及16A B C D h h h h r +++=有1111316A B C D V r S S S S ⎛⎫⋅+++= ⎪⎝⎭.注意到()13A B C D V S S S S r =+++⋅, 则()111116A B C D AB C D S S S S S S S S ⎛⎫++++++= ⎪⎝⎭. 而()111116A B C D AB C D S S S S S S S S ⎛⎫++++++ ⎪⎝⎭≥,取等号是当且仅当A B C D S S S S ===.由此即证. 推论42x x h r r ==.注对外接球半径也有一条性质见本章例13.性质26四面体为等面四面体的充要条件是它的切点四面体(内切球切侧面的切点)为等腰四面体. 分析充分性:设O 为四面体ABCD 的内心,亦即它是切点四面体A B C D ''''的外心.当A B C D ''''为等腰四面体时,由性质2的推论推之.性质27四面体为等面四面体的充要条件是四面体的内切球与各侧面的切点为该面的外接圆圆心. 性质28四面体为等面四面体的充要条件是四面体的重心(或外心)在各侧面内的射影为该面的外接圆圆心.性质29四面体为等面四面体的充要条件是各侧面都具有相等外接圆半径的锐角三角形. 性质30四面体为等面四面体的充要条件是四面体各侧面外接圆半径与内切圆半径之积相等. 分析充分性:在四面体ABCD 中,设BC a =,AC b =,AB c =,1DA a =,1DB b =,1DC c =,R ',r '分别为侧面三角形外接、内切圆半径,则2abcR r a b c''=++.同理,1111111111112ab c a bc a b cR r a b c a b c a b c''===++++++.由此得()()()()11110c a c b b b b a c c +-++-=, ()()()()11110c c b a a a b a c c +-++-=, ()()()()11110b b c a a a a c b b +-++-=.将上述三式看作1a a -,1b b -,1c c -为未知数的三元一次方程组,它只有唯一的一个零解.即证. 性质31四面体为等面四面体的充要条件是四面体的四条中线长相等(中线长即为四面体的每一顶点和对面重心的连结线段长).分析充分性:注意到中线长相等及四面体重心性质,推得重心与外心重合. 性质32性质33四面体为等面四面体的充要条件是四面体的四条中线长的平方和等于2649R . 分析由性质31及25推导.性质34四面体为等面四面体的充要条件是四面体的四条高线长相等(即A B C D h h h h ===).性质35等面四面体的过某棱及所对棱中点的截面,就是过此棱及与所对棱垂直的截面,也就是过此棱且平分此棱所在二面角的截面.性质36在等面四面体ABCD 中,设分别过棱BC 、BD 、CD 且平分α、β、γ的截面面积为a S 、S β、S γ,则cos2x S S αα=⋅,cos2x S S ββ=⋅,cos 2x S S γγ=⋅,且22222x S S S S αβγ++=.性质37四面体为等面四面体的充要条件是其棱均作为外接平行六面体的侧面对角线时,平行六面体为长方体.性质38四面体为等面四面体的充要条件是四面体在平行于两对棱的每一个平画上的射影为矩形. 性质39四面体为等面四面体的充要条件是四面体的展开图是一个引出了三条中位线的锐角三角形. 性质40四面体为等面四面体的充要条件是四面体内任意一点到各侧面的距离之和为定值.分析充分性:设定值为l ,取点为内心时有4l r =,再取点为重心时有4A B C D h h h h l +++=,再由性质25即证. 7.正四面体称六条棱相等的四面体为正四面体.性质1正四面体的每个面是正三角形.反之亦然. 性质2正四面体是三组对棱都垂直的等面四面体. 推论正四面体是两组对棱垂直的等面四面体.性质3倍,反之亦真. 性质4正四面体的各棱的中点是正八面体的六顶点. 性质5正四面体的每个三面角均是面角为60︒的三面角,因而都是全等的三面角,且每个三面角的特征,即()2S x ==.性质6正四面体的六个二面角都相等.若记其大小为θ,则1arccos 3θ=或.其逆命题亦成立.性质712倍,即2S 全=,3V =. 推论设S △为侧面三角形面积,则4228cos 2a S θ=⋅⋅△;22sin 3S a V θ=⋅⋅△;V S ⋅全.性质8正四面体的内切球与其外接球是同心球,内切球半径r =(等于高线的14);外接球半径R =;两球面面积之比为1∶9. 性质9在各类四面体的比值R r ∶中,以正四面体的比值3R r =∶为最小. 性质10正四面体的体积与其内切球的内接正四面体的体积之比为27.且若内切球半径为r ,则其体积为3.性质11正四面体的四个旁切球半径均相等,等于内切球半径的2倍,即x r =,或等于正四面体高线的一半.性质12正四面体的内切球与各侧面的切点是侧面三角形的外心,或内心,或垂心,或重心.除外心外,其逆命题均成立.性质13正四面体的外接球球心到四面体四顶点的距离之和,小于空间中其他任一点到四顶点的距离之和.分析利用正四面体的外接球球心O 是过四面体的一棱AB 与对棱CD 中点N 的平面(共有六个这样的平面)的交点的特性,我们将指出,如果点P (空间中任一点)不在这些平面之一上即如果它不是O ,则和S PA PB PC PD =+++不是最小.由此得出结论:使S 最小的点位于所有这些平面上,因此最小值只可能在点O 达到.假定P 不在平面ABN 上,设l 为过P 平行于CD 的直线,因此垂直于平面ABN ,且设P '为l 和ABN 的交点,则PC PD P C P D ''+>+.①事实上,CPD △和CP D '△有相同的底和高,但后者是等腰三角形,它有较小的周长.又PA P A '>,PB P B '>.② 因为PA 是Rt APP '△的斜边,PB 是Rt BPP '△的斜边,把①和②中三个不等式加起来,得PA PB PC PD P A P B P C P D ''''+++>+++,这就是我们要证的.性质14四面体为正四面体的充要条件是,存在五个球与四面体的六条棱或其延长线相切. 此性质的充分性证明见本章例14.性质15正四面体内任意一点到各侧面的垂线长的和等于这四面体的高.性质16对于四个相异的平行平面,总存在一个正四面体,其顶点分别在这四个平面上.性质17以正四面体的每条棱为直径作球,设S 是所作六个球的交集,则S 中含有两点,它们的距离为性质18 性质19四面体为正四面体的充要条件是,其棱均作为外接平行六面体的侧面对角线时,平行六面体为正方体.性质20四面体为正四面体的充要条件是,其共顶点三棱作为外接平行六面体的棱时,平行六面体为一个三面角面角均为60︒的菱形六面体.性质21囚面体为正四面体的充要条件是,四面体在平行于两棱的每一个平面上的射影是正方形. 性质22四面体为正四面体的充要条件是,四面体的展开图是一个引出了三条中位线的正三角形. 性质23正四面体每条高的中点与底面三角形三顶点均构成直角四面体的四顶点,且高的中点为直三面角顶点.性质24正四面体是垂心四面体(四条高共点的四面体),且四面体的垂心、重心、内心、外心这四心合一.性质25设P 为正四面体1234A A A A 的外接球面上任一点,R 为该球的半径. (I )42218i i PA R ==∑;(Ⅱ)若1B ,2B ,…,6B 分别为23A A ,34A A ,24A A ,12A A ,13A A ,14A A 的中点,则42218i i PB R ==∑;(Ⅲ)若i O 为i A 所对面的中心(1,2,3,4i =),则22409i PO R =∑. 证明(I )设i O 为正四面体1234A A A A 的中心,则。
数学特殊四边形的归纳总结

数学特殊四边形的归纳总结在数学中,四边形是指由四条线段组成的图形。
然而,有一些特殊的四边形具有独特的性质和特征。
本文将对几种常见的数学特殊四边形进行归纳总结,包括矩形、正方形、菱形、平行四边形和梯形。
一、矩形矩形是一种特殊的四边形,它具有以下性质:1. 两组对边相等且平行。
2. 对角线相等。
3. 内角为直角(90度)。
矩形是一种常见的四边形,它有许多实际应用,如建筑设计中的房间布局和绘画中的画框。
二、正方形正方形是一种特殊的矩形,它具有以下性质:1. 所有边相等且平行。
2. 所有角为直角(90度)。
3. 对角线相等且相互平分。
正方形是一种非常对称且稳定的四边形,它在几何学和工程学中经常被使用。
三、菱形菱形是一种特殊的四边形,它具有以下性质:1. 所有边相等。
2. 对角线相互垂直且相等。
菱形是一种具有双重对称性的四边形,它在纺织品设计和室内装饰中经常出现。
四、平行四边形平行四边形是一种特殊的四边形,它具有以下性质:1. 对边相等且平行。
2. 对角线不相交。
3. 相对角相等。
平行四边形是一种常见的四边形,它在计算机图形学和建筑设计中得到广泛应用。
五、梯形梯形是一种特殊的四边形,它具有以下性质:1. 有两条平行边。
2. 其他两条边不平行。
3. 对角线不相交。
梯形是一种常见的四边形,它在建筑设计和地形测量中具有重要意义。
综上所述,数学特殊四边形包括矩形、正方形、菱形、平行四边形和梯形,每种特殊四边形都有独特的性质和特征。
熟练掌握这些特殊四边形的性质,对于解决与几何学相关的问题和应用具有重要意义。
无论是在学习数学知识还是日常生活中,这些特殊四边形都有广泛的应用和重要性。
立体几何中的平行四面体

立体几何中的平行四面体平行四面体是立体几何中的一种特殊形状,由四个平行的三角形构成,具有一些独特的性质和特点。
在本文中,我们将探讨平行四面体的定义、性质以及与其他形状的关系。
一、定义与性质平行四面体是由四个平行的三角形所围成的立体。
它具有以下性质:1. 四个面都是平行的:平行四面体的四个面平行于另一个面,且互相平行。
2. 所有边的长度相等:平行四面体的四条边长度相等,因此它是一个等边四面体。
3. 所有角度相等:平行四面体的四个顶点所形成的内角都是相等的。
4. 对角平分:平行四面体的对角线相交于一个点,并且这个点所在的直线平分对角线。
二、与其他形状的关系1. 与立方体的关系:平行四面体可以被看作是一个正立方体的一半。
当一个正立方体沿着一条对角线剖分时,剩余的两个部分就构成了一个平行四面体。
2. 与正四面体的关系:平行四面体与正四面体是两个不同的立体形状。
平行四面体具有平行的底面和顶面,而正四面体的四个面是等边的三角形。
3. 与长方体的关系:平行四面体可以被视为一个长方体的一部分。
当一个长方体沿着一条对角线剖分时,剩余的两个部分就构成了一个平行四面体。
三、实际应用与意义平行四面体在实际生活中有着广泛的应用和意义。
以下是一些例子:1. 建筑设计:平行四面体的形状常被用于建筑设计中,用于创造独特的外观和视觉效果。
2. 晶体结构:某些晶体的结构可以被近似地看作是平行四面体的形状,这对于研究材料的物理和化学性质非常重要。
3. 几何学教育:平行四面体是几何学教育中重要的概念之一,通过学习和理解平行四面体的性质,可以提高学生的空间想象力和几何思维能力。
结论平行四面体是立体几何中的一种特殊形状,由四个平行的三角形组成。
它具有独特的定义和性质,与其他形状如立方体、正四面体和长方体有一些关联和区别。
在实际应用中,平行四面体在建筑设计、晶体结构研究以及几何学教育等领域发挥着重要的作用。
通过深入理解和学习平行四面体,我们能够更好地探索立体几何的奥秘。
特殊四边形性质与判定

②两组对边分别相等的四边形是平行四边形。
③一组对边平行且相等的四边形是平行四边形。
④两组对角分别相等的四边形是平行四边形。
⑤对角线互相平分的四边形是平行四边形。
中
心
对
称
矩
形
①两组对边分别平行且相等
②四个角都是直角
③对角线互相平分且相等
①有一个角是直角的平行四边形是矩形。(矩形的定义)
⑤每一条对角线平分一组对角的四边形是菱形。
中轴
心对
对称
称
正
方
形
(1)具有平行四边形、矩形、菱形的一切性质,即:①正方形的对边分别平行且四条边都相等;四个角都是直角;②正方形的两条对角线互相垂直平分且相等,每一条对角线平分一组对角。
(2)对角线与边的夹角为45o
①有一组邻边相等并且有一个角是直角的平行四边形是正方形(正方形的定义)
类类别性性质质判判定定对称性平行四边形两组对边分别平行两组对边分别相等两组对角分别相等两条对角线互相平分邻角互补两组对边分别平行的四边形是平行四边形平行四边形、菱形、矩形、正来自形性质和判定归纳表:类别
性质
判定
对称性
平
行
四
边
形
①两组对边分别平行
②两组对边分别相等
③两组对角分别相等④两条对角线互相平分
⑤邻角互补
②有一组邻边相等的矩形是正方形。
③有一个角是直角的菱形是正方形。
④对角线垂直且相等的平行四边形是正方形。
中轴
心对
对称
称
②有三个角是直角的四边形是矩形。
③对角线相等的平行四边形是矩形。
中轴
心对
几何体的平行四面体

几何体的平行四面体平行四面体是一种特殊的多面体,具有一些独特的性质和特点。
在几何学中,平行四面体是指具有四个平行的面的多面体。
本文将介绍平行四面体的定义、性质和一些相关的应用。
一、平行四面体的定义平行四面体是一个四面体,它的四个面都是平行的。
具体来说,对于一个平行四面体,任意两个相邻面之间的平行线相交于一条公共直线,这条公共直线被称为平行四面体的高。
二、平行四面体的性质1. 面的平行性:平行四面体的四个面都是平行的。
这意味着这个几何体的上下底面是平行的,并且侧面也都是平行的。
2. 边的平行性:平行四面体的对边边平行。
也就是说,连接两个相对面的边都是平行的。
3. 高的关系:平行四面体的高是由相邻面间的平行线构成的。
这条高与底面的交点、底面上的一点和顶点构成一个平行四边形。
4. 相对边长比例:对于一个平行四面体,底面上的任意两条边与对应顶点的连线构成的三角形相似。
5. 体积计算:平行四面体的体积可以通过公式V = (1/3) * S * h来计算,其中S表示底面积,h表示高。
三、平行四面体的应用1. 建筑与工程:平行四面体被广泛应用于建筑与工程领域,特别是设计和建造金字塔形状的建筑物时。
例如,埃及的金字塔就是一个平行四面体结构。
2. 数学学科:平行四面体是数学学科中的一个重要概念,学生们在几何学和立体几何的学习中经常会遇到平行四面体相关的问题和计算。
3. 游戏和娱乐:平行四面体也被广泛应用于游戏和娱乐产业。
在一些游戏中,设计师会使用平行四面体来创建虚拟世界中的建筑和物体。
4. 科学和工业应用:平行四面体的概念也在科学研究和工业应用中得到了应用。
例如,在晶体学中,晶体的结构有时可以用平行四面体的概念来描述。
总结:平行四面体是一个具有四个平行面的几何体,它具有一些独特的性质和特点。
平行四面体在建筑、数学、游戏和科学领域中有着广泛的应用。
通过研究平行四面体的性质和应用,可以加深对立体几何学的理解,同时也可以拓宽我们的知识领域。
特殊四边形的性质与判定
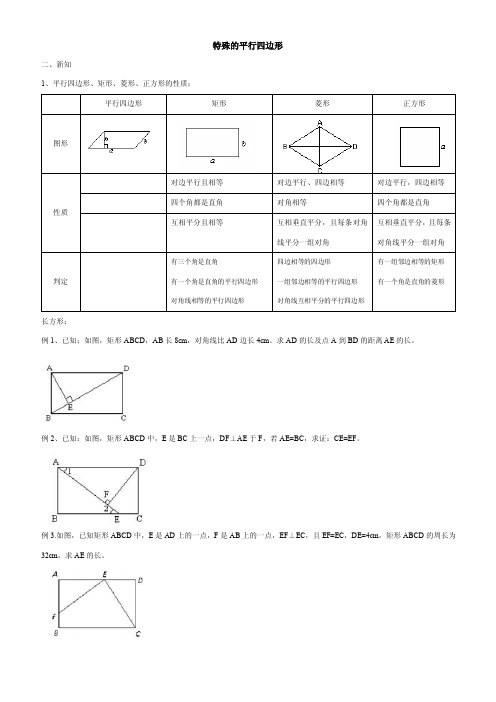
特殊的平行四边形二、新知1、平行四边形、矩形、菱形、正方形的性质:长方形:例1、已知:如图,矩形ABCD,AB长8cm,对角线比AD边长4cm。
求AD的长及点A到BD的距离AE的长。
例2、已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC,求证:CE=EF。
例3.如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长。
例4、如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F。
(1)求证:AB=CF;(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由。
菱形:例1、已知如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E。
求证:∠AFD=∠CBE。
例2、已知:如图平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F。
求证:四边形AFCE是菱形例3、如图,在平行四边形ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F,求证:四边形AECF是菱形。
例4、已知如图,菱形ABCD中,E是BC上一点,AE、BD交于M,若AB=AE,∠EAD=2∠BAE。
求证:AM=BE。
例5、如图,在菱形ABCD中,角A=60°,AB=4,O 为对角线BD的中点,过O点作OE⊥AB,垂足为E。
求线段BE的长例6、如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于E,DF⊥BC,交BC的延长线于F。
请你猜想DE与DF的大小有什么关系?并证明你的猜想。
例7、如图菱形ABCD的边长为2,BD=2,EF分别是边AD、CD上的两个动点,且满足AE+CF=2(1)求证△BDE≌△BCF(2)判断△BEF的形状,并说明理由;(3)设△BEF的面积为S,求S的取值范围。
正方形例1、已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F。
