冀教版数学八年级上册14.3 第1课时 无理数及实数的概念
八年级数学上册14.3《实数》

问题1:无理数是否也可以用数轴上的点来表示吗?
如图,直径为1个单位长度的圆从原点O沿数轴向
Байду номын сангаас
右滚动一周,圆上一点从原点到达A点,则OA的长
度是 点A表示的数就是
。
-4 -3 -2 -1 0O 1 2 3A 4
可以用数轴上的点来表示.
有两个边长为1的小正方形,请大家 拿出剪刀把它剪成四个同样大小的直 角三角形,设法拼成一个大得正方形。
大正方形的面积是 2 ,边长
是
2
。
我们把这个正方形的一个顶点和原点O重合,一条 边恰好落在数轴的正方向上,其另一个顶点为数轴 上的点A.
线段OA的长是多少? 点A 在数轴上对应的数哪个数?
面积为5
面积为2
O
A
-1 2
0
1
2B
可以用数轴上的点来表示.
回顾:一个有理数的相反数的概念
首先回顾 有理数的相反数在数轴上的特点:
冀教版数学 八年级上册
§14.3 实数(二)
承德市双桥区双峰寺镇中学 李振江
昨日点滴
(1)无限不循环小数叫做__无__理__数__ (2)无理数的常见三种形式: ①圆周率π及一些含有π的;如 5π
②开不尽方的数,如 2 ;
③有一定的规律,但不循环的无限小数,如 0.101 001 000 1… (3)
也就是说有理数关于相反数的概念同样适用于无理数。
2+ 2 = 0
的相反数是
3 8 的相反数是
回顾:一个有理数的绝对值的概念 我们再来回顾有理数的绝对值的概念:
-2
0
2
一个数的绝对值是该数在数轴上所对应的 点到原点的距离
《14.3实数》作业设计方案-初中数学冀教版12八年级上册

《实数》作业设计方案(第一课时)一、作业目标本次作业的目标是帮助学生巩固《实数》第一课时的知识点,包括实数的概念、分类、性质以及实数在数轴上的表示等。
通过作业练习,加深学生对实数基本概念的理解,提高其应用实数知识解决实际问题的能力。
二、作业内容1. 基础练习:包括填空题和选择题,内容涵盖实数的定义、分类以及数轴上点的表示。
要求学生准确理解实数的概念,并能正确判断实数的类型和在数轴上的位置。
2. 概念应用:设计几道应用题,让学生运用实数的性质解决实际问题。
例如,通过温度的表示理解正负数的实际意义,通过长度单位的换算理解有理数的大小关系等。
3. 拓展提高:设计一些稍具难度的题目,如探索实数与数轴的关系、实数的加减法运算等。
旨在培养学生的逻辑思维能力和解决问题的能力。
三、作业要求1. 独立完成:要求学生独立完成作业,不得抄袭他人答案。
2. 认真审题:仔细阅读题目,明确题目要求,避免因理解错误导致答案错误。
3. 规范答题:答案要规范、清晰,步骤要完整,尽量使用数学语言进行表述。
4. 及时提交:按照教师的要求,按时提交作业。
四、作业评价1. 评价标准:根据学生完成作业的准确性、规范性、解题思路的清晰程度以及是否独立完成等方面进行评价。
2. 评价方式:教师批改作业时,采用多种评价方式相结合,如过程性评价与结果性评价相结合、自评与互评相结合等。
3. 反馈形式:通过批改作业,及时向学生反馈学习情况,指出错误并给出正确答案及解题思路。
对于表现优秀的学生给予表扬和鼓励。
五、作业反馈1. 课堂讲解:教师利用课堂时间,针对学生作业中普遍存在的问题进行讲解,帮助学生掌握正确的解题方法和思路。
2. 个别辅导:对于个别学生存在的问题,教师可进行个别辅导,帮助学生解决学习中的困难。
3. 互动交流:鼓励学生之间进行互动交流,分享解题经验和技巧,共同提高学习成绩。
4. 复习巩固:要求学生将错题整理成错题本,以便于后期复习巩固,减少同类错误的再次发生。
新冀教版初中数学八年级上册精品学案14.3 第1课时 无理数及实数的概念
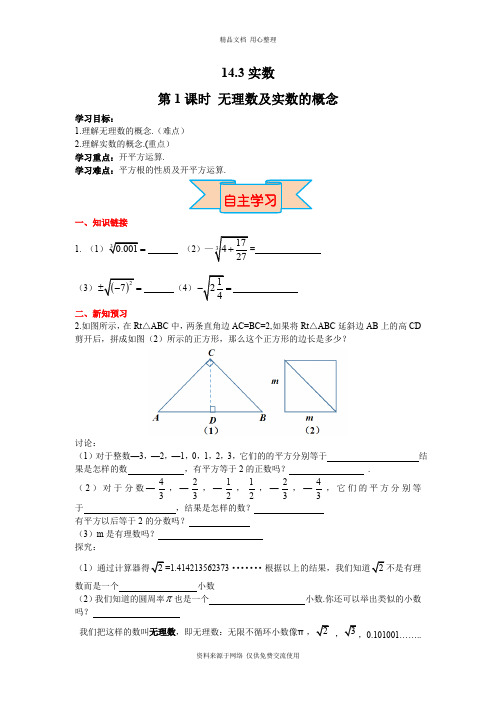
14.3实数第1课时无理数及实数的概念学习目标:1.理解无理数的概念.(难点)2.理解实数的概念.(重点)学习重点:开平方运算.学习难点:平方根的性质及开平方运算.一、知识链接1. (1=(2=(3)=(4)=二、新知预习2.如图所示,在Rt△ABC中,两条直角边AC=BC=2,如果将Rt△ABC延斜边AB上的高CD剪开后,拼成如图(2)所示的正方形,那么这个正方形的边长是多少?讨论:(1)对于整数—3,—2,—1,0,1,2,3,它们的的平方分别等于结果是怎样的数,有平方等于2的正数吗?.(2)对于分数—43,—23,—12,12,—23,—43,它们的平方分别等于,结果是怎样的数?有平方以后等于2的分数吗?(3)m是有理数吗?探究:(1······不是有理数而是一个小数(2)我们知道的圆周率π也是一个小数.你还可以举出类似的小数吗?我们把这样的数叫无理数,即无理数:无限不循环小数像π0.101001……..实数:_______和_________统称为实数.三、自学自测1、判断下列说法是否正确:(1)无限小数都是无理数.( )(2)无理数都是无限小数.( )(3)带根号的数都是无理数.( )2.在下列各数中,哪些数是有理数,哪些数是无理数?3.14,2.847四、我的疑惑_____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________一、要点探究探究点:无理数及实数的概念问题:下列各数中,哪些是有理数?哪些是无理数?3.14,-53,0.58··,-0.125,-5π,0.35,227,5.3131131113…(相邻两个3之间1的个数逐次加1).【归纳总结】准确理解有理数和无理数的概念是解答本题的关键.任何有限小数或无限循环小数都是有理数;无限不循环小数称为无理数,故-5π,5.3131131113…是无理数,其他都是有理数.【针对训练】1.把下列各数分别填入相应的集合里:-|-3|,21.3,-1.234,722-,0,9-,381--,2π-,8,0)32(-,3-2,1.212 112 111 2….(1)无理数集合{_____________…};(2)有理数数集合{___________…}.2.下列说法正确的有( )⑴不存在绝对值最小的无理数;⑵不存在绝对值最小的实数;⑶不存在与本身的算术平方根相等的数;⑷比正实数小的数都是负实数;⑸非负实数中最小的数是0.A. 2个B. 3个C. 4个D.5个1.下列说法中正确的是 ( )A.不存在最小是实数B.有理数、是有限小数C.无限小数都是无理数D.带根号的数都是无理数2.把下列各数分别填入相应的集合内:,23,41,7,π,25-,320,94,0,5-,83-⋅⋅⋅3737737773.0(相邻两个3之间的7的个数逐次加1)有理数集合 无理数集合 3.已知长方体的体积是1 620,它的长、宽、高的比是5∶4∶3,问该长方体的长、宽、高是无理数吗?为什么?当堂检测参考答案:1.A2.有理数集合:,41,25-,94,0,83-无理数集合:,23,7,π,320,5-⋅⋅⋅3737737773.0(相邻两个3之间的7的个数逐次加1)3.该长方体的长、宽、高不是无理数.理由如下:设长方体的长、宽、高分别是5k、4k、3k.根据题意得5k·4k·3k=1 620,k3=27,k=3.所以5k=15,4k=12,3k=9. 所以该长方体的长、宽、高均为有理数,不是无理数.。
冀教版八年级数学上册14.3《实数》(共28张PPT)

知识归纳:
也可以这样来分类:
正实数
实 数
0
负实数
正有理数 正无理数 负有理数 负无理数
当堂检测
一、判断:
1.实数不是有理数就是无理数。( ) 2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
×
概念辨析:
2
=1.4142135623730950488016887242096980 78569671875376…
这个数的特点是:
无限的,
不循环小数
类似的还有下面的数:
2 -1.414213562…
=3.14159265358 …
… …
5 =-2.236067977 …
…
7 3
(3)整数集合: (4)负数集合: (5)分数集合: (6)实数集合:
9
3 4
0.6
9 35
64 3
3 9
3
0.13
4
64
0.6
3 4
3 9
3
0.13
自学指导二: 阅读课本P73 探究: 无理数是否也可以用数轴上的点来表示呢?
你能在数轴上找到表示
知识归纳:
有理数和无理数统称 实数
学由学过于过的生的数活数和生产实践的白需天的要古气代温.猎是人.5射℃.落,几晚只上老的鹰气?温是零下5℃,如何表 示右呢图? 中红色正方形面积的边长是多少(?3只)
——人们(发+现5(并℃使、用)-了5自℃然)数 2
?
1
——人—们—发人现们并发使现用并了使正用数了1和无负理数数 ?
冀教版八年级数学上册14.3《实数》(共16张PPT)

结论
实数和数轴上的点是一一对应的,即每 一个实数都可以用数轴上的一个点来表示; 反过来,数轴上的每一个点都表示一个实 数.
实数的性质
参照有理数的有关概念,谈谈实数的下列概念: (1)实数的绝对值. (2)互为相反数的实数. (3)—个实数的倒数.
在有理数范围内的一些基本概念(如绝对值、相反数、
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
实数与数轴的关系
1.如图1所示,将面积分别为2和3的两个正方形放置在 数轴上,使得正方形的一个顶点和原点O重合,一条 边恰好落在数轴正方向上,其另一个顶点分别为数 轴上的点A和点B.
(1)线段OA,OB的长分别是多少? (2)点A,B在数轴上对应的数分别是哪两个数?
2.如图2所示,设一枚5角硬币的直径为1个单位长度, 将这枚硬币放置在平面内一条数轴上,使硬币边缘 上的一点P与原点O重合.让这枚硬币沿数轴的正方向 无滑动滚动一周,这时点P转到数轴上点P′的位置.
(1)线段OP′的长是多少? (2)在数轴上与点P′,对应的数是哪个数?
14.3 实 数
第十四章 实 数
第2课时 实数的性质
回顾旧知
学习有理数时,我们知道 整数 和_分_数___
统称为有理数.
任意一个整数都可以看成一个有限小数,任
意一个分数都可以化成有限小数或无限循环
小数.所以说 有限小数 和_无_限__循_环__小_数__称为有
理数.
无限不循环小数
叫做无理数.
有理数 和 无理数 统称为实数.
例2 :
1、-5的相反数是
冀教版数学八年级上册14.3《实数》说课稿2

冀教版数学八年级上册14.3《实数》说课稿2一. 教材分析冀教版数学八年级上册14.3《实数》是学生在掌握了有理数和无理数的基础上,进一步对实数进行系统学习。
本节内容主要包括实数的定义、实数的分类以及实数与数轴的关系。
通过学习,使学生了解实数的广泛性,加深对实数概念的理解,为后续学习函数、方程等知识打下基础。
二. 学情分析八年级的学生已经掌握了有理数和无理数的基本概念,对数轴有一定的认识。
但实数作为一个全新的概念,可能对学生产生一定的困惑。
因此,在教学过程中,要注重引导学生从已有知识出发,逐步过渡到实数的概念。
三. 说教学目标1.知识与技能:理解实数的定义,掌握实数的分类,了解实数与数轴的关系。
2.过程与方法:通过观察、思考、讨论等方法,培养学生分析问题、解决问题的能力。
3.情感态度与价值观:激发学生对数学学习的兴趣,培养学生的团队协作精神,提高学生自主学习能力。
四. 说教学重难点1.重点:实数的定义,实数的分类,实数与数轴的关系。
2.难点:实数的概念的理解,实数与数轴的关系的运用。
五. 说教学方法与手段1.采用问题驱动法,引导学生从已有知识出发,探索实数的概念。
2.利用数轴辅助教学,帮助学生直观地理解实数与数轴的关系。
3.分组讨论,合作学习,提高学生团队协作能力和自主学习能力。
六. 说教学过程1.导入新课:回顾有理数和无理数的概念,引出实数的概念。
2.自主学习:学生自主探究实数的定义,理解实数的广泛性。
3.讲解演示:教师讲解实数的分类,利用数轴展示实数与数轴的关系。
4.实践练习:学生分组讨论,解决实际问题,运用实数与数轴的关系。
5.总结提升:教师引导学生总结本节课的主要内容,加深对实数概念的理解。
七. 说板书设计板书设计如下:实数的定义实数的分类实数与数轴的关系有理数无理数八. 说教学评价1.课堂提问:检查学生对实数概念的理解程度。
2.课后作业:检验学生对实数与数轴关系的掌握情况。
3.小组讨论:评价学生在团队合作中的表现,以及自主学习能力。
冀教版八年级数学上册第十四章《实数》PPT课件
也就是说,非负数的“算术”平方根是非负数;
负数不存在算术平方根,即当 a 0时, a 无意义.
练一练
1.若一个数的算术平方根是 7 ,那么这个数
是7 ;
2. 9 的算术平方根是 3
;
3.( 2)2 的算术平方根是 3
2 3
;
4.若 m 2 2 ,则(m 2)2 16 .
当堂练习
1.若 a 的算术平方根是3,则a =___8_1____.
(D)
B.一个数的立方根不是正数,就是负数 C.一个数的立方根等于它本身,这个数一定是0 D.一个非负数的立方根和这个数同好,0的立方根是0
2.已知a2=4,b3=27,则ab的值为__8_或__-_8_____.
3.求下列各式的值 :
1 3 8;
2 3 0.064;
3 3 8 ;
3
4 3 9 .
36
4
面积/dm2
25
正方形的
边长/dm
1
3
2
4
6
5
你能指出它们的共同特点吗? 都是已知一个正数的平方,求这个正数.
讲授新课
一 平方根的概念及性质
问题1 如果一个数的平方等于9,这个数是多少?
解析:
由于3 2 =9,
所以这个数是3或-3.
想一想 3和-3有什么特征?
问题2 根据上面的研究过程填表:
因为(
1 2
)3 =0.125,所以0.125的立方是(
1 2
);
3
因为( 0 ) =0,所以0的立方根是( 0);
因为 ( -2)3=-8,所以-8的立方根是( -2);
因为(
2 3
3
) =
冀教版数学八年级上册14.3《实数》教学设计1
冀教版数学八年级上册14.3《实数》教学设计1一. 教材分析冀教版数学八年级上册14.3《实数》是学生在学习了有理数、无理数相关知识的基础上,进一步对实数进行系统地认识和理解。
本节内容主要包括实数的定义、实数的分类、实数的性质等。
通过本节课的学习,使学生掌握实数的概念,了解实数的分类,理解实数的性质,为学生进一步学习函数、几何等知识打下基础。
二. 学情分析八年级的学生已经学习了有理数、无理数的相关知识,对数的运算、性质有一定的了解。
但是,学生对实数的认识还比较模糊,对实数的分类和性质的理解还有待提高。
此外,学生的数学思维能力、逻辑表达能力等方面也有待提高。
三. 教学目标1.了解实数的概念,掌握实数的分类,理解实数的性质。
2.培养学生运用数学知识解决实际问题的能力。
3.培养学生的数学思维能力、逻辑表达能力。
四. 教学重难点1.实数的定义、分类和性质。
2.实数与实际问题的结合。
五. 教学方法采用问题驱动法、案例分析法、小组合作法等教学方法,引导学生主动探究、积极思考,提高学生的数学思维能力和逻辑表达能力。
六. 教学准备1.教材、教案、课件。
2.相关实数的学习资料。
3.投影仪、白板等教学设备。
七. 教学过程导入(5分钟)教师通过引入生活中实际问题,如身高、体重等,引导学生认识到实数在生活中的重要性。
然后,教师提问:“你们已经学习了有理数和无理数,那么,实数与有理数、无理数有什么关系呢?”从而引出本节课的主题——实数。
呈现(15分钟)教师通过课件展示实数的定义、分类和性质,让学生初步了解实数的概念。
接着,教师通过举例说明实数的性质,如实数的大小比较、实数的加减乘除运算等。
在此过程中,教师引导学生积极参与,提问解答,确保学生对实数的理解。
操练(15分钟)教师布置一些有关实数的练习题,让学生独立完成。
题目包括实数的分类、实数的性质等。
完成后,教师选取部分学生的作业进行讲评,指出其中的错误和不足,帮助学生巩固实数知识。
冀教版初中数学八年级上册 14.3 实数 教案 (1)
学过程教师导学及学生主体活动过程随堂问题简记即0.3 =0.333…=31根据上面提供的方法,你能把0.7 ,0.41 化成分数吗?且想一想是不是任何无限循环小数都可以化成分数?在此基础上与学生一起得到结论:任何一个有限小数或无限循环小数都能化成分数,所以任何一个有限小数或无限循环小数都是有理数。
思考:还有其它类型的小数吗?问题:课本102页,如图,在Rt △ABC 中,两条直角边AC=BC=2,如果将Rt △ABC 沿斜边AB上的高CD剪开后,拼成如图所示的正方形,那么这个正方形的边长是多少呢?如果用计算机计算结果为1.41421356237309504880168872420969807856967187537694……问题:小数点后面的数是循环的吗?那么它属于什么小数?学生命名无限不循环小数--------叫做无理数例如:0.1010010001…〔两个1之间依次多1个0〕—168.3232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕无理数和有理数一样也有正负之分,例如正无理数:π,,负无理数:-π,- ,-现在我们不仅学过了有理数,而且又定义了无理数,显然我们所学的数的范围又扩大了,我们把有理数和无理数统称为实数,这是我们今天学习的又一新的概念.2.实数的定义:有理数和无理数统称为实数.3.实数的分类:对于实数,我们可按定义分类如下:32,3,5,6,,232323由上述分类,我们发现有理数和无理数都有正负之分,所以对实数我们还可以按大小分类如下:对于这两种分类的方法,同学们应牢固地掌握.二、练一练例1(1)你能尝试着找出三个无理数来吗?(2)下列各数中,哪些是有理数?哪些是无理数?解决问题后,可以再问同学:“用根号形式表示的数一定是无理数吗?”例2把下列各数填人相应的集合内:整数集合{ … }负分数集合{ …} 正数集合{ …} 负数集合{ …} 有理数集合{ …} 无理数集合{ …}三、探一探我们知道,在有理数中只有符号不同的两个数叫做互为相反数,例如3和-3,43和-43等,实数的相反数的意义与有理数一样。
冀教版数学八年级上册14.3《实数》教学设计2
冀教版数学八年级上册14.3《实数》教学设计2一. 教材分析冀教版数学八年级上册14.3《实数》是学生在掌握了有理数和无理数的基础上,进一步对实数进行系统学习。
本节课的内容包括实数的定义、实数的分类、实数的性质等。
通过本节课的学习,使学生能够理解实数的意义,掌握实数的分类和性质,为后续的数学学习打下基础。
二. 学情分析学生在学习本节课之前,已经掌握了有理数和无理数的相关知识,对数的运算也有一定的了解。
但学生在理解实数的本质和实数的分类上可能会存在一定的困难。
因此,在教学过程中,需要结合学生的实际情况,用生动形象的例子和生活中的实际问题,帮助学生理解和掌握实数的概念。
三. 教学目标1.理解实数的定义,掌握实数的分类。
2.理解实数的性质,能够运用实数的性质解决实际问题。
3.培养学生的逻辑思维能力,提高学生的数学素养。
四. 教学重难点1.实数的定义和分类。
2.实数的性质及其运用。
五. 教学方法1.采用问题驱动法,引导学生主动探究实数的定义和性质。
2.用生活中的实际问题,帮助学生理解实数的意义。
3.采用小组合作学习,培养学生的团队协作能力。
六. 教学准备1.准备相关的生活实例和数学实例,用于解释实数的概念和性质。
2.准备PPT,用于展示实数的定义、分类和性质。
3.准备练习题,用于巩固所学知识。
七. 教学过程导入(5分钟)教师通过提问方式引导学生回顾有理数和无理数的概念,为新课的学习做好铺垫。
例如:“同学们,你们能举例说明有理数和无理数吗?”呈现(10分钟)教师通过PPT展示实数的定义、分类和性质,同时结合生活实例和数学实例,帮助学生理解实数的概念。
例如:用尺子测量物体长度,涉及到整数、分数和小数;用π表示圆周率,涉及到无理数。
操练(15分钟)教师提出练习题,让学生分组讨论、解答。
例如:判断以下数是有理数还是无理数?并说明理由。
巩固(10分钟)教师引导学生总结实数的性质,并通过实例说明实数的性质在实际问题中的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14.3实数
第1课时无理数及实数的概念
学习目标:
1.理解无理数的概念.(难点)
2.理解实数的概念.(重点)
学习重点:开平方运算.
学习难点:平方根的性质及开平方运算.
一、知识链接
1. (1
=(2
=
(3)
=(
4)=
二、新知预习
2.如图所示,在Rt△ABC中,两条直角边AC=BC=2,如果将Rt△ABC延斜边AB
上的高CD
剪开后,拼成如图(2)所示的正方形,那么这个正方形的边长是多少?
讨论:
(1)对于整数—3,—2,—1,0,1,2,3,它们的的平方分别等于结果是怎样的数,有平方等于2的正数吗?.
(2)对于分数—4
3
,—
2
3
,—
1
2
,
1
2
,—
2
3
,—
4
3
,它们的平方分别等
于,结果是怎样的数?有平方以后等于2的分数吗?
(3)m是有理数吗?
探究:
(
1·····
·不是有理
数而是一个小数
(2)我们知道的圆周率π也是一个小数.你还可以举出类似的小数吗?
我们把这样的数叫无理数
,即无理数:无限不循环小数像π
0.101001……
..
实数:_______和_________统称为实数.
三、自学自测
1、判断下列说法是否正确:
(1)无限小数都是无理数.( )
(2)无理数都是无限小数.( )
(3)带根号的数都是无理数.( )
2.在下列各数中,哪些数是有理数,哪些数是无理数?
3.14,2.8
47
四、我的疑惑
_____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________
一、要点探究
探究点:无理数及实数的概念
问题:下列各数中,哪些是有理数?哪些是无理数?
3.14,-53,0.58··,-0.125,-5π,0.35,227
,5.3131131113…(相邻两个3之间1的个数逐次加1).
【归纳总结】准确理解有理数和无理数的概念是解答本题的关键.任何有限小数或无限循环小数都是有理数;无限不循环小数称为无理数,故-5π,5.3131131113…是无理数,其他都是有理数.
【针对训练】
1.把下列各数分别填入相应的集合里:
-|-3|,21.3,-1.234,722-
,0,9-,381--,2π-,8,0)32(-,3-2,1.212 112 111 2….
(1)无理数集合{_____________…};
(2)有理数数集合{___________…}.
2.下列说法正确的有( )
⑴不存在绝对值最小的无理数;
⑵不存在绝对值最小的实数;。
