高等数学建模案例
数学建模数学实验插值及案例

数学建模数学实验插值及案例在科学研究和工程实践中,数学建模扮演着至关重要的角色。
通过建立数学模型,我们可以对现实世界的现象进行模拟和预测。
其中,插值方法是一种重要的数学建模工具,用于估计在给定数据点之间的未知值。
本文将探讨插值方法的基础理论以及一个具体的数学实验案例。
插值方法是一种数学技术,通过在给定的数据点之间估计未知的值。
最常用的插值方法包括线性插值、多项式插值和样条插值等。
线性插值是最简单的插值方法,它将数据点之间的变化视为线性的,即变化率保持恒定。
多项式插值方法则通过构建一个多项式函数来逼近数据点的变化趋势。
样条插值则通过将数据点连接成平滑的曲线来进行插值。
本案例将利用多项式插值方法对房价进行预测。
我们收集了一组房屋价格数据,包括房屋的面积、房龄、位置等信息。
然后,我们使用多项式插值方法构建一个函数来描述房价与这些因素之间的关系。
通过调整多项式的阶数,我们可以控制模型的复杂性。
我们使用该模型来预测新的房价。
在本案例中,我们使用了200个样本数据进行训练,并使用另外100个数据点进行测试。
我们发现,通过增加多项式的阶数,模型的预测精度可以得到提高。
然而,当阶数增加到一定程度后,模型的性能改善不再明显。
我们还发现模型的预测结果对训练数据的分布非常敏感,对于分布偏离较大的新数据点,预测结果可能会出现较大误差。
通过本次数学实验,我们深入了解了插值方法在数学建模中的应用。
在实际问题中,插值方法可以帮助我们更好地理解数据的变化趋势和预测未知的值。
然而,插值方法也存在一定的局限性,如本实验中模型对训练数据分布的敏感性。
未来工作中,我们可以尝试采用其他更加复杂的模型,如神经网络、支持向量机等来提高预测精度。
我们还应充分考虑数据的分布特性,以提高模型的泛化能力。
插值方法是数学建模中的重要工具之一,它可以让我们更好地理解和预测数据的趋势。
通过本次数学实验,我们深入了解了多项式插值方法的工作原理和实现过程,并成功地将其应用于房价预测问题中。
数学建模案例在高等数学教学中的应用
经 过 一 些 合 理 假 设 后 , 到 如 图 2 2坐 标 系 , 中 A, , D正 方 形 A D 的 中 心 为 坐 标 原 点 . BC 0为 A 连 线 与 轴 的 夹 角 , ( C 厂 0)
首 先 , 们 把 易 拉 罐 近 似 看 成 一 个 正 圆 柱 形 进 行 建 模 是 有 一 定 合 理 性 的 . 一 步 观 察 我 们 发 现 罐 体 的侧 边 我 进
材 料 很 薄 , 顶 盖 材 料 很 硬 ( , 为 要 使 劲 拉 ); 说 明 实 际 建 模 必 须 考 虑 不 同 部 位 的 体 积 ( 同 部 位 材 料 不 而 厚 因 这 不 同 , 应 的 价 格 也 不 同 ) 因此 , 们 可 简 化 为 如 下 模 型 : 拉 罐 内 部 体 积 一 定 , 盖 厚 度 为 其 余 部 分 厚 度 的 相 . 我 易 顶 倍 时 , 易 拉罐 材料 的体 积最 小 的罐体 内部 的尺寸 为 多少 ? 使 设 饮 料 罐 的 半 径 为 r 因 此 , 径 为 d=2 ), 的 高 为 h, 内 体 积 为 ; 盖 外 的 材 料 的 厚 度 为 b 项 盖 的 厚 ( 直 r 罐 罐 顶 ,
.
为 A, c两 脚 与 地 面 距 离 之 和 , ) g( 为 , 两 脚 与 地 面 距 离 之 和 , 0) 0, D f( g ( 0 ) .由假 设 ( ) g都 是 连 续 函 数 . 假 设 ( ), 于 任 意 0 厂 ) g( )中 2 ,, 由 3 对 ( 和 0
案 例 2: 点 存 在 定 理 与 椅 子 放 平 问 题 零
在 介 绍 闭 区 问 上 连 续 函 数 的 零 点 存 在 定 理 时 , 们 可 以 给 出 下 面 来 自 日常 生 活 中 的 问 题 : 把 四 条 腿 长 我 一
高等数学建模题目及答案

典型谱方法的缺点:
当解u存在奇异点时,典型谱方法在奇异点 处不收敛,这时需要加密在奇异点附近的离散点。 对于奇异解的问题,多区域谱方法可以解决。
以下介绍多区域谱方法。
4.多区域谱方法
① p-refinement (M固定,N不固定)
x∈[-1,1],先将[-1,1]等分为M个均分小区间, 再将每个小区间分为Ni (i=1,2,...M) 个小区间,分 别求M个小区间上的求导矩阵,然后按照相应规 则组装。
② 同样,对于简单函数u,可以利用定义直接计算它 的分数阶积分/导数,但是对于复杂函数u,无法利用 定义求解其分数阶积分/导数。解决方法是用正交多 项式逼近u,通过求正交多项式的分数阶积分/导数代 替求u的分数阶积分/导数。
2.第一种形式的谱方法
其中,正交系数Cij的求法如下:
3.第二种形式的谱方法
分数阶谱方法
1.分数阶积分/导数的定义 2.第一种形式的谱方法 3.第二种形式的谱方法 4.多区域谱方法 5.数值例子
1.分数阶积分/导数的定义
思考:
① 联想数学分析中的泰勒级数展开,对于简单函数u, 可以直接计算并讨论它的收敛性、连续性、可微性和 可积性,但对于复杂函数u,无法直接讨论它的以上 性质。解决方法是用泰勒级数逼近u,通过讨论级数 的性质代替讨论u的性质。
(cosx
i
sin
x)
(it
(
( 1) 1)
t
)
x [0,2 ], t [0,1]
IC : u(x,0) 0, BC:u(0,t) t 2, u(2 ,t) t 2
exact solution: u(x,t) t (cosx i sin x)
解题原理:
误差图:
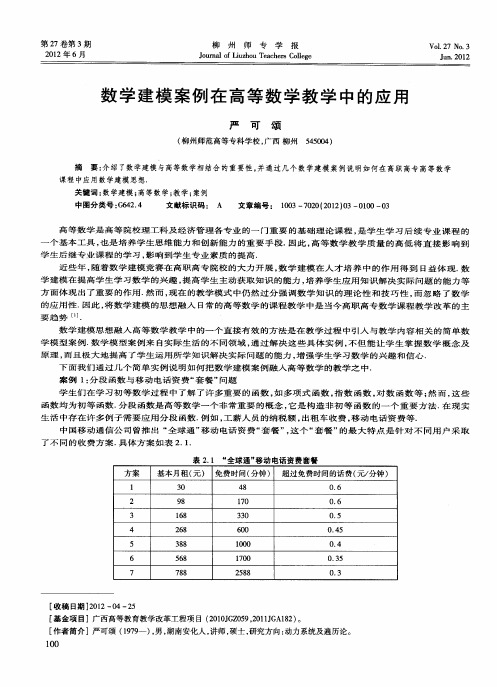
数学建模案例在高等数学教学中的应用

高等数学是高等院校理工科 和经管类学生必修的一门数学基础课 程, 直接关系到学生后续数学课程和专业课程 的学习。然而 , 现在 的 教学模式 过分强调数 学知识 的理 论性和技巧 性 ,忽略 了数学的应用 性。而数 学建模在提高学生学习数学的兴趣 ,提高学生主动获取 知识 的能力 ,培养学生应用知识解决实际问题的能力等方面体现 了重要 的 作用。因此, 将数学建模的思想融人日常的高等数学的课程教学中是 当今高等数学课程教学改革 的主要趋势。 1 在高等t学教学过程中啊入救掌t■思想 的必要性 传 统 的数 学课程体 系偏重理 论 、注 重推理 ,淡 化知识 的实际背 景 ,使教学与实际割裂开来 ,导致学生 即使学了很多的公式 、定理 , 也不能用其解决实际问题。而数学建模就为我们提供了这一平 台,使 学 生在熟练掌握数学基本知识的同时 , 增强 了分析 、解决实际问题 的
教学文件教学业务部门的管理教学理论教育和研究活动等方面构成保管文件材料这是一种间接的教学活动的原始记录包括教师的教学价值结果的分析分析的论文研究项目教案反思在教学理论以及其他活动间接声像档案如教学实践视频等这些图像表达并辅以简短的文字澄清历史纪录纪录片直观典型的特点学校档案馆协助完成任务中占据重要地位的教育活动知识和信息的方式因为他们是存储详细真实地反映了大学的教学历史图片审查后传送的文件如教师教学教案实验报告研究论文毕业设计论论文等可以快速了解高等教育教学情境的基本使命而且还作为一种教学管理评估的基础上基本参考
证 明 :将 椅 子 旋 转 9 0 。 ,对 角 线 A c和 B D互 换 , 由
g ( o J = 0 , - 厂 【 0 ) > 0可知 g (  ̄ / 2 ) > 0 , , 2 ) = 0。令 ^ ) = g ( a ) - f ( o )
高等数学在交通领域的建模

高等数学在交通领域的建模
高等数学在交通领域具有重要的建模作用,以下是一些例子:
1. 微积分建模:交通领域需要处理大量数据,例如交通流量、速度、密度等,这些数据通常可以用微积分来建模。
例如,可以用微积分来建立交通流量方程,以预测未来交通状况。
2. 偏微分方程建模:偏微分方程在交通规划中发挥着重要作用。
例如,可以用偏微分方程来描述交通流的运动和变化,预测交通流量和拥堵情况。
3. 概率论建模:交通领域涉及到很多随机因素,例如交通事故、道路状况、天气等。
因此,概率论在交通领域中具有重要的建模作用,可以用来预测交通流量和拥堵情况。
4. 线性代数建模:交通领域中也需要处理很多矩阵和向量运算,例如交通信号控制、道路维修等。
因此,线性代数在交通领域中也具有重要的建模作用。
高等数学在交通领域中具有重要的建模作用,可以帮助交通领域更好地理解和处理交通问题。
高数数学建模题目

高数数学建模题目
以下是一个高数数学建模题目的示例:
题目:某品牌手机生产商生产了100万部手机,其中有5%的手机存在电池寿命不足的问题。
为了解决这个问题,生产商决定对所有手机进行电池更换。
每部手机更换电池的成本为30元,求总成本和平均每部手机更换电池的成本。
假设手机数量为 N=100万部,电池寿命不足的手机比例为 p=5%,更换电池的单价为 c=30元。
总成本可以通过以下公式计算:
总成本= N × p × c
其中,N 是手机数量,p 是电池寿命不足的手机比例,c 是更换电池的单价。
平均每部手机更换电池的成本可以通过以下公式计算:
平均成本 = 总成本 / N
请使用以上信息,求解总成本和平均每部手机更换电池的成本。
总成本为:元
平均每部手机更换电池的成本为:15 元。
数学建模-猎狗追兔子问题

数学建模论文《数学建模》(2014春)课程期末论文摘要(一)对于问题一:自然科学中存在许多变量,也有许多常量,而我们要善于通过建立合适的模型找到这些变量之中的不变量。
猎狗追赶兔子的问题是我们在生活中常见的实例,而题目把我们生活中的普通的例子抽象成为高等数学中微分方程的例子,通过对高阶微分方程的分析,建立微分方程模型,并用数学软件编写程序求解,得出结论,解决生活中常见的实际问题。
(二)对于问题二:学习使用matlab进行数学模型的求解,掌握常用计算机软件的使用方法。
关键词微分方程导数的几何意义猎狗追兔子数学建模数学软件一、问题重述如图1所示,有一只猎狗在B 点位置,发现了一只兔子在正东北方距离它250m 的地方O 处,此时兔子开始以8m/s 的速度正向正西北方向,距离为150m 的洞口A 全速跑去. 假设猎狗在追赶兔子的时候,始终朝着兔子的方向全速奔跑。
请回答下面的问题:⑴ 猎狗能追上兔子的最小速度是多少? ⑵ 在猎狗能追上兔子的情况下,猎狗跑过的路程 是少?⑶ 假设猎狗在追赶过程中,当猎狗与兔子之间的距离为30m 时,兔子由于害怕导致奔跑速度每秒减半, 而狗却由于兴奋奔跑速度每秒增加0.1倍,在这种情 况下回答前面两个问题。
二、问题分析与假设在猎狗追赶兔子的时候猎狗一直朝着兔子的方向追赶,所以可以建立平面直角坐标系,通过导数联立起猎狗运动位移,速度和兔子的运动状态。
1.假设兔子的运动是匀速的。
2.假设猎狗的运动轨迹是一条光滑并且一阶导数存在的曲线。
3.猎狗的运动时匀速或者匀变速的。
4.猎狗运动时总是朝向兔子。
三、模型的建立及求解3.1 符号规定1.(x ,y ):猎狗或者兔子所在位置的坐标。
2. t :从开始到问题结束经过的时间。
3. a:猎狗奔跑的路程。
4. v:猎狗的奔跑速度。
3.2 模型一的建立与求解猎狗能够抓到兔子的必要条件:猎狗的运动轨迹在OA 要有交点以OA 为y 轴,以OB 为x 轴建立坐标系,则由图有O(0,0),A(0,150),B(250,0),兔子的初始位置0点,而猎狗初始位置是B 点,t (s )后猎狗到达了C (x ,y ),而兔子到达了D (0,8t ),则有CD 的连线是猎狗运动轨迹的一条切线,由导数的几何意义有:NW8dy y tdx x-=dav dt =da =三式联立消去t ,得到;设:若猎狗可以追上兔子则有当兔子在OA,猎狗在OB 之间运动时此方程有解,设:得到:得到:两式联立相加得到:1.如果q=1即v=8 m/s 得到所以此情况无交点,所以v=8m/s 猎狗无法追上兔子; 2.如果q<1即v>8m/s 得到此情况有交点,所以有可能能够追上兔子,如果要追上兔子需要y<=150; 解得到: 即所以这种情况下能够追上的最小速度是 .3.如果q>1 利用上式得到,所以这种情况不能追上兔子。
数学建模案例

2021/10/10
13
建模示例五:轮廓模型
轮廓模型是以量纲模型为基础,利用量 的比例关系而构造简单数学模型的一种方法。 因为这种比例关系比较粗糙,因而成为轮廓 模型。
(货物的包装成本)在超市中可以看到许 多商品(如面粉、白糖、奶粉等)都以包装 的形式出售,同一种商品的包装也经常有大 小不同的规格,出售的价格也高低不同。下 表是一些例子。
周 期 中 南 北 方 向 亮 红 灯 的 比 率 是 t/T,需 停 车 等 待 的 车 辆
数 是 V t/T.这 些 车 辆 等 待 时 间 最 短 为 0(刚 停 下 ,红 灯 就 转
换 为 绿 灯 ),最 长 为 t(到 达 路 口 时 ,绿 灯 刚 转 换 为 红 灯 ),由 假
设 2"车 流 量 均 匀 "可 知 ,它 们 的 平 均 等 待 时 间 是 t/2.由 此 可
它 也 是 货 物 量 的 减 函 数 .因 而 当 包 装 比 较 大 时 单 位 重 量 货物的成本的减低将越来越慢.
我们来计算总的节省率,即购买单位包装的商品的
花 费 随 着 包 装 的 增 大 而 改 变 的 速 率 r ( ) (q / 3) 1/3 , 它
仍 然 是 的 减 函 数 .这 说 明 总 的 节 省 率 也 是 随 着 所 包 装 的
1588)2 27
27(152 88
882 272
)1588
12
当t
88 30 30 24
48.8889时,ymin
587(秒).
由此可见,我们计算所得的结果和同学们实际观测
到的数据是比较接近的.这也说明此路口红灯与绿灯设
置的时间比较合理.
评 注: 由上述结果可知,两个方向绿灯时间之比恰好等于
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学建模案例
1. 水桶模型:用高等数学的积分和微分知识模拟水桶的溢出情况,以确定最大容量和最快的流出速度。
2. 热传导模型:通过热传导方程式和边界条件,建立热传导模型,研究热量在物体内的传递和分布。
3. 光学模型:运用高等数学的微积分和波动方程式,描述光线在介质中的传播和干涉现象,以及各种光学器件的工作原理。
4. 风电场建设模型:利用高等数学的多元函数、梯度和偏导数等知识,分析风电场建设的最佳布局、风能利用效率和风机数量等问题。
5. 市场建模:运用高等数学的统计学和概率论知识,对市场需求、供给、价格等因素进行建模,预测市场走向和未来的趋势。
6. 股票交易策略模型:通过高等数学的时间序列分析和随机过程模型,研究股票价格的波动规律和交易策略的制定。
7. 电力系统建模:利用高等数学的电路分析和微分方程式,建立电力系统的模型,预测电力系统的稳定性和故障情况。
8. 机器人运动模型:通过高等数学的向量和矩阵知识,描述机器人的运动轨迹和姿态变化,以及机器人的工作空间和运动范围。
9. 交通流模型:运用高等数学的微分方程式和概率论知识,建立交通流模型,分析交通拥堵的原因和解决方案。
10. 化学反应动力学模型:通过高等数学的微积分和差分方程式,建立化学反应动力学模型,研究反应速率、反应机理和反应过程中的状态变化。
