Maple13入门教程
Maple 入门教程
Quick Help Details
。求值多项式在 x = 10,求输出
Part 2:整合思想
西希安工程模拟软件(上海)有限公司,2008
2.0 介绍
第二部分:整合你的思想,你将学习使用一些基本工具创建出版文件,以及在文字中使用 排版数学。此外,你将使用Maple符号和数值求解方程,了解Maple中赋值语句、表达式、 函数之间的区别。
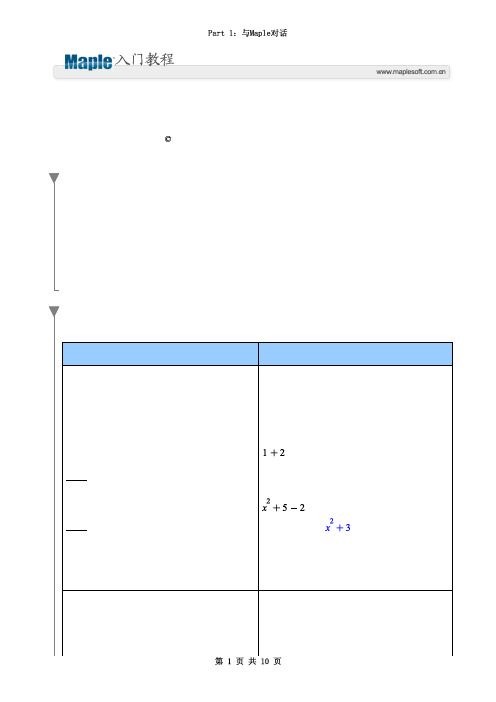
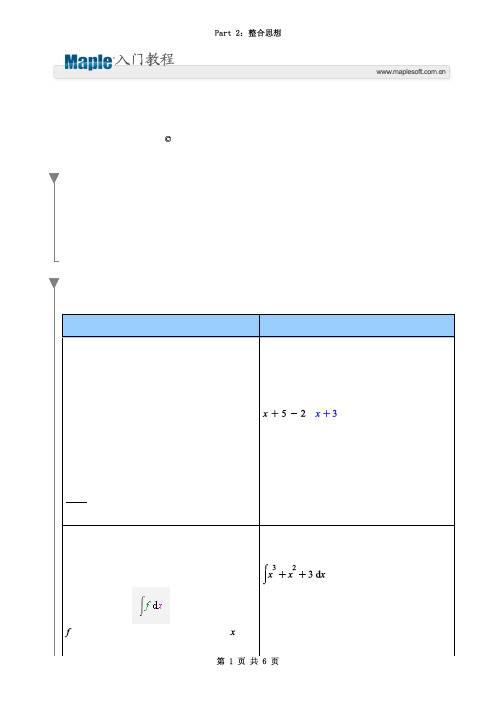
例子:键入 "x+5-2" 然后按 [Ctrl][=]。
组合文字和数学
例子: 1. 输入一个简单的计算。从表达式面板中
选择积分模板
。 用被积函数代替
。按 [Tab] 键移到下一个占位符,用 替 换。
2. 使用 [Ctrl][=] 积分计算。
3. 将光标放置在表达式的左边,切换到文
字模式
,或者按 [F5]
是一
例子:输入上面的方程(使用单引号作为 微分符号),为了验证它是一个微分方 程,从关联菜单中选择 Solve DE 求解。
标签 无论你何时使用【回车键】获得一个计算 结果,工作表将自动给出一个公式标签。 如果想引用前面的计算结果,使用 C t r l + L 并输入标签数字。
例子:将上面的结果 标签。
操作步骤
结果
求精确解和数值近似 Maple 计算精确结果,也就是说,分数计算 时保持分数形式,e 和 在整个计算过程中 保留为符号形式。这些将减少在多步计算 中由于近似产生的误差。
例子:在新的一行,输入 1/2 + 1/3。 我们注意到光标 / 自动移到分母的位置。按 回车键得到计算结果。
Maple也可以计算数值近似解。 例子:鼠标右击上面的结果表达式,选择 关联菜单的Approximate,精度位选择 5。
Maple入门教程Part2_整合思想
Part 2:整合思想
西希安工程模拟软件(上海)有限公司,2008
2.0 介绍
第二部分:整合你的思想,你将学习使用一些基本工具创建出版文件,以及在文字中使用排版数学。
此外,你将使用Maple符号和数值求解方程,了解Maple中赋值语句、表达式、函数之间的区别。
2.1 组合文字和数学
在Maple中,你可以在文件中任意组合文字和数学,创建专业的技术文件。
,重新计算。
提示:快捷键 【F5】用于切换数学/文字输入。
在数学模式下,光标显示为斜体,周围有虚线框。
在文字模式下,光标显示为垂直线。
2.2 求解方程
Maple 能够求方程和不等式中未知量的值。
用数学软件Maple做线性代数(2013.5.15)

用数学软件Maple做线性代数作者:徐小湛四川大学数学学院xuxzmail@目录前言第一章行列式行列式克拉默法则第二章矩阵及其运算矩阵的线性运算矩阵的乘法矩阵的转置逆矩阵矩阵方程第三章矩阵的初等变换与线性方程组矩阵的行最简形矩阵的秩齐次线性方程组基础解系非齐次线性方程组求通解用Solve求线性方程组的解第四章向量组的线性相关性向量的线性表示极大无关组第五章相似矩阵及二次型正交矩阵矩阵的特征值矩阵的特征向量矩阵的对角化二次型的标准化补充:向量参考文献前言Maple是著名的数学软件,具有强大的的数学运算能力和绘图功能。
本文档用Maple来进行线性代数中的各种运算。
本文档中所有的例子都是用Maple 8编程和计算的。
如有对本文档中的内容任何问题,请发邮件与作者讨论。
邮箱:xuxzmail@2012-5-11返回目录第一章 行列式行列式 det(A)例 计算三阶行列式124221342A -=---(同济5版,3页)输入:with(linalg):A:=matrix([[1,2,-4],[-2,2,1],[-3,4,-2]]);detA:=det(A);输出: := A ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥12-4-221-34-2:= detA -14例 计算四阶行列式3112513420111533A ---=---(同济5版,12页) 输入:with(linalg):A:=matrix([[3,1,-1,2],[-5,1,3,-4],[2,0,1,-1],[1,-5,3,-3]]);detA:=det(A);输出: := A ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥31-12-513-4201-11-53-3,:= d e t A 40例 求解方程211123049x x =(同济5版,3页)输入:with(linalg):A:=array([[1,1,1],[2,3,x],[4,9,x^2]]);solve(det(A)=0,x);输出:,32例 计算行列式2324323631063a b c da ab a bc a b cd a a b a b c a b c da ab a bc a b c d++++++++++++++++++(同济5版,13页)输入:with(linalg):A:=array([[a,b,c,d],[a,a+b,a+b+c,a+b+c+d],[a,2*a+b,3*a+2*b+c,4*a+3*b+2*c+d],[a,3*a+b,6*a+3*b+c,10*a+6*b+3*c+d]]); DetA:=det(A);输出: := A ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥a b c d a + a b + + a b c + + + a b c d a + 2a b + + 3a 2b c + + + 4a 3b 2c d a + 3a b + + 6a 3b c + + + 10a 6b 3c d ,,:= DetA a 4例 计算行列式000000000000000000000000a b a b a bc dc d c d (同济5版,15页)输入:with(linalg):A:=array([[a,0,0,0,0,b],[0,a,0,0,b,0],[0,0,a,b,0,0],[0,0,c,d,0,0],[0,c,0,0,d,0],[c,0,0,0,0,d]]);DetA:=det(A);输出: := A ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥a 0000b 0a 00b 000a b 0000c d 000c 00d 0c 0000d ,:= DetA () - d a b c 3 返回目录克拉默法则例 用克拉默法则解线性方程组:123412423412342583692254760x x x x x x x x x x x x x x +-+=⎧⎪--=⎪⎨-+=-⎪⎪+-+=⎩(同济5版,22页) 输入:with(linalg):A:=array([[2,1,-5,1],[1,-3,0,-6],[0,2,-1,2],[1,4,-7,6]]); b:=array([8,9,-5,0]);A1:=augment(b,col(A,2),col(A,3),col(A,4));A2:=augment(col(A,1),b,col(A,3),col(A,4));A3:=augment(col(A,1),col(A,2),b,col(A,4));A4:=augment(col(A,1),col(A,2),col(A,3),b);x1:=det(A1)/det(A);x2:=det(A2)/det(A);x3:=det(A3)/det(A);x4:=det(A4)/det(A);输出: := A ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥21-511-30-602-1214-76 := b [],,,89-50:= A1⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥81-519-30-6-52-1204-76 := A2⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥28-51190-60-5-1210-76:= A3⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥21811-39-602-521406 :=A4⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥21-581-30902-1-514-70方程组的解: := x13 := x2-4 := x3-1 := x41返回目录第二章 矩阵及其运算矩阵的线性运算 matadd(A,B) 或 evalm(A+B); k*B例 设352078A -⎛⎫= ⎪-⎝⎭,3912418B -⎛⎫= ⎪-⎝⎭,求A B +和43A B +输入:with(linalg):A:=array([[2,5,-2],[0,7,-8]]);B:=array([[-3,9,12],[-4,1,8]]);matadd(A,B);evalm(A+B);matadd(4*A,3*B);evalm(4*A+3*B);输出: := A ⎡⎣⎢⎢⎤⎦⎥⎥25-207-8 := B ⎡⎣⎢⎢⎤⎦⎥⎥-3912-418⎡⎣⎢⎢⎤⎦⎥⎥-11410-480 ⎡⎣⎢⎢⎤⎦⎥⎥-11410-480 ⎡⎣⎢⎢⎤⎦⎥⎥-14728-1231-8 ⎡⎣⎢⎢⎤⎦⎥⎥-14728-1231-8 返回目录矩阵的乘法 multiply(A,B) 或 evalm(A&*B)例 设10312102A -⎛⎫= ⎪⎝⎭,410113201134B ⎛⎫⎪- ⎪= ⎪ ⎪⎝⎭,求AB输入:with(linalg):A:=array([[1,0,3,-1],[2,1,0,2]]);B:=array([[4,1,0],[-1,1,3],[2,0,1],[1,3,4]]);AB:=multiply(A,B);AB:=evalm(A&*B);结果: := A ⎡⎣⎢⎢⎤⎦⎥⎥103-12102, := B ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥410-113201134,:= AB ⎡⎣⎢⎢⎤⎦⎥⎥9-2-19911 := AB ⎡⎣⎢⎢⎤⎦⎥⎥9-2-19911例 设2412A -⎛⎫= ⎪-⎝⎭,2436B ⎛⎫= ⎪--⎝⎭,求AB 和BA (同济5版,35页)输入:with(linalg):A:=array([[-2,4],[1,-2]]);B:=array([[2,4],[-3,-6]]);AB:=multiply(A,B);BA:=multiply(B,A);结果: := A ⎡⎣⎢⎢⎤⎦⎥⎥-241-2, := B ⎡⎣⎢⎢⎤⎦⎥⎥24-3-6, := AB ⎡⎣⎢⎢⎤⎦⎥⎥-16-32816, := BA ⎡⎣⎢⎢⎤⎦⎥⎥0000例 证明:cos sin cos sin sin cos sin cos n t t nt nt tt nt nt --⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭(同济5版,38页) 解 取n=7输入 with(linalg):A:=array([[cos(t),-sin(t)],[sin(t),cos(t)]]);evalm(A^7);map(combine,%);结果: := A ⎡⎣⎢⎢⎤⎦⎥⎥()cos t -()sin t ()sin t ()cos t()- () - ()cos t 2()sin t 224()cos t 2()sin t 2[()- () - ()cos t 2()sin t 2()cos t 2()cos t ()sin t 24() - ()cos t 2()sin t 2()cos t ()sin t () + 2()cos t 2()sin t () - ()cos t 2()sin t 2()sin t - ,() - () - ()cos t 2()sin t 224()cos t 2()sin t 2()- - () - ()cos t 2()sin t 2()sin t 2()cos t 2()sin t 4() - ()cos t 2()sin t 2()cos t ()sin t () - () - ()cos t 2()sin t 2()cos t 2()cos t ()sin t 2 - ]4() - ()cos t 2()sin t 2()cos t ()sin t () - () - ()cos t 2()sin t 2()cos t 2()cos t ()sin t 2 + [()- () - ()cos t 2()sin t 224()cos t 2()sin t 2() + 2()cos t 2()sin t () - ()cos t 2()sin t 2()sin t ,4() - ()cos t 2()sin t 2()cos t ()sin t ()- - () - ()cos t 2()sin t 2()sin t 2()cos t 2()sin t + ()- () - ()cos t 2()sin t 224()cos t 2()sin t 2() - () - ()cos t 2()sin t 2()cos t 2()cos t ()sin t 2]化简的结果:⎡⎣⎢⎢⎤⎦⎥⎥()cos 7t -()sin 7t ()sin 7t ()cos 7t返回目录矩阵的转置 transpose(A)例 设120311A ⎛⎫= ⎪-⎝⎭,求其转置矩阵T A (同济5版,39页) 输入:with(linalg):A:=array([[1,2,0],[3,-1,1]]);B:=transpose(A);结果:原矩阵: := A ⎡⎣⎢⎢⎤⎦⎥⎥1203-11 转置矩阵: := B ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥132-101例 设201132A -⎛⎫= ⎪⎝⎭,171423201B -⎛⎫⎪= ⎪ ⎪⎝⎭,求()T AB ,并验证:()T T TAB B A= (同济5版,39页)输入with(linalg):A:=array([[2,0,-1],[1,3,2]]);B:=array([[1,7,-1],[4,2,3],[2,0,1]]); transpose(multiply(A,B));multiply(transpose(B),transpose(A)); 结果: := A ⎡⎣⎢⎢⎤⎦⎥⎥20-1132, := B ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥17-1423201⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥0171413-310这是()T AB ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥0171413-310这是T TB A 可见:()T T T AB B A =返回目录逆矩阵 inverse(A) 或 evalm(A^(-1))例 设123221343A ⎛⎫⎪= ⎪ ⎪⎝⎭,求其逆矩阵1A -,并验证1AA E -=(单位矩阵) (同济5版,44页)输入:with(linalg):A:=array([[1,2,3],[2,2,1],[3,4,3]]);B:=inverse(A); C:=evalm(A^(-1)); AB:=multiply(A,B); CA:=multiply(C,A);结果: := A ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥123221343, 逆矩阵: := B ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥13-2-3-3511-1 := C ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥13-2-3-3511-1验证1AA E -=: := AB ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥10001001,:= CA ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥100010001 返回目录矩阵方程例 设123221343A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,2153B ⎛⎫= ⎪⎝⎭,132031C ⎛⎫⎪= ⎪ ⎪⎝⎭,且AXB C =,求矩阵X (同济5版,45页)解 11AXB C X A CB --=⇒=输入with(linalg):A:=array([[1,2,3],[2,2,1],[3,4,3]]); B:=array([[2,1],[5,3]]);C:=array([[1,3],[2,0],[3,1]]);X:=multiply(inverse(A),C,inverse(B));结果: := A ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥123221343,:= B ⎡⎣⎢⎢⎤⎦⎥⎥2153, := C ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥132031, := X ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥-2110-4-104例 设213122132A -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭,112025B -⎛⎫ ⎪= ⎪ ⎪-⎝⎭,求解矩阵方程AX B =(同济5版,65页) 解 1AX B X A B -=⇒=输入with(linalg):A:=array([[2,1,-3],[1,2,-2],[-1,3,2]]); B:=array([[1,-1],[2,0],[-2,5]]); X:=multiply(inverse(A),B);结果: := A ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥21-312-2-132, := B ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥1-120-25, := X ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥-4201-32 返回目录第三章 矩阵的初等变换与线性方程组矩阵的行最简形和标准型 阶梯形: gausselim(A)行最简形:gaussjord(A) 或 rref(A),例 设21112112144622436979B --⎛⎫⎪-⎪= ⎪--⎪-⎝⎭,求B 的阶梯形和秩(同济5版,59页) 输入:with(linalg):B:=array([[2,-1,-1,1,2],[1,1,-2,1,4],[4,-6,2,-2,4],[3,6,-9,7,9]]);GL:=gausselim(B);输出: := B ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥2-1-11211-2144-62-2436-979 阶梯形: := GL ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥2-1-1120-44-40000-1300000 阶梯形有一行全为零,矩阵的秩为3。
Maple13+入门教程

=
菜单有数百个命令,但只是跟对应表达式
相关的命令才会显示。
例:将鼠标放在最后的输出结果上,右击 鼠标右键。弹出的右键菜单将显示跟该表 达式相关的操作。为了求表达式的积分: Integrate x
=
integrate w.r.t. x
例:绘制积分结果的图形,在结果表达式 上鼠标右击,在弹出的右键菜单中选择: Plots > 2-D Plot.
(8.3)
例:输入一个几何,并赋值给变量名 .
常规操作 例:使用符号识别面板找到几何交集符
号,求
步骤
结果
定义方程
在Maple中,使用 = (等于号)定义等式。
例:求方程 "
"中x的
值,使用右键菜单 Solve > Solve for a
Variable.
求精确解
默认情况下,Maple显示方程的精确解。
例: 求方程 "
"中x的
值,使用 右键菜单Solve > Solve.
求数值解
如果您想求数值解,需要直接使用数值求
(6.6)
过程(程序) 一个函数实际上就是特殊的过程。
例: 右侧是一个简单的过程。 关于Maple 程序设计更多的内容见用户手册第八章。
提 示 :程序语句较长时,使用【S h i f t】+ 【ENTER】 在新的一行继续输入语句。
(6.7)
5
(6.8)
5 方程求解
Maple 能够求方程和不等式中未知量的值。
提示: 还有一个比较明显的提示是,当在文本(text)模式时,光标显示为竖线,而当在数 学(math)格式时,光标显示为斜线。
练习: 回到最后的练习,在多项式中添加文本说明,改变原多项式并更新计算结果。
maple入门

数的进制转换
convert 函数 binary二进制 decimal 十进制 octal 八进制 hex十六进制
小数划为分数运算
convert(x,rational) 将实数(有理数)x转换为 精确分数 convert(x,rational,n) 将实数(无理数)x转换 为分子与分母非零数码的个数和为n的分数
Maple入门 Maple入门
1.Maple概述 Maple概述
什么是Maple, 怎么学习Maple? Maple软件是加拿大Waterloo大学在1980年开始 开发,到现在最新的版本是Maple11, Maple具有强 大的数值计算能力,图形处理能力,特别是符号 计算能力. 常用的数学软件除Maple外,有Matlab等, 统计 软件: SAS,SPSS,运筹学软件:Lingo, WINQSB.
ifactor 求因子 iquo 求商 iquo(a,b,'r') irem 余数 irem(a,b,'q') isqrt 近似的平方跟整数
sqrt(x) 平方根函数 exp(x), ln(x) 指数函数和自然对数函数 log[b](x) 以b为底的对数函数 Abs(x) 绝对值函数 round(x) 最接近x的整数rand ()12位的随机数 Max(a,b,c,…),min(a,b,c,…) a, b, c, … 中的最 大(小)数 floor(x) 不大于x的最大整数 ceil(x) 不小于x的最小整数 trunc(x) x靠近0的整数部分 frac(x) x的分数部分(=x-trunc(x))signum(x)符号函数
1.5.1 fprintf
fprintf函数是用来输出到文件中,在使用该函数前,先用 fopen打开一个文件,再使用fprintf函数输出到fopen打开的文件 中,最后用fclose关闭文件. 格式:fopen(filename,mode); 其中,mode分为:WRITE和APPEND fprintf(fd,format,vars); 其中fd,为fopen打开的文件,format输出的格式,vars为变量组 fclose(fd); 演示
Maple基础教程

目录第二章MAPLE基础 (1)2.1与M APLE对话 (1)2.2使用命令和函数包 (18)2.3微积分 (23)2.4线性代数 (28)2.5微分方程 (35)2.6优化 (45)2.7动态系统 (53)2.8基础编程知识 (58)2.9M APLE使用中常犯的错误 (78)第二章Maple基础Maple是目前应用非常广泛的科学计算软件之一,具有非常强大的符号计算和数值计算功能。
Maple 提供智能界面求解复杂数学问题和创建技术文件,用户可在易于使用的智能文件环境中完成科学计算、建模仿真、可视化、程序设计、技术文件生成、报告演示等,从简单的数字计算到高度复杂的系统,满足各个层次用户的需要。
与传统工程软件不同,甚至有别于旧版本的Maple,新版本Maple为工程师提供了大量的专业计算功能,庞大的数学求解器可用于各种工程领域,如微分方程、矩阵、各种变换包括FFT、统计、小波、等等,超过5000个计算命令让用户通常只需要一个函数就可以完成复杂的分析任务。
本章主要介绍Maple的基本功能,包括:数值和符号计算计算、求解方程、微积分计算、向量及矩阵计算、微分方程求解等。
Maple是一个全面的系统,提供多种方式完成同一个任务。
在本章中,我们将通过简单、易于重复的方式求解常见的问题,但它不是唯一的操作方式。
当用户熟悉本章中的各种操作方式后,用户可以通过帮助系统了解如何使用相似的技术完成各种任务。
2.1 与Maple对话2.1.1 Maple环境Maple的用户界面是一个典型的Windows或Mac风格的操作环境。
工作环境界面如图2-1所示。
图2-1:Maple工作界面在图2-1的工作界面中,窗体的主要部分包括:●主文档,即主工作区。
事实上,用户大可以把它想象成包含有各种数学和绘图工具的Microsoft Word。
●面板区。
汇集了数学工具和特殊的数学符号,用户可以将它们直接拖拽到工作区中使用。
面板区中最重要的面板当属Expressions,Matrix,Common Symbols和Greek。
Maple13数学实验初级篇

>restart; #restart - clear internal memory > f:=int(exp(x^3),x=0..1); evalf(f); evalf(cos(1)+sin(1)I); >Product(k^3,k=1..4): value(%); #value - evaluate inert functions
SDAU
2.2.2 函数值运算
定义表达式 f:=数 或 表达式; #后赋值将替换以前的赋值, 加单引号表示符号变量 >f:=x^2; eval(f,x=3); #定义表达式并计算器在x=3处的值 右键点击输入f 后的蓝色结果 x2 可以从事多种运算! 定义函数 f:=x->x的表达式; >f:=x->x^2; f(3); #定义函数f(x)并计算其在x=3处的值 >G:=(a,b)->a^2-b^3; G(3,2); #定义多变量函数并求函数值 右键点击输入f 后的蓝色结果 x→x2 可以从事多种运算! >y:=x->piecewise(x<=1,sin(Pi*x/2),x>1,log(x)); # 定义分段函 数 y= log x (x>1), sin(x/2) (x≤1) >y:=s^2-5*s+3; z:=s^2-5*t+3; 表达式运算 >y*z+3;
常用数学常数
数学常数 I Pi False, true Catalan Infinity Fall
Gamma
意义 虚数单位 圆周率 逻辑表达式的值 Catalan常数,值为0.9159… 无穷大 表示不确定的数或操作失败
Euler 常数,值为0.577215…
MAPLE讲稿

快 速 进 入
Maple
Jan,8, 2004
毕业指导培训
M1-9
第一讲 MAPLE简介
Maple
小结:
本章仅就Maple 的基本功能作一个简短的解说, Maple的操 作界面尚有许多功能,例如,可以加入试算表,可以将文件存成 HTML格式等.限于时间的关系,本次培训不一一介绍.如果需要更 详细的说明,你可以从 Maple在线帮助系统里的Worksheet interface中查询. 当然,你也可以到 Maple 加拿大总公司的网站逛逛,收集最 新的资料,其网址为:
快 速 进 入
Maple
Jan,8, 2004
毕业指导培训
M1-10
第二讲 数值计算
2.1Maple 简介
数值运算可概括地分为精确与近似值运算.
2.1.1数值运算 一. 精确运算
通常我们把整数称为精确数,因为它不带任何小数.其它诸如3/4, sin2等数也叫精 确数.数值运算的结果为一个精确数,则称此运算为精确运算. > 1+3/7; 的结果为10/7,不是将它化为小数(1.42857142…)
Jan,8, 2004
快 速 进 入
Maple
毕业指导培训
M1-11
第二讲 数值计算
2.2 Maple 的基本运算
基本指令(一)
factorial(n)或n! irem(m,n) iquo(m,n)
基本指令(二)
计算n的阶乘 计算m/n的整数余数,其中m,n必须为整数 计算m/n的整数商,其中m,n必须为整数
快 速 进 入
Maple
Jan,8, 2004
毕业指导培训
M1-12
n e
第二讲 数值计算
