周益春-材料固体力学习题解答习题二
周益春-材料固体力学习题解答习题三备课讲稿

--第三章 弹性本构关系和弹性问题的求解习题习题1、试利用各向异性理想弹性体的广义虎克定律导出:在什么条件下,理想弹性体中的主应力方向和主应变方向相重合?解:各向异性理想弹性体的广义虎克定律为:zxyz xy zz yy xx zx zx yz xy zz yy xx yz zx yz xy zz yy xx xy zx yz xy zz yy xx zz zx yz xy zz yy xx yy zx yz xy zz yy xx xx c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c γγγεεετγγγεεετγγγεεετγγγεεεσγγγεεεσγγγεεεσ666564636261565554535251464544434241363534333231262524232221161514131211+++++=+++++=+++++=+++++=+++++=+++++= (a )当0===zx yz xy τττ时,三个互相垂直的应力方向为主应力方向。
当0===zx yz xy γγγ时,三个互相垂直的应变方向为主应变方向。
在主应变方向上,剪应力分量为:zzyy xx zx zz yy xx yz zzyy xx xy c c c c c c c c c εεετεεετεεετ636261535251434241++=++=++= (b ) 若使0===zx yz xy τττ,则式中xx ε,yy ε,zz ε具有非零解的条件为0636261535251434241=c c c c c c c c c (c ) 上式即为x ,y ,z 轴同时为应力主轴和应变主轴的条件。
如果材料性能对称于一个平面,如Oxy 平面,则04645363526251615========c c c c c c c c ,而且ji ij c c =,此时(c )式恒等于零。
周益春-材料固体力学习题解答6-1
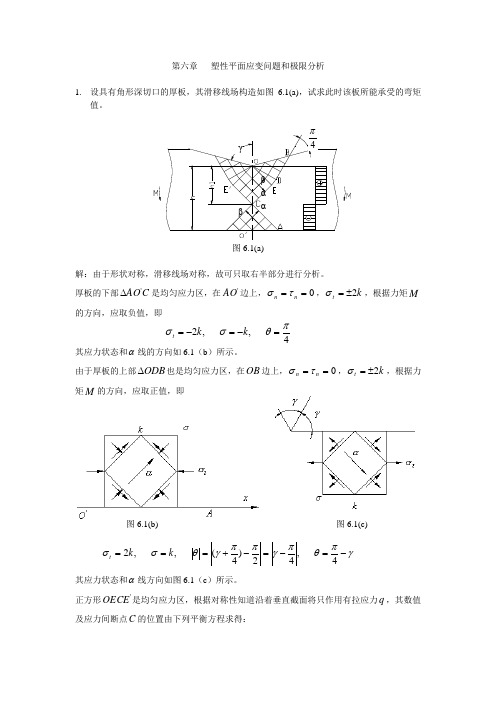
第六章 塑性平面应变问题和极限分析1. 设具有角形深切口的厚板,其滑移线场构造如图6.1(a),试求此时该板所能承受的弯矩值。
的方向,应取负值,即4,,2πθσσ=-=-=k k t其应力状态和α线的方向如6.1(b )所示。
由于厚板的上部ODB ∆也是均匀应力区,在OB 边上,0==n n τσ,k t 2±=σ,根据力矩M 的方向,应取正值,即γπθπγππγθσσ-=-=-+===4,42)4(,,2k k t其应力状态和α线方向如图6.1(c )所示。
正方形'OECE 是均匀应力区,根据对称性知道沿着垂直截面将只作用有拉应力q ,其数值及应力间断点C 的位置由下列平衡方程求得:图6.1(c)图6.1(b)⎪⎭⎪⎬⎫=---=--0)(210)(2212111h h k qh M h h k qh 由此得出Mkh kMq khMh h -==-212,由于CEDB 是同一根β线,故B BC C k k θσθσ22+=+)21()4(2)4(2γππγπσ-+=---+=k k k k C取OC 边上的单元体进行分析,如图6.1(d )所示得:4,0,πθτσ-===n n qk q k t t n 2,2-==-σσσ)2(21)(21k q q t n -+=+=σσσk q k C -=-+=)21(γπσMkh kMk q -=-+=22)21(γπγπγπ24)22(2-+-+=kh M 令2021kh M =则可得γπγπ24210-+-+=M M 图6.1(d )2. 设两边有对称角形深切口的厚板,角形深切口处的高度为h ,试求在极限状态时,该板所能承受的弯矩值。
解:此题滑移线场与上一题(a )图中上部的滑移线场一样,因此在极限状态下应力为)2()21(22=--+=hq M k q γπ故由此应力所承受的弯矩为22)21(2141h k qh M γπ-+==令2021kh M =则得γπ-+=210M M3.图6.2解:作滑移线场如图6.3(b)所示,由于对称,只考虑板条的一半。
材料固体力学答案1-6章

第一章习题1 证明δ-e 恒等式jtks kt js ist ijke e δδδδ-=[证明]()()()jtks kt js ktjs jtks jtks ktjs jtks kt js itjs jtis ki it ks ktis ji jtks kt js ii ktks ki jtjsjiitis ii ist ijk e e δδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδ-=-++--=-+---==33习题2 证明若jiij ji ijb b a a -==;,则0=ij ijb a[证明]jiij jiijbb aa-==; jiji ij ij b a b a -=∴,0=+=+∴pq pq ij ij ji ji ij ijb a b a b a b a又因为所有的指标都是哑指标,ijij pq pqb a b a =,所以02=aijbij,即0=ij ijb a习题3 已知某一点的应力分量xxσ,yyσ,zzσ,xyσ不为零,而0==yzxzσσ,试求过该点和z 轴,与x 轴夹角为α的面上的正应力和剪应力。
[解] 如图1.1,过该点和z 轴,与x 轴夹角为α的面的法线,其与x 轴,y 轴和z 轴的方向余弦分别为cos α,sin α,0,则由斜面应力公式的分量表达式,iji jσνσν=)(,可求得该面上的应力为ασασσνσνsin cos 11)(xyxxj j +== ασασσνσνsin cos 22)(yyyxjj +== 033==j j v σνσ)(由斜面正应力表达式ji ij nννσσ=,可求得正应力为ασαασασσ22sinsin cos 2cosyyxyxxn++=剪应力为ασασσστ2cos 2sin )(2122)()(xyxx yynn n +-=-=-=σσσn习题4 如已知物体的表面由0),,(=z y x f 确定,沿物体表面作用着与其外法线方向一致分布载荷()z y x p ,,。
周益春-材料固体力学习题解答习题三

--第三章 弹性本构关系和弹性问题的求解习题习题1、试利用各向异性理想弹性体的广义虎克定律导出:在什么条件下,理想弹性体中的主应力方向和主应变方向相重合?解:各向异性理想弹性体的广义虎克定律为:zxyz xy zz yy xx zx zx yz xy zz yy xx yz zx yz xy zz yy xx xy zx yz xy zz yy xx zz zx yz xy zz yy xx yy zx yz xy zz yy xx xx c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c γγγεεετγγγεεετγγγεεετγγγεεεσγγγεεεσγγγεεεσ666564636261565554535251464544434241363534333231262524232221161514131211+++++=+++++=+++++=+++++=+++++=+++++= (a )当0===zx yz xy τττ时,三个互相垂直的应力方向为主应力方向。
当0===zx yz xy γγγ时,三个互相垂直的应变方向为主应变方向。
在主应变方向上,剪应力分量为:zzyy xx zx zz yy xx yz zzyy xx xy c c c c c c c c c εεετεεετεεετ636261535251434241++=++=++= (b ) 若使0===zx yz xy τττ,则式中xx ε,yy ε,zz ε具有非零解的条件为0636261535251434241=c c c c c c c c c (c ) 上式即为x ,y ,z 轴同时为应力主轴和应变主轴的条件。
如果材料性能对称于一个平面,如Oxy 平面,则04645363526251615========c c c c c c c c ,而且ji ij c c =,此时(c )式恒等于零。
周益春-材料固体力学习题解答7
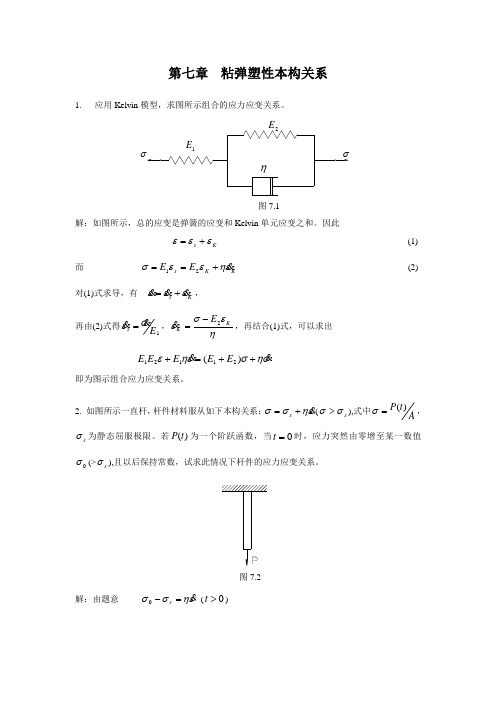
第七章 粘弹塑性本构关系1. 应用Kelvin 模型,求图所示组合的应力应变关系。
解:如图所示,总的应变是弹簧的应变和Kelvin 单元应变之和。
因此K s εεε+= (1)而 K K s E E εηεεσ +==21 (2) 对(1)式求导,有 K s εεε +=, 再由(2)式得1E s σε=,ηεσεKK E 2-= ,再结合(1)式,可以求出 σησεηε ++=+)(21121E E E E E 即为图示组合应力应变关系。
2. 如图所示一直杆,杆件材料服从如下本构关系:εησσ +=s (s σσ>),式中At P )(=σ,s σ为静态屈服极限。
若)(t P 为一个阶跃函数,当0=t 时,应力突然由零增至某一数值0σ(>s σ),且以后保持常数,试求此情况下杆件的应力应变关系。
解:由题意 εησσ =-s 0 (0>t) 图7.1图7.2即 )(10s σσηε-=对上式积分可得 C t s +-=)(10σσηε其中C 为积分常数。
若0=t 时已有应变0ε存在,则由上式可得0ε=C 。
从而有00)(1εσσηε+-=t s3. 假定介质的流动是缓慢的轴对称的定常流,即介质在管中没有转动,讨论粘塑性材料在圆管中的流动。
解:如图所示的圆柱坐标系z r ,,ϕ中,其径向和环向速度为零,即0==ϕυυr于是应变率分量为0====z r r ϕϕϕεεεεrzzrz zz ∂∂=∂∂=υευε, 如果我们假定材料是不可压缩的,则有0=z ε,从而有)(r z z υυ=。
若进一步假定应力分量可分解为塑性和粘性两部分,其塑性部分服从与Mises 屈服条件相关的流动法则,而粘性部分服从牛顿线性粘性定律,则不难得到0===z r σσσϕ0==z r ϕϕττ图7.3drd zs rz υηττ+-= (1) s τ为剪切屈服极限很显然,当,s rz ττ≥且0≤drd zυ时才有意义。
周益春-材料固体力学习题解答习题十.docx

第十章热应力习题及解习题1、如图10-1所不,将一圆锥体固定在两壁间,计算温度由77升高到门时所产生的压缩 热应力。
解:设圆锥体棒温度升高为0 = G 其线胀系数为&。
在自由膨胀时,其仲长为o 若假设壁给予的压缩力为P,而棒应缩短o 各截面的粗细不同,因此各截面产生的热应力 不同。
与左端距离x 的截面AB 处的直径为dx ,dx = d l +(d 2-d l )x/l 。
设AB 截面的面积为S x ,于是该截面上的压缩热应力为-4P故AB 处的应变为与AB 距离dx 微段的缩短了 g/x,因此整个棒缩短那么P = jcEoalyd^ I ,于是热应力为-Ead.d.O6 = -----------£ +仏F1I最大热应力发生在截面积最小的左端,为Umax =~Ed 2a0!=习题2、如图10-2所不,两根材料和长度都不相同的平行棒,它们的一端各自被固定,而另一 端连接在刚体板上可以一起轴向活动,通过弹簧受到另一壁的反作用,设两棒分别从最初的无应力-4P4Pdx4PIJiEd'd ?=ccOl状态下温度升高了「和T2,试计算两棒中的热应力。
解:假定N >几。
2 > a,,贝U棒1的自山膨胀量为厶,而棒2的自山膨胀量为a2T2L2。
棒2自由膨胀时伸长量大,故棒2除自由膨胀外,受到压缩而缩短,因压应力的缩短量为£2L2 = cr?厶2 / E?,其最终伸长量为a2T2L2 + cr?厶2 /丘2。
而棒1除自山膨胀外,还因相应拉应力的伸长刍厶=5厶/耳,其最终伸长量为+ b]厶 / E]其中bj, O'?中包含了应力符号。
因右端连接在冈!I体板上一起轴向活动,两棒的总伸长量应相等,即务片厶 + CF]厶 / 耳=a2T2L2 + cr2L2 / E2 = -Z(设弹簧的弹性常数为& ,则其压缩力为F = k s l ,故有CF]S] + c2S2 = P(b) 可求得S、E, (洛厶5並卜也严]V 厶 + S Q E Q L I砧S'E.—害吕-(也乙厶2 — ap]厶)-厶26 _—]_|_ V厶2 _(_ S]E]厶2S°E° S2E2L]讨论:⑴若k s =0,弹簧非常柔软的情况下,刚体板仅起连接作用,此时a = 一耳(&1冲厶一色笃厶2)/厶1 + S]E]厶2 / S Q E Q L、再假设厶二厶2,卩1 =笃=厂,贝I」_ _-EJ G1 —也)O 1 —O1 + S^/S2E2(2)若& = 8,弹簧不能伸缩,即为全约束下(即为上题情形),此时<7,=―耳內”对于CT?,以上讨论完全类似。
周益春-材料固体力学课后习题解答
第一章习题1 证明δ-e 恒等式jt ks kt js ist ijk e e δδδδ-= [证明] 习题20=ij ij b a[证明]ji ij ji ij b b a a -==; ji ji ij ij b a b a -=∴,0=+=+∴pq pq ij ij ji ji ij ij b a b a b a b a 又因为所有的指标都是哑指标,ij ij pq pq b a b a =,所以02=aijbij ,即0=ij ij b a习题3 已知某一点的应力分量xx σ,yy σ,zz σ,xy σ不为零,而0==yz xz σσ,试求过该点和z 轴,与x 轴夹角为α的面上的正应力和剪应力。
[解] 如图1.1,过该点和z 轴,与x 轴夹角为α的面的法线,其与x 轴,y 轴和z 轴的方向余弦分别为cos α,sin α,0,则由斜面应力公式的分量表达式,ij i j σνσν=)(,可求得该面上的应力为 由斜面正应力表达式j i ij n ννσσ=,可求得正应力为ασαασασσ22sin sin cos 2cos yy xy xx n ++=剪应力为习题4 如已知物体的表面由0),,(=z y x f 确定,沿物体表面作用着与其外法线方向一致分布载荷()z y x p ,,。
试写出其边界条件。
[解] 物体表面外表面法线的方向余弦为 带入应力边界条件,()3,2,1,,==j i n T j ij i σ,得习题5 已知某点以直角坐标表示的应力分量为xx σ,yy σ,zz σ,xy σ,xz σ,yz σ,试求该点以柱坐标表示的应力分量。
[解] 如图1.2,两个坐标轴之间的方向余弦如下表所示:由应力分量转换公式''''jn i m ij n m ββσσ=,求得 利用三角公式可将上面的式子改写为 习题6 一点的应力状态由应力张量()⎪⎪⎪⎭⎫⎝⎛=σσσσσσσσσσc b c a b a ij 给定,式中,a ,b ,c 为常数,σ是某应力值,求常数a ,b ,c ,以使八面体面)e e e (n 321++=31上的应力张量为零[解] 由斜面应力公式的分量表达式,ij i j σνσν=)(,知八面体面上应力张量为零需满足如下方程组:解得21-===c b a 习题7 证明(1)应力的三个主方向互相垂直;(2)三个主应力1σ,2σ,3σ必为实根 [证明](1)设任意两个不同的主应力为k σ、l σ,对应的主方向为k n 、l n 。
周益春-材料固体力学习题解答5-1
由此得
p2
3(
r0 t0
)2
6(
r0 t0
)
4
4
2 s
p
2 s
3( r0 )2 6( r0 ) 4
t0
t0
由于式(b)成立,故将式(a)中的 和 r 的表达式代入 Tresca 屈服条件,即
r s
则得
p s 1 r0 t0
3. 求出 Tresca 屈服准则的等向强化模型和随动强化模型的屈服函数,并在 平面上进行讨
解: 根据薄壁圆管的平衡条件,有
pr0 t0
,
z
pr0 2t0
,
r p
(a)
由式(a)可见:
z r
(b)
将式(a)代入 Mises 屈服条件
( r )2 (r z )2 ( z )2 2 s2
则得
3 ( pr0 )2 2 t0
2p2
3p
pr0 t0
2
2 s
将上式整理后,得
论。 解:(1) 在 Tresca 屈服准则下,等向强化模型可以表示为:
s 0
式中 F( dW p ) H ( d p ) , max 1 2 , 2 3 , 3 1
由上式可知: s ,即为所求屈服函数 。
很明显,在强化过程中,随着 的增加,产生屈服所需的最大有效应力 相应增大, 对应于 平面上的正六边形的面积也将增大。
第五章
屈服准则和塑性本构关系
1. 如图 5.1 所示的薄壁圆管受拉力 p 和扭矩 M 的作用,试写出此情况下的 Mises 条件和
Tresca 条件。
τ
σ
σ
τ
图 5.1
解:如图所示:
1
周益春-材料固体力学课后习题解答
第一章习题1 证明δ-e 恒等式jt ks kt js ist ijk e e δδδδ-= [证明] 习题20=ij ij b a[证明]ji ij ji ij b b a a -==; ji ji ij ij b a b a -=∴,0=+=+∴pq pq ij ij ji ji ij ij b a b a b a b a 又因为所有的指标都是哑指标,ij ij pq pq b a b a =,所以02=aijbij ,即0=ij ij b a习题3 已知某一点的应力分量xx σ,yy σ,zz σ,xy σ不为零,而0==yz xz σσ,试求过该点和z 轴,与x 轴夹角为α的面上的正应力和剪应力。
[解] 如图1.1,过该点和z 轴,与x 轴夹角为α的面的法线,其与x 轴,y 轴和z 轴的方向余弦分别为cos α,sin α,0,则由斜面应力公式的分量表达式,ij i j σνσν=)(,可求得该面上的应力为 由斜面正应力表达式j i ij n ννσσ=,可求得正应力为ασαασασσ22sin sin cos 2cos yy xy xx n ++=剪应力为习题4 如已知物体的表面由0),,(=z y x f 确定,沿物体表面作用着与其外法线方向一致分布载荷()z y x p ,,。
试写出其边界条件。
[解] 物体表面外表面法线的方向余弦为 带入应力边界条件,()3,2,1,,==j i n T j ij i σ,得习题5 已知某点以直角坐标表示的应力分量为xx σ,yy σ,zz σ,xy σ,xz σ,yz σ,试求该点以柱坐标表示的应力分量。
[解] 如图1.2,两个坐标轴之间的方向余弦如下表所示:由应力分量转换公式''''jn i m ij n m ββσσ=,求得 利用三角公式可将上面的式子改写为 习题6 一点的应力状态由应力量()⎪⎪⎪⎭⎫⎝⎛=σσσσσσσσσσc b c a b a ij 给定,式中,a ,b ,c 为常数,σ是某应力值,求常数a ,b ,c ,以使八面体面)e e e (n 321++=31上的应力量为零[解] 由斜面应力公式的分量表达式,ij i j σνσν=)(,知八面体面上应力量为零需满足如下方程组: 解得21-===c b a 习题7 证明(1)应力的三个主方向互相垂直;(2)三个主应力1σ,2σ,3σ必为实根 [证明](1)设任意两个不同的主应力为k σ、l σ,对应的主方向为k n 、l n 。
完整版材料力学性能课后习题答案整理
完整版材料⼒学性能课后习题答案整理材料⼒学性能课后习题答案第⼀章单向静拉伸⼒学性能1、解释下列名词。
1弹性⽐功:⾦属材料吸收弹性变形功的能⼒,⼀般⽤⾦属开始塑性变形前单位体积吸收的最⼤弹性变形功表⽰。
2.滞弹性:⾦属材料在弹性范围内快速加载或卸载后,随时间延长产⽣附加弹性应变的现象称为滞弹性,也就是应变落后于应⼒的现象。
3.循环韧性:⾦属材料在交变载荷下吸收不可逆变形功的能⼒称为循环韧性。
4.包申格效应:⾦属材料经过预先加载产⽣少量塑性变形,卸载后再同向加载,规定残余伸长应⼒增加;反向加载,规定残余伸长应⼒降低的现象。
5.解理刻⾯:这种⼤致以晶粒⼤⼩为单位的解理⾯称为解理刻⾯。
6.塑性:⾦属材料断裂前发⽣不可逆永久(塑性)变形的能⼒。
脆性:指⾦属材料受⼒时没有发⽣塑性变形⽽直接断裂的能⼒韧性:指⾦属材料断裂前吸收塑性变形功和断裂功的能⼒。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成⼀个⾼度为b的台阶。
8.河流花样:解理台阶沿裂纹前端滑动⽽相互汇合,同号台阶相互汇合长⼤,当汇合台阶⾼度⾜够⼤时,便成为河流花样。
是解理台阶的⼀种标志。
9.解理⾯:是⾦属材料在⼀定条件下,当外加正应⼒达到⼀定数值后,以极快速率沿⼀定晶体学平⾯产⽣的穿晶断裂,因与⼤理⽯断裂类似,故称此种晶体学平⾯为解理⾯。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有⼀定韧性的⾦属材料当低于某⼀温度点时,冲击吸收功明显下降,断裂⽅式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变2、说明下列⼒学性能指标的意义。
答:E 弹性模量 G 切变模量 r σ规定残余伸长应⼒ 2.0σ屈服强度 gt δ⾦属材料拉伸时最⼤应⼒下的总伸长率 n 应变硬化指数P153、⾦属的弹性模量主要取决于什么因素?为什么说它是⼀个对组织不敏感的⼒学性能指标?答:主要决定于原⼦本性和晶格类型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-第二章习题1 初始时刻位于()321,,a a a 的质点在某时刻t 的位置为33322311;;a x ka a x ka a x =+=+=,其中510-=k ,求格林应变张量的分量。
[解] 采用拉格朗日描述法,),,(321a a a u a x u i i i i =-=,得0;;33231===u ka u ka u 由格林应变张量,j i e e E ij E =,()j m i m i j j i u u u u Eij ,,,,21++=,得 021131312121111111111=⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂+∂∂=a u a u a u a u a u a u a u a u E 02123132212211112212112=⎪⎪⎭⎫⎝⎛∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂+∂∂==a u a u a u a u a u a u a u a u E E 6331332123111133131131052121-⨯==⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂+∂∂==k a u a u a u a u a u a u a u a u E E 021232322222121222222=⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂+∂∂=a u a u a u a u a u a u a u a u E 6332332223121233232231052121-⨯==⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂+∂∂==k a u a u a u a u a u a u a u a u E E 021333332323131333333=⎪⎪⎭⎫⎝⎛∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂+∂∂=a u a u a u a u a u a u a u a u E习题2 证明j i ε是二阶对称张量的分量,而ij γ不是任何张量的分量。
[证明] (1) ()i j j i ij u u ,,21+=ε,显然可得其对称性 对于笛卡尔直角坐标系oxyz 和z y x o ''',各坐标轴之间的方向余弦如下表由弹性力学理论知,ij j j i i j i εββε''''=,恰与张量定义相吻合,∴ j i ε是二阶对称张量的分量(2)设有一剪应变张量γ,其分量()ij ij ij ij ij ij εδεδεγ-=-=22 取任一矢量k k e n k n =,则()()k j i j i k e e e e e n γ•-=•-=•k ij ij k ij ij n n εδεδ22m k j i e e e e jk β=•,但()jk k ij ij n βεδ-2不能缩并为m ε,与假设γ是张量矛盾。
根据张量的商判则,ij γ不是任何张量的分量。
习题3 为求平面应变分量x ε、y ε、xy γ,将电阻应变片分别贴在x 方向,与x 成ο60和ο120方向上,测得应变值以0ε、60ε、120ε表示,试求x ε、y ε、xy γ[解] 平面应变状态下,沿x 方向,与x 成ο60和ο120方向上的方向余弦分别为)23,21();23,21();0,1(-321v v v根据v 方向线元的工程正应变公式,j i ij v v v εε=,得⎪⎪⎪⎭⎪⎪⎪⎬⎫-+=++==xy y x xy y x xγεεεγεεεεε434341434341120600求得⎪⎪⎪⎭⎪⎪⎪⎬⎫-=-+==322322120600120600εεγεεεεεεxy y x习题4 假设体积不可压缩位移),(211x x u 与),(212x x u 很小,03≡u ,在一定区域内已知()()2112211cx bx a x u ++-=,其中a ,b ,c 为常数,求()212,x x u 。
[解] 题目条件适用小变形,()i j ji ij u u ,,21+=ε,得()()()()⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂∂∂+++-∂∂+++-+-=0210212102121323222122112122112122x u x u x u x u cx bx a x x u cx bx a x cx b x εΘ 体积不可压缩,0332211=++=∴εεεεii ()()122222221cx b x x u +-=∂∂=∴ε 即()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+==⎰202202221222231312220x x x x cx b dx u xx ε习题5 在平面应变状态下,使用直角坐标和极坐标中应变分量、位移分量的转换公式,写出在极坐标中的应变和位移的关系式。
[解] 在平面应变状态下,由应变分量转换公式,ij j j i i j i εββε''''=,得⎪⎪⎪⎭⎪⎪⎪⎬⎫++-=-+=++=θεθεθεεθεθεθεεθεθεθεεθθθ2cos 2sin 22sin 22sin cos sin 2sin sin cos 2222xy yy xxr xy yy xx xy yy xx rr (1)代入()i j j i ij u u ,,21+=ε,即 ⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂=∂∂∂∂+∂∂∂∂=∂∂=y v y r r v y u y r r u y v y u yu y r r u y u x u x r r u x u xyyy xx θθθθεθθεθθε2121 (2) ⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫∂∂∂∂+∂∂∂∂=∂∂∂∂∂∂+∂∂∂∂=∂∂∂∂∂∂+∂∂∂∂=∂∂∂∂∂∂+∂∂∂∂=∂∂θθθθθθθθθθθθθθu u v u u v v u u u u u u u r u u v r u u v r v r u u u r u u u r u r r r r r r r r (3)⎭⎬⎫+=-=θθθθθθcos sin sin cos u c u v u u u r r (4)因此,⎪⎪⎭⎪⎪⎬⎫=∂∂=∂∂-=∂∂=∂∂θθθθθθcos ,sin sin ,cos u vu v u u u u r r (5)⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫=⎪⎭⎫ ⎝⎛∂∂=∂∂-=⎪⎭⎫ ⎝⎛∂∂=∂∂=⎪⎭⎫ ⎝⎛+∂∂=∂∂=⎪⎭⎫ ⎝⎛+∂∂=∂∂θθθθθθcos 1sin 1sin cos 2222r x y arctg y y rx y arctg x x y x y y r y x x x r (6) 将式(2)-(6)代入式(1),得平面应变状态下,极坐标中的应变和位移的关系式:⎪⎪⎪⎭⎪⎪⎪⎬⎫∂∂+-∂∂=+∂∂=∂∂=θεθεεθθθθθθr r r rrr u r r u r u r u u r ru 11习题7 证明由下式确定的应变()i j j i ij u u ,,21+=ε恒满足变形协调方程,0,=kl ij nil mjk e e ε。
[证明] ()i j j i ij u u ,,21+=εΘ ()()ikl j nil mjk jkl i mjk nil ikl j jkl i nil mjk kl ij nil mjk u e e u e e u u e e e e .,,,,2121+=+=∴ε 对于单值连续位移场,并存在三阶以上连续偏导数时,偏导数的值与求导顺序无关jkl i u ,∴关于j ,k 对称;ikl j u ,关于i ,l 对称对于排列符号mjk e 关于j ,k 反对称;l ni e 关于i ,l 反对称0;0,,==∴ikl j nil jkl i mjk u e u e即应变()i j j i ij u u ,,21+=ε恒满足变形协调方程,0,=kl ij nil mjk e e ε习题8 假定物体被加热至定常温度场()321,,x x x T 时,应变分量为T αεεε===332211;0323112===γγγ,其中α为线膨胀系数,试根据应变协调方程确定温度场T 的函数形式。
[解] 由应变协调方程,0,,,,=--+ik jl jl ik ij kl kl ij εεεε,得()()()()()()0132322212232222212=∂∂∂=∂∂∂=∂∂∂=∂∂=∂∂=∂∂x x T x x T x x T x T x T x T αααααα又定常温度场()321,,x x x T 应满足拉普拉斯方程,0)(232222212=∂∂+∂∂+∂∂T x x x故()321,,x x x T 的函数形式中不应含有高于或等于2次的项 温度场T 的函数形式为()c x k x k x k x x x T +++=332211321,,其中,1k ,2k ,3k 和c 均为常数。
习题9 试导出平面应变轴对称情况下的应变协调方程 [解] 轴对称平面应变情况下,应变分量为0;;===θθεεεr rrr r u drduru dr du drr u d rdr du r rr r -=⎪⎪⎭⎫ ⎝⎛=∴θ 因此,平面应变轴对称情况下的应变协调方程为ru dr du dr du rrr -=θ习题10 在某一平面轴对称变形情况下,轴向应变z ε为常数,试确定其余两个应变分量r ε和θε的表达式(材料是不可压缩的)[解] 平面轴对称情况下,变形协调条件为:0=-+r drd rεεεθθ当材料不可压缩时,体积应变为零,即0=++φθεεεr ,代入上式,得02=-+z drd rεεεθθ解得222;2rC rC z r z --=+-=εεεεθ,式中,C 是右边界条件确定的常数习题11 试问什么类型的曲面在均匀变形后会变成球面。
[解] 均匀变形状态可表示为321;;;;;d d d c b a xz zx zy yz yx xy z y x =========γγγγγγεεε其中,321;;;;;d d d c b a 为常量设均匀变形前的坐标为000;;z y x ,则变形后的坐标为()()()0001;1;1z z y y x x z y x εεε+=+=+=曲面在均匀变形后变成球面,即2222R z y x =++略去刚体位移,当x 、y 、z 为主轴时,变形前的坐标000;;z y x 满足()()()1111222022202220=+++++c Rz b Ry a Rx变形前半轴为a R +1,b R +1,cR +1的椭球面在均匀变形后会变成球面。
