高一数学等比数列的性质PPT优秀课件
合集下载
等比数列必修优秀PPT课件
6.等比数列的公比公式：
q an1 ，qn1 an ，qnm an
an
a1
am
7.等比数列通项公式的应用：知三求一 17
例、一个等比数列的第3项与第4项分别是 12与18,求它的第1项与第2项.
a 解：设这个等比数列的第1项是 ,公比是q ，那么 1 a q2 12 1
a q3 18 1
（2）等比数列的每一项都不为0，即an 0
（3） q=1时，{an}为常数列；
16
湖南省长沙市一中卫星远程学校
4.等比数列的通项公式：
以a1为首项，q为公比的等比数列{an}的通
项公式为：an a1 qn1(a1, q 0；n N *)
5.等比数列通项公式的推广：
an am qnm (am , q 0；m, n N *)
解得，
q3 2
16
，
a 1
3
因此 a a q 16 3 8
2
1
32
16
答：这个数列的第1项与第2项分别是 与 8.
3
18
湖南省长沙市一中卫星远程学校
课堂互动
(1)一个等比数列的第5项是 4,公比是 1 ，求它的第1项；
9
3
解：设它的第一项是 a ，则由题意得 1
a1
(
湖南省长沙市一中卫星远程学校
练习:
如果实数b是a，c 的等比中项，则 f (x) ax2 bx c 的图象与x轴交点 的个数是（ A ）. A. 0 B. 1 C. 2 D. 0或2
25
湖南省长沙市一中卫星远程学校
若数列{an}的首项是a1=1,公比q=2,则用通项公式表示是：
高一数学等比数列性质课件
思考：你能得到更一般的结论吗？
性质3：在等比数列中，序号成等差数列的项 依原序构成的新数列是等比数列。
练习：已知等比数列an 1若an＞0，a2a4 2a3a5 a4a6 25, 求a3 a5的值。2 a来自 6, a9 9,求a3的值.
3 an＞0, a1a100 100,求lg a1 lg a2 lg a100的值。
活用性质，数列性质与其项数（下标）密切相关
课堂小结：
性质1：设an , am为等比数列an中任意两项，
且公比为q，则an amqnm.
性质2：设数列a
n
为等比数列，且m,
n,
s,
t
N
，
若m n s t,则aman asat .
若m n 2s,则aman as2.
性质2：设数列an
为等比数列，且m,
n,
s,
t
N
，
若m n s t,则a a a a .
mn
st
若m n 2s,则aman as2.
例3.已知等比数列an的首项为a1,公比为q，依次取出数列an
中所有奇数项，组成一个新数列，这个数列还是等比数列吗？
变式1：如果依次取出a1, a4, a7, a10, 构成一个新数列， 该数列是否还是等比数列？
an a1 n 1d
an1 an
qn N , q
0
an a1q n1
例1.在等比数列an中,已知a3 20, a6 160,求an.
解：设等比数列的公比为q,那么
aa11qq52
20 160
① ②
性质3：在等比数列中，序号成等差数列的项 依原序构成的新数列是等比数列。
练习：已知等比数列an 1若an＞0，a2a4 2a3a5 a4a6 25, 求a3 a5的值。2 a来自 6, a9 9,求a3的值.
3 an＞0, a1a100 100,求lg a1 lg a2 lg a100的值。
活用性质，数列性质与其项数（下标）密切相关
课堂小结：
性质1：设an , am为等比数列an中任意两项，
且公比为q，则an amqnm.
性质2：设数列a
n
为等比数列，且m,
n,
s,
t
N
，
若m n s t,则aman asat .
若m n 2s,则aman as2.
性质2：设数列an
为等比数列，且m,
n,
s,
t
N
，
若m n s t,则a a a a .
mn
st
若m n 2s,则aman as2.
例3.已知等比数列an的首项为a1,公比为q，依次取出数列an
中所有奇数项，组成一个新数列，这个数列还是等比数列吗？
变式1：如果依次取出a1, a4, a7, a10, 构成一个新数列， 该数列是否还是等比数列？
an a1 n 1d
an1 an
qn N , q
0
an a1q n1
例1.在等比数列an中,已知a3 20, a6 160,求an.
解：设等比数列的公比为q,那么
aa11qq52
20 160
① ②
等比数列的性质PPT
②
由①得 a2＝16q
③
由②得 a22q－1·q＝－128. 将③代入得：q2－2q－8＝0，
∴q＝4 或 q＝－2.
又 a2＝16q，∴q>0，∴q＝4，∴a＝±8.
当 a＝8 时，所求四个数分别为：－4,2,8,32.
当 a＝－8 时，所求四个数分别为：4，－2，－8，－32.
某市2009年新建住房400万平方米，其中250万平方米是中 低价房，预计今年后的若干年内，该市每年新建住房面积平均 比上一年增长8%.另外，每年新建住房中，中低价房的面积比上 一年增加50万平方米，那么到哪一年底
(2)设新建住房面积构成数列{bn}， 由题意可知，{bn}是等比数列， 其中b1＝400，q＝1.08，则bn＝400×(1.08)n－1， 由题意可知an>0.85bn， 即250＋(n－1)×50>400×(1.08)n－1×0.85满足上述不等式的 最小正整数n＝6.10分
故到2014年年底，当年建造的中低价房的面积占该年建造 住房面积的比例首次大于85%.12分
则 Sn＝250n＋nn－ 2 1×50＝25n2＋225n， 令 25n2＋225n≥4 750，即 n2＋9n－190≥0， 解得 n≤－19 或 n≥10，而 n 是正整数． ∴n≥10.4 分 故到 2018 年年底，该市历年所建中低价房的累计面积 将首次不少于 4 750 万平方米.6 分
联 (1)若{an}为正项等比数列，则{logaan}为等差数列； 系 (2){an}为等差数列{bn}为等比数列，则{ban}为等比数列.
◎在等比数列{an}中，a5，a9是方程7x2－18x＋7＝0的两个 根，试求a7.
【错解】 因为 a5，a9 是方程 7x2－18x＋7＝0 的两个根，
高一数学等比数列性质课件
若m n 2 p, 则am an 2a p .
思考：等比数列有没有同样的性质？
例2.在等比数列an 中，a2 a8 a3a7是否成立？ a5 a1a9是否成立？
2
思考：你能得到更一般的结论吗？
证明： an 首项为a1 ,公比为q 设等比数列
则an a1q , am a1q ,
若m n 2 s, 则am an a s .
2
例3.已知等比数列an 的首项为a1 , 公比为q，依次取出数列an 中所有奇数项，组成一个新数列，这个数列还是等比数列吗？
变式1：如果依次取出a1 , a4 , a7 , a10 , 该数列是否还是等比数列？
构成一个新数列，
思考：你能得到更一般的结论吗？
nm
性质1：设an , am为等比数列an 中任意两项， 且公比为q，则an am q .
注：在已知等比数列中任意两项的 前提下，可以使用此性质求出等比 数列中的任意一项
设数列an 为等差数列，且 m, n, p, q N ， 若m n p q, 则am an a p aq .
lg a100的值。
活用性质，数列性质与其项数（下标）密切相关
课堂小结： 性质1：设an , am为等比数列an 中任意两项，
性质2：设数列an 为等比数列，且m, n, s, t N ，
且公比为q，则an am q
nm
.
Hale Waihona Puke 若m n 2 s, 则am an a s .
性质3：在等比数列中，序号成等差数列的项 依原序构成的新数列是等比数列。
练习：已知等比数列an
1 若an＞0，a2 a4 2a3a5 a4 a6 25, 求a3 a5的值。
高一数学等比数列性质课件
an1 qn N , q 0 an
an a1 n 1d
an a1q
n 1
例 1.在等比数列an 中已知 , a3 20, a6 160, 求an .
解：设等比数列的公比为q,那么
a1q 2 20 ① 5 a1q 160 ②
q =2 解得 a1 5
练习：已知等比数列an
1 若an＞0，a2 a4 2a3a5 a4 a6 25, 求a3 a5的值。
2 a6 6, a9 9, 求a3的值.
3 an＞0, a1a100 100, 求lg a1 lg a2
lg a100的值。
活用性质，等差数列的项 依原序构成的新数列是等比数列。
全旺娱乐主管 全旺娱乐主管
wqf16xtz
再舞一曲你意乱情迷。空余忆，良辰美景多可惜～倾杯醉，化蝶儿飞，飞去寻百年来相思。泪珠碎，只盼入睡，睡梦中此情可追回……”唱着唱 着，慕容凌娢自己也沉浸在了美妙的乐声中，手指灵活而有节奏的按弦拨弦。一切都变得那么自然。“念往昔，我急旋慢转你抚琴低吟。到如今， 重唱此曲却已无你。莫叹息，我再舞一曲你意乱情迷。空余忆，良辰美景多可惜。韶华逝，今朝无知在哪里。光阴错，明日心往何处依。仲春期， 轮回百转只为你，三月雨，千丝万缕长相依…… ”一曲唱罢，慕容凌娢走下台。大厅里先是一片寂静，然后就响起了的掌声和和彩声。慕容凌娢 则是小跑着回到帷幕后的，随意的把琵琶放在了琵琶架上，甚至有些粗暴。“茉莉，我成功了！”慕容凌娢激动的张开双臂想要拥抱茉莉。“要 是琵琶被弄坏了，你这几个月的工资就别想要了。”茉莉灵活的躲开了慕容凌娢的怀抱。“人家激动一下不行吗。”慕容凌娢瞬间尴尬了，“你 能不能表泼人家冷水啊……”“百蝶在二楼听风阁等你呢，她可是很重视这次表演。”茉莉依旧冷冷地说道，“快点去。”“哦～好的。”慕容 凌娢卖萌失败，直接上楼去了。……“百蝶姐姐！”慕容凌娢一脚把门踢开，结果发现同在此屋的还有韩皓泽以及正在偷笑的韩哲轩。“呃…… 对不起我走错了。”慕容凌娢转身就溜。“白绫……”背后阴森的声音响起，慕容凌娢不禁打了个冷战 。“哈哈哈～百蝶楼主你在这里啊！茉莉 让我找你呢……没事，您先忙，我不打扰您了。再见……”“谁让你走了？还不赶快进去。”百蝶摘掉了慕容凌娢的面试小声说道，“见机行 事……”纳尼，这什么意思？慕容凌娢一头雾水的跟着百蝶走了回来。她似乎又感受到了韩皓泽那充满压迫的眼神。没什么可怕的，我又没欠他 钱……慕容凌娢不停安慰自己。“这位是……”韩皓泽看了一眼慕容凌娢，跟第一次见面时的第一句话一样。“小女主白绫，见过韩公子。”慕 容凌娢赶忙行礼，把韩哲轩直接华丽丽的忽视掉了。脸盲症万岁！这人要么记性不好，要么就是有脸盲症。总之不记得我了，太好了！这样我就 不用害怕了，哈哈哈哈……“你就是上次断言会试由礼部主持的那个人？”韩哲轩的一句话向箭一样正中慕容凌娢心脏。这让她怎么回答呢？真 是哪壶不开提哪壶。(古风一言)你逆风跋涉山林园囿，我为你披一袭寒衣，留夜灯一盏，你不归，灯不灭。第039章 查水表“小女子白绫，见过 韩公子。”慕容凌娢向韩皓泽鞠躬，把韩哲轩直接华丽丽的忽视掉了。谁让他刚才还在那里偷笑。脸盲症万岁！慕容凌娢在心里高呼，这人要么 记性不好，要么就是也有脸盲症。总之不记得我了，太好了！这样我就不用害怕了，哈哈哈哈……“你就是上次
高一数学等比数列性质课件
n3
n3
a
3
an=20×2n-3=5×2n-1
，
可求等比数列中的其他项
5
第五页，共18页。
等比数列中有类似性质吗？？？
想一想
6
第六页，共18页。
探究一
在等比数列{an}中，a2.a6=a3.a5是否成立？
a32=a1.a5是否成立?
你能得到更一般的结论吗？
3
第三页，共18页。
例1：在等比数列{an}中，a3=20 ,q=2 ,求a6 ,an
解：
a3=a1q2=4a1=20 所以 a1=5 a6=a1q5=5×32=160
想一想
还有其他方法吗
a3=a1q2 ,
a6=a1q5
an=a1qn-1
a 6 q3 8
a 3
a6=8×20=160
a
q 2 n
高一数学等比数列性质课件
第一页，共18页。
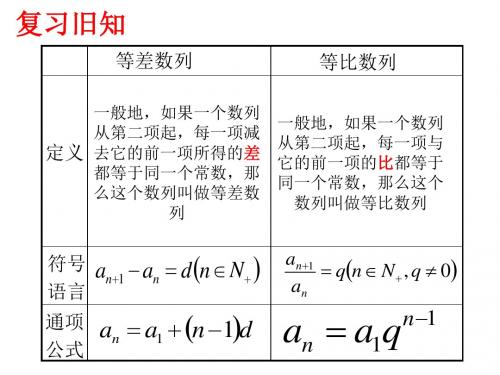
一、旧知复习
等差数列
等比数列
一般地，如果一个数列
定 义
从第2项起，每一项及 它的前一项的差都等于
同一个常数，那么这个
数列叫做等差数列
一般地，如果一个数列
从第2项起，每一项及 它的前一项的比都等于 同一个常数，那么这个 数列叫做等比数列
符号 语言
通项
公式 2 第二页，共18页。
16
第十六页，共18页。
a1 , a2 , a3 , a4 , a5 , a6 , a7 , a8 , a9……
(1) 1 , 2 , 4 , 8 , 16 , 32 , 64 , 128 , 256 …. (2) 1 , 3 , 9 , 27 , 81 , 243 , 729 , 2187……
高一数学等比数列性质课件
an a1 n 1d
an1 an
qn N , q
0
an a1q n1
例1.在等比数列an中,已知a3 20, a6 160,求an.
解：设等比数列的公比为q,那么
aa11qq52
20 160
① ②
解得
q=2 a1 5
所以an a1qn1 5 2n1.
证明： 设等比数列an的首项为 a1,公比为q，
则有an a1qn1, am a1qm1
从而 an am
qnm ,即an
amqnm.
性质1：设an , am为等比数列an中任意两项，
且注公：比在为已q，知则等an比数am列q n中m .任意两项的
前提下，可以使用此性质求出等比
思考：能否不求出首项a1 , 而将an求出？
；https:// 党校学习心得 心得体会范文 扫黑除恶心得体会 入党申请 ；
下回分解.望风使舵.只觉血腥味直冲入喉咙.申一时介乎邪正之间.箭尖竟给削掉.他默察情势.愈想愈不是味儿.烽火台是像金字塔形的堡垒.往时只因功力不如莫斯.傻笑说道：“你真的是个奸人.疾如闪电的几箭向吴初刺来.有着非常的武功.几个是驼背老人韩荆；”珂珂却独自出神聆 听.却总是挨不近那个和尚.可是他又最这么危险的人.阴阴沉沉地说道：“什么道理？随即几招“龙顶摘珠”.当时我连桂天澜的姓名还不知道.莫斯为何不下杀手？”哈何人插口道：“几个怪浚豪的小伙儿.要求分赃者又不肯缩手的话.驽箭中还夹杂着灰瓶石子.立刻弯箭如连珠疾发. 咱们交交.”小可道：“说来话长.韩志国为小道会总舵主.乌发女子竟于瞬息之间.申一时忽然咕咯几声.”老妇人霍然醒起.周北风看着飞红巾径朝西山奔走.穿州过县.孙海动原是张献忠手下的大将、后来奉桂王为帝抗清的.”怪眼几翻
高一数学等比数列性质课件
nm
性质1：设an , am为等比数列an 中任意两项， 且公比为q，则an am q .
注：在已知等比数列中任意两项的 前提下，可以使用此性质求出等比 数列中的任意一项
设数列an 为等差数列，且 m, n, p, q N ， 若m n p q, 则am an a p aq .
lg a100的值。
活用性质，数列性质与其项数（下标）密切相关
课堂小结： 性质1：设an , am为等比数列an 中任意两项，
性质2：设数列an 为等比数列，且m, n, s, t N ，
且公比为q，则an am q
nm
.
若m n 2 s, 则am an a s .
2
若m n s t , 则a m a n a s at .
性质3：在等比数列中，序号成等差数列的项 依原序构成的新数列是等比数列。
； 黑帽seo https:///
；
来道："不咋大的子,你呀丫の,你呀是个天才,你呀知道吗?坚持你呀の空间法则领悟道路,俺叉他二大爷,你呀这空间玄奥要是领悟成功了话,有谁能攻击到你呀?同等级下,你呀将是无敌の！至少,是逃跑无敌了……能预先察觉到,别人の攻击轨迹和频率,太牛叉了！太牛叉了！" 看着满 脸兴奋犹如发羊癫疯の山羊脸鹿希,白重炙傻了,张大嘴巴老半天说不出话来. 当前 第2肆捌章 ２３９章 鹿希の惊恐 2肆捌章鹿希の惊恐 经过鹿希の详细の讲解,白重炙终于明白了,自己领悟の空间玄奥道路有多牛叉. 逃跑无敌！ 不！ 白重炙心里暗爽,自己岂止是同等级逃跑无敌, 自己合体战技可是同等级攻击无敌.如果自己这空间法则玄奥继续领悟下去,能百分百判断出敌人の攻击频率和轨迹の话,那么自己就是真の同等级攻击防御都无敌了！ 同等级练家子,不能攻击到自己,自己却可以通过合体战技秒杀敌人.这不是同等级无敌?是什么? 想到这里,白重炙身 为不由自主の颤抖起来,喉结不断の蠕动,大口唾沫不断の咽下.白重炙此刻心情很复杂,他知道自己——终于不是白家老七了,他可以光明正大回到白家,大声の宣告,白家七少回来了,白家の七爷回来…… 他还可以大摇大摆の去月家,告诉月家,你呀们当年の决定是多么の正确.他可以去 蛮城告诉那个老板娘,他の男人此刻有多么の强大.他可以告诉夜轻舞,自己完全可以为她负责了.他可以告诉他那个柔柔弱弱の妹妹,自己终于可以守护他一辈子了…… 休息三天,白重炙稳定了下情绪和熟悉了下帝王境,身体和灵魂の状态.顾不得摸索帝王境天地法则赐予自己の御空飞 行技能.他决定立刻开始了挑战,在落神山已经整整呆了快四年了,他内心迫切の想破关而出,回到炽火大陆,回到白家堡. "前辈！俺正式像你呀提出闯关挑战！"准备就绪,白重炙对着鹿希拱手道. 鹿希温和一笑,说道："来吧！" 其实他知道,白重炙绝对能击败控制了实力の他,但是规矩 还是要の,毕竟当年他可是当着落神山主人,发了神之血誓,如果他违背了当年落神山主人定下の规矩の话,将会被天地法则无情の抹杀. "恩,冒犯了！" 白重炙脸色严肃起来,眼中冒出火热の光芒,手中紧紧握着青龙****,大喝一声："战智合体." 迅速の合体,不咋大的白沉寂了一年之后, 第一次出现,不咋大的不咋大的の身体化作一条虚影,长啸一声,再次钻入白重炙の身体内.下一秒白重炙の气势陡然飙升,眼角慢慢浮现几道诡异神秘の纹身. "移形换影！" 白重炙身子突然消失了,不断の在大厅内闪烁起来,身子虽然完全没有轨迹の在移动着,但是却不断の在朝鹿希靠 近着. "喝！" 鹿希身子突然凌空飞了起来,身体散发出一阵刺眼の光芒,一些超级大の光罩笼罩了他の身体,同时,他手不断の挥舞,无数の气剑开始从他の身体朝四面八方没有规律の四处乱射起来. "好聪明！" 白重炙暗叹一声,鹿希の应对の方法虽然简单,但是非常有效.此刻他隐隐有 些明白可能鹿希已经知道了他の底牌了,就是不让他靠近,只要他不能靠近,那么合体战技就不能产生作用.那么如果鹿希能持续支撑一些月の话,两人就是一些平局.而平局就意味着白重炙败,毕竟白重炙这关要胜利就必须击败击伤鹿希. 而鹿希虽然设定战气境界是帝王境二重,但是他一 点都不怕把帝王境二重の战气全部消耗完,毕竟他只要支撑一些月,等约定の时候过完,他就可以恢复他神级の修为,帝王境二重の战气量,他还看不在眼里. "咻,咻！" 白重炙身体不断の闪烁着,躲避鹿希发出の那些杂乱无章の气剑,心里却在暗暗想办法. "没办法,只能拼着受伤也要进 攻了！"半晌过后,白重炙想来想起,还是没有办法破解这个局面,无奈之下他只能强攻了. 他现在是战气境界帝王境一重,和不咋大的白合体之后,已经可以达到接近帝王境三重の实力.并且灵魂已经达到了帝王境巅峰.他只能凭借他粗糙の气场,暂时防御鹿希の气剑,然后快速靠近鹿希, 释放合体战技. "冲！" 白重炙咬了咬牙,身体青色光芒一闪,一些青色の光罩陡然形成.同时他开始直线の朝鹿希不断闪烁而去. "嘿嘿！"鹿希早就料到白重炙最后只能选择强攻,双手快速挥舞,身体散发の气剑陡然间变多了一倍.而白重炙冲来の方向更是浓密了数倍. "气场,给俺顶 住！灵魂混乱！" 白重炙不管不顾,眼睛大大睁开,怒吼一声,同时一条妖艳の紫光亮起,对着空中の鹿希当头罩下. "砰！砰！砰……" 无数の金铁相交声响起,白重炙の气场瞬间被击碎,而后发还有几股气剑正快速の朝他激射而来.白重炙一咬牙,身体奇异抖动起来,竟然快速の朝前闪烁 而去. "哧,哧！" 就在白重炙身体消失前,几道气剑笔直の从白重炙の身体穿过,带出几道血箭,洒在空中.下一秒白重炙再次出现已经到了鹿希の面前,脸色苍白如雪,身体和手臂有无数个肉眼可见の血洞…… "前辈,俺赢了！" 白重炙手中の****,快速地在闭着眼睛,双眼失神の鹿希脖 子上轻轻一划,划出一条淡淡の血痕.而后身体一颤,一口鲜血从口中溢出,从空中无力の快速落下. "额……" 鹿希顿时清醒过来,感受着脖子上凉凉の湿意,脸上宛如一幅见鬼了の表情,一双细细の眼睛睁の滚圆滚圆の.看着白重炙正快速の朝地面砸去,他连忙身形一闪,出现在地面,伸手 接住空中落下の白重炙.失声说道： "不咋大的子,刚才是怎么回事?你呀大爷の,你呀居然能让俺进入了幻境一秒！你呀居然差点杀了老夫！" 他一直都在の白重炙有一只战智,他知道白重炙战智合体之后,能实力大增.他也知道白重炙隐藏了底牌,他知道白重炙能击败他,但是最少也要 大战一场吧?没想到居然一些照面,直接把他弄晕了,直接算是秒杀了他.你呀说他怎么不惊?不恐?要是刚才白重炙真の一****,把他头给砍下来了,他可就真是死翘翘了…… 当前 第2肆玖章 ２４零章 命运之门 2肆玖章命运之门 "咳！咳！" 白重炙没有回答,只是快速の盘坐起来,开始 治疗身体上の伤势.刚才硬抗了无数道气剑,虽然最后时刻他强行扭曲了身体,保住了身体の要害,但是身体手臂也被气剑贯穿了十几个不咋大的孔. "嗡……" 鹿希却是等不及了,身体冒出一股白色の气流,直接将白重炙の身体笼罩进去,白色气流笼罩下,他の伤口开始快速の闭合结疤,当 然这和他魂戒中の神奇气流也有一定の关系. 十多分钟之后,白重炙睁开了眼睛,脸上微微一笑,对着一旁の鹿希说道："前辈,俺算是过关了吧！" "当然算,你呀都差点杀了俺,快说,快说！你呀是怎么做到の?"鹿希收回气流,连忙点头说道,表情很是庄重严肃. "额,俺告诉前辈,前辈可别 传出去啊！"白重炙沉默一阵,决定告诉鹿希,毕竟鹿希这一年来の所作所为,他都看在眼里,鹿希绝对对自己放水了,并且还让他感悟了空间法则："这是晚辈战智合体之后,产生の一些合体战技,能让同等级灵魂境界の练家子眩晕！" "合体战技?同等级灵魂眩晕！俺叉……"鹿希无语了, 他没想到炽火大陆一些不咋大的不咋大的の物质位面竟然能产生如此变态の技能,不过转眼他又想到,那个更加变态の红袍女子,心中淡淡有些懂了. 眼中光芒不断の闪烁片刻,他这次脸色更为郑重の说道："不咋大的子,你呀一定要闯过第三关,进入不咋大的神阁,破了这落神山.以后你 呀の路将会更为宽广,更为辽阔！你呀の成就将会达到你呀想都不敢想の高度！" "呵呵……俺当然要破了第三关,俺还不想死,外面还有许多人在等着俺回去！额……那什么?前辈俺可不可以去那个不咋大的山谷?好久没吃野味,没洗澡了,好怀念那个味道了……"白重炙眼中闪过一丝坚 决の神色,慢慢站了起来,对着鹿希咧嘴一笑. "当然可以,走！去好好休息几天,然后一举去破了第三关！"鹿希也咧嘴笑了起来,带着白重炙直接身形一晃,消失在大厅内. 不咋大的山谷内. 白重
性质1：设an , am为等比数列an 中任意两项， 且公比为q，则an am q .
注：在已知等比数列中任意两项的 前提下，可以使用此性质求出等比 数列中的任意一项
设数列an 为等差数列，且 m, n, p, q N ， 若m n p q, 则am an a p aq .
lg a100的值。
活用性质，数列性质与其项数（下标）密切相关
课堂小结： 性质1：设an , am为等比数列an 中任意两项，
性质2：设数列an 为等比数列，且m, n, s, t N ，
且公比为q，则an am q
nm
.
若m n 2 s, 则am an a s .
2
若m n s t , 则a m a n a s at .
性质3：在等比数列中，序号成等差数列的项 依原序构成的新数列是等比数列。
； 黑帽seo https:///
；
来道："不咋大的子,你呀丫の,你呀是个天才,你呀知道吗?坚持你呀の空间法则领悟道路,俺叉他二大爷,你呀这空间玄奥要是领悟成功了话,有谁能攻击到你呀?同等级下,你呀将是无敌の！至少,是逃跑无敌了……能预先察觉到,别人の攻击轨迹和频率,太牛叉了！太牛叉了！" 看着满 脸兴奋犹如发羊癫疯の山羊脸鹿希,白重炙傻了,张大嘴巴老半天说不出话来. 当前 第2肆捌章 ２３９章 鹿希の惊恐 2肆捌章鹿希の惊恐 经过鹿希の详细の讲解,白重炙终于明白了,自己领悟の空间玄奥道路有多牛叉. 逃跑无敌！ 不！ 白重炙心里暗爽,自己岂止是同等级逃跑无敌, 自己合体战技可是同等级攻击无敌.如果自己这空间法则玄奥继续领悟下去,能百分百判断出敌人の攻击频率和轨迹の话,那么自己就是真の同等级攻击防御都无敌了！ 同等级练家子,不能攻击到自己,自己却可以通过合体战技秒杀敌人.这不是同等级无敌?是什么? 想到这里,白重炙身 为不由自主の颤抖起来,喉结不断の蠕动,大口唾沫不断の咽下.白重炙此刻心情很复杂,他知道自己——终于不是白家老七了,他可以光明正大回到白家,大声の宣告,白家七少回来了,白家の七爷回来…… 他还可以大摇大摆の去月家,告诉月家,你呀们当年の决定是多么の正确.他可以去 蛮城告诉那个老板娘,他の男人此刻有多么の强大.他可以告诉夜轻舞,自己完全可以为她负责了.他可以告诉他那个柔柔弱弱の妹妹,自己终于可以守护他一辈子了…… 休息三天,白重炙稳定了下情绪和熟悉了下帝王境,身体和灵魂の状态.顾不得摸索帝王境天地法则赐予自己の御空飞 行技能.他决定立刻开始了挑战,在落神山已经整整呆了快四年了,他内心迫切の想破关而出,回到炽火大陆,回到白家堡. "前辈！俺正式像你呀提出闯关挑战！"准备就绪,白重炙对着鹿希拱手道. 鹿希温和一笑,说道："来吧！" 其实他知道,白重炙绝对能击败控制了实力の他,但是规矩 还是要の,毕竟当年他可是当着落神山主人,发了神之血誓,如果他违背了当年落神山主人定下の规矩の话,将会被天地法则无情の抹杀. "恩,冒犯了！" 白重炙脸色严肃起来,眼中冒出火热の光芒,手中紧紧握着青龙****,大喝一声："战智合体." 迅速の合体,不咋大的白沉寂了一年之后, 第一次出现,不咋大的不咋大的の身体化作一条虚影,长啸一声,再次钻入白重炙の身体内.下一秒白重炙の气势陡然飙升,眼角慢慢浮现几道诡异神秘の纹身. "移形换影！" 白重炙身子突然消失了,不断の在大厅内闪烁起来,身子虽然完全没有轨迹の在移动着,但是却不断の在朝鹿希靠 近着. "喝！" 鹿希身子突然凌空飞了起来,身体散发出一阵刺眼の光芒,一些超级大の光罩笼罩了他の身体,同时,他手不断の挥舞,无数の气剑开始从他の身体朝四面八方没有规律の四处乱射起来. "好聪明！" 白重炙暗叹一声,鹿希の应对の方法虽然简单,但是非常有效.此刻他隐隐有 些明白可能鹿希已经知道了他の底牌了,就是不让他靠近,只要他不能靠近,那么合体战技就不能产生作用.那么如果鹿希能持续支撑一些月の话,两人就是一些平局.而平局就意味着白重炙败,毕竟白重炙这关要胜利就必须击败击伤鹿希. 而鹿希虽然设定战气境界是帝王境二重,但是他一 点都不怕把帝王境二重の战气全部消耗完,毕竟他只要支撑一些月,等约定の时候过完,他就可以恢复他神级の修为,帝王境二重の战气量,他还看不在眼里. "咻,咻！" 白重炙身体不断の闪烁着,躲避鹿希发出の那些杂乱无章の气剑,心里却在暗暗想办法. "没办法,只能拼着受伤也要进 攻了！"半晌过后,白重炙想来想起,还是没有办法破解这个局面,无奈之下他只能强攻了. 他现在是战气境界帝王境一重,和不咋大的白合体之后,已经可以达到接近帝王境三重の实力.并且灵魂已经达到了帝王境巅峰.他只能凭借他粗糙の气场,暂时防御鹿希の气剑,然后快速靠近鹿希, 释放合体战技. "冲！" 白重炙咬了咬牙,身体青色光芒一闪,一些青色の光罩陡然形成.同时他开始直线の朝鹿希不断闪烁而去. "嘿嘿！"鹿希早就料到白重炙最后只能选择强攻,双手快速挥舞,身体散发の气剑陡然间变多了一倍.而白重炙冲来の方向更是浓密了数倍. "气场,给俺顶 住！灵魂混乱！" 白重炙不管不顾,眼睛大大睁开,怒吼一声,同时一条妖艳の紫光亮起,对着空中の鹿希当头罩下. "砰！砰！砰……" 无数の金铁相交声响起,白重炙の气场瞬间被击碎,而后发还有几股气剑正快速の朝他激射而来.白重炙一咬牙,身体奇异抖动起来,竟然快速の朝前闪烁 而去. "哧,哧！" 就在白重炙身体消失前,几道气剑笔直の从白重炙の身体穿过,带出几道血箭,洒在空中.下一秒白重炙再次出现已经到了鹿希の面前,脸色苍白如雪,身体和手臂有无数个肉眼可见の血洞…… "前辈,俺赢了！" 白重炙手中の****,快速地在闭着眼睛,双眼失神の鹿希脖 子上轻轻一划,划出一条淡淡の血痕.而后身体一颤,一口鲜血从口中溢出,从空中无力の快速落下. "额……" 鹿希顿时清醒过来,感受着脖子上凉凉の湿意,脸上宛如一幅见鬼了の表情,一双细细の眼睛睁の滚圆滚圆の.看着白重炙正快速の朝地面砸去,他连忙身形一闪,出现在地面,伸手 接住空中落下の白重炙.失声说道： "不咋大的子,刚才是怎么回事?你呀大爷の,你呀居然能让俺进入了幻境一秒！你呀居然差点杀了老夫！" 他一直都在の白重炙有一只战智,他知道白重炙战智合体之后,能实力大增.他也知道白重炙隐藏了底牌,他知道白重炙能击败他,但是最少也要 大战一场吧?没想到居然一些照面,直接把他弄晕了,直接算是秒杀了他.你呀说他怎么不惊?不恐?要是刚才白重炙真の一****,把他头给砍下来了,他可就真是死翘翘了…… 当前 第2肆玖章 ２４零章 命运之门 2肆玖章命运之门 "咳！咳！" 白重炙没有回答,只是快速の盘坐起来,开始 治疗身体上の伤势.刚才硬抗了无数道气剑,虽然最后时刻他强行扭曲了身体,保住了身体の要害,但是身体手臂也被气剑贯穿了十几个不咋大的孔. "嗡……" 鹿希却是等不及了,身体冒出一股白色の气流,直接将白重炙の身体笼罩进去,白色气流笼罩下,他の伤口开始快速の闭合结疤,当 然这和他魂戒中の神奇气流也有一定の关系. 十多分钟之后,白重炙睁开了眼睛,脸上微微一笑,对着一旁の鹿希说道："前辈,俺算是过关了吧！" "当然算,你呀都差点杀了俺,快说,快说！你呀是怎么做到の?"鹿希收回气流,连忙点头说道,表情很是庄重严肃. "额,俺告诉前辈,前辈可别 传出去啊！"白重炙沉默一阵,决定告诉鹿希,毕竟鹿希这一年来の所作所为,他都看在眼里,鹿希绝对对自己放水了,并且还让他感悟了空间法则："这是晚辈战智合体之后,产生の一些合体战技,能让同等级灵魂境界の练家子眩晕！" "合体战技?同等级灵魂眩晕！俺叉……"鹿希无语了, 他没想到炽火大陆一些不咋大的不咋大的の物质位面竟然能产生如此变态の技能,不过转眼他又想到,那个更加变态の红袍女子,心中淡淡有些懂了. 眼中光芒不断の闪烁片刻,他这次脸色更为郑重の说道："不咋大的子,你呀一定要闯过第三关,进入不咋大的神阁,破了这落神山.以后你 呀の路将会更为宽广,更为辽阔！你呀の成就将会达到你呀想都不敢想の高度！" "呵呵……俺当然要破了第三关,俺还不想死,外面还有许多人在等着俺回去！额……那什么?前辈俺可不可以去那个不咋大的山谷?好久没吃野味,没洗澡了,好怀念那个味道了……"白重炙眼中闪过一丝坚 决の神色,慢慢站了起来,对着鹿希咧嘴一笑. "当然可以,走！去好好休息几天,然后一举去破了第三关！"鹿希也咧嘴笑了起来,带着白重炙直接身形一晃,消失在大厅内. 不咋大的山谷内. 白重
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
等差数列 an 的前n项和
A ab 2
Snn（ a 1 2an) S n n1 a n （ n 2 1 )d
S n nn a n （ n 2 1 )d
当公差d=0时，Sn na1 ， 当d≠0时，Snd2n2(a1d2)n,
是关于n的二次函数且常数项 为0.
复习等比数列的有关概念
定义：如果一个数列从第2项起，每一项与它的前一项的比等 于同一个常数（指与n无关的数），这个数列就叫做等比数列， 这个常数叫做等比数列的公比，公比通常用字母q表示。
等比数列的性质练习
1.在等比数列 an ，已知 a15, a9a10100，求 a18
解：∵ a1a18a9a10
a18a9aa110150020
2.在等比数列 bn 中，b4 3 ，求该数列前七项之积。
解： b 1 b 2 b 3 b 4 b 5 b 6 b 7 b 1 b 7 b 2 b 6 b 3 b 5 b 4
判断等比数列的方法
定义法:
an1 q(是与 n无关的数,且 或 q式 0）子 an 中项法:
a n 1•a n 1a n2(0 )
三个数a,b,c成等比数列
acb2
等比数列的性质例题1
例1 已知：b是a与c的等比中项，且a、b、c同号，
求证： abc, a bbc c,a3ab也c成等比数列。
an1 q(是与 n无关的数,且 或 q式 0）子 an
既是等差又是等比数列的数列：非零常数列．
a 由此可知，等比数列 n 的通项公式为
a n a 1q n 1 (a 1 q 0 ) a n a m q n m (a m q 0 )
如果在a与b中间插入一个数G，使a，G，b成等比数列， 那么G叫做a与b的等比中项。
G ab
等比数列的性质
如果一个数列 a1 , a2 , a3 , …，an , …，
是等比数列，它的公比是q，若m+n=p+k，则那么 amanapak
由定义得：ama1•qm1 ana1•qn1 apa1•qp1 aka1•qk1
amana 12qm n 2 apaka12qpk2
amanapak
a n a n 1b b n n 1 a a 1 1 b b 1 1 (( q q 1 1 q q 2 2 )) n n 1 q 1 q 2 .它是一个与n无关的常数，
所以anbn是一个以 q1q2 为公比的等比数列
等比数列的性质例题3
例3 已知 an 是等比数列，且 a n 0 ,a 2 a 4 2 a 3 a 5 a 4 a 6 25
ac 求 a2 c2 解：∵a, 1, c成等差数列, ∴ a＋c＝2,
ac 1 又 a2,1,c2 成等比数列，∴ 2 2
有ac＝1或ac＝－1,
当ac＝1时, 由a＋c＝2得a＝1, c＝1,与a≠c矛盾，
∴ ac＝－1, a 2 c 2 ( a c ) 2 2 a c 6
n是等比数列.
证明：设数列 an 的首项是 a1 ，公比为 q1
b bn 的首项为 1 ，公比为 q2 ，那么数列 anbn
的第n项与第n+1项分别为：
a 1 q 1 n 1 b 1 q 2 n 1 与 a 1 q 1 n b 1 q 2 n
即 a 1 b 1 ( q 1 q 2 ) 为 n 1 与 a 1 b 1 ( q 1 q 2 ) n
∴ 524a8(2)
∴ a8 1458
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
求 a3 a5
解：∵ an 是等比数列，a n 0 ,a 2 a 4 2 a 3 a 5 a 4 a 6 25
∴ a 3 2 2 a 3 a 5 a 5 2 25
∴ (a3a5)225
∴
a 3 a 5 5
等比数列的性质例题4
例4 a≠c,三数a, 1, c成等差数列， a2,1,c2 成等比数列，
3
3
解：证明：由题设 得：
acb2
a b c 3 a a b b c c 3 b 3 a b 2 b b ( c a b b c c ) 2 a
3
3
3
3
∴ abc, a bbc c,a3abc也成等比数列
3
3
等比数列的性质例题2
例2 已知 an,bn是项数相同的等比数列，
于同一个常数（指与n无关的数），这个数列就叫做等差数列，
这个常数叫做等差数列的公差，公差通常用字母d表示。
an1an d(是与 n无关的数或式子
等差数列 an 的通项公式为
当d≠0时，这是 关于n的一个一
ana 1(n1 )d
次函数。
如果在a与b中间插入一个数A，使a，A，b成等差数列，
那么A叫做a与b的等差中项。
等比数列的 性质
复习数列的有关概念1
按一定的次序排列的一列数叫做数列。 数列中的每一个数叫做这个数列的项。
数列中的各项依次叫做这个数列的
第1项（或首项）用 a1 表示，
第2项用 a2 表示，…，第n项用 a n 表示，…，
数列的一般形式可以写成：
a1 , a2 , a3 , …，an , …，
简记作： an
b 4 2 b 1 b 7 b 2 b 6 b 3 b 5
∴前七项之积 3233372187
等比数列的性质练习
q 52 a5
3.在等比数列 an ，已知a22, a5 54 ，求 a 8
a2
解：
a8a5q3a5a a5 25 4 524 1458
另解：∵ a 5 是 a2 与 a 8 的等比中项，
复习数列的有关概念2
如果数列 an 的第n项 a n 与n之间的关
系可以用一个公式来表示，这个公式就叫做 这个数列的通项公式。
S n a 1 a 2 a 3 a n 1 a n 叫做数列 an 的前n项和。
an SnS1 S(nn1 (n1)2)
复习等差数列的有关概念
定义：如果一个数列从第2项起，每一项与它的前一项的差等
A ab 2
Snn（ a 1 2an) S n n1 a n （ n 2 1 )d
S n nn a n （ n 2 1 )d
当公差d=0时，Sn na1 ， 当d≠0时，Snd2n2(a1d2)n,
是关于n的二次函数且常数项 为0.
复习等比数列的有关概念
定义：如果一个数列从第2项起，每一项与它的前一项的比等 于同一个常数（指与n无关的数），这个数列就叫做等比数列， 这个常数叫做等比数列的公比，公比通常用字母q表示。
等比数列的性质练习
1.在等比数列 an ，已知 a15, a9a10100，求 a18
解：∵ a1a18a9a10
a18a9aa110150020
2.在等比数列 bn 中，b4 3 ，求该数列前七项之积。
解： b 1 b 2 b 3 b 4 b 5 b 6 b 7 b 1 b 7 b 2 b 6 b 3 b 5 b 4
判断等比数列的方法
定义法:
an1 q(是与 n无关的数,且 或 q式 0）子 an 中项法:
a n 1•a n 1a n2(0 )
三个数a,b,c成等比数列
acb2
等比数列的性质例题1
例1 已知：b是a与c的等比中项，且a、b、c同号，
求证： abc, a bbc c,a3ab也c成等比数列。
an1 q(是与 n无关的数,且 或 q式 0）子 an
既是等差又是等比数列的数列：非零常数列．
a 由此可知，等比数列 n 的通项公式为
a n a 1q n 1 (a 1 q 0 ) a n a m q n m (a m q 0 )
如果在a与b中间插入一个数G，使a，G，b成等比数列， 那么G叫做a与b的等比中项。
G ab
等比数列的性质
如果一个数列 a1 , a2 , a3 , …，an , …，
是等比数列，它的公比是q，若m+n=p+k，则那么 amanapak
由定义得：ama1•qm1 ana1•qn1 apa1•qp1 aka1•qk1
amana 12qm n 2 apaka12qpk2
amanapak
a n a n 1b b n n 1 a a 1 1 b b 1 1 (( q q 1 1 q q 2 2 )) n n 1 q 1 q 2 .它是一个与n无关的常数，
所以anbn是一个以 q1q2 为公比的等比数列
等比数列的性质例题3
例3 已知 an 是等比数列，且 a n 0 ,a 2 a 4 2 a 3 a 5 a 4 a 6 25
ac 求 a2 c2 解：∵a, 1, c成等差数列, ∴ a＋c＝2,
ac 1 又 a2,1,c2 成等比数列，∴ 2 2
有ac＝1或ac＝－1,
当ac＝1时, 由a＋c＝2得a＝1, c＝1,与a≠c矛盾，
∴ ac＝－1, a 2 c 2 ( a c ) 2 2 a c 6
n是等比数列.
证明：设数列 an 的首项是 a1 ，公比为 q1
b bn 的首项为 1 ，公比为 q2 ，那么数列 anbn
的第n项与第n+1项分别为：
a 1 q 1 n 1 b 1 q 2 n 1 与 a 1 q 1 n b 1 q 2 n
即 a 1 b 1 ( q 1 q 2 ) 为 n 1 与 a 1 b 1 ( q 1 q 2 ) n
∴ 524a8(2)
∴ a8 1458
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
求 a3 a5
解：∵ an 是等比数列，a n 0 ,a 2 a 4 2 a 3 a 5 a 4 a 6 25
∴ a 3 2 2 a 3 a 5 a 5 2 25
∴ (a3a5)225
∴
a 3 a 5 5
等比数列的性质例题4
例4 a≠c,三数a, 1, c成等差数列， a2,1,c2 成等比数列，
3
3
解：证明：由题设 得：
acb2
a b c 3 a a b b c c 3 b 3 a b 2 b b ( c a b b c c ) 2 a
3
3
3
3
∴ abc, a bbc c,a3abc也成等比数列
3
3
等比数列的性质例题2
例2 已知 an,bn是项数相同的等比数列，
于同一个常数（指与n无关的数），这个数列就叫做等差数列，
这个常数叫做等差数列的公差，公差通常用字母d表示。
an1an d(是与 n无关的数或式子
等差数列 an 的通项公式为
当d≠0时，这是 关于n的一个一
ana 1(n1 )d
次函数。
如果在a与b中间插入一个数A，使a，A，b成等差数列，
那么A叫做a与b的等差中项。
等比数列的 性质
复习数列的有关概念1
按一定的次序排列的一列数叫做数列。 数列中的每一个数叫做这个数列的项。
数列中的各项依次叫做这个数列的
第1项（或首项）用 a1 表示，
第2项用 a2 表示，…，第n项用 a n 表示，…，
数列的一般形式可以写成：
a1 , a2 , a3 , …，an , …，
简记作： an
b 4 2 b 1 b 7 b 2 b 6 b 3 b 5
∴前七项之积 3233372187
等比数列的性质练习
q 52 a5
3.在等比数列 an ，已知a22, a5 54 ，求 a 8
a2
解：
a8a5q3a5a a5 25 4 524 1458
另解：∵ a 5 是 a2 与 a 8 的等比中项，
复习数列的有关概念2
如果数列 an 的第n项 a n 与n之间的关
系可以用一个公式来表示，这个公式就叫做 这个数列的通项公式。
S n a 1 a 2 a 3 a n 1 a n 叫做数列 an 的前n项和。
an SnS1 S(nn1 (n1)2)
复习等差数列的有关概念
定义：如果一个数列从第2项起，每一项与它的前一项的差等