1.2《点线面之间的位置关系--平面的基本性质3》教案(苏教版必修2)
数学1.2《点、线、面之间的位置关系》教案十一(苏教版必修2)

1.通过观察身边的实物发现直线与平面的位置关系语言表示:符号表示:4.直线和平面平行的性质定理 语言表示:符号表示:例题剖析例1 如图,已知E 、F 分别是三棱锥A -BCD 的侧棱AB 、AD中点,求证:EF//平面BCD .[变式]:若M 、N 分别是△ABC 、△ACD 的重心,则MN//平面BCD 吗?例2 一个长方体木块如图所示,要经过平面A 1C 1内一点P 和棱BC 将木块锯开,应怎样画线?[思考]:在平面A 1B 1C 1D 1内所画的线与平面ABCD 有何位置关系?例3 求证: 如果三个平面两两相交于直线,并且其中两条直线平行,那么第三条直线也和它们平行.图形表示:图形表示:P A B CDA 1 D 1C 1 B 1 · AEFBCD[思考]:如果三个平面两两相交于三条直线,并且其中的两条直线相交, 那么第三条直线和这两条直线有怎样的位置关系?巩固练习1.指出下列命题是否正确,并说明理由:(1)如果一条直线不在某个平面内,那么这条直线就与这个平面平行; (2)过直线外一点有无数个平面与这条直线平行; (3)过平面外一点有无数条直线与这个平面平行.2.已知直线a ,b 与平面α,下列命题正确的是( )A 、若a //α, b ⊂α,则a //bB 、若a //α,b //α,则a //bC 、若a //b ,b ⊂α,则a //αD 、若a //b ,b ⊂α,则a //α或a ⊂α3.如图,在长方体1AC 的侧面和底面所在的平面中:(1)与直线AB 平行的平面是 (2)与直线1AA 平行的平面是 (3)与直线AD 平行的平面是4.如图:一块矩形木板ABCD 的一边AB 在平面α内, 把这块矩形木板绕AB 转动,在转动过程中,AB 的对边CD 是否都和平面α平行?为什么?课堂小结直线与平面的位置关系,直线与平面平行的判定定理和性质定理.ABC DA 1 D 1 C 1B 1课后训练班级:高一( )班 姓名:____________一 基础题1.梯形ABCD 中, AB //CD , AB ⊂α, CD ⊄α, 则CD 与平面α内的直线的位置关系只能是 ( )A .平行B .平行或异面C .平行或相交D .异面或相交 2.直线l 在平面α外,则下列说法:(1)l //α;(2)l 与α至少有一个公共点;(3) l 与α 至多有一个公共点;(4) l 与α有且仅有一个公共点.其中正确的是 (填序号) 3.证明直线a 与平面α平行的步骤:①首先说明a α;②然后在 内找到 直线b ,并证明直线a 与它平行,再由直线和平面的 得a //平面α. 4.若直线a 、b 都平行于平面α,则a ,b 的位置关系为 . 二 提高题5.如图,AB //α,AC //BD ,αα∈∈D C ,,求证:AC =BD .6.如图,αγβγαβα//,,,AB AB EF CD =⋂=⋂=⋂,求证:EF CD //.三 能力题7.如图, E 、F 、G 、H 分别是空间四边形ABCD 的边AB 、BC 、CD 、DA 的中点, 求证:(1)四点E 、F 、G 、H 共面;(2)BD //平面EFGH ,AC //平面EFGH .AB C E F D β αγ AC FB E HD G8.如图,在三棱柱111C B A ABC -中,C C EF C B F BC E 111//,,∈∈,点∈M 侧面B B AA 11,点F E M ,,确定平面γ,试作出平面γ与三棱柱111C B A ABC -表面的交线.9.如图,在四棱锥P -ABCD 中,M 、N 分别是AB 、PC 的中点,若ABCD 是平行四边形,求证:MN //平面PAD .PNC B A MD CE 1C 1BF 1AB A ∙M。
苏教版高中数学(必修2)1.2《点、线、面之间的位置关系》(两平面平行)word学案
周次
4
课题
两平面平行
2课时
授课形式
新授课
主编
审核
教学目标
1.理解平面与平面的平行与相交的含义
2.掌握两平面平行的判定定理与性质定理
重点难点
1.利用判定定理证明两平面平行,利用性质定理证明直线间的平行。
2.判定定理与性质定理的综合应用,线线、线面、面面之间平行的转化。
教学方法
尝试指导法
课堂结构
一、自主探究
1.两个平面的位置关系
位置关系
两平面平行
两平面相交
公共点
符号表示
图形表示
2.两个平面平行
文字表述
符号表示
判定
定理
如果一个平面内有都平行于另一个平面,那么这两个平面平行,简称:线面平行 面面平行
若
性质
定理
如果两个平行平面同时和第三个平面相交,那么所得的两条交线,简称:面面平行 线线平行。
[变式训练]:如图所示,线段PQ分别交两个平行平面 于A、B两点,线段PD分别交 于C、D两点,线段QF分别交 于F、E两点,若PA=9,AB=12,BQ=12,△ACF面积为72,求△BDE的面积。
四、归纳小结:
在空间平行的判断与证明时要熟练掌握线线、线面、面面平行关系的相互转化。
学后、教后反思:
[变式训练]:在如图所示的几何体中,三个侧面AA1B1B,BB1C1C,CC1A1A都是平行四边形,求证:平面ABC//平面A1B1C1
类型二 面面平行的性质定理的应用
例2、如图,已知 ,点P是平面 外的一点(不在 和 之间),直线PB、PD分别与 相交于点A、B和C、D
(1)求证:AC//BD(2)已知PA=4cm,AB=5cm,PC=3cm,求PD的长。
苏教版高中数学必修二—学同步教学案立体几何平面的基本性质

§1.2 点、线、面之间的位置关系1.2.1 平面的基本性质【课时目标】 1.了解平面的概念及表示法.2.了解公理1、2、3及推论1、2、3,并能用文字语言、图形语言和符号语言分别表述.1.公理1:如果一条直线上的________在一个平面内,那么这条直线上所有的点都在这个平面内.用符号表示为:________________.2.公理2:如果________________________________,那么它们还有其他公共点,这些公共点的集合是经过这个公共点的______________.用符号表示为:⎭⎪⎬⎪⎫P ∈αP ∈β⇒α∩β=l 且P ∈l . 3.公理3:经过不在同一条直线上的三点,________________________.公理3也可简单地说成,不共线的三点确定一个平面.(1)推论1 经过________________________________________,有且只有一个平面. (2)推论2 经过____________,有且只有一个平面. (3)推论3 经过____________,有且只有一个平面.一、填空题 1.下列命题: ①书桌面是平面;②8个平面重叠起来,要比6个平面重叠起来厚; ③有一个平面的长是50 m ,宽是20 m ;④平面是绝对的平、无厚度,可以无限延展的抽象数学概念. 其中正确命题的个数为________. 2.若点M 在直线b 上,b 在平面β内,则M 、b 、β之间的关系用符号可记作____________. 3.已知平面α与平面β、γ都相交,则这三个平面可能的交线有________条.4.已知α、β为平面,A 、B 、M 、N 为点,a 为直线,下列推理错误的是__________(填序号).①A ∈a ,A ∈β,B ∈a ,B ∈β⇒a ⊂β;②M ∈α,M ∈β,N ∈α,N ∈β⇒α∩β=MN ; ③A ∈α,A ∈β⇒α∩β=A ;④A 、B 、M ∈α,A 、B 、M ∈β,且A 、B 、M 不共线⇒α、β重合. 5.空间中可以确定一个平面的条件是________.(填序号) ①两条直线; ②一点和一直线; ③一个三角形; ④三个点.6.空间有四个点,如果其中任意三个点不共线,则经过其中三个点的平面有__________个.7.把下列符号叙述所对应的图形(如图)的序号填在题后横线上.(1)AD/∈α,a ⊂α________.(2)α∩β=a,PD/∈α且PD/∈β________.(3)a⊄α,a∩α=A________.(4)α∩β=a,α∩γ=c,β∩γ=b,a∩b∩c=O________.8.已知α∩β=m,a⊂α,b⊂β,a∩b=A,则直线m与A的位置关系用集合符号表示为________.9.下列四个命题:①两个相交平面有不在同一直线上的三个公共点;②经过空间任意三点有且只有一个平面;③过两平行直线有且只有一个平面;④在空间两两相交的三条直线必共面.其中正确命题的序号是________.二、解答题10.如图,直角梯形ABDC中,AB∥CD,AB>CD,S是直角梯形ABDC所在平面外一点,画出平面SBD和平面SAC的交线,并说明理由.11.如图所示,四边形ABCD中,已知AB∥CD,AB,BC,DC,AD(或延长线)分别与平面α相交于E,F,G,H,求证:E,F,G,H必在同一直线上.能力提升12.空间中三个平面两两相交于三条直线,这三条直线两两不平行,证明三条直线必相交于一点.13.如图,在正方体ABCD -A 1B 1C 1D 1中,对角线A 1C 与平面BDC 1交于点O ,AC 、BD 交于点M ,E 为AB 的中点,F 为AA 1的中点.求证:(1)C 1、O 、M 三点共线; (2)E 、C 、D 1、F 四点共面; (3)CE 、D 1F 、DA 三线共点.1.证明几点共线的方法:先考虑两个平面的交线,再证有关的点都是这两个平面的公共点,或先由某两点作一直线,再证明其他点也在这条直线上.2.证明点线共面的方法:先由有关元素确定一个基本平面,再证其他的点(或线)在这个平面内;或先由部分点线确定平面,再由其他点线确定平面,然后证明这些平面重合.注意对诸如“两平行直线确定一个平面”等依据的证明、记忆与运用.3.证明几线共点的方法:先证两线共点,再证这个点在其他直线上,而“其他”直线往往归结为平面与平面的交线.§1.2 点、线、面之间的位置关系1.2.1 平面的基本性质答案知识梳理1.两点⎭⎪⎬⎪⎫A ∈αB ∈α⇒AB ⊂α 2.两个平面有一个公共点 一条直线3.有且只有一个平面 (1)一条直线和这条直线外的一点 (2)两条相交直线 (3)两条平行直线作业设计 1.1解析 由平面的概念,它是平滑、无厚度、可无限延展的,可以判断命题④正确,其余的命题都不符合平面的概念,所以命题①、②、③都不正确.2.M ∈b ⊂β 3.1,2或3 4.③解析 ∵A ∈α,A ∈β,∴A ∈α∩β.由公理可知α∩β为经过A 的一条直线而不是A .故α∩β=A的写法错误.5.③6.1或4解析四点共面时有1个平面,四点不共面时有4个平面.7.(1)C(2)D(3)A(4)B8.A∈m解析因为α∩β=m,A∈a⊂α,所以A∈α,同理A∈β,故A在α与β的交线m上.9.③10.解很明显,点S是平面SBD和平面SAC的一个公共点,即点S在交线上,由于AB>CD,则分别延长AC和BD交于点E,如图所示.∵E∈AC,AC⊂平面SAC,∴E∈平面SAC.同理,可证E∈平面SBD.∴点E在平面SBD和平面SAC的交线上,连结SE,直线SE是平面SBD和平面SAC的交线.11.证明因为AB∥CD,所以AB,CD确定平面AC,AD∩α=H,因为H∈平面AC,H∈α,由公理3可知,H必在平面AC与平面α的交线上.同理F、G、E都在平面AC与平面α的交线上,因此E,F,G,H必在同一直线上.12.证明∵l1⊂β,l2⊂β,l1P l2,∴l1∩l2交于一点,记交点为P.∵P∈l1⊂β,P∈l2⊂γ,∴P∈β∩γ=l3,∴l1,l2,l3交于一点.13.证明(1)∵C1、O、M∈平面BDC1,又C1、O、M∈平面A1ACC1,由公理3知,点C1、O、M在平面BDC1与平面A1ACC1的交线上,∴C1、O、M三点共线.(2)∵E,F分别是AB,A1A的中点,∴EF∥A1B.∵A1B∥CD1,∴EF∥CD1.∴E、C、D1、F四点共面.(3)由(2)可知:四点E、C、D1、F共面.又∵EF=12A1B.∴D1F,CE为相交直线,记交点为P.则P∈D1F⊂平面ADD1A1,P∈CE⊂平面ADCB.∴P∈平面ADD1A1∩平面ADCB=AD.∴CE、D1F、DA三线共点.。
数学1.2点、线、面之间的位置关系教案一苏教版必修2
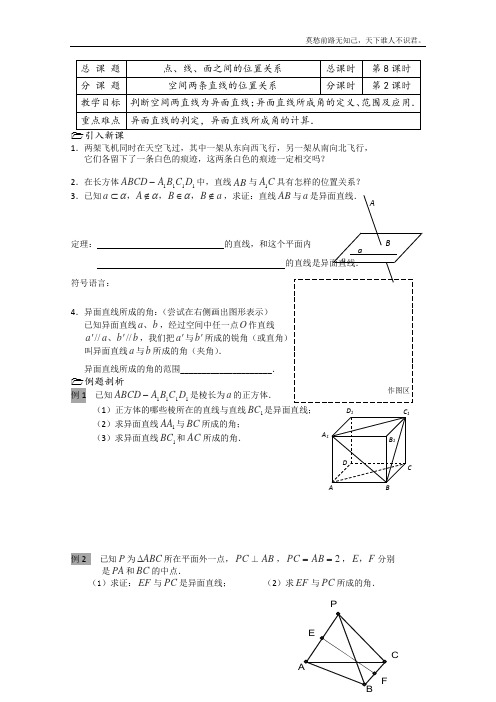
1.两架飞机同时在天空飞过,其中一架从东向西飞行,另一架从南向北飞行, 它们各留下了一条白色的痕迹,这两条白色的痕迹一定相交吗?2.在长方体1111D C B A ABCD -中,直线AB 与C A 1具有怎样的位置关系? 3.已知a B B A a ∉∈∉⊂,,,ααα,求证:直线AB 与a 是异面直线.定理:的直线,和这个平面内的直线是异面直线. 符号语言:4.异面直线所成的角:(尝试在右侧画出图形表示) 已知异面直线b a 、,经过空间中任一点O 作直线b b a a ////''、,我们把a '与b '所成的锐角(或直角) 叫异面直线a 与b 所成的角(夹角). 异面直线所成的角的范围_____________________.例题剖析例1 已知1111D C B A ABCD -是棱长为a 的正方体.(1)正方体的哪些棱所在的直线与直线1BC 是异面直线; (2)求异面直线1AA 与BC 所成的角; (3)求异面直线1BC 和AC 所成的角.例2 已知P 为ABC ∆所在平面外一点,PC ⊥AB ,2==AB PC ,F E ,分别是PA 和BC 的中点.(1)求证:EF 与PC 是异面直线; (2)求EF 与PC 所成的角.A Baα 作图区CA 1P C巩固练习1.在三棱锥所有的棱中互为异面直线的有_____________对. 2.下列说法正确的有________________.(填上正确的序号) ①.过直线外一点可作无数条直线与已知直线成异面直线. ②.过直线外一点只有一条直线与已知直线垂直. ③.若a c b a ⊥,//,则b c ⊥. ④.若c b c a ⊥⊥,,则b a //.3.已知长方体1111D C B A ABCD -中,2321===AA AD AB ,. (1)直线BC 与11C A 所成的角; (2)直线1AA 与1BC 所成的角.课堂小结异面直线的判定,异面直线所成角的计算.A 1课后训练一 基础题1.两条异面直线所成角的取值范围是____________________________. 2.在正方体1111D C B A ABCD -中,面11A ABB 的对角线1AB 所在直线 与直线1DD 所成角的大小是________________________________.3.已知1111D C B A ABCD -是棱长为a 的正方体,F E ,分别是AB AA ,1的中点. (1)哪些棱所在直线与直线DC 是异面直线? (2)哪些棱所在直线与直线EF 垂直? (3)直线11D C 与EF 的夹角是多少?二 提高题4.长方体1111D C B A ABCD - 中,221===AB AA AD ,,则异面直线1AB 与1BC 所成角的余弦值是_______________. 三 能力题5.在空间四边形ABCD 中,F E 、分别是CD AB 、中点,且5=EF , 又86==BC AD ,.求AD 与BC 所成角的大小.6.如图,已知c b a 、、不共面,P c b a =⋂⋂,点c C b B a D a A ∈∈∈∈,,,,求证:BD 和AC 是异面直线.7.空间四边形ABC P -中,CA BC AB PC PB PA =====.ABA 1EF A DB C Pacb(1)写出图中几组异面直线;(2)画出与PC AB ,都垂直且相交的直线. PC。
1.2《点线面之间的位置关系--平面的基本性质3》教案(苏教版必修2)

第7课时平面的基本性质(三)教学目标:使学生能够进行性质与推论的简单应用、正确运用平面的基本性质及三个推论进行共面、共线、共点问题的证明;要通过知识的应用,使学生掌握方法、规律,学会正确推理,以理服人。
教学重点、难点:共面、共线、共点问题的证明。
教学过程:一、复习回顾:三个公理及推论;各个公理及推论的作用。
二、新课讨论:例1:直线AB、BC、CA两两相交,交点分别为A、B、C,证明这三条直线共面.[师]空间的几个点和几条直线,如果都在同一个平面内,那么可以简单地说它们“共面”.分析:两两相交,是说每两条直线都相交.此题是让我们证明三条直线共面,我们学过的公理和推论中都没有关于三条直线的,怎么办呢?[生丙]先由两条直线确定一个平面,再证第三条直线也在这个平面内(学生已作了预习,回答出这样的思路应该是没有问题的).[师]生丙同学的回答正确吗?若正确,怎样证明第三条直线也在这个平面内呢?[生丁]生丙的回答正确.先由两条直线确定一个平面是容易的,要证第三条直线也在这个平面内,只要证第三条直线上有两点在这个平面内就行了,如图,先由AB、AC 确定一个平面,由于B点、C点在确定的平面内,根据公理1可知,直线BC也在这个平面内.[师]生丁所述有道理吗?[生]有道理,完全正确.[师]下面我们根据生丙、生丁两位同学的思路,写出此题的证明过程.证明:∵AB、AC相交,∴AB、AC确定一个平面,设为α∵B∈AB,C∈AC∴B∈α,C∈α∴BC α因此AB、AC、BC都在平面α内.即AB、AC、BC共面.注意:确定的平面叫成什么是无所谓的.不一定非要叫α不可,叫成其他如β、γ都行.[师]谁还有其他不同于生丙同学的意见?[生戊]每两条相交直线都能确定一个平面,若能证明这些平面重合,则也能说明这三条直线共面.[师]同学们想一想,生戊同学的思路可行吗?(同学们积极思考,但无人回答,留出几分钟时间,让同学们继续思考是非常必要的)[生戊]AB、AC可确定一个平面,AB、BC也可确定一个平面,由于点A、B、C 既在第一个平面内,又在第二个平面内.根据公理3,经过A、B、C三点有且只有一个平面,所以这两个平面重合,即AB、AC、BC共面.[师]很好!下面我们根据生戊同学的思路,写出此题的另一种证明.证明:∵AB、AC相交∴AB、AC确定一个平面α∴点A、B、C∈α,且不共线∵AB、BC相交∴AB、BC确定一个平面β∴点A、B、C∈β,且不共线根据公理3,经过不共线的三点A、B、C有且只有一个平面,∴面α与面β重合∴AB、AC、BC共面.[师]从刚才我们的分析讨论中,可以知道,证明共面问题的方法至少有两种:①先由某些条件确定一个平面,然后证明其余已知的都在这个平面内.②所有已知条件确定若干个平面,然后证明这些平面重合.两种证明方法的关键都在“然后”,要注意练习掌握.这两种证明方法比较,第一种更为常用,因为证明若干个平面重合,实在不是一件容易的事情.希望大家都能像生戊同学那样.遇到问题善于思考,多动脑子去想,办法总会是有的.下面再来看一个例子.例2:如图,已知△ABC的各顶点在平面α外,直线AB、BC、AC分别交平面α于P、Q、R,求证:P、Q、R三点共线.分析:平面几何中证明三点共线是怎样证明的?[生]先由两点确定一条直线,然后证明第三点也在这条直线上.[师]这里的三点共线能用这种办法证明吗?比如说,连结点P、点Q,得直线PQ,大家能够证明点R也在直线PQ上吗?[生己]能!由已知条件可知,直线PQ实质上是面ABC与面α的交线,只要证明点R是面ABC与面α的交点,那么R必在直线PQ上.[生庚]既然这样,只要证明点P、Q、R都是面ABC与面α的交点,那么点P、Q、R就共线,它们都在面ABC与面α的交线上.[师]两位同学分析得都很好!在立体几何中,要证明三点共线,只要证明三点都是某两个平面的公共点即可.证明若干点共线的问题,思路同样也是这样的.下面大家一起来写出此题的证明:证明:∵AB∩α=P ∴P∈AB,P∈平面α又AB 平面ABC ∴P∈平面ABC∴由公理2可知,点P在平面ABC与平面α的交线上∴P、Q、R三点共线例3:三个平面两两相交于三条直线,若这三条直线不平行,求证:这三条直线交于一点. 已知:平面α、β、γ两两相交于三条直线l1、l2、l3,且l1、l2、l3不平行.求证:l1、l2、l3相交于一点证明:如图,α∩β=l1,β∩γ=l2,α∩γ=l3,∵l1⊂β,l2⊂β,且l1、l2不平行∴l1与l2必相交,设l1∩l2=P,①则P∈l1⊂α,P∈l2⊂γ∴P∈α∩γ= l3 ②∴l1、l2、l3相交于一点P.例4:已知一条直线与三条平行直线都相交,求证:这四条直线共面.已知:直线a∥b∥c,直线l∩a=A,l∩b=B,l∩c=C.求证:l与a、b、c共面.证明:∵a∥b∴a、b确定一个平面,设为α又l∩a=A,l∩b=B ∴A∈α,B∈α又A∈l,B∈l ∴AB⊂α,即l⊂α同理b、c确定一个平面β,l⊂β.∴平面α与β都过两相交直线b与l.由推论2,两条相交直线确定一个平面.∴α与β重合.故l与a、b、c共面.例5:画出四面体ABCD中过E、F、G三点的截面。
数学知识点苏教版高中数学(必修2)1.2《点、线、面之间的位置关系》(平面的基本性质)word学案-总结

周次
2
课题
平面的基本性质
第 课时
授课形式
新授
主编
审核
教学目标
1.利用生活中的实物对平面进行描述
2.掌握平面的表示法及画法
3.掌握平面的基本性质的三条公理、三个推论及作用
重点
平面的概念及表示,平面性质的三条公理、三个推论
难点
平面性质的三条公理、三个推论的掌握及运用
例2.已知, ,求证:直线AD、BD、CD共面。
变式训练1:求证:两两相交且不公共点的四条直线共面。
变式训练2:证明:如果三条平行线都与一条直线相交,那么这四条直线共面。
【例3】如右图,在四面体ABCD中作截面PQR,若PQ与CB的延
长线交于M,RQ与DB的延长线交于N,RP与DC的延长线交于K,
求证:M、N、K三点共线。
变式训练:如右图,已知空间四边形ABCD中,E、F分别是
AB、AD的中点G、H分别是BC、CD上的点,且 ,
求证:直线EG、FH、AC相交于一点。
【例4】已知 是两两平行的四条直线,试求由 四直线所确定的平面的个数。
变式训练:(1)两个不重合的平面将空间分成个部分。
(2)三个平面把空间分成最我 个部分,最少分成 个部分,则 =。
解决这类问题的要点,一是要将所给出的条件与公理中的条件相比较;二是任意条件中是否有分类讨论的必要性。
确定平面的方法主要依据为公理3和三个推论。
三、例题讲解
【例1】在下列各种面中,不能认为是平面一部分的应该为。
①黑板面;②乒乓球桌面;③篮球的表面;④平静的水面
变式训练:按照给出的要求,完成下面两个相交平面的作图,下图的(1),(2),(3),(4),(5),(6)中,线段AB分别是两个平面的交线。
2013苏教版必修二1.2《点、线、面之间的位置关系》word教案

1.2点、线、面之间的位置关系1.2.1平面的基本性质与推论教学目标:理解公理1、2、3的内容及应用 教学重点:理解公理1、2、3的内容及应用 教学过程:1.平面的基本性质(一) 公理一:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内1、直线与平面的位置关系:直线在这个平面内或者平面经过这条直线。
2、符号:点A 在直线上,记作a A ∈,点A 在平面α内,记作α∈A ,直线a 在平面α内,记作α⊂a3、作用:判断直线是否在平面内生活中,我们看到三脚架可以牢固地支撑照相机或测量用的平板仪等等…… (二) 公理二:经过不在同一条直线上的三点,有且只有一个平面.作用:确定一个平面的依据。
(三) 公理三:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线.今后所说的两个平面(或两条直线),如无特殊说明,均指不同的平面(直线).两个平面有且只有一条公共直线,称这两个平面相交,公共直线称为两个平面的交线,记作l =⋂βα.符号表示为:P ∈α∩β =>α∩β=L ,且P ∈L 公理3作用:判定两个平面是否相交的依据(四) 问题:(1)如果一条线段在平面内,那么这条线段所在直线是否在这个平面内?(2)一条直线经过平面内一点和平面外一点,它和这个平面有几个公共点?为什么?(3)有没有过空间一点的平面?这样的平面有多少个? (4)有没有过空间两点的平面?这样的平面有多少个? (5)有没有过一条直线上三点的平面?这样的平面有多少个? (6)有没有过不在同一条直线上三点的平面?这样的平面有多少个?小结:1.理解公理一、三,并能运用它解决点、线共面问题.2.理解公理二,并能运用它找出两个平面的交线及“三线共点”和“三点共线”问题.3.初步掌握“文字语言”、“符号语言”、“图形语言”三种语言之间的转化.2.平面基本性质的推论(一) 推论1:直线及其外一点确定一个平面 (二) 推论2:两相交直线确定一个平面 (三) 推论3:两平行直线确定一个平面例1已知:空间四点A 、B 、C 、D 不在同一平面内. 求证:AB 和CD 既不平行也不相交.证明:假设AB 和CD 平行或相交,则AB 和CD 可确定一个平面α,则α⊂AB ,α⊂CD ,故α∈A ,α∈B ,α∈C ,α∈D .这与已知条件矛盾.所以假设不成立,即AB 和CD 既不平行也不相交.卡片:1、反证法的基本步骤:假设、归谬、结论;2、归谬的方式:与已知条件矛盾、与定理或公理矛盾、自相矛盾.例2已知:平面α⋂平面β=a ,平面α⋂平面γ=b ,平面γ⋂平面β=c 且c b a 、、不重合.求证:c b a 、、交于一点或两两平行.证明:(1)若三直线中有两条相交,不妨设a 、b 交于A . 因为,β⊂a ,故β∈A , 同理,γ∈A , 故c A ∈.所以c b a 、、交于一点.(2)若三条直线没有两条相交的情况,则这三条直线两两平行. 综上所述,命题得证.例3已知ABC ∆在平面α外,它的三边所在的直线分别交平面α于R Q P 、、.求证:R Q P 、、三点共线.证明:设ABC ∆所在的平面为β,则R Q P 、、为平面α与平面β的公共点,所以R Q P 、、三点共线.卡片:在立体几何中证明点共线,线共点等问题时经常要用到公理2.例4正方体1111D C B A ABCD -中,E 、F 、G 、H 、K 、L 分别是、、、111D A DD DC BC BB B A 、、111的中点.求证:这六点共面. 证明:连结BD 和KF ,因为 L E 、是CB CD 、的中点, 所以 BD EL //. 又 矩形11B BDD 中BD KF //,所以 EL KF //,所以 EL KF 、可确定平面α,所以 L K F E 、、、共面α,同理 KL EH //,故 L K H E 、、、共面β. 又 平面α与平面β都经过不共线的三点L K E 、、,故 平面α与平面β重合,所以E 、F 、G 、H 、K 、L 共面于平面α.同理可证α∈G ,所以,E 、F 、G 、H 、K 、L 六点共面. 卡片:证明共面问题常有如下两个方法:A BC P Q R αCA AB BCD DEFG HK L1111(1)接法:先确定一个平面,再证明其余元素均在这个平面上;(2)间接法:先证明这些元素分别在几个平面上,再证明这些平面重合.课堂练习:1.判断下列命题是否正确(1)如果一条直线与两条直线都相交,那么这三条直线确定一个平面.( )(2)经过一点的两条直线确定一个平面.( )(3)经过一点的三条直线确定一个平面.( )(4)平面α和平面β交于不共线的三点A、B、C.( )(5)矩形是平面图形. ( )2.空间中的四点,无三点共线是四点共面的条件.3.空间四个平面两两相交,其交线条数为 .4.空间四个平面把空间最多分为部分.5.空间五个点最多可确定个平面.6.命题“平面α、β相交于经过点M的直线a”可用符号语言表述为 .7.梯形ABCD中,AB∥CD,直线AB、BC、CD、DA分别与平面α交于点E、G、F、H.那么一定有G直线EF,H直线EF.8.求证:三条两两相交且不共点的直线必共面.小结:本节课学习了平面的基本性质的推论及其应用。
1.2《 点线面位置关系-两个平面平行的判定和性质习题课》教案(苏教版必修2)

第22课时 两个平面平行的判定和性质习题课教学目标:使学生能够充分运用所学定理进行分析、论证。
教学重点、难点:如何根据条件、定理分析问题。
教学过程:复习位置关系,判定与性质定理,距离例1:如图,P 是△ABC 所在平面外的一点,A ′、B ′、C ′分别是△PBC 、△PCA 、 △PAB 的重心(1)求证:平面ABC ∥平面A ′B ′C ′;(2)求△A ′B ′C ′与△ABC 的面积之比。
证明:(1)连结PA ′、PB ′、PC ′并延长交BC 、AC 、AB 于D 、E 、F ,连结DE 、EF 、DF∵A ′、C ′分别是△PBC 、△PAB 的重心∴PA ′=23 PD ,PC ′=23PF ∴A ′C ′∥DF , ∵A ′C ′⊂\平面ABC ,DF ⊂平面ABC∴A ′C ′∥平面ABC同理 A ′B ′∥平面ABC又A ′C ′∩A ′B ′=A ′,A ′C ′、A ′B ′⊂平面A ′B ′C ′∴平面ABC ∥平面A ′B ′C ′(2)由(1)知A ′C ′∥= 23 DF , 又DF ∥= 12AC ∴A ′C ′∥= 13AC 同理:A ′B ′∥= 13 AB ,B ′C ′∥= 13BC ∴△A ′B ′C ′∽△ABC∴S △A ′B ′C ′︰S △ABC =1︰9例2:如图,两条线段AB 、CD 所在的直线是异面直线,CD ⊂平面α,AB ∥α,M 、N 分别是AC 、BD 的中点,且AC 是AB 与CD 的公垂线段(1)求证:MN ∥α;(2)若AB =CD =b ,AC =a ,BD =c ,求线段MN 的长。
(1)证明:过AB 、AC 有一个平面与平面α相交,过B 作此交线的垂线,垂足为F ,由线面平行的性质定理知:AB ∥CF又AC ⊥AB ∴AC ⊥CF得:AC ∥BF∴四边形ABFC 是平行四边形由AC ⊥CF ,AC ⊥CD 知:AC ⊥平面α, ∴BF ⊥平面α 取BF 中点E ,连接EM 、EN ,则:EM ∥CF可得:EM ∥平面α,同理EN ∥平面α∴平面EMN ∥平面α 又MN 平面EMN∴MN ∥α(2)即求等腰三角形CDF 底边上的高例3:如图,棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 、N 、E 、F 分别是棱A 1B 1、A 1D 1、B 1C 1、C 1D 1的中点(1)求证:平面AMN ∥平面EFDB ;(2)求平面AMN 与平面EFDB 之间的距离;(23) (3)求异面直线BE 与FN 之间的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第7课时平面的基本性质(三)
教学目标:
使学生能够进行性质与推论的简单应用、正确运用平面的基本性质及三个推论进行共面、共线、共点问题的证明;要通过知识的应用,使学生掌握方法、规律,学会正确推理,以理服人。
教学重点、难点:共面、共线、共点问题的证明。
教学过程:
一、复习回顾:
三个公理及推论;各个公理及推论的作用。
二、新课讨论:
例1:直线AB、BC、CA两两相交,交点分别为A、B、C,证明这三条直线共面.
[师]空间的几个点和几条直线,如果都在同一个平面内,那么可以简单地说它们“共面”.
分析:两两相交,是说每两条直线都相交.
此题是让我们证明三条直线共面,我们学过的公理和推论中都没有关于三条直线的,怎么办呢?
[生丙]先由两条直线确定一个平面,再证第三条直线也在这个平面内(学生已作了预习,回答出这样的思路应该是没有问题的).
[师]生丙同学的回答正确吗?若正确,怎样证明第三条直线也在这个平面内呢?
[生丁]生丙的回答正确.先由两条直线确定一个平面是容易的,要证第三条直线也在这个平面内,只要证第三条直线上有两点在这个平面内就行了,如图,先由AB、AC 确定一个平面,由于B点、C点在确定的平面内,根据公理1可知,直线BC也在这个平面内.
[师]生丁所述有道理吗?
[生]有道理,完全正确.
[师]下面我们根据生丙、生丁两位同学的思路,写出此题的证明过程.
证明:∵AB、AC相交,
∴AB、AC确定一个平面,设为α
∵B∈AB,C∈AC
∴B∈α,C∈α
∴BC α
因此AB、AC、BC都在平面α内.
即AB、AC、BC共面.
注意:确定的平面叫成什么是无所谓的.不一定非要叫α不可,叫成其他如β、γ都行.
[师]谁还有其他不同于生丙同学的意见?
[生戊]每两条相交直线都能确定一个平面,若能证明这些平面重合,则也能说明这三条直线共面.
[师]同学们想一想,生戊同学的思路可行吗?(同学们积极思考,但无人回答,留出几分钟时间,让同学们继续思考是非常必要的)
[生戊]AB、AC可确定一个平面,AB、BC也可确定一个平面,由于点A、B、C 既在第一个平面内,又在第二个平面内.根据公理3,经过A、B、C三点有且只有一个平面,所以这两个平面重合,即AB、AC、BC共面.
[师]很好!下面我们根据生戊同学的思路,写出此题的另一种证明.
证明:∵AB、AC相交
∴AB、AC确定一个平面α
∴点A、B、C∈α,且不共线
∵AB、BC相交
∴AB、BC确定一个平面β
∴点A、B、C∈β,且不共线
根据公理3,经过不共线的三点A、B、C有且只有一个平面,
∴面α与面β重合
∴AB、AC、BC共面.
[师]从刚才我们的分析讨论中,可以知道,证明共面问题的方法至少有两种:
①先由某些条件确定一个平面,然后证明其余已知的都在这个平面内.
②所有已知条件确定若干个平面,然后证明这些平面重合.
两种证明方法的关键都在“然后”,要注意练习掌握.这两种证明方法比较,第一种更为常用,因为证明若干个平面重合,实在不是一件容易的事情.
希望大家都能像生戊同学那样.遇到问题善于思考,多动脑子去想,办法总会是有的.下面再来看一个例子.
例2:如图,已知△ABC的各顶点在平面α外,直线AB、BC、AC分别交平面α于P、Q、R,求证:P、Q、R三点共线.
分析:平面几何中证明三点共线是怎样证明的?
[生]先由两点确定一条直线,然后证明第三点也在这条直
线上.
[师]这里的三点共线能用这种办法证明吗?比如说,连结
点P、点Q,得直线PQ,大家能够证明点R也在直线PQ上吗?
[生己]能!由已知条件可知,直线PQ实质上是面ABC与
面α的交线,只要证明点R是面ABC与面α的交点,那么R必在直线PQ上.
[生庚]既然这样,只要证明点P、Q、R都是面ABC与面α的交点,那么点P、Q、R就共线,它们都在面ABC与面α的交线上.
[师]两位同学分析得都很好!在立体几何中,要证明三点共线,只要证明三点都是某两个平面的公共点即可.证明若干点共线的问题,思路同样也是这样的.
下面大家一起来写出此题的证明:
证明:∵AB∩α=P ∴P∈AB,P∈平面α
又AB 平面ABC ∴P∈平面ABC
∴由公理2可知,点P在平面ABC与平面α的交线上
∴P、Q、R三点共线
例3:三个平面两两相交于三条直线,若这三条直线不平行,求证:这三条直线交于一点. 已知:平面α、β、γ两两相交于三条直线l1、l2、l3,且l1、l2、l3不平行.
求证:l1、l2、l3相交于一点
证明:如图,α∩β=l1,β∩γ=l2,α∩γ=l3,
∵l1⊂β,l2⊂β,且l1、l2不平行
∴l1与l2必相交,设l1∩l2=P,①则P∈l1⊂α,P∈l2⊂γ
∴P∈α∩γ= l3 ②∴l1、l2、l3相交于一点P.
例4:已知一条直线与三条平行直线都相交,求证:这四条直线共面.
已知:直线a∥b∥c,直线l∩a=A,l∩b=B,l∩c=C.
求证:l与a、b、c共面.
证明:∵a∥b
∴a、b确定一个平面,设为α
又l∩a=A,l∩b=B ∴A∈α,B∈α
又A∈l,B∈l ∴AB⊂α,即l⊂α
同理b、c确定一个平面β,l⊂β.
∴平面α与β都过两相交直线b与l.
由推论2,两条相交直线确定一个平面.
∴α与β重合.
故l与a、b、c共面.
例5:画出四面体ABCD中过E、F、G三点的截面。
例6:如图正方体中,点C在与A、B不共面的其余8条棱上,画出过A、B、C三点的截面。
三、课堂练习:
课本P28习题6.
四、课堂小结:
本节课我们讨论了平面基本性质——三个公理及其推论的简单应用,讨论了共面、共线、共点问题的证明,请同学们注意:
对于共面问题的证明,一般地是先由某些条件确定一个平面,然后证明其余已知的都在这个平面内;
对于点共线问题的证明,只要证明这些点都是某两个平面的公共点即可;
对于线共点问题的证明,一般地是先证明某两条直线相交,然后再证明这个交点在其余直线上或者证明其余直线过这个交点.
无论怎样的问题的证明、推理必须严谨严密、有条有理、完整无纰漏,绝对不能东拉西扯、杂乱无章.
五、课后作业:
补充:
1.不共点的四条直线两两相交,求证:这四条直线在同一个平面内.
已知:直线a、b、c、d两两相交,且不过同一点.(注意:两两相交的意思是,如果n 条直线两两相交,那么任一条直线与另外(n-1)条直线都相交,都有公共点.)求证:直线a、b、c、d共面.
(证明略)
2.如图,AB∩α=P,CD∩α=P,A、D与B、C分别在面α的两侧,AC∩α=Q,BD∩α=R. 求证:P、Q、R三点共线.
证明:∵AB∩α=P,CD∩α=P ∴AB∩CD=P
∴AB、CD可确定一个平面,设为β.
∵A∈AB,C∈CD,B∈AB,D∈CD
∴A∈β,C∈β,B∈β,D∈β
∴AC⊂β,BD⊂β,平面α、β相交,
∵AB∩α=P,AC∩α=Q,BD∩α=R
∴P、Q、R三点是平面α与平面β的公共点
∴P、Q、R都在α与β的交线上
故P、Q、R三点共线.
3.在正方体ABCD—A1B1C1D1中,A1C与面DBC1交于O点,AC、BD交于M,
求证:C1、O、M三点共线.
证明:∵C1、O、M∈面BDC1
又C1、O、M∈面A1ACC1
由公理2,C1、O、M在平面BDC1与平面A1ACC1的交线上.
∴C1、O、M三点共线.
4.已知:a ⊂α,b ⊂α,a ∩b =A ,P ∈b ,PQ ∥a ,
求证:PQ ⊂α.
证明:∵PQ ∥a ,∴PQ 、a 确定一个平面,设为β,
∴P ∈β,a ⊂β,P ∉a
又P ∈α,a ⊂α,P ∉a
由推论1:过P 、a 有且只有一个平面
∴α、β重合. ∴PQ ⊂α.
5.如图,在棱长为a 的正方体ABCD —A 1B 1C 1D 1中,M 、N 分别是AA 1、D 1C 1的中点,过D 、M 、N 三点的平面与正方体的下底面相交于直线l ,
(1)画出l 的位置;
(2)设l ∩A 1B 1=P ,求PB 1的长.
解:(1)平面DMN 与平面AD 1的交线为DM ,设DM ∩D 1A 1=Q . 则平面DMN 与平面A 1C 1的交线为QN .
QN 即为所求作的直线l .
(2)设QN ∩A 1B 1=P .
∵△MA 1Q ≌△MAD ,∴A 1Q =AD =a =A 1D 1
∴A 1是QD 1的中点,又A 1P ∥D 1N
∴A 1P =12 D 1N =14 C 1D 1=14
a ∴PB 1=A 1B 1-A 1P =a -14 a =34
a (二)1.预习课本P 24~P 25空间直线——空间两条直线的位置关系和平行直线.
2.预习提纲
(1)空间两条直线的位置关系有几种?各有什么特征?
(2)怎样理解两条直线不同在任何一个平面?
(3)公理4的具体内容是什么?
(4)公理4用符号语言如何表示?。
