伯努利方程习题
化工原理伯努利方程练习题

第一章 流体流动【例1-1】 已知硫酸与水的密度分别为1830kg/m 3与998kg/m 3,试求含硫酸为60%(质量)的硫酸水溶液的密度为若干。
解:根据式1-49984.018306.01+=mρ =(3.28+4.01)10-4=7.29×10-4ρm =1372kg/m 3【例1-2】 已知干空气的组成为:O 221%、N 278%和Ar1%(均为体积%),试求干空气在压力为9.81×104Pa 及温度为100℃时的密度。
解:首先将摄氏度换算成开尔文100℃=273+100=373K再求干空气的平均摩尔质量M m =32×0.21+28×0.78+39.9×0.01=28.96kg/m 3根据式1-3a 气体的平均密度为:3kg/m 916.0373314.896.281081.9=⨯⨯⨯=m ρ【例1-3 】 本题附图所示的开口容器内盛有油和水。
油层高度h 1=0.7m 、密度ρ1=800kg/m 3,水层高度h 2=0.6m 、密度ρ2=1000kg/m 3。
(1)判断下列两关系是否成立,即 p A =p'A p B =p'B(2)计算水在玻璃管内的高度h 。
解:(1)判断题给两关系式是否成立 p A =p'A 的关系成立。
因A 与A '两点在静止的连通着的同一流体内,并在同一水平面上。
所以截面A-A'称为等压面。
p B =p'B 的关系不能成立。
因B 及B '两点虽在静止流体的同一水平面上,但不是连通着的同一种流体,即截面B-B '不是等压面。
(2)计算玻璃管内水的高度h 由上面讨论知,p A =p'A ,而p A =p'A 都可以用流体静力学基本方程式计算,即p A =p a +ρ1gh 1+ρ2gh 2p A '=p a +ρ2gh于是 p a +ρ1gh 1+ρ2gh 2=p a +ρ2gh简化上式并将已知值代入,得800×0.7+1000×0.6=1000h解得 h =1.16m【例1-4】 如本题附图所示,在异径水平管段两截面(1-1'、2-2’)连一倒置U 管压差计,压差计读数R =200mm 。
伯努利方程习题参考(课后给学生)

3
v3
3
180N
对平板冲击力 F R 180 N
【例2】 有一贮水装置如图5-4所示,贮水池足够大,当阀 门关闭时,压强计读数为2.8个大气压强。而当将阀门全 开,水从管中流出时,压强计读数是0.6个大气压强,试 求当水管直径d=12cm时,通过出口的体积流量(不计流动 损失)。
1
沿流向取为x 方向 列动量方程
2
d1
v1 p1
1
R d 2 R
2
2
v2
R′
d1 Q2 d2 2 R p1 0 Q(v2 x v1x ) ) [1 ( ) ] 2 4 d1 d 2 4
2 25 2 4 0.02 2 0 . 05 5 R 1000( ) [ 1 ( ) ] 2 . 38 10 2 3600 0.02 0.05 4
2014-12-15
(5-6)
3
考虑到实际情况
qV实 Cd qV Cd
4
d
2 2
2 g ( 液 )h液
式中Cd为流量系数,通过实验测定。
[1 ( A2 / A1 ) 2 ]
(5-7)
文特里流量计是节流装置中的一种,除此之外还有孔 板,喷嘴等,其基本原理与文特里流量计基本相同,不再 叙述。
将式(5-4)代入到式(5-3),则
(5-4)
(5-5)
V2
2 g ( 液 )h液 [1 ( A2 / A1 ) 2 ]
式(5-5)表明,若ρ液, ρ ,A2,A1已知,只要测量出h 液,就可以确定流体的速度。流量为:
2 2 g ( 液 )h液 qV A2V2 d 2 4 [1 ( A2 / A1 ) 2 ]
伯努利方程习题
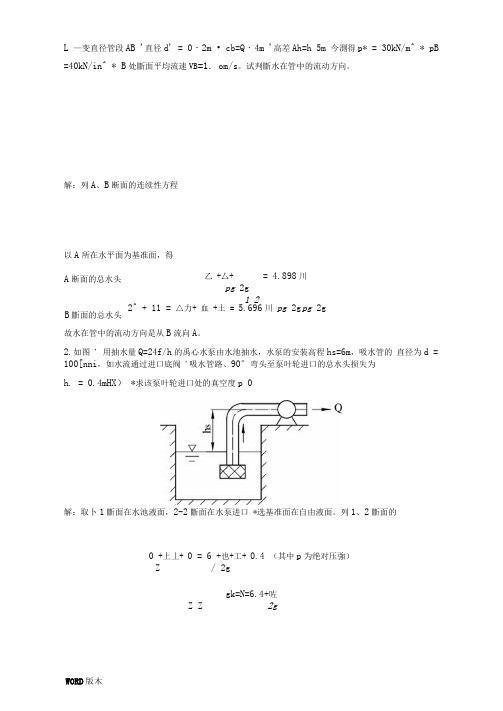
L —变直径管段AB '直径d' = 0・2m • cb=Q ・4m '高差Ah=h 5m 今測得p* = 30kN/m^ * pB =40kN/in^ * B 处斷面平均流速VB =1. om/s 。
试判斷水在管中的流动方向。
解:列A 、B 断面的连续性方程以A 所在水平面为基准面,得1 22^ + 11 = △力+ 血 +土 = 5.696川 pg 2g pg 2g 故水在管中的流动方向是从B 流向A 。
2.如图 ' 用抽水量Q=24f/h 的禹心水泵由水池抽水,水泵的安装高程hs=6m ,吸水管的 直径为d = 100[nni ,如水流通过进口底阀 '吸水管路、90°弯头至泵叶轮进口的总水头损失为h. = 0.4mHX ) *求该泵叶轮进口处的真空度p 0解:取卜1斷面在水池液面,2-2斷面在水泵进口 *选基准面在自由液面。
列1、2斷面的0 +上丄+ 0 = 6 +也+工+ 0.4 (其中p 为绝对压強)Z / 2ggk=N=6.4+咗Z Z 2gA 断面的总水头乙 +厶+ = 4.898川pg 2g B 斷面的总水头4Q 4x24----- 5 ----- = 0.849/M /SPvI 0 849 1= 9.8x 6,4 + -^—1 = 63. U/i2x9.83.如图,高压水箱的泄水管*当阀门关闭时,测得安装在此管路上的压力表读数为pi = 280kPa *当阀门开启后,庄力表上的读数变为p2=60kPa,已知此泄水管的直径D=25mm *求每小时的泄水流量。
(不计水头损失)解:取管中心轴为尿准面 ' 水箱中取17断面,压力表处为2・2斷面*闸门关闭时所以自由液面至管中心轴距离h=28・ 57m闸门打开后*列1一1 ' 2-2斷面能量方程/ 2gV2=2O・ 98ni/sQ=V2A2=37.4.如图,大水箱中的水经水箱底部的竖管流入大%,竖管直径为di = 200nini - 道出口处为收缩喷嘴,其直径d2=100nini,不计水头损失,求管道的泄流量Q及A点相对压强p\。
伯努利方程习题参考(课后给学生)

思考题
(1)欧拉法研究----------的变化情况 (A) 每个质点的速度 (B) 每个质点的轨迹
( C) 每个空间点的速度
(D) 每个空间点的质点轨迹
( C)
思考题
(2). 二元流动的速度分布为 u=2x+t, v=y2+2t, 则 t=0时, 点(1,2)的流体加 速度分量 ax 和ay 为---------(A) 1,2 ( C) 2,4 (B) 3,16 (D) 5,18
则
p1 Hg h h1 13.6 0.2 0.72 2 (mH2O) g
列1-1和2-2断面的伯努利方程
Hg gh p1 gh1 p1 Hg gh gh1
p1 V12 p 2 V 22 z1 z2 g 2 g g 2 g
3
v3
3
180N
对平板冲击力 F R 180 N
【例2】 有一贮水装置如图5-4所示,贮水池足够大,当阀 门关闭时,压强计读数为2.8个大气压强。而当将阀门全 开,水从管中流出时,压强计读数是0.6个大气压强,试 求当水管直径d=12cm时,通过出口的体积流量(不计流动 损失)。
将式(5-4)代入到式(5-3),则
(5-4)
(5-5)
V2
2 g ( 液 )h液 [1 ( A2 / A1 ) 2 ]
式(5-5)表明,若ρ液, ρ ,A2,A1已知,只要测量出h 液,就可以确定流体的速度。流量为:
2 2 g ( 液 )h液 qV A2V2 d 2 4 [1 ( A2 / A1 ) 2 ]
15
2014-12-15
16
2014-12-15
伯努利方程的应用(例题)

将以上各值代入(b)式,可求得输送碱 液所需的外加能量:
We
18.59.81
2.452 2
29.4 103 1100
30.8
242.0
j
/
kg
碱液的质量流量:
qm
4
d 2 2u2
0.785 0.072
2.451000
10.37kg
/
s
泵的有效功率:
Ne Weqm 24210.37 2510W 2.51kW
2019/7/29
Z3 1m,Z4 0.2m,
P4 0(表压),P3 ? 1000kg / m3
将已知数据代入柏努利方程式得:
g p3 1.96
P3 11770Pa(表压)
计算塔前管路,取河水表面为1-1’截面,喷头内侧为2-2’ 截面,在1-1’和2-2’截面间列柏努利方程。
截面2-2’处压强为 :
P2 gh 10009.810.5 4905Pa(表压)
流经截面1-1’与2-2’的压强变化为:
P1 P2 (101330 3335) (10330 4905)
P1
(101330 3335)
0.079 7.9% 20%
u2
qV A
qV
d2
5
3600 0.0332
1.62m / s
4
4
由连续性方程 u1 A1 u2 A2 ∵A1>>A2,
因为u1<<u2, 所以:u1≈0
已知:We=0 ,
R 30J / kg
伯努利方程习题

伯努利方程习题1. 一变直径管段AB ,直径d A =0.2m ,d B =0.4m ,高差Δh =1.5m 。
今测得p A =30kN/m 2,p B =40kN/m 2,B 处断面平均流速v B =1.5m/s 。
试判断水在管中的流动方向。
解:列A 、B 断面的连续性方程 v v A A B BA A = 得 v v 6m/sB BA AA A ==以A 所在水平面为基准面,得 A 断面的总水头 24.8982A AA p v z m g gρ++=B断面的总水头225.69622B B B BB p v p v z h m g g g gρρ++=∆++=故水在管中的流动方向是从B 流向A 。
2. 如图,用抽水量Q =24m 3/h 的离心水泵由水池抽水,水泵的安装高程h s =6m ,吸水管的直径为d =100mm ,如水流通过进口底阀、吸水管路、90º弯头至泵叶轮进口的总水头损失为h w =0.4mH 2O ,求该泵叶轮进口处的真空度p v 。
Q解:取1-1断面在水池液面,2-2断面在水泵进口,选基准面在自由液面。
列1、2断面的能量方程,有4.02600222+++=++gvp p aγγ(其中p 为绝对压强)即gvp p p va 24.6222+==-γγ其中s m d Q v /849.036001.02444222=⨯⨯⨯==ππ故a v kPp 1.638.92849.04.68.92=⎪⎪⎭⎫⎝⎛⨯+⨯=3. 如图,高压水箱的泄水管,当阀门关闭时,测得安装在此管路上的压力表读数为p 1=280kPa ,当阀门开启后,压力表上的读数变为p 2=60kPa ,已知此泄水管的直径D =25mm ,求每小时的泄水流量。
(不计水头损失)解:取管中心轴为基准面,水箱中取1-1断面,压力表处为2-2断面,闸门关闭时h p γ=1所以自由液面至管中心轴距离h =28.57m闸门打开后,列1-1、2-2断面能量方程gvp h 2000222++=++γ即: v 2=20.98m/sQ =v 2A 2=37.1m 3/h4. 如图,大水箱中的水经水箱底部的竖管流入大气,竖管直径为d 1=200mm ,管道出口处为收缩喷嘴,其直径d 2=100mm ,不计水头损失,求管道的泄流量Q 及A 点相对压强p A 。
伯努利方程的应用(例题)

截面2-2’处压强为 :
P2 gh 10009.810.5 4905Pa(表压)
流经截面1-1’与2-2’的压强变化为:
P1 P2 (101330 3335) (10330 4905)
P1
(101330 3335)
0.079 7.9% 20%
2019/7/29
gz1
u12 2
p1
We
gz2
u22 2
p2
R
式中 :
Z1 1m,Z2 6m
u1
0, u2
VS A
84.82
3600
0.12
3m / s
4
P1 0(表压),
p2 0.02106 11770 8230Pa(表压)
gz1
u12 2
p1
We
gz2
u22 2
p2
R
其中: z1=0; p1=147×103 Pa(表压);
u1
qV A
qm
d2
1000 / 3600 0.785 0.0532 1000
1.26m / s
4
2019/7/29
z2=0;喷嘴出口速度u2可直接计算或由 连续性方程计算
喷射泵是利用流体流动时静压能与动能的转换 原理进行吸、送流体的设备。当一种流体经过喷 嘴时,由于喷嘴的截面积比管道的截面积小得多 ,流体流过喷嘴时速度迅速增大,使该处的静压 力急速减小,造成真空,从而可将支管中的另一 种流体吸入,二者混合后在扩大管中速度逐渐降 低,压力随之升高,最后将混合流体送出。
伯努利方程计算题

伯努利方程计算题一、一根内径均匀的细玻璃管,开口向上竖直放置,管内有一段长15cm的水银柱封闭着一段空气柱,当玻璃管在竖直平面内缓慢转动至开口向下时,发现管内水银柱长度变为18cm,则大气压强为多少cmHg?(答案:C)A. 60cmHgB. 55cmHgC. 65cmHgD. 70cmHg二、一端封闭的粗细均匀的玻璃管,开口向下竖直插入水银槽中,管内封闭有一定质量的气体,管内水银面比槽内水银面高4cm,现将玻璃管缓慢向上提起(管口未离开槽内水银面),直到管内外水银面相平,则此过程中(答案:A)A. 气体体积增大,压强减小B. 气体体积减小,压强增大C. 气体体积不变,压强不变D. 无法判断气体体积和压强的变化三、一端封闭的粗细均匀的玻璃管,开口向下竖直插入水银槽中,管内封闭有一定质量的气体,管内水银面比槽内水银面高4cm,若使玻璃管绕其下端在槽内水银面内匀速转动,则转动后(答案:D)A. 管内气体体积增大B. 管内气体体积减小C. 管内气体压强增大D. 管内气体压强不变四、一端封闭的粗细均匀的玻璃管,开口向下竖直插入水银槽中,管内封闭有一定质量的气体,管内水银面比槽内水银面高4cm,若环境温度升高,则管内水银面比槽内水银面高度差将(答案:B)A. 增大B. 减小C. 不变D. 无法判断五、一端封闭的粗细均匀的玻璃管,开口向下竖直插入水银槽中,管内封闭有一定质量的气体,管内水银面比槽内水银面高4cm,若将玻璃管稍微上提一些(管口未离开槽内水银面),则(答案:A)A. 管内气体体积增大,压强减小B. 管内气体体积减小,压强增大C. 管内气体体积不变,压强不变D. 无法判断气体体积和压强的变化六、一根两端开口的玻璃管,下端附一塑料片(塑料片重力不计),竖直压入水面下20cm 深处,然后向管内缓慢注入某种液体,当管内液面高出水面5cm时,塑料片刚好脱落,则该液体的密度是多大?(答案:B)A. 0.8g/cm³B. 1.2g/cm³C. 1.0g/cm³D. 0.5g/cm³七、一端封闭的粗细均匀的玻璃管,开口向下竖直插入水银槽中,管内封闭有一定质量的气体,管内水银面比槽内水银面高4cm,若将玻璃管稍微倾斜一些(管口未离开槽内水银面),则(答案:D)A. 管内气体体积增大,压强减小B. 管内气体体积减小,压强增大C. 管内气体体积不变,压强不变D. 无法判断气体体积和压强的变化八、一根两端开口的玻璃管,下端附一塑料片(塑料片重力不计),竖直压入水面下10cm 深处,然后向管内缓慢注入水,当管内水面比管外水面高出多少时,塑料片刚好脱落?(答案:A)A. 10cmB. 5cmC. 15cmD. 20cm九、一端封闭的粗细均匀的玻璃管,开口向下竖直插入水银槽中,管内封闭有一定质量的气体,管内水银面比槽内水银面高4cm,若将玻璃管上端开口封闭,再将玻璃管缓慢向上提起(管口未离开槽内水银面),直到管内外水银面相平,则此过程中(答案:C)A. 气体体积增大,压强增大B. 气体体积减小,压强减小C. 气体体积不变,压强增大D. 无法判断气体体积和压强的变化十、一根两端开口的玻璃管,下端附一塑料片(塑料片重力不计),竖直压入水面下20cm 深处,然后向管内缓慢注入酒精,当管内酒精面高出水面多少时,塑料片刚好脱落?(答案:B)A. 10cmB. 25cmC. 30cmD. 35cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
伯努利方程习题
1. 一变直径管段AB ,直径d A =0.2m ,d B =0.4m ,高差Δh =1.5m 。
今测得p A =30kN/m 2,p B =40kN/m 2,B 处断面平均流速v B =1.5m/s 。
试判断水在管中的流动方向。
解:列A 、B 断面的连续性方程 v v A A B B
A A = 得 v v 6m/s
B B
A A
A A =
=
以A 所在水平面为基准面,得 A 断面的总水头 2
4.8982A A
A p v z m g g
ρ++=
B
断
面
的
总
水头
22
5.69622B B B B
B p v p v z h m g g g g
ρρ++=∆++=
故水在管中的流动方向是从B 流向A 。
2. 如图,用抽水量Q =24m 3/h 的离心水泵由水池抽水,水泵的安装高程h s =6m ,吸水管的直径为d =100mm ,如水流通过进口底阀、吸水管路、90º弯头至泵叶轮进口的总水头损失为h w =0.4mH 2O ,求该泵叶轮进口处的真空度p v 。
d
解:取管中心轴为基准面,水箱中取1-1断面,压力表处为2-2断面,闸门关闭时
h p γ=1
所以自由液面至管中心轴距离
h =28.57m
闸门打开后,列1-1、2-2断面能量方程
g
v
p h 20002
2
2
++=++γ
即: v 2=20.98m/s
Q =v 2A 2=37.1m 3/h
4. 如图,大水箱中的水经水箱底部的竖管流入大气,竖管直径为d 1=200mm ,管道出口处为收缩喷嘴,其直径d 2=100mm ,不计水头损失,求管道的泄流量Q 及A 点相对压强p A 。
4m
7m
A
d 1
d 2
解:取1-1断面在A 处,2-2断面在喷嘴出口,自由液面为0-0断面,选基准面在喷嘴出口。
列0、2断面的能量方程,有
g
v
2000072
2
++=++
v 2=11.71m/s Q =v 2A 2=0.09m 3/s v 1=Q/A 1=2.93m/s
又列0、1断面的能量方程,有
g
v p A
240072
11αγ
+
+
=++
p A =25.1kN
5. 如图,虹吸管从水池引水至C 端流入大气,已知a =1.6m ,b =3.6m 。
若不计损失,试求:(1)管中流速v 及B 点的绝对压强p B 。
(2)若B 点绝对压强水头下降到0.24m 以下时,将发生汽化,设C 端保持不动,问欲不发生汽化,a 不能超过多少?
C
a
b
解:取1-1断面在C 处,2-2断面在B 处,自由
液面为0-0断面,基准面选在过C 面中心的水平面。
列0、1断面的能量方程,有
g
v
200006.32
1
++=++
v 1=v 2=8.4m/s
又列0、2断面的能量方程,有
g
v
p B
22.50106.32
2
++=++γ
p B =47.04kPa
g
v
a 224.06.30106.32
2
+++=++
a =6.16m
6. 如图,由水池通过等直径虹吸管输水,A 点为虹吸管进口处,H A =0;B 点为虹吸管中与水池液面齐高的部位,H B =6m ;C 点为虹吸管中的最高点,H C =7m ;D 点为虹吸管的出口处,H D =4m 。
若不计流动中的能量损失,求虹吸管
的断面平均流速和A 、B 、C 各断面上的绝对压强。
B
6m
1m
4m
C D
A
解:A 、B 、C 、D 各断面上的平均流速相等,用v 表示,
列自由液面与出口断面D 的能量方程
g
v 2040062
+
+=++
v =6.26m/s
列自由液面与A 断面的能量方程
g
v p p A
a
20062
+
+=++γγ p A =140.2kPa
列自由液面与B 断面的能量方程 g
v p p B
a
26062
+
+=++γγ p B =81.4 kPa
列自由液面与C 断面的能量方程 g
v p p C
a
27062
++=++γγ p C =71.6 kPa
7. 如图,水从敞口水池沿一截面有变化的管路排出,若质量流量q m =15kg/s ,d 1=100mm ,d 2=75mm ,不计损失,试求所需的水头H 以及第二管段中央M 点的相对压强。
d 1
H
d 2
M
解:取管中心轴为基准面,列自由液面与出口断面的能量方程
g
v
H 200002
2
++=++
其中:
s m d q v m
/395.34222==
ρ
π
故 H =0.588m
又列自由液面与M 处断面的能量方程
g
v
p H m
20002
1
++=++γ
其中
s m d q v m
/9.14211==
ρ
π
故 p m =3.94kPa。
