2019—2020学年度福建省福州市第一学期八县(市、区)一中期中联考【含解析】
2019-2020学年福建省福州市八县(市、区)一中高二上学期期中联考化学试题 Word版

2019---2020学年度第一学期八县(市)一中期中联考高中二年化学科试卷考试时间:11月14日完卷时间:90分钟满分:100分相对原子质量:H-1 Li-7 C-12 N-14 O-16 Cu-64一、选择题:(共22小题,共44分,每小题只有一个选项符合题意)1、下列我国科技创新的产品设备在工作时,能量转化过程与氧化还原反应有关的是()A.①②B. ③④C.②③D.①④2、下列食品添加剂中,其使用目的与反应速率有关的是()A. 调味剂B. 防腐剂C. 着色剂D. 增稠剂3、在酸性条件下,可发生如下反应:ClO-3+2M3++4H2O=M2O7n-+Cl-+8H+,M2O7n-中M的化合价是()A.+4B.+5C.+6D.+74、下列反应中,在任何温度下都不自发进行的是()A.2O 3(g)=3O2(g) △H<0 B.2CO(g)=2C(s)+O2(g) △H>0C.N2(g)+3H2(g)=2NH3(g ) △H<0 D.CaCO3(s)=CaO(s)+CO2(g) △H>05、在N2+3H22NH3的反应中,经过一段时间后,NH3的浓度增加了0.8 mol/L,在此段时间内用H2表示的平均反应速率为0.25mol/(L·s),则此段时间是()A.2 s B.3.2 s C.4.8 s D.5.6 s6、对于反应2NO2(g)N2O4(g),关于反应速率的说法正确的是()A.6mol·L﹣1·s﹣1的反应速率一定比3.5mol·L﹣1·s﹣1的反应速率大B.反应速率越大,可逆反应进行的越完全C.恒温恒容下,充入N2,压强增大但正逆反应速率都不变D.升温或加压都能增大反应物活化分子百分数,从而加快速率7、某反应过程能量变化如右图所示,下列说法正确的是()A.该反应为放热反应,热效应ΔH=E1-E2B.有催化剂条件下,反应的活化能等于E1+E2C.使用催化剂后,整个反应的速率快慢由E2对应反应决定D.曲线b说明催化剂参与反应过程,降低反应的活化能,但不改变ΔH8、一定温度下,在 2 L密闭容器中发生反应:2N2O5(g) 4NO2(g)+O2(g)ΔH>0。
福建省福州市八县(市区)一中2019-2020学年高二英语上学期期中联考试题

福建省福州市八县(市、区)一中20192020学年高二英语上学期期中联考试题考试日期:11月15日完卷时间:120分钟满分:150分第I卷(共90分)第一部分:听力(共两节,满分30分)第一节(共5小题,每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the woman suggest the man bring?A. Milk.B. Coffee.C. Tea.2. What does the man like to do before an exam?A. Do sports.B. Read a lot.C. Relax at home.3. What did the man do last night?A. He held a party.B. He lost his phone.C. He bought something in a shop.4. How many people will go to the football match?A. Two.B. Three.C. Four.5. What's the probable relationship between the speakers?A. Mother and son.B. Brother and sister.C. Teacher and student.第二节听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题, 每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6. Where does the conversation take place?A. At a bookshop.B. At a museum.C. At a library.7. Which direction does the woman point the man?A. Straight ahead.B. To the right.C. To the left.听第7段材料,回答第810题。
福建省福州市八县(市、区)一中2019-2020学年高三上学期期中联考英语试题及答案解析

福建省福州市八县(市、区)一中2019-2020学年高三上学期期中联考英语试题注意事项:1.答题前填写好自己的姓名、班级、考号等信息;2.请将答案正确填写在答题卡上。
第I卷(选择题)一、短对话1.What are the speakers mainly talking about?A.Driving license. B.Car accidents. C.How to drive. 2.How long would the man work in the library?A.5 hours. B.3 hours. C.4 hours. 3.Why does Tim apologize?A.He made Helen embarrassed.B.He asked for a public apology.C.He took the dictionary without asking.4.How is Andrew?A.Fine. B.Sick. C.Tired.5.In what school is the man’s daughter?A.Kindergarten. B.Primary school. C.College二、长对话听下面一段较长对话,回答以下小题。
6.Where was Jason kicked out of yesterday?A.A restaurant. B.A work place. C.A food store. 7.What did the man ask Jason about?A.His motion. B.His food. C.His job.听下面一段较长对话,回答以下小题。
8.Where does the conversation take place probably?A.In a hotel. B.In a shopping mall. C.In a party.9.What does the woman thank the man for?A.The lunch. B.The boots. C.The shoes.听下面一段较长对话,回答以下小题。
福建省福州市八县(市)联考2019-2020学年高一上学期期中物理试卷 (含答案解析)

福建省福州市八县(市)联考2019-2020学年高一上学期期中物理试卷一、单选题(本大题共8小题,共32.0分)1.第29届杭州国际马拉松鸣枪开跑,来自45个国家和地区的3万名路跑爱好者参加了本次比赛.下列说法正确的是()A. 研究运动员平均时速时,不能将运动员看作质点B. 出发后前2小时内与第2小时内是指同一段时间C. 不同观众观察同一名运动员的运动,其结果可能有所不同D. 位移是描述物体位置变化的物理量,“全马”42.195公里指的就是位移2.如图所示是一沿笔直公路做匀加速直线运动的汽车的速度计.某同学在汽车中观察速度计指针位置的变化,开始时指针指示在如图(甲)所示的位置,经过7s后指针位置如图(乙)所示.有关上述运动过程,下列说法中正确的是()A. 甲图直接读出的是汽车运动的平均速度B. 乙图不能读出汽车的瞬时速率C. 汽车运动的加速度约为1.6m/s2D. 汽车运动的加速度约为5.7m/s23.如图所示,一本物理书静止在水平桌面上,下列说法正确的是()A. 由于桌面很硬,所以桌面没有发生形变B. 由于桌面发生微小的形变,对书本产生垂直于桌面向上的弹力C. 书对桌子的压力,是由于桌子的形变产生的D. 书对桌子的压力就是书受到的重力4.关于重力和重心,以下说法中正确的是()A. 地球上的物体只有静止时才受重力,而落向地面时不受重力作用B. 物体受到的重力与地理纬度及海拔高度有关,与物体是否运动无关C. 重心是物体所受重力的等效作用点,所以重心一定在物体上D. 对形状有规则的物体,其重心就在物体的几何中心5.以v0=10m/s速度匀速行驶的汽车,突然刹车,刹车过程中汽车以a=−2m/s2的加速度继续前进,则刹车后()A. 5s内的位移是8mB. 5s内的位移是12mC. 1s末的速度是0m/sD. 3s末的速度是4m/s6.如图所示为一个做直线运动物体的位移图象,则下列说法正确的是()A. OA段物体向东北方向运动,AB段物体向东运动,BC做又向东北方向运动B. OA段与BC段物体运动方向相反,AB段物体静止不动C. 因OA段和BC段物体通过的位移相等,所用时间相等,所以OA与BC的斜率相同D. OA段、AB段、BC段物体通过的位移均相同7.下雨时雨水从屋檐滴落是生活中常见的现象,如图所示。
【解析】福建省福州市八县(市、区)一中2019-2020学年高二上学期期中考试数学试题

2019-2020学年第一学期八县(市、区)期中联考高中二年数学科试卷第Ⅰ卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求.)1.已知命题0:1p x ∃>,使得0lg 0x …,则p ⌝为( ) A. 1x ∀…,总有lg 0x > B. 1x ∀>,总有lg 0x > C. 01x ∃>,使得0lg 0x > D. 01x ∃…,使得0lg 0x >【答案】B 【分析】根据特称命题的否定是全称命题进行求解即可.【详解】命题是特称命题,则命题的否定是:1,p x ⌝∀>总有lg 0x >成立, 故选:B【点睛】本题主要考查含有量词的命题的否定,根据特称命题的否定是全称命题是解决本题的关键.属于基础题2.已知中心在原点的等轴双曲线()2222:10,0x y C a b a b-=>>,右顶点为),则双曲线C 的焦距等于( )A. 2B.C. 4D. 【答案】C 【分析】根据等轴双曲线的定义,右顶点以及双曲线中,,a b c 的关系式,计算可求解.【详解】因为双曲线()2222:10,0x y C a b a b-=>>为等轴双曲线,所以a b =,因为右顶点为0),所以a b ==所以焦距24c ===. 故选:C【点睛】本题考查了等轴双曲线的定义,双曲线的几何性质,属于基础题. 3.不等式22530x x +-<的一个必要不充分条件是( ) A. 61x -<<B. 132x -<<C. 30x -<<D.132x -<< 【答案】A 【分析】解一元二次不等式得132x -<<,根据充分,必要条件的概念分析可求解. 【详解】由不等式22530x x +-<得(21)(3)0x x -+<,解得132x -<<,因为1(3,)2-=1(3,)2-,所以选项B 为充要条件,因为(3,0)- 1(3,)2-,所以选项C 为充分不必要条件,因为1(,3)2- 1(3,)2-,且1(3,)2- 1(,3)2-,所以选项D 是既不充分也不必要条件,因为1(3,)2- (6,1)-,所以选项A 是必要不充分条件.故选:A【点睛】本题考查了必要不充分条件,属于基础题. 4.下列命题中正确的是( )A. 命题“若2320x x -+=,则1x =”的否命题为“若2320x x -+=,则1x ≠”;B. 命题“若平面向量,a b r r 共线,则,a b r r方向相同”的逆否命题为假命题;C. 命题“若3a ≠或2b ≠,则5a b +≠”是真命题;D. 命题“若4a b +…,则a b 、中至少有一个大于等于2”的逆命题是真命题. 【答案】B 【分析】根据写否命题时,既要否定条件,又要否定结论可知,A 不正确;根据原命题为假命题且逆否命题与原命题同真假可知,B 正确; 根据逆否命题为假且原命题与逆否命题同真假可知,C 不正确; 根据否命题为假命题且逆命题与否命题同真假可知,,D 不正确.【详解】对于A ,命题“若2320x x -+=,则1x =”的否命题为“若2320x x -+≠,则1x ≠”,故A 不正确;对于B ,因为0a r r =时,满足向量,a b r r 共线,但是不能说,a b r r 方向相同,所以命题“若平面向量,a b r r 共线,则,a b r r方向相同”是假命题,所以其逆否命题也是假命题,故B 正确;对于C ,因为命题“若3a ≠或2b ≠,则5a b +≠”的逆否命题”若5a b +=,则3a =且2a =”是假命题,所以原命题也是假命题,故C 不正确;对于D ,因为命题“若4a b +…,则a b 、中至少有一个大于等于2”的否命题”若4a b +<,则a b 、都小于2”是假命题,所以逆命题也是假命题,故D 不正确. 故选:B【点睛】本题考查了四种命题及其真假的判断,属于基础题.5.已知椭圆的中心在原点,长轴长为12,且两个焦点恰好将长轴三等分,则此椭圆的标准方程是( )A. 221364x y+=B. 221364x y +=或221436x y += C. 2213632x y +=D. 2213632x y+=或2213632y x +=【答案】D 【分析】根据椭圆的几何性质得到22236,4,32a c b ===后,讨论焦点的位置可得椭圆方程. 【详解】设椭圆长半轴长,短半轴长,半焦距分别为,,a b c , 因为椭圆的长轴长为12,且两个焦点恰好将长轴三等分, 所以2212,23aa c ==, 所以6,2a c ==,所以22236432b a c =-=-=,当焦点在x 轴上时,椭圆的标准方程为2213632x y+=,当焦点在y轴上时,椭圆的标准方程为2213236x y+=, 故选:D 【点睛】本题考查了椭圆的标准方程和几何性质,属于基础题. 6.如图所示,在平行六面体1111ABCD A B C D-中,AB a=u u u r r,AD b=u u u r r,1AA c=u u u r r,M是11A D 的中点,点N是1CA上的点,且1:1:4CN NA=.用,,a b cr r r表示向量MNu u u u r的结果是()A.12a b c++r r rB.114555a b c++r r rC.1315105a b c--r r rD.4345105a b c+-r r r【答案】D【分析】根据向量加法的平行四边形,向量减法的三角形法则可得.【详解】如图所示:因为MN AN AM=-u u u u r u u u r u u u u r11AC CN AA AM=+--u u u r u u u r u u u r u u u u r111152AC CA AA AD=+--u u u r u u u r u u u r u u u r1111()52AC AA AC AA AD =+---u u u r u u u r u u u r u u u r u u u r1441552AC AA AD =--u u ur u u u r u u u r 1441()552AB AD AA AD =+--u u ur u u u r u u u r u u u r 14345105AB AD AA =+-u u ur u u u r u u u r 4345105a b c =+-r r r . 故选:D【点睛】本题考查了向量加法的平行四边形,向量减法的三角形法,属于基础题.7.空间四边形ABCD 中若,,2,1,AB BD CD BD AC BD ⊥⊥==则AC BD ⋅=u u u r u u u r( )A.12B. 1D. 0【答案】B 【分析】根据向量加法的三角形法则以及平面向量的数量积计算可得.【详解】因为AC BD ⋅=u u u r u u u r()AB BC BD +u u u r u u u r u u u r g ()AB BD DC BD =++⋅u u u r u u u r u u u r u u u r 2AB BD BD DC BD =⋅++⋅u u u r u u u r u u u r u u u r u u u r ,因为AB BD ⊥,DC BD ⊥,所以0,0AB BD DC BD ⋅=⋅=u u u r u u u r u u u r u u u r,所以AC BD ⋅=u u u r u u u r20101++=, 故选:B【点睛】本题考查了向量加法的三角形法则以及平面向量的数量积,属于基础题. 8.已知点P 为抛物线214y x =上的动点,点P 在x 轴上的射影为点H ,点A 的坐标为(12,6),则+PA PH 的最小值是( ) A. 13 B. 12 C. 11 D. 10【答案】B 【分析】利用抛物线的定义,得||||PA PH +||||11PA PH =++-=||||1PA PF +-,再利用两点之间连线段最短可得. 【详解】如图所示:设抛物线的焦点为F ,则(0,1)F , 因为||||PA PH +||||11PA PH =++-=||||1PA PF +-||1AF ≥-22(120)(61)112-+-=,当且仅当,,A P F 三点共线,且P 在线段AF 上时,取得等号. 故选:B【点睛】本题考查了抛物线的定义,属于基础题.9.如图,在正方体1111ABCD A B C D -中,M 、N 分别为11A B 、1CC 的中点,P 为AD 上一动点,记α为异面直线PM 与1D N 所成的角,则α的集合是( )A. {}2πB. {|}62ππαα≤≤C. {|}42ππαα≤≤D. {|}32ππαα≤≤【答案】A分别以边1,,DA DC DD所在直线为x轴,y轴,z轴,建立如图所示空间直角坐标系:设正方体边长为1,()(),0,001P x x≤≤,并能确定以下几点坐标:()1111,,1,0,0,1,0,1,22M D N⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭;∴1111,,1,0,1,22PM x D N⎛⎫⎛⎫=-=-⎪ ⎪⎝⎭⎝⎭u u u u r u u u u r∴1PM D N⋅=u u u u r u u u u r∴1PM D N⊥u u u u r u u u u r∴2πα=故选A10.已知双曲线()222210,0x y a b a b-=>>的一个焦点F 与抛物线()220y px p =>的焦点相同,点A 是两曲线的一个交点,且AF 垂直x 轴,则双曲线的离心率为( )C. 1D. 1+【答案】C 【分析】分别在双曲线和抛物线中求出A 的坐标为2(,)b c a和(,)2p p ,由此列式可求得.【详解】不妨设A 在第一象限内,则在双曲线()222210,0x y a b a b-=>>中,(c,0)F ,2(,)b A c a ,在抛物线()220y px p =>中(,02p F ),(,)2pA p , 所以2p c =,且2b p a=,所以22b ac =,所以222c a ac -=,所以2()12cc aa-=, 所以2210e e --=,所以1e =1e =舍). 故选:C【点睛】本题考查了双曲线和抛物线的几何性质,属于基础题.11.已知椭圆222116x y a +=与双曲线22215x ym -=有公共焦点12,,F F 且两条曲线在第一象限的交点为P 点,则12PF F △的面积为( )A.112B.212C. D.【答案】C 【分析】根据双曲线方程可知焦点在x 轴上,所以22165a m -=+,再联立椭圆与双曲线方程解得点P 的纵坐标的绝对值,然后利用面积公式121||||2F F y 可求得. 【详解】因为双曲线22215x ym -=的焦点在x 轴上,所以椭圆222116x ya +=的焦点在x 轴上,所以22165a m -=+,即2221a m =+,联立22222211615x y a x y m ⎧+=⎪⎪⎨⎪-=⎪⎩ ,所以22222222165a y x a m y x m ⎧+=⎪⎪⎨⎪-=⎪⎩,所以222222165a y m y a m -=+, 所以22222()165a m y a m +=-,所以22222516a m y m a -=+ 22222121516m m m m +-=++222116510580m m =++2218021105m ⨯=+2805m =+,所以||y =即点P,又12||F F =, 所以12PF F △的面积为121||||2F Fy 12=⨯=. 故选:C点睛】本题考查了椭圆和双曲线共焦点问题,三角形面积公式,属于中档题.12.已知椭圆22221(0)x y a b a b+=>>的内接ABC ∆的顶点B 为短轴的一个端点,右焦点F ,线段AB 中点为K ,且2CF FK =u u u r u u u r,则椭圆离心率的取值范围为( )A. 03⎛ ⎝⎭, B. 03⎛⎫⎪ ⎪⎝⎭,C. ,13⎛⎫⎪ ⎪⎝⎭D. 13⎛⎫⎪ ⎪⎝⎭【答案】A 【分析】设1122(,),(,)A x y C x y ,所以11(,)22x y bK +,根据定比分点坐标公式可得弦AC 的中点坐标,再根据弦AC 的中点在椭圆内列不等式可解得. 【详解】设1122(,),(,)A x y C x y , 因为(0,)B b ,(c,0)F ,所以11(,)22x y b K +, 因为2CF FK =u u u r u u u r,所以2CF FK =,由定比分点坐标公式得,1212221222012x x c y b y ⎧+⨯⎪=⎪⎪+⎨+⎪+⨯⎪=⎪+⎩,化简得12123x x c y y b +=⎧⎨+=-⎩,所以弦AC 的中点坐标为3(,)22c b-,根据弦AC 的中点在椭圆内可得22223()()221c b a b -+<, 所以29344e <,所以213e <,又离心率(0,1)e ∈,所以(0,3e ∈. 故选:A【点睛】本题考查了椭圆的几何性质,定比分点的坐标公式,点与椭圆的位置关系,椭圆的离心率,属于中档题.第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在答题卡相应位置.) 13.命题“2,210x R mx mx ∀∈-+>”是真命题,则实数m 的取值范围为_____________.【答案】01m <… 【分析】依题意列式0m =或0m >且2(2)40m m --<,可解得.【详解】因为命题“2,210x R mx mx ∀∈-+>”是真命题,所以2210mx mx -+>对任意实数x 都成立,所以0m =或0m >且2(2)40m m --<,所以0m =或01m <<,综上所述:实数m 的取值范围是01m ≤<.故答案为: 01m ≤<【点睛】本题考查了一元二次不等式恒成立,分类讨论思想,属于基础题.14.双曲线2244x y -=的一条弦恰被点()8,1P 平分,则这条弦所在的直线方程是_____________.【答案】2150x y --=【分析】设弦为AB ,11(,)A x y ,22(,)B x y ,将,A B 的坐标代入椭圆方程作差,可求出弦的斜率,再由点斜式可解得.【详解】设弦为AB ,11(,)A x y ,22(,)B x y ,所以221144x y -=,222244x y -=,所以222212124()x x y y -=-, 所以121212124()y y x x x x y y -+=-+, 又弦AB 的中点为(8,1),所以122816x x +=⨯=,12212y y +=⨯=, 所以121216242AB y y k x x -===-⨯, 由点斜式得弦AB 所在直线的方程为:12(8)y x -=-,即2150x y --=.故答案为: 2150x y --=.【点睛】本题考查了点差法求弦的斜率,直线方程的点斜式,属于基础题.15.已知A 、B 是过抛物线22(0)y px p =>焦点F 的直线与抛物线的交点,O 是坐标原点,满足2,OAB AF FB S ==V u u u v u u u v ,则p 的值为_______【答案】【分析】由题意首先求得倾斜角的三角函数值,然后结合面积公式和三角函数的定义可得p 的值.【详解】设焦点弦的倾斜角为α, 由抛物线焦点弦的焦半径公式可知:1cos p AF α=-,1cos p BF α=+,故:21cos 1cos p p αα=⨯-+,解得:1cos 3α=,故sin 3α=,设原点到直线AB 的距离为h ,则1,2OAB S AB h h ==⨯⨯∴=V由三角函数的定义可得:sin 2α==,解得:p =【点睛】本题主要考查抛物线的焦半径公式,抛物线中的三角形问题等知识,意在考查学生的转化能力和计算求解能力.16.如图所示,在直四棱柱1111ABCD A B C D -中,底面ABCD 为菱形,ABC ∠=60o 且1=AA AB ,M 为侧棱1AA 的中点,,E F 分别是线段1BB 和线段1CC 上的动点(含端点),且满足1BE C F =,当,E F 运动时,下列结论中正确的序号是_____________.①在△MEF 内总存在与平面ABCD 平行的线段;②平面MEF ⊥平面11BCC B ;③三棱锥1A MEF -的体积为定值;④△MEF 可能为直角三角形.【答案】①②③【分析】对于①,取EF 的中点G ,则可证MG 就是满足条件的线段;对于②,可证MG 与平面11BCC B 垂直,再由平面与平面垂直的判定定理可证;对于③,可用等体积法求得三棱锥1A MEF -的体积为定值;对于④, 设1A A AB a ==,BE t =,可求得三角形三边长,再用余弦定理判断三角形不可能是直角三角形.【详解】如图所示:取EF 的中点G ,BC 的中点H ,AB 的中点N ,连GH ,,,MG AH ,AC CN ,对于①,根据梯形的中位线有11111()()222GH BE CF C F CF CC AM =+=+==,又////GH BE AM ,所以//GH AM ==, 所以四边形AHGM 为平行四边形,所以//MG AH ,又AH ⊂平面ABCD ,MG ⊄平面ABCD ,所以//MG 平面ABCD ,故①正确;对于②,在直四棱柱1111ABCD A B C D -中,底面ABCD 为菱形,ABC ∠=60o ,所以AH BC ⊥,又直四棱柱的侧面与底面垂直,所以AH ⊥平面11BCC B ,而//MG AH ,所以MG ⊥平面11BCC B ,因为MG ⊂平面MEF ,所以平面MEF ⊥平面11BCC B ,故②正确, 对于③,设1A A AB a ==,则11A MEF F A ME V V --==131131133322A ME a CN S a a ⋅=⨯⨯=V 为定值,故③正确; 对于④, 设1A A AB a ==,BE t =,则EF =22(2)a t a -+221()2ME a t a =-+221()2MF a a t =+-因为ME MF =,所以△MEF 为等腰三角形,所以M MEF FE =∠∠不可能为直角,又2222222122()(2)2ME MF EF a a t a t a +-=+----221(44)2a at t =+- 2212()2t at a =--+2212()2t a a =--+, 因为0t a ≤≤,所以0t =或t a =时, 2212()2t a a --+取得最小值,最小值为212a , 所以222ME MF EF +-2102a ≥>, 所以222cos 2ME MF EF EMF ME MF+-∠=⋅>0,所以EMF ∠恒为锐角,不可能为直角,故④不正确.故答案为:①②③【点睛】本题考查了线面平行的判定定理,面面垂直的判定定理,等体积法求体积,余弦定理判断三角形形状,属于中档题.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.若命题:p 实数x 满足240x x -…,命题q :实数x 满足(1)(1)0x a x a -+--…()0a >. (1)当2a =且p q ∧为真命题时,求实数x 的取值范围;(2)若p 是q ⌝的必要不充分条件,求实数a 的取值范围.【答案】(1)34x 剟(2)01a <≤【分析】(1) p q ∧为真命题时,p 与q 都是真命题,用04x 剟和1x -…或3x ≥取公共部分即可得到; (2)利用真子集关系列式即可得到.【详解】解:(1)由:p ()40x x -…,得04x 剟, 当2a =时,由q :()(12)120x x -+--…,得1x -…或3x ≥, ∴:q 1x -…或3x ≥,p q ∧Q 为真命题,p ∴真且q 真,34x ∴剟,∴实数x 的取值范围为34x 剟. (2)因为0a >,由:q ⌝(1)(1)0x a x a -+--<,得()110a x a a -<<+>,设{|04},{|11,0}A x x B x a x a a ==-<<+>剟, p Q 是q ⌝的必要不充分条件,B A ∴Ü,1014a a -⎧∴⎨+⎩……, 又0a >Q ∴01a <≤,∴实数a 的取值范围为01a <≤.【点睛】本题考查了一元二次不等式的解法,命题的真假,必要不充分条件,属于中档题.18.(1)已知中心在原点的双曲线C的焦点坐标为(0,(0-,且渐近线方程为y =,求双曲线C 的标准方程;(2)在圆223x y +=上任取一点P ,过点P 作y 轴的垂线段PD ,D 为垂足,当点P 在该圆上运动时,求线段PD 的中点M 的轨迹方程.【答案】(1)2212y x -=(2)221334x y +=【分析】(1)根据c =,ab=,,联立解方程组可解得a =1b =,从而可得; (2)设出M 的坐标为(),x y ,根据中点公式可得P 的坐标,再将P 的坐标代入椭圆方程可得.【详解】解:(1)依题可知双曲线的焦点在y 轴上, 则设其方程为:22221(0,0)y x a b a b-=>>,且c =①双曲线的渐近线方程为y =,即a b =② 又222a b c +=Q③,由①②③得1a b == 得双曲线方程为:2212y x -= (2)设轨迹上任一点M 的坐标为(),x y ,点P 的坐标为()00,x y ,则依题意可知D 点坐标为()00,yQ PD 的中点为M ,00,2x x y y ⎧=⎪∴⎨⎪=⎩即002x x y y =⎧⎨=⎩ Q 点P 圆223x y +=上运动,02203x y ∴+=,所以22(2)3x y +=, 2243x y ∴+=,经检验所求方程符合题意,∴点M 的轨迹方程为221334x y +=. 【点睛】本题考查了双曲线的标准方程,代入法求曲线的轨迹方程,属于基础题.19.如图,已知正方形ABCD 和矩形ACEF 所在的平面互相垂直,2AB =,1AF =,M是线段EF 的中点.(1)求证://AM 平面BDE ;(2)求二面角A DF B --的大小.【答案】(Ⅰ)见解+析(Ⅱ)60o试题分析:(1)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(2)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(3)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.试题详细分析:(I )记AC 与BD 的交点为O ,连接OE ,∵O 、M 分别是,AC EF 的中点,ACEF 是矩形∴四边形AOEM 是平行四边形,∴AM ∥OE ,∵OE ⊂平面BDEAM ⊄平面BDE ,∴AM ∥平面BDE 6分(Ⅱ)在平面AFD 中过A 作AS DF ⊥于S ,连接BS ,∵,,AB AF AB AD AD AF A ⊥⊥⋂=∴AB ⊥平面ADF ,∴AS 是BS 在平面ADF 上的射影,由三垂线定理点得BS DF ⊥∴BSA ∠是二面角A DF B --的平面角,在Rt ASB ∆中,6,23AS AB ==, ∴tan 3,60ASB ASB ∠=∠=o二面角A DF B --的大小为60o 8分另解:以C 为原点,CD 所在直线为x 轴,CB 所在直线为y 轴,CE 所在直线为z 轴,建立空间直角坐标系,则(0,0,0)C ,(2,0,0)D ,(2,2,0)A ,(0,2,0)B ,(0,0,1)E ,(2,2,1)F22(,,0)22M ,设AC 与BD 交于点O ,则 (I )易得:,则∥,由OE ⊂面BDE ,故AM ∥面BDE ;(Ⅱ)取面ADF 的一个法向量为,面BDF 的一个法向量为, 则,故二面角A DF B --的大小为60o .考点:证明线面平行及求二面角20.已知抛物线C 的方程为()220y px p =>,C 上一点3,2M m ⎛⎫ ⎪⎝⎭到焦点的距离为2.(1)求抛物线C 的方程及点M 的坐标;(2)过点()1,0P 的直线l 与抛物线C 交于点,A B ,与y 轴交于点Q ,设QA PA λ=u u u r u u u r ,QB PB μ=u u u r u u u r ,求证:λμ+是定值..【答案】(1)22y x =,3,2M ⎛ ⎝(2)证明见解+析【分析】(1)利用抛物线的定义列式可解得1p =,可得抛物线2:2C y x =,令32x =,可得m 的值; (2) 设直线l 的方程为()()10y k x k =-≠,并代入抛物线,由韦达定理以及向量关系可解得.【详解】解:(1)依题意得抛物线的准线为2p x =-, Q 抛物线上一点3,2M m ⎛⎫ ⎪⎝⎭到焦点的距离为2,由抛物线的定义可得3222p +=,1p ∴=, ∴抛物线的方程为22y x =,232,2m m =⨯∴=Q 3,2M ⎛∴ ⎝. (2)当直线l 的斜率不存在时不符合题意,故直线l 的斜率k 必存在且不为0.Q 直线l 过点()1,0P ,∴设直线l 的方程为()()10y k x k =-≠,当0x =时,y k =-,∴点Q 坐标()0,k -,设()()1122,,,A x y B x y ,由22y kx k y x=-⎧⎨=⎩,得22y y k k =-,整理得2220ky y k --=, 20,480k k ≠∴∆=+>Q ,12122,2y y y y k∴+==-, ()11,QA x y k ∴=+u u u r ,()111,PA x y =-u u u r ,QA PA λ=u u u r u u u r Q ,()()1111,1,x y k x y λ∴+=-,11,y k y λ∴+=即11,y k yλ+=同理可得22,y k y μ+= ()121212121222212y y k y y y k y k k k y y y y λμ++++∴+=+==+=-,即λμ+是定值. 【点睛】本题考查了抛物线的定义,直线与抛物线的位置关系,韦达定理,向量的线性运算,属于中档题.21.如图所示,等腰梯形ABCD 中,AB CD ∥,2AD AB BC ===,4CD =,E 为CD 中点,AE 与BD 交于点O ,将ADE V 沿AE 折起,使点D 到达点P 的位置(P ∉平面ABCE ).(1)证明:平面POB ⊥平面ABCE ;(2)若PB =6,试判断线段PB 上是否存在一点Q (不含端点),使得直线PC 与平面AEQ 所成角的正弦值为155,若存在,求出PQ QB 的值;若不存在,说明理由. 【答案】(1)证明见解+析(2)存在点Q 为PB 的中点时,使直线PC 与平面AEQ 所成角的正弦值为155,1PQ QB =【分析】 (1)利用线面垂直的判定定理证AE ⊥平面POB,利用面面垂直的判定定理证平面POB⊥平面ABCE 可得;(2)利用222OP OB PB +=证明OP⊥OB,然后以O 为原点,,,OE OB OP u u u r u u u r u u u r 分别为x 轴,y 轴,z 轴,建立空间直角坐标系O xyz -,利用向量可求得直线PC 与平面AEQ 所成角的正弦值,根据已知列等式可解得.【详解】解:(1)证明:连接BE ,在等腰梯形ABCD 中,2AD AB BC ===,4CD =,E 为CD 中点,∴四边形ABED 为菱形,BD ∴⊥AE,,OB AE OD AE ∴⊥⊥,即,OB AE OP AE ⊥⊥,且,OB OP O =I OB ⊂平面,POB OP ⊂平面POB ,∴AE⊥平面POB又AE ⊂平面ABCE ,∴平面POB⊥平面ABCE .(2)由(1)可知四边形ABED 为菱形,2,AD DE ∴==在等腰梯形ABCD 中2,AE BC ==PAE ∴∆正三角形3OP ∴=,同理3OB =6PB =Q ,222OP OB PB ∴+=,∴OP⊥OB,由(1)可知,OP AE OB AE ⊥⊥,以O 为原点,,,OE OB OP u u u r u u u r u u u r分别为x 轴,y 轴,z 轴,建立空间直角坐标系O xyz -,由题意得,各点坐标为(3P ,()1,0,0A -,()3,0B,()3,0C ,()1,0,0E ,∴3,3)3,3)PB PC ==-u u u r u u u r ,,(2,0,0),AE =u u u r设()01PQ PB λλ=<<u u u r u u u r , 3)3,3)333)AQ AP PQ AP PB λλλλλ=+=+=+=u u u r u u u r u u u r u u u r u u u r,设平面AEQ 的一个法向量为(,,)n x y z =r,则00n AE n AQ ⎧⋅=⎨⋅=⎩u u u v v u u u v v ,即)203330x x y z λλ=⎧⎪⎨++=⎪⎩,取0,1x y ==,得1z λλ=-,所以n r=(0,1,1λλ-),设直线PC 与平面AEQ 所成角为02πθθ⎡⎤∈⎢⎥⎣⎦,,,则sin cos ,PC n PC n PC nθ⋅=<>==u u u r r u u u r r u u u r r5=, 化简得:24410λλ-+=,解得12λ=, ∴存在点Q 为PB 的中点时,使直线PC 与平面AEQ.【点睛】本题考查了直线与平面垂直的判定,平面与平面垂直的判定,线面角的向量求法,属于中档题.22.已知椭圆()2222:10x y C a b a b +=>>的离心率为2,椭圆C 截直线1x =所得线段的长.过椭圆C 上的动点P 作圆22(1)1x y -+=的两条切线分别交y 轴于,M N 两点.(1)求椭圆C 的方程;(2)求线段MN 长度的最大值,并求此时点P 的坐标.【答案】(1)2212x y +=(2)||MN取得最大值P位置是椭圆的左顶点(【分析】 (1)根据离心率为2,椭圆C 截直线1x =,列式可解得; (2)先求出点P 的横坐标的取值范围,再设出过点P 的圆的切线方程为y kx b =+,根据圆心到直线的距离求出212b k b-=,可得2(2)20x b yb x --+=,根据韦达定可得001212002,22y x b b b b x x --+==--,再求出弦长,并利用单调性求出最大值即可. 【详解】解:(1)∵椭圆()2222:10x y C a b a b +=>>,所以2ca=,所以222a c=,又222a b c=+,∴,2b c a b==,当1x=时,22211y ba⎛⎫=-⋅⎪⎝⎭221()2==,∴222,1a b==,∴椭圆的方程是2212xy+=.(2)设00)(,P x y,由22221,2(1)1,xyx y⎧+=⎪⎨⎪-+=⎩得22x=-,22x=+(舍去),因为P在椭圆上,过P作椭圆的切线有两条,如图所示:∴)(2,00,22x⎡∈--⎣U.设过点P的圆的切线方程为y kx b=+,∵圆心()10,到直线PM的距离为1,211k=+,化简得212bkb-=,∴212by x bb-=+.所以2(2)20x b yb x--+=,设()00,P x y则()2000220x b y b x--+=,∴001212002,22y xb b b bx x--+==--,∴12||MN b b=-====.∵()00,P x y是椭圆上的点,∴2212xy+=,所以22012xy=-,∴||MN====,令()f x=((0,2x∈⋃-,∴()f x=[上单调递减,在(0,2内也是单调递减,所以2x=时,()f x取得最小值1,x=,()f x取得最大值又0x≠,所以()(0)1f x f≠= ,∴()()(0,1f x∈U,所以当x=||MN取得最大值此时点P位置是椭圆的左顶点(.【点睛】本题考查了求椭圆标准方程,,点到直线距离,圆的切线方程,利用单调性求最大值,属于难题.。
2020届福建省福州市八县(市、区)一中高三上学期期中联考语文试题

2019—2020学年度高中三年级第一学期八县(市、区)一中期中联考语文科试卷完卷时间:150分钟满分:150分一、现代文阅读(36分)(一)论述类文本阅读(本题3小题,9分)阅读下面的文字,完成1-3题。
①“人类命运共同体”理念是中国特色大国外交思想的重要内容。
那么,它的特色究竟“特”在哪里?我们究竟应该如何认识其思想文化本源?②客观地说,世界上主要文明地区的政治文化中都有命运与共、共同体、世界主义的政治思想,例如西方基督教世界秩序及西方永久和平论、印度思想中的“不害”、伊斯兰世界的“天下一家”、中国古代的“天下大同”等观念。
总的来说,早期这些共同体观念解决的只是内部秩序问题,还没有很好地解决不同文明之间如何共生共处的问题。
其中,历史上不少共同体思想还受到二元对立世界观的局限,它们所强调构建的共同体是以一个假想或现实的敌人为目标的,这种思想很容易导致世界陷入对抗之中。
事实上,直到今天,这种思想还在影响着个别大国的外交政策,值得我们去辨别和防范。
③我们倡导的“人类命运共同体”,其思想文化本源来自传统和现代两部分。
所谓传统,中国古代有丰富的中外秩序资源,在当时地理所及的范围内,形成了一套处理中外关系的思想和实践做法,这套思想和做法在今天需要创造性转化。
所谓现代,“打造人类命运共同体”还需要从马克思主义中寻找本源。
马克思主义关于社会共同体和人类解放的思想中,包含着国际主义以及很多“人类命运与共”的资源。
马克思主义政治经济学中关于世界不平等、剥削以及世界政治经济秩序根源、改造的论述等等,都是我们理解“人类命运共同体”的重要思想本源。
同时,这些思想也是“人类命运共同体”理念从学理上区别于既往及现在流行的一些共同体理论,如各种带有宗教色彩的联盟、大西洋共同体、“民主”价值观联盟等的重要依据。
④以往绝大多数国际秩序思想和实践,要么服务于强者,要么用来结成一个国家联盟以反对另一个国家联盟,要么是一种宗教秩序的外在表现。
福建省福州八县(市、区)一中2019-2020学年高一地理上学期期中联考试题
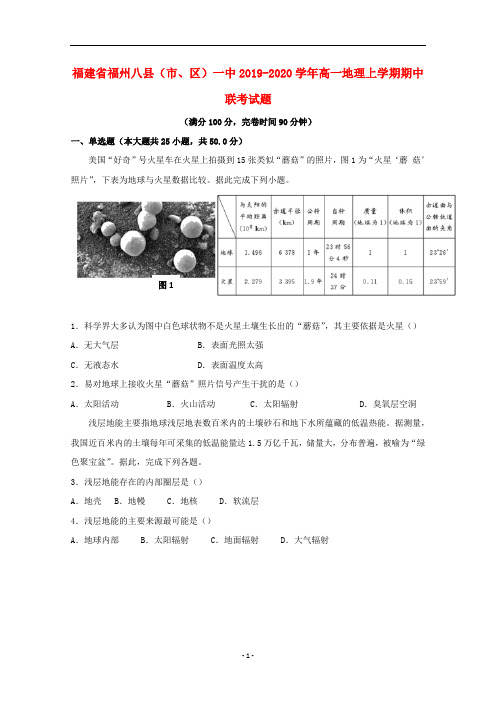
福建省福州八县(市、区)一中2019-2020学年高一地理上学期期中联考试题(满分100分,完卷时间90分钟)一、单选题(本大题共25小题,共50.0分)美国“好奇”号火星车在火星上拍摄到15张类似“蘑菇”的照片,图1为“火星‘蘑菇’照片”,下表为地球与火星数据比较。
据此完成下列小题。
图11.科学界大多认为图中白色球状物不是火星土壤生长出的“蘑菇”,其主要依据是火星()A.无大气层 B.表面光照太强C.无液态水 D.表面温度太高2.易对地球上接收火星“蘑菇”照片信号产生干扰的是()A.太阳活动 B.火山活动 C.太阳辐射 D.臭氧层空洞浅层地能主要指地球浅层地表数百米内的土壤砂石和地下水所蕴藏的低温热能。
据测量,我国近百米内的土壤每年可采集的低温能量达1.5万亿千瓦,储量大,分布普遍,被喻为“绿色聚宝盆”。
据此,完成下列各题。
3.浅层地能存在的内部圈层是()A.地壳 B.地幔 C.地核 D.软流层4.浅层地能的主要来源最可能是()A.地球内部B.太阳辐射C.地面辐射D.大气辐射图2为2017年11月13日印度尼西亚锡纳朋火山喷发时情景。
据此回答下列小题。
图25.这些蔓延的火山灰物质在地球圈层的迁移顺序是()A. 大气圈→水圈、生物圈→岩石圈B. 岩石圈→大气圈→水圈、生物圈C. 水圈、生物圈→大气圈→岩石圈D. 水圈、生物圈→岩石圈→大气圈6.火山喷发产生的火山灰云团对其覆盖地区的影响是()A. 增强了大气反射作用,使气温升高B. 削弱了大气反射作用,使气温降低C. 增强了大气逆辐射作用,使昼夜温差变小D. 削弱了大气逆辐射作用,使昼夜温差变小读图3北非和亚洲南部、西部局部图,回答下面小题图37. M地的年日照时数比N地的多,主要原因是M地()A. 纬度较低B. 地势较高C. 气候干旱D. 白昼较长8. N地的年太阳辐射总量比M地的丰富,其主要原因是N地()A. 地势高,大气稀薄B. 海拔高,多冰雪C. 纬度低,太阳高度大D. 气候干旱,光照强随着脱欧的最后期限日益逼进,某记者于当地时间2019年10月19日晚8时许抵达伦敦,对英国进行采访调研。
【英语】福建省福州八县(市、区)一中2019-2020学年高一上学期期中联考试题

福建省福州八县(市、区)一中2019-2020学年高一上学期期中联考英语试题第一部分听力(共两节,满分30 分)第一节(共 5 小题;每小题 1.5 分,满分7.5 分)听下面 5 段对话,每段对话后有一个小题。
从题中所给的A,B,C 三个选项中选出最佳选项。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the man prefer?A. Apples.B. Oranges.C. Bananas.2. What will the man do tomorrow?A. Work at his office.B. Attend a basketball game.C. Take the girl to see a doctor.3. What will the weather be like tonight according to the woman?A. Rainy.B. Cloudy.C. Clear.4. What meal is the man going to eat?A. Breakfast.B. Lunch.C. Dinner.5. What are the speakers mainly talking about?A. A meeting.B. Fire practice.C. Plans for the weekend.第二节(共15 小题;每小题 1.5 分,满分22.5 分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6. How many cats does the woman want?A. Three.B. Two.C. One.7. What color cat does the woman choose?A. Black.B. Gray.C. White.听第7段材料,回答第8至10题。
