统计学实验作业
统计学实验题根据图形说明大学生每月生活开支

统计学实验题根据图形说明大学生每月生活开支1、消费方式:在消费方式上面,大多数人的态度为能省则省,但是也有大部分人毫不在乎,想花就花。
事先做好消费计划的好习惯拥有的人不多。
2、生活费来源:大学生由于没有完全独立,所以绝大多数学生的生活费来源还是以父母给予为主。
但是,勤工助学,奖学金等自力更生的学生也有一小部分。
3、生活费主要花销:大学生主要在校园里生活,所以还是以伙食消费为主。
这是比较健康的合理的消费方式,同时,大学生在学习上面的花销很少,说明学生或许不太重视学业。
4、买东西钱不够时的选择:买东西钱不够,大多数学生选择向父母要钱,这说明学生任然缺乏独立自主的意识,而且向同学借钱的消费观念需要改进。
5、消费倾向:消费时,绝大部分学生选择经济实惠的东西,这跟大学生有限的生活费有关。
6、消费时考虑的因素:大学生对商品要求不高,主要考虑商品的价格。
7、大学生买东西看重的方面:大学生买东西更喜欢外形美观和质量好的商品。
8、学生外出打工的原因:学生校外打工的主要原因还是补贴日用和渴望独立,可见大学生已经具有独立意识,脱离父母的佑护。
9、周围同学消费情况:大多数学生消费比较实际,说明学生活比较朴素,没有盲目消费。
通过以上的统计分析,我们基本得出以下结论:第一、对于生活费均值的分析结果:1.通过对本校大二学生生活费的总体计量,发现学生的月生活费平均数为764,生活费500元~800元所占频数最高。
;2.单因素分析的结果表明,性别对生活费均值没有显著影响。
第二、对于生活费来源的分析结果:1.描述统计的结果显示,生活费的主要来源都集中在父母供给中,其他来源依次是:勤工俭学、助学贷款及其他。
2.男女生而言,男生的生活费主要来源中来自父母的比女生稍低,而勤工俭学的比女生稍多,助学贷款比例相差不大。
3.本科生还是传统的以靠父母读书为主。
第三、对于生活费主要支出的分析结果:1.就抽样总体而言,生活费的主要支出集中在伙食费上,其他支出依次是:衣着、娱乐休闲、学习用品、日化用品。
统计学作业

统计学作业
将抗生素注入人体会产生抗生素与血浆蛋白质结合现象,以致减少了药性,下表列出5种常用的抗生素注入牛的体内时,抗生素与血浆蛋白质结合的百分比
抗生素青霉素四环素链霉素红霉素氯霉素
1 29.6 27.3 5.8 21.6 29.2
2 24.
3 32.6 6.2 17.
4 32.8
3 28.5 30.8 11.0 18.3 25.0
4 32.0 34.8 8.3 19.0 24.2
试在显著性水平a=0.05下检验这些百分比的均值有无显著性差异。
解:以u1,u2,u3,u4,u5依次表示青霉素,四环素,链霉素,红霉素,氯霉素与血浆蛋白质结合的百分比均值,本题需假设检验
Ho:u1=u2=u3=u4=u5,
H1:u1,u2,u3,u4,u5不全相等。
折线散点图:
SUMMARY
组观测数求和平均方差
青霉素 4 114.4 28.6 10.35333
四环素 4 125.5 31.375 10.05583
链霉素 4 31.3 7.825 5.6825
红霉素 4 76.3 19.075 3.2625
氯霉素 4 111.2 27.8 15.92
方差分析
差异源SS df MS F P-value F crit 组间1480.823 4 370.2058 40.88488 6.73978E-08 3.055568 组内135.8225 15 9.054833
总计1616.646 19
Fa(4,15)=3.06 <F=40.88488 所以接受H0,认为这些均值无显著性差异。
统计学作业
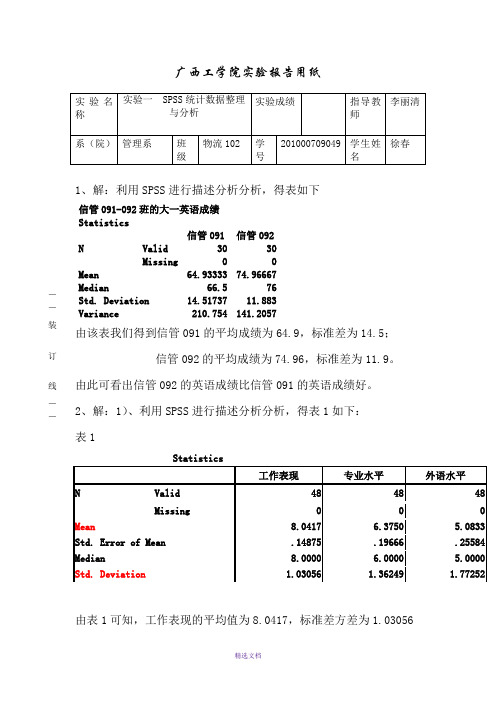
广西工学院实验报告用纸1、解:利用SPSS 进行描述分析分析,得表如下信管091-092班的大一英语成绩 Statistics信管091 信管092N Valid 30 30 Missing 0 0Mean 64.93333 74.96667Median 66.5 76 Std. Deviation 14.51737 11.883 Variance 210.754141.2057由该表我们得到信管091的平均成绩为64.9,标准差为14.5;信管092的平均成绩为74.96,标准差为11.9。
由此可看出信管092的英语成绩比信管091的英语成绩好。
2、解:1)、利用SPSS 进行描述分析分析,得表1如下: 表1由表1可知,工作表现的平均值为8.0417,标准差方差为1.03056— — 装订线— —专业水平的平均值为6.3750,标准差方差为 1.36249外语水平的平均值为5.0833,标准差方差为1.77252由此可见,用人单位对该校毕业生工作表现方面最为满意。
外语水平方面最不满意。
应在外语水平方面作出教学改革。
措施:1、在入学前就针对性的对英语成绩进行筛选2、入学后分班进行上课3、加强对英语课程的教育4、开展一些有关英语互动的活动5、要求每个班每天早上用一定时间读英语2)、由表1可知,工作表现的标准误差为0.14875,全距为4专业水平的标准误差为0.19666,全距为5外语水平的标准误差为0.25584,全距为7由此可见,用人单位对该校毕业生外语水平方面的满意程度差别最大。
产生的原因是:从抽取的样本看来,学生的外语水平参差不齐,有的学生外语水平很高,而有的学生水平非常低,同时大多数学生的外语水平都较低。
所以使得用人单位对该校毕业生外语水平方面的满意程度差别较大。
3)、利用SPSS进行,得表1、表2和表3如下:商学院表1Statistics工作表现专业水平外语水平N Valid 17 17 17Missing 0 0 0Mean 8 5.823529 4.764706Std. Deviation 1.118034 0.951006 1.601929Variance 1.25 0.904412 2.566176生物学院表2Statistics工作表现专业水平外语水平N Valid 17 17 17Missing 0 0 0Mean 8 6.647059 5.294118Std. Deviation 1.06066 1.271868 1.611083Variance 1.125 1.617647 2.595588医学院表3Statistics工作表现专业水平外语水平N Valid 14 14 14Missing 0 0 0Mean 8.142857 7.214286 3.714286Std. Deviation 0.949262 1.368805 1.489893Variance 0.901099 1.873626 2.21978由以上三个表对比可知社会对三个学院的毕业生工作表现方面的满意程度近于一致。
大学生统计学实验操作题目及解析

大学生统计学实验操作题目及解析在大学统计学的学习中,实验操作是巩固理论知识、提升实践能力的重要环节。
以下为大家呈现一些常见的大学生统计学实验操作题目,并进行详细的解析。
一、数据收集与整理题目:对某高校一个班级学生的身高数据进行收集和整理。
解析:首先,需要确定收集数据的方法。
可以采用直接测量、问卷调查或者从学校的学生信息系统中获取。
在收集数据时,要确保数据的准确性和完整性。
对于测量身高,要使用标准的测量工具,并多次测量取平均值以减小误差。
收集完数据后,需要对数据进行整理。
可以按照身高的数值从小到大或从大到小进行排序,然后将数据分组,例如以 5 厘米为一组,统计每个组内的人数。
通过这样的整理,可以更直观地了解身高数据的分布情况。
二、描述性统计分析题目:计算给定数据集中的均值、中位数、众数和标准差。
解析:均值是所有数据的平均值,通过将所有数据相加然后除以数据的个数来计算。
中位数是将数据按照从小到大或从大到小的顺序排列后,位于中间位置的数值(如果数据个数为奇数)或者中间两个数值的平均值(如果数据个数为偶数)。
众数是数据集中出现次数最多的数值。
标准差则反映了数据的离散程度,其计算相对复杂,需要先计算每个数据与均值的差值的平方,然后求这些平方值的平均值,最后取平方根。
以数据集10, 20, 20, 30, 40为例,均值为(10 + 20 + 20 + 30 +40) / 5 = 24;中位数是 20;众数是 20;标准差的计算过程为:首先计算均值 24,然后计算差值的平方分别为(10 24)²= 196, (20 24)²= 16, (20 24)²= 16, (30 24)²= 36, (40 24)²= 256,这些平方值的平均值为(196 + 16 + 16 + 36 + 256) / 5 = 100,标准差为√100 = 10 。
三、概率计算题目:一个盒子里有 5 个红球和 3 个白球,从中随机取出 2 个球,求取出的 2 个球都是红球的概率。
统计学实验

统计学实验内容一、频数统计1.A公司在招聘时采用了综合能力测试(满分为100分),由于应聘的人数较多,现随机抽取了157名应聘者的测试成绩,其测试分数的数据如book1所示。
(1)根据上面的资料,进行分组,并确定组数和组距。
根据资料判断,进行分组,分为六组,组距为10。
(2)编制频率分布表上限成绩频数频率19 10~20 16 0.10191129 20~30 27 0.17197539 30~40 56 0.35668849 40~50 39 0.24840858 50~60 14 0.08917268 60~70 5 0.031847合计157接收频率累积 %19 16 10.19%29 27 27.39%39 56 63.06%49 39 87.90%59 14 96.82%69 5 100.00%其他0 100.00%(3)画出直方图。
2. 为评价家电行业售后服务的质量,随机抽取了由100家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C.一般;D.差;E.较差。
调查结果见book2。
(1) 指出表中的数据属于什么类型?定序型(2) 制作一张频数分布表;服务质量等级频数频率1 A 14 0.142 B 21 0.213 C 32 0.324 D 18 0.185 E 15 0.15合计100(3)绘制一张条形图,反映服务质量的分布。
等量质计数项:服务质量等级服务质量等级汇总A 14B 21C 32D 18E 15总计100二、参数估计1.已知灯管使用寿命服从正态分布,其标准差为50小时。
现从一批产品中抽取25个作为样本,测得其平均使用寿命为1600小时,要求在95%的概率保证下估计该批产品平均使用寿命的置信区间。
(运用CONFIDENCE函数)标准差50置信度0.95样本容量25平均值1600极限误差19.59964置信区间1580.4 1619.6抽样平均误差 19.59964,置信区间即(1580.4003~1619.59964)2.在一篇关于“通货紧缩”的文章中,作者考察了各种各样投资的收益情况。
统计学四篇实验报告

《统计学》四篇实验报告实验一:用Excel构建指数分布、绘制指数分布图图1-2:指数分布在日常生活中极为常见,一般的电子产品寿命均服从指数分布。
在一些可靠性研究中指数分布显得尤为重要。
所以我们应该学会利用计算机分析指数分布、掌握EXPONDIST函数的应用技巧。
指数函数还有一个重要特征是无记忆性。
在此次实验中我们还学会了产生“填充数组原理”。
这对我们今后的工作学习中快捷地生成一组有规律的数组有很大的帮助。
实验二:用Excel计算置信区间一、实验目的及要求1、掌握总体均值的区间估计2、学习CONFIDENCE函数的应用技巧二、实验设备(环境)及要求1、实验软件:Excel 20072、实验数据:自选某市卫生监督部门对当地企业进行检查,随机抽取当地100家企业,平均得分95,已知当地卫生情况的标准差是30,置信水平0.5,试求当地企业得分的置信区间及置信上下限。
三、实验内容与步骤某市卫生监督部门对当地企业进行检查,随机抽取当地100家企业,平均得分95,已知当地卫生情况的标准差是30,置信水平0.5,试求当地企业得分的置信区间及置信上下限。
第1步:打开Excel2007新建一张新的Excel表;第2步:分别在A1、A2、A3、A4、A6、A7、A8输入“样本均值”“总体标准差”“样本容量”“显著性水平”“置信区间”“置信上限”“置信下限”;在B1、B2、B3、B4输入“90”“30”“100”“0.5”第3步:在B6单元格中输入“=CONFIDENCE(B4,B2,B3)”,然后按Enter键;第4步:在B7单元格中输入“=B1+B6”,然后按Enter键;第5步:同样在B8单元格中输入“=B1-B6”,然后按Enter键;计算结果如图2-1四、实验结果或数据处理图2-1:实验二:用Excel产生随机数见图3-1实验二:正态分布第1步:同均匀分布的第1步;第2步:在弹出“随机数发生器”对话框,首先在“分布”下拉列表框中选择“正态”选项,并设置“变量个数”数值为1,设置“随机数个数”数值为20,在“参数”选区中平均值、标准差分别设置数值为30和20,在“输出选项”选区中单击“输出区域”单选按钮,并设置为D2 单元格,单击“确定”按钮完成设置。
统计学实验例题实验报告(3篇)

第1篇一、实验课程名称:统计学实验二、实验项目名称:例题分析与解决三、实验日期:2023年10月26日四、实验者信息:- 专业班级:经济与管理学院经济学专业- 姓名:张三- 学号:20190001五、实验目的:1. 理解统计学的基本概念和原理。
2. 掌握统计学中的常用方法和技巧。
3. 提高运用统计学知识解决实际问题的能力。
六、实验原理:统计学是一门应用数学的分支,主要用于收集、整理、分析数据,从而对现象进行描述、解释和预测。
本实验主要通过分析例题,加深对统计学理论和方法的理解。
七、实验内容:1. 例题一:计算一组数据的平均数、中位数、众数(1)数据:10, 15, 20, 25, 30, 35, 40(2)计算过程:- 平均数 = (10 + 15 + 20 + 25 + 30 + 35 + 40) / 7 = 25- 中位数 = 30- 众数 = 30(出现次数最多)2. 例题二:求解一组数据的方差和标准差(1)数据:10, 15, 20, 25, 30, 35, 40(2)计算过程:- 方差 = [(10 - 25)^2 + (15 - 25)^2 + (20 - 25)^2 + (25 - 25)^2 + (30 - 25)^2 + (35 - 25)^2 + (40 - 25)^2] / 7 = 91.43- 标准差= √方差= √91.43 ≈ 9.533. 例题三:分析两组数据的关联性(1)数据集A:身高(cm):160, 165, 170, 175, 180体重(kg):50, 55, 60, 65, 70(2)数据集B:身高(cm):165, 170, 175, 180, 185体重(kg):55, 60, 65, 70, 75(3)计算过程:- 相关系数= (Σ(xy) - nΣxΣy) / √[(Σx^2 - nΣx^2)^2 (Σy^2 -nΣy^2)]- 其中,x为身高,y为体重,n为数据个数计算得出两组数据的关联性较强,说明身高和体重之间存在正相关关系。
实验报告统计实训(3篇)

第1篇一、实验目的本次实验旨在通过实际操作,加深对统计学基本概念和方法的理解,提高运用统计方法分析数据的能力。
通过本次实训,学生应掌握以下内容:1. 熟悉统计软件的基本操作;2. 掌握描述性统计、推断性统计的基本方法;3. 能够运用统计方法对实际问题进行分析;4. 提高数据收集、整理和分析的能力。
二、实验内容1. 数据收集:通过查阅相关资料,收集一组实际数据,例如某地区居民消费水平、学生成绩等。
2. 数据整理:对收集到的数据进行整理,包括数据的清洗、缺失值的处理等。
3. 描述性统计:运用统计软件对数据进行描述性统计,包括计算均值、标准差、方差、中位数、众数等。
4. 推断性统计:运用统计软件对数据进行推断性统计,包括t检验、方差分析、回归分析等。
5. 结果分析:根据统计结果,对实际问题进行分析,并提出相应的建议。
三、实验步骤1. 数据收集:从网络、书籍或实地调查等方式收集一组实际数据。
2. 数据整理:将收集到的数据录入统计软件,并进行数据清洗和缺失值处理。
3. 描述性统计:(1)打开统计软件,选择数据文件;(2)运用统计软件的描述性统计功能,计算均值、标准差、方差、中位数、众数等;(3)观察统计结果,分析数据的分布情况。
4. 推断性统计:(1)根据实际问题,选择合适的统计方法;(2)运用统计软件进行推断性统计;(3)观察统计结果,分析数据之间的关系。
5. 结果分析:(1)根据统计结果,对实际问题进行分析;(2)结合实际情况,提出相应的建议。
四、实验结果与分析1. 描述性统计结果:根据实验数据,计算得到以下统计量:均值:X̄ = 100标准差:s = 15方差:σ² = 225中位数:Me = 95众数:Mo = 105分析:从描述性统计结果可以看出,该组数据的平均值为100,标准差为15,方差为225,中位数为95,众数为105。
这表明数据分布较为集中,且波动较大。
2. 推断性统计结果:(1)t检验:假设检验H₀:μ = 100,H₁:μ ≠ 100。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、一家大型商业银行在多个地区设有分行,其业务主要是进行基础设施建设、国家重点项目建设、固定资产投资等项目的贷款。
近年来,该银行的贷款额平稳增长,但不良贷款额也有较大比例的增长,这给银行业务的发展带来较大压力。
为弄清楚不良贷款形成的原因,管理者希望利用银行业务的有关数据做些定量分析,以便找出控制不良贷款的办法。
该银行所属的25家分行2002年的有关业务数据是“例11.6.xls”。
(1)试绘制散点图,并分析不良贷款和贷款余额、累计应收贷款、贷款项目个数、固定资产投资额之间的关系;
2计算不良贷款、贷款余额、累计应收贷款、贷款项目个数、固定资产投资额之间的相关系数
(2) 求不良贷款对贷款余额的估计方程;
Anova b
模型 平方和 df
均方 F Sig.
1
回归 249.371 4 62.343 19.704
.000a
残差 63.279 20 3.164
总计
312.650
24
相关性
不良贷款 (亿元)
各项贷款余
额 (亿元) 本年累计应收贷款 (亿元)
贷款项目个
数 (个) 本年固定资产投资额 (亿元)
不良贷款 (亿元)
Pearson 相关性
1
.844**
.732**
.700**
.519**
显著性(双侧)
.000 .000 .000 .008 N
25 25 25 25 25 各项贷款余额 (亿元)
Pearson 相关性
.844**
1
.679**
.848**
.780**
显著性(双侧) .000
.000 .000 .000 N
25 25 25 25 25 本年累计应收贷款 (亿元)
Pearson 相关性
.732**
.679**
1
.586**
.472*
显著性(双侧) .000 .000
.002 .017 N
25 25 25 25 25 贷款项目个数 (个)
Pearson 相关性
.700**
.848**
.586**
1
.747**
显著性(双侧) .000 .000 .002
.000 N
25 25 25 25 25 本年固定资产投资额 (亿元)
Pearson 相关性
.519**
.780**
.472*
.747**
1
显著性(双侧) .008 .000 .017 .000
N
25
25
25
25
25
**. 在 .01 水平(双侧)上显著相关。
*. 在 0.05 水平(双侧)上显著相关。
a. 预测变量: (常量), 本年固定资产投资额 (亿元), 本年累计应收贷款 (亿元), 贷款项目个数 (个), 各项贷款余额 (亿元)。
b. 因变量: 不良贷款 (亿元
模型汇总
模型 R R 方 调整 R 方 标准 估计的
误差
更改统计量
R 方更改 F 更改
df1
df2
Sig. F 更
改 1
.893a
.798
.757
1.7788
.798 19.704
4
20
.000
a. 预测变量: (常量), 本年固定资产投资额 (亿元), 本年累计应收贷款 (亿元), 贷款项目个数 (个), 各项贷款余额 (亿元)。
从表系数可以看出常量、应收贷款、项目个数、固定资产投资额,都接受原假设,只有贷款余额拒绝原假设,所以只有贷款余额对不良贷款起作用。
系数a
模型 非标准化系数
标准系数 t Sig.
B 标准 误差
试用版
1
(常量) -1.022 .782
-1.306
.206 各项贷款余额 (亿元)
.040
.010
.891
3.837
.001
本年累计应收贷款 (亿元) .148
.079
.260
1.879
.075
贷款项目个数 (个)
.015
.083
.034
.175
.863
本年固定资产投资额 (亿元)
-.029
.015
-.325
-1.937
.067
a. 因变量: 不良贷款 (亿元)
共线性诊断a
从共线性可以看出,第五个特征值对贷款余额解释87%,对应收账款解释度为12%、对贷款个数解释度为63%、对固定资产投资解释度为5%。
所以不是太共线。
、
线性方程为 Y=0.01X Y 为不良贷款,X 为贷款余额。
4 检验不良贷款和贷款余额之间线性关系的显著性(α=0.05);回归系数的显回归系数a
模型 非标准化系数
标准系数
t Sig. 共线性统计量 B 标准 误差 试用版
容差
VIF
1
(常量) -.830 .723 -1.147
.263
各项贷款余额 (亿元)
.038
.005
.844
7.534
.000
1.000
1.000
a. 因变量: 不良贷款 (亿元)
共线性诊断a
模型 维数 特征值
条件索引
方差比例
(常量)
各项贷款余额
(亿元)
1
1 1.837 1.000 .08 .08 2
.163
3.354
.92
.92
a. 因变量: 不良贷款 (亿元)
模型 维数 特征值 条件索引 方差比例 (常量) 各项贷款余额
(亿元)
本年累计应收
贷款 (亿元)
贷款项目个数
(个)
本年固定资产
投资额 (亿元)
1
1 4.538 1.000 .01 .00 .01 .00 .00
2 .20
3 4.733 .68 .03 .02 .01 .09 3 .157 5.378 .16 .00 .66 .01 .13
4 .066 8.287 .00 .09 .20 .36 .72 5
.036
11.215
.15
.87
.12
.63
.05
a. 因变量: 不良贷款 (亿元)
通过
对上表分析得出:贷款余额线性关系通过显著性检验,回归系数通过显著性检验。
5绘制不良贷款和贷款余额回归的残差图。
2.练习《统计学》教材P330 练习题11.1、11.6、11.7、11.8、11.15,对应的数据文件为“习题11.1.xls”、“习题11.6.xls”、“习题11.7.xls”、“习题11.8.xls”、“习题11.15.xls”。
(任选两题)
11.1
(1)绘制产量和生产费用之间的散点图,判断二者之间的关系形态.
正向相关
相关性
产量(台)
生产费用(万元)
产量(台)
Pearson 相关性 1
.920**
显著性(双侧)
.000
N
12
12 生产费用(万元) Pearson 相关性 .920**
1
显著性(双侧) .000
N
12
12
**. 在 .01 水平(双侧)上显著相关。
(3)对相关系数的显著性进行检验,并说明二者间的关系强度
11.8
设月租金为自变量,出租率为因变量,回归并对结果进行解释和分析。
模型汇总
模型 R R 方 调整 R 方
标准 估计的误
差 更改统计量
R 方更改 F 更改
df1
df2
Sig. F 更改 1
.920a
.847
.832
14.791
.847
55.286
1
10
.000
a. 预测变量: (常量), 生产费用(万元)。
答:二者的关系强度为92%,P 值较小拒绝原假设所以关系强
模型汇总
模
型R R 方调整
R 方
标准
估计的
误差
1 .795
a
.632 .612 2.6858
a. 预测变量: (常量), 每平方米月租金(元)。
Anova b
模型平方
和df 均方 F Sig.
1 回
归223.
140
1 223.
140
30.9
33
.000
a
残差129.
845
18 7.21
4
总计352.
986
19
a. 预测变量: (常量), 每平方米月租金(元)。
模型汇总
模
型R R 方调整
R 方
标准
估计的
误差
1 .795
a
.632 .612 2.6858
b. 因变量: 出租率(%)
系数a
模型非标准化
系数
标准
系数
t Sig. B
标准
误差
试用
版
1 (常量) 49.3
18 3.80
5
12.9
61
.000
每平方米月租金(元).249 .045 .795 5.56
2
.000
a. 因变量: 出租率(%)
常量和每平米月租金都通过显著性检验,拒绝原假设所以方程成立。
相关系数为0.795中度相关。
