人教版九年级数学下册 26.1 反比例函数 同步测试题(有答案)
【九年级】九年级数学下26.1反比例函数(一)同步测试题(人教版有答案)

【九年级】九年级数学下26.1反比例函数(一)同步测试题(人教版有答案)反比例函数测试题姓名、班级、学号、分数___________一、选择题1.以下功能,① y=2x,② y=x,③ y=X-1,④ y=是反比例函数的数量,有()a.0个b.1个c.2个d.3个2.逆比例函数y=的图像位于()a.第一、二象限b.第一、三象限c.第二、三象限d.第二、四象限3.假设矩形的面积为10,则其长度y和宽度x之间的关系由图像表示,大致为()4.已知关于x的函数y=k(x+1)和y=-(k≠0)它们在同一坐标系中的大致图象是(•)5.如果已知点(3,1)是双曲线y=(K)上的点≠ 0),图像上以下点中的点为()a.(,-9)b.(3,1)c.(-1,3)d.(6,-)6.气球装满一定质量的气体后,当温度不变时,气球内气体的气压P(kPa)与气体体积V(M3)成反比函数,其图像如图所示。
当气球内气压大于140kpa时,气球将爆炸。
出于安全考虑,气体体积应为()a.不大于m3b.不小于m3c.不大于m3d.不小于m37.在闭合电路中,电源电压恒定,电流IA。
和电阻R(ω)成反比,如右图所示,是电路中电流I和电阻R之间函数关系的图像,然后用电阻R表示电流I,函数的解析表达式为()a.i=b.i=-c.i=d.i=8.函数y=和函数y=x在同一平面直角坐标系中的图像交点数为()a.1个b.2个c.3个d.0个9.如果函数y=(M+2)|M |-3是一个反比函数,则M的值为()a.2b.-2c.±2d.×210.已知点a(-3,Y1)、B(-2,Y2)和C(3,Y3)都在反比例函数y=,然后()a.y1<y2<y3b.y3<y2<y1c.y3<y1<y2d.y2<y1<y3二、填空11.一个反比例函数y=(k≠0)的图象经过点p(-2,-1),则该反比例函数的解析式是________.12.已知主函数y=KX+1和反比例函数y=X的图像通过点(2,m),则主函数的解析公式为___13.一批零件300个,一个工人每小时做15个,用关系式表示人数x•与完成任务所需的时间y之间的函数关系式为________.14.正比例函数y=x和反比例函数y=x的图像在两点a和点C以及点ab处相交⊥ X轴在B和CD处⊥ X轴在D轴,如图所示,则四边形abcd的为_______.图14、图15、图1915.如图,p是反比例函数图象在第二象限上的一点,且矩形peof的面积为8,则反比例函数的表达式是_________.16.在具有逆比例函数y=的图像的每个象限中,y随X的增加而增加,然后n=___17.已知一次函数y=3x+m与反比例函数y=的图象有两个交点,当m=_____时,有一个交点的纵坐标为6.18、如果主函数y= x+b和反比例函数y=图像,则在第二象限中有两个交点,即k×0,b,α,0(用“>”、“<”、“=”)填空。
人教版九年级数学下册 26.1 反比例函数 同步测试题(有答案)

26.1 反比例函数同步测试题(满分120分;时间:120分钟)一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 下列等式中是的反比例函数的是()A. B. C. D.2. 已知反比例函数的图像经过点,则它的图像一定也经过( )A. B. C. D.3. 已知反比例函数的图象经过点,则函数可为()A. B. C. D.4. 函数与(在同一坐标系内的图象可能是( )A. B.C. D.5. 反比例函数的图象经过点,则的值是()A. B.C. D.上述答案都不对6. 已知函数的图象如图,以下结论:①;②分支上随的增大而增大;③若点、点在图象上,则;④若点在图象上,则点也在图象上.其中正确的个数是( )A.个B.个C.个D.个7. 已知一个函数中,两个变量与的部分对应值如下表:…………………………如果这个函数图象是轴对称图形,那么对称轴可能是()A.轴B.轴C.直线D.直线8. 如图,在直角坐标系中,正方形的中心在原点,且正方形的一组对边与轴平行,点是反比例函数的图象上与正方形的一个交点,若图中阴影部分的面积等于,则的值为()A. B. C. D.9. 如图,第四象限的射线与反比例函数的图象交于点,已知,垂足为,已知的面积为,则该函数的解析式为()A. B. C. D.10. 如图,的三个顶点分别为,,.若反比例函数在第一象限内的图象与有交点,则的取值范围是( )A. B. C. D.二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 若反比例函数的图象经过点,则的图象在第________象限.12. 反比例函数,当________时,在每一象限内,的值随的值的增大而减小.13. 如图,反比例函数的图象经过点与点,则的面积为________.14. 过反比例函数的图象上一点分别作轴和轴的垂线,这两条垂线与两坐标轴围成的矩形面积是________.15. 已知两点、、在反比例函数的图象上,当时,________.16. 反比例函数的函数值为时,自变量的值是________.17. 若函数中,当时,,则函数解析式是________.18. 如图,在平面直角坐标系中,四边形是一个边长为的正方形,若反比例函数在第一象限的图象正好经过它的顶点,则的值为________.19. 一个函数具有下列性质:①它的图象经过点;②它的图象在二、四象限内;③在每个象限内,函数值随自变量的增大而增大.则这个函数的解析式可以为________.20. 一定质量的二氧化碳,其体积是密度的反比例函数,请你根据图中的已知条件,写出反比例函数的关系式,当时,________.三、解答题(本题共计6 小题,共计60分,)21. 在平面直角坐标系中,已知:直线反比例函数的图象的一个交点为.(1)试确定反比例函数的解析式;(2)写出该反比例函数与已知直线的另一个交点坐标.22. 已知函数,其中与成正比列,与成反比例,且时,,时,,求出与的函数关系及时,的值.23. 如图,点是反比例函数的图象上任意一点,延长交该图象于点,轴,轴,求的面积.24. 已知点,,点和在反比例函数的图象上.(1)若、、、构成正方形,求、的值;(2)若、、、构成一个邻边比为的矩形,则________.25. 已知双曲线经过矩形边的中点,交边于点.(1)求的值;(2)求四边形的面积.26. 如图,已知等边在平面直角坐标系中,点,函数(,为常数)的图象经过的中点,交于.(1)求的值;(2)若第一象限的双曲线与没有交点,请直接写出的取值范围.参考答案与试题解析一、选择题(本题共计10 小题,每题 3 分,共计30分)1.【答案】D【解答】解:、是正比例函数,故错误;、是正比例函数,故错误;、是一次函数,故错误;、是反比例函数,故正确;故选:.2.【答案】B【解答】解:因为反比例函数的图像经过点,故,只有答案中.故选.3.【答案】A【解答】解:由题意,,∴为.故选.4.【答案】A【解答】解:当时,函数过一、二、三象限,函数在第一、三象限上;当时,函数过二、三、四象限,函数在二、四象限上,综上所述,只有选项符合题意.故选.5.【答案】A【解答】解:∵函数经过点,∴,得.故选.6.【答案】B【解答】解:①根据反比例函数的图象的两个分支分别位于二、四象限,可得,故正确;②在每个分支上随的增大而增大,故正确;③若点、点在图象上,则,故错误;④若点在图象上,则点也在图象上,故正确.故选.7.【答案】D【解答】解:由表格可得:,所以该函数图象是经过第一、三象限的双曲线,故可得这个函数图象是轴对称图形,对称轴是.故选.8.【答案】C【解答】解:∵图中阴影部分的面积等于,∴正方形的面积,∵点坐标为,∴,∴(舍去),∴点坐标为,把代入,得.故选:.9.【答案】D【解答】解:∵的面积为,∴,解得,由图可知,反比例函数图象位于第二四象限,所以,,所以,,该函数的解析式为.故选.10.【答案】C【解答】解:∵是直角三角形,∴当反比例函数经过点时最小,经过点时最大,∴,,∴.故选.二、填空题(本题共计10 小题,每题 3 分,共计30分)11.【答案】二、四【解答】解:∵反比例函数的图象经过点,∴,∵,∴图象过二、四象限,故答案为二、四.12.【答案】【解答】解:∵反比例函数在每一象限内,的值随的值的增大而减小,∴,解得,.故答案是:.13.【答案】【解答】解:过点,分别作轴于,轴于,∵反比例函数的图象经过点与点,∴,,∴.故答案为:.14.【答案】【解答】解:设点坐标为,由函数解析式可知,,则可知,故答案为:.15.【答案】【解答】解:把、、代入得,,因为时,∴.故答案为.16.【答案】【解答】解:∵是反比例函数,则有,解得,因而函数解析式是,当函数值为时,即,解得.故自变量的值是.17.【答案】【解答】解:把,代入中得,,所以函数解析式是.故答案为:.18.【答案】【解答】解:∵四边形是一个边长为的正方形,∴,∴.故答案为:.19.【答案】【解答】解:设符合条件的函数解析式为,∵它的图象经过点把此点坐标代入关系式得,∴这个函数的解析式为.20.【答案】【解答】解:设函数关系式为:,由图象可得,当,,代入得:,故,当时,.故答案为:.三、解答题(本题共计6 小题,每题10 分,共计60分)21.【答案】解:(1)因为在直线上,则,即,又因为在的图象上,可求得,所以反比例函数的解析式为;(2)另一个交点坐标是.【解答】解:(1)因为在直线上,则,即,又因为在的图象上,可求得,所以反比例函数的解析式为;(2)另一个交点坐标是.22.【答案】解:设,,则,把时,,时,分别代入得,解得,所以与的函数关系式为,当时,.【解答】解:设,,则,把时,,时,分别代入得,解得,所以与的函数关系式为,当时,.23.【答案】解:设点的坐标为,则点坐标为,所以,,所以的面积为.【解答】解:设点的坐标为,则点坐标为,所以,,所以的面积为.24.【答案】.【解答】解:(1)如图,作轴于,轴于,根据题意,,∴,,∴,,∴,解得;(2)根据题意,,∴,,∴,,∴,解得.25.【答案】解:(1)∵点在双曲线的图象上,∴,∴;(2)∵为边的中点,∴,,,∴.∴四边形的面积.【解答】解:(1)∵点在双曲线的图象上,∴,∴;(2)∵为边的中点,∴,,,∴.∴四边形的面积.26.【答案】若第一象限的双曲线与没有交点,的取值范围为或.【解答】解:(1)过点作于点,如图所示.∵点,∴,又∵为等边三角形,∴,.∴点的坐标为.∵点为线段的中点,∴点的坐标为.∵点为函数(,为常数)的图象上一点,∴有,解得:.(2)设过点的反比例函数的解析式为,∵点的坐标为,∴有,解得:.若要第一象限的双曲线与没有交点,只需或即可,∴或.答:若第一象限的双曲线与没有交点,的取值范围为或.。
人教版初三数学9年级下册 第26章(反比例函数)26.1反比例函数 课后练习

人教九下26.1反比例函数一、选择题1. 下列函数中,是反比例函数的是( )A.y=−x2B.y=−12xC.y=1x−1D.y=1x22. 已知函数y=kx,当x=1时,y=−3,那么这个函数的解析式是( )A.y=3x B.y=−3xC.y=13xD.y=−13x3. 下列函数关系中,是反比例函数的是( )A.等边三角形面积S与边长a的关系B.直角三角形两锐角A与B的关系C.长方形面积一定时,长y与宽x的关系D.等边三角形的顶角A与底角B的关系4. 若点(3,6)在反比例函数y=kx(k≠0)的图象上,那么下列各点在此图象上的是( ) A.(−3,6)B.(2,9)C.(2,−9)D.(3,−6)5. 在反比例函数y=k−1x的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )A.k>1B.k>0C.k≥1D.k<16. 下列反比例函数的图象一定在第一、三象限的是( )A.y=mx B.y=m+1xC.y=m2+1xD.y=−mx7. 已知函数y=kx的图象经过(2,3),下列说法正确的是( )A.y随着x增大而增大B.函数的图象只在第一象限C.当x<0时,必有y<0D.点(−2,−3)不在此函数的图象上8. 已知A(x1,y1),B(x2,y2)是反比例函数y=kx(k≠0)的图象上的两点,当x1<x2<0时,y1 >y2,那么一次函数y=kx−k的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限9. 一次函数y=kx+b(k≠0)与反比例函数y=kx(k≠0)的图象在同一平面直角坐标系中的大致图象如图所示,则k,b的取值范围是( )A.k>0,b>0B.k<0,b>0C.k<0,b<0D.k>0,b<010. 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上,反比例函数y=kx (x>0)的图象经过顶点B,则k的值为( )A.12B.20C.24D.3211. 在反比例函数y=k(k<0)的图象上有两点A(x1,y1),B(x2,y2),且x1>x2>0,则y1−y2的x值为( )A.正数B.负数C.非正数D.非负数二、填空题12. 设三角形的底边、对应高、面积分别为a,ℎ,S.(1)当a=10时,S与ℎ的关系式为,是函数;(2)当S=18时,a与ℎ的关系式为,是函数.13. 已知变量y,x成反比例,且当x=2时,y=6,则这个函数关系是.14. 若函数y=(n−1)x n2−2是反比例函数,则n=.15. 点(1,3)在反比例函数y=k的图象上,则k=,在图象的每一支上,y随x的增大x而.16. 如图所示,某反比例函数的图象经过点(−2,1),则此反比例函数表达式为.17. 反比例函数y=2a−1的图象有一支位于第一象限,则常数a的取值范围是.x18. 已知点A(2,y1),B(4,y2)都在反比例函数y=k(k<0)的图象上,则y1y2(填“>”“<”x或“=”).19. 已知函数y=(m+1)x m2−5是反比例函数,且图象在第一、三象限内,则m=.20. 反比例函数y=k+1,点(x1,y1),(x2,y2)在其图象上,当x1<0<x2时,有y1>y2,则k x的取值范围是.图象上的概率21. 从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数y=12x是.三、解答题22. 已知y−1与x成反比例,当x=3时,y=5,求y与x的函数关系式.23. 作出反比例函数y=−4的图象,并结合图象回答:x(1) 当x=2时,y的值;(2) 当1<x≤4时,y的取值范围;(3) 当1≤y<4时,x的取值范围.的图象的一支位于第一象限.24. 已知反比例函数y=m−7x(1) 判断该函数图象的另一支所在的象限,并求出m的取值范围;(2) 如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.25. 如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA,OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数y=k(x>0,k≠0)的图象经过线段BC的中点D.x(1) 求k的值;(2) 若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式,并写出x的取值范围.26. 已知反比例函数的图象过点(1,−2).(1) 求这个函数的解析式,并画出图象;(2) 若点A(−5,m)在该图象上,则点A关于两坐标轴和原点的对称点是否也在图象上?27. 如图,一次函数y=kx+b的图象l分别与x轴,y轴交于点E,F,与双曲线y=−4x (x<0)交于点P(−1,n),F是PE的中点.(1) 求直线l的解析式;(2) 若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?答案一、选择题1. 【答案】B2. 【答案】B3. 【答案】C4. 【答案】B5. 【答案】A6. 【答案】C7. 【答案】C8. 【答案】B9. 【答案】D10. 【答案】D11. 【答案】A二、填空题12. 【答案】S=5ℎ;正比例;a=36;反比例ℎ13. 【答案】y=12x14. 【答案】−115. 【答案】3;减小16. 【答案】y=−2x17. 【答案】a>1218. 【答案】<19. 【答案】220. 【答案】k<−121. 【答案】16三、解答题22. 【答案】y=12+x.x23. 【答案】(1) y=−2.(2) −4<y≤−1.(3) −4≤x<−1.24. 【答案】(1) 第三象限;m−7>0,则m>7.(2) m=13.25. 【答案】(1) k=2.(2) S=2x−2,x>12−2x,0<x<1.26. 【答案】(1) y=−2,图略.x(2) m=2,点A−5,关于两坐标轴对称的点均不在函数图象上,关于原点对称的点在函数图5象上.27. 【答案】(1) y=−2x+2.(2) 当a=−2时,PA=PB(提示:过点P作PD⊥AB).。
人教版九年级数学下册《26.1反比例函数》练习题(含答案)

人教版九年级数学下册《26.1反比例函数》练习题(含答案)一、选择题1.下列函数是反比例函数的是( )A .B .y=x 2+xC .y=3xD .y=4x+82.已知变量y 与x 成反比例,当x =4时,8y =-;则当y =4时,x 的值是 ( )A .8B .-8C .12D .-12 3.函数k y x =的图象经过点()2,3,那么k 等于( ) A .6 B .16 C .23 D .324.已知反比例函数2k y x -=,其图象在第二、四象限内,则k 的值可为( ) A .0 B .2 C .3 D .55.点()13,A y -,()21,B y ,()33,C y 在反比例函数3y x -=的图象上,则1y ,2y ,3y 的大小关系是( )A .231y y y >>B .132y y y >>C .221y y y >>D .312y y y >> 6.在平面直角坐标系xOy 中,若函数)(0k y x x =<的函数值y 随着自变量x 的增大而增大,则函数)(0k y x x=<的图象所在的象限为( ) A .第一象限 B .第二象限C .第三象限D .第四象限 7.下列坐标是反比例函数3y x =图象上的一个点的坐标是( )A.(1,3) B .(3,1)- C .(3,1)- D .(8.对于反比例函数y =4x,下列说法不正确的是( ) A .这个函数的图象分布在第一、三象限B .点(1,4)在这个函数图象上C .这个函数的图象既是轴对称图形又是中心对称图形D .当x >0时,y 随x 的增大而增大9.如图,反比例函数a y x=-与6y x =的图像上分别有一点A ,B ,且AB x ∥轴,AD x ⊥轴于D ,BC x ⊥轴于C ,若矩形ABCD 的面积为8,则=a ( )A .-2B .-6C .2D .610.如图,已知反比例函数()>0k y x x=的图象上有一点P ,PA x ⊥轴于点A ,点B 在y 轴上,PAB △的面积为3,则k 的值为( )A .6B .12C .3-D .6-二、填空题11.正比例函数与反比例函数的一个交点为 123⎛⎫- ⎪⎝⎭,,当正比例函数的图像在反比例函数图像的上方时,则 x 的取值范围是_____________12.如图,四边形ABCD 为矩形,E 为对角线AC 的中点,A 、B 在x 轴上.若函数y =4x (x >0)的图像过D 、E 两点,则矩形ABCD 的面积为_______________13.如图,直线AB 与x 轴交于点()2,0A -,与x 轴夹角为30°,将ABO 沿直线AB 翻折,点O 的对应点C 恰好落在双曲线()0k y k x=≠上,则k 的值为______.14.如图,已知()11,A y ,()22,B y 是反比例函数2y x=图象上的两点,动点(),0P x 在x 轴正半轴上运动,当AP BP -达到最大时,点P 的坐标是______.15.如图,在平面直角坐标系中,菱形OABC 的面积为12,点B 在y 轴上,点C 在反比例函数y =k x(x <0)的图象上,则k 的值为______.三、解答题16.若函数y=(m+1)231m m x ++是反比例函数,求m 的值17.(1)已知y 与x ﹣2成反比例,当x =4时,y =3,求y 关于x 的解析式;(2)在平面直角坐标系中,点O 为坐标原点,直线l 与抛物线2y mx nx =+相交于A (1,,B (4,0)两点.求出抛物线的解析式.18.已知反比例函数y =8m x-(m 为常数) (1)若函数图象经过点A (-1,6),求m 的值:(2)若函数图象在第二、四象限,求m 的取值范围.19.如图,已知函数1k y x=的图象与一次函数222y x =+的图象交于点(),4A m 和点B .(1)求反比例函数的关系式;(2)如果点C 与点A 关于x 轴对称,求ABC 的面积.20.如图,在平面直角坐标系中,正比例函数y kx =的图象1L 与反比例函数6k y x-=的图象2L 的两个交点分别为()1,A a ,(),B m n . (1)则=a ______________,m =______________,n =______________;(2)求双曲线2L 的函数表达式;(3)若()3,C c 在双曲线2L 上,过点C 作CD x ⊥轴,垂足为D .求四边形AODC 的面积; (4)若6k kx x->,请根据图象,直接写出x 的取值范围.21.如图一次函数113y k x =+的图象与坐标轴相交于点()2,0A -和点B ,与反比例函数22(0)k y x x=>的图象相交于点()2,C m .(1)求出一次函数与反比例函数的解析式;(2)若点P 是反比例函数图象上的一点,连接CP 并延长,交x 轴正半轴于点D ,若:1:2PD CP =时,求COP 的面积;(3)在(2)的条件下,在y 轴上是否存在点Q ,使PQ CQ +的值最小,若存在请直接写出PQ CQ +的最小值,若不存在请说明理由.22.如图(1),一次函数y =ax +b 的图象与反比例函数k y x=的图象交于A (4,4),B (m ,﹣2)两点.(1)求反比例函数与一次函数的关系式.(2)C (0,n )为y 轴负半轴上一动点,作CD AB 与x 轴交于点D ,交反比例函数于点E . ①如图(1),当D 为CE 的中点时,求n 的值.①如图(2),过点E 作y 轴的垂线,交直线AB 于点F ,若48EF <≤,请直接写出n 的取值范围.23.如图,在平面直角坐标系xOy 中,正方形ABCD 的边AB 在x 轴的正半轴上,顶点C ,D 在第一象限内,正比例函数y 1=3x 的图象经过点D ,反比例函数2(0)k y x x =>的图象经过点D ,且与边BC 交于点E ,连接OE ,已知AB =3.(1)点D 的坐标是 ;(2)求tan ①EOB 的值;(3)观察图象,请直接写出满足y 2>3的x 的取值范围;(4)连接DE ,在x 轴上取一点P ,使98DPE S =,过点P 作PQ 垂直x 轴,交双曲线于点Q ,请直接写出线段PQ 的长.【参考答案】1.A 2.B 3.A 4.A 5.B 6.B 7.A 8.D 9.C 10.D 11.2x <-或02x <<12.813.14.3,015.6-16.m 的值是﹣2.17.(1)62y x =-(2)2y =+ 18.(1)2;(2)8m <19.(1)反比例函数表达式为4y x =;(2)12ABC S = 20.(1)3,-1,-3;(2)3y x =;(3)112;(4)-1<x <0或x >121.(1)212(0)y x x =>;(2)S ①OPC = 16;(3) 22.(1)y =16x;y =12x +2;(2)①n =2±;①20n -≤<. 23.(1)(1,3);(2)316;(3)01x <<;(4)12或34。
人教版初三数学9年级下册 第26章(反比例函数)单元测试卷1(含答案)
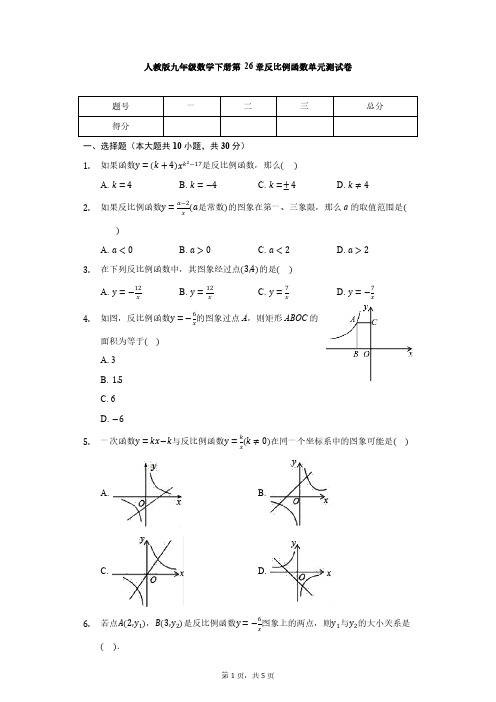
第1页,共5页人教版九年级数学下册第 26章反比例函数单元测试卷题号一二三总分得分一、选择题(本大题共10小题,共30分)1.如果函数y =(k +4)x k 2−17是反比例函数,那么( )A. k =4B. k =−4C. k =±4D. k ≠42.如果反比例函数y =a−2x(a 是常数)的图象在第一、三象限,那么a 的取值范围是()A. a <0 B. a >0C. a <2D. a >23.在下列反比例函数中,其图象经过点(3,4)的是( )A. y =−12xB. y =12xC. y =7xD. y =−7x4.如图,反比例函数y =−6x 的图象过点A ,则矩形ABOC 的面积为等于( )A. 3B. 1.5C. 6D. −65.一次函数y =kx−k 与反比例函数y =kx (k ≠0)在同一个坐标系中的图象可能是( )A. B.C. D.6.若点A(2,y 1),B(3,y 2)是反比例函数y=−6x 图象上的两点,则y 1与y 2的大小关系是( ).A. y1<y2B. y1>y2C. y1=y2D. 3y1=2y27.若点A(x1,−6),B(x2,−2),C(x3,2)均在反比例函数y=k2+1x的图象上,则x1,x2,x3的大小关系正确的是()A. x1<x2<x3B. x2<x1<x3C. x2<x3<x1D. x3<x2<x18.点M(a,2a)在反比例函数y=8x的图象上,那么a的值是( )A. 4B. −4C. 2D. ±29.点A(−1,1)是反比例函数y=m+1x的图象上一点,则m的值为( )A. −1B. −2C. 0D. 110.如图,直线y=−3x+3与x轴交于点A,与y轴交于点B,以AB为边在直线AB的左侧作正方形ABDC,反比例函数y=kx的图象经过点D,则k的值是( )A. −3B. −4C. −5D. −6二、填空题(本大题共5小题,共15分)11.反比例函数y=6x的图象经过点(m,−3),则m=________.12.反比例函数y=1−2mx的图象有一支位于第一象限,则常数m满足的条件是__.13.反比例函数y=2m−5x的图象的两个分支分别在第二、四象限,则m的取值范围为______,在每个象限内y随x的增大而______.14.已知同一个反比例函数图象上的两点P1(x1,y1)、P2(x2,y2),若x2=x1+2,且1y2=1 y1+12,则这个反比例函数的解析式为______.15.如图,一次函数y=−x+b与反比例函数y=4x(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D 两点,连结OA,OB,过A作AE⊥x轴于点E,交OB 于点F,设点A的横坐标为m.(1)b=______ (用含m的代数式表示);第3页,共5页(2)若S △OAF +S 四边形EFBC =4,则m 的值是______ .三、解答题(本大题共6小题,共55分)16.在一个不透明的布袋里,装有完全相同的3个小球,小球上分别标有数字1,2,5;先从袋子里任意摸出1个球,记其标有的数字为x ,不放回;再从袋子里任意摸出一个球,记其标有的数字为y ,依次确定有理数xy .(1)请用画树状图或列表的方法,写出xy 的所有可能的有理数;(2)求有理数xy 为整数的概率.17.已知平面直角坐标系xOy 中,O 是坐标原点,点A(2,5)在反比例函数y =kx 的图象上,过点A 的直线y =x +b 交x 轴于点B .(1)求反比例函数解析式;(2)求△OAB 的面积.18.如图,已知反比例函数y =6x 的图象与一次函数y =kx +b 的图象交于点A(1,m),B(n,2)两点.(1)求一次函数的解析式;≥kx+b的解集;(2)直接写出不等式6x在第一象限的图像,如图所示,过点A(1,0)作x轴的垂线,交反比19.反比例函数y=kx的图像于点M,△AOM的面积为3.例函数y=kx(1)求反比例函数的解析式.(2)设点B的坐标为(t,0),其中t>1,若以AB为一边的正方形ABCD有一个顶点的图像上,求t的值.在反比例函数y=kx20.阅读材料:公元前3世纪,古希腊学者阿基米德发现了著名的“杠杆原理”.杠杆平衡时,阻力×阻力臂=动力×动力臂.第5页,共5页问题解决:若工人师傅欲用提棍动一块大石头,已知阻力和阻力臂不变,分别为1500N 和0.4m .(1)动力F(N)与动力臂l(m)有怎样的函数关系⋅当动力臂为1.5m 时,提动石头需要多大的力⋅(2)若想使动力F(N)不超过题(1)中所用力的一半,则动力臂至少要加长多少⋅数学思考(3)请用数学知识解释:我们使用攉棍,当阻力与阻力臂一定时,为什么动力臂越长越省力.21.某商场出售一批名牌衬衣,衬衣进价为60元,在营销中发现,该衬衣的日销售量y(件)是日销售价x 元的反比例函数,且当售价定为100元/件时,每日可售出30件.(1)请写出y 关于x 的函数关系式;(2)该商场计划经营此种衬衣的日销售利润为1800元,则其售价应为多少元?。
人教版九年级数学下册 26.1 反比例函数 同步训练(含答案)

26.1反比例函数同步训练一.选择题1.下列图象中是反比例函数y=x2-的图象的是( )2.当x >0时,函数y =-x5的图象在()A .第四象限B .第三象限C .第二象限D .第一象限3.已知点A(-2,y 1),B(3,y 2)是反比例函数y =xk(k <0)图象上的两点,则有( ) A .y 1<0<y 2B .y 2<0<y 1C .y 1<y 2<0D .y 2<y 1<04.若反比例函数ky x=(k≠0)的图象经过点P(-2,3),则该函数的图象不经过的点是( )A .(-1,-6)B .(1,-6)C .(-1,6)D .(3,-2)5. 在反比例函数y =1-3mx 的图象上有两点A(x 1,y 1),B(x 2,y 2),x 1<0<x 2,y 1<y 2,则m 的取值范围是( )A .m>13B .m ≥13C m<13D .m ≤136.若点A(a ,b)在反比例函数2y x=的图象上,则代数式ab -4的值为( ) A .0 B .-2 C .2 D .-67.在同一直角坐标系中,函数y =-kx +k 与y = (k ≠0)的图象大致是( )A. B. C. D.8.如图,在函数的图像上有A ,B ,C 三点,过这三点分别向轴、轴作垂线,过每一点所作的两条垂线段与轴、轴围成的矩形的面积分别为S 1,S 2,S 3,则( )A.S1>S2>S3 B.S1<S2<S3 C.S1<S3<S2 D.S1=S2=S39.如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=(x>0)的图象经过顶点B,则k的值为( )A.12 B.20 C.24 D.3210.若在同一直角坐标系中,直线y=k1x与双曲线y=有两个交点,则有( )A.k1+k2>0 B.k1+k2<0 C.k1k2>0 D.k1k2<011.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=()A. B.9 C. D.312.已知反比例函数y=K/X的图象经过点(2,-2),则k的值为()A. 4 B.-1 C.-4 D.-213.已知反比例函数(k≠0),当x=2时,y=﹣7,那么k等于()A.14 B.2 C. 6 D.﹣1414.下列关于y 与x 的表达式中,反映y 是x 的反比例函数的是( ) A .y=4x B .y=﹣2x C .xy=4 D .y=8x ﹣315.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(Pa)是气体体积V(cm 3)的反比例函数,其图象如图所示。
人教版九年级数学下册《第26章反比例函数》测试卷-含参考答案

人教版九年级数学下册《第26章反比例函数》测试卷-含参考答案(考试时间:90分钟 试卷满分:100分)一、选择题:(本大题共10小题,每小题3分,满分30分) 1.已知点()()()1232,,3,,2,y y y --在函数0.8y x=-的图象上,则( ) A .123y y y << B .213y y y << C .312y y y << D .321y y y <<【答案】D【详解】解:∵反比例函数解析式为0.8y x =-,0.80k =-<∵反比例函数图象经过第二、四象限,在每个象限内y 随x 增大而增大 ∵点()()()1232,,3,,2,y y y --在函数0.8y x =-的图象上,3202-<-<<∵3210y y y <<<故选D .2.若反比例函数3ky x-=的图像分布在第二、四象限,则k 的取值范围是( ) A .3k <- B .3k <C .3k >D .3k >-【答案】C【详解】解:∵反比例函数3ky x -=的图像分布在第二、四象限∵30k -< 解得:3k > 故选:C . 3.反比例函数ky x=经过点(2,1),则下列说法错误的是( ) A .函数图象经过点(1,2)-- B .函数图象分布在第一、三象限 C .当0x >时,y 随x 的增大而增大 D .当0x <时,y 随x 的增大而减小 【答案】C【详解】解:∵反比例函数ky x =经过点(2,1)∵2120k =⨯=>∵函数图象分布在第一、三象限,当0x >时,y 随x 的增大而减小∵1(2)2k -⨯-== ∵函数图象经过点(1,2)-- ∵选项C 错误 故选:C .4.如图,已知双曲线()0ky k x=<经过Rt OAB △斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为6,4,则AOC 的面积为( )A .92B .6C .9D .10【答案】C【详解】解:∵OA 的中点是D ,点A 的坐标为6,4∵()3,2D - ∵双曲线()0ky k x=<经过点D ∵326k =-⨯=- ∵BOC 的面积132k =. 又∵AOB 的面积164122=⨯⨯=∵AOC 的面积AOB =△的面积BOC -△的面积1239=-=. 故选C .5.如图,正方形ABCD 位于第一象限,边长为3,点A 在直线y x =上,点A 的横坐标为2,正方形ABCD 的边分别平行于x 轴、y 轴.若双曲线()0ky k x=≠与正方形ABCD 有两个公共点,则k 的取值范围为( )A .25k <<B .116k ≤≤C .425k ≤≤D .425k <<【答案】D【详解】解:把2x =代入y x = 解得∵2y = ∵A 的坐标是()2,2∵正方形ABCD 位于第一象限,边长为3 ∵C 点的坐标是()5,5 ∵当双曲线()0ky k x=≠经过点()2,2时,4k =; 当双曲线()0ky k x=≠经过点()5,5时,25k = ∵双曲线()0ky k x=≠与正方形ABCD 有两个公共点 ∵425k <<. 故选D .6.如图,已知双曲线(0)k y x x=>与矩形OABC 的对角线OB 相交于点D ,若53OB OD =,矩形OABC 的面积为1003,则k 等于( )A .6B .12C .24D .36【答案】B【详解】解:设D 的坐标是(3,3)m n ,则B 的坐标是(5,5)m n . ∵矩形OABC 的面积为1003∵100553m n = ∵43=mn . 把D 的坐标代入函数解析式得:33k n m= ∵499123k mn ==⨯=. 故选:B .7.二次函数2y ax bx c ++=的图象如图所示,则一次函数y ax b =-+与反比例函数c y x=在同一坐标系内的大致图象是( )A .B .C .D .【答案】A【详解】解:∵二次函数图象开口方向向上 ∵a >0,即-a <0又∵对称轴为直线x =-2ba <0∵b >0∵与y 轴的负半轴相交 ∵c <0∵y =-ax +b 的图象经过第一、二、四象限,反比例函数cy x =图象在第二、四象限只有A 选项图象符合. 故选:A .8.如图,A 、B 两点在反比例函数1k y x=的图像上,C 、D 两点在反比例函数2ky x =的图像上,AC ∵y 轴于点E ,BD ∵y 轴于点F ,AC =2,BD =1,EF =3 则12k k -的值是( )A .6B .4C .3D .2【答案】D【详解】解:由题意 设点A 的坐标为1,k A a a ⎛⎫ ⎪⎝⎭ 点B 的坐标为1,B b k b ⎛⎫ ⎪⎝⎭ 则12,C a a k ⎛⎫- ⎪⎝⎭ 11,D b b k ⎛⎫+ ⎪⎝⎭ 10,E k a ⎛⎫ ⎪⎝⎭ 10,F k b ⎛⎫⎪⎝⎭ 将点12,C a a k ⎛⎫- ⎪⎝⎭ 11,D b b k ⎛⎫+ ⎪⎝⎭代入2k y x =得:21121k a k k a b b -+==解得2a b =-3EF =113k k a b ∴-= 即1132b b k k--=解得12k b=-2111222b b k b b b b k ++===⋅-∴--()122222k k b b --∴---==故选:D .9.如图 在平面直角坐标系xoy 中 点A C 分别在坐标轴上 且四边形OABC 是边长为3的正方形 反比例函数()0ky x x=>的图像与BC AB ,边分别交于E D ,两点 DOE 的面积为4 点P 为y 轴上一点 则PD PE +的最小值为( )A .3B .C .D .5【答案】B【详解】正方形OABC 的边长是3 ∴点D 的横坐标和点E 的纵坐标为3(3,)3kD ∴ (3kE 3) 33k BE ∴=-33kBD =-ODE △的面积为421113333(3)4232323k k k∴⨯-⨯⨯-⨯⨯-⨯-=3k ∴=或3-(舍去)(3,1)D ∴ ()1,3E作E 关于y 轴的对称点E ' 连接DE '交y 轴于P 则DE '的长PD PE =+的最小值1CE CE AD ='==4BE ∴'= 2BD ='DE ∴=即PD PE +的最小值为故选:B . 10.函数 4y x =和1y x =在第一象限内的图象如图 点P 是4y x=的图象上一动点PC x ⊥轴于点C 交1y x=的图象于点A PD y ⊥轴于点D 交1y x=的图象于点B .给出如下结论: ∵ODB △与OCA 的面积相等; ∵PA 与PB 始终相等;∵四边形PAOB 的面积大小不会发生变化; ∵13CA AP =. 其中所有正确结论有( )个.A .1个B .2个C .3个D .4个【答案】C【详解】解:∵AB 、是反比函数1y x=上的点 12OBD OAC S S ==△△ 故∵正确; ∵由图的直观性可知 P 点至上而下运动时 PB 在逐渐增大 而PA 在逐渐减小 只有当P 的横纵坐标相等时PA PB = 故∵错误; ∵P 是4y x=的图像上一动点 ∵矩形PDOC 的面积为4 ∵114322ODBOACPDOC PAOB S S SS=----=矩形四边形= 故∵正确;连接OP∵2412POC OAC S PC S AC ===△△∵1344AC PC PA PC ==, ∵3PAAC= ∵13AC AP =故∵正确; 综上所述 正确的结论有∵∵∵. 故选:C .二、填空题:(本大题共6小题 每小题3分 满分18分) 11.已知反比例函数ky x=的图象经过()4,2- 求y 关于x 的函数解析式_______.【答案】8y x=-【详解】解:∵反比例函数ky x=的图象经过()4,2- ∵24k-=解得8k =-. ∵y 关于x 的函数解析式为8y x=-. 故答案为:8y x=-. 12.已知一次函数12y k x =+的图象经过点()3A m ,()21B m +-, 反比例函数2k y x=的图象位于一、三象限 则1k ______2k .(填> <或=) 【答案】<【详解】解:∵一次函数12y k x =+的图象经过点()3A m ,()21B m +-, ∵1123(2)21k m k m +=⎧⎨++=-⎩ 得1212k m =-⎧⎪⎨=-⎪⎩∵反比例函数2k y x=的图象位于一、三象限 ∵20k > ∵12k k < 故答案为:<.13.如图 点A 、B 分别是双曲线4y x=和1y x =第一象限分支上的点 且AB y ∥轴 BC y⊥轴于点C 则AB BC ⋅的值是_____________.【答案】3【详解】解:延长AB 交x 轴于点D 过点A 作AE y ⊥轴于点E∵AB y ∥轴 BC y ⊥轴∵四边形ADOE ABCE BDOC 、、都是矩形 ∵点A 、B 分别是双曲线4y x =和1y x =第一象限分支上的点∵矩形ADOE 的面积为4 矩形BDOC 的面积为1 ∵矩形ABCE 的面积为413-= ∵3AB BC ⋅= 故答案为:3.14.如图 点A 、B 是反比例4y x=图像上任意两点 过点A 、B 分别作x 轴、y 轴的垂线 2S =阴影 则12S S =+ ________.【答案】4【详解】解:∵点A 、B 是反比例4y x=图像上任意两点 过点A 、B 分别作x 轴、y 轴的垂线∵124S S S S +=+=阴影阴影 ∵2S 阴影= ∵122S S == ∵124S S +=. 故答案为:4.15.如图 已知一次函数26y x =+的图象与反比例函数ky x=的图象交于A B 两点 点B 的横坐标是1 过点A 作AC y ⊥轴于点C 连接BC 则ABC 的面积是________.【答案】20【详解】解:∵一次函数26y x =+的图象与反比例函数ky x=的图象交于A B 两点 点B 的横坐标是1∵把1x =代入26y x =+ 得:2168y =⨯+= ∵(18)B ,. 将(18)B ,代入ky x = 得:81k = 解得:8k∵反比例函数解析式为8y x=. 联立268y x y x =+⎧⎪⎨=⎪⎩ 解得:18x y =⎧⎨=⎩或42x y =-⎧⎨=-⎩ ∵(42)A --,. ∵AC y ⊥轴于点C ∵4AC = ∵()()114822022ABCB A SAC y y =⨯-=⨯⨯+=. 故答案为:20.16.瑞泰工程组安排甲、乙、丙、丁四辆货车用于一批建筑材料运输 已知这四辆货车每一次的运货量都保持不变且为整数(单位:吨) 乙车每次运货量比甲车高50% 丙车每次运货量比甲车多12吨 甲、丙两车运输2次的货物总量与丁车独自运输3次的货物量相等、当甲、乙、丙、丁四辆货车运输次数之比为5:2:3:1恰好运完这一批建筑材料 此时甲车共运输了120吨 则这批建筑材料最多有 ___________吨. 【答案】376【详解】解:设甲车每次运x 吨乙车每次运货量比甲车高50% 丙车每次运货量比甲车多12吨 ∴乙车每次运3(150%)2x x+=(吨) 丙车每次运(12)x +吨甲、丙两车运输2次的货物总量与丁车独自运输3次的货物量相等∴丁车每次运22(12)4(8)33x x x ++=+吨x 32x 12x + 483x +都是整数x ∴是6的倍数 x 最小为6设这一批建筑材料共W 吨 运完这一批建筑材料 丁车运输k 次 则甲车运输5k 次 乙车运输2k 次 丙车运输3k 次 甲车共运输了120吨5120kx ∴= 24k x ∴=根据题意得:34523(12)(8)23W kx k x k x k x =+⋅+⋅++⋅+37203kx k =+ 3724203k =⨯+ 29620k =+480296x =+∴当x 最小时 W 取最大值6x ∴=时 W 最大为4802963766+=(吨)∴这批建筑材料最多有376吨故答案为:376.三、解答题(本大题共6题 满分52分) 17.(7分)已知反比例函数1ky x=的图象与一次函数2y ax b =+的图象交于点(1,4)A 和点(),2B m -.(1)求这两个函数的关系式;(2)观察图象 直接写出使得12y y >成立的自变量x 的取值范围; (3)如果点C 与点A 关于x 轴对称 求ABC 的面积. 【答案】(1)14y x=222y x =+ (2)<2x -或01x << (3)12【详解】(1)解:将(1,4)A 代入1k y x=得 41k=解得4k =∴反比例函数的解析式为14y x=又点(),2B m -在14y x=上 42m∴-=解得2m =-∴点B 的坐标为()2,2--点A 和点B 在一次函数2y ax b =+上422a b a b +=⎧∴⎨-+=-⎩ 解得22a b =⎧⎨=⎩∴一次函数的解析式为222y x =+综上可得14y x=222y x =+. (2)解:12y y >时 反比例函数图象在一次函数图象上方 观察图象可知 当<2x -或01x <<时 12y y >.(3)解:如图 作点A 关于x 轴的对称点C 连接AC 作BD AC ⊥于点D点A 的坐标为()1,4∴点C 的坐标为()1,4-又点B 的坐标为()2,2--448AC ∴=+-= 213BD =-+=∴ABC 的面积11831222S AC BD =⋅=⨯⨯=. 18.(7分)王叔叔计划购买一套商品房 首付30万元后 剩余部分用贷款并按“等额本金”的形式偿还 即贷款金额按月分期还款 每月所还贷款本金数相同.设王叔叔每月偿还贷款本金y 万元 x 个月还清 且y 是x 的反比例函数 其图象如图所示.(1)求y 与x 的函数关系式; (2)求王叔叔购买的商品房的总价;(3)若王叔叔计划每月偿还贷款本金不超过2000元 则至少需要多少个月还清? 【答案】(1)60y x=(2)90万元 (3)300个月【详解】(1)解:设()0ky k x=≠ 由图象可知:()120,0.5在函数图象上 ∵1200.560k =⨯= ∵60y x=;(2)解:∵60y x=∵王叔叔贷款总额为:60万元 ∵房子总价为:306090+=万元; (3)解:20000.2=万 由题意得: 当0.2y ≤时 即:600.2x ≥解得300x ≥∵至少需要300个月还清.19.(9分)如图 一次函数25y x =-的图象与反比例函数ky x=的图象交于A 、B 两点 其中(3,1)A .(1)求该反比例函数的解析式及点B 的坐标; (2)根据所给条件 直接写出不等式25kx x-≤的解集. (3)C 是第三象限内反比例函数图象上的点 是否存在点C 使得OC OA =?若存在请直接写出C 的坐标;若不存在 请说明理由.【答案】(1)反比例函数的解析式为3y x =;1(6)2B --,; (2)12x ≤-或03x <≤;(3)存在 点C 的坐标为()31--,或()13,--. 【详解】(1)解:∵反比例函数ky x=的图象经过点(31)A , ∵313k =⨯=∵反比例函数的解析式为3y x=; 解方程325x x =-得:3x =或12x =- 经检验 3x =或12x =-都是方程的解当12x =-时3612y ==-- ∵1(6)2B --,; (2)解:∵(31)A , 1(6)2B --, ∵不等式25k x x -≤的解集为:12x ≤-或03x <≤; (3)解:存在设点C 的坐标为3m m ⎛⎫⎪⎝⎭,且0m <∵OA OC = 即22OA OC =∵2222331m m ⎛⎫+=+ ⎪⎝⎭整理得421090m m -+=解得29m =或21m = ∵3m =-或1m =-∵点C 的坐标为()31--,或()13,--. 20.(9分)已知一次函数1(0)y kx b k =+≠的图象与反比例函数2(0)my m x=≠的图象交于A 、B 两点 已知点(1,4)A -- 点B 的横坐标为2.(1)求一次函数与反比例函数的表达式 并在图中画出一次函数的图象; (2)根据函数图象 直接写出不等式12y y >的解集;(3)若点C 是点B 关于x 轴的对称点 连接AC 、BC 求ABC 的面积. 【答案】(1)一次函数122y x =- 反比例函数为:24y x= 画图见解析; (2)10x -<<或>2x . (3)6ABCS=.【详解】(1)解:∵反比例函数2(0)my m x =≠的图象过点(1,4)A --∵()144m =-⨯-= ∵反比例函数为:24y x =∵B 在反比例函数图象上 且2B x =∵2B y = 即()2,2B∵一次函数1(0)y kx b k =+≠的图象过A B∵224k b k b +=⎧⎨-+=-⎩ 解得:22k b =⎧⎨=-⎩∵一次函数122y x =-描点 画图如下:(2)由函数图象可得:当12y y >时 x 的取值范围为:10x -<<或>2x .(3)如图 点C 是点B 关于x 轴的对称点∵()2,2C - 可得4BC =∵()1,4A -- 可得A 到BC 的距离为()213--=∵14362ABC S =⨯⨯=△.21.(10分)如图 已知一次函数y ax b =+与反比例函数(0)my x x=<的图象交于(2)A -,3 (32)B -,两点 且与x 轴和y 轴分别交于点C 、点D .(1)根据图象直接写出不等式max b x<+的解集; (2)求反比例函数与一次函数的解析式; (3)点P 在y 轴上 且2AOPAOBS S= 请求出点P 的坐标.【答案】(1)31x -<<- (2)6(0)y x x =-< 5y x =+(3)(05)P ,或(05)-, 【详解】(1)∵当my x =的图象在y ax b =+图象的下方时 m ax b x<+成立 又∵由图象可知当31x -<<-时 my x=的图象在y ax b =+图象的下方 ∵不等式max b x<+的解集为31x -<<-. (2)将(2)A -,3代入m y x= 得:32m =-解得:6m =-∵反比例函数为:6(0)y x x=-<;将(2)A -,3 (32)B -,代入y ax b =+ 得:3223a ba b =-+⎧⎨=-+⎩解得:15a b =-⎧⎨=⎩ ∵一次函数的表达式为:5y x =+; (3)对于5y x =+ 当0y =时 5x =- ∵(50)C -,. ∵()11512225ABOAOC BOCA B S SSOC y y =-=⨯-=⨯⨯= ∵5AOPS=.∵P 在y 轴上 ∵112522AOPA SOP x OP =⨯=⨯= 解得:5OP =. ∵(05)P ,或(05)-,. 22.(10分)已知平面直角坐标系中 直线AB 与反比例函数(0)ky x x=>的图象交于点()3,4A 和点()6,B t 与x 轴交于点C 与y 轴交于点D .(1)求反比例函数的表达式和直线AB 的表达式;(2)若在x 轴上有一异于原点的点P 使PAB 为等腰三角形 求点P 的坐标;(3)若将线段AB 沿直线()0y mx n m =+≠进行对折得到线段11A B 且点1A 始终在直线OA 上 当线段11A B 与x 轴有交点时 求n 的取值的最大值. 【答案】(1)反比例函数的表达式为12y x=直线AB 的解析式为263y x =-+(2)PAB 为等腰三角形时 点P 的坐标为5,02⎛⎫⎪⎝⎭或()3,0或()9,0(3)当线段11A B 与x 轴有交点时 n 的取值的最大值为7916【详解】(1)反比例函数(0)k y x x=>的图象经过点()3,4A 和点()6,B t346k t ∴=⨯=12k ∴= 2t =∴反比例函数的表达式为12y x=设直线AB 的解析式为y cx d =+()3,4A ()6,2B 3462c d c d +=⎧∴⎨+=⎩ 解得:236c d ⎧=-⎪⎨⎪=⎩ ∴直线AB 的解析式为263y x =-+;(2)设(),0P t则2222(3)(04)625PA t t t =-+-=-+ 2222(6)(02)1240PB t t t =-+-=-+ 222(36)(42)13AB =-+-=PAB △为等腰三角形PA PB ∴=或PA AB =或PB AB =当PA PB =时 22PA PB =226251240t t t t ∴-+=-+解得:52t =5,02P ⎛⎫∴ ⎪⎝⎭;当PA AB =时 22PA AB = 262513t t ∴-+=2(6)4112120∆=--⨯⨯=-<∴此方程无解;当PB AB =时 22PB AB = 2124013t t ∴-+=解得:13t = 29t =()3,0P ∴或()9,0;综上所述 PAB 为等腰三角形时 点P 的坐标为5,02⎛⎫⎪⎝⎭或()3,0或()9,0;(3)当点1B 落到x 轴上时 n 的取值的最大 如图设直线OA 的解析式为y ax = 点A 的坐标为()3,434a ∴= 即43a =. ∴直线OA 的解析式为4.3y x =点1A 始终在直线OA 上∴直线y mx n =+与直线OA 垂直.413m ∴=-. 34m ∴=-.34y x n ∴=-+由于1//BB OA 因此直线1BB 可设为43y x e =+.点B 的坐标为()6,2 4623e ∴⨯+= 即6e =-. ∴直线1BB 解析式为463y x =-. 当0y =时460.3x -=则有92x =.∴点1B 的坐标为902,⎛⎫⎪⎝⎭.1BB 的中点坐标为96202,22⎛⎫+ ⎪+ ⎪ ⎪⎝⎭即21,14⎛⎫ ⎪⎝⎭ 点21,14⎛⎫⎪⎝⎭在直线34y x n =-+上321144n ∴-⨯+=.解得:7916n =. 故当线段11A B与x 轴有交点时 n 的取值的最大值为7916.。
人教版九年级数学下册《第二十六章 反比例函数》测试题-带参考答案

人教版九年级数学下册《第二十六章反比例函数》测试题-带参考答案一、选择题1.已知y与x成反比例函数,且x=2时,y=3,则该函数表达式是()A.y=6x B.y= C.y= 6x D.y= 6x−12.若点(−2,−6)在反比例函数y=kx上,则k的值是()A.3B.−3C.12D.−123.已知反比例函数y=k−2x的图象位于第一、第三象限,则k的取值范围是()A.k>2 B.k≥2 C.k≤2 D.k<25.在同一平面直角坐标系中,函数y=mx+n与y=mnx(mn≠0)的图象可能是()A.B.C.D.6.若正比例函数y=-4x与反比例函数y=kx的图像相交于A,B两点,其中点A的横坐标为2,则k的值为()A.-16 B.-8 C.16 D.87.如图,函数y=6x与函数y=kx(k>0)的图象相交于A、B两点,AC//y轴,BC∥x轴,则△ABC的面积等于()A.18 B.12 C.6 D.38.如图,在平面直角坐标系中,A是反比例函数y=1x图象上第三象限上的点,连结AO并延长交该函数第一象限的图象于点B,过点B作BC//x轴交函数y=kx(k>1)的图象于点C,连结AC.若ΔABC的面积为3,则k的值为()A.3 B.52C.4 D.7二、填空题9.当m= 时,y=(m−3)x m2−10是反比例函数.10.一批零件300个,一个工人每小时做15个,用关系式表示人数x与完成任务所需的时间y之间的函数关系式为.11.若点(2,1)是反比例函数y= m2+2m−1x的图象上一点,当y=6时,则x= .12.如图,已知点P(1,2)在反比例函数y=kx的图象上,观察图象可知,当x>1时,y的取值范围是.13.如图,点A在双曲线y=5x 上,点B在双曲线y=7x上,且AB//x轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为.三、解答题14.如图,直线AB交双曲线y=kx(x>0)于A、B两点,交x轴于点C(4a,0),AB=2BC,过点B作BM⊥x 轴于点M,连接OA,若OM=3MC,S△OAC=8求k的值.15.如图,在平面直角坐标系中,一次函数y =x +b 的图象与x 轴交于点B(1,0),与y 轴交于点C ,与反比例y =kx(k >0,x >0)的图象交于点A.点B 为AC 的中点.求一次函数y =x +b 和反比例y =kx的解析式.16.某市政府计划建设一项水利工程,工程需要运送的土石方总量为106立方米,某运输公司承担了运送土石方的任务.(1)设该公司平均每天运送土石方总量为y 立方米,完成运送任务所需时间为t 天. ①求y 关于t 的函数表达式; ②当0<t ≤80时,求y 的取值范围.(2)若1辆卡车每天可运送土石方102立方米,工期要求在80天内完成,则公司至少要安排多少辆相同型号的卡车运送?17.如图,正比例函数112y x =和反比例函数2(0)ky x x=>的图像交于点(),2A m .(1)求反比例函数的解析式;(2)将直线OA 向上平移3个单位后,与y 轴交于点B ,与2(0)ky x x =>的图像交于点C ,连接AB,AC ,求ABC 的面积.18.如图,在平面直角坐标系xOy 中,点A (a ,﹣)在直线y =﹣上,AB ∥y 轴,且点B 的纵坐标为1,双曲线y=经过点B.(1)求a的值及双曲线y=的解析式;(2)经过点B的直线与双曲线y=的另一个交点为点C,且△ABC的面积为.①求直线BC的解析式;②过点B作BD∥x轴交直线y=﹣于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.参考答案 1.C 2.C 3.A 4.D 5.D 6.A 7.B 8.C 9.﹣3 10.y =20x11.13 12.0<y <2 13.214.解:连接OB ,设B(a ,b).∵点B 在函数y =k x 上∴ab =k ,且OM =a ,BM =b ∵OM =3MC ∴MC =13a ∴S △BOM =12ab =12k ,S △BMC =12×13ab =16ab =16k ∴S △BOC =S △BOM +S △BMC =12k +16k =23k ∵AB =2BC 设点O 到AC 的距离为h 则S △BOCS△AOB=12BC·h 12AB·h =BC AB =12∴S △AOB =2S △BOC =43k ∴S △AOC =S △AOB +S △BOC =43k +23k =2k ∵S △AOC =8∴2k =8∴k =4.15.解:把点B(1,0)代入y =x +b 得:0=1+b 解得:b =−1∴一次函数的解析式y =x −1当x =0时,y =−1∴C(0,−1)如图,作AD ⊥x 轴,垂足为D在△OBC 和△DBA 中{∠OBC =∠ABD∠BOC =∠ADB AB =CB∴△OBC ≌△DBA(AAS)∴BD =OB =1,AD =OC =1∴A(2,1)∵点A(2,1)在反比例函数y =kx ∴k =2×1=2∴反比例的解析式y =2x . 16.(1)①由题意得y=106t∴y 关于t 的函数表达式为y=106t.②当0<t ≤80时,y 随t 的增大而减小 ∴当t=80时,y 有最小值,为10680=12 500当t 逐渐接近0时,y 值趋于无穷大 ∴y 的取值范围为y ≥12 500. (2)设安排x 辆相同型号的卡车运送 依题意得102x ×80≥106,解得x ≥125∴公司至少要安排125辆相同型号的卡车运送.17.(1)解:把(),2A m 代入112y x =中,122m =解得4m =∴()4,2A 把()4,2A 代入2(0)ky x x=>中,24k =解得8k ∴反比例函数解析式为28y x=; (2)解:将直线OA 向上平移3个单位后,其函数解析式为132y x =+当0x =时,3y =∴点B 的坐标为()0,3设直线AB 的函数解析式为AB y mx n =+将()4,2A,()0,3B 代入可得423m n n +=⎧⎨=⎩解得143m n ⎧=-⎪⎨⎪=⎩∴直线AB 的函数解析式为134AB y x =-+联立方程组1328y x y x⎧=+⎪⎪⎨⎪=⎪⎩,解得1181x y =-⎧⎨=-⎩ 2224x y =⎧⎨=⎩∴C 点坐标为()2,4过点C 作CM x ⊥轴,交AB 于点N在134BC y x =-+中,当2x =时52y =∴53422CN =-=∴134322ABC S =⨯⨯=△.18.解:(1)∵点A (a ,)在直线y =﹣上∴﹣a ﹣=,解得a =2则A (2,﹣)∵AB∥y 轴,且点B 的纵坐标为1∴点B 的坐标为(2,1).∵双曲线y =经过点B (2,1)∴m =2×1=2∴反比例函数的解析式为y =; (2)①设C (t ,)∵A (2,﹣),B (2,1)∴×(2﹣t )×(1+)=解得t =﹣1∴点C 的坐标为(﹣1,﹣2)设直线BC 的解析式为y =kx+b 把B (2,1),C (﹣1,﹣2)代入得解得∴直线BC 的解析式为y =x ﹣1; ②当y =1时,﹣=1,解得x =﹣1,则D (﹣1,1)∵直线BCy =x ﹣1为直线y =x 向下平移1个单位得到∴直线BC 与x 轴的夹角为45°而BD ∥x 轴∴∠DBC =45°当△PBD 为等腰直角三角形时,以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形若∠BPD =90°,则点P 在BD 的垂直平分线上,P 点的横坐标为,当x =时,y =x ﹣1=﹣,此时P (,﹣)若∠BDP =90°,则PD ∥y 轴,P 点的横坐标为﹣1,当x =﹣1时,y =x ﹣1=﹣2,此时P (﹣1,﹣2)综上所述,满足条件的P 点坐标为(﹣1,﹣2)或(,).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
26.1 反比例函数同步测试题(满分120分;时间:120分钟)一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 下列等式中y是x的反比例函数的是()A.y=4xB.yx=3 C.y=6x+1 D.xy=22. 已知反比例函数的图像经过点(a, b),则它的图像一定也经过()A.(a, −b)B.(−a, −b)C.(−a, b)D.(0, 0)3. 已知反比例函数y=kx的图象经过点(1, 2),则函数y=−kx可为()A.y=−2xB.y=−12x C.y=12x D.y=2x4. 函数y=kx+k与y=kx(k≠0)在同一坐标系内的图象可能是() A. B.C. D.5. 反比例函数y=k−1的图象经过点(−2, 3),则k的值是()xA.−5B.−6C.−7D.上述答案都不对的图象如图,以下结论:6. 已知函数y=mx①m<0;②分支上y随x的增大而增大;③若点A(−1, a)、点B(2, b)在图象上,则a<b;④若点P(x, y)在图象上,则点P1(−x, −y)也在图象上.其中正确的个数是()A.4个B.3个C.2个D.1个7. 已知一个函数中,两个变量x与y的部分对应值如下表:如果这个函数图象是轴对称图形,那么对称轴可能是()A.x轴B.y轴C.直线x=1D.直线y=x8. 如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,(k>0)的图象上与正方形的一个交点,若图中阴影部分的点P(4a, a)是反比例函数y=kx面积等于16,则k的值为()A.16B.1C.4D.−169. 如图,第四象限的射线OM与反比例函数y=kx(k≠0)的图象交于点A,已知AB⊥x,垂足为B,已知△ABO的面积为4.5,则该函数的解析式为()A.y=3x B.y=−3xC.y=9xD.y=−9x10. 如图,△ABC的三个顶点分别为A(1, 2),B(4, 2),C(4, 4).若反比例函数y=kx在第一象限内的图象与△ABC有交点,则k的取值范围是()A.1≤k≤4B.2≤k≤8C.2≤k≤16D.8≤k≤16二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 若反比例函数y=kx 的图象经过点(−2, 5),则y=kx的图象在第________象限.12. 反比例函数y=m−2x,当m________时,在每一象限内,y的值随x的值的增大而减小.13. 如图,反比例函数y=kx的图象经过点A(2, 2)与点B(4, m),则△AOB的面积为________.14. 过反比例函数y=kx的图象上一点分别作x轴和y轴的垂线,这两条垂线与两坐标轴围成的矩形面积是________.15. 已知两点P1(x1, y1)、P2(x2、y2)在反比例函数y=3x的图象上,当x1>x2>0时,y1________y2.16. 反比例函数y=(m−2)x2m+1的函数值为13时,自变量x的值是________.17. 若函数y=kx中,当x=2时,y=−3,则函数解析式是________.18. 如图,在平面直角坐标系中,四边形OABC是一个边长为3的正方形,若反比例函数y=kx在第一象限的图象正好经过它的顶点B,则k的值为________.19. 一个函数具有下列性质:①它的图象经过点(−1, 1);②它的图象在二、四象限内;③在每个象限内,函数值y随自变量x的增大而增大.则这个函数的解析式可以为________.20. 一定质量的二氧化碳,其体积V(m3)是密度ρ(kg/m3)的反比例函数,请你根据图中的已知条件,写出反比例函数的关系式,当V=1.9m3时,ρ=________.三、解答题(本题共计6 小题,共计60分,)21. 在平面直角坐标系xOy中,已知:直线y=−x反比例函数y=k的图象的一个交点为xA(a, 3).(1)试确定反比例函数的解析式;(2)写出该反比例函数与已知直线l的另一个交点坐标.22. 已知函数y=y1+y2,其中y1与−2x成正比列,y2与x2成反比例,且x=1时,y=−5,x=−1时,y=7,求出y与x的函数关系及x=2时,y的值.23. 如图,点A是反比例函数y=12的图象上任意一点,延长AO交该图象于点B,AC⊥xx轴,BC⊥y轴,求Rt△ACB的面积.24. 已知点A(0, 2),B(a, 0),点C和D在反比例函数y=k的图象上.x(1)若A、B、C、D构成正方形,求a、k的值;(2)若A、B、C、D构成一个邻边比为2:1的矩形,则k=________.经过矩形ABCD边AB的中点F(4, 1),交BC边于点25. 已知双曲线y=kxE.(1)求k的值;(2)求四边形OEBF的面积.26. 如图,已知等边△ABO在平面直角坐标系中,点A(4√3, 0),函数y=k(x>0,k为x常数)的图象经过AB的中点D,交OB于E.(1)求k的值;与△BDE没有交点,请直接写出m的取值范围.(2)若第一象限的双曲线y=mx参考答案与试题解析一、选择题(本题共计10 小题,每题 3 分,共计30分)1.【答案】D【解答】解:A、是正比例函数,故A错误;B、是正比例函数,故B错误;C、是一次函数,故C错误;D、是反比例函数,故D正确;故选:D.2.【答案】B【解答】解:因为反比例函数y=k的图像经过点(a, b),x故k=a×b=ab,只有B答案中(−a)×(−b)=ab=k.故选B.3.【答案】A【解答】解:由题意,k=1×2=2,∴ y=−kx为y=−2x.故选A.4.【答案】A【解答】解:当k>0时,函数y=kx+k过一、二、三象限,在第一、三象限上;函数y=kx当k<0时,函数y=kx+k过二、三、四象限,函数y=k在二、四象限上,x综上所述,只有A选项符合题意.故选A.5.【答案】A【解答】解:∴ 函数经过点P(−2, 3),,∴ 3=k−1−2得k=−5.故选A.6.【答案】B【解答】解:①根据反比例函数的图象的两个分支分别位于二、四象限,可得m<0,故正确;②在每个分支上y随x的增大而增大,故正确;③若点A(−1, a)、点B(2, b)在图象上,则a>b,故错误;④若点P(x, y)在图象上,则点P1(−x, −y)也在图象上,故正确.故选B.7.【答案】D【解答】,所以该函数图象是经过第一、三象限的双曲线,解:由表格可得:y=6x故可得这个函数图象是轴对称图形,对称轴是y=x.故选D.8.【答案】C【解答】解:∴ 图中阴影部分的面积等于16,∴ 正方形OABC的面积=16,∴ P点坐标为(4a, a),∴ 4a×4a=16,∴ a=1(a=−1舍去),∴ P点坐标为(4, 1),把P(4, 1)代入y=k,得xk=4×1=4.故选:C.9.【答案】D【解答】解:∴ △ABO的面积为4.5,|k|=4.5,∴ 12解得|k|=9,由图可知,反比例函数图象位于第二四象限,所以,k<0,所以,k=−9,.该函数的解析式为y=−9x故选D.10.【答案】C【解答】解:∴ △ABC是直角三角形,经过点A时k最小,经过点C时k最大,∴ 当反比例函数y=kx∴ k min=1×2=2,k max=4×4=16,∴ 2≤k≤16.故选C.二、填空题(本题共计10 小题,每题 3 分,共计30分)11.【答案】二、四【解答】的图象经过点(−2, 5),解:∴ 反比例函数y=kx∴ k=−10,∴ k=−10<0,∴ 图象过二、四象限,故答案为二、四.12.【答案】>2【解答】解:∴ 反比例函数y=m−2在每一象限内,y的值随x的值的增大而减小,x∴ m−2>0,解得,m>2.故答案是:>2.13.【答案】3【解答】解:过点A,B分别作AC⊥x轴于C,BD⊥x轴于D,的图象经过点A(2, 2)与点B(4, m),∴ 反比例函数y=kx∴ k=4,m=1,(1+2)(4−2)=3.∴ S△AOB=S△AOC+S四边形ACDB−S△BOD=S四边形ACDB=12故答案为:3.14.【答案】|k|【解答】解:设B 点坐标为(x, y),由函数解析式可知,xy =k ,则可知S 矩形ABCO =|xy|=|k|,故答案为:|k|.15.【答案】<【解答】解:把P 1(x 1, y 1)、P 2(x 2、y 2)代入y =3x 得y 1=3x 1,y 2=3x 2,因为x 1>x 2>0时,∴ 0<y 1<y 2.故答案为<.16.【答案】−9【解答】解:∴ y =(m −2)x 2m+1是反比例函数,则有{2m +1=−1m −2≠0, 解得m =−1,因而函数解析式是y =−3x , 当函数值为13时,即−3x =13, 解得x =−9.故自变量x 的值是−9.17.【答案】y =−6x【解答】解:把x=2,y=−3代入y=kx中得,k=−6,所以函数解析式是y=−6x.故答案为:y=−6x.18.【答案】9【解答】解:∴ 四边形OABC是一个边长为3的正方形,∴ B(3,3),∴ k=3×3=9.故答案为:9.19.【答案】y=−1 x【解答】解:设符合条件的函数解析式为y=kx,∴ 它的图象经过点(−1, 1)把此点坐标代入关系式得k=−1,∴ 这个函数的解析式为y=−1x.20.【答案】5kg/m3【解答】解:设函数关系式为:V=kρ,由图象可得,当V=5,ρ=1.9,代入得:k=5×1.9=9.5,故V=9.5ρ,当V=1.9时,ρ=5kg/m3.故答案为:5kg/m3.三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )21.【答案】解:(1)因为A(a, 3)在直线y =−x 上,则a =−3,即A(−3, 3),又因为A(−3, 3)在y =k x 的图象上,可求得k =−9,所以反比例函数的解析式为y =−9x ; (2)另一个交点坐标是(3, −3).【解答】解:(1)因为A(a, 3)在直线y =−x 上,则a =−3,即A(−3, 3),又因为A(−3, 3)在y =k x 的图象上,可求得k =−9,所以反比例函数的解析式为y =−9x ; (2)另一个交点坐标是(3, −3).22.【答案】解:设y 1=−2ax ,y 2=b x 2,则y =−2ax +b x 2,把x =1时,y =−5,x =−1时,y =7分别代入得{−2a +b =−52a +b =7,解得{a =3b =1, 所以y 与x 的函数关系式为y =−6x +1x 2,当x =2时,y =−6x +1x 2=−12+14=−474. 【解答】解:设y 1=−2ax ,y 2=b x ,则y =−2ax +b x ,把x =1时,y =−5,x =−1时,y =7分别代入得{−2a +b =−52a +b =7,解得{a =3b =1, 所以y 与x 的函数关系式为y =−6x +1x 2, 当x =2时,y =−6x +1x =−12+14=−474.【答案】解:设点A 的坐标为(x, y),则点B 坐标为(−x, −y),所以AC =2y ,BC =2x ,所以Rt △ACB 的面积为12AC ⋅BC =12×2x ⋅2y =2xy =2|k|=24. 【解答】解:设点A 的坐标为(x, y),则点B 坐标为(−x, −y),所以AC =2y ,BC =2x ,所以Rt △ACB 的面积为12AC ⋅BC =12×2x ⋅2y =2xy =2|k|=24. 24.【答案】3.【解答】解:(1)如图,作CE ⊥x 轴于E ,DF ⊥y 轴于F ,根据题意,△AOB ≅△DFA ≅△BEC ,∴ DF =BE =OA =2,AF =CE =OB =a ,∴ C(2+a, a),D(2, 2+a),∴ {a =k 2+a 2+a =k 2, 解得{a =2k =8; (2)根据题意,△AOB ∽△DFA ≅△BEC ,∴ DF =BE =12OA =1,AF =CE =12OB =12a , ∴ C(1+a, a 2),D(1, 2+a2), ∴ {a 2=ka+1a 2+2=k , 解得k =3.【答案】解:(1)∴ 点F(4, 1)在双曲线y=kx的图象上,∴ 1=k4,∴ k=4;(2)∴ F(4, 1)为边AB的中点,∴ B(4, 2),S四边形OABC =4×2=8,S△OEC=S△OAF=12|k|=2,∴ S四边形OEBF =S四边形OABC−S△OEC−S△OAF=8−2−2=4.∴ 四边形OEBF的面积=4.【解答】解:(1)∴ 点F(4, 1)在双曲线y=kx的图象上,∴ 1=k4,∴ k=4;(2)∴ F(4, 1)为边AB的中点,∴ B(4, 2),S四边形OABC =4×2=8,S△OEC=S△OAF=12|k|=2,∴ S四边形OEBF =S四边形OABC−S△OEC−S△OAF=8−2−2=4.∴ 四边形OEBF的面积=4.26.【答案】若第一象限的双曲线y=mx与△BDE没有交点,m的取值范围为m<9√3或m>12√3.【解答】解:(1)过点B作BM⊥OA于点M,如图所示.∴ 点A(4√3, 0),∴ OA=4√3,又∴ △ABO为等边三角形,∴ OM=12OA=2√3,BM=√32OA=6.∴ 点B的坐标为(2√3, 6).∴ 点D为线段AB的中点,∴ 点D的坐标为(2√3+4√32, 62)=(3√3, 3).∴ 点D为函数y=kx(x>0,k为常数)的图象上一点,∴ 有3=k3√3,解得:k=9√3.(2)设过点B的反比例函数的解析式为y=nx,∴ 点B的坐标为(2√3, 6),∴ 有6=2√3,解得:n=12√3.若要第一象限的双曲线y=mx与△BDE没有交点,只需m<k或m>n即可,∴ m<9√3或m>12√3.答:若第一象限的双曲线y=mx与△BDE没有交点,m的取值范围为m<9√3或m> 12√3.。
