第二届华罗庚金杯少年数学邀请赛初赛试题
第二届华罗庚金杯少年数学邀请赛一试试题

第二届华罗庚金杯少年数学邀请赛一试试题
1. 图55的30个格子中各有一个数字,最上面一横行和最左面一竖列的数字已经填好,其余每个格子中的数字等于同一横行最左面数字与同一竖到最上面数字之和(例如a=14+17=31)。
问这30个数字的总和等于多少?
2. 平行四边形ABCD周长为75厘米,以BC为底时高是14厘米(图57);以CD为底时高是16厘米。
求:平行四边形ABCD的面积。
3. 一段路程分成上坡、平路、下坡三段。
各段路程长之比依次是1∶2∶3 三人走各段路所用时间之比次依是4∶5∶6。
已知他上坡时速度为每小时3公里.路程全长50公里。
问此人走完全程用了多少时间?
4. 小玲有两种不同形状的纸板。
一种是正方形的,一种是长方形的(图58)。
正方形纸板的总数与长方形纸板的总数之比是1∶2。
她用这些纸板做成一些竖式和横式的无盖纸盒(图59)。
正好将纸板用完,在小玲所做的纸盒中、竖式纸盒的总数与横式纸盒的总数之比是
多少?
5. 在一根长木棍上,有三种刻度线、第一种刻度线将木棍分成十等份;第于种将木棍分成十二等份;第三仲将木棍分成十五等份。
如果沿每条刻度先将木的锯断,木棍总共被锯成多少段?
6. 已知:
问:a的整数部分是多少?
7. 图60算式中,所有分母都是四位数。
请在每个方格中各填入一个数字,使等式成立。
图60。
2019年香港华罗庚金杯少年数学邀请赛(决赛)初中二年级、初一年级组试题含答案

一小時三十分鐘完卷 (上午 10:00 至上午 11:30) 比賽須知:
1. 全卷共 10 題,滿分 100 分。包括填空題 6 道,每題 10 分;詳答題 4 道,每題 10 分。 2. 參賽學生必須全部作答,所有答案寫在答題紙上。 3. 填空題無需書寫步驟,只須填寫答案;詳答題要求寫出詳細過程。 4. 比賽時使用自備文具,例如鉛筆、原子筆及橡皮擦膠等。不准使用計算器。違規者將被
若 | x1-x2|=2 2,則 k 的值為
.
答案:1. 解:令 x+2=kxx2+2x-k=0,△=22+4k≥0k≥-1.
x1+x2=-2,x1x2=-k,|x1-x2|= (x1+x2)2-4x1x2= 4+4k=2 2 k=1.
9. 如圖,方格紙中的每個小正方形的邊長為 1.記圖中陰影部分的面積 A
中二組 F.2 (10 marks for each question)
1. (3x-1)2=0x=3,故3x+3x=2
2.
24+1=4( 2-1),3-4 5=3+ 5即滿足要求的 m 可以取 2,3,4,
5,共 4 個數
3. 取(0,2)關於直線 y=x 的對稱點(2,0),過(-4,-2),(2,0)的直線為 y= 13(x-2),與 y=x 交於點(-1,-1).即為周長最小時的點 C.故 a=-1
二、解答下列各題 (每小題 10 分,共 40 分,要求寫出詳細過程。)
7. 求 − 2 + 2 (− 2 )2 − 4 (− 2 )4 的值。
2
2
2
8. 設 k 為非零實數, 兩個函數 y = x + 2 與 y = k 的圖像相交於 A(x1,y1)、B(x2,y2) x
历届“华杯赛”初赛决赛试题汇编【小中组(附答案)】

二、简答题(每小题 15 分, 共 60 分, 要求写出简要过程)
9. 用 4 个数码 4 和一些加、减、乘、除号和小括号, 写出值分别等于 2、3、4、 5、6 的五个算式. 10. 右图是 U, V, W, X 四辆不同类型的汽车每百千米的耗油 量. 如果每辆车都有 50 升油, 那么这四辆车最多可行驶 的路程总计是多少千米? 11. 某商店卖出一支钢笔的利润是 9 元, 一个小熊玩具的进 价为 2 元. 一次, 商家采取 “买 4 支钢笔赠送一个小熊玩具”的打包促销, 共 获利润 1922 元. 问这次促销最多卖出了多少支钢笔? 12. 编号从 1 到 10 的 10 个白球排成一行, 现按照如下方法涂红色: 1)涂 2 个球; 2)被涂色的 2 个球的编号之差大于 2. 那么不同的涂色方法有多少种?
四百米比赛进入冲刺阶段,甲在乙前面 30 米,丙在丁后面 60 米,乙在丙前面 20 米. 这时,跑在最前面的两位同学相差( (A)10 (B)20 )米. (D)60
(C)50
5.
在右图所示的两位数的加法算式中, 已知 A B C D 22 , ). (B)4 (C)7 (D)13
一、选择题 (每小题 10 分, 满分 60 分. 以下每题的四个选项中, 仅 有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号 内.)
五年级计算数阵图与数字谜学生版
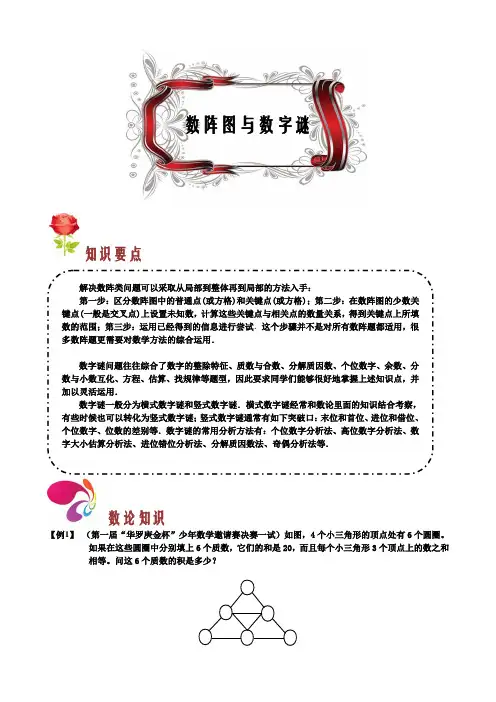
数阵图与数字谜知识要点解决数阵类问题可以采取从局部到整体再到局部的方法入手:第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.数字谜问题往往综合了数字的整除特征、质数与合数、分解质因数、个位数字、余数、分数与小数互化、方程、估算、找规律等题型,因此要求同学们能够很好地掌握上述知识点,并加以灵活运用.数字谜一般分为横式数字谜和竖式数字谜.横式数字谜经常和数论里面的知识结合考察,有些时候也可以转化为竖式数字谜;竖式数字谜通常有如下突破口:末位和首位、进位和借位、个位数字、位数的差别等.数字谜的常用分析方法有:个位数字分析法、高位数字分析法、数字大小估算分析法、进位错位分析法、分解质因数法、奇偶分析法等.数论知识【例1】(第一届“华罗庚金杯”少年数学邀请赛决赛一试)如图,4个小三角形的顶点处有6个圆圈。
如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形3个顶点上的数之和相等。
问这6个质数的积是多少?【例2】 一个整数乘以13后,乘积的最后三位数是123,这样的整数中最小的是多少?【例3】 红、黄、蓝和白色卡片各一张,每张上写有一个数字。
小明将这4张卡片如图放置,使它们构成一个四位数,并计算这个四位数与它的数字之和的10倍的差。
结果小明发现,无论白色卡片上是什么数字,计算结果都是1998。
问:红、黄、蓝3张卡片上各是什么数字?蓝白黄红【例4】 如图算式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字,请求出这个算式。
春夏秋冬四季季年年年年年年【例5】 将1~9分别填入这九个区域,使得每个圆里的数字和相等。
【例6】已知76⨯=⨯,相同的字母代表相同的数字,不同的字母代表不同的数字,求ABCXYZ XYZABCABCXYZ是多少?【例7】三位数AAA乘三位数AAB等于六位数CCCDDD,求A,B,C,D分别是多少?【例8】(第二届“华罗庚金杯”少年数学邀请赛复赛)试将1,2,3,4,5,6,7分别填入下面的方框中,每个数字只用一次:(这是一个三位数)、(这是一个三位数)、(这是一个一位数),使得这三个数中任意两个都互质。
第五讲 最大公因数与最小公倍数

第五讲最大公因数与最小公倍数学法探讨大家知道我们在研究因数和倍数时,0是一个特殊的数;O不是任何自然数的因数(除数不能为O),但0是任何非0自然数的倍数(任何非0自然数的O倍等于0)在本讲中我们只讨论正整数。
几个数公有的因数叫做这几个数的公因数,其中最大的一个,叫做这几个数的最大公因数。
为了书写简便,a、b两数的最大公因数记为(a,b)。
几个数公有的倍数叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数,为了书写简便,a、b两数的最小公倍数记为[a,b]。
最大公因数与最小公倍数有以下重要性质:1.两个数的公因数都是它们的最大公因数的因数;2.两个数的公倍数都是它们的最小公倍数的倍数;3.两个数的积,等于它们的最大公因数与最小公倍数的积;即a×b=(a,b)×[a,b]4.两个自然数分别除以它们的最大公因数,所得的商为互质数。
关于“最大公因数和最小公倍数”你还有什么需要补充?请你写在下面:例题选讲【例题1】育才小学拿出一块长方体木料,长180厘米,宽144厘米,高108厘米,请王师傅把它锯成棱长是整厘米数,大小相同的正方体木块,木块的体积要最大,木料又不能剩余,算一算,可以锯成多少块?【分析】要把长方体木料锯成棱长是整厘米数,大小相同的正方体木块,则正方体的棱长应是长方体的长、宽、高的公因数,又要求每小块正方体的体积最大,因此锯成的正方体的棱长必须是长方体的长、宽、高的最大公因数,由此便可得出问题的解答。
【解答】【练习5-1】把一张长60厘米、宽48厘米的长方形纸,裁成若干面积相等边长为整厘米数的小正方形而没有剩余,小正方形的面积最大是多少?【例题2】有一个班的同学去划船,他们算了一下,如果增加一条船,正好每船坐6人,如果减少一条船,正好每船坐9人,这个班有多少人?(第二届全国“华罗庚金杯”少年数学邀请赛初赛试题) 【分析】根据题意,这个班的人数应是6的倍数,又是9的倍数,从而是6和9的公倍数,故只要在6和9的公倍数中寻找符合条件的解,便能得到问题的解答。
小学数学竞赛学习材料(五年级上期)

小学数学竞赛学习材料五年级上期第一讲速算与巧算(一)例1 计算72.19+6.48+27.81-1.38-5.48-0.62。
解:观察发现,有些加数可以凑整;有的加数和减数尾数相同,可以抵消。
于是:72.19+6.48+27.81-1.38-5.48-0.62=(72.19+27.81)+(6.48-5.48)-(1.38+0.62)=100+1-2=99例2用简便方法计算 1.25×67.875+125×6.7875+1250×0.053375。
解:观察发现:相加的三个乘积中分别有1.25、125、250,因此想到利用积不变的性质,使三个积有相同的因数。
于是:1.25×67.875+125×6.7875+1250×0.053375=1.25×67.875+1.25×678.75+1.25×53.375=1.25×(67.875+678.75+53.375)=1.25×800=1000例3 计算1999+199.9+19.99+1.999。
解法一:观察发现,构成这四个加数的数字和排列顺序完全相同,因此可以把它们都看作1999与某个数的积,于是:1999+199.9+19.99+1.999=1999×(1+0.1+0.01+0.001)=1999×1.111=(2000-1)×1.111=2222-1.111=2220.889解法二:观察发现这四个加数分别接近2000、200、20、2,于是1999+199.9+19.99+1.999=2000+200+20+2-1.111=2220.889例4 计算(1+0.33+0.44)×(0.33+0.44+0.55)-(1+0.33+0.44+0.55)×(0.33+0.44)。
解:观察发现这些因数中有一些相同的部分,可以进行代换。
华杯赛小中组试题 解析.
3、 如右图,在由 1x1 的正方形组成的网格中,写有 2015 四个数字(阴影部分)。其边线要 么是水平或竖直的直线段、要么是连接 1x1 的正方形相邻两边中点的线段,或者是 1x1 正 方 形 的 对 角 线 。 则 图 中 2015 四 个 数 字 ( 阴 影 部 分 ) 的 面 积 是 ( )
7. 计算1000 257 84 43 16
.
8. 已知动车的时速是普快的两倍, 动车的时速提高 25% 即达到高铁的时速, 高铁
与普快的平均时速比特快快15 千米/小时, 动车与普快的平均时速比特快慢10
千米/小时, 则高铁和普快列车的时速分别是
千米/小时和
千米
/小时.
9. 《火星救援》中, 马克不幸没有跟上其他 5 名航天员飞回地球, 独自留在了
(B)两个直角三角形
(C)两个钝角三角形
(D)一个锐角三角形和一个钝角三
角形
2. 从1 至10 这10 个整数中, 至少取( )个数, 才能保证其中有两个数的和等
于10 .
(A)4
(B)5
(C)6
(D)7
3. 小明行李箱锁的密码是由两个数字 8 与 5 构成的三位数. 某次旅行, 小明忘
记了密码, 他最少要试( )次, 才能确保打开箱子.
5. 如右图, 在 5×5 的空格内填入数字, 使每行、每列及每个粗线框中的数字为 1, 2, 3, 4, 5, 且不重复. 那么五角星所在的空格内的数字是( ).
四年级三大原理抽屉原理学生版
抽屉原理知识要点最不利原则所谓“最不利原则”是指完成某一项工作先从最不利的情况下考虑,然后研究任意情况下可能的结果。
由此得到充分可靠的结论。
抽屉原理又称鸽巢原理或Dirichlet原理如果把1n+个苹果任意放入n个抽屉,那么必定有一个抽屉里至少有两个苹果。
这个现象就是我们所说的抽屉原理。
抽屉原理在国外又称为鸽巢原理。
(“如果有五个鸽子笼,养鸽人养了6只鸽子,那么当鸽子飞回笼中后,至少有一个笼子中装有2只鸽子”)。
它是由德国数学家狄利克雷(G.Lejeune Dirichlet,18051859~)首先明确的提出来并用以证明一些数论中的问题,因此,也称为狄利克雷原理。
它是组合数学中一个重要的原理。
抽屉原理1:如果把多于n件物品任意放到n个抽屉中,那么必有1个抽屉至少有2件物品。
抽屉原理2:如果把多于m nm+件物品。
⨯件物品任意放到n个抽屉中,那么必有1个抽屉至少有1抽屉原理3:如果把无穷多件物品任意放到n个抽屉中,那么必有1个抽屉至少有无穷多件物品。
最不利原则【例 1】一副扑克牌共54张,其中有2张王牌,还有黑桃、红心、草花和方块4种花色的牌各13张。
那么至少从中摸出多少张牌,才能保证在摸出的牌中有黑桃?【例 2】一副扑克牌共54张,其中有2张王牌,还有黑桃、红心、草花和方块4种花色的牌各13张。
那么至少从中摸出多少张牌,才能保证至少有3张牌是红桃?【例 3】一副扑克牌共54张,其中有2张王牌,还有黑桃、红心、草花和方块4种花色的牌各13张。
那么至少从中摸出多少张牌,才能保证有5张牌是同一花色的?【例 4】(2004年第九届“华罗庚金杯”少年数学邀请赛小学组初赛第8题)一副扑克牌有54张,最少要抽取几张牌,方能使其中至少有2张牌有相同的点数?【例 5】(1988年第二届“华罗庚金杯”少年数学邀请赛小学组初赛第11题)一副扑克牌有四种花色,每种花色有13张,从中任意抽牌。
问:最少要抽多少张牌,才能保证有4张牌是同一花色?【例 6】(2006年3月8日第十一届“华罗庚金杯”少年数学邀请赛小学组初赛第13题)自制的一幅玩具牌共计52张(含4种牌:红桃、红方、黑桃、黑梅。
华罗庚金杯数学邀请赛决赛初二组练习题(含答案)
第二十三届华罗庚金杯少年数学邀请赛决赛试题(初中二年级组) 总分第二十三届华罗庚金杯少年数学邀请赛决赛试题(初中二年级组·练习用)一、填空题(每小题10 分, 共80 分)2019 2 2 1009 2 20181.计算1 2 2018.2. 一块正三角形草坪边长为 12 米,三个顶点处都安有喷水装置,每个喷水装置都可以从三角形的一边到另一边旋转60º来回喷水.假定三个喷水装置的射程相等,要使草坪上所有区域都可以被喷水覆盖,那么被重复喷水的最小面积是平方米.3. 从 2, 3, 4, 5 这四个数中,任取两个数p,q( p q) ,构成函数y px 2 和y x q ,如果这两个函数图象的交点在直线x 2 的左侧,那么这样的有序数对( p,q) 共有个.4. 设p 为质数,如果二次方程x2 2px p2 5p 1 0的两个根都是整数,那么p 可能取的值有个.5. 如果1295 (6n 1) (其中n 是整数,且1986≤n≤2018 ),那么满足条件的n 的个数是.6. 如图所示,在正六边形ABCDEF 内放有一个正方形MNPQ ,正方形的顶点分别在正六边形的 4 条边上,且MN //BC .若正方形MNPQ 的面积为12 6 3 平方厘米,则正六边形ABCDEF 的面积是平方厘米.7. 将 1,2,3,4,5,6,7,8,9,10,11 这 11 个数排成一行,使得任意 5个相邻的数的和都是 5 的倍数.那么这样的排列方法有种.8. 四张卡片,每张写着一个自然数,任取 2 张,或者 3 张,或者 4 张,把卡片上的数求和,可以得到 11 个不同的和,那么 4 张卡片上所有数的和最小为.第二十三届华罗庚金杯少年数学邀请赛决赛试题(初中二年级组)二、解答下列各题(每小题10 分, 共40 分, 要求写出简要过程)9. 有 A ,B 两队野外徒步旅行,A 队在 B 队的西偏北 45 度处,两队相距8 2千米.如果 A 队向东继续行走, B 队同时沿西偏南45 度路线行走,且 A队与 B 队的速度比是 2 ,求A,B 两队最近时的距离.10. 如果实数x, y,z 同时满足关系式x( y2 z) z(z xy) ,y(z2 x) x(x yz) ,z(x2 y) y( y zx) ,那么,实数x, y,z 是否一定都相等?请给出证明.11. 如图,在四边形ABCD 中, ABC BCD 120 ,AB BC .对角线AC ,BD 相交于点E .若AE 3CE ,求证:AB 2CD .12. 从 76 个连续自然数 1,2,…,76 中任取 39 个数,其中必有 2 个数的差是p ,求p 的值.三、解答下列各题(每小题15 分, 共30 分, 要求写出详细过程)13. 如图,在五边形ABCDE 中,AB AE 1 , CAD 45 , E DE EAB B 90 ,求点A到直线CD 的距离. CA B14. 如图,一个由 81 个小方格组成的9 9 网格.先将其中的任意n 个方格染黑,然后按照以下规则继续染色:如果某个方格至少与 2 个黑格都恰好有 1 个公共顶点,那么就将这个方格染黑.现在要按照这个方法将整个棋盘都染成黑色,那么n的最小值是多少?说明你的结论.第二十三届华罗庚金杯少年数学邀请赛决赛试题参考答案(初中二年级组)第二十三届华罗庚金杯少年数学邀请赛决赛试题·练习用参考答案(初中二年级组)一、填空题(每小题10 分, 共 80 分)题号 1 2 3 4 5 6 7 8答案2018 1 24π 36 3 5 2 83 322304 14二、解答下列各题(每小题10 分, 共 40 分, 要求写出简要过程)16 1059. 【答案】A ,B 两队最近时的距离是千米.【解答】如图,以B 队初始位置为原点,正东、正北方向为x 轴和y 轴的正方向,建立平面直角坐标系,B(0,0) ,A( 8,8).不妨y设B 队的速度为 1,那么A队的速度为 2 ,经过时间t A A1x后,B 队所在位置是 2 2B ( t, t) ,A队所在位置是12 2B1BA1( 8 2t,8) ,于是此时两队的距离d 满足2 2 2 2 2 28 2d ( 8 2t t) (8 t) 5t 16 2t 128,当t 时,d取到最2 2 5小值512 16 10千米.5 510. 【答案】x, y,z 一定都相等.【证明】将原关系式变形,得xy(y z) z(z x) ①,yz(z x) x(x y) ②,zx(x y) y(y z) ③.(1)当(x y()y z ()zx) 0 时,不妨设x y ,由③得y 0 或者y z .若y z ,则x y z ;若y 0 ,有x 0 ,代入①,得z 0 或者z x 0 ,即x y z 0 .(2)当(x y)(y z)(z x) 0 时,将①②③相乘得xyz(xyz 1) 0,即xyz 0 或xyz .如果xyz 0 ,不妨设y 0 ,由(1)知z 0或者z x ,矛盾!如果xyz 1,1- 1 -不妨设x≥y≥z ,显然x 0 .假设x y ,考虑②式,有x(x y) 0 ,又1yz 0,xz x ,所以yz(z x) 0 .矛盾!所以x y z .证毕!11. 【证明】作BM AC于M.因为△ABC 中,AB BC , ABC=120 ,所以AM CM, CAB ACB 30 .因此AB 2BM .由于 ACB 30 ,所以 ACD 90 .又由AE 3CE 和AM CM 得:AM ME 3CE ,即CM ME 3CE .即(ME CE) ME 3CE 所以2ME 2CE ,故ME CE .在 Rt△BME 与 Rt△DCE 中,因为ME CE , BEM DEC ,所以Rt△BME ≌Rt△DCE .因此BM CD .由于AB 2BM (已证),所以AB 2CD .12. 【答案】p 的值为 1,2,19,38.【解答 1】p 的值是 1,2,19,38.做抽屉,每个抽屉内有差为p 的两个数,或仅有一个数:当p≥39 时, 有两类抽屉,第一类,每个抽屉有 2 个非零自然数,差是p :{76,76 p},{75, 75 p},…,{p 2,2},{p 1,1},个数是76 p ;第二类,每个抽屉仅有 1 个不大于p 的非零自然数,但与p 的和大于76:{77 p},{78 p},…,{p}个数是76 2 (76 p) 2p 76 .此时,抽屉总数是p 个.从每个抽屉各取一个数,因为p≥39 ,这些数中不存在差是p 的两个数.当p≤38时,做抽屉:{1, p 1},{2, p 2},{3, p 3} ,{4, p 4}…{p,2 p} ,{2p 1,3p 1},{2p 2,3p 2},{2p 3,3p 3} ,…{3p,4p} ,……,- 2 -76 76 76 762p 1 1, 2p 1 p 1 , 2p 1 2, 2p 1 p 2 ,2p 2p 2p2p76 76.2p p,2p2p2p①若76 762p 2p,则抽屉到此为止,共有 38 个抽屉,从中任取 39 个,必有2 个取自同一个有两个数的抽屉,差是p .所以,p 1, 2,19, 38 .②若76 762p 2p,则还有抽屉:76 762p 1 , 2p 2 ,{76},2p 2p76个数是76 2p2p.得到抽屉的个数是:76 76 76 76 76 76p p p p p76 2 76 76 38p p p p p p2 2 2 2 2 276 76 76其中,2p 2p2p ,此时,p76≥1,抽屉的个数≥39.从其中 392p个抽屉各取 1 个数,不存在两个数的差是p .所以,p 的值是 1, 2, 19, 38.【解答 2】记76 kp r ,0 r p ,把 1 到 76 按照下面排成p 行,1 2r p 1 p2 pr 2p2p1 (k1)2rp(k1) p(k1) pkp1kp2kprkpk 为偶数时,记k 2l (注,当k 为偶数时,由于 76 是偶数,r 也是偶数),则前r 行可以取l 1个数,后p r 行可以取l 个数,这lp 个数任意两个数的差不等于p .kp 76 r rr r r 382 2 2k 为奇数时,记k 2l 1(注,当k 为奇数时,由于 76 是偶数,p r 也是偶数),则前r 行可以取l 1个数,后p r 行也可以取l 1个数,这2(l 1) p (2l 1) p p kp p 76 r p p r(l 1) p 38 个数任意两个数2 2 2 2 2的差不等于p .r 当r 0时, 02p r与 0,因此任取 38+1=39 个数时,任意两个数的差2- 3 -。
“华罗庚金杯”少年数学邀请赛(口试)试题1-10届
华罗庚金杯少年数学邀请赛口试试题第01届华罗庚金杯少年数学邀请赛口试试题1. 这是七巧板拼成的正方形,正方形边长20厘米,问七巧板中平行四边形的一块(如右图中阴影部分)的面积是多少?2.从所有分母小于10的真分数中,找出一个最接近0.618的分数。
3.有49个小孩子,每人胸前有一个号码,号码从1到49各不相同,请你挑选出若干个小孩,排成一个圆圈,使任何相邻两个小孩的号码数的乘积小于100,你最多能挑选出多少个小孩子?4.有一路公共汽车,包括起点和终点站共有15个车站,如果有一辆车,除终点到站外,每一站上车的乘客中,恰好各有一位乘客从这一站到以后的每一站,为了使每位乘客都有座位,问这辆公共汽车最少要有多少个座位?5.正方形的树林每边长1000米,里面有白杨树和榆树,小明从树林的西南角走入树林,碰见一株白杨树就往正北走,碰见一株榆树就往正东走,最后他走了东北角上,问:小明一共走了多少米的距离?6.自然数按从小到大的顺序排成螺旋形,在2处拐第一个弯,在3处拐第二个弯,在5处拐第三个弯……问拐第二十个弯的地方是哪一个数?第02届华罗庚金杯少年数学邀请赛口试试题1、如下图是一个对称的图形,黑色部分面积大还是阴影部分面积大?2、你能不能将自然数1到9分别填入右面的方格中,使得每个横格中的三个数之和都是偶数?3、司机开车按顺序到五个车站接学生到学校(如下图),每个站都有学生上车,第一站上了一批学生,以后每站上车的人数都是前一站上车人数的一半,车到学校时,车上最少有多少学生?4、如图中五个正方形的边长分别是1米、2米、3米、4米、5米。
问:白色部分面积与阴影部分面积之比是多少?5、用1、2、3、4、5这五个数两两相乘,可以得到10个不同的乘积,问乘积中是偶数多还是奇数多?6、7、将右边的硬纸片沿虚线折起来,便可作成一个正方体,问:这个正方体的2号面对面是几号面?(如下图)8、下面是一个11位数,它的每三个相邻数之和都是20,你知道打“?”的数字是几?9、有八张卡片,右图分别写着自然数1到8,从中取出三张,要使这三张卡片上的数字之和为9,问有多少种不同的取法?第03届华罗庚金杯少年数学邀请赛团体决赛口试1.一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道红条,如右图阴影所示部分,红条宽都是2厘米.问:这条手帕白色部分的面积是多少?2.伸出你的左手,从大拇指开始如图所示的那样数数字,1,2,3,……,问:数到1991时,你数在那个手指上?3.有3个工厂共订300份吉林日报,每个工厂订了至少99份,至多101份.问:一共有多少种不同的订法?4.图上有两条垂直相交的直线段AB、CD,交点为E(如下图).已知:DE=2CE,BE=3AE.在AB和CD上取3个点画一个三角形.问:怎样取这3个点,画出的三角形面积最大?5.如下图中有两个红色的圆,两个蓝色的圆,红色圆的直径分别是1992厘米和1949厘米,蓝色圆的直径分别是1990厘米和1951厘米.问:红色二圆面积大还是蓝色二圆面积大?6.在一张9行9列的方格纸上,把每个方格所在的行数和列数加起来(如下图),填在这个方格中,例如a=5+3=8.问:填入的81个数字中,奇数多还是偶数多?7.能不能在下式:1□2□3□4□5□6□7□8□9=10的每个方框中,分别填入加号或减号,使等式成立?8.把一个时钟改装成一个玩具钟(如右图),使得时针每转一圈,分针转16圈,秒针转36圈.开始时3针重合.问:在时针旋转一周的过程中,3针重合了几次?(不计起始和终止的位置).9.将1,2,3,4,5,6,7,8这8个数分成3组,分别计算各组数的和.已知这3个和互不相等,且最大的和是最小的和的2倍.问:最小的和是多少?10.这是一个棋盘,将一个白子和一个黑子放在棋盘线交叉点上,但不能在同一条棋盘线上.问:共有多少种不同的放法(如下图)?11.这是两个圆,它们的面积之和为1991平方厘米,小圆的周长是大圆周长的90%(如右图).问:大圆的面积是多少?12.有一根1米长的木条,第一次去掉它的,第二次去掉余下木条的;第三次又去掉第二次余下木条的,等等;这样一直下去,最后一次去掉上次余下木条的.问:这根木条最后还剩下多长?13.这是一个楼梯的截面图(如下图),高2.8米,每级台阶的宽和高都是20厘米.问:此楼梯截面的面积是多少?14.请找出6个不同的自然数,分别填入6个括号中,使这个等式成立.第04届华罗庚金杯少年数学邀请赛团体决赛口试1.2×3×5×7×11×13×17这个算式中有七个数连乘,请回答:最后得到的乘积中,所有数位上的数字和是多少?请讲一讲你是怎样算的?2.这是一个中国象棋盘(图中小方格都是相等的正方形,“界河”的宽等于小正方形边长),黑方有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12, 13,14中的两个位置.问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?3.将一根长为374厘米的合金铝管截成若干根36厘米和24厘米两种形状的短管(加工损耗忽略不计)问:剩余部分的管子最少是多少厘米?4.乙两人同时从A出发向B行进,甲速度始终不变,乙在走前面路程时,速度为甲的2倍,而走后面路程时,速度是甲的,问甲、乙二人谁选到B?请你说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二届华罗庚金杯少年数学邀请赛初赛试题
“华罗庚金杯”少年数学邀请赛每隔一年举行一次。
今年是第二届。
问2000年是第几届?
一个充气的救生圈(如图32)。
虚线所示的大圆,半径是33厘术。
实线所示的小圆,半径是9厘米。
有两只蚂蚁同时从A点出发,以同样的速度分别沿大圆和小圆爬行。
问:小圆上的蚂蚁爬了几圈后,第一次碰上大圆上的蚂蚁?
图33是一个跳棋棋盘,请你算算棋盘上共有多少个棋孔?
有一个四位整数。
在它的某位数字前面加上一个小数点,再和这个四位数相加,得数是2000.81。
求这个四位数。
图35是一块黑白格子布。
白色大正方形的边长是14厘米,白色小正方形的边长是6厘米。
问:这块布中白色的面积占总面积的百分之几?
图37是两个三位数相减的算式,每个方框代表一个数字。
问:这六个方框中的数字的连乘积等于多少?
图 37
图38中正方形的边长是2米,四个圆的半径都是1米,圆心分别是正方形的四个顶点。
问:这个正方形和四个圆盖住的面积是多少平方米?
有七根竹竿排成一行。
第一根竹竿长1米,其余每根的长都是前一根的一半。
问:这七根竹竿的总长是几米?
有三条线段A、B、C,A长2.12米,B长2.71米,C长3.53米,以它们作为上底、下底和高,可以作出三个不同的梯形。
问:第几个梯形的面积最大?
有一个电子钟,每走9分钟亮一次灯,每到整点响一次铃。
中午12点整,电子钟响铃又亮灯。
问:下一次既响铃又亮灯是几点钟?
一副扑克牌有四种花色,每种花色有13张。
从中任意抽牌。
问:最少要抽多少张牌,才能保证有四张牌是同一花色的?
有一个班的同学去划船。
他们算了一下,如果增加一条船,正好每条船坐6人;如果减少一条船,正好每条船坐9人。
问:这个班共有
多少同学?
四个小动物换座位。
一开始,小鼠坐在第1号位子,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号。
以后它们不停地交换位子。
第一次上下两排交换。
第二次是在第一次交换后再左右两排交换。
第三次再上下两排交换。
第四次再左右两排交换……这样一直换下去。
问:第十次交换位子后,小兔坐在第几号位子上?(参看图39)
用1、9、8、8这四个数字能排成几个被11除余8的四位数?
图41是一个围棋盘,它由横竖各19条线组成。
问:围棋盘上有多少个与图42中的小正方形一样的正方形?
计算
有三张卡片,在它们上面各写有一个数字(图43)。
从中抽出一张、二张、三张,按任意次序排起来,可以得到不同的一位数、二位数、
三位数。
请你将其中的素数都写出来。
有大、中、小三个正方形水池,它们的内边长分别是6米、3米、2米。
把两堆碎石分别沉没在中、小水池的水里,两个水池的水面分别升高了6厘米和4厘米。
如果将这两堆碎石都沉没在大水池的水里,大水池的水面升高了多少厘米?
在一个圆圈上有几十个孔(不到100个),如图44。
小明像玩跳棋那样,从A孔出发沿着逆时针方向,每隔几个孔跳一步,希望一圈以后能跳回到A孔。
他先试着每隔2孔跳一步,结果只能跳到B孔。
他又试着每隔4孔跳一步,也只能跳到B孔。
最后他每隔6孔跳一步,正好跳回到A孔。
你知道这个圆圈上共有多少个孔吗?
试将1,2,3,4,5,6,7分别填入图45的方框中,每个数字只用一次:
使得这三个数中任意两个都互质。
其中一个三位数已填好,它是714。
图47是一张道路图,每段路上的数字是小王走这段路所需的分钟数。
请问小王从A出发走到B,最快需要几分钟?
梯形 ABCD的中位线EF长15厘米(见图53),∠ABC=∠AEF=90°,G是EF上的一点。
如果三角形ABG的面积是梯形ABCD面积的1/5,那么EG的长是几厘米?
有三堆砝码,第一堆中每个法码重3克,第二堆中每个砝码重5克,第三堆中每个砝码重7克。
请你取最少个数的砝码,使它们的总重量为130克写出的取法:需要多少个砝码?其中3克、5克和7克的砝码各有几个?
有5块圆形的花圃,它们的直径分别是3米、4米、5米、8米、9米;请将这5块花圃分成两组,分别交给两个班管便两班所管理的面积尽可能接近。
一串数排成一行,它们的规律是这样的:头两个数都是1,从第三个数开始,每一个数都是前两个数的和,也就是:1,2,3,5,8,13,21,34,55,问:这串数的前100个数中(包括第100个数)有多
少个偶数?
王师傅驾车从甲地开乙地交货。
如果他往返都以每小时60公里的速度行驶,正好可以按时返回甲地。
可是,当到达乙地时、他发现他从甲地到乙地的速度只有每小时55公里,如果他想按时返回甲地,他应以多大的速度往回开?
图54大圈是400米跑道,由A 到B的跑道长是200米,直线距离是50米。
父子俩同时从A点出发逆时针方向沿跑道进行长跑锻炼,儿于跑大圈,父亲每跑到B点便沿各直线跑。
父亲每100米用20秒,儿子每100米用 19秒。
如果他们按这样的速度跑,儿子在跑第几圈时,第一次与父亲再相遇?。
