第九届“华罗庚金杯赛”初赛试题
第九届华罗庚金杯少年数学邀请赛总决赛二试试题

第九届华罗庚金杯少年数学邀请赛总决赛二试试题
1.一正方形苗圃,栽种桃树和李树,一圈一圈地相间种植,即最外一圈种的是桃树,往内一圈是李树,然后是桃树,…,最内一圈种了4棵李树.已知树苗的的行距和列距都相等,桃树比李树多40棵.问:
桃树和李树一共有多少棵?
2.如右图,在以AB为直径的半圆上取一点C,分别以AC和BC为直径在△ABC外作半圆AEC和BFC.当C点在什么位置时,图中两个弯月型(阴影部分)AEC和BFC的面积和最大.
3、甲、乙两家医院同时接受同样数量的病人,每个病人患x病或y 病中的一种,经过几天治疗,甲医院治好的病人多于乙医院治好的病人.问:经过这几天治疗后,是否可能甲医院对x病的治愈率和对y 病的治愈率均低于乙医院的?举例说明.(x病治愈率
=)
4、完成某项工程,甲单独工作需要18小时,乙需要24小时,丙需要30小时.现甲、乙和丙按如下顺序工作:甲、乙、丙、乙、丙、甲、丙、甲、乙、…,每人工作一小时换班,直到工程完成.问:当工程完成时,甲、乙、丙各干了多少小时?
5、求同时满足下列三个条件的自然数a,b:1)a>b;2)
3)a+b是平方数
6.如图,正方形跑道ABCD.甲、乙、丙三人同时从A点出发同向跑步,他们的速度分别为每秒5米、4米、3米.若干时间后,甲首次开始看到乙和丙都与自己在正方形的同一条边上,且他们在自己的前方.从此时刻算起,又经过21秒,甲乙丙三人处在跑道的同一位置,这是出发后三人第一次处在同一位置.请计算出正方形的周长的所有可能值.。
第九届全国“华罗庚金杯”少年数学邀请赛决赛试题及参考答案(初二组)
第九届全国“华罗庚金杯”少年数学邀请赛决赛试题参考答案 (初二组)第九届全国“华罗庚金杯”少年数学邀请赛决赛试题参考答案(初二组)一、填空(每题10分)二、解答下列各题,要求写出简要过程(每题10分)7.解答:.922=+n m ① 解方程⎩⎨⎧-=+-=+.965,543y x y x 得到x=-3,y=1;② 代入原方程组中后两个方程,得到⎩⎨⎧=+=-.35,68n m n m 再解上面关于m 和n 的方程,得到;,136139-==n m③ 计算.911722==+n m 8.解答:重叠部分的面积是.)(22332r -π 如图A,两圆重叠部分是两段小圆弧B AO AOB 1和围成的区域,它由两部分构成:① 第一部分是四边形1AOBO ,因为,111r B O A O OB OA OO =====所以1AOO ∆和1BOO ∆均是边长为r 的正三角形,AD 垂直和等分1OO ,由勾股定理,23212222)(r r r OD AO AD =-=-=,所以r AD 23=,1BOO ∆的面积=,24322321r r =⨯四边形.2231r AOBO =的面积 ② 第二部分是四个弓形AO 、1AO 、BO 、1BO ,四个弓形相同,只需求出一个弓形面积即可。
因为 601=∠AOO ,所以扇形AO O 1的面积=261236060r r ππ=、弓形AO 的面积=扇形AO O 1的面积-AO O 1∆的面积=.)(24361r -π 9.解答:42圈. ① 设A 、B 、C 三个微型机器人的速度分别为u 、v 和w ,圆形轨道周长是S ,5.2,2==--w u S v u S或 5.22,S S w u v u =-=-第九届全国“华罗庚金杯”少年数学邀请赛主试委员会,2004/04/10 1第九届全国“华罗庚金杯”少年数学邀请赛决赛试题参考答案 (初二组)所以,.105.22S S Sv w =-=-…………………………………………………………(1) ②又有,231010=v w…………………………………………………………………(2) 解(1)和(2),得到.5S v = ③代入2Sv u =-,得到.4260,107107S u S S =⨯=10.解答===321a a a ….1010==a①将10个不等式累加得),(3)(2)(103211032110321a a a a a a a a a a a a ++++≥+++++++++ (3)只有10个式子都取等号,(3)式才成立.②由23132a a a =+ 可以得到 ),(23221a a a a -=- (3.1)由34232a a a =+ 可以得到 ),(24332a a a a -=- (3.2)………………………………由121032a a a =+ 可以得到 ),(221110a a a a -=- (3.10)由(3.1)和(3.2)可推知).(243221a a a a -=-类似地,可以推知),(2211021a a a a -=-所以,21a a =,同理可得10321a a a a ==== .所以,.1010321====a a a a11.解答:共有16种填法.① 如图B1,数字1只能填在左上角的格子中,数字9只能填到右下角的格子中.② 数字7和数字8都不能填在中心的格子中;当它们分别填在第三列和第三行时,它们只能填在图B2阴影格子中.③ 数字7和数字8都填在第三列时,只能是图B3的填法.此时,数字6只能填在图B3空的阴影格子中,数字4和5可以分别填在空的白格子中,共有2种填法.类似地,数字7和数字8都填在第三行时,同样有2种填法(见图B4).④ 数字7和数字8可以分别填在图B2空的阴影格中,显然,有两种类型,对每一种类型,数字4、5、6可以随意填入图B2空的白格子中,此时数字4、5、6有6种填法。
第九届 华罗庚杯 赛总决赛(决赛)试题及解答汇编

第九届华杯赛总决赛一试试题及解答1. 计算:2.00×2. 0(结果用最简分数表示)2.水池装有一个水管和若干每小时注水量相同的注水管,注水管注水时,排水管同时排水.若用12个注水管注水,8小时可注满水池;若用9个注水管注水,24小时可注满水池.现在用8个注水管注水,那么需要多少小时注满水池?3.在操场上做游戏,上午8:00从A地出发,匀速地行走,每走5分钟就折转90o。
问:(1)上午9:20能否恰好回到原处?(2)上午9:10能否恰好回到原处?如果能,请说明理由,并设计一条路线.如果不能,请说明理由。
4. 1到100所有自然数中与100互质各数之和是多少?5. 老王和老张各有5角和8角的邮票若干张,没有其它面值的邮票,但是他们邮票的总张数一样多.老王的5角邮票的张数与8角邮票张数相同,老张的5角邮票的金额等于8角邮票的金额.用他们的邮票共同支付110元的邮资足够有余,但不够支付160元的邮资.问他们各有8角邮票多少张?6. 在下面一列数中,从第二个数开始,每个数都比它前面相邻的数大7,8,15,22,29,36,43,……。
它们前n-1个数相乘的积的末尾0的个数比前n个数相乘的积的末尾0的个数少3个,求n 的最小值.答案1.答:2.00×2. 0原式=2.解:设单开水管需x小时将满池水排完,单开一个注水管需要y小时,则可知排水管每小时排整池水的,注水管每小时注水,可知有即为……………………………①同时由2小时用9个注水管注满水知即为……………………………②将①-②得可知代入①中得所以用8个注水管注水每小时注水故需用时(小时)答:用8个注水管注水,需要72小时注满水池.3.答:(1)上午9:20分恰好回到原地.我们可以设计如下的路线:我们若没定每走5分钟都按顺时针方向(或逆时针方向)折转90°,则可知每过20分钟回到原处,而到9:20恰好过了80分钟,故可知9:20恰好第4次回原处.(2)上午9:10不能回到原地.因为到上午9:10共走了70分钟,而我们可以验证不管每一步为逆时针折转90°,还是顺时针折转90°都不能在70分钟内回原地.4.解:我们可以先去考虑到100的所有自然数中与100不可质的数,因为100=2×2×5×5,故1到100中所有含因子2或5的数都与100不互质.其中含因子2的有2,4,6,8…,100(即为50个数),含因子5的有5,10,15,20…,100但其中10,20,30,…100已经包括在上面内,故与100不互质的1到100之内的数为:2,4,6,…100,5,15,25,…95。
2004年第九届华罗庚金杯赛初赛

第九屆“華羅庚金杯賽”初賽試題 (2004.3.7)說明:轉載3A 奧數網試題需注明出處,否則3A 將追究法律責任1、“華杯賽”是爲了紀念和學習我國傑出的數學家華羅庚教授而舉辦的全國性大型少年數學競賽。
華羅庚教授生於1910年,現在用“華杯”代表一個兩位數。
已知1910與“華杯”之和等於2004,那麽“華杯”代表的兩位數是多少? 1 9 1 0+ 華 杯2 0 0 42、長方形的各邊長增加10%,那麽它的周長和麵積分別增加百分之幾?3、題目中的圖是一個正方體木塊的表面展開圖。
若在正方體的各面填上數,使得對面兩數之和爲7,則A 、B 、C 處填的數各是多少?4、在31,53,75,97,119,1311,…中,從哪一個數開始,1與每個數之差都小於10001?5、“神舟五號”載人飛船載著航太英雄楊利偉於2003年10月16日清晨6時51分從太空返回地球,實現了中華民族的飛天夢。
飛船繞地球共飛行14圈,其中後10圈沿離地面343千米的圓形軌道飛行。
請計算飛船沿圓形軌道飛行了多少千米?(地球半徑爲6371千米,圓周率 =3.14)6、如圖,一塊圓形的紙片分成4個相同的扇形,用紅、黃兩種顔色分別塗滿各扇形,問共有幾種不同的塗法?7、在9點至10點之間的某一時刻,5分鐘前分針的位置與5分鐘後時針的位置相同。
問:此時刻是9點幾分?8、一副撲克牌有54張,最少要抽取幾張牌,才能使其中至少有2張牌有相同的點數?9、任意寫一個兩位數,再將它依次重復3遍成一個8位數。
將此8位數除以該兩位數所得到的商再除以9,問:得到的餘數是多少?10、一塊長方形的木板,長爲90釐米,寬爲40釐米,將它鋸成2塊,然後拼成一個正方形,你能做到嗎?11、如圖,大小兩個半圓,它們的直徑在同一直線上,弦AB與小圓相切,且與直徑平行,弦AB長12釐米。
求圖中陰影部分的面積。
(圓周率取3.14)12、半徑爲25釐米的小鐵環沿著半徑爲50釐米的大鐵環的內側作無滑動的滾動,當小鐵環沿大鐵環滾動一周回到原位時,問:小鐵環自身轉了幾圈?。
历届小学华罗庚少年金杯赛试题及解答
历届⼩学华罗庚少年⾦杯赛试题及解答历届⼩学华罗庚少年⾦杯赛试题及解答2010年第⼗五届华杯赛决赛试题C及…2010年第⼗五届华杯赛决赛试题A及…2010年第⼗五届华杯赛决赛试题B及…第⼗四届华罗庚⾦杯少年数学邀请赛…第⼗四届华罗庚⾦杯少年数学邀请赛…第⼗三届“华罗庚⾦杯”少年数学邀请…第⼗三届“华罗庚⾦杯”少年数学邀请…第⼗⼆届华杯赛总决赛⼆试试题及解…第⼗⼆届华杯赛总决赛⼀试试题及解…第⼗⼆届华杯赛决赛试题及解答第⼗⼆届华杯赛初赛试题及解答第⼗⼀届华杯赛决赛试题及解答第⼗⼀届华杯赛初赛试题及解答第⼗届华罗庚⾦杯少年数学邀请赛⼝…第⼗届华杯赛总决赛⼆试试题及解答第⼗届华杯赛总决赛⼀试试题及解答第⼗届华杯赛决赛试题及解答第⼗届华杯赛初赛试题及解答第九届华杯赛总决赛⼆试试题及解答第九届华杯赛总决赛⼀试试题及解答第九届华杯赛决赛试题及解答第九届华杯赛初赛试题及解答第⼋届华杯赛决赛⼆试试题及解答第⼋届华杯赛决赛⼀试试题及解答第⼋届华杯赛复赛试题及解答第七届华杯赛决赛⼆试试题及解答第七届华杯赛决赛⼀试试题及解答第七届华杯赛复赛试题及解答第七届华杯赛初赛试题及解答第六届华罗庚⾦杯少年数学邀请赛团…第六届华杯赛决赛⼆试试题及解答第六届华杯赛决赛⼀试试题及解答第六届华杯赛复赛试题及解答第六届华杯赛初赛试题及解答第五届华杯赛团体决赛⼝试备⽤题第五届华杯赛团体赛⼝试试题第五届华杯赛决赛⼆试试题及解答第五届华杯赛决赛⼀试试题及解答第五届华杯赛复赛试题及解答第五届华杯赛初赛试题及解答第四届华罗庚⾦杯少年数学邀请赛团…第四届华杯赛决赛⼆试试题及解答第四届华杯赛决赛⼀试试题及解答第四届华杯赛复赛试题及解答第四届华杯赛初赛试题及解答第三届华罗庚⾦杯少年数学邀请赛团…第三届华杯赛决赛⼆试试题及解答第三届华杯赛决赛⼀试试题及解答第三届华杯赛复赛试题及解答第三届华杯赛初赛试题及解答第⼆届华罗庚⾦杯少年数学邀请赛⼝…第⼆届华杯赛决赛⼆试试题及解答第⼆届华杯赛决赛⼀试试题及解答第⼆届华杯赛复赛试题及解答第⼆届华杯赛初赛试题及解答第⼀届华杯赛团体赛⼝试试题第⼀届华杯赛决赛⼆试试题及解答第⼀届华杯赛决赛⼀试试题及解答。
六年级下册数学试题-华罗庚金杯少年数学邀请赛小学组初赛试题(含答案PDF)全国通用

的都是假话.那么,昨天这5个人中复习数学的有( )个人.
(A) 0
(B) 1
(C) 2
(D) 3
l
(
华罗庚金杯少年数学邀请赛小学组初赛试题 答案
(
一、 选择题(每小题10分, 满分60分)
1:: I�I : I : I : I : I : I
华罗庚金杯少年数学邀请赛小学组初赛试题
一、选择题(每小题10 分以下每题的四个选项中,仅有一个是正确的,诮将表示正确答案的英文 字母写在每题的圆括号内.)
1. 若连续的四个自然数都为合数,那么这四个数之和的最小伯为( ) 书
(A) 100
CB) 101
(C) 102
(D) 103
· 2. m火柴棍摆放数字0�9的方式如下;\曰Fra bibliotek叶55丁日日D
(1
'··
现在,去掉;, 9,, 的左下创 一根,就成了数字 “ 千,我们称"9"对应1; 去掉"8"的上下呐
o, 根和左下角 一根,就成了数字 ” 中,我们称 "4,, 对应3. 规定 "B,, 本身对应 按照这杆的
规则,可以对应出( )个不同的数字.
(A) 10
(B) 8
(C) 6
:二、填空题(每小题10分, 满分40分)
7 -8
8 1- 2
9
·一
一1·0
65
1769
(
(
,`�
90
(D) 5
3. -�Jj数之和与两数之商都为6, Jjl么这两数之积减这两数之差(大减小)等于( ) .
第九届“华罗庚金杯”少年数学邀请赛总决赛,初一组一试试题及解答
第九届“华罗庚金杯”少年数学邀请赛总决赛初一组一试试题及解答1. 下面的等式成立:1110110110010099433221=======x x x x x x x x x x x x ,求10110021 , , , ,x x x x 的值解:由已知:10199531x x x x x ===== ,10098642x x x x x ===== 。
又1001x x =,所以10110099321x x x x x x ====== 。
因此,110110099321=======x x x x x x或110110099321-=======x x x x x x2.滚柱轴承(如图),外圈大圆是外轴瓦,内圈小圆是内轴瓦,中间是滚柱。
内轴瓦固定,转动时没有相对滑动。
若外轴瓦的直径是内轴瓦的直径的1.5倍,当外轴瓦转动一周时,滚柱自转了几周?解。
滚柱的半径=2r R -,其中R 是外轴瓦的半径,r 是内轴瓦的半径。
外轴瓦转动一周,它上面的每一个点的运动路程为R π2,由于没有滑动,滚柱上的每一个点相对于小球求心的运动路程也是R π2,滚柱自转一周,它上面的点的路程是)(r R -π,所以,滚柱自转了65.0312)(2==-=-r r Rr R R ππ(周)。
3.已知z y x ,,满足:)3(3.1][}{)2(2.0}{][)1(9.0}{][=++=++-=++z y x z y x z y x 其中记号:对于数a ,][a 表示不大于a 的最大整数,][}{a a a -=。
求z y x ,,的值。
解:首先注意到,.0}{,][,≥≤a a a a 所以,对于任意有理数 (1)+(2)+(3)得到6.0222=++z y x 即 3.0=++z y x (4)(4)-(1)得到 2.1][}{=+z y 从而 1][,2.0}{==z y 。
(4)-(2)得到 1.0][}{=+y x从而 0][,1.0}{==y x ,(4)-(3)得到 1}{][-=+z x 因此, 0}{1][=-=z x故 9.0-=x ,2.0=y ,1=z 。
1-16届华罗庚金杯赛试题
第一届“华罗庚金杯”少年数学邀请赛(初赛试题)1.1966、1976、1986、1996、2006这5个数的总和是多少?2.每边长是10厘米的正方形纸片,正中间挖一个正方形的洞,成为一个宽度是1厘米的方框。
把5个这样的方框放在桌面上,成为这样的图案。
问桌面上被这些方框盖住的部分面积是多少平方厘米?3.105的约数共有几个?4.妈妈让小明给客人烧水沏茶。
洗开水壶要用1分钟,烧开水要用15分钟,洗茶壶要用1分钟,洗茶杯要用1分钟,拿茶叶要用2分钟。
小明估算了一下,完成这些工作要花20分钟,为了使客人早点喝上茶,按你认为最合理的安排,多少分钟就能沏茶了?5.右面的算式里,4个小纸片各盖住了一个数字。
被盖住的4个数字总和是多少?6.松鼠妈妈采松籽。
晴天每天可以采20个。
有雨的天每天只能采12个。
它一连几天采了112个松籽,平均每天采14个。
问这几天当中有几天有雨?7.边长1米的正方体2100个,堆成一个实心的长方体。
它的高是10米,长、宽都大于高。
问长方体的长与宽的和是几米?8.早晨8点多钟,有两辆汽车先后离开化肥厂,向幸福村开去。
两辆汽车的速度都是每小时60公里。
8点32分的时候,第一辆汽车离开化肥厂的距离是第二辆汽车的3倍。
到了8点39分的时候,第一辆汽车离开化肥厂的距离是第二辆汽车的2倍.那么,第一辆汽车是8点几分离开化肥厂的?9.有一个整数,除300、262、205,得到相同的余数.问这个整数是几?10.甲、乙、丙、丁4个人比赛乒乓球,每两个人都要赛一场.结果甲胜了丁,并且甲、乙、丙3个胜的场数相同.问丁胜了几场?11.两个十位数1111111111和9999999999的乘积有几个数字是奇数?12.黑色、白色、黄色的筷子各有8根,混杂地放在一起。
黑暗中想从这些筷子中取出颜色不同的两双筷子。
问至少要取多少根才能保证达到要求?13.有一块菜地和一块麦地,菜地的21和麦地的31放在一起是13亩,麦地的21和菜地的31放在一起是12亩,那么,菜地是几亩?14.71427和19的积被7除,余数是几?15.科学家进行一项实验,每隔5小时做一次记录.做第十二次记录时,挂钟的时针恰好指向9,问做第一次记录时,时针指向几?16.有一路电车的起点站和终点站分别是甲站和乙站。
第9届华杯赛决赛试题及解答
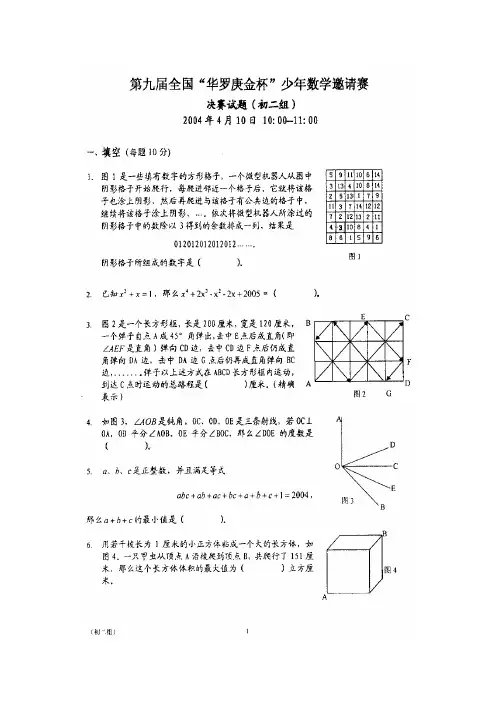
第九届华杯赛决赛试题及解答一、填空(每题10分)1.计算:2004.05×1997.05-2001.05×1999.05=( )2.如图所示,是一些填有数字的方形格子,一个微型机器人从图中阴影格子开始爬行,每爬进邻近一个格子后,它就将该格子也涂上阴影,然后再爬进与该格子有公共边的格子中,继续将该格子涂上阴影,…。
依次将微型机器人所涂过的阴影格子中的数除以3得到的余数排成一列,结果是012012012012012…… 阴影格子所组成的数字是( )。
3.等式: =39× 恰好出现1、2、3、4、…、9九个数字,“潮州市”代表的三位数是( )。
4.一个半径为1厘米的圆盘沿着一个半径为4厘米的圆盘外侧做无滑动的滚动,当小圆盘的中心围绕大圆盘中心转动90度后(如图2),小圆盘运动过程中扫出的面积是( )平方厘米。
(=3.14)5.甲、乙、丙三只蚂蚁从A 、B 、C 三个不同的洞穴同时出发,分别向洞穴B 、C 、A爬行,同时到达后,继续向洞穴C 、A 、B 爬行,然后返回自己出发的洞穴。
如果甲、乙、丙三只蚂蚁爬行的路径相同,爬行的总距离都是7.3米,所用时间分别是6分钟、7分钟和8分钟,蚂蚁乙从洞穴B 到达洞穴C 时爬行了( )米,蚂蚁丙从洞穴C 到达洞穴A 时爬行了( )米。
6.如图3,甲、乙二人分别在A 、B 两地同时相向而行,于E 处相遇后,甲继续向B 地行走,乙则休息了14分钟,再继续向A 地行走。
甲和乙到达B 和A 后立即折返,仍在E 处相遇,已知甲分钟行走60米,乙每分钟行走80米,则A 和B 两地相( )米。
图3二、解答下列各题,要求写出简要过程(每题10分)7.李家和王家共养了521头牛,李家的牛群中有67%是母牛,而王家的牛群中仅有113是母牛,李家和王家各养了多少头牛?8.在3×3的方格纸上(如图4),用铅笔涂其中的5个方格,要求每横行和每竖行列被涂方格的个数都是奇数,如果两种涂法经过旋转后相同,则认为它们是相同类型的涂法,否则是不同类型的涂法。
9第九届华罗庚金杯少年数学邀请赛
第九届华罗庚金杯少年数学邀请赛初赛
复赛
决赛一试
1.计算:2.004 × 2.008 (循环节分别是4和8)
(结果用最简分数表示)
2.水池装有一个排水管和若干个每小时注水量相同的注水管,注水管注水时,排水管同时排水。
若用12个注水管注水,8小时可注满水池;若用9个注水管注水,24小时可注满水池。
现在用8个注水管注水,那么需要多少小时可注满水池?
3.在操场上做游戏,上午8:00从A地出发,均匀地行走,每走5分钟就折转90°。
问:
(1)上午9:20能否恰好回到原处?
(2)上午9:10能否恰好回到原处?
如果能,请说明理由,并设计一条路线;如果不能,请说明理由
4.1到100所有自然数中与100互质各数之和是多少?
5.老王和老张各有5角和8角的邮票若干张,没有其它-面值的邮票,但是他们邮票的总张数一样多。
老王的5角邮票的张数和8角邮票的张数一样多,老张5角邮票的金额等于85角邮票的金额,用他们的邮票共同支付110元的邮资足够有余,但不够支付160元的邮资,问他们各有8角的邮票多少张?
6.在下面一列数中,第二个数开始,每个数都比它前面相邻的数大7:
8,15,22,29,36,43,……
它们前n-1个数相乘的积的末尾0的个数比前n个数相乘的积的末尾0的个数少3个,求n的最小值。
决赛二试。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九届“华罗庚金杯赛”初赛试题第九届“华罗庚金杯赛”初赛试题1、“华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛。
华罗庚教授生于1910年,现在用“华杯”代表一个两位数。
已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少,2、长方形的各边长增加10%,那么它的周长和面积分别增加百分之几,3、题目中的图是一个正方体木块的表面展开图。
若在正方体的各面填上数,使得对面两数之和为7,则A、B、C处填的数各是多少,13579114、在一列数:中,从哪一个数开始,1与每个数之差,,,,,,?357911131都小于, 10005、“神舟五号”载人飞船载着航天英雄杨利伟于2003年10月16日清晨6时51分从太空返回地球,实现了中华民族的飞天梦。
飞船绕地球共飞行14圈,其中后10圈沿离地面343千米的圆形轨道飞行。
请计算飞船沿圆形轨道飞行了多少千米(地球半径为6371千米,圆周率π=3.14)。
6、如图,一块圆形的纸片分为4个相同的扇形,用红、黄两种颜色分别涂满各扇形,问共有几种不同涂法,7、在9点至10点之间的某一时刻,5分钟前分针的位置与5分钟后时针的位置相同。
问:此时刻是9点几分,8、一副扑克牌有54张,最少要抽取几张牌,方能使其中至少有2张牌有相同的点数,9、任意写一个两位数,再将它依次重复3遍成一个8位数。
将此8位,问:得到的余数是多少, 数除以该两位数所得到的商再除以910、一块长方形木板,长为90厘米,宽为40厘米,将它锯成2块,然后拼成一个正方形,你能做到吗,、如图,大小两个半圆,它们的直径在同一条直线上,弦AB与小圆11相切,且与直径平行,弦AB长12厘米。
求图中阴影部分的面积(圆周率π=3.14)。
12、半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿滚动一周回到原位时,问小铁环自身转了几圈,4(在下列数中,从哪一个数开始,l与每个数之差都小于5(“神舟五号”载人飞船载着航天英雄杨利伟,于M年 10月16日清晨6时sl分从太空返回地球,实现了中华民族的飞天梦。
飞船绕地球共飞行14圈,其中后10 M沿离地面343千米的圆形轨道飞行。
请计算飞船沿圆形轨道飞行了多少千米 (地球半径为6371千米,圆周率一3。
14)。
6(如右图,一块圆形的纸片被分成4个相同的扇形,用红、黄两种颜色分别涂满扇形,问共有几种不同的涂法,(通过旋转能得到相同的图案看作相同的涂法)7(在9点至10点之间的某一时刻,5分钟前分针的位置与 5分钟后时针的位置相同。
问:此时刻是9点几分,8(一副扑克牌有54张,最少要抽取几张牌,方能使其中至少有2张牌有相同的点数,9(任意写一个两位数,再将它依次重复3遍成一个8位数,将此8位数除以该两位数所得到的商再除以9,问;得到的余数是多少,10(一块长方形的木板,长为p厘米,宽为40厘米,将它锯成2块,再拼成一个正方形,你能做到吗,11(如左下图,大、小两个半圆,它们的直径在同一直线上,弦 AB与小半圆相切,且与直径平行,弦 AB长 12厘米。
求图中阴影部分的面积(圆周率二3二4)。
11(半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问:小铁环自身转了几圈,。
决赛(2004年4月11日)一、填空(每题10分,如果一道题中有两个空,则每个5分) 1.计算:2004.05×1997.05,2001.05×1999.05,( )。
2.右图是一些填有数字的方形格子,一个微型机器人从图中画有大的格子开始爬行,每爬进邻近一个格子后,它就将该格子涂上阴影,然后再爬进与该格子有公共边的格子中,继续将该格子涂上阴影……依次将微型机器人所涂过的阴影格子中的效除以3得到的余数排成一列,结果是0 1 2 0 1 2 0 1 2……如果机器人不能爬进已经被涂上阴影的格子,那么机器人最多将( )个格子涂上了阴影。
(注:本题略有改动) 3.等式,恰好出现1,2,3,4…??9九个数字,“潮州潮州54,39,1市6市”代表的三位数是( )。
4.一个半径为1厘米的圆盘沿着一个半径为尽厘米的圆盘外侧做无滑动的滚动,当小圆盘的中心围绕大圆盘中心转动叨度后(如右图),小圆盘运动过程中扫出的面积是( )平方厘米。
(π=3.14)5.甲、乙、丙三只蚂蚁从A,B,C三个不同的洞穴同时出发,分别向洞穴B,C,A爬行,同时到达后,继续向洞穴C,A,B爬行,然后返回自己出发的洞穴。
如果甲、乙、而三只蚂蚁爬行的路径相同,爬行的总距离都是7.3米,所用时间分别是6分钟、7分钟和8分钟,则蚂蚁乙从洞穴B到达洞穴C时爬行了( )米,蚂蚁丙从洞穴C到达洞穴A时爬行了( )米。
6.如下图,甲、乙二人分别在A,B两地同时相向而行,于E处相遇后,甲继续向B地行走,乙则休息了14分钟,再继续向A地行走。
甲和乙到达B和A后立即折返,仍在E处相遇。
已知甲每分钟行走60米,乙每分钟行走80米,则A和B 两地相距〔 )米。
二、解答下列各题,要求写出简要过程(每题10分)7.李家和王家共养了521头牛,李家的牛群中有67,是母牛,而王家的牛群中仅有下1/13是母牛,李家和王家各养了多少头牛, 8.一个最简真分数M/7,化成小数。
,如果从小数点后第一位起连续若干位的数字之和等于2004,求M的值。
9.小丽计划用31元买走每支2元、3元、4元三种不同价格的圆珠笔,每种至少买1支,问她最多能买多少支,最少能买多少支, 10.在3×3的方格纸上(如左下图),用铅笔涂其中的5个方格,要求每横行和每竖列被涂方格的个数都是奇数。
如果两种涂法经过旋转后相同,则认为它们是相同类型的涂法,否则是不同类型的涂法。
例如下中图和右下图是相同类型的涂法。
最多有多少种不同类型的涂法,说明理由。
11.三个连续正整数,中间一个是完全平方数,将这样的三个连续正整数的积称为“美妙数”。
问所有的小于2008的“美妙数”的最大公约数是多少,11.用455个棱长为1的小正方体粘成一个大的长方体,若拆下沿校的小正方体,则尚余下的1个小正方体,问所粘成的大长方体的棱长各是多少,拆下沿棱的小正方体后的多面体(如下图)的表面积是多少,总决赛第一试(2004年5月13日),,,2.004,2.0081.计算:(结果用最简分数表示)2.水池装有一个排水管和若干每小时注水量相同的注水管,注水管注水时,排水管同时排水。
若用,12个注水管注水,8小时可注满水池;若用9个注水管注水,24小时可注满水池,现在用8个注水管注水,那么需要多少小时注满水池,3.在操场上做游戏,上午8:00从A地出发,匀速地行走,每走5分钟就折转90?。
问(1)上午9:20能否恰好回到原处,(2)上午9:10 能否恰好回到原处,如果能,请说明理由,并设计一条路线。
如果不能请说明理由。
4.在1到100的所有自然数中,与100互质的各数之和是多少,5.老王和老张各有5角和8角的邮票若干张,没有其它面值的邮票,但是他们邮票的总张数一样多。
老王的5角邮票的张数与8角邮票张数相同,老张的5角邮票的总金额等于8角邮票的总金额。
用他们的邮票共同支付 110元的邮资足够有余,但不够支付160元的邮资。
问他们各有8角邮票多少张,6.在下面一列数中,从第M个数开始,每个数都比它前面相邻的数大7:8,15,22,29,36,43……它们前(n,l)个数相乘的积的末尾0的个数比前n个数相乘的积的末尾0的个数少3个,求n的最小值。
总决赛第二试(2004年5月13日)1.如左下图所示,一正方形苗圃,栽种桃树和李树,一圈一圈地相间种植,即最外一圈种的是桃树,往内一圈是李树,然后是桃树。
……最内一圈种了4棵李树。
已知树苗的行距和列距都相等,桃树比李树多40棵。
问:桃树和李树一共有多少棵,2.如右上图所示,在以AB为直径的半圆上取一点C,分别以AC和BC为直径在LABC外作半圆AEC和BFC。
当C点在,什么位置时,图中两个弯月型(阴影部分)AEC和BFC的面积和最大,(提示:?ACB是直角三角形)3.甲、乙两家医院同时接收同样数量的病人,每个病人患x病或y病中的一种,经过几天治疗,甲医院治好的病人多于乙医院治好的病人。
问:经过这几天治疗后,是否可能甲医院对x病的治愈率和对y病的治愈率均低于乙医院的,举例说明。
x病治好人数,, x病治愈率,,100%,,患x并总人数,,4.完成某项工程,甲单独工作需要18小时,乙单独工作需要24小时,丙单独工作需要30小时。
现在甲、乙和丙按如下顺序换班工作:甲、乙、丙、乙、丙、甲、丙、甲、乙……每人工作一小时换班,直到工程完成。
问:当工程完成时,甲、乙、丙各干了多少小时,ab5.求同时满足下列三个条件的自然数a,b:(l)a,b;(2);,169a,b(3)(a,b)是平方数。
6.如下图所示,正方形跑道ABCD,甲、乙、雨三人同时从A点出发同向跑步,他们的速度分别为每秒5米、4米。
3米。
若干时间后,甲首次开始看到乙和丙都与自己在正方形的同一条边上,且他们在自己的前方。
从此时刻算起,又经过21秒,甲、乙。
丙三人处在跑道的同一位置,请计算出正方形的周长的所有可能值。
