华罗庚金杯少年数学邀请赛决赛
第23届华罗庚金杯少年数学邀请赛 决赛试题(小学高年级组·练习用)

第二十三届华罗庚金杯少年数学邀请赛决赛试题(小学高年级组)第二十三届华罗庚金杯少年数学邀请赛 决赛试题(小学高年级组·练习用) 一、填空题(每小题 10 分, 共 80 分) 1. 如图,一个4 ⨯ 4 方形点阵,每个点与其相邻的上、下、左、右点的距离都相等. 以这些点为端点的、不同长度的线段共有 条. 2. a , b , c , d 四个数,每次去掉 2 个数,将其余 2 个数求平均数, 这样计算了 6 次,得到 6 个数是: 23,26,29,32,24,31,则四个数a , b , c , d 的平均数是 . 3. 甲、乙两车从同一地点出发沿同一高速公路从 A 地到 B 地。
甲车先出发 2 小时,乙车出发后经 5 小时与甲车同时到达 B 地。
如果乙车时速增加 8 千米, 那么,出发后 4 小时可追上甲车。
A 地与 B 地的距离是 千米. 4. 如图, 一个6⨯9 方格网. 先将其中的任意几个方格染黑, 然后按照以下规则继续染色: 如果某个方格至少与2 个黑格都有公共边, 那么就将这个方格染黑. 要按照这个规则将整个棋盘都染成黑色, 所需要的最少初始染黑方格是 个。
5. 有五张标有 A ,B ,C ,D ,E 的卡片,从左到右排成一行,已知: (1)C 和 E 都不和 B 相邻; (2)C 和 E 都不和 D 相邻; (3)B 和 E 都不和 A 相邻; (4)A 的右边是 D 。
请问:这个五张卡片的从左到右排列顺序是 。
6. 如图,由 6 个正方形与 12 个等边三角形构成的图形,整个图形的面积是 2018,阴影部分的面积是 .7. 圆周有 101 个格子,从某格 A 开始,沿着逆时针方向,第一次移动1格,第二次移动2 格, ,每次比前次多移动1格,移动到的格子中放一枚棋子,最多有 个格子放有棋子.总分 学校姓名参赛证号密封线内请勿答题第二十三届华罗庚金杯少年数学邀请赛决赛试题(小学高年级组)8. 从 1 到 2018 这 2018 个数中,任取 2 个数 x , y ,使得9| x 3 + y 3 ,这样的数对(x , y ) 有 对.二、解答下列各题(每题 10 分, 共 40 分, 要求写出简要过程)9. 求 22 + 3 + 32 + 3 + 42 + 3 + 52 + 3 + 22 -1 32 -1 42 -1 52 -1 + 20172 + 3 的整数部分。
第十四届全国“华罗庚金杯”少年数学邀请赛决赛
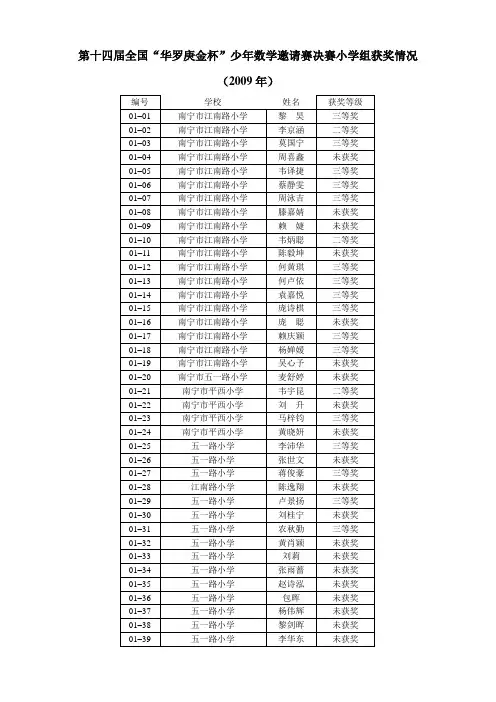
05–16 05–17 05–18 05–19 05–20 05–21 05–22 05–23 05–24 05–25 05–26 05–27 05–28 05–29 05–30 05–31 05–32 05–33 05–34 05–35 05–36 05–37 05–38 05–39 05–40 05–41 05–42 05–43 05–44 05–45 05–46 05–47 05–48 05–49 05–50 06–01 06–02 06–03 06–04 06–05 06–06 06–07 06–08 06–09
玉国圣 谭喜校 巫柳柳 廖小莹 覃 敏
未获奖 未获奖 未获奖 三等奖 未获奖 未获奖 未获奖 未获奖 三等奖 未获奖 一等奖 未获奖 二等奖 二等奖 未获奖 未获奖 二等奖 未获奖 三等奖 二等奖 一等奖 未获奖 未获奖 二等奖 未获奖 未获奖 未获奖 未获奖 未获奖 未获奖 三等奖 三等奖 未获奖 三等奖 三等奖 三等奖 三等奖 二等奖 三等奖 三等奖 三等奖 未获奖 三等奖 未获奖
南宁市荣和实验学校 南宁市荣和实验学校 南宁市荣和实验学校 南宁市菠萝岭小学 南宁市菠萝岭小学 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 五一中路学校 五一中路学校 五一中路学校 五一中路学校 五一中路学校 五一中路学校 五一中路学校 江南区淡村小学 江南区淡村小学 江南区淡村小学 江南区淡村小学 江南区淡村小学 南宁市壮锦学校 南宁市壮锦学校 南宁市壮锦学校 南宁市壮锦学校 南宁市壮锦学校 南宁市壮锦学校 南宁市五一西路学校 白沙小学 白沙小学
数学竞赛第七届“华罗庚金杯”少年数学邀请赛决赛第一试及答案

数学竞赛 第七届“华罗庚金杯”少年数学邀请赛决赛第一试及答案1.公园只售两种门票:个人票每张5元,元,l0l0人一张的团体票每张30元,购买10张以上团体票者可优惠l0l0%。
%。
%。
(1) (1)甲单位甲单位45人逛公园,按以上规定买票,最少应付多少钱人逛公园,按以上规定买票,最少应付多少钱? ?(2) (2)乙单位乙单位208人逛公园,按以上规定买票,最少应付多少钱人逛公园,按以上规定买票,最少应付多少钱? ?2.用无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体(如图如图)),大正方体内的对角线,,,所穿过的小正方体都是红色玻璃小正方体,其它部分都是无色透明玻璃小正方体,小红正方体共用了40l 个。
问:无色透明小正方体用了多少个个。
问:无色透明小正方体用了多少个? ?3.a 是自然数,且17a=,求a 的最小值。
的最小值。
4.对一个自然数作如下操作:如果是偶数则除以2,如果是奇数则加l 。
如此进行直到为l 时操作停止。
问:经过9次操作变为1的数有多少个的数有多少个? ?5.已知m ,n ,k 为自然数,m≥n≥k,是100的倍数,求m +n -k 的最小值。
的最小值。
6.1998个小朋友围成一圈,从某人开始,逆时针方向报数,从l 报到6464,再依次从,再依次从l 报到6464,一,一直报下去,直到每人报过l0次为止。
问:次为止。
问:(1) (1)有没有报过有没有报过5,又报过l0的人的人??有多少有多少??说明理由;说明理由;(2) (2)有没有报过有没有报过5,又报过ll 的人的人??有多少有多少??说明理由;说明理由;参考答案1.1.【解】【解】【解】(1)45(1)45个人,应当买4张团体票张团体票((每张10人),5张个人票,共用:30×4+5×5=张个人票,共用:30×4+5×5=145145元(比5张团体票省张团体票省))。
(2)208个人,可以买21张团体票张团体票((每张10人),共用:30×21×(1-,共用:30×21×(1-101010%%)=3×21×9==3×21×9=567567元,元, 如果买20张团体票,张团体票,88张个人票,共用:30×20×(1-张个人票,共用:30×20×(1-10%)10%)10%)+5×8=+5×8=+5×8=580580元由于购买10张以上团体票的可以优惠1010%,所以%,所以208人买21张团体票反而省钱。
第二十届华罗庚金杯少年数学邀请赛决赛试题B

word专业资料-可复制编辑-欢迎下载详解第二十届华罗庚金杯少年数学邀请赛决赛小学高年级组B卷题特级教师吴迺华一、填空题(每小题10分,共80分)1.计算:57.6×85+28.8×1845-14.4×80+1112解:原式=57.6×85+(28.8×2)×(1845×12)-(14.4×4)×(80÷4)+1112=57.6×85+57.6×925-57.6×20+1112=57.6×(85+925-20)+1112=111 22.甲、乙、丙、丁四人共植树60棵,己知,甲植树的棵数是其余三人的二分之一,乙植树的棵数是其余三人的三分之一,丙植树的棵数是其余三人的四分之一,那么丁植树多少棵?解:本题中的12、13、14,单位“1”的量都不相同,可以以甲、乙、丙、丁四人共植树的棵数为单位“1”来统一。
甲植树的棵数是其余三人的二分之一,即甲植树的棵数是四人共植棵数的11+2;乙植树的棵数是其余三人的三分之一,即乙植树的棵数是四人共植棵数的11+3;丙植树的棵数是其余三人的四分之一,即丙植树的棵数是四人共植棵数的11+4;所以,丙植树的棵数是:60×(1―11+2―11+3―11+4)=13(棵)3、当时间为5点8分时,钟表面上的时针与分针成度的角。
解:分针每分钟走6°,5:00时,分针与时针夹角为:25×6°=150°八分钟分针走了8×6°=48°;时针每分钟走0.5°,八分钟走8×0.5°=4°。
所以,5:08时,时针与分针成的夹角为:150°-(48°-4°) =106°4.某个三位数是2的倍数,加1是3的倍数,加2是4的倍数,加3是5的倍数,加4是6的倍数,那么这个数最小为。
华罗庚金杯数学邀请赛决赛初二组练习题(含答案)

第二十三届华罗庚金杯少年数学邀请赛决赛试题(初中二年级组) 总分第二十三届华罗庚金杯少年数学邀请赛决赛试题(初中二年级组·练习用)一、填空题(每小题10 分, 共80 分)2019 2 2 1009 2 20181.计算1 2 2018.2. 一块正三角形草坪边长为 12 米,三个顶点处都安有喷水装置,每个喷水装置都可以从三角形的一边到另一边旋转60º来回喷水.假定三个喷水装置的射程相等,要使草坪上所有区域都可以被喷水覆盖,那么被重复喷水的最小面积是平方米.3. 从 2, 3, 4, 5 这四个数中,任取两个数p,q( p q) ,构成函数y px 2 和y x q ,如果这两个函数图象的交点在直线x 2 的左侧,那么这样的有序数对( p,q) 共有个.4. 设p 为质数,如果二次方程x2 2px p2 5p 1 0的两个根都是整数,那么p 可能取的值有个.5. 如果1295 (6n 1) (其中n 是整数,且1986≤n≤2018 ),那么满足条件的n 的个数是.6. 如图所示,在正六边形ABCDEF 内放有一个正方形MNPQ ,正方形的顶点分别在正六边形的 4 条边上,且MN //BC .若正方形MNPQ 的面积为12 6 3 平方厘米,则正六边形ABCDEF 的面积是平方厘米.7. 将 1,2,3,4,5,6,7,8,9,10,11 这 11 个数排成一行,使得任意 5个相邻的数的和都是 5 的倍数.那么这样的排列方法有种.8. 四张卡片,每张写着一个自然数,任取 2 张,或者 3 张,或者 4 张,把卡片上的数求和,可以得到 11 个不同的和,那么 4 张卡片上所有数的和最小为.第二十三届华罗庚金杯少年数学邀请赛决赛试题(初中二年级组)二、解答下列各题(每小题10 分, 共40 分, 要求写出简要过程)9. 有 A ,B 两队野外徒步旅行,A 队在 B 队的西偏北 45 度处,两队相距8 2千米.如果 A 队向东继续行走, B 队同时沿西偏南45 度路线行走,且 A队与 B 队的速度比是 2 ,求A,B 两队最近时的距离.10. 如果实数x, y,z 同时满足关系式x( y2 z) z(z xy) ,y(z2 x) x(x yz) ,z(x2 y) y( y zx) ,那么,实数x, y,z 是否一定都相等?请给出证明.11. 如图,在四边形ABCD 中, ABC BCD 120 ,AB BC .对角线AC ,BD 相交于点E .若AE 3CE ,求证:AB 2CD .12. 从 76 个连续自然数 1,2,…,76 中任取 39 个数,其中必有 2 个数的差是p ,求p 的值.三、解答下列各题(每小题15 分, 共30 分, 要求写出详细过程)13. 如图,在五边形ABCDE 中,AB AE 1 , CAD 45 , E DE EAB B 90 ,求点A到直线CD 的距离. CA B14. 如图,一个由 81 个小方格组成的9 9 网格.先将其中的任意n 个方格染黑,然后按照以下规则继续染色:如果某个方格至少与 2 个黑格都恰好有 1 个公共顶点,那么就将这个方格染黑.现在要按照这个方法将整个棋盘都染成黑色,那么n的最小值是多少?说明你的结论.第二十三届华罗庚金杯少年数学邀请赛决赛试题参考答案(初中二年级组)第二十三届华罗庚金杯少年数学邀请赛决赛试题·练习用参考答案(初中二年级组)一、填空题(每小题10 分, 共 80 分)题号 1 2 3 4 5 6 7 8答案2018 1 24π 36 3 5 2 83 322304 14二、解答下列各题(每小题10 分, 共 40 分, 要求写出简要过程)16 1059. 【答案】A ,B 两队最近时的距离是千米.【解答】如图,以B 队初始位置为原点,正东、正北方向为x 轴和y 轴的正方向,建立平面直角坐标系,B(0,0) ,A( 8,8).不妨y设B 队的速度为 1,那么A队的速度为 2 ,经过时间t A A1x后,B 队所在位置是 2 2B ( t, t) ,A队所在位置是12 2B1BA1( 8 2t,8) ,于是此时两队的距离d 满足2 2 2 2 2 28 2d ( 8 2t t) (8 t) 5t 16 2t 128,当t 时,d取到最2 2 5小值512 16 10千米.5 510. 【答案】x, y,z 一定都相等.【证明】将原关系式变形,得xy(y z) z(z x) ①,yz(z x) x(x y) ②,zx(x y) y(y z) ③.(1)当(x y()y z ()zx) 0 时,不妨设x y ,由③得y 0 或者y z .若y z ,则x y z ;若y 0 ,有x 0 ,代入①,得z 0 或者z x 0 ,即x y z 0 .(2)当(x y)(y z)(z x) 0 时,将①②③相乘得xyz(xyz 1) 0,即xyz 0 或xyz .如果xyz 0 ,不妨设y 0 ,由(1)知z 0或者z x ,矛盾!如果xyz 1,1- 1 -不妨设x≥y≥z ,显然x 0 .假设x y ,考虑②式,有x(x y) 0 ,又1yz 0,xz x ,所以yz(z x) 0 .矛盾!所以x y z .证毕!11. 【证明】作BM AC于M.因为△ABC 中,AB BC , ABC=120 ,所以AM CM, CAB ACB 30 .因此AB 2BM .由于 ACB 30 ,所以 ACD 90 .又由AE 3CE 和AM CM 得:AM ME 3CE ,即CM ME 3CE .即(ME CE) ME 3CE 所以2ME 2CE ,故ME CE .在 Rt△BME 与 Rt△DCE 中,因为ME CE , BEM DEC ,所以Rt△BME ≌Rt△DCE .因此BM CD .由于AB 2BM (已证),所以AB 2CD .12. 【答案】p 的值为 1,2,19,38.【解答 1】p 的值是 1,2,19,38.做抽屉,每个抽屉内有差为p 的两个数,或仅有一个数:当p≥39 时, 有两类抽屉,第一类,每个抽屉有 2 个非零自然数,差是p :{76,76 p},{75, 75 p},…,{p 2,2},{p 1,1},个数是76 p ;第二类,每个抽屉仅有 1 个不大于p 的非零自然数,但与p 的和大于76:{77 p},{78 p},…,{p}个数是76 2 (76 p) 2p 76 .此时,抽屉总数是p 个.从每个抽屉各取一个数,因为p≥39 ,这些数中不存在差是p 的两个数.当p≤38时,做抽屉:{1, p 1},{2, p 2},{3, p 3} ,{4, p 4}…{p,2 p} ,{2p 1,3p 1},{2p 2,3p 2},{2p 3,3p 3} ,…{3p,4p} ,……,- 2 -76 76 76 762p 1 1, 2p 1 p 1 , 2p 1 2, 2p 1 p 2 ,2p 2p 2p2p76 76.2p p,2p2p2p①若76 762p 2p,则抽屉到此为止,共有 38 个抽屉,从中任取 39 个,必有2 个取自同一个有两个数的抽屉,差是p .所以,p 1, 2,19, 38 .②若76 762p 2p,则还有抽屉:76 762p 1 , 2p 2 ,{76},2p 2p76个数是76 2p2p.得到抽屉的个数是:76 76 76 76 76 76p p p p p76 2 76 76 38p p p p p p2 2 2 2 2 276 76 76其中,2p 2p2p ,此时,p76≥1,抽屉的个数≥39.从其中 392p个抽屉各取 1 个数,不存在两个数的差是p .所以,p 的值是 1, 2, 19, 38.【解答 2】记76 kp r ,0 r p ,把 1 到 76 按照下面排成p 行,1 2r p 1 p2 pr 2p2p1 (k1)2rp(k1) p(k1) pkp1kp2kprkpk 为偶数时,记k 2l (注,当k 为偶数时,由于 76 是偶数,r 也是偶数),则前r 行可以取l 1个数,后p r 行可以取l 个数,这lp 个数任意两个数的差不等于p .kp 76 r rr r r 382 2 2k 为奇数时,记k 2l 1(注,当k 为奇数时,由于 76 是偶数,p r 也是偶数),则前r 行可以取l 1个数,后p r 行也可以取l 1个数,这2(l 1) p (2l 1) p p kp p 76 r p p r(l 1) p 38 个数任意两个数2 2 2 2 2的差不等于p .r 当r 0时, 02p r与 0,因此任取 38+1=39 个数时,任意两个数的差2- 3 -。
第十六届华赛杯小学组决赛试题及答案

第十六届华罗庚金杯少年数学邀请赛决赛试题(深圳赛区小学组)(时间: 2011年4月16日)一、填空(每题 10 分, 共80分)1.11122181819 .2320320192020⎛⎫⎛⎫⎛⎫++++++++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2.甲车从A 出发驶向B,往返来回;乙车从B 同时出发驶向A,往返来回.两车第一次相遇后,甲车继续行驶4小时到达B ,乙车继续行驶1小时到达A. 若A,B 两地相距100千米,那么当甲车第一次到达B 时,乙车的位置距离A 千米。
3.每个铅字上刻有一个数码.如果印刷十二页书,所用的页码铅字要以下15个:1,2,3,4,5,6,7,8,9,1,0,1,1,1,2。
现要印刷一本新书,从库房领出页码铅字共2011个,排版完成后有剩余.那么,这本书最多有页.最少剩余 个铅字.4. 一列数:8,3,1,4,.….., 从第三个开始,每个数都是最靠近它前两个数的和的个位数.那么第2011个数是 .5.编号从1到50的50个球排成一行,现在按照如下方法涂色:1)涂2个球;2)被涂色的2个球的编号之差大于2.如果一种涂法被涂色的两个球与另一种涂法被涂色的两个球至少有一个是不同号的,这两种涂法就称为”不同的”.那么不同的涂色方法有种.6. A,B两地相距100千米。
甲车从A到B要走m个小时,乙车从A 到B要走n个小时,m ,n是整数.现在甲车从A,乙车从B同时出发,相向而行,经过5小时在途中C点相遇。
若甲车已经走过路程的一半,那么C到A路程是千米。
7. 自然数b与175的最大公约数记为d. 如果176(111)51⨯-⨯+=⨯+,b d d则b = .8. 如右图. ABCD为平行四边形.AE=2EB.若三角形CEF的面积=1.那么,平行四边形ABCD的面积= .二、解答下列各题(每题10 分, 共40分, 要求写出简要过程)9.三位数的十位数字与个位数字的和等于百位数字的数,称为”好数”.共有多少个好数?10.在下列2n 个数中,最多能选出多少个数,使得被选出的数中任意两个数的比都不是2或12?2345213, 32, 32, 32, 32, 32,, 32.n -⨯⨯⨯⨯⨯⨯11 .一个四位数abcd 和它的反序数dcba 都是65 的倍数.求这个数.12. 用写有+1和-1的长方块放在10n方格中,使得每一列和每一行的数的乘积都是正的,n的最小值是多少?三、解答下列各题(每题15 分, 共30分, 要求写出详细过程)13. 十五个盒子,每个盒子装一个白球或一个黑球.,且白球不多于 12个.你可以任选三个盒子来提问:“这三个盒子中的球是否有白球?”并得到真实的回答. 那么你最少要问多少次,就能找出一个或更多的白球?14. 求与2001互质,且小于2001的所有自然数的和。
奥数竞赛 第十二届全国华罗庚金杯少年数学邀请赛决赛试卷及答案
第十二届全国华罗庚金杯少年数学邀请赛决赛试卷及答案一、填空(每题10分,共80分)1.“华”、“杯”、“赛”三个字的四角号码分别是“2440”、“4199”和“3088”,将“华杯赛”的编码取为244041993088,如果这个编码从左起的奇数位的数码不变,偶数位的数码改变为关于9的补码,例如:0变9,1变8等,那么“华杯赛”新的编码是 。
2.计算;=÷÷-+75.41]25239)21274.3(75.20[ 。
图13.如图书1所示,两个正方形ABCD 和DEFG 的边长都是整数厘米,点E 在线段CD 上,且CE<DE ,线段CF=5厘米,则五边形ABCFG 的面积等于 平方厘米。
4.将52.0523.0523.0....,,4021,250131 ,从小到大排列,第三个数是 。
5.图2a 是一个密封水瓶的切面图,上半部为圆锥状,下半部为圆柱关,底面直径都是10厘米,水瓶高度是26厘米,瓶中液面的高度为12厘米,将水瓶倒置后,如图2b ,瓶中液面的高度是16厘米,则水瓶的容积等于 立方厘米。
(取π=3.14,水瓶壁厚不计)6.一列数是按以下条件确定的:第一个是3,第二个是6,第三个是18,以后每个数是前面所有数的和的2倍,则第六个数等于 ,从这列数的第 个数开始,第个都大于2007。
7.一个自然数,它的最大的约数和次大的约数的和是111,这个自然数是 。
8.用一些棱长是1的小正方体码放成一个立体,从上向下看这个立体,如图3 ,从正面看这个立体,如图4,则这个立体的表面积最多是 。
二、简答下列各题(每题10分,共40分,要求写出简要过程) 9.如图5,在三角形ABC中,点D在BC上,且∠ABC=∠ACB,∠ADC=∠DAC,∠DAB=21°,求∠ABC的度数;并且回答:图中哪些三角形是锐角三角形。
图510.李云靠窗坐在一列时速60千米的火车里,看到一辆有30节车厢的货车迎面驶来,当货车车头经过窗口时,他开始记时,直到最后一节车厢驶过窗口时,所记的时间是18秒,已知货车车厢长15.8米,车厢间距1.2米,货车车头长10米,问货车行驶的速度是多少?11.图6是一个9×9的方格图,由粗线隔为9个横竖各有3个格子的“小九宫”格,其中,有一些小方格填有1至9的数字,小青在第4列的空格中各填入了一个1至9中的自然数,使每行、每列和每个“小九宫”格内的数字都要不重复,然后小青将第4列的数字从上向下写成一个9位数,请写出这个9位数,并且简单说明理由。
第十四届华罗庚金杯少年数学邀请赛决赛含详解(树人学校)
a
b
c 题图13
d
e
利用对称的性质,如图 2 和图 3 所示,蓝边等边三角形的面积是: 是 7 的等边三角形有 2×4×2=16 个; 利用对称性的性质,如图 4,黄色等边三角形的面积是 示,灰色难道正三角形的面积为
1 ×4×3+1=7,面积 2
1 ×24=12 的有 2 个。如图 5 所 2
1 ×6×3+4=13,面积为 13 的正三角形共有 4 个。 2
11.已知 a,b,c 是三个自然数,且 a 与 b 的最小公倍数是 60,a 与 c 的最小公 倍数是 270。求b与c的最小公倍数。 12.在 51 个连续的奇数 1,3,5,„,101 中选取 k 个数,使得他们的和为 1949, 那么 k 的最大值是多少?
三、 解答下列各题 (每小题 15 分, 共 30 分, 要求写出详细解答过程)
8.已知 1+2+3+„„+n(n﹥2)的和的个位数为 3,十位数为 0,则 n 的最小值 为__________。
二、解答下列各题(每题 10 分,共 40 分,要求写出简要过程)
1 1 1 1 1 1 9.六个分数 , , , , , 的和在哪两个连续自然数之间? 2 3 5 7 11 13
10.2009 年的元旦是星期四,问:在 2009 年,哪几个月的第一天也是星期四? 哪几个月有 5 个星期日?
a,b 一定是 2
2
的倍数,但是 a,2
的倍数,所以 b 是 2
2
的倍数,
同理可得 c 是 3 的倍数,所以 b, c 应被 2 2 .3 整除。
3
3
因为 a , b =60, a , c =270,所以 60 是 b 的倍数,270 是 c 的倍数,
第十六届全国“华罗庚金杯”少年数学邀请赛总决赛
第十六届全国“华罗庚金杯”少年数学邀请赛总决赛数学文化节方案一、指导思想第十六届全国“华罗庚金杯”少年数学邀请赛总决赛数学文化节旨在传承华罗庚精神,引导青少年热爱数学,立志成才。
让青少年在活动中感受数学与生活的自然融合,感受数学的奇巧和缜密。
在活动中提升思维、在挑战中享受快乐。
让数学不仅成为智者的游戏,更成就游戏者的智慧。
二、活动主题快乐与数学同行,智慧随思维生长三、活动目的以丰富多彩、趣味纷呈的数学活动为载体,让学生充分感受数学文化,品味数学魅力。
激发学生“爱数学,数学有无尽的乐趣;学数学,数学有无穷的奥妙;用数学,数学有无限的未来”的热情。
四、活动时间2011年7月24日上午9:00---11:30五、活动地点惠州市华罗庚中学六、活动内容及时间安排(一)华罗庚足迹1、参观华罗庚纪念馆负责人:龙静瑶2、华罗庚事迹循环播放负责人:易舒婷(二)数学文化展示1、分“数学之史、数学之美、数学之思、数学之用、数学之语”五个主题布置展板。
地点:华罗庚广场解说:数学社学生负责人:戴辉2、数学文化节优秀宣传语展、数学文化节优秀会标展、数学海报展。
负责人:张启龙实施:由数学社征集数学文化节宣传语和数学文化节会标,集训部、高一和高二开展数学海报比赛3、活动主题展板、活动内容展板、悬挂宣传条幅(每一个游戏场地一条标语)和彩旗。
负责人:刘卫忠4、数学PPT图片和学校简介(电脑播放)(高一阶梯教室)负责人: 熊伟(三)数学智慧活动数学智慧活动九项(专家讲座除外)若晴天则全部放在华罗庚广场举行,各摊位图附后:数学智慧活动九项(专家讲座除外)若雨天则活动地点如下:七、华杯赛数学文化节活动指南(见附件一)八、组织机构和保障措施(一)成立华杯赛数学文化节领导小组市教育局分管领导:骆平书记组长:戴立波副组长:吴永丹、宋词、黄进添、姜前勇、涂光峰成员:戴辉、杨永强、范恩辉、李京华、陈翰生、谢林海、张毅、丁志勇、刘卫忠、周淼淼、甄红、韩荣兰、张启龙、解凤英、陈冠宁、黄伟周、陈倬飞、黎润秋、刘宝林、陈宇祥、曾中华、向才兵、罗衾、何小华、袁劲竹、游兆龙、汪毅刚、吉世龙、钟跟、石丹慧、左静、谭卉、张丽君宣传接待:杨永强、陈翰生、周淼淼、凌丽聪保卫:杨永强、黄伟周及护校队成员音响:谢林海、张毅、熊伟、曾雨挺奖品:张启龙、吉世龙、熊伟、林惠琦(二)第十六届华杯赛数学文化节所需材料清单(见附件二)、所需奖品清单(见附件三)。
【小中组】第20届华杯赛决赛
第二十届华罗庚金杯少年数学邀请赛决赛(A )卷【小中组】1. 森林里举行比赛,要派出狮子、老虎、豹子和大象中的两个动物去参加,如果派狮子去,那么也要派老虎取;如果不派豹子去,那么也不能派老虎去;要是豹子参加的话,大象可不愿意去,那么,最后能去参加比赛的是( )A. 狮子、老虎B.老虎、豹子C.狮子、豹子D.老虎、大象2. 小明有多张面额为1元,2元和5元的人民币,他想用其中不多于10张的人民币购买一只价格为18元的风筝,要求至少用两种面额的人民币,那么不同的付款方式有( )种. A.3 B.9 C.11 D.83. 如右图,在有1×1的正方形组成的网格中,写有2015四个数字(阴影部分),其边线要么是水平,要么是竖直的直线段,要么是连接1×1正方形相邻两边中点的线段,或者是1×1的正方形的对角线,则图中2015四个数字(阴影部分)的面积是( ) A.47 B.2147C.48D.21484. 新生入校后,合唱队,田径队,舞蹈队共招收学员100人,如果合唱队招收的人数比田径队多一倍,舞蹈队比合唱队多10人,那么舞蹈队招收( )人.(注:每人限加入一个队) A.30 B.42 C.46 D.525.一只旧钟的时针和分针每重合一次,需要经过标准时间66分钟,那么这只旧钟的24小时比标准时间的24小时()A.快12分B.快6分C.慢6分D.慢12分6.一次考试共有6道选择题,评分规则如下:每人先给6分,答对一题加4分,答错一题减一分,不答得0分,现有51名同学参加考试,那么,至少有()人得分相同.A.3B.4C.5D.67.计算:_____(=⨯+314-151000+++.⨯)-+-+)110(15(314360)360201201110)1000(8.角可以用它的两边上的两个大写字母和顶点的字母表示,(如右图的AOB∠表示,∠,也可以用0顶点处只有一个角时),下面的三角形ABC中,οBCO∠ACO=∠AOCABOBAO,则_____CAO∠CBO,,==110∠,∠∠∠=∠CBO.=9.张叔叔和李叔叔的年龄和是56岁,当张叔叔的年龄是李叔叔现在年龄的一半时,李叔叔当时的年龄是张叔叔现在的年龄,那么张叔叔现在有______岁.10.妈妈决定假期带小花驾车去10个城市旅游,小花查完地图后惊奇地发现:10个城市的任意三个城市之间或者都开通了高速公路,或者只有两个城市间没有开通高速路,那么这10个城市间至少开通了______条高速公路.(注:两个城市间最多只有一条高速公路)第二十届华罗庚金杯少年数学邀请赛决赛(A )卷参考答案【小中组】1.解析:【知识点】逻辑推理假设派狮子去,那么老虎也去,那么豹子就不去,这样老虎也不能去,矛盾,A 排除; 假设派狮子去,那么老虎也去,C 排除; 不派豹子去,那么也不能派老虎去,D 排除; 故只能派老虎和豹子去,答案选B 2.解析:【知识点】计数,枚举 付款方式有以下几种:3×5+1×2+1×1=18,3×5+1×3=18,2×5+4×2=18,2×5+3×2+2×1=18,2×5+2×2+4×1=18, 2×5+1×2+6×1=18,2×5+8×1=18,1×5+6×2+1×1=18,1×5+5×2+3×1=18,1×5+4×2+5×1, 8×2+2×1=18;总共11种,答案选C 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四届华罗庚金杯少年数学邀请赛决赛
一、填空题:
1)计算:
2)如图1所示,在边长为1的小正方形组成的4×4方格图形中,共有25个格点,在以格点为顶点的直角三角形中,两条直角边长分别是1和3的直角三角形共有个。
3)将七位数1357924重复写287次组成一个2009位数“13579241357924……”。
删去
这个新数中所有位于奇数位(从左往右数)上的数字组成一个新数,再删去新数中所有
位于奇数位上的数字,按上述方法一直删下去直到剩下一个数字为止,则最后剩下的数
字是。
图1
4)如图2所示,在由七个小正方形组成的图形中,直线l将原图形分为面积相等的两部
分,l与AB的交点为E,与CD的交点为F,若线段CF与线段AE的长度之和为91厘米,
那么小正方形的边长是厘米。
5)某班学生要栽一批树苗,若每个人分k棵树苗,则剩下38棵;若每个学生分配9棵树苗,则还差3棵,那么这个班共有名学生。
6)已知三个合数A、B、C两两互质,且A×B×C=11011×28,那么A+B+C的最大值是。
7)方格中的图形符号“◇”,“○”,“▽”“☆”代表填入方格内的数,相同的符号表示相同的数。
如图所示。
若第一列,第三列,第二行,第四行的四个数的和分别为36,50,41,37。
则第三行的四个数的和是。
8)已知1+2+3+……+n(n>2)的和的个位数为3,十位数为0,则n的最小值
为。
二、解答下列各题(要求写出简要过程):
9)下列六个分数的和在哪两个连续自然数之间?
10)2009年的元旦是星期四。
问:在2009年,哪几个月的第一天也是星期四?哪几个月有5个星期日?
11)已知a,b,c是三个自然数,且a与b的最小公倍数是60,a与c的最小公倍数是270,求b与c的最小公倍数是多少?
12)在51个连续奇数1,3,5,……,101中选取k个数,使得他们的和为1949,那么k的最大值是多少?
三、解答下列各题(要求写出详细解答过程)
13)如图所示,在梯形ABCD中,AB∥CD,对角线AC,BC相交于O点,已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积。
14)如下算式,汉字代表1至9这9个数字,不同的汉字代表不同的数字。
若“祝”字和“贺”字分别代表数字“ 4”和“8”,求出“华杯赛”所代表的整数。
第十四届华罗庚金杯少年数学邀请赛决赛
一、填空题:
1)=2。
2)64个。
3)3。
4)a=26。
5)41。
6)A+B+C的最大值=2×2 + 7×7+ 11×11×13 7)33。
8)37。
二、解答下列各题(要求写出简要过程):
9) 1<1/2+1/3+1/51/7+1/11+1/13<2。
10)10月1日星期四;有五个星期日的是:3月、5月、8月、11月。
11)∴p/q=2/9。
60,[b,c] =108或360 。
12)3+5+7+……+83+85+101=1949。
三、解答下列各题(要求写出详细解答过程)
13)△AOB面积16/25 。
14)答案是:159×48=7632。
(注:素材和资料部分来自网络,供参考。
请预览后才下载,期待你的好评与关注!)。
