2011-2016年第16-22届华罗庚杯少年数学邀请赛几何试题(小学高年级组)全解析
第十六届“华杯赛”小学组决赛试题b答案

第十六届华罗庚金杯少年数学邀请赛决赛试题 B 参考答案(小学组)一、填空题 (每小题 10 分,共 80 分)题号 1 2 3 4 5 6 7 8答案27 4320 15 43 4 7100017120 3二、解答下列各题 (每题 10 分,共 40 分, 要求写出简要过程)9.答案: 416.解答. 连接FD的直线与AE的延长线相交于H.则△DFG绕点D逆时针旋转180o与△DHE重合,DF=DH.梯形 AEGF 的面积=△AFH的面积=2×△AFD的面积=长方形ABCD的面积 =416(平方厘米).10.答案:62.解答. 设一班有x人,二班有y人.则7(x-1) =13( y-1) ,所以,13 | (x-1) ,7 | ( y-1) . 于是x =13m +1,y =7m +1,其中 m 是自然数.因为250 ≤ 7(x-1) =13( y-1) ≤ 300 ,所以250 ≤ 91m≤ 300 ,解得m =3.最终得到x + y =13m +1+7m +1=62.11.答案: 1111, 1212, 2424, 3636, 1515.解答. 设n=abab=101ab.依题(3),有a2b2|n2,所以ab|n,即ab| 101ab.由于101是质数, (ab, 101) =1,故ab|ab,即ab | (10a+b) ,于是有a | b且b| 10a.讨论:I.当 b = a 时,a2| 11a⇒a| 11.∴a=b=1⇒n1=1111II.当 b =2a 时,2a2| 12a⇒a| 6⇒i. a =1, b =2⇒ n2=1212ii. a =2, b =4⇒ n3=2424iii. a =3, b =6⇒ n4=3636III.当 b =5a 时,5a2| 15a⇒a| 3.∴a=1,b=5⇒n5=1515.12.答案: 3344.解答. 每一个自然数n都可以表示成n=2r g,其中r≥0,g是奇数,是n的最大奇因子. 现在将自然数 1~100 如下分类.0类 ( r= 0 ): 1,3,5,…,99, 和为 1+3 +5 + +99 = 2500.1类 ( r=1 ): 2,6,10,…,98, 奇因子之和为1+3 +5 + + 49 = 625.2类 ( r=2 ): 4,12,20,…,100, 奇因子之和为1+3 +5 + + 25 =169.3类 ( r= 3 ): 8,24,40,…,88, 奇因子之和为1+3 +5 + +11 = 36 .4类 ( r=4 ): 16,48,80, 奇因子之和为1+3 + 5 = 9 .5 类 ( r= 5 ): 32,96, 奇因子之和为 1+3 = 4 .6 类 ( r= 6 ): 64, 奇因子为 1.因此,所有运动员在黑板上写下的数之和是 3344.三、解答下列各题 (每小题 15 分,共 30 分,要求写出详细过程)13.解答. 由题设知,水箱底面积 S 水箱=40×25=1000.水箱体积 V 水箱=1000×50=50000,铁块底面积 S 铁=10×10=100.铁块体积 V 铁=10×10×10=1000.(1)若放入铁块后,水箱中的水深恰好为 50 时,1000a+1000=50000, 得a=49.所以,当 49≤a≤50 时,水深为 50(多余的水溢出).(2)若放入铁块后,水箱中的水深恰好为 10 时,1000a+1000=10000, 得a=9.a×40×25+10×10×10所以,当 9≤a<49 时,水深为= a+1.(3)由(2)知,当 0<a<9 时,设水深为x,则101000x=1000a+100x.得x=9a.10答:当 0<a<9 时,水深为9a;当 9≤a<49 时,水深为a+1;当 49≤a≤50 时,水深为 50.14.答案: 100.解答.等式成立时有第十六届华罗庚金杯少年数学邀请赛决赛试题 B 参考答案(小学组)1793 = 2011-169 - 49 ≤华杯决赛≤ 2011-160 - 40 = 1811.进而得到, 华=1, 杯=7 或 8.(1)当杯=8 时, 共 72 种情况.10决+赛+日+月= 2011-1800-160 - 40 =11.①决=1 时, 赛, 月, 日中有一个为 1, 其它为 0, 共 3 种情况.②决=0 时, 赛+月+日=11,赛=0, 月+日=11 有 8 种情形;赛=1, 月+日=10 有 9 种情形;赛分别为 2,3,…9 时, 对应的情形为 10,9, …,3, 计 52 种情形(2)当杯=7 时, 共 28 种情况.10决+赛+日+月= 2011-1700-160 - 40 =111.不可能有决< 9 的情况, 否则需要, 赛+月+日要大于 30, 所以决=9. 此时赛+月+日=21,赛不能小于 3, 否则要求, 月+日大于 18.赛分别为 3,4,…9 时, 对应的情形为 1, 2, …, 7, 计 28 种情形综合上述讨论, 满足要求的不同算式共有 100 种.。
第十六届“华罗庚金杯”少年数学邀请赛总决赛试卷(小学组第2试)

2011年第十六届“华罗庚金杯”少年数学邀请赛总决赛试卷(小学组第2试)一、填空题(共3题,每题10分)1.(10分)某班共36人都买了铅笔,共买了50支,有人买了1支,有人买了2支,有人买了3支.如果买1支的人数是其余人数的2倍,则买2支铅笔的人数是.2.(10分)如图中,四边形ABCD的对角线AC与BD相交于O,E为BC的中点,三角形ABO的面积为45,三角形ADO的面积为18,三角形CDO的面积为69.则三角形AED的面积等于.3.(10分)一列数的前三个依次是1,7,8,以后每个都是它前面相邻三个数之和除以4所得的余数,则这列数中的前2011个数的和是.二、解答题(共3题,每题10分,写出解答过程)4.有57个边长等于1的小等边三角形拼成一个内角都不大于180的六边形,小等边三角形之间既无缝隙,也没有重叠部分.则这个六边形的周长至少是多少?5.(10分)黑板上写有1,2,3,…,2011一串数.如果每次都擦去最前面的16个数,并在这串数的最后再写上擦去的16个数的和,直至只剩下1个数,则:(1)最后剩下的这个数是多少?(2)所有在黑板上出现过的数的总和是多少?6.(10分)试确定积(21+1)(22+1)(23+1)…(22011+1)的末两位的数字.2011年第十六届“华罗庚金杯”少年数学邀请赛总决赛试卷(小学组第2试)参考答案与试题解析一、填空题(共3题,每题10分)1.(10分)某班共36人都买了铅笔,共买了50支,有人买了1支,有人买了2支,有人买了3支.如果买1支的人数是其余人数的2倍,则买2支铅笔的人数是10 .【分析】买1支的人数是其余人数的2倍,也就是说全班人数相当于其余人数的1+2=3倍,先根据除法意义,求出买2支和3支铅笔的人数,再设买2支铅笔的有x人,进而用x表示出买3支铅笔的人数,最后依据买笔总数=人数×买笔支数,用x表示出买笔总人数,根据铅笔总数是50支列方程,依据等式的性质即可求解.【解答】解:36÷(1+2)=36÷3=12(人);设买2支铅笔的人数是x人12×2×1+2x+(12﹣x)×3=5024+2x+36﹣3x=5060﹣x+x=50+x60﹣50=50+x﹣50x=10;答:买2支铅笔的人数是10.故答案为:10.2.(10分)如图中,四边形ABCD的对角线AC与BD相交于O,E为BC的中点,三角形ABO的面积为45,三角形ADO的面积为18,三角形CDO的面积为69.则三角形AED的面积等于75 .【分析】若将AD作为底边,因为点E为BC的中点,那么△ADB,△ADE,△ADC的高为等差数列(可以认为中间三角形的高是两边三角形的高的平均数),所以面积也呈等差数列(可以认为中间三角形的面积是两边三角形的面积的平均数).据此可解.【解答】解:若将AD作为底边,因为点E为BC的中点,所以△ADE的高为△ADB和△ADC的高的平均数,因此△ADE的面积就等于△ADB和△ADC的面积的平均数.所以,S△ADE=(S△ADB+S△ADC)÷2=(45+18+18+69)÷2=75;答:三角形AED的面积等于75.3.(10分)一列数的前三个依次是1,7,8,以后每个都是它前面相邻三个数之和除以4所得的余数,则这列数中的前2011个数的和是3028 .【分析】根据题意,列出这个数列是:1、7、8、0、3、3、2、0、1、3、0、0、3、3、2、0、1、3、0、0…易见,从第4个数开始每8个数一个循环.由于前面还有3个数,所以需用2011减去3的得数除以8,求出有多少组,再相加即可解答.【解答】解:这个数列:1、7、8、0、3、3、2、0、1、3、0、0、3、3、2、0、1、3、0、0…(2011﹣3)÷8=251(0+3+3+2+0+1+3+0)×251+1+7+8=12×251+16=3028故答案为:3028.二、解答题(共3题,每题10分,写出解答过程)4.有57个边长等于1的小等边三角形拼成一个内角都不大于180的六边形,小等边三角形之间既无缝隙,也没有重叠部分.则这个六边形的周长至少是多少?【分析】在面积不变的情况下,要使得这些等边三角形堆成的边长最短,则使它们堆城一个六边形,且六边形的每个内角都是120度.然后构建一个大三角形:把大三角形每条边n等分,连结各边n等分点一共构成n×n个小等边三角形解答即可.【解答】解:我们把一个等边三角形每条边2等分,可以连结各边中点一共构成2×2=4个小等边三角形;如果把每条边3等分,连结各边三等分点一共构成3×3=9个小等边三角形;以此类推,把每条边n等分,连结各边n等分点一共构成n×n个小等边三角形.7×7<57<8×8<9×9,8×8=64,64﹣57=7,7不能分解成为3个完全平方数之和的形式,9×9=81,81=4+4+16,所以我们就可以把这57个小三角形放在如图所示的等边三角形中,每条边被9等分,△ABC的边长为9,三个角各被切除一部分,此时DE=5,EF=2,FG=3,GH=4,HI=3,DI=2,则DE+EF+FG+GH+HI+DI=19,即这个六边形的周长至少是19.答:这个六边形的周长至少是19.故答案为:19.5.(10分)黑板上写有1,2,3,…,2011一串数.如果每次都擦去最前面的16个数,并在这串数的最后再写上擦去的16个数的和,直至只剩下1个数,则:(1)最后剩下的这个数是多少?(2)所有在黑板上出现过的数的总和是多少?【分析】(1)每操作一次,不影响黑板上所有数的总和,因此最后剩下的和=1+2+3+…+2011,根据高斯求和公式完成即可.(2)由于倒数第2次操作,黑板上就16个数,总和是2023066,这16个数来源于16×16=256个数,这256个数的和也同上.2011﹣(16﹣1)x=256,x=117次显然,从开始,只要117次操作,黑板上就剩256个数.据此依据规则分析即可.①原有2011个数,和2023066②操作117次,黑板剩余256个数:1873到2011,新出现117个和.这117个和=2023066﹣(1873+2011)*139/2=1753128③操作16次,黑板剩余16个数都是新出现,和=2023066④操作1次,黑板剩余1个数=2023066;综上,所有出现过的数=2023066+1753128+2023066+2023066=7822326 【解答】解:(1)1+2+3+…+2011=(1+2011)×2011÷2=2012×2011÷2=2023066答:最后剩下的这个数是2023066.(2)由于倒数第2次操作,黑板上就16个数,总和是2023066,这16个数来源于16×16=256个数,这256个数的和也同上.2011﹣(16﹣1)x=256,x=117次,显然,从开始,只要117次操作,黑板上就剩256个数.①原有2011个数,和2023066②操作117次,黑板剩余256个数:1873到2011,新出现117个和.这117个和=2023066﹣(1873+2011)×139÷2=1753128③操作16次,黑板剩余16个数都是新出现,和=2023066④操作1次,黑板剩余1个数=2023066综上,所有出现过的数=2023066+1753128+2023066+2023066=7822326.6.(10分)试确定积(21+1)(22+1)(23+1)…(22011+1)的末两位的数字.【分析】首先判断出积能被25整除,由于各因数均为奇数,则判断积的末两位数字为25或75,结合各因数被4整除的余数特点判断积的余数,进而判断出末两位数字为75.【解答】解:设n=(21+1)×(22+1)×(23+1)×…×(22011+1),由于各因数2k+1均为奇数,其中22+1=5,26+1=65=5×13,所以n≡0(mod25),此时知n的末两位数字要么为25,要么为75.又21+1≡3(mod4),对k≥2,都有2k+1≡1(mod4),所以n≡3(mod4),即n的末两位数字被4除余3,而25≡1(mod4),75≡3(mod4),所以n 的末两位数字为75.答:(21+1)(22+1)(23+1)…(22011+1)的末两位的数字75.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/7 10:51:42;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
第22届华杯赛小学中年级组初赛试题及答案解析

第22届华罗庚金杯少年数学邀请赛初赛试卷(小学中年级组)一、选择题(每小题10分,共60分。
以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内。
)1、两个小三角形不重叠放置可以拼成一个大三角形,那么这个大三角形不可能由()拼成。
A、两个锐角三角形B、两个直角三角形C、两个钝角三角形D、一个锐角三角形和一个钝角三角形2、从1至10这10个整数中,至少取()个数,才能保证其中有两个数的和等于10。
A、4B、5C、6D、73、小明行李箱锁的密码是由两个数字8与5构成的三位数。
某次旅行,小明忘记了密码,他最少要试()次,才能确保打开箱子。
A、9B、8C、7D、64、猎豹跑一步长为2米,狐狸跑一步长为1米,猎豹跑2步的时间狐狸跑3步,猎豹距离狐狸30米,则猎豹跑()米可追上狐狸。
A、90B、105C、120D、1355、图1中的八边形是将大长方形纸片剪去一个小长方形得到的,则至少需要知道()条线段的长度,才可以算出这个八边形的周长。
A、4B、3C、5D、106、一个数串219……,从第4个数字开始,每个数字都是前面3个数字和的个位数字,下面有4个四位数:1113,2226,2125,2215。
其中共有()个不出现在该数串中。
A、1B、2C、3D、4二、填空题(每小题10分,满分40分)7、计算:1000—257—84—43—16=。
8、已知动车的时速是普快的两倍,动车的时速提高25%即达到高铁的时速。
高铁与普快的平均时速比特快快15千米/小时,动车与普快的平均时速比特快慢10千米/小时,则高铁和普快的时速分别是千米小/时和千米//小时。
9、《火星救援》中,马克不幸没有跟上其他5名航天员飞回地球,独自留在了火星,马克必须想办法生存,等待求援。
马克的居住舱内留有每名航天员5天的食品和50千克的非饮用水,还有一个足够大的菜园,马克计划用来种植土豆,30天后每平方米可以收获2.5千克,但是需要灌溉4千克的水。
华罗庚金杯少年数学邀请赛(小学数学奥数)竞赛试题

华罗庚金杯少年数学邀请赛(小学数学奥数)决赛试题一、填空题(每小题10 分, 共80 分)1.计算: (2014⨯2014 +2012) -2013⨯2013 = ________.2.将长方形的纸片ABCD 按右图的方式折叠后压平, 使三角形DCF 落在三角形DEF 的位置, 顶点E 恰落在边AB 上. 已知∠1=22°, 那么∠2 是________度.3.亮亮上学, 若每分钟行40 米, 则8 : 00 准时到校; 若每分钟行50 米, 则7 : 55到校. 亮亮的家与学校的距离是________米.4.第一次操作将图a 左下角的正方形分为四个小正方形, 见图b, 第二次操作再将图b 左下角的小正方形分为四个更小的正方形, 见图c. 这样继续下去, 当完成第五次操作时, 得到的图形上共有________个正方形.5.“熊大”⨯“熊二”=“熊兄弟”. 若相同的汉字代表0 至9 中的相同数字, 不同的汉字代表不同的数字, 且“大”>“二”, 则所有满足条件的“熊兄弟”代表的三位数之和是________.6.鸡兔同笼, 共有40 个头, 兔脚的数目比鸡脚的数目的10 倍少8 只, 那么兔有________只.7.如图所示的手串中, 从挂坠的珠子开始逆时针将珠子1 至22 依次编号. 小明玩数珠子游戏, 规则是: 从1 号珠子开始顺时针逐个珠子连续地数自然数, 但每当数到含数字7 或7 的倍数的数时就跳过它, 直接数下一个数. 例如: 数到6 时下一个数8, 数到13 时下一个数15, ……. 那么数到100 时应落在第________号珠子上.8.布袋中有60 个彩球, 每种颜色的球都有 6 个. 蒙眼取球, 要保证取出的球中有三个同色的球, 至少要取出________个球.二、简答题(每小题15 分, 共60 分, 要求写出简要过程)9.一块长方形的地ABCD 分成如图所示的两个长方形, 分别承包给甲、乙两户.甲户的蔬菜大棚与乙户的鸡场面积相等, 剩下的部分甲户比乙户的面积多96 亩. 已知BF=3CF, 那么长方形ABCD 的总面积是多少亩?10.右图是U, V, W, X 四辆不同类型的汽车每百千米的耗油量. 如果每辆车都有50升油, 那么这四辆车最多可行驶的路程总计是多少千米?11.甲、乙、丙、丁四人分2013 块糖果, 甲分得的糖果比乙的2 倍多10 块, 比丙的3 倍多18 块, 比丁的 5 倍少55 块. 那么甲分得糖果多少块?12.编号从1 到10 的10 个白球排成一行, 现按照如下方法涂红色: 1)涂2 个球; 2)被涂色的 2 个球的编号之差大于2. 不同的涂色方法有多少种?。
第二十二届“华杯赛”决赛小高组试题A详细解答

第二十二届华罗庚金杯少年数学邀请赛决赛试题A(小学高年级组)详细解答【解】:∵201711=183+411∴[201711×3] = [183×3+411×3]= 183×3+1类似地,可知:[201711×4]= 183×4+1;[201711×5]= 183×5+1[201711×6]= 183×6+2;[201711×7]= 183×7+2;[201711×8]= 183×8+2∴原式= 183×[3+4+5+6+7+8]+1+1+1+2+2+2=6048【答】:所求值为6048。
【解】:假设原来四个整数分别为a,b,c,d,则按照题意所求的四个数的表达式分别为:a+b+c3+d,a+b+d3+ca+c+d3+b,b+c+d3+a∵a+b+c3+d+a+b+d3+c+a+c+d3+b+b+c+d3+a=3(a+b+c+d)3+(a+b+c+d)=2(a+b+c+d)∴a+b+c+d=12×(8+12+1023+913)=12×(20+20) =20【答】:原来给定的4个整数的和为20。
【解】:分三种情形,共有10种不同摆法,如下图:(1)两个点都在第一行;(2)两个点不在同一行但相邻;(3)两个点不在同一行且不相邻;【答】:共有10种不同的摆放方法。
【解】:设甲的速度为V甲,乙的速度为V乙,AB两地距离为SAB,BC两地距离为SBC 根据题意可知:V甲=80÷2=40 (千米/小时) ,甲原来的速度的2倍为80(千米/小时) 所以,BC两地距离:SBC=2×80=160 (千米)又,乙从B地到C地花了2.5小时,所以,乙的速度为:V乙=SBC÷2.5=160÷2.5=64(千米/小时)【答】:乙的速度为64 千米/小时。
2016年第22届“华杯赛”初赛小高组试卷

第二十二届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组)第二十二届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组)(时间: 2016年12月10日10:00—11:00)一、选择题 (每小题10分, 共60分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内.)1. 两个有限小数的整数部分分别是7和10,那么这两个有限小数的积的整数部分有( )种可能的取值.(A )16 (B )17 (C )18 (D )192. 小明家距学校,乘地铁需要30分钟,乘公交车需要50分钟.某天小明因故先乘地铁,再换乘公交车,用了40分钟到达学校,其中换乘过程用了6分钟,那么这天小明乘坐公交车用了( )分钟.(A )6 (B )8 (C )10 (D )123. 将长方形ABCD 对角线平均分成12段,连接成右图,长方形ABCD 内部空白部分面积总和是10平方厘米,那么阴影部分面积总和是( )平方厘米.(A )14 (B )16 (C )18 (D )204. 请在图中的每个方框中填入适当的数字,使得乘法竖式成立.那么乘积是( ).(A )2986 (B )2858 (C )2672 (D )2754CDB A第二十二届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组)5. 在序列20170……中,从第5个数字开始,每个数字都是前面4个数字和的个位数,这样的序列可以一直写下去.那么从第5个数字开始,该序列中一定不会出现的数组是( ).(A )8615 (B )2016 (C )4023 (D )20176. 从0至9中选择四个不同的数字分别填入方框中的四个括号中,共有( )种填法使得方框中话是正确的.(A )1 (B )2 (C )3 (D )4二、填空题(每小题 10 分,共40分)7. 若1532 2.254553923741A ⎛⎫-⨯÷+= ⎪ ⎪ ⎪+ ⎪⎝⎭,那么A 的值是________. 8. 右图中,“华罗庚金杯”五个汉字分别代表1—5这五个不同的数字.将各线段两端点的数字相加得到五个和,共有________种情况使得这五个和恰为五个连续自然数.9. 右图中,ABCD 是平行四边形,E 为CD 的中点,AE 和BD 的交点为F ,AC 和BE 的交点为H ,AC 和BD 的交点为G ,四边形EHGF 的面积是15平方厘米,则ABCD 的面积是__________平方厘米.10. 若2017,1029与725除以d 的余数均为r ,那么d r -的最大值是________. 华庚 金 杯。
第十六届“华杯赛”小学组决赛试题A答案
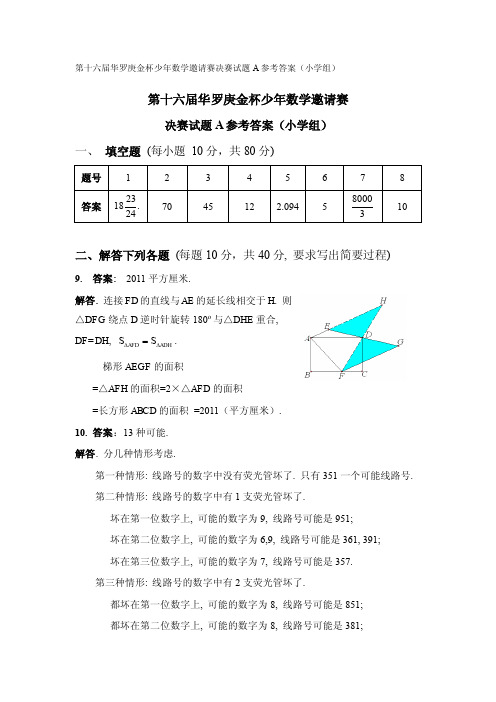
第十六届华罗庚金杯少年数学邀请赛决赛试题A 参考答案(小学组)一、 填空题 (每小题 10分,共80分)二、解答下列各题 (每题10分,共40分, 要求写出简要过程)9. 答案: 2011平方厘米.解答. 连接FD 的直线与AE 的延长线相交于H . 则△DFG 绕点D 逆时针旋转180o 与△DHE 重合,DF=DH , ADH AFD S S ∆∆=.梯形AEGF 的面积=△AFH 的面积=2×△AFD 的面积=长方形ABCD 的面积 =2011(平方厘米).10. 答案:13种可能.解答. 分几种情形考虑.第一种情形: 线路号的数字中没有荧光管坏了. 只有351一个可能线路号. 第二种情形: 线路号的数字中有1支荧光管坏了.坏在第一位数字上, 可能的数字为9, 线路号可能是951;坏在第二位数字上, 可能的数字为6,9, 线路号可能是361, 391;坏在第三位数字上, 可能的数字为7, 线路号可能是357.第三种情形: 线路号的数字中有2支荧光管坏了.都坏在第一位数字上, 可能的数字为8, 线路号可能是851;都坏在第二位数字上, 可能的数字为8, 线路号可能是381;都坏在第三位数字上, 可能的数字为4, 线路号可能是354;坏在第一、二位数字上, 第一位数字可能的数字为9,第二位数字可能的数字为6,9, 线路号可能是961, 991;坏在第一、三位数字上, 第一位数字可能的数字为9,第三位数字可能的数字为7, 线路号可能是957;坏在第二、三位数字上,第二位数字可能的数字为6,9, 第三位数字可能的数字为7,线路号可能是367, 397.所以可能的线路号有13个:351,354,357,361,367,381,391,397,851,951,957,961,991.11. 答案: 3, 5.解答. 设这个月的第一个星期日是a 日(71≤≤a ), 则这个月内星期日的日期是a k +7, k 是自然数, 317≤+a k . 要求有三个奇数.当a =1时, 要使7k +1是奇数, k 为偶数, 即k 可取0, 2, 4三个值, 此时,177+=+k a k 分别为1, 15, 29, 这时20号是星期五.当a =2时, 要使7k +2是奇数, k 为奇数, 即k 可取1, 3两个值, 7k +2不可能有三个奇数.当a =3时, 要使7k +3是奇数, k 为偶数, 即k 可取0, 2, 4三个值, 此时377+=+k a k 分别为3, 17, 31, 这时20号是星期三.当74≤≤a 时, a k +7不可能有三个奇数.12. 答案: 253.解:令k m 15=, k 是自然数, 首先考虑满足下式的最大的m ,.201115151153152151≤⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡m m 于是.2011213152)1(1515)1(152151150151511531521512≤-=+-=+⨯-++⨯+⨯+⨯=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡k k k k k kk m m 因此.402213152≤-k k 又40224114171317152>=⨯-⨯, 40223632161316152<=⨯-⨯,得知k 最大可以取16. 当16=k 时, m =240. 注意到这时312161952363220112131520112+⨯==-=--k k . 注意到20112024131618161513151615121516152151615115161515161511516152151>=⨯+=⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡+⨯++⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡⨯+⎥⎦⎤⎢⎣⎡-⨯++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡ 而201120081216181615121516153152151<=⨯+=⎥⎦⎤⎢⎣⎡+⨯++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡ .所以253 是满足题目要求的n的最小值.三、解答下列各题(每小题15分,共30分,要求写出详细过程)13.答案: 312解答. 由于2+0+1+1=4 且0+1+2+3+4+6+7+8+9=40, 4≡40(mod 9), 所以, 九个不同的汉字代表的数字:0, 1, 2, 3, 4, 6, 7, 8, 9.易知:40-4=36, 36÷9=4(次), 说明此算式共发生四次进位.“4=2+2=1+1+2=1+2+1”显然:①华=1, “4=2+2”无解②华=1, “4=1+1+2”有解A:28+937+1046=2011, 可组成算式36种(6×6×1=36)B:69+738+1204=2011, 可组成算式48种(6×4×2=48)C:79+628+1304=2011, 可组成算式48种(6×4×2=48)③华=1, “4=1+2+1”有解A:46+872+1093=2011, 可组成算式36种(6×6×1=36)B:98+673+1240=2011, 可组成算式72种(6×6×2=72)C:97+684+1230=2011, 可组成算式72种(6×6×2=72)总计:72×3+96=216+96=312(种).14.解答. 如左下图, 设M, N, P分别为棱GC, GF, GH的中点, 'M, 'N, 'P 分别为棱AE, AD, AB的中点, O为正方体的中心(长方形BDHF的中心).(1)第一只蜘蛛甲可以把爬虫控制在右上图所示的范围内.首先蜘蛛甲做与爬虫关于点O的对称方向的移动, 不妨设爬虫由G沿棱GC 向点M移动, 蜘蛛甲由A沿棱AE向点'M移动, 爬虫被限制在GM上. 当爬虫到达点M时, 蜘蛛甲也同时到达点'M. 然后蜘蛛甲改变策略, 做与爬虫关于平面BDHF对称的方向移动.a) 当爬虫到达点B, D, F, H时, 蜘蛛甲捉住爬虫.b) 当爬虫未到达点B, D, F, H时, 爬虫被控制在左上图所示的范围内.(2) 蜘蛛乙先移动到点G, 由于右上图无环路, 蜘蛛乙可以跟在爬虫后面, 总可以捉住爬虫.。
2016第二十二届华罗庚金杯少年数学邀请赛初赛试题解析(小学中年级)

2016第二十二届华罗庚金杯少年数学邀请赛初赛试题解析(小学中年级)第二十二届华罗庚金杯少年数学邀请赛初赛试卷(小学中年级组)(时间:2016年12月10日10:00-11:00)一、选择题(每小题10分,共60分,以下每题的四个选项,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内)1、两个小三角形不重叠放置可以拼成一个大三角形,那么这个大三角形不可能由()拼成。
(A)两个锐角三角形(B)两个直角三角形(C)两个钝角三角形(D)一个锐角三角形和一个钝角三角形解析:此题主要考察学生图片组合分析能力由图显然可知,锐角、直角、钝角这三种角,只有锐角与锐角,锐角与直角不能不重叠组合,其余4种均能组合,则(B)、(C)、(D)均有可能组成一个大三角形,故选(A)2、从1至10这10个整数中,至少取()个数,才能保证其中有两个数的和等于10。
(A)4 (B)5 (C)6 (D)7解析:此题属于抽屉原理。
分析如下:10 =1+9=2+8=3+7=4+6即1至10这10个数字中能保证两个数字之和为10的可能情况只有以上4种,那么当取1,2,3,4,5,10时任意两数之和都不等于10,再取5,6,7,8这4个数中的1个数时,就有以上4种等式成立。
则至少要取6+1=7。
故选(D)3、小明行李箱锁的密码是由两个数字8与5构成的三位数。
某次旅行,小明忘记了密码,他最少要试()次,才能确保打开箱子。
(A)9 (B)8 (C)7 (D)6解析:此题考察学生的数字组合能力。
分析如下:(1)当三位数为2个8和1个5时:885,858,588;即有3种可能情况。
(2)当三位数为1个8和2个5时:855,585,558;即有3种可能情况。
综上分析,行李箱密码的可能性总和:3+3=6(种),即要确保打开箱子,至少要试6次。
故选(D)4、猎豹跑一步长为2米,狐狸跑一步长为1米。
猎豹跑2步的时间狐狸跑3步。
猎豹距离狐狸30米,则猎豹跑动()米可追上狐狸。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
序4:基本几何模型
燕尾模 型
蝴蝶模 型
沙漏模 型
金字塔 模型
鸟头模 型
一半模 型
几何 模型
等积变 形模型
华罗庚杯少年数学邀请赛 历年几何典型题库
鸟头
等积 変换
燕尾
几何 蝴蝶
漏斗
一半
比例
金字塔
2011年第16届华罗庚金杯少年数学邀请赛决赛试题D 如图所示,AB∥CE,AC ∥ DE,且AB=AC=5,CE=DE=10。若三角形COD的 面积为10,求四边形ABDE的面积。
一个长40、宽25、高60的无盖长方体容器(厚度忽略不计)盛有水,深度为a,其中0 ˂a ≤60,现将棱长尾10的长方体铁块放在容器底面,问放入铁块后水深是()。
1
2
3
分析:无盖长方体容器盛有水情况有三种: 1、水很满;放入铁块后,水溢出; 2、水深很浅,放入铁块后,铁块一部分在水中,另一部分露出水面,水面也有升高。 3、水很深,则放入铁块后,铁块全部沉入水中,水面升高;
2011年第16届华罗庚杯少年数学邀请赛决赛B几何试题 如右图,两条线段将边长为10的正方形分为两个高度相等的直角梯形S1、S2和一个直角 三角形,其中两个梯形的面积差为10,则直角三角形图示的边长是()。
A
E
D
S1
S2
x
B
F
C
如右图,两条线段将边长为10的正方形分为两个高度相等的直角梯形S1、S2和一个直角 三角形,其中两个梯形的面积差为10,则直角三角形图示的边长x是()。
(10×10×h)]÷(40×25) ,经简化计算,得h=������������a。
������
3、水很深,则放入铁块后,铁块全部沉入水中,水面升高。 放入铁块后水全部漫完铁块时,即当容器水深大于9小于59时,放入铁块后水深是 h=[(40×25×a)+(10×10×10)]÷(40×25) =a+1。
E
A O
BC
D
如图所示,AB∥CE,AC ∥ DE,且AB=AC=5,CE=DE=10。若三 角形COD的面积为10,求四边形ABDE的面积。
E
A
2a
a O4a
2a
BC
D
解:由AC∥DE,AC:DE=1:2 根据蝴蝶模型,在梯形ACDE中: S△COD=������������ 5=������ 由OC∥AB,OA:OD=BC:CD=1:2 根据鸟头模型,在三角形ABD中, S△ACD: S△ABC =������������ • ������������: ������������ • ������������ = 1:2 S△ABC =������. ������������ S△ABDE=10.5a=52.5
2011年第16届华罗庚杯少年数学邀请赛决赛B几何试题 已知某个几何体的三视图,如右图,根据图中标示的尺寸,求几何体的体积是()。
5 10
5
10
10
10
已知某个几何体的三视图,如右图,根据图中标示的尺寸,求几何体的体积是()。
5 10
5
10
10
10
10
解:由三视图可知该几何体为四棱锥;四棱锥底面为边长为10的正方形,棱锥的高为10; 所以四棱锥的体积为:底面积×高÷3=10×10×10÷3=1000/3
解2:根据一半模型:
E
三角形ADF是梯形AEGF的一半
A
D
三角形ADF是长方形ABCD的一半
长方形ABCD的面积等于梯形AFGE的面积,
G 则梯形AFGE的的面积是70。
B
F
C
2011年第16届华罗庚杯少年数学邀请赛决赛C几何试题 一个长40、宽25、高60的无盖长方体容器(厚度忽略不计)盛有水,深度为a,其中0 ˂a ≤60,现将棱长尾10的长方体铁块放在容器底面,问放入铁块后水深是()。
A B
E O C
解:梯形ACDE中,AC:DE=1:2,
根据梯形蝴蝶模型
S△AOC: S△AOE: S△COD: S△DOE=1:2:2:4
S△AOC=5
S△AOE= S△COD=10
S△DOE=20
S□ACDE= ������������
梯形ABCE中,根据等积变换模型,
S △ ABC: S △ ACE=1:2
E A
B
F
解1:连接DF,
利用蝴蝶模型,在梯形AFGE中, D
S△ADF= ������ S□ AFGE
������
G 利用蝴蝶模型,在长方形ABCD�
S□
ABCD
C
故: S□ AFGE= S□ ABCD=70
长方形ABCD的面积为70,梯形AFGE的顶点F在BC上,D是EG的中点,则梯形AFGE的 的面积是()。
解: 1、水很满;放入铁块后,水溢出; 放入铁块后水刚要溢出时,容器水深a=[(40×25×60)-(10×10×10)]÷(40×25) =59 当容器水深大于59时,放入铁块后水深是60。 2、水深很浅,放入铁块后,铁块一部分在水中,另一部分露出水面,水面也有升高; 放入铁块后水刚要全部漫完铁块时,容器水深a=[(40×25×10)-(10×10×10)]÷(40×25) =9 所以,当容器水深大于0小于9时,放入铁块后水深是h=[(40×25×a)+
D
S △ ABC=7.5
S□ABCD=S △ ABC+S□ACDE=7.5+45=52.5
2011年第16届华罗庚杯少年数学邀请赛决赛C几何试题 长方形ABCD的面积为70,梯形AFGE的顶点F在BC上,D是EG的中点,则梯形AFGE的 的面积是()。
E
A
D
G
B
F
C
长方形ABCD的面积为70,梯形AFGE的顶点F在BC上,D是EG的中点,则梯形AFGE的 的面积是()。
2011年第16届华罗庚杯少年数学邀请赛决赛D几何试题 AB∥CE, AC∥DE,且AB=AC=5,CE=DE=10,若三角形COD的面积为10,四边形 ABDE的面积是()。
E
A O
D
B
C
AB∥CE, AC∥DE,且AB=AC=5,CE=DE=10,若三角形COD的面积为10,四边形
ABDE的面积是()。
华罗庚杯少年数学邀请赛
2011-2016年 第16-22届几何试题(小学高年级组)
目录
基本几 基本几 何单位 何图形
基本几 何关系
基本几何模型
华罗庚杯少年数学邀请赛 历年题库
序1:基本几何单位
长度
几何
体积
单位
周长
面积
序2:基本几何图形
几何图形
三四多正圆 线角边边方柱
形形形体体
序3:基本几何关系
