全等三角形基础题
全等三角形经典题型50题(含答案)

全等三角形证明经典50 题(含答案)1. 已知: AB=4, AC=2, D 是 BC 中点, AD 是整数,求ADAB CD延伸 AD 到 E,使 DE=AD,则三角形ADC全等于三角形EBD即 BE=AC=2 在三角形 ABE 中 ,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又 AD 是整数 ,则 AD=512. 已知: D 是 AB 中点,∠ ACB=90°,求证:CD AB2ADC B3.已知: BC=DE,∠ B=∠ E,∠ C=∠ D, F 是 CD中点,求证:∠ 1=∠ 2A21B EC F D证明:连结 BF 和 EF。
由于 BC=ED,CF=DF,∠ BCF=∠ EDF。
因此三角形 BCF 全等于三角形 EDF(边角边 )。
因此 BF=EF,∠ CBF=∠ DEF。
连结 BE。
在三角形BEF 中 ,BF=EF。
因此∠ EBF=∠ BEF。
又由于∠ ABC=∠AED。
因此∠ABE=∠AEB。
因此 AB=AE。
在三角形 ABF 和三角形 AEF中, AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠ AEB+∠ BEF=∠ AEF。
因此三角形 ABF 和三角形 AEF全等。
因此∠ BAF=∠ EAF (∠ 1=∠ 2)。
A4. 已知:∠ 1=∠ 2, CD=DE, EF//AB,求证: EF=AC 1 2证明:过 E 点,作 EG//AC,交 AD 延伸线于 G 则∠ DEG=∠ DCA,F ∠DGE=∠ 2又∵CD=DE∴ ⊿ADC≌ ⊿ GDE(AAS)∴EG=AC∵ EF//AB∴∠ DFE=∠ 1∵ ∠ 1=∠ 2∴ ∠ DFE=∠ DGE∴ EF=C EG∴ EF=AC DEB5.已知:AD均分∠ BAC,AC=AB+BD,求证:∠B=2∠C ACB D证明:在 AC上截取AD=AD∴ ⊿ AED≌ ⊿ ABD AE=AB,连结(SASED∵ AD)均分∠ BAC∴ ∠∴ ∠ AED=∠ BEAD=∠ BAD 又∵ AE=AB,,DE=DB∵ AC=AB+BDAC=AE+CE∴ CE=DE∴ ∠ C=∠ EDC∵∠ AED=∠ C+∠ EDC=2∠ C∴∠ B=2∠C6. 已知: AC 均分∠ BAD,CE⊥ AB,∠ B+∠ D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连结 CF 由于 CE⊥AB 因此∠CEB=∠ CEF= 90 °由于 EB= EF, CE= CE,所以△CEB≌△CEF 所以∠B =∠ CFE 由于∠ B+∠ D= 180 ,°∠CFE+∠ CFA= 180°因此∠ D=∠ CFA 由于AC 均分∠ BAD 因此∠ DAC=∠ FAC 又由于AC= AC因此△ ADC≌ △ AFC( SAS)因此 AD= AF 因此 AE= AF+ FE= AD+ BE12.如图,四边形 ABCD 中, AB∥ DC, BE、 CE 分别均分∠ ABC、∠ BCD,且点 E 在 AD 上。
北师七年级下册数学全等三角形的基础、判定、经典、精选拔高证明题

七年级下册数学全等三角形的基础,判定,经典,精选证明题(一)全等三角形的基础1、已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF.2、如图,已知: AD是BC上的中线 ,且DF=DE.求证:BE∥CF.3、如图, 已知:AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF.求证:AC=EF.4、如图,在ΔABC中,AC=AB,AD是BC边上的中线。
求证:AD⊥BC,5、如图,已知AB=DE,BC=EF,AF=DC。
求证:∠EFD=∠BCA 6、如图,ΔABC的两条高AD、BE相交于H,且AD=BD,试说明下列结论成立的理由。
(1)∠DBH=∠DAC;(2)ΔBDH≌ΔADC。
7、已知等边三角形ABC中,BD=CE,AD与BE相交于点P,求∠APE的大小。
8、如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.9、在△ABC中,,AB=AC, 在AB边上取点D,在AC延长线上了取点E ,使CE=BD , 连接DE交BC于点F,求证DF=EF .(二) 全等三角形的判定1.已知∠BAC=∠DAE,∠1=∠2,BD=CE,问ABD≌⊿ACE.吗?为什么?ADEBC122.已知CD∥AB,DF∥EB,DF=EB,问AF=CE吗?说明理由。
ADCEFB3.已知BE=CF,AB=CD,∠B=∠C.问AF=DE吗?ACDBEF4.已知AD=CB,∠A=∠C,AE=CF,问EB∥DF吗?说明理由。
BADFEC5.已知,M是AB的中点,∠1=∠2,MC=MD,问∠C=∠D吗?说明理由。
MABCD126.已知,AE=DF,BF=CE,AE∥DF,问AB=CD吗?说明理由。
DCFEAB7.已知∠1=∠2,∠3=∠4,问AC=AD吗?说明理由。
ACDB12348.已知∠E=∠F,∠1=∠2,AB=CD,问AE=DF吗?说明理由。
全等三角形基础题

全等三角形基础题1、如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:△ABD ≌△ACD 。
2、如图(2):AC ∥EF ,AC=EF ,AE=BD 。
求证:△ABC ≌△EDF 。
3、 如图(4):AB=AC ,AD=AE ,AB ⊥AC ,AD ⊥AE 。
求证:(1)∠B=∠C ,(2)BD=CE4.如图(8):A 、B 、C 、D 四点在同一直线上,AC=DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
5、如图(10)∠BAC=∠DAE ,∠ABD=∠ACE ,BD=CE 。
求证:AB=AC 。
(图1)D C B A F (图2)D C B A E(图4)D C B A FE(图8)D C B A E(图10)D CB A6、如图(11)在△ABC 和△DBC 中,∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA=PD 。
7.如图:在△ABC 中,AD ⊥BC 于D ,AD=BD ,CD=DE ,E 是AD 上一点,连结BE 并延长交AC 于点F 。
求证:(1)BE=AC ,(2)BF ⊥AC 。
8、如图:在△ABC 中,∠ACB=90°,AC=BC ,D 是AB 上一点,AE ⊥GD 于E ,BF ⊥CD 交CD的延长线于F 。
求证:AE=EF+BF 。
9、如图:AB=DC ,BE=DF ,AF=DE 。
求证:△ABE ≌△DCF 。
10.如图:CD ⊥AB 于D ,BE ⊥AC 于E ,OD=OE 。
求证:AB=AC 。
11.如图:AB=AC ,EB=EC ,AE 的延长线交BC 于D 。
求证:BD=DC 。
P 4321(图11)D B A F (图17)ED C B AF(图18)E D C B A F(图19)ED C B A O (图25)E D C BA12.如图:△ABC 和△DBC 的顶点A 和D 在BC 的同旁,AB=DC ,AC=DB ,AC 和DB 相交于O 。
全等三角形经典题型50题(含答案)
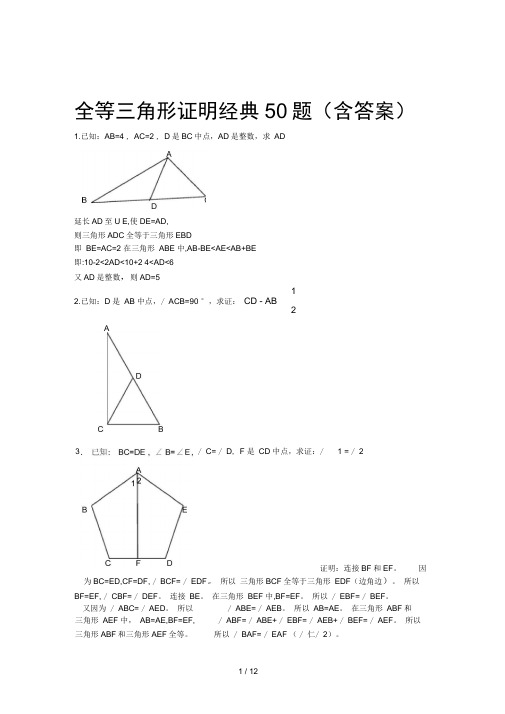
全等三角形证明经典50题(含答案)1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=512.已知:D 是 AB 中点,/ ACB=90 °,求证: CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。
所以 三角形BCF 全等于三角形 EDF (边角边)。
所以BF=EF, / CBF= / DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 / EBF= / BEF 。
/ ABE= / AEB 。
所以 AB=AE 。
在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。
所以/ C= / D , F 是 CD 中点,求证:/ 1 = / 2证明:连接BF 和EF 。
因又因为 / ABC= / AED 。
所以 三角形 AEF 中, AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF ( / 仁/ 2)。
A3因为 EB = EF ,CE = CE , 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图,四边形 ABCD 中,AB // DC ,BE 、CE 分别平分/ ABC 、/ BCD ,且点 E 在AD 上。
全等三角形的练习题(100题)

1、如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC.2、如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.(1)求证:△ABE≌DCE;(2)当∠AEB=50°,求∠EBC的度数?3、如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF4、如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.5、如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l 于点C,BD⊥l交l于点D.求证:AC=OD.6、如图,已知AD是△ABC的中线,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.7、如图,已知点B、E、C、F在同一条直线上,BE=CF,AB∥DE,∠A=∠D.求证:AB=DE.8、如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB9、如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C作CF∥AB交DE延长线于点F.求证:AD=CF10、如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.(1)求证:CF=DG;(2)求出∠FHG的度数.11、如图,C是AB的中点,AD=BE,CD=CE.求证:∠A=∠B.12、已知:如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.13、已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.14、如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.(1)求证:△ADE≌△BFE;(2)连接EG,判断EG与DF的位置关系并说明理由.15、在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:;结论:。
全等三角形基础练习题及答案

全等三角形基础练习题及答案一、选择题1. △ABC和△A.△ABC≌△C. △ABC≌△2. 如图,已知AB=CD,AD=BC,则下列结论中错误的是A.AB∥DCB.∠B=∠DC.∠A=∠CD.AB=BC 中,若AB=,BC=,AC= .则B. △ABC≌△ D. △ABC≌△3. 下列判断正确的是A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4. 如图,AB、CD、EF相交于O,且被O点平分,DF =CE,BF=AE,则图中全等三角形的对数共有A. 1对B.对C.对D.对5. 如图,将两根钢条,的中点O连在一起,使,可以绕着点O自由的转动,就做成了一个测量工件,则理由是的长等于内槽宽AB,那么判定△OAB≌△A.边角边B.角边角C.边边边D.角角边6. 如图,已知AB⊥BD于B,ED⊥BD于D,AB=CD,BC=ED,以下结论不正确的是A.EC⊥ACB.EC=ACC.ED +AB =DBD.DC =CB二、填空题7. 如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=_________.8. 如图,在四边形ABCD中,对角线AC、BD互相平分,则图中全等三角形共有_____对.9. 如图,在△ABC和△EFD中,AD=FC,AB=FE,当添加条件_______时,就可得△ABC≌△EFD10. 如图,AC=AD,CB=DB,∠2=30°,∠3=26°,则∠CBE=_______.11. 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B =20°,则∠C=______. 12. 已知,如图,AB=CD,AC=BD,则△ABC≌______,△ADC≌ ______.三、解答题13. 已知:如图,四边形ABCD中,对角线AC、BD相交于O,∠ADC=∠BCD,AD=BC,求证:CO=DO.14. 已知:如图,AB∥CD,AB=CD.求证:AD∥BC.分析:要证AD∥BC,只要证∠______=∠______,又需证______≌______.证明:∵ AB∥CD ,∴ ∠______=∠______ ,在△______和△______中,∴ Δ______≌Δ______ .∴ ∠______=∠______ .∴ ______∥______.15. 如图,已知AB=DC,AC=DB,BE=CE求证:AE =DE.答案与解析一.选择题1. B;注意对应顶点写在相应的位置.2. D;连接AC或BD证全等.3. D;4. C;△DOF≌△COE,△BOF≌△AOE,△DOB≌△COA.5. A;将两根钢条再由对顶角相等可证.6. D;△ABC≌△EDC,∠ECD+∠ACB=∠CAB+∠ACB=90°,所以EC⊥AC,ED +AB =BC+CD=DB.,的中点O连在一起,说明OA=,OB=,二.填空题7. 66°;可由SSS证明△ABC≌△DCB,∠OBC=∠OCB=∠ABC=25°+41°=66°.8. 4;,所以∠DCB=△AOD≌△COB,△AOB≌△COD,△ABD≌△CDB,△ABC≌△CDA.9. BC=ED;10.56°;∠CBE=26°+30°=56°.11.20°;△ABE≌△ACD12.△DCB,△DAB;注意对应顶点写在相应的位置上.三.解答题13.证明:在△ADC与△BCD中,14.3,4;ABD,CDB;已知;1,2;两直线平行,内错角相等;ABD,CDB;AB,CD,已知;全等三角形 one 姓名一.填空题1.如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC 是对应角,其对应边:_______.2.如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边_________.. 已知:如图,△ABC≌△FED,且BC=DE.则∠A=__________,A D=_______.. 如图,△ABD≌△ACE,则AB的对应边是_________,∠BAD的对应角是______.5. 已知:如图,△ABE≌△ACD,∠B=∠C,则∠AEB=_______,AE=________.6.已知:如图, AC⊥BC于C , DE⊥AC于E , AD⊥AB 于 A , BC=AE.若AB=, 则AD=___________..已知:△ABC≌△A’B’C’,△A’B’C’的周长为12cm,则△ABC 的周长为 .8.如图, 已知:∠1=∠, ∠3=∠, 要证BD=CD , 需先证△AEB≌△A EC , 根据是_________再证△BDE≌△______ , 根据是__________.AC’A’AACBC9.如图,∠1=∠2,由AAS判定△ABD≌△ACD,则需添加的条件是____________.10.如图,在平面上将△ABC绕B点旋转到△A’BC’的位置时,AA’∥BC,∠ABC=70°,则∠CBC’为________度.二.选择题11、下列条件中,不能判定三角形全等的是 A.三条边对应相等 B.两边和一角对应相等C.两角的其中一角的对边对应相等D.两角和它们的夹边对应相等12. 如果两个三角形全等,则不正确的是A.它们的最小角相等B.它们的对应外角相等C.它们是直角三角形D.它们的最长边相等13. 如图,已知:△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是A.AB=ACB.∠BAE=∠CAD C.BE=DC D.AD=DE14. 图中全等的三角形是A.Ⅰ和ⅡB.Ⅱ和ⅣC.Ⅱ和ⅢD.Ⅰ和Ⅲ15. 下列说法中不正确的是 A.全等三角形的对应高相等 B.全等三角形的面积相等 C.全等三角形的周长相等D.周长相等的两个三角形全等16. AD=AE , AB=AC , BE、CD交于F , 则图中相等的角共有A.5对B.4对C.3对D.2对CADO17.如图,OA=OB,OC=OD, ∠O=60°, ∠C=25°则∠BED 的度数是A.70°B.5°C.5°D. 以上都不对18. 已知:如图,△ABC≌△DEF,AC∥DF,BC∥EF.则不正确的等式是A.AC=DFB.AD=BEC.DF=EFD.BC=EF19.如图, ∠A=∠D , OA=OD , ∠DOC=50°, 求∠DBC的度数为A.50°B.30°C.45°D.25°20. 如图, ∠ABC=∠DCB=70°, ∠ABD=40°, AB=DC , 则∠BAC=A.70°B.80°C.100°D.90° 三.解答题21. 已知:如图, 四边形ABCD中, AB∥CD , AD∥BC.求证:△ABD≌△CDB.22. 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使EC=CB,连结DE,量出DE的长,就是A、B的距离.写出你的证明.23. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF.24. 如图,已知: AD是BC上的中线 ,且DF=DE.求证:BE∥CF.25.如图, 已知:AB⊥BC于B , EF⊥AC于G , DF⊥BC 于D , BC=DF.求证:AC=EF.BEDCAGF全等三角形 two一.填空题:1.如图1,AD⊥BC,D为BC的中点,则△ABD≌_________.图1图24. 如图4,△ABC≌△AED,若AB?AE,?1?27?,则?2? .5.如图5,已知AB∥CD,AD∥BC,E.F是BD上两点,且BF=DE,则图中共有对全等三角形.图56.如图6,四边形ABCD的对角线相交于O点,且有AB∥DC,AD∥BC,则图中有___对全等三角形..“全等三角形对应角相等”的条件是 .8.如图8,AE=AF,AB=AC,∠A=60°,∠B=24°,则∠BOC=__________.图9图8图6A9.若△ABC≌△A′B′C′,AD和A′D′分别是对应边BC和B′C′的高,则△ABD≌△A′B′D′,理由是_______________.10.在Rt△ABC中,∠C=90°,∠A.∠B的平分线相交于O,则∠AOB=_________. 二.选择题:11.如图9,△ABC≌△BAD,A和B.C和D分别是对应顶点,若AB=6cm,AC=4cm,BC=5cm,则AD的长为A.4cmB.5cmC.6cmD.以上都不对 12.下列说法正确的是 A.周长相等的两个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C.面积相等的两个三角形全等D.有两角和其中一角的对边对应相等的两个三角形全等13.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是A.∠AB.∠BC.∠CD.∠B或∠C 14.下列条件中,能判定△ABC≌△DEF的是 A.AB=DE,BC=ED,∠A=∠D B.∠A=∠D,∠C=∠F,AC=EF C.∠B=∠E,∠A=∠D,AC=EF D.∠B=∠E,∠A=∠D,AB=DE15.AD是△ABC中BC边上的中线,若AB=4,AC=6,则AD的取值范围是 A.AD>1B.AD<5C.1<AD< D.2<AD<10 16.下列命题正确的是 A.两条直角边对应相等的两个直角三角形全等; B.一条边和一个锐角对应相等的两个直角三角形全等C.有两边和其中一边的对角对应相等的两个三角形全等D.有两条边对应相等的两个直角三角形全等17.如图10.△ABC中,AB=AC,BD⊥AC于D,CE⊥AB 于E,BD和CE交于点O,AO的延长线交BC于F,则图中全等直角三角形的对数为A.3对B.4对C.5对D.6对OBD图 11CA图10全等三角形测试题一、选择题 1.下列命题中真命题的个数有⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等, A、3个 B、2个 C、1个D、0个2.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是 A.甲和乙B.乙和丙C.只有乙D.只有丙3.在⊿ABC和⊿A′B′C′中,AB=A′B′,∠A=∠A′,若证⊿ABC≌⊿A′B′C′还要从下列条件中补选一个,错误的选法是A. ∠B=∠B′B. ∠C=∠C′C. BC=B′C′D. AC=A′C′4.P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD_____P点到∠AOB两边距离之和.A.小于B.大于 C.等于D.不能确定两直角三角形全等的是6.有以下条件:①一锐角与一边对应相等;②两边对应相等;③两锐角对应相等。
3.5全等三角形判定(基础题)

第一板块-认识三角形-三角形三线一、训练平台1.如图1所示,在△ABC中,∠BAC=80°,∠B=35°,AD平分∠BAC,则∠ADC的度数为()A.90° B.95° C.75° D.55°(1) (2) (3) (4)2.如图2所示,在△ABC中,∠ABC=40°,AD,CD•分别平分∠BAC,•∠ACB,•则∠ADC等于()A.110° B.100° C.190° D.120°3.如图3所示,D,E分别为△ABC的边AC,BC的中点,则下列说法中不正确的是()A.DE是△BDC的中线 B.图中∠C的对边是DE C.BD是△ABC的中线 D.AD=DC,BE=EC4.如图4所示,BD平分∠ABC,DE∥BC,且∠D=30°,则∠AED的度数为()A.50° B.60° C.70° D.80°5.如图5所示,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,且CD,BE•交于一点P,若∠A=50°,则∠BPC的度数是()A.150° B.130° C.120° D.100°6.在如图6所示的方格纸中,每个方格都是边长为1的正方形,点A,B是方格纸中的两个格点(即正方形的格点),在这个5×5的方格纸中,找出格点C使△ABC的面积为2个平方单位,则满足条件的格点C的个数是()A.5个 B.4个 C.3个 D.2个(5) (6) (7)7.已知,如图7所示,在△ABC中,AD⊥BC于D,AE平分∠BAC,若∠B=28°,•∠DAE=16°,求∠C的度数.二、提高训练(9) (10) (11)1.如图9所示,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB的中线,•将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A等于_______.2.若一个三角形三条高线的交点在这个三角形的一个顶点上,•则这个三角形是__________三角形.3.如图10所示,△ABC中,BD=DE=EC,则AD,AE分别是________的中线.4.如图11所示,若∠ACB=90°,CD⊥AB于D,则AC边上的高是______,CD是____边上的高.5.已知△ABC中,AB=5cm,BC=8cm,若AD是BC边上的中线,则中线AD•的取值范围是________.第二板块-全等三角形1.重叠型(边):已知:如图,A、B、C、D在同一条直线上,AC=BD,AM=CN,BM=DN.求证:AM∥CN,BM∥DN。
全等三角形基础(详解版)

30 (5分)在正 ,求
内取一点 ,使 的度数.
,在
外取一点 ,使
,且
A
E
答案
解析 如图所示,连接 ,
∵
,
,
,
D
B
C
∴
≌
.
∴
.
∵
,
,
.
∴
≌
.
∴
.
A
E
D
B
C
考点 三角形 > 全等三角形 > 全等形判定 > 题型:全等三角形之二次全等
C1
A.
B.
C.
D.
答案 C
解析 A选项:符合全等三角形的判定定理 ,即能推出
≌
B选项:符合全等三角形的判定定理 ,即能推出
≌
C选项:不符合全等三角形的判定定理,即不能推出
≌
D选项:符合全等三角形的判定定理 ,即能推出
≌
故选C.
考点 三角形 > 全等三角形 > 全等形判定 > 题型:SSA反例
,故本选项错误. ,故本选项错误. ,故本选项正确. ,故本选项错误.
,
( )分别以 、 为圆心,以大于 长为半径画弧,两弧相交于点 ,所以
,
( )作射线 所以 是
与
的公共边.
故它所用到的识别方法是边边边公理,即 .
考点 三角形 > 全等三角形 > 全等三角形性质 > 题型:对应边与角
12 (3分)在
和
中,已知
,
≌
的是( ).
A
,下列添加的条件中,不能判定
A1
B
C
B1
,
,垂足分别为 、 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、如图1,共有______个三角形.
2、若三角形的两边长分别为2cm和6cm,则它的第三边范围是。
3、若等腰三角形的两边长分别为3cm和8cm,则它的周长是。
4.三角形的三边长分别为5,1+2x,8,则x的取值范围是________.
5.在△ABC中,若∠A+∠B=∠C,则此三角形为_______三角形;若∠A+∠B <∠C,则此三角形是_____三角形.
6.适合条件∠A=1
2
∠B=
1
3
∠C的△ABC是
7.在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132°,则∠A=___
____度.
8.如图所示,已知∠1=20°,∠2=25,∠A=35°,则∠BDC的度数为________.
9.如图3,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,
求△ABD•与△ACD的周长之差.
10.如图,在△ABC中,D、E分别是BC、
AD的中点,S△ABC=4cm2,求S△ABE.
11.如图,在锐角△ABC中,CD、BE分别是AB、AC上的高,•且CD、BE交于一点P,
若∠A=50°,求∠BPC的度数。
12.如图(1),△ABC中,AD是角平分线,AE⊥BC于点E.∠C=80°,∠B=50°,求∠DAE 的度数.
13.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;
(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.
14.(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=_________,∠XBC+∠XCB= _________.
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.。
