(完整版)全等三角形基础练习证明题
全等三角形证明经典40题(含答案)
1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 的长.解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：BC=ED ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
AD B C已知：∠1=∠2，CD=DE，EF如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。
求证：BC=AB+DC。
在BC上截取BF=AB，连接EF∵BE平分∠ABC∴∠ABE=∠FBE又∵BE=BE∴⊿ABE≌⊿FBE（SAS）∴∠A=∠BFE∵AB知：AB=CD，∠A=∠D，求证：∠B=∠C证明：设线段AB,CD所在的直线交于E，则：△AED是等腰三角形。
∴AE=DE而AB=CD∴BE=CE∴△BEC是等腰三角形∴∠B=∠C.是∠BAC平分线AD上一点，AC>AB，求证：PC-PB<AC-AB在AC上取点E，使AE＝AB。
∵AE＝ABBACDF21EAAP＝AP∠EAP＝∠BAE，∴△EAP≌△BAP∴PE＝PB。
PC＜EC＋PE∴PC＜（AC－AE）＋PB∴PC－PB＜AC－AB。
完整版)全等三角形基础练习证明题
完整版)全等三角形基础练习证明题1.已知三角形ABC中，AD为中线，BE⊥AD，CF⊥AD，证明BE=CF。
2.已知四边形ACBD中，AC=BD，AE=CF，BE=DF，证明AE∥CF。
3.已知四边形ABCD中，AB=CD，BE=DF，AE=CF，证明AB∥CD。
4.已知四边形ABCD中，AB=CD，AD=CB，证明AB∥CD。
5.已知两个三角形中，∠BAC=∠DAE，∠1=∠2，BD=CE，证明三角形ABD≌三角形ACE。
6.已知四边形ABED中，CD∥AB，DF∥EB，DF=EB，证明AF=CE。
7.已知四边形BEFC中，BE=CF，AB=CD，∠B=∠C，证明AF=DE。
8.已知四边形ABED中，AD=CB，∠A=∠C，AE=CF，证明EB∥DF。
9.已知三角形ABC中，M为AB的中点，∠1=∠2，MC=MD，证明∠C=∠D。
10.已知四边形ABFE和CDFE中，AE=DF，BF=CE，AE∥DF，证明AB=CD。
11.已知四边形ABCD中，∠1=∠2，∠3=∠4，证明AC=AD。
12.已知四边形ABCD中，∠E=∠F，∠1=∠2，AB=CD，证明AE=DF。
13.已知四边形ABCDEF中，ED⊥AB，EF⊥BC，BD=EF，证明BM=ME。
14.已知三角形ABC中，高AD与BE相交于点H，且AD=BD，证明三角形BHD≌三角形ACD。
15.已知四边形ABCDE中，∠A=∠D，AC∥FD，AC=FD，证明AB∥DE。
16.已知三角形ABC和三角形ADE中，AC=AB，AE=AD，∠1=∠2，证明∠3=∠4.17.已知三角形ABC和三角形DEF中，EF∥BC，AF=CD，AB⊥BC，DE⊥EF，证明三角形ABC≌三角形DEF。
18.已知四边形ABED中，AD=AE，∠B=∠C，证明AC=AB。
19.已知三角形ABC中，AD⊥BC，BD=CD，证明AB=AC。
20.已知三角形ABC和三角形BAD中，∠1=∠2，BC=AD，证明三角形ABC≌三角形BAD。
(完整版)全等三角形基础练习及答案
全等三角形判断一一、选择题1.△ABC和△中，若AB＝，BC＝，AC＝. 则（）A. △ABC≌△B. △ABC≌△C. △ABC≌△D. △ABC≌△2.如图，已知 AB＝ CD， AD＝ BC，则以下结论中错误的选项是（）∥DC B. ∠B＝∠ D C.∠A＝∠ C＝ BC3.以下判断正确的选项是（）A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4.如图，AB、CD、EF订交于O，且被O点均分，DF＝CE，BF＝AE，则图中全等三角形的对数共有（）A. 1 对B. 2 对C. 3 对D. 4 对5.如图，将两根钢条，的中点O连在一起，使，能够绕着点O自由转动，就做成了一个测量工件，则的长等于内槽宽AB，那么判断△ OAB≌△的原由是( )A. 边角边B. 角边角C. 边边边D. 角角边6.如图，已知AB⊥BD 于 B，ED⊥BD 于 D， AB＝CD， BC＝ ED，以下结论不正确的选项是（）⊥AC＝ AC＋AB＝DB D.DC ＝ CB二、填空题7.如图，AB＝CD，AC＝DB，∠ ABD＝25°，∠ AOB＝82°，则∠ DCB＝_________.8.如图，在四边形 ABCD中，对角线 AC、BD互相均分，则图中全等三角形共有_____对 .9.如图，在△ ABC和△ EFD中，AD＝FC，AB＝FE，当增加条件_______时，即可得△ ABC≌△ EFD（SSS）10.如图，AC＝AD，CB＝DB，∠ 2＝30°，∠ 3＝26°，则∠ CBE＝_______.11.如图，点 D在 AB上，点 E 在 AC上， CD与 BE 订交于点 O，且 AD＝AE， AB＝AC，若∠ B ＝20°，则∠C ＝______．12.已知，如图，AB＝CD， AC＝BD，则△ ABC≌______，△ ADC≌ ______.三、解答题13.已知：如图，四边形 ABCD中，对角线 AC、 BD订交于 O，∠ ADC＝∠ BCD， AD＝BC，求证： CO＝ DO．14.已知：如图， AB∥CD， AB＝CD．求证： AD∥BC．解析：要证AD∥BC，只要证∠ ______＝∠ ______，又需证 ______≌______．证明：∵ AB∥CD （），∴ ∠______＝∠ ______ （），在△ ______和△ ______中，∴______≌Δ ______ （）．∴∠______＝∠ ______ （）．∴______ ∥______（）．15.如图，已知AB＝DC， AC＝ DB， BE＝ CE求证： AE＝ DE.答案与解析一. 选择题1.【答案】 B；【解析】注意对应极点写在相应的地址.2.【答案】 D；【解析】连接 AC或 BD证全等 .3.【答案】 D；4.【答案】 C；【解析】△ DOF≌△ COE，△ BOF≌△ AOE，△ DOB≌△ COA.5.【答案】 A；【解析】将两根钢条，的中点O连在一起，说明OA＝，OB＝，再由对顶角相等可证.6.【答案】 D；【解析】△ ABC≌△ EDC，∠ ECD＋∠ ACB＝∠ CAB＋∠ ACB＝90°，所以EC⊥AC， ED ＋ AB ＝ BC＋CD ＝ DB.二. 填空题7.【答案】 66°；【解析】可由SSS证明△ ABC≌△ DCB，∠ OBC＝∠ OCB＝，所以∠ DCB＝∠ABC＝25°＋ 41°＝ 66°.8.【答案】 4；【解析】△ AOD≌△ COB，△ AOB≌△ COD，△ ABD≌△ CDB，△ ABC≌△ CDA.9.【答案】 BC＝ ED；10.【答案】 56°；【解析】∠ CBE＝26°＋ 30°＝ 56°.11.【答案】 20°；【解析】△ ABE≌△ ACD（ SAS）12.【答案】△ DCB，△ DAB；【解析】注意对应极点写在相应的地址上.三. 解答题13. 【解析】证明：在△ ADC 与△ BCD中，14.【解析】3 ， 4；ABD，CDB；已知；1， 2；两直线平行，内错角相等；ABD， CDB；AB， CD，已知；∠1＝∠ 2，已证；BD＝ DB，公共边；ABD， CDB， SAS；3， 4，全等三角形对应角相等；AD， BC，内错角相等，两直线平行.15.【解析】证明：在△ ABC 和△ DCB中∴△ ABC≌△ DCB（ SSS）∴∠ ABC＝∠ DCB，在△ ABE和△ DCE中∴△ ABE≌△ DCE（ SAS）∴AE＝ DE.全等三角形判断二一、选择题1.能确定△ ABC≌△ DEF的条件是（）A． AB＝ DE， BC＝ EF，∠ A＝∠EB． AB＝ DE， BC＝ EF，∠ C＝∠EC．∠ A＝∠ E， AB＝ EF，∠ B＝∠DD．∠ A＝∠ D， AB＝ DE，∠ B＝∠E2．如图，已知△ ABC 的六个元素，则下面甲、乙、丙三个三角形中，和△ABC全等的图形是（）图4－ 3A．甲和乙 B ．乙和丙 C ．只有乙 D ．只有丙3． AD是△ ABC的角均分线，作A． DE＝ DF B ． AE＝ AF DE⊥AB 于 E，DF⊥AC于 C ．BD＝ CDF，以下结论错误的选项是（D．∠ ADE＝∠ ADF）4．如图，已知MB＝ND，∠ MBA＝∠ NDC，以下条件不能够判断△ ABM≌△ CDN的是（）A．∠ M＝∠N B ． AB＝ CD C ．AM＝ CN D ．AM∥CN5.某同学把一块三角形的玻璃打碎成了3块 , 现在要到玻璃店去配一块完满相同的玻璃, 那么最省事的方法是()A. 带①去B. 带②去C. 带③去D.①②③都带去6．如图，∠ 1＝∠ 2，∠ 3＝∠ 4，下面结论中错误的选项是（）A．△ ADC≌△ BCD B ．△ ABD≌△ BACC．△ ABO≌△ CDO D ．△ AOD≌△ BOC二、填空题7.如图 , ∠1＝∠ 2，要使△ ABE≌△ ACE，还需增加一个条件是 _________.( 填上你认为合适的一个条件即可).8.在△ ABC和△中，∠ A＝44°，∠ B＝67°，∠＝69°，∠＝44°，且AC＝，则这两个三角形 _________全等 . （填“必然”或“不用然”）9.已知，如图，AB∥CD，AF∥DE，AF＝ DE，且 BE＝ 2， BC＝ 10，则 EF＝ ________.10.如图， AB∥CD，AD∥BC， OE＝ OF，图中全等三角形共有 ______ 对.11.如图, 已知：∠ 1 ＝∠ 2 , ∠3 ＝∠ 4 , 要证BD ＝CD , 需先证△ AEB ≌△ AEC , 依照是_________ ，再证△ BDE ≌△ ______ ___，依照是_________．12.已知 : 如图，∠ B＝∠ DEF， AB＝ DE，要说明△ ABC≌△ DEF，（1）若以“ ASA”为依照，还缺条件_________（2）若以“ AAS”为依照，还缺条件_________（3）若以“ SAS”为依照，还缺条件_________三、解答题13．阅读下题及一位同学的解答过程：如图，AB和CD订交于点O，且 OA＝ OB，∠A＝∠ C．那么△ AOD与△COB全等吗？若全等，试写出证明过程；若不全等，请说明原由．答：△ AOD≌△ COB．证明：在△ AOD和△ COB中，∴△AOD≌△ COB（ ASA）．问：这位同学的回答及证明过程正确吗？为什么？14.已知如图， E、 F 在 BD上，且 AB＝ CD， BF＝ DE， AE＝ CF，求证： AC与 BD互相均分 .15.已知：如图, AB∥CD,OA＝OD, BC 过 O点 ,点E、F在直线AOD上,且AE＝DF.求证： EB∥CF.答案与解析【答案与解析】一.选择题1.【答案】 D；【解析】 A、 B 选项是 SSA，没有这种判断， C 选项字母不对应 .2.【答案】 B；【解析】乙可由 SAS证明，丙可由 ASA证明 .3.【答案】 C；【解析】可由AAS证全等，获取A、 B、 D 三个选项是正确的.4.【答案】 C；【解析】没有 SSA定理判断全等 .5.【答案】 C；【解析】由 ASA定理，能够确定△ ABC.6.【答案】 C；【解析】△ ABO 与△ CDO中，只能找出三对角相等，不能够判断全等.二、填空题7.【答案】∠ B＝∠ C；【解析】可由 AAS来证明三角形全等 .8.【答案】必然；【解析】由题意，△ ABC≌△，注意对应角和对应边.9.【答案】 6；【解析】△ ABF≌△ CDE， BE＝CF＝ 2，EF＝ 10－2－ 2＝ 6.10.【答案】 5；【解析】△ ABO≌△ CDO，△ AFO≌△ CEO，△ DFO≌△ BEO，△ AOD≌△ COB，△ ABD≌△ CDB.11.【答案】 ASA， CDE， SAS；【解析】△ AEB ≌△ AEC 后可得 BE＝ CE.12.【答案】（1）∠ A＝∠D；（ 2）∠ ACB＝∠F； (3) BC ＝ EF.三、解答题13.【解析】解：这位同学的回答及证明过程不正确.因为∠D 所对的是AO，∠C所对的是OB，证明中用到了OA＝ OB，这不是一组对应边，所以不能够由ASA去证明全等 .14.【解析】证明：∵ BF＝ DE，∴B F－ EF＝ DE－EF，即 BE＝ DF在△ ABE和△ CDF中，∴△ ABE≌△ CDF（ SSS）∴∠ B＝∠ D，在△ ABO和△ CDO中∴△ ABO≌△ CDO（ AAS）∴AO＝ OC， BO＝DO， AC与 BD互相均分 .15.【解析】证明：∵ AB∥CD,∴∠ CDO＝∠ BAO在△ OAB和△ ODC中，∴△ OAB≌△ ODC（ ASA）∴OC＝ OB又∵ AE ＝ DF ，∴AE＋ OA＝ DF＋ OD，即 OE＝ OF 在△ OCF和△ OBE中∴△ OCF≌△ OBE（ SAS）∴∠ F＝∠ E，∴CF∥EB.。
全等三角形证明题及答案(15道)
全等三角形的判定与性质．
7.如图，D、E分别是AB、AC上的点，且 AB=AC，AD=AE．求证：∠B=∠C．
在△ABE和△ACD中， ∵ AB=AC ∠A=∠A AE=AD ， ∴△ABE≌△ACD〔SAS〕， ∴∠B=∠C．
证明：∵AB∥DE， ∴∠B=∠DEF． ∵BE=CF， ∴BC=EF． ∵∠ACB=∠F， ∴ ∠B=∠DEF BC=EF∠ACB=∠F ， ∴△ABC≌△DEF．
全等三角形的判定；平行线的性质．
10.：如图，E、F在AC上，AD∥CB且AD=CB，∠D=∠B． 求证：AE=CF．
证明：∵AD∥CB， ∴∠A=∠C， 在△ADF和△CBE中， ∠A=∠C AD=CB ∠D=∠B ， ∴△ADF≌△CBE〔ASA〕， ∴AF=CE， ∴AF+EF=CE+EF，即AE=CF．
∴△BCF≌△CBD〔ASA〕． 全等三角形的判定．
如图，在△ABC中，D是BC的中点，DE⊥AB， DF⊥AC，垂足分别是E，F，BE=CF． 求证：AD是△ABC的角平分线．
证明：∵DE⊥AB，DF⊥AC， ∴Rt△BDE=Rt△DCF=90°． BD=DC BE=CF ， ∴Rt△BDE≌Rt△DCF〔HL〕， ∴DE=DF， 又∵DE⊥AB，DF⊥AC， ∴AD是角平分线．
系和位置关系？并加以证明．
• 证明：∵AB∥CD， • ∴∠A=∠D， • ∵在△ABF和△DCE中 • AB=CD ∠A=∠D
AF=DE ， • ∴△ABF≌△DCE， • ∴CE=BF，
全等三角形练习(基础证明题)
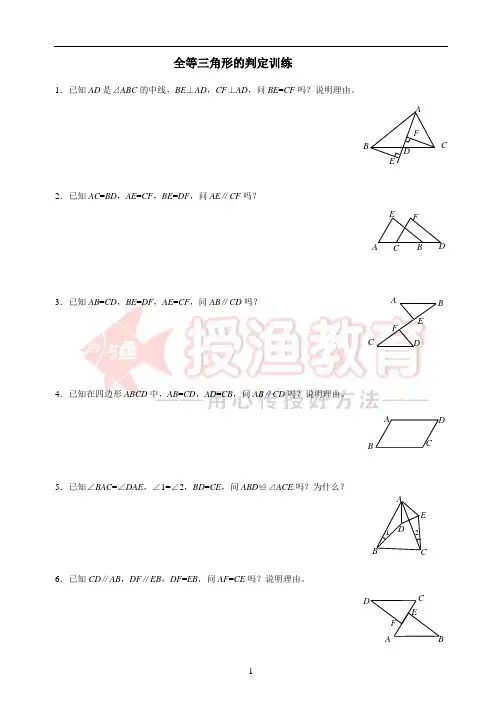
全等三角形的判定训练1．已知AD是⊿ABC的中线，BE⊥AD，CF⊥AD，问BE=CF吗？说明理由。
2．已知AC=BD，AE=CF，BE=DF，问AE∥CF吗？3．已知AB=CD，BE=DF，AE=CF，问AB∥CD吗？4．已知在四边形ABCD中，AB=CD，AD=CB，问AB∥CD吗？说明理由。
5．已知∠BAC=∠DAE，∠1=∠2，BD=CE，问ABD≌⊿ACE.吗？为什么？6．已知CD∥AB，DF∥EB，DF=EB，问AF=CE吗？说明理由。
AB CDFEA C DE FDCFEA BAB CADEB C1 2AD CEFB7．已知BE=CF，AB=CD，∠B=∠C.问AF=DE吗？8．已知AD=CB，∠A=∠C，AE=CF，问EB∥DF吗？说明理由。
9．已知，M是AB的中点，∠1=∠2，MC=MD，问∠C=∠D吗？说明理由。
10．已知，AE=DF，BF=CE，AE∥DF，问AB=CD吗？说明理由。
11．已知∠1=∠2，∠3=∠4，问AC=AD吗？说明理由。
12．已知∠E=∠F，∠1=∠2，AB=CD，问AE=DF吗？说明理由。
13．已知ED⊥AB，EF⊥BC，BD=EF，问BM=ME吗？说明理由。
ACDB1234A B C DE F1 2ACDB E FBA DFECMA BC D1 2DCFEA B14．在⊿ABC 中，高AD 与BE 相交于点H ，且AD =BD ，问⊿BHD ≌⊿ACD ，为什么？15．已知∠A =∠D ，AC ∥FD ，AC =FD ，问AB ∥DE 吗？说明理由。
16．已知AC =AB ，AE =AD ， ∠1=∠2，问∠3=∠4吗？17．已知EF ∥BC ，AF =CD ，AB ⊥BC ，DE ⊥EF ，问⊿ABC ≌⊿DEF 吗？说明理由。
18．已知AD =AE ，∠B =∠C ，问AC =AB 吗？说明理由。
A B C EH DACME F B D A B C E FD AB C ED F ADE AD E B C 1 23 419．已知AD⊥BC，BD=CD，问AB=AC吗？20．已知∠1=∠2，BC=AD，问⊿ABC≌⊿BAD吗？21．已知AB=AC，∠1=∠2，AD=AE，问⊿ABD≌⊿ACE.说明理由。
全等三角形证明经典50题(含答案)
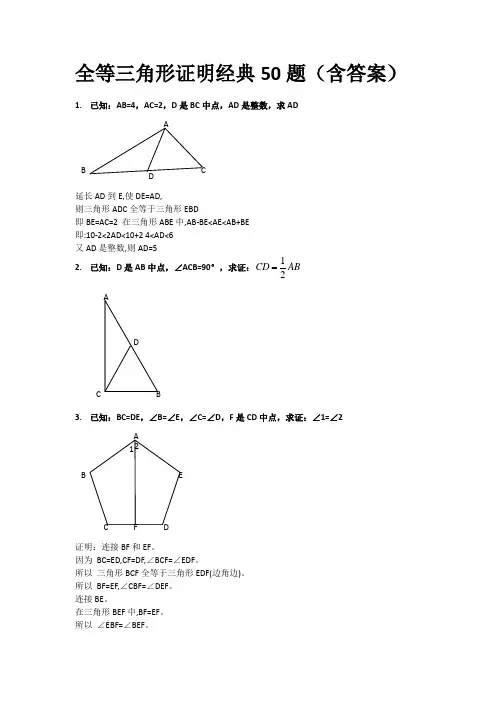
全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
BC ADBC又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中， AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2 又∵CD=DE∴⊿ADC ≌⊿GDE （AAS ） ∴EG=AC ∵EF//AB ∴∠DFE=∠1 ∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD∴⊿AED ≌⊿ABD （SAS ） ∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠CCDB BA CDF2 1 EA6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE 证明：在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC所以△ADC ≌△AFC （SAS ） 所以AD ＝AF所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。
(完整版)全等三角形证明经典50题(含答案)
全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。
求证：BC=AB+DC 。
13.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C14. P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-AB15. 已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BED C B A FE PD A CB16. 已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC18．如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．19．如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA20．（5分）如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．21．如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B22．（6分）如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．F AEDCB P E D CB A DC B A23．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点， （1）求证：△AED ≌△EBC ． （2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：24．（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．证明：25、如图：DF=CE ，AD=BC ，∠D=∠C 。
全等三角形证明100题(经典).docx
1 :已知：AB=4 , AC=2 , D是BC中点，AD是整数，求AD长。
A2:已知：D 是AB 中点，∠ ACB=90 °,求证：CD=I AB2:3 :已知：BC=DE , ∠ B= ∠ E,∠ C= ∠ D , F 是CD 中点，求证：∠ 1 = ∠ 2:4 :已知：∠ 1 = ∠ 2, CD=DE , EF//AB ,求证：EF=ACB5:已知：AC 平分∠ BAD , CE 丄AB , ∠ B+ ∠ D=180 °,求证：AE=AD+BE6:.:如图，四边形ABCD中，AB // DC , BE、CE分别平分∠ ABC、/ BCD ,且点E在AD 上。
求证：BC=AB+DC。
7：P 是∠ BAC 平分线AD 上一点，AC>AB ,求证：PC-PB<AC-AB8 :已知∠ ABC=3 ∠ C ,∠ 1= ∠ 2,B E 丄AE ,求证：AC-AB=2BEC9:已知，E 是AB 中点，AF=BD , BD=5 , AC=7 ,求DC10:如图，在△ ABC 中，BD=DC , ∠ 1 = ∠ 2,求证：AD丄BC .11:如图，OM平分∠ PoQ , MA丄OP,MB丄OQ , A、B为垂足，AB交OM于点N. 求证：∠ OAB= ∠ OBAO12:如图①，E、F分别为线段AC上的两个动点，且DE丄AC于E,BF丄AC于F,若AB=CD ,AF=CE, BD 交AC 于点M .(1)求证：MB = MD , ME=MF(2)当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由.13:已知：如图，DC // AB,且DC =AE, E为AB的中点，(1) 求证：△ AED ◎△ EBC .(2) 观看图前，在不添辅助线的情况下，除△EBC夕卜，请再写出两个与△ AED的面积相等的三角形.(直接写出结果，不要求证明)：14:如图：DF=CE AD=BC ∠ D=∠ CO 求证：△ AED^△ BFGR15:如图：AE、BC交于点M, F 点在AMk, BE// CF, BE=CF求证：AM>△ ABC的中线。
(完整版)全等三角形证明经典50题(含答案)
证明：连接 BF 和 EF T BC=ED,CF=DF, / BCF= / EDF 三角形BCF 全等于三角形 EDF （边角边）1.已知：AB=4 , AC=2 , D 是BC 中点，AD 是整数，求 ADD • BF=EF, / CBF= / DEF 连接 BE 在三角形 BEF 中,BF=EF • / EBF= / BEF 。
： / ABC= / AED 。
二 / ABE= / AEB 。
• AB=AE 。
在三角形 ABF 和三角形 AEF 中AB=AE,BF=EF, / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF • 三角形 ABF 和三角形 AEF 全等。
•/ BAF= / EAF （ /仁/ 2）4.已知：/ 1 = / 2, CD=DE , EF//AB ，求证：EF=AC解：延长 AD 到E,使AD=DE •/ D 是BC 中点二BD=DC 在厶 ACD 和^ BDE 中 AD=DE / BDE= / ADCBD=DC /•△ ACD ◎△ BDE ••• AC=BE=2 •••在△ ABE 中 AB-BE V AE V AB+BE •/ AB=4 即 4-2 V 2AD V 4+21 V AD V 3 • AD=21 2.已知：D 是 AB 中点，/ ACB=90 °，求证：CD —AB 2A CG// EF ,可得，/• △ EFD ^A CGD•，/ EFD =Z 1过C 作CG // EF 交AD 的延长线于点GEFD = CGDDE = DC / FDE =Z GDC （对顶角） EF = CG / CGD =Z EFD 又，EF // AB / 1= / 2 •/ CGD =Z 2 • △ AGC 为等腰三角形， AC = CG 又 EF = CG 「. EF = AC 延长CD 与P ,使D 为CP 中点。
连接 AP,BP •/ DP=DC,DA=DB • ACBP 为平行四边形又/ ACB=90 •平行四边形 ACBP 为矩形 • AB=CP=1/2AB 3.已知：BC=DE ，/ B= / E ,Z C=Z D , F 是 CD 中点，求证：/ 1 = / 2 5.已知：AD 平分/ BAC , AC=AB+BD ，求证：/ B=2 / C证明：延长 AB 取点E ,使AE = AC ,连接DE •/ AD 平分/ BAC• / EAD =Z CAD•/ AE = AC , AD = AD • △ AED 也厶 ACD （ SAS ）•••/ E = Z C•/ AC = AB+BD •AE = AB+BD•/ AE = AB+BE •BD = BE •••/ BDE =Z E •••/ ABC =Z E+ / BDE •••/ ABC = 2 / E •••/ ABC = 2 / C ••• AE = AF + FE = AD + BE12.如图，四边形ABCD中，AB 在AD上。
全等三角形证明50题(含答案)
全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=2ADBC2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。
连接AP ,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ，可得，∠EFD ＝CGD DE ＝DC∠FDE ＝∠GDC （对顶角）BA CDF2 1 EEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF ∵CE ⊥AB∴∠CEB ＝∠CEF ＝90° ∵EB ＝EF ，CE ＝CE ， ∴△CEB ≌△CEF ∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° ∴∠D ＝∠CFA ∵AC 平分∠BAD ∴∠DAC ＝∠FAC ∵AC ＝AC∴△ADC ≌△AFC （SAS ） ∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DEADB C∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=28. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB解：延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=29.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF。
三角形全等证明题60题(有答案)
全等三角形证明题专项练习60题（有答案）1．已知如图，△ABC≌△ADE，∠B=30°，∠E=20°,∠BAE=105°，求∠BAC的度数．∠BAC=_________．2．已知：如图，四边形ABCD中，AB∥CD,AD∥BC．求证:△ABD≌△CDB．3．如图，点E在△ABC外部，点D在边BC上,DE交AC于F．若∠1=∠2=∠3,AC=AE，请说明△ABC≌△ADE 的道理．4．如图，△ABC的两条高AD，BE相交于H，且AD=BD．试说明下列结论成立的理由．（1）∠DBH=∠DAC;（2）△BDH≌△ADC．5．如图，在△ABC中，D是BC边的中点，DE⊥AB，DF⊥AC,垂足分别为E、F，且DE=DF，则AB=AC，并说明理由．6．如图，AE是∠BAC的平分线，AB=AC，D是AE反向延长线的一点，则△ABD与△ACD全等吗？为什么？7．如图所示，A、D、F、B在同一直线上，AF=BD，AE=BC，且AE∥BC．求证:△AEF≌△BCD．8．如图,已知AB=AC,AD=AE，BE与CD相交于O,△ABE与△ACD全等吗？说明你的理由．9．如图，在△ABC中，AB=AC,D是BC的中点,点E在AD上,找出图中全等的三角形，并说明它们为什么是全等的．10．如图所示,CD=CA，∠1=∠2，EC=BC，求证：△ABC≌△DEC．11．已知AC=FE，BC=DE,点A、D、B、F在一条直线上，要使△ABC≌△FDE，应增加什么条件？并根据你所增加的条件证明：△ABC≌△FDE．12．如图，已知AB=AC，BD=CE，请说明△ABE≌△ACD．13．如图，△ABC中，∠ACB=90°，AC=BC，将△ABC绕点C逆时针旋转角α（0°＜α＜90°)得到△A1B1C,连接BB1．设CB1交AB于D,A1B1分别交AB，AC于E,F，在图中不再添加其他任何线段的情况下,请你找出一对全等的三角形，并加以证明．(△ABC与△A1B1C1全等除外）14．如图，AB∥DE，AC∥DF，BE=CF．求证:△ABC≌△DEF．15．如图，AB=AC,AD=AE，AB，DC相交于点M，AC，BE相交于点N,∠DAB=∠EAC．求证：△ADM≌△AEN．16．将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内．从图1中抽象出一个几何图形（如图2）,B、C、E三点在同一条直线上，连接DC．求证：△ABE≌△ACD．17．如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE,连接DE并延长至点F，使EF=AE，连接AF、BE和CF．请在图中找出所有全等的三角形，用符号“≌"表示，并选择一对加以证明．18．如图，已知∠1=∠2，∠3=∠4,EC=AD．（1）求证:△ABD≌△EBC．（2）你可以从中得出哪些结论?请写出两个．19．等边△ABC边长为8，D为AB边上一动点，过点D作DE⊥BC于点E,过点E作EF⊥AC于点F．（1）若AD=2，求AF的长；（2）求当AD取何值时,DE=EF．20．巳知:如图，AB=AC,D、E分别是AB、AC上的点，AD=AE，BE与CD相交于G．（Ⅰ）问图中有多少对全等三角形？并将它们写出来．（Ⅱ）请你选出一对三角形，说明它们全等的理由（根椐所选三角形说理难易不同给分，即难的说对给分高，易的说对给分低）21．已知：如图，AB=DC，AC=BD,AC、BD相交于点E,过E点作EF∥BC，交CD于F，(1）根据给出的条件，可以直接证明哪两个三角形全等？并加以证明．（2）EF平分∠DEC吗？为什么？22．如图，己知∠1=∠2,∠ABC=∠DCB,那么△ABC与△DCB全等吗?为什么？23．如图，B，F，E，D在一条直线上，AB=CD,∠B=∠D，BF=DE．试证明：(1）△DFC≌△BEA;（2）△AFE≌△CEF．24．如图，AC=AE，∠BAF=∠BGD=∠EAC,图中是否存在与△ABE全等的三角形？并证明．25．如图,D是△ABC的边BC的中点,CE∥AB,E在AD的延长线上．试证明：△ABD≌△ECD．26．如图，已知AB=CD，∠B=∠C，AC和BD相交于点O，E是AD的中点，连接OE．（1）求证：△AOB≌△DOC；（2）求∠AEO的度数．27．如图，已知AB∥DE，AB=DE，AF=DC．(1)求证：△ABF≌△DEC；（2）请你找出图中还有的其他几对全等三角形．(只要直接写出结果，不要证明）28．如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．（1）求证：△ABD≌△GCA；（2）请你确定△ADG的形状，并证明你的结论．29．如图，点D、F、E分别在△ABC的三边上,∠1=∠2=∠3，DE=DF,请你说明△ADE≌△CFD的理由．30．如图，在△ABC中,∠ABC=90°，BE⊥AC于点E，点F在线段BE上，∠1=∠2，点D在线段EC上，给出两个条件:①DF∥BC；②BF=DF．请你从中选择一个作为条件，证明:△AFD≌△AFB．31．如图，在△ABC中，点D在AB上，点E在BC上，AB=BC，BD=BE，EA=DC，求证：△BEA≌△BDC．32．阅读并填空：如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E,AD⊥CE于点D．请说明△ADC≌△CEB的理由．解:∵BE⊥CE于点E(已知），∴∠E=90°_________，同理∠ADC=90°，∴∠E=∠ADC（等量代换)．在△ADC中，∵∠1+∠2+∠ADC=180°_________,∴∠1+∠2=90°_________．∵∠ACB=90°（已知）,∴∠3+∠2=90°,∴_________．在△ADC和△CEB中，.∴△ADC≌△CEB （A．A．S）33．已知：如图所示，AB∥DE，AB=DE,AF=DC．（1）写出图中你认为全等的三角形(不再添加辅助线)；（2）选择你在（1）中写出的全等三角形中的任意一对进行证明．34．如图,点E在△ABC外部,点D在BC边上,DE交AC于点F，若∠1=∠2=∠3，AC=AE．试说明下列结论正确的理由：（1）∠C=∠E；（2）△ABC≌△ADE．35．如图，在Rt△ABC中，∠ACB=90°，AC=BC,D是斜边AB上的一点,AE⊥CD于E,BF⊥CD交CD的延长线于F．求证：△ACE≌△CBF．36．如图，在△ABC中，D是BC的中点，DE∥CA交AB于E，点P是线段AC上的一动点，连接PE．探究：当动点P运动到AC边上什么位置时,△APE≌△EDB？请你画出图形并证明△APE≌△EDB．37．已知：如图，AD∥BC，AD=BC,E为BC上一点，且AE=AB．求证：(1）∠DAE=∠B；（2）△ABC≌△EAD．38．如图,D为AB边上一点,△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=90°，CA=CB,CD=CE，图中有全等三角形吗？指出来并说明理由．39．如图，AB=AC，AD=AE,∠BAC=∠DAE．求证：△ABD≌△ACE．40．如图，已知D是△ABC的边BC的中点，过D作两条互相垂直的射线，分别交AB于E，交AC于F，求证：BE+CF＞EF．41．如图所示，在△MNP中，H是高MQ与NE的交点，且QN=QM，猜想PM与HN有什么关系?试说明理由．42．如图，在△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥GF，交AB于点E，连接EG．(1）求证：BG=CF;（2）请你判断BE+CF与EF的大小关系，并证明你的结论．43．如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D，AD=2。
全等三角形证明经典10题((含答案)
全等三角形证明经典10题(含答案)1 如图,已知: AD 是BC 上的中线 ,且DF=DE ．求证:BE ∥CF ．2.如图，在ΔABC 中，D 是边BC 上一点，AD 平分∠BAC ，在AB 上截取AE=AC ，连结DE ，已知DE=2cm ，BD=3cm ，求线段BC 的长。
3.已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE∠BDE=∠ADC BD=DC∴△ACD ≌△BDE∴AC=BE=2 ∵在△ABE 中AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=24.已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2ADBCA BCDE1.证明：连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边) ∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF (∠1=∠2)。
5.已知：∠1=∠2，CD=DE，EF//AB，求证：EF=AC证明：过C作CG∥EF交AD的延长线于点GCG∥EF，可得，∠EFD＝CGDDE＝DC∠FDE＝∠GDC（对顶角）∴△EFD≌△CGDEF＝CG ∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CGBACDF21EEDC B A F又 EF ＝CG ∴EF ＝AC6.已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：延长AB 取点E ，使AE ＝AC ，连接DE∵AD 平分∠BAC ∴∠EAD ＝∠CAD ∵AE ＝AC ，AD ＝AD∴△AED ≌△ACD （SAS ） ∴∠E ＝∠C ∵AC ＝AB+BD∴AE ＝AB+BD ∵AE ＝AB+BE ∴BD ＝BE ∴∠BDE ＝∠E∵∠ABC ＝∠E+∠BDE ∴∠ABC ＝2∠E ∴∠ABC ＝2∠C7.如图所示,△ABC 中,∠ACB=90°,AC=BC,AE 是BC 边上的中线,过C 作CF ⊥AE, 垂足为F,过B 作BD ⊥BC 交CF 的延长线于D.求证:(1)AE=CD;(2)若AC=12cm,求BD 的长.8.如图(1), 已知△ABC 中, ∠BAC=900, AB=AC, AE 是过A 的一条直线, 且B 、C 在A 、E 的异侧, BD ⊥AE 于D, CE ⊥AE 于E 试说明: BD=DE+CE9已知∠ABC=3∠C，∠1=∠2，BE⊥AE，求证：AC-AB=2BE证明：在AC上取一点D，使得角DBC=角C∵∠ABC=3∠C∴∠ABD=∠ABC-∠DBC=3∠C-∠C=2∠C；∵∠ADB=∠C+∠DBC=2∠C;∴AB=AD∴AC – AB =AC-AD=CD=BD在等腰三角形ABD中，AE是角BAD的角平分线，∴AE垂直BD∵BE⊥AE∴点E一定在直线BD上，在等腰三角形ABD中，AB=AD，AE垂直BD∴点E也是BD的中点∴BD=2BE∵BD=CD=AC-AB∴AC-AB=2BE22．（6分）如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．（1）求证：MB=MD，ME=MF（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．（1）连接BE，DF．∵DE⊥AC于E，BF⊥AC于F，∴∠DEC=∠BFA=90°，DE∥BF，在Rt△DEC和Rt△BFA中，∵AF=CE，AB=CD，∴Rt△DEC≌Rt△BFA（HL），∴DE=BF．∴四边形BEDF是平行四边形．∴MB=MD，ME=MF；（2）连接BE，DF．∵DE⊥AC于E，BF⊥AC于F，∴∠DEC=∠BFA=90°，DE∥BF，在Rt△DEC和Rt△BFA中，∵AF=CE，AB=CD，∴Rt△DEC≌Rt△BFA（HL），∴DE=BF．∴四边形BEDF是平行四边形．∴MB=MD，ME=MF．。
(完整版)全等三角形证明经典30题
全等三角形经典题目精选1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CAD BCB ACDF21 ECD B A6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE7. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。
求证：BC=AB+DC 。
8.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C9.已知：AB=CD ，∠A=∠D ，求证：∠B=∠C10.P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-AB11.已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE12.已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DCDC B A F E A B C DPD A CB13.如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．14．如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA15．如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．PED CB A16．如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠BD C B A17．如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，F A E DCBAF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF （2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．18．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：O E DC B A19．如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．FEDC B A20、如图：DF=CE ，AD=BC ，∠D=∠C 。
全等三角形证明题(完整版)
全等三角形证明题全等三角形证明题第一篇：全等三角形证明题全等三角形证明题1在直角坐标系中,有两个点a△ab≌△aed；ob＝oe .e8.如图，在△ab和△db中，ab = d，a = db，a与db交于点m．（1）求证：△ab≌△db ；（2）过点作n∥bd，过点b作bn∥a，n与bn交于点n，试判断线段bn与n的数量关系，并证明你的结论．bn9.在⊿ab中，∠b＝60。
，∠ba和∠ba的平分线ad和f交于i 点。
试猜想：af、d、a三条线段之间有着怎样的数量关系，并加以证明。
10. 在?ab中，ab=a，de∥b.（1）试问?ade是否是等腰三角形，说明理由.（2）若m为de上的点，且bm平分?ab，m平分?ab，若?ade的周长20，b=8.求?ab的周长.amdeb11. 如图, 已知: 等腰rt△oab中,∠aob=900, 等腰rt△eof 中,∠eof=900, 连结ae、bf. 求证:ae=bf;ae⊥bf.1如图，△ab中，d是b的中点，过d点的直线gf交a于点f，交a的平行线bg于点g，de⊥gf交ab于点e，连接eg。
（1）求证：bg=f；（2）请你判断be+f与ef的大小关系，并证明。
13.如图:△ab和△ade是等边三角形.证明：bd=e.bg dabde14. 如图，一艘轮船从点a向正北方向航行，每小时航行15海里，小岛p在轮船的北偏西15°，3小时后轮船航行到点b，小岛p此时在轮船的北偏西30°方向，在小岛p的周围20海里范围内有暗礁，如果轮船不改变方向继续向前航行，是否会有触礁危险？请说明理由。
北b15.如图若直线ae绕a点旋转到图若直线ae绕a点旋转到图.a. 全等三角形周长相等b. 全等三角形能够完全重合. 形状相同的图形就是全等图形d.全等图形的形状和大小都相同9.如图，已知△ab ≌△def，且ab＝4，b＝5，a＝6，则de的长为.ａ.４ｂ.５ｃ.６ｄ.不能确定10．如图，若△oad≌△ob，且∠0=65°，∠=20°，则∠oad等于（）.ａ. 85°ｂ. 95°ｃ. 65°ｄ.105°11. 如图，已知∠1＝∠2，要使△ab≌△ade，还需条件（）.a. ab＝ad，b＝deb. b＝de，a＝ae. ∠b＝∠d，∠＝∠ed.a＝ae，ab＝adaeebdbfbd1如图，△ab≌△aef，ab＝ae，∠b＝∠e，则对于结论①a＝af；②∠fab＝∠eab；③ef＝b；④∠eab＝∠fa，其中正确结论的个数是（）.a. 1个b. 2个. 3个d. 4个13.如图，已知△ab中，ab＝a，它的周长为24，又ad⊥b于d，△abd的周长为20，则ad的长为（）.a. 6b.8. 10d. 12三、证明题1．已知：如图点是ab的中点，d∥be，且d=be.求证：∠d=∠e.adbe、f是ab上的两点，ae=bf，又a∥db，且a=db.求证：f=de。
全等三角形证明经典题(含答案)
全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形AD BC∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）B ACDF21 E∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD BCAD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE ∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=28.已知：D是AB中点，∠ACB=90°，求证：12 CD AB9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。
全等三角形证明经典40题(含答案)
1.已知：AB=4，AC=2，D是BC中点，AD是整数，求AD的长.解：延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=22.已知：BC=ED，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴ AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF (∠1=∠2)。
ADB C3. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG∥EF 交AD 的延长线于点GCG∥EF，可得，∠EFD＝CGDDE ＝DC∠FDE＝∠GDC（对顶角）∴△EFD ≌△CGDEF ＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC 为等腰三角形，AC ＝CG又 EF ＝CG∴EF ＝AC4. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：延长AB 取点E ，使AE ＝AC ，连接DE∵AD 平分∠BAC∴∠EAD ＝∠CAD∵AE ＝AC ，AD ＝AD∴△AED ≌△ACD （SAS ）∴∠E ＝∠C∵AC ＝AB+BD∴AE ＝AB+BD∵AE ＝AB+BE∴BD ＝BE∴∠BDE ＝∠E∵∠ABC ＝∠E+∠BDEBACDF21 EA∴∠ABC＝2∠E∴∠ABC＝2∠C5.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF(SAS)∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6. 如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。
(完整版)全等三角形证明经典50题(含答案)
1.已知： AB=4 ， AC=2 ， D 是 BC 中点， AD 是整数，求 AD AB CD解：延伸 AD 到 E,使 AD=DE ∵ D 是 BC 中点∴ BD=DC在△ ACD 和△ BDE 中 AD=DE ∠ BDE= ∠ ADCBD=DC ∴△ ACD ≌△ BDE∴AC=BE=2 ∵在△ ABE 中 AB-BE ＜ AE ＜AB+BE ∵ AB=4即4-2＜ 2AD ＜ 4+21＜ AD ＜ 3∴AD=22. 已知： D 是 AB 中点，∠ ACB=90 °，求证：CD 1 AB2ADC B延伸 CD 与 P，使 D 为 CP 中点。
连结AP,BP∵DP=DC,DA=DB ∴ ACBP 为平行四边形又∠ ACB=90 ∴平行四边形 ACBP 为矩形∴AB=CP=1/2AB3.已知： BC=DE ，∠ B=∠ E，∠ C=∠ D ，F 是 CD 中点，求证：∠ 1=∠ 2A12B EC F D证明：连结 BF 和 EF∵ BC=ED,CF=DF, ∠ BCF= ∠ EDF∴三角形 BCF 全等于三角形 EDF( 边角边 )∴BF=EF, ∠CBF= ∠ DEF 连结 BE 在三角形 BEF 中 ,BF=EF∴∠EBF= ∠ BEF 。
∵ ∠ ABC= ∠ AED 。
∴ ∠ABE= ∠ AEB 。
∴AB=AE 。
在三角形 ABF 和三角形 AEF 中 AB=AE,BF=EF,∠ABF= ∠ ABE+ ∠ EBF= ∠ AEB+ ∠ BEF= ∠AEF∴三角形 ABF 和三角形 AEF 全等。
∴∠ BAF=∠ EAF (∠ 1=∠ 2) 4.已知：∠ 1=∠2， CD=DE ， EF//AB ，求证： EF=ACA12FCDEB过 C 作 CG∥ EF 交 AD 的延伸线于点G CG∥ EF，可得，∠ EFD＝ CGDDE＝ DC ∠ FDE＝∠ GDC（对顶角）∴ △ EFD≌ △ CGD EF＝ CG ∠ CGD＝∠ EFD 又， EF∥AB ∴，∠ EFD＝∠ 1 ∠ 1= ∠2 ∴∠ CGD＝∠ 2∴ △AGC 为等腰三角形，AC＝ CG 又 EF＝ CG∴ EF＝AC5.已知： AD 均分∠ BAC ，AC=AB+BD ，求证：∠ B=2 ∠ C A证明：延伸AB 取点 E，使 AE ＝ AC ，连结 DE∵AD 均分∠ BAC∴∠ EAD ＝∠ CAD∵AE ＝AC ， AD ＝ AD∴△ AED ≌△ ACD（SAS）∴∠ E＝∠ C∵AC ＝AB+BD∴AE ＝ AB+BD∵AE ＝ AB+BE∴ BD ＝BE∴∠ BDE ＝∠ E∵∠ ABC ＝∠ E+ ∠ BDE∴∠ ABC ＝ 2∠E∴∠ ABC ＝ 2∠C6.已知： AC 均分∠ BAD ，CE⊥AB ，∠ B+ ∠ D=180 °，求证： AE=AD+BE证明：在AE 上取 F，使 EF＝EB ，连结 CF∵ CE⊥ AB∴∠ CEB ＝∠ CEF＝ 90°∵ EB＝ EF， CE＝ CE，∴△ CEB ≌△ CEF∴∠ B ＝∠ CFE∵∠ B ＋∠ D＝ 180°，∠ CFE＋∠ CFA ＝ 180°∴∠ D ＝∠ CFA∵AC 均分∠ BAD∴∠ DAC ＝∠ FAC∵AC ＝AC∴△ ADC ≌△ AFC （ SAS）∴AD ＝AF ∴AE ＝AF ＋ FE＝AD ＋ BE12.如图，四边形 ABCD 中， AB ∥ DC ，BE、CE 分别均分∠ ABC 、∠ BCD ，且点 E在AD 上。
全等三角形基础证明题练习题不含辅助线
全等三角形基础证明题练习题不含辅助线【类型一】平移模型1如图，点C是AE的中点，∠A=∠ECD，AB=CD，求证：△ABC≌△CDE．2如图，已知点B、E、C、F在同一直线上，AB=DE，∠A=∠D，AB∥DE．求证：(1)△ABC≌△DEF；(2)AC∥DF．3如图，在△ABC和△DEF中，AB∥DE，AC∥DF，BC∥EF，BC=EF．(1)求证：△ABC≌△DEF；(2)分别连接AD，BE，CF，探索线段AD，CF，BF之间的位置关系和数量关系，并证明结论．4已知：如图，BC∥EF，AB=DE，BC=EF．证明：△ABC≌△DEF．【类型二】轴对称模型5如图，AE=AF,AC=AD, 求证：∠C=∠D．6如图，在Rt△ABC和Rt△DEF中，∠B=∠E=90°，AC=DF，BF=EC，求证：AB=DE．7如图，AB=AD，CB⊥AB于点B，CD⊥AD于点D．求证：∠1=∠2．8如图，AC=AE，∠C=∠E，∠1=∠2．(1)求证：AB=AD(2)求证：EM=CN【类型三】旋转模型9如图，点E在AB上，CD=CA，DE=AB，∠DCA=∠DEA．求证：CE平分∠BED．10如图，△ABC和△DAE中，∠BAC=∠DAE，AB=AE，AC=AD，连接BD，CE．(1)求证：∠ABC=∠AED；(2)求证：BD=CE．11如图，点B在CD上，OB=OD，AB=CD，∠OBA=∠D；(1)求证：△ABO≌△CDO；(2)当AO∥CD，∠BOD=30°，求∠A的度数．12如图，点E在△ABC边AC上，AE=BC，BC∥AD，∠D=∠BAC．求证：AB=DE．【类型四】角平分线模型13在△ABC中，∠C=90°，AC=4cm，AB=7cm，AD平分∠BAC，DE⊥AB于E．(1)求证：△ACD≌△AED；(2)求EB的长．14如图，已知DE⊥AB垂足为E，DF⊥AC垂足为F，BD=CD，BE=CF．(1)求证：AD平分∠BAC；(2)丁丁同学观察图形后得出结论：AB+AC=2AE，请你帮他写出证明过程．15如图，在△ABC中，AD是它的角平分线，DE⊥AB于点E,DF⊥AC于点F，且BE=CF．线段BD与CD相等吗？说明理由．16已知AD、CD分别是△ABC内角和外角平分线，它们的交点为D，过点D作DF⊥BC，垂足为F 点，作DE⊥AB，垂足为E点，连接BD．求证：BF=BE．【类型五】三垂线模型17如图，在△ABC中，∠ACB=90°，AC=BC，AE为BC边上的中线，过点C作CF⊥AE，垂足为点F，在直线CF上截取CD=AE．求证：BD⊥BC．18如图1，点A是线段DE上一点，∠BAC=90°，AB=AC，BD⊥DE，CE⊥DE，(1)求证：DE=BD+CE．(2)如图2，点A是线段DE上一点，∠BAC=90°，AB=AC，BD⊥DE，CE⊥DE，BD、CE、DE有什么数量关系？并证明．19如图，∠ACB=90°，AC=BC，AD⊥MN，BE⊥MN，垂足分别是D，E．(1)求证：△ADC≌△CEB；(2)猜想线段AD，BE，DE之间具有怎样的数量关系，并说明理由．20如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于D，CE⊥DE于点E；(1)若B、C在DE的同侧(如图1所示)且AD=CE．求证：AB⊥AC；(2)若B、C在DE的两侧(如图2所示)，且AD=CE，其他条件不变，AB与AC仍垂直吗？若是请给出证明；若不是，请说明理由．【类型六】“8”字型21如图，在△ABC中，BD，CE分别是AC，AB边上的高，在BD上载取BF=AC，延长CE至点G 使CG=AB，连接AF，AG．(1)求证：AG=AF；(2)求∠GAF的度数；22如图，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E三点在同一条直线上，连接BD．(1)△BAD与△CAE全等吗？为什么？(2)请判断BD、CE有何大小、位置关系，并说明理由．23如图，AC⊥BC，CE⊥DC，CA=CB，CE=CD，AE与BD交于点F，AE与BC交于点G，BD 与CE交于点H．(1)求证：AE=BD；(2)求证：AE⊥BD．24如图，△ACD和△BCE都是等腰三角形，∠ACD=∠BCE=90°，AC=DC，BC=EC，AE交CD 于点F，BD分别交CE，AE于点G，H．试猜想线段AE和BD的数量和位置关系，再说明理由．【类型七】手拉手模型25如图, AB=CB, BD=BE, ∠ABC=∠DBE=a.(1)当a=60°, 如图①则，∠DPE的度数(2)若△BDE绕点B旋转一定角度，如图②所示，求∠DPE(用a表示)26已知：如图1，在ΔABC和ΔADE中，∠C=∠E，∠CAE=∠DAB，BC=DE．(1)请说明ΔABC≌ΔADE．(2)如图2，连接CE和BD，DE，AD与BC分别交于点M和N，∠DMB=56°，求∠ACE的度数．(3)在(2)的条件下，若CN=EM，请直接写出∠CBA的度数．27如图，△ABC和△DCE是等腰直角三角形，∠ACB=∠DCE=90°，且∠EBD=52°，求∠AEB的度数．28如图，△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=α，AC、BD交于M．(1)如图1，当α=90°时，∠AMD的度数为；(2)如图2，当α≠90°使，求证：△BOD≌△AOC；(3)如图3，当△OCD绕O点任意旋转时，∠AMD与α是否存在着确定的数量关系?如果存在，请直接写出数量关系；若不确定，说明理由．【类型八】一线三等角29已知CD是经过∠BCA顶点C的一条直线，CA=CB．E、F分别是直线CD上两点，且∠BEC=∠CFA=∠α．(1)若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面问题：①如图1，若∠BCA=90°，∠α=90°，求证：BE=CF；②如图2，若∠α+∠BCA=180°，探索三条线段EF，BE，AF的数量关系，并证明你的结论；(2)如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，题(1)②中的结论是否仍然成立？若成立，请给予证明；若不成立，请你写出正确的结论再给予证明．30(1)如图1，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC．求证：△ABE≌△CAF；(2)如图2，在△ABC中，AB=AC，AB>BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为18，求：△ABE与△CDF的面积之和．31“一线三等角”模型是平面几何图形中的重要模型之一，“一线三等角”指的是图形中出现同一条直线上有3个相等的情况，在学习过程中，我们发现“一线三等角”模型的出现，还经常会伴随着出现全等三角形．根据对材料的理解解决以下问题：(1)如图1，∠ADC=∠CEB=∠ACB=90°，AC=BC．猜想DE，AD，BE之间的关系：；(2)如图2，将(1)中条件改为∠ADC=∠CEB=∠ACB=α90°<α<180°，AC=BC，请问(1)中的结论是否成立？若成立，请给出证明；若不成立，请说明理由；(3)如图3，在△ABC中，点D为AB上一点，DE=DF，∠A=∠EDF=∠B，AE=3，BF=5，请直接写出AB的长．32【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一，请根据以下问题，把你的感知填写出来：①如图1，△ABC是等腰直角三角形，∠C=90°，AE=BD，则△AED≌；②如图2，△ABC为正三角形，BD=CF,∠EDF=60°，则△BDE≌；③如图3，正方形ABCD的顶点B在直线l上，分别过点A、C作AE⊥l于E，CF⊥l于F．若AE=1，CF=2，则EF的长为．【模型应用】(2)如图4，将正方形OABC放在平面直角坐标系中，点O为原点，点A的坐标为1,3，则点C的坐标为．【模型变式】(3)如图5所示，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D，DE=4cm，AD=6cm，求BE的长．【类型九】动点问题33如图，在△ABC中，D为AB的中点，AB=AC=10cm，BC=8cm，动点P从点B出发，沿BC方向以每秒3cm的速度向点C运动；同时动点Q从点C出发，沿CA方向以每秒3cm的速度向点A运动，运动时间是t秒．(1)在运动过程中，当点C位于线段PQ的垂直平分线上时，求出t的值；(2)在运动过程中，是否存在某一时刻t，使△BPD和△CQP全等，若存在，求出t的值．若不存在，请说明理由．34如图1，在△ABC中，AB=AC=BC，∠ABC=∠ACB=∠CAB=60°，点P、Q分别是△ABC边AB、BC上的动点(端点除外)，点P从点A、点Q从点B同时出发，且它们的运动速度相同，连接AQ、CP 交于点M．(1)求证：△ABQ≌△CAP；(2)点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，请求出它的度数．(3)如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，直接写出11∠QMC 的度数．35如图，在△ABC 中，∠BAD =∠DAC ，DF ⊥AB ，DM ⊥AC ，AF =10cm ，AC =14cm ，动点E 以2cm/s 的速度从A 点向F 点运动，动点G 以1cm/s 的速度从C 点向A 点运动，当一个点到达终点时，另一个点随之停止运动，设运动时间为t．(1)求证：AF =AM ；(2)当t 取何值时，△DFE 与△DMG 全等．36如图(1)，AB =8cm ，AD ⊥AB ，BC ⊥AB ，垂足为A 、B ，AD =BC =6cm ，点P 在线段AB 上以每秒2cm 的速度由点A 向点B 运动，同时，点Q 在线段BC 上由点B 向点C 运动．连接PD ，PQ ，设它们运动的时间为t s．(1)PA =cm ，PB =cm ；(用含t 的代数式表示)(2)若点Q 的运动速度与点P 的运动速度相等，当t =1时，判断线段PD 和线段PQ 的数量关系和位置关系，并请说明理由；(3)如图(2)，将图(1)中的“AD ⊥AB ，BC ⊥AB ”，改为“∠DAB =∠CBA =α”，其他条件不变．设点Q 的运动速度为xcm /s ，当x 为何值时，△ADP 与△BPQ 全等，请求出x 的值．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
全等三角形的判定 班级： 姓名：
1．已知AD 是⊿ABC 的中线，BE ⊥AD ，CF ⊥AD ，求证BE =CF 。
2．已知AC =BD ，AE =CF ，BE =DF ，求证AE ∥CF
3．已知AB =CD ，BE =DF ，AE =CF ，求证AB ∥CD
4．已知在四边形ABCD 中，AB =CD ，AD =CB ，求证AB ∥CD
5．已知∠BAC =∠DAE ，∠1=∠2，BD =CE ，求证⊿ABD ≌⊿ACE .
6．已知CD ∥AB ，DF ∥EB ，DF =EB ，求证AF =CE
7．已知BE =CF ，AB =CD ， ∠B =∠C ，求证AF =DE 8．已知AD =CB ， ∠A =∠C ，AE =CF ，求证EB ∥DF
9．已知M 是AB 的中点，∠1=∠2，MC =MD ，求证∠C =∠D 。
10．已知，AE =DF ，BF =CE ，AE ∥DF ，求证AB =CD 。
11．已知∠1=∠2，∠3=∠4，求证AC =AD
12．已知∠E =∠F ，∠1=∠2，AB =CD ，求证AE =DF
13．已知ED ⊥AB ，EF ⊥BC ，BD =EF ，求证BM =ME 。
14．在⊿ABC 中，高AD 与BE 相交于点H ，且AD =BD ，求证⊿BHD ≌⊿ACD 。
A
C
D
B 1
2 3 4
A B C
D
E
F
1 2
A
B
C
E H
A
C M E F B
D
A B
C
D
F
E A C
B
D
E
F D
C
F E A
B A
D
E
B C
1 2
A
D
C E
F B
A D
B
A
D
F
E
C
M
A
B
C D 1 2
D
C
F E A B
15．已知∠A =∠D ，AC ∥FD ，AC =FD ，求证AB ∥DE 。
16．已知AC =AB ，AE =AD ， ∠1=∠2，求证∠3=∠4。
17．已知EF ∥BC ，AF =CD ，AB ⊥BC ，DE ⊥EF ，求证⊿ABC ≌⊿DEF 。
18．已知AD =AE ，∠B =∠C ，求证AC =AB 。
19．已知AD ⊥BC ，BD =CD ，求证AB =AC
20．已知∠1=∠2，BC =AD ，求证⊿ABC ≌⊿BAD 。
21．已知AB =AC ， ∠1=∠2，AD =AE ，求证⊿ABD ≌⊿ACE .
22．已知BE ∥DF ，AD ∥BC ，AE =CF ，求证⊿AFD ≌⊿CEB
23．已知AD =AE ，BD =CE ，∠1=∠2，求证⊿ABD ≌⊿ACE
24．已知AB =AC ，AD =AE ，∠1=∠2，求证CE =BD 。
25．已知CE ⊥AB ，DF ⊥AB ，AC ∥DB ，AC =BD ，求证CE =DF
26．如图，AD =BC ，AE =BE ，求证∠C =∠D 。
A B
C
E
F
D
C
A
E
B
F
D
A B
C
E D
F A D E B
C
A
B
C
D
A B
A D
F
E C
A
B C
D E
1 2 A C
D
B
E F
G 1 2 A
D E B
C
1 2
3
4
A
C D
E
B
A D
B
E
C
1
2
27．已知∠1=∠2，AC =BD ，E ，F ，A ，B 在同一直线上，求证∠3=∠4
28．已知D O ⊥BC ，O C =O A ，O B =O D ，求证CD =AB
29．已知CE=DF ，AE =BF ，AE ⊥AD ，FD ⊥AD ，求证⊿EAB ≌⊿FDC
30．已知AB 与CD 相交于点E ，EA =EC ，ED =EB ，求证⊿AED ≌⊿CEB
31．已知AB =AC ，D ，E 分别是AB ，AC 的中点。
求证BE =CD 。
32．已知DE =FE ，FC ∥AB ，求证AE =CE 。
33．已知CE ⊥AB ，DF ⊥AB ，CE =DF ，AE =BF ，求证⊿CEB ≌⊿DF A 。
34．如图，D ，E ，F ，B 在一条直线上，AB =CD ，∠B =∠D ，BF =DE ，求证(1)AE =CF (2)AE ∥CF 。
35．已知，点C 是AB 的中点，CD ∥BE ，且CD =BE ，求证∠D =∠E 。
36．已知，E 、F 是AB 上的两点，AE =BF ，又AC ∥DB ，AC =DB ，求证CF =DE 。
A E D C
B
O
C D
A
E F
B 2
1 3
4 B
A
C D E
F
C
D
E
F A B
D
A E C
B 1 2
B
A
D
F
E
C A
C
B
D
E
C
A
E
B
F
D
A D B
E F C
A C
B
E D
37．已知，AC⊥CE，AC=CE，∠ABC=∠DEC=900，求证BD=AB+ED。
38．⊿ABC≌⊿A′B′C′，AD与A′D′分别是中线，求证AD=A′D′。
39．已知：如图, E, B, F, C四点在同一直线上, ∠A=∠D=90° , BE=FC, AB=DF．求证：∠E=∠C
40．已知：如图, DN=EM , 且DN AB于D , EM AC于E , BM=CN．求证：∠B=∠C.
41．已知：如图, AE , FC都垂直于BD , 垂足为E、F , AD=BC , BE=DF．求证：OA=OC. 42．已知：如图, AB=CD , D、B到AC的距离DE=BF．求证：AB∥CD．
43．已知：如图, OC=OD , AD OB于D , BC OA于C，求证：EA=EB．
44．如图, 已知：∠ACB和∠ADB都是直角, BC=BD , E
是AB上任一点,求证：CE=DE．
45．已知：如图，∠A=∠D=90°，AC，BD交于O，AC=BD，求证：OB=OC．
A
B C D
E
A
B C
D
A′B′C′
D′。