1——matlab——二分法求解非线性方程的近似解_共3页
matlab二分法

matlab二分法MATLAB二分法是一种常用的求解非线性方程的数值解法,它通过不断地将定义域分成若干个子区间,从而找到近似解。
与梯形法和牛顿迭代法相比,MATLAB 二分法又称为“分治法”,是一种简单、直观、快速和有效的求解非线性方程的数值解法。
1. 二分法原理MATLAB 二分法是根据“分而治之”的思想来求解非线性方程的数值解的。
它的基本思想是,将定义域分成两个子区间,其中一个子区间的函数值的符号一定是固定的,另一个子区间的函数值的符号也是固定的,只有当它们的符号相反时,才能确定解存在于这两个子区间之间。
然后,再对缩小的子区间重复以上操作,进而确定非线性方程的近似解,也就是所谓的“黄金分割法”。
2. MATLAB 二分法的步骤(1)始条件首先,要将定义域分成两个子区间,在每一个子区间内,假定函数值的符号是固定的;确定迭代初值 $x_0,比如$x_0=0.5;(2)代计算求出迭代第二值 $x_1,即 $x_1=x_0+frac{b-x_0}{2},计算出$x_1$值,计算函数值的符号;(3)晕条件当求得的函数值的符号与定义域中一边的函数值的符号相反时,认为解存在于此子区间之间,继续将所取得的子区间继续缩小,直到定义域中的某两个端点接近,或者函数值的绝对值小于指定的误差范围,此时称为收敛;(4)的输出将收敛时的根 $x_n$ 作为解的输出。
3. MATLAB 二分法的优缺点(1) MATLAB 二分法的优点MATLAB 二分法具有简单、直观、快速和有效的特点,只要能够确定函数在定义域中的一边的函数值的符号,就可以求出近似解。
(2) MATLAB 二分法的缺点MATLAB 二分法容易收敛到局部极小值,而无法收敛到全局最优值;同时,它也不适用于函数值在定义域内不连续或周期变化的情况。
4. MATLAB 二分法的应用MATLAB 二分法在实际工程中广泛应用,主要用于求解非线性方程、解决二次规划问题、求解非线性最小化问题、结构优化问题等。
MATLAB应用 求解非线性方程

第7章 求解非线性方程7.1 多项式运算在MATLAB 中的实现一、多项式的表达n 次多项式表达为:n a +⋯⋯++=x a x a x a p(x )1-n 1-n 1n 0,是n+1项之和在MATLAB 中,n 次多项式可以用n 次多项式系数构成的长度为n+1的行向量表示[a0, a1,……an-1,an]二、多项式的加减运算设有两个多项式n a +⋯⋯++=x a x a x a p1(x )1-n 1-n 1n 0和m b +⋯⋯++=x b x b x b p2(x )1-m 1-m 1m 0。
它们的加减运算实际上就是它们的对应系数的加减运算。
当它们的次数相同时,可以直接对多项式的系数向量进行加减运算。
当它们的次数不同时,应该把次数低的多项式无高次项部分用0系数表示。
例2 计算()()1635223-+++-x x x xa=[1, -2, 5, 3]; b=[0, 0, 6, -1]; c=a+b例 3 设()6572532345++-+-=x x x x x x f ,()3532-+=x x x g ,求f(x)+g(x)f=[3, -5, 2, -7, 5, 6]; g=[3, 5, -3]; g1=[0, 0, 0, g];%为了和f 的次数找齐 f+g1, f-g1三、多项式的乘法运算conv(p1,p2)例4 在上例中,求f(x)*g(x)f=[3, -5, 2, -7, 5, 6]; g=[3, 5, -3];conv(f, g)四、多项式的除法运算[Q, r]=deconv(p1, p2)表示p1除以p2,给出商式Q(x),余式r(x)。
Q,和r 仍为多项式系数向量 例4 在上例中,求f(x)/g(x)f=[3, -5, 2, -7, 5, 6]; g=[3, 5, -3];[Q, r]=deconv(f, g)五、多项式的导函数p=polyder(P):求多项式P 的导函数p=polyder(P ,Q):求P ·Q 的导函数[p,q]=polyder(P ,Q):求P/Q 的导函数,导函数的分子存入p ,分母存入q 。
用Matlab编写二分法和Newton迭代法求解非线性函数
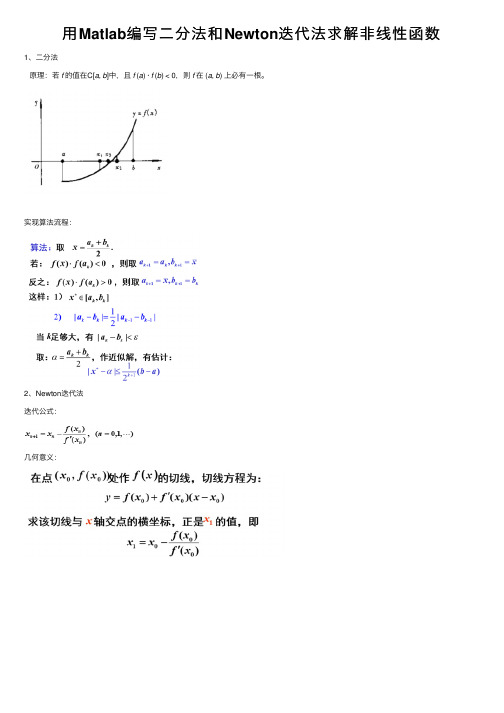
⽤Matlab编写⼆分法和Newton迭代法求解⾮线性函数1、⼆分法原理:若f的值在C[a, b]中,且f (a) · f (b) < 0,则f在 (a, b) 上必有⼀根。
实现算法流程:2、Newton迭代法迭代公式:⼏何意义:3、求解问题⽤Newton法和⼆分法求的解。
4、代码实现1 clear;close;clc2 a=0;b=1;%根区间3 e=10^(-6);%根的容许误差4 [X , N]=dichotomy(e,a,b);%⼆分法5 p0=0.5;%初始值6 N=15;%迭代次数7 [X1]=Newdon(p0,e,N);%Newton迭代法89 function [X , N]=dichotomy(deta,a,b)10 % 函数dichotomy:⼆分法11 %输⼊值:12 %fun:⽅程函数13 %deta:根的容许误差14 %有根区间:[a,b]15 %输出值16 %X:求解到的⽅程的根17 %N:总的迭代次数18 N=1+fix(log2((b-a)/deta));%由公式7.2求得,取整数|X_N-X*|<=(b-a)/2^N<deta,求N19 n=1;20 f1=myfunction(a);21 f2=myfunction(b);22if (f1*f2>0)23 disp('根不在输⼊的区间⾥,请重新输⼊区间');24else25while n <= N26 x=(a+b)/2;27if myfunction(a)*myfunction(x)>028 a=x;29else30 b=x;31 end32 n=n+1;33 end34 X=x;35 fprintf('第%d次⼆分法求出的⽅程的根:\n',N);36 fprintf('X=\n');37 disp(X);38 end39 end4041 function [P]=Newdon(p0,TOL,N)42 %求⽅程组的解43 %输⼊参数44 %初始值:p045 %误差容限:TOL46 %最⼤迭代次数:N47 %输出参数:48 %⽅程近似解:p49 %或失败信息“Method failed”50 format long;51 n=1;%初始迭代次数52 syms x;53while n<=N54if abs(subs(diff(myfunction(x)),x,p0))<TOL55 P=p0;56break;57else58if subs(diff(myfunction(x),2),x,p0)==059 disp('Method failed');60break;61else62 p=p0-myfunction(p0)/subs(diff(myfunction(x)),x,p0);63 p=eval(p);%将exp的值转为⼩数值64if(abs(p-p0)<TOL)65 P=p;66break;67else68 p0=p;69 end70 end71 end72 n=n+1;73 end74 % P=vpa(P,10);%将分数转为⼩数并保留8位⼩数75 fprintf('第%d次NeWton迭代法求出的⽅程的根:\n',N);76 fprintf('P=\n');77 disp(P);78 end7980 function f=myfunction(x)81 f=x*exp(x)-1;82 end5、求解结果。
数值分析 第二章 基于MATLAB的科学计算—非线性方程(组)

科学计算—理论、方法及其基于MATLAB 的实现与分析解非线性方程(组)(一)直接法二分法:设方程()0=x f 在区间[]b a ,上有唯一解,并且()()0<b f a f ,如方程()f x x x x x =-++=3223030.sin .(1)首先要确定适当的包含根的区间,这可以依据闭区间上连续函数的介值定理来确定,例如,()f 1110=-+<sin ,()f 222090=->sin .,所以方程 (1)至少有一个实根属于区间[]12,,图1表明区间[]12,中只含有一个根,显然方程 (1)的根不易直接求得。
在区间[-1,0]、[0,1]和[1,2]的情形,如下图1所示 例1 plotNL_fun01.mplotNL_fun01clearx=-1:0.05:2;f=x.^3-2.3*x.^2+x.*sin(x)+0.3; plot(x,f,'r',x,0*x,'k')title('The Image of f(x)=x^3-2.3*x^2+x*sin(x)+0.3') xlabel('\fontsize {12} \fontname {宋体} 图1') axis square二分法的求根过程:用*x 表示方程()0=x f 在区间[]b a ,上的根,对于给定的精度要求0>ε,取区间[]b a ,的中点21ba x +=,并按下式进行判断: ()()()()()⎪⎩⎪⎨⎧∈⇒<∈⇒<=⇒=],[0],[001*11*1*11b x x b f x f x a x a f x f x x x f (2) 以()()01<a f x f 为例,如果ε≤-2ab ,那么区间[]1,x a 内的任何一点都可以作为方程()0=x f 的近似根。
二分法适用于一个方程的场合,收敛速度是线性的,二分次数的估计:()b aN b a N-≤⇒≥--22εεln ln ln (3) 2、黄金分割法:在区间[]b a ,内取对称的两点:()()()⎩⎨⎧-+=--+=a b a x a b a x ββ211 (4) 使得()()()()()618.025125101102221≈+-=−−→−±-=⇒=-+⇒--=--=--=--->ββββββββa b a b ab a x a x a x a b a b按这种方法选取点1x 和2x ,每次去掉的区间长度至少是原区间长度的0.618倍,()()()()()()()()⎪⎪⎩⎪⎪⎨⎧∉∈⇒<⋃∉∈⇒<∉∈⇒<=⇒==⇒=],[],[0],[],[],[0],[],[0002*2*221*21*211*1*1*22*11x a x b x x b f x f b x x a x x x x x f x f b x x x a x a f x f x x x f x x x f (5) 适用于一个方程的场合,收敛速度是线性的,迭代次数的估计:()()215lnln ln 215--->⇔<⎪⎪⎭⎫ ⎝⎛--a b N a b Nεε (6) (二)迭代法首先将方程(组)写成等价的迭代形式:()()0f x x x ϕ=⇔= (7)由此确定了相应的迭代法:()[]10,n n x x x a b ϕ+=⎧⎪⎨∀∈⎪⎩ (8)迭代收敛的图像解释对于非线性方程(组)的迭代法来说,同样面临收敛性问题,为说明收敛性条件,先看下面的例子:例2:让我们来求如下方程的根()f x x x x x =-++=3223030.sin .下面,我们采用迭代法求方程 (1)位于区间]01[,-中的根,为此构造迭代算法如下:()()x x xx g x -+==3.2sin 3.0 (9)()()x g x x x x n n nn n +==+-10323.sin ., n =12,, (10)在区间]01[,-中任取一个迭代初值x 0,如取初值8.00-=x .执行下面的程序:EqutIteration.m:open EqutIteration.m EqutIterationN =29下面欲求1.5附近的根,为此分别取初值4.10=x ,9.10=x ,迭代的结果如下:open Ex_IteraConv01 Ex_IteraConv01N = 31收敛性定理:(收敛的充分性条件)设方程()f x =0在[]a b ,上存在唯一解,()x g x =是方程的等价形式,如果1、()g x 在[]a b ,上连续可微; 2、对任何x a b ∈[],,()g x a b ∈[],; 3、()'≤<g x L 1,则对任何x a b 0∈[],,由迭代算法()x g x n n +=1, (11)生成的序列{}x n 收敛于方程()f x =0在[]a b ,上的唯一解。
用二分法求方程的近似解 课件

________,第二次应计算________.以上横线应填的内容
分别为( )
A.(0,0.5),f(0.25)
B.(0,1),f(0.25)
C.(0.5,1)f(0.75)
D.(0,0.5),f(0.125)
解析:因为 f(0)<0,f(0.5)>0,故 x0∈(0,0.5).依二 分法,第二次应计算 f(0.25).
答案:A
3.用二分法求函数 f(x)的一个正实数零点时,经计
算,得 f(0.64)<0,f(0.72)>0,f(0.68)<0,f(0.74)>0,则函
数的一个精确度为 0.1 的正实数零点的近似值为( )
A.0.64
B.0.74
C.0.7
D.0.6
解析:因为 f(0.72)>0,f(0.68)<0,所以零点在区间
用二分法求方程的近似解
1.二分法 对于在区间[a,b]上连续不断且 f(a)f(b)<0 的函数 y =f(x),通过不断地把函数 f(x)的零点所在的区间一分为 二,使区间的两个端点逐步逼近零点,进而得到零点近 似值的方法叫作二分法.
温馨提示 二分法求函数零点的适用条件:①y=f(x) 的图象在区间[a,b]上连续不断;②f(a)f(b)<0.
易错警示:解答本题时,极易由于忽视精确度而致错. 防范措施:利用二分法求方程的根,要注意在计算到 第几步时,区间(an,bn)的长度才小于精确度.
区间是[-2,4],则第三次所取的区间可能是( )
A.[1,4]
B.[-2,1]
C.[-2,2.5]
D.[-0.5,1]
解析:(1)由图象可知,选项 B 中的函数的零点左右
二分法,牛顿迭代法,matlab

二分法、牛頓迭代法求方程近似解在一些科學計算中常需要較為精確的數值解,本實驗基於matlab 給出常用的兩種解法。
本實驗是以解決一個方程解的問題說明兩種方法的精髓的。
具體之求解方程e^(-x)+x^2-2*x=0,精度e<10^-5;;程序文本文檔如下%%%%%%二分法求近似解cleardisp('二分法求方程的近似解')format longsyms xf=inline('exp(-x)+x^2-2*x');%原函數%通過[x,y]=fminbnd(f,x1,x2)求出極小值點和極小值,進而確定%區間端點,從而確定解區間矩陣CX=[];C=[0 1.16;1.16 2] ; %C(:,1)為解區間的左端點,C(:,2)為解區間右端點ss=length(C); %統計矩陣C的行數,即為方程解的個數for i=1:ssa=C(i,1);b=C(i,2);%f(a)>=0,f(b)<=0e1=b-a;%解一的精度e0=10^-5;%精度ya=f(a);while e1>=e0x0=1/2*(a+b);y0=f(x0);if y0*ya<=0b=x0;elsea=x0;ya=y0;ende1=b-a;endA=[a,b,e1];%解的區間和精度X=[X;A];%解與精度構成的矩陣endX%%%%%%%牛頓迭代法disp('牛頓迭代法解方程的近似解')clear %清空先前變量syms x %定義變量y=exp(-x)+x^2-2*x;%原函數f=inline(y);f1=diff(y); %一階導函數g=inline(f1);format long %由於數值的默認精度為小數點后四位,故需要定義長形X=[];C=[0 1.16;1.16 2] ; %C(:,1)為解區間的左端點,C(:,2)為解區間右端點ss=length(C); %統計矩陣C的行數,即為方程解的個數for i=1:ssa=C(i,1);b=C(i,2);%f(a)>=0,f(b)<=0e0=10^-5; %要求精度i=1; %迭代次數x0=(a+b)/2;A=[i,x0]; %迭代次數,根值的初始方程t=x0-f(x0)/g(x0); %%%%迭代函數while abs(t-x0)>=e0 %%迭代循環i=i+1;x0=t;A=[A;i,x0];t=x0-f(x0)/g(x0);endA ;B=A(i,:);%迭代次數及根值矩陣X=[X;B];endX運行結果如下如若使用matal內置函數fzero,得到如下結果由兩者求得的結果知,使用函數fzero求得的結果精度不夠。
数值分析中求解非线性方程的MATLAB求解程序

数值分析中求解非线性方程的MATLAB求解程序1. fzero函数:fzero函数是MATLAB中最常用的求解非线性方程的函数之一、它使用了割线法、二分法和反复均值法等多种迭代算法来求解方程。
使用fzero函数可以很方便地求解单变量非线性方程和非线性方程组。
例如,要求解方程f(x) = 0,可以使用以下语法:``````2. fsolve函数:fsolve函数是MATLAB中求解多维非线性方程组的函数。
它是基于牛顿法的迭代算法来求解方程组。
使用fsolve函数可以非常方便地求解非线性方程组。
例如,要求解方程组F(x) = 0,可以使用以下语法:``````3. root函数:root函数是MATLAB中求解非线性方程组的函数之一、它采用牛顿法或拟牛顿法来求解方程组。
使用root函数可以非常方便地求解非线性方程组。
例如,要求解方程组F(x) = 0,可以使用以下语法:``````4. vpasolve函数:vpasolve函数是MATLAB中求解符号方程的函数。
它使用符号计算的方法来求解方程,可以得到精确的解。
vpasolve函数可以求解多变量非线性方程组和含有符号参数的非线性方程。
例如,要求解方程组F(x) = 0,可以使用以下语法:```x = vpasolve(F(x) == 0, x)```vpasolve函数会返回方程组的一个精确解x。
5. fsolve和lsqnonlin结合:在MATLAB中,可以将求解非线性方程转化为求解最小二乘问题的形式。
可以使用fsolve函数或lsqnonlin函数来求解最小二乘问题。
例如,要求解方程f(x) = 0,可以将其转化为最小二乘问题g(x) = min,然后使用fsolve或lsqnonlin函数来求解。
具体使用方法可以参考MATLAB官方文档。
6. Newton-Raphson法手动实现:除了使用MATLAB中的函数来求解非线性方程,还可以手动实现Newton-Raphson法来求解。
用二分法求方程的近似解 课件

探究二 利用二分法求方程的近似值 [典例 2] 求方程 x2=2x+1 的一个近似解(精确度为 0.1). [解析] 设 f(x)=x2-2x-1. ∵f(2)=-1<0,f(3)=2>0, ∴在区间(2,3)内,方程 x2-2x-1=0 有一实数根,记为 x0 取 2 与 3 的平均 数 2.5,∵f(2.5)=0.25>0, ∴2<x0<2.5. 再取 2 与 2.5 的平均数 2.25,∵f(2.25)=-0.437 5<0 ∴2.25<x0<2.5.
二分法的应用问题的解决思路: (1)将实际问题抽象成数学模型,提取数据. (2)建立关系式,并求出定义域或解的区间. (3)利用二分法求其近似值.
3.在 16 枚崭新的金币中,混入了一枚外表与它们完全相同的假币(真币重量大 于假币重量),现在只有一台天平,请问:如何才能发现这枚假币? 解析:用二分法,第一次把 16 枚金币分成两组,每组 8 枚,称重后确定出假币 所在的那一组(较轻的一组),再把较轻的一组的 8 枚金币分成两组,每组 4 枚, 称重后确定假币在哪一组(较轻的一组),依次下去,即可发现这枚假币.
f(1.187 5)·f(1.25)<0, ∴x0∈(1.187 5,1.25). ∵|1.25-1.187 5|=0.062 5<0.1, ∴1.187 5 可作为这个方程的实数解.
探究三 二分法的实际应用 [典例 3] 如图所示,有一块边长为 15 cm 的正方形铁皮,将其四 个角各截去一个边长为 x cm 的小正方形,然后折成一个无盖的 盒子. (1)求出盒子的体积 y(cm3)以 x(cm)为自变量的函数解析式,并讨 论这个函数的定义域; (2)如果要做成一个容积是 150 cm3 的无盖盒子,那么截去的小正方形的边长 x 是 多少?(精确到 0.1 cm).
