【离散数学】知识点典型例题整理
离散数学知识点

绪论研究对象:离散量研究方法:解的存在性解的能行性研究内容:数理逻辑集合代数系统图论离散概率组合数学例题1、A、B、C、D四人参加四次长跑,问:“A在B前三次,B在C前三次,C在D前三次,D在A前三次”是否有解,若有求出,否则说明理由。
方法一: A A B C D n个元素的环形排列可拆成n个元素的B C D A 线性排列D B C D A BD A B CC方法二:集合Sa={X|A在B前} Sa∩Sb∩Sc={A B C D}Sb={X|B在C前} Sa∩Sb∩Sd={D A B C}Sc={X|C在D前} Sa∩Sc∩Sd={C D A B}Sd={X|D在A前} Sb∩Sc∩Sd={B C D A}例题2:在边长为1的正方形中任取五个点,则至少有两个点的距离≤√2/2。
“中点分隔”将边长为1的正方形分成四个边长为1/2的小正方形,从中任取五个小点,必有两个小点来自一个小正方形。
例题3:“布鲁英序列”----应用旋转鼓的设计,设旋转鼓有8个区域,旋转一圈可识别三位二进制数,如何确定磁粉位置。
(阴影0,非阴影1)0—1—1—1 000 0010001 0—1—1—1 010 0111 0 100 1011 110 1111思考题:四位二进制a1 a2 a3 a4例题4:有五位小姐排成一排,所有小姐姓不同,穿的衣服颜色不同,喝不同的饮料,养不同的宠物,吃不同的水果,已知:1.钱小姐穿红衣服2.翁小姐养了一只狗3.陈小姐喝茶4.穿绿衣服的小姐在穿白色衣服小姐的左边,穿绿衣服的小姐在喝咖啡5.吃西瓜的小姐养鸟6.穿黄衣服的小姐吃梨7.站中间的小姐喝牛奶8.赵小姐站最左边9.吃桔子的小姐站在养猫的小姐旁边10.养鱼的小姐旁边小姐吃梨11.吃苹果的小姐喝香槟12.江小姐吃香蕉13.赵小姐站在穿蓝色衣服小姐旁边14.喝开水的小姐站在吃桔子的小姐旁边问每位小姐怎么站,她们分别养什么宠物,吃什么水果,喝什么饮料,穿什么颜色衣服,姓什么。
离散数学在密码学中的应用例题和知识点总结

离散数学在密码学中的应用例题和知识点总结在当今数字化的时代,信息安全变得至关重要。
密码学作为保护信息安全的核心手段,其背后离不开离散数学的强大支撑。
离散数学中的众多概念和方法,为密码学提供了坚实的理论基础和有效的工具。
下面我们将通过一些具体的例题来深入理解离散数学在密码学中的应用,并对相关的知识点进行总结。
一、离散数学在密码学中的重要知识点(一)数论基础1、素数和整除性:素数在密码学中起着关键作用,例如在 RSA 加密算法中,选择两个大素数的乘积作为公钥和私钥的一部分。
2、同余和模运算:同余关系在加密和解密过程中被广泛应用,帮助确定加密后的数值与原始数值之间的关系。
(二)群论1、群的定义和性质:群的概念用于构建加密算法的数学结构,保证加密的安全性和有效性。
2、循环群和置换群:在密码算法的设计中,循环群和置换群可以提供高效的加密和解密操作。
(三)图论1、图的遍历和最短路径:图论可以用于分析密码算法的复杂性和效率。
2、网络安全中的图模型:帮助理解和防范网络攻击中的信息传播路径。
(四)布尔代数1、逻辑运算和布尔函数:在加密算法中用于数据的编码和解码。
2、布尔电路设计:实现加密和解密的硬件逻辑电路。
二、应用例题(一)RSA 加密算法中的数论应用RSA 算法是一种广泛使用的非对称加密算法。
假设选取两个素数 p = 11,q = 13,计算 n = p q = 143,φ(n) =(p 1) (q 1) = 120。
选择一个整数 e = 7(1 < e <φ(n),且 e 与φ(n) 互质),通过扩展欧几里得算法求出 d,使得e d ≡ 1 (mod φ(n)),得到 d = 103。
加密过程:对于明文 m = 8,计算密文 c = m^e mod n = 8^7 mod 143 = 11。
解密过程:接收方收到密文 c = 11,计算明文 m = c^d mod n =11^103 mod 143 = 8,成功恢复明文。
离散数学知识点总结

离散数学知识点总结 一、各章复习要求与重点第一章 集 合[复习知识点]1、集合、元素、集合的表示方法、子集、空集、全集、集合的包含、相等、幂集2、集合的交、并、差、补等运算及其运算律(交换律、结合律、分配律、吸收律、 De Morgan 律等),文氏(V enn )图3、序偶与迪卡尔积本章重点内容:集合的概念、集合的运算性质、集合恒等式的证明 [复习要求]1、理解集合、元素、子集、空集、全集、集合的包含、相等、幂集等基本概念。
2、掌握集合的表示法和集合的交、并、差、补等基本运算。
3、掌握集合运算基本规律,证明集合等式的方法。
4、了解序偶与迪卡尔积的概念,掌握迪卡尔积的运算。
[本章重点习题]P5~6,4、6; P14~15,3、6、7; P20,5、7。
[疑难解析] 1、集合的概念因为集合的概念学生在中学阶段已经学过,这里只多了一个幂集概念,重点对幂集加以掌握,一是掌握幂集的构成,一是掌握幂集元数为2n 。
2、集合恒等式的证明通过对集合恒等式证明的练习,既可以加深对集合性质的理解与掌握;又可以为第三章命题逻辑中公式的基本等价式的应用打下良好的基础。
实际上,本章做题是一种基本功训练,尤其要求学生重视吸收律和重要等价式在B A B A ~⋂=-证明中的特殊作用。
[例题分析]例1 设A ,B 是两个集合,A={1,2,3},B={1,2},则=-)()(B A ρρ 。
解}}3,2,1{},3,2{},3,1{},2,1{},3{},2{},1{,{)(φρ=A}}2,1{},2{},1{,{)(φρ=B于是}}3,2,1{},3,2{},3,1{},3{{)()(=-B A ρρ例2 设{}{}Φ=,,,,b a b a A ,试求:(1){}b a A ,-; (2)Φ-A ; (3){}Φ-A ; (4){}{}A b a -,; (5)A -Φ; (6){}A -Φ。
解 (1){}{}{}Φ=-,,,b a b a A (2)A A =Φ- (3){}{}{}b a b a A ,,,=Φ- (4){}{}Φ=-A b a , (5)Φ=-ΦA (6){}Φ=-ΦA 例3 试证明()()()()B A B A B A B A ~~~~⋂⋃⋂=⋃⋂⋃ 证明()()()()()()()()()()()()()()()()()()B A B A B A B A B B B A A B A A B B A A B A B A B A ~~~~~~~~~~~~~⋂⋃⋂=Φ⋃⋂⋃⋂⋃Φ=⋂⋃⋂⋃⋂⋃⋂=⋂⋃⋃⋂⋃=⋃⋂⋃第二章 二元关系[复习知识点]1、关系、关系矩阵与关系图2、复合关系与逆关系3、关系的性质(自反性、对称性、反对称性、传递性)4、关系的闭包(自反闭包、对称闭包、传递闭包)5、等价关系与等价类6、偏序关系与哈斯图(Hasse )、极大/小元、最大/小元、上/下界、最小上界、最大下界7、函数及其性质(单射、满射、双射)8、复合函数与反函数本章重点内容:二元关系的概念、关系的性质、关系的闭包、等价关系、半序关系、映射的概念 [复习要求]1、理解关系的概念:二元关系、空关系、全关系、恒等关系;掌握关系的集合表示、关系矩阵和关系图、关系的运算。
【离散数学】知识点及典型例题整理

【半群】G非空,·为G上的二元代数运算,满足结合律。
【群】(非空,封闭,结合律,单位元,逆元)恰有一个元素1适合1·a=a·1=a,恰有一个元素a-1适合a·a-1=a-1·a=1。
【Abel群/交换群】·适合交换律。
可能不只有两个元素适合x2=1【置换】n元置换的全体作成的集合Sn对置换的乘法作成n 次对称群。
【子群】按照G中的乘法运算·,子集H仍是一个群。
单位子群{1}和G称为平凡子群。
【循环群】G可以由它的某元素a生成,即G=(a)。
a所有幂的集合an,n=0,±1,±2,…做成G的一个子群,由a生成的子群。
若G的元数是一个质数,则G必是循环群。
n元循环群(a)中,元素ak是(a)的生成元的充要条件是(n,k)=1。
共有ϕ(n)个。
【三次对称群】{I(12)(13)(23)(123)(132)}【陪集】a,b∈G,若有h∈H,使得a =bh,则称a合同于b(右模H),a≡b(右mod H)。
H有限,则H的任意右陪集aH的元数皆等于H的元数。
任意两个右陪集aH和bH或者相等或者不相交。
求右陪集:H本身是一个;任取a∉H而求aH又得到一个;任取b∉H∪aH而求bH又一个。
G=H∪aH∪bH∪…【正规子群】G中任意g,gH=Hg。
(H=gHg-1对任意g∈G都成立)Lagrange定理G为有限群,则任意子群H的元数整除群G的元数。
1有限群G的元数除以H的元数所得的商,记为(G:H),叫做H在G中的指数,H的指数也就是H的右(左)陪集的个数。
2设G为有限群,元数为n,对任意a∈G,有an=1。
3若H在G中的指数是2,则H必然是G的正规子群。
证明:此时对H的左陪集aH,右陪集Ha,都是G中元去掉H的所余部分。
故Ha=aH。
4G的任意多个子群的交集是G的子群。
并且,G的任意多个正规子群的交集仍是G的正规子群。
5 H是G的子群。
《离散数学》典型例题
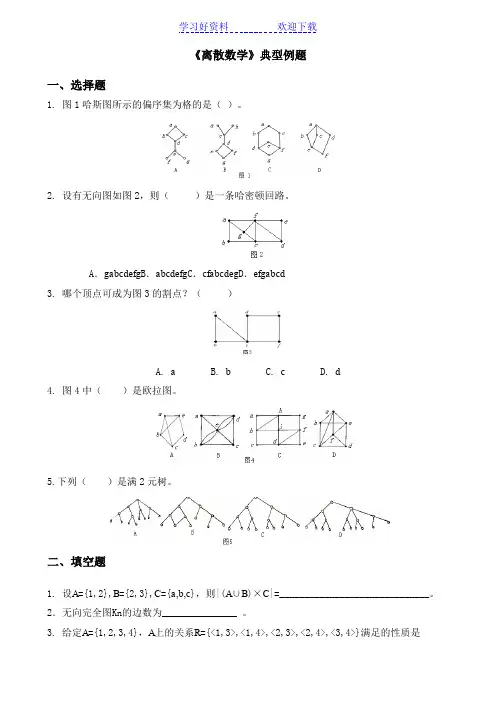
《离散数学》典型例题一、选择题1. 图1哈斯图所示的偏序集为格的是()。
2. 设有无向图如图2,则()是一条哈密顿回路。
A.gabcdefg B.abcdefg C.cfabcdeg D.efgabcd3. 哪个顶点可成为图3的割点?()A. aB. bC. cD. d4. 图4中()是欧拉图。
5.下列()是满2元树。
二、填空题1. 设A={1,2},B={2,3},C={a,b,c},则|(A∪B)×C|=______________________________。
2.无向完全图Kn的边数为_______________ 。
3. 给定A={1,2,3,4},A上的关系R={<1,3>,<1,4>,<2,3>,<2,4>,<3,4>}满足的性质是_________________________。
4. 设A ={a,b,c },F 是A 上的二元关系,F ={<a,a >,<b,b >,<c,c >},则其自反闭包为r (F )=______________________________。
5. 设A 和B 是有穷集合,|A |=m ,|B |=n ,A 到B 有_______多少个不同一对一映射。
三、判断题1.每个正整数都可以唯一地表示为素数的乘积。
( )2.集合X 上的关系R 如果是自反的、反对称的、传递的则称此关系为相容关系。
( )3.一条基本回路一定是简单回路,但一条简单回路不一定是基本回路。
( )4.树是不包含回路的连通图,在(n ,m )树中必有m=n+1( )5.一个有限群<G ,*>的阶n 一定被它的任一个子群的阶m 所等分。
( )四 、综合题1. 求公式(~P →Q) →(Q →~P)的主析取范式和主合取范式。
2. 6个人一起吃饭,围绕圆桌就餐,有多少种就座方式?如果要从4种不同的菜系中点足6道菜,问有多少种点法?3. 一个面包店里有5种不同口味的面包,要挑选8个面包,并且至少有2个奶油味面包和不超过2个咸味面包。
离散数学应用题总结分类及经典例题

离散数学应用题总结分类及经典例题一、命题逻辑1. 命题逻辑基本概念和运算规则- 命题、命题公式、真值表- 与、或、非、异或运算- 逻辑等价、逻辑蕴含、逻辑等值、逻辑与式、逻辑析式等概念2. 命题公式的简化和合取范式- 联结词的法则与性质- 逻辑表达式的简化- 布尔函数的合取范式3. 命题逻辑的演绎推理- 推理规则:假言推理、析取引入、逆否命题引入等- 短路原理和证明方法二、谓词逻辑1. 一阶逻辑的基本概念- 常量、变量、函数、谓词、连接词- 全称量词、存在量词- 函数与数学归纳法2. 谓词公式的形式化定义和语义解释- 语义解释和真值表- 等值逻辑、矢列逻辑3. 谓词逻辑的演绎推理和运算规则- 等效变换和替换规则- 归结演算和合一术- 基本规则和证明方法三、图论与树1. 图的基本概念和性质- 顶点、边、路径、圈- 连通图、欧拉图、哈密顿图- 对偶图、平面图、可平面图2. 图的数据结构和遍历算法- 图的表示方法与存储结构- 广度优先搜索、深度优先搜索- 最小生成树和最短路径算法3. 树的基本概念和性质- 根节点、叶节点、子树、森林- 二叉树、平衡二叉树、哈夫曼树- B树、B+树4. 树的应用- 排序算法:二叉排序树、AVL树、红黑树- 堆、优先队列四、组合数学1. 排列与组合的基本概念- 排列、组合、幂集、二项式系数- 齐次线性递推关系2. 容斥原理和抽屉原理- 容斥原理的应用- 抽屉原理的应用3. 连通图的计数- 生成函数的定义和使用- 应用实例分析五、图的着色与平面分区1. 图的着色问题- 四色定理和五色定理- 补图和可着色图- 哈密顿图和Hamilton回路2. 平面分区问题- 固定多边形的划分- 平面图的着色问题六、离散数学在计算机科学中的应用1. 逻辑电路设计- 逻辑门电路- 布尔代数和真值表2. 算法设计与分析- 递归算法、回溯算法、动态规划等- 时间复杂度和空间复杂度这份文档总结了离散数学的应用题,并对每个分类进行了简要介绍和例题演示。
试题:离散数学基础概念
1.集合理论中,如何表示A集合中所有元素均为B集合中元素的子集关系?o A. A∪Bo B. A∩B=Ao C. A−B=∅o D. B⊆A参考答案: B解析:集合A中所有元素均为B集合中的元素,意味着A是B的子集,但在选项中直接表示子集的方式不出现,而A∩B=A表示A与B的交集等于A,只有当A中的所有元素都在B中时,此等式才成立,故B正确。
2.下列哪个语句是命题?o A. 今天天气很好。
o B. 我希望你考试顺利。
o C. 2 + 3 = 6o D. 请不要再这样做了。
参考答案: C解析:命题是能够判断真假的陈述句。
选项C中“2 + 3 = 6”能够被判断为假(正确值应为5),因此是一个命题。
3.在图论中,完全图是指:o A. 图中任意两个顶点都有边相连。
o B. 图中每个顶点的度数相等。
o C. 图中不存在环。
o D. 图中所有顶点形成一个环。
参考答案: A解析:完全图的定义是图中任意两个不同的顶点之间都有一条边相连。
4.若命题P为真,命题Q为假,则复合命题P ∧Q(P且Q)的真假值为:o A. 真o B. 假o C. 可能真可能假o D. 无法判断参考答案: B解析:在命题逻辑中,P ∧Q(P且Q)成立的条件是P和Q都为真,若Q为假,则P ∧Q为假。
5.以下哪个是逻辑等价的?o A. P∨Q和¬P∨Qo B. P∧Q和¬P∧Qo C. P→Q和¬Q→¬Po D. P∨Q和¬(¬P∧¬Q)参考答案: C解析:P→Q与¬Q→¬P为逻辑等价,代表原命题与它的逆否命题。
6.有向图中,顶点的入度是指:o A. 连接此顶点的边的数量。
o B. 从此顶点出发,指向其它顶点的边的数量。
o C. 指向此顶点的边的数量。
o D. 顶点的度数减去出度。
参考答案: C解析:有向图中,顶点的入度定义为指向该顶点的边的数量。
7.集合A和B的笛卡尔积表示为:o A. A×Bo B. A+Bo C. A∩Bo D. A−B参考答案: A解析:笛卡尔积表示为两个集合的所有可能的有序对的集合,即A×B。
离散数学知识点
离散数学知识点第⼀章1. 将下列命题符号化:解:令p:天下⾬,q:我骑⾃⾏车上班,则(1)只要不下⾬,我就骑⾃⾏车上班?p是q的充分条件,所以符号化为:?p→q (2)只有不下⾬,我才骑⾃⾏车上班?p是q 的必要条件,所以符号化为:q→? p (3)除⾮下⾬,否则我就骑⾃⾏车上班?p仍然是q的充分条件,所以符号化为:?p→q (4)如果下⾬,我就不骑⾃⾏车上班p是?q的充分条件,所以符号化为:p→?q2.命题: 判断结果惟⼀的陈述句(注意: 感叹句、祈使句、疑问句都不是命题陈述句中的悖论以及判断结果不惟⼀确定的也不是命题)3.p→q为假当且仅当p 为真q 为假4.p→q (q 为p 的必要条件)“如果p,则q ” 的不同表述法很多:若p,就q只要p,就qp 仅当q只有q 才p除⾮q, 才p 或除⾮q, 否则⾮p因为….所以5.p?q为真当且仅当p与q同真或同假6.p 0层p 1层p→q 2层(p→q)?r 3层((?p∧q) →r)?(?r∨s) 4层7.双重否定律??A?A等幂律:A∨A?A, A∧A?A交换律: A∨B?B∨A, A∧B?B∧A结合律: (A∨B)∨C?A∨(B∨C) (A∧B)∧C?A∧(B∧C)分配律: A∨(B∧C)?(A∨B)∧(A∨C) A∧(B∨C)? (A∧B)∨(A∧C)德·摩根律: ?(A∨B)??A?∧B?(A∧B)??A?∨B吸收律: A∨(A∧B)?A, A∧(A∨B)?A零律: A∨1?1, A∧0?0同⼀律: A∨0?A, A∧1?A排中律: A?∨A?1⽭盾律: A?∧A?0蕴涵等值式: A→B??A∨B等价等值式: A?B?(A→B)∧(B→A)假⾔易位: A→B??B?→A等价否定等值式: A?B??A??B归谬论: (A→B)∧(A?→B) ??A8.对偶原理设A,B为两个命题公式,若A ? B,则A* ? B*.9.求公式A的范式的步骤:(1) 消去A中的→, ?(若存在)(2) 否定联结词?的内移或消去(3) 使⽤分配律∧对∨分配(析取范式)∨对∧分配(合取范式)(公式的范式存在,但不惟⼀)10.设A 含n 个命题变项,则A 为重⾔式?A 的主析取范式含2n 个极⼩项A 的主合取范式为1.A 为⽭盾式? A 的主析取范式为0A 的主合取范式含2n 个极⼤项A 为⾮重⾔式的可满⾜式A 的主析取范式中⾄少含⼀个且不含全部极⼩项A 的主合取范式中⾄少含⼀个且不含全部极⼤项第⼆章第三章1.相对补 A -B = { x | x ∈A ∧ x ?B }=A - (A ?B)对称差 A ⊕B = (A -B)?(B -A)= (A ?B)-(A ?B)绝对补 ~A = E -A第四章1. R=M1 S=M2 R °S = M2 * M12. (1) (F -1)-1=F (2) domF -1=ranF, ranF -1=domF(1) (F °G)°H=F °(G °H) (2) (F °G)-1= G -1°F -13.关系性质的充要条件设R 为A 上的关系, 则(1) R 在A 上⾃反当且仅当 IA ?R(2) R 在A 上反⾃反当且仅当 R ∩IA =?(3) R 在A 上对称当且仅当 R =R -1(4) R 在A 上反对称当且仅当 R ∩R -1?IA(5) R 在A 上传递当且仅当 R ?R ?R4.定理1 设R 为A 上的关系, 则有(1)⾃反闭包 r (R ) = R ∪R 0(2)对称闭包s (R ) = R ∪R -1(3)传递闭报 t (R ) = R ∪R 2∪R 3∪…5. Mr = M + E E 是和 M 同阶的单位矩阵, M ’是 M 的转置矩阵.Ms = M + M ’ 注意在上述等式中矩阵的元素相加时使⽤逻辑加Mt = M + M2 + M 3 + … |...|)1(...|||||||||...|2111121m m m k j i k j i mi m j i j i i m A A A A A A A A A S A A A -++??-?+-=∑∑∑≤<<≤=≤<≤6.集合A 上的恒等关系 IA 是A 上的偏序关系.⼩于或等于关系, 整除关系和包含关系也是相应集合上的偏序关系7.数集上的⼩于或等于关系是全序关系;整除关系不是正整数集合上的全序关系8.哈斯图特点:每个结点没有环,两个连通的结点之间的序关系通过结点位置的⾼低表⽰,位置低的元素的顺序在前,具有覆盖关系的两个结点之间连边9.特殊元素的性质:对于有穷集,极⼩元和极⼤元必存在,可能存在多个.最⼩元和最⼤元不⼀定存在,如果存在⼀定惟⼀.最⼩元⼀定是极⼩元;最⼤元⼀定是极⼤元.孤⽴结点既是极⼩元,也是极⼤元10.哈斯图应注意:(1).哈斯图不应出现三⾓形第七章1.握⼿定理任意⽆向图和有向图的所有顶点度数之和都等于边数的2倍, 并且有向图的所有顶点⼊度之和等于出度之和等于边数2.环是长度为1的圈, 两条平⾏边构成长度为2的圈3. Kn ⽆点割集n 阶零图既⽆点割集,也⽆边割集.若G 连通,E '为边割集,则p (G -E ')=2若G 连通,V '为点割集,则p (G -V ')≥24.强连通?单向连通?弱连通5. 定理(强连通判别法) D 强连通当且仅当D 中存在经过每个顶点⾄少⼀次的回路定理(单向连通判别法) D 单向连通当且仅当D 中存在经过每个顶点⾄少⼀次的通路6.⽆向图的关联矩阵性质:(1) 每⼀列恰好有两个1或⼀个27.有向图的关联矩阵性质:(1) 每⼀列恰好有⼀个1和⼀个-1(2) 第i ⾏1 的个数等于d +(vi ), -1 的个数等于d -(vi )(3) 1的总个数等于-1的总个数, 且都等于m (4) 平⾏边对应的列相同8.有向图的邻接矩阵性质:平⾏边的列相同)4(2)3(),...,2,1()()2(,1m m n i v d m j i ij i m j ij ===∑∑=的回路数中长度为的通路数中长度为1)4(1)3(,...,2,1),()2(,...,2,1),()1(1)1(,)1(1 )1(1)1(D a D m a n j v d a n i v d a n i ii ji ij j n i ij i n j ij ------=====∑∑∑∑=-=+=9有向图的可达矩阵性质:P(D)主对⾓线上的元素全为1. D强连通当且仅当P(D)的元素全为1第⼋章1.定理8.1 ⽆向图G=是⼆部图当且仅当G中⽆奇圈2.欧拉图的判别法定理8.4 ⽆向图G为欧拉图当且仅当G连通且⽆奇度顶点.⽆向图G是半欧拉图当且仅当G连通且恰有两个奇度顶点定理8.5 有向图D是欧拉图当且仅当D连通且每个顶点的⼊度都等于出度.有向图D具有欧拉通路当且仅当D连通且恰有两个奇度顶点, 其中⼀个⼊度⽐出度⼤1, 另⼀个出度⽐⼊度⼤1, 其余顶点的⼊度等于出度.3.环不影响图的欧拉性. 环与平⾏边不影响图的哈密顿性4.定理8.6 设⽆向图G=是哈密顿图, 则对于任意V1?V且V1≠?, 均有p(G-V1)≤|V1|.5.定理8.7 设G是n阶⽆向简单图, 若任意两个不相邻的顶点的度数之和⼤于等于n-1, 则G中存在哈密顿通路.当n≥3时, 若任意两个不相邻的顶点的度数之和⼤于等于n, 则G中存在哈密顿回路, 从⽽G为哈密顿图.6.定理8.10 (欧拉公式) 设G为n阶m条边r个⾯的连通平⾯图,则n-m+r=2第九章1.定理9.2 设T 是n 阶⾮平凡的⽆向树,则T中⾄少有两⽚树叶2.求带权图的最⼩⽣成树检验:边数达到n-1 (n:顶点数)。
离散数学习题讲解
1、求公式(p→q)→r对应的主析取范式和主合取范式。
解:1、真值表法:p q r p→q (p→q)→r 极小项:m1,m3,m4,m5,m70 0 0 1 0 极大项:M0,M2,M60 0 1 1 1 公式主析取范式为:0 1 0 1 0 (p∨q)→r⇔ m1∨m3∨m4∨m5∨m70 1 1 1 1 ⇔(⌝p∧⌝q∧r)∨(⌝p∧q∧r)∨( p∧⌝q∧⌝r)1 0 0 0 1 ∨(p∧⌝q∧r)∨(p∧q∧r)1 0 1 0 1 公式的主合取范式为:1 1 0 1 0 (p∨q)→r⇔ M0∧M2∧M61 1 1 1 1 ⇔(p∨q∨r)∧(p∨⌝q∨r)∧(⌝p∨⌝q∨r)(2、等值演算法也可,略)2、在自然推理系统P中构造下面推理的证明:(要求有符号化、前提、结论、推理及理由)如果乙不参加篮球赛,那么甲就不参加;如果乙参加篮球赛,那么甲和丙就参加。
因此,如果甲参加篮球赛,那么丙就参加。
解:设:p:乙队参加比赛;q:甲队参加比赛;r:丙队参加比赛。
前提:⌝p→⌝q, p→(q∧r),结论:q→r证明①q 附加前提引入②⌝p→⌝q 前提引入③p ①②拒取式规则④p→(q∧r) 前提引入⑤q∧r ③④假言推理⑥r化简推理成立。
3、自然推理系统F中,证明下面推理:(要求有符号化、前提、结论、推理及理由)所有的舞蹈者都很有风度;李霞是个学生并且是个舞蹈者。
因此,有些学生很有风度。
解:设F(x) :x是舞蹈者;G(x):x是学生;H(x):x很有风度;a:李霞。
前提:∀x(F(x)→H(x)), G(a)∧F(a)结论:∃x(G(x)∧H(x))证明:①G(a)∧F(a) 前提引入②G(a) ①化简③F(a) ①化简④∀x(F(x)→H(x)) 前提引入⑤F(a)→H(a) ④UI规则⑥H(a) ③⑤假言推理⑦G(a)∧H(a) ②⑥合取引入⑧∃x(G(x)∧H(x)) ⑦EG规则所以推理成立。
离散数学复习提纲(完整版)解析
《离散数学》期末复习大纲(完整版)(含例题和考试说明)一、命题逻辑[复习知识点]1、命题与联结词(否定¬、析取∨、合取∧、蕴涵→、等价↔),复合命题2、命题公式与赋值(成真、成假),真值表,公式类型(重言、矛盾、可满足),公式的基本等值式3、范式:析取范式、合取范式,极大(小)项,主析取范式、主合取范式4、公式类型的判别方法(真值表法、等值演算法、主析取/合取范式法)5、命题逻辑的推理理论本章重点内容:命题与联结词、公式与解释、(主)析取范式与(主)合取范式、公式类型的判定、命题逻辑的推理[复习要求]1、理解命题的概念;了解命题联结词的概念;理解用联结词产生复合命题的方法。
2、理解公式与赋值的概念;掌握求给定公式真值表的方法,用基本等值式化简其它公式,公式在解释下的真值。
3、了解析取(合取)范式的概念;理解极大(小)项的概念和主析取(合取)范式的概念;掌握用基本等值式或真值表将公式化为主析取(合取)范式的方法。
4、掌握利用真值表、等值演算法和主析取/合取范式的唯一性判别公式类型和公式等价方法。
5、掌握命题逻辑的推理理论。
[疑难解析]1、公式类型的判定判定公式的类型,包括判定公式是重言的、矛盾的或是可满足的。
具体方法有两种,一是真值表法,二是等值演算法。
2、范式求范式,包括求析取范式、合取范式、主析取范式和主合取范式。
关键有两点:一是准确理解掌握定义;另一是巧妙使用基本等值式中的分配律、同一律和互补律(排中律、矛盾律),结果的前一步适当使用幂等律,使相同的短语(或子句)只保留一个。
3、逻辑推理掌握逻辑推理时,要理解并掌握12个(除第10,11)推理规则和3种证明法(直接证明法、附加前提证明法和归谬法)。
例1.试求下列公式的主析取范式:(1)))()((P Q Q P P ⌝∨⌝⌝∧→→;(2))))((R Q Q P P →⌝∨→⌝∨())()(())()((:)1P Q Q P Q P P P Q Q P P ∧∧∨∧∧⌝∨⌝=∧∧∨⌝∨⌝=原式解 Q P P P Q P P Q P ∨⌝=∨⌝∧∨⌝=∧∨⌝=)()()())(())((Q P P Q Q P ∧∨⌝∨∨⌝∧⌝=)()()(Q P Q P Q P ∧∨∧⌝∨⌝∧⌝=)))((()))(((:)2R Q Q P P R Q Q P P ∨∨∨∨=→⌝∨→⌝∨解)()()()(R Q P R Q P R Q P R Q P R Q P ∧⌝∧∨∧∧⌝∨⌝∧∧⌝∨∧⌝∧⌝=∨∨=)()()(R Q P R Q P R Q P ∧∧∨⌝∧∧∨⌝∧⌝∧∨)2.用真值表判断下列公式是恒真?恒假?可满足?(1)(P ∧⌝P )↔Q(2)⌝(P →Q )∧Q(3)((P →Q )∧(Q →R ))→(P →R )解:(1) 真值表因此公式(1)为可满足。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【半群】G非空,·为G上的二元代数运算,满足结合律。
【群】(非空,封闭,结合律,单位元,逆元)恰有一个元素1适合1·a=a·1=a,恰有一个元素a-1适合a·a-1=a-1·a=1。
【Abel群/交换群】·适合交换律。
可能不只有两个元素适合x2=1【置换】n元置换的全体作成的集合Sn对置换的乘法作成n 次对称群。
【子群】按照G中的乘法运算·,子集H仍是一个群。
单位子群{1}和G称为平凡子群。
【循环群】G可以由它的某元素a生成,即G=(a)。
a所有幂的集合an,n=0,±1,±2,…做成G的一个子群,由a生成的子群。
若G的元数是一个质数,则G必是循环群。
n元循环群(a)中,元素ak是(a)的生成元的充要条件是(n,k)=1。
共有ϕ(n)个。
【三次对称群】{I(12)(13)(23)(123)(132)}【陪集】a,b∈G,若有h∈H,使得a =bh,则称a合同于b(右模H),a≡b(右mod H)。
H有限,则H的任意右陪集aH的元数皆等于H的元数。
任意两个右陪集aH和bH或者相等或者不相交。
求右陪集:H本身是一个;任取a∉H而求aH又得到一个;任取b∉H∪aH而求bH又一个。
G=H∪aH∪bH∪…【正规子群】G中任意g,gH=Hg。
(H=gHg-1对任意g∈G都成立)Lagrange定理G为有限群,则任意子群H的元数整除群G的元数。
1有限群G的元数除以H的元数所得的商,记为(G:H),叫做H在G中的指数,H的指数也就是H的右(左)陪集的个数。
2设G为有限群,元数为n,对任意a∈G,有an=1。
3若H在G中的指数是2,则H必然是G的正规子群。
证明:此时对H的左陪集aH,右陪集Ha,都是G中元去掉H的所余部分。
故Ha=aH。
4G的任意多个子群的交集是G的子群。
并且,G的任意多个正规子群的交集仍是G的正规子群。
5 H是G的子群。
N是G的正规子群。
命HN为H的元素乘N的元素所得的所有元素的集合,则HN是G的子群。
【同态映射】K是乘法系统,G到K的一个映射σ(ab)=σ(a)σ(b)。
设(G,*),(K,+)是两个群,令σ:x→e,∀x∈G,其中e是K的单位元。
则σ是G到K 内的映射,且对a,b∈G,有σ(a*b)=e=σ(a)+ σ(b)。
即,σ是G到K的同态映射,G~σ(G)。
σ(G)={e}是K的一个子群。
这个同态映射是任意两个群之间都有的。
【同构映射】K是乘法系统,σ是G到σ(G)上的1-1映射。
称G与σ(G)同构,G≅G′。
同构的群或代数系统,抽象地来看可以说毫无差别。
G和G′同态,则可以说G′是G的一个缩影。
【同态核】σ是G到G′上的同态映射,核N为G中所有变成G′中1′的元素g的集合,即N=σ-1(1′)={g∈G∣σ(g)=1′}。
N是G的一个正规子群。
对于Gˊ的任意元素aˊ,σ-1(aˊ)={x|x∈G ,σ(x)= aˊ}是N在G 中的一个陪集。
Gˊ的元素和N在G中的陪集一一对应。
设N是G的正规子群。
若A,B是N的陪集,则AB也是N的陪集。
【环】R非空,有加、乘两种运算a+b=b+a2)a+(b+c)=(a+b)+c,3)R中有一个元素0,适合a+0=a,4)对于R中任意a,有-a,适合a+(-a)=0,5)a(bc)=(ab)c,6)a(b+c)=ab+ac,(a+b)c=ac+bc。
交换环:乘法适合交换律ab=ba 。
含壹环:R不只有一个元素且有一个元素1适合1a =a1=a。
1不为零。
无零因子环:不含a,b∈R,a≠0,b≠0,但ab=0,a,b为零因子。
又叫消去环。
消去环:消去律成立。
不为0的元素在加法下的周期或为0或为质数。
整区:有壹无零因子的交换环。
体:如果去掉0,环R的其余元素作成一个乘法群。
体有壹而且无零因子,其中任意非零元素有逆。
域是交换体。
单纯环:R除自己和{0}外没有别的理想。
【子环】环R的非空子集S在R的加法和乘法下仍是环。
若a∈S,b∈S,则a-b∈S;若a∈S,b∈S,则ab∈S。
对于乘法群,其壹恒与子群的壹一致;但对于环,其壹却未必与子环的壹一致。
【理想】环R的子集N (理想子环)N非空;若a∈N,b∈N,则a-b∈N;若a∈N,х∈R,则aх∈N,хa∈N。
1理想一定是子环,但子环未必是理想。
2任意体R只有平凡理想。
3设R是有壹的交换环,a∈R,则aR={ar|r∈R}是R的理想,且包含a。
【主理想(a)】R是有壹的交换环,a∈R,则aR称为由a生成的。
(0)={0},(1)=R。
环R的主理想(a)是R中包含a的理想中最小的理想。
【合同】设R是环,N是理想。
a,b∈R,如果a-b=n∈N,或a=b+n,n∈N,则称a和b模N合同,记为a≡b(mod N)。
在环R中,对于模N,有:反身性:a≡a;对称性:若a≡b,则b≡a;传递性:若a≡b,b ≡c,则a≡c;加法同态性:若a≡b,c≡d,则a±c≡b±d。
乘法同态性:若a≡b,c≡d,则ac≡bd。
【环同态】R是环,S有加乘两种运算,R到S中的一个映射σ(a+b)=σ(a)+σ(b),σ(ab)=σ(a)σ(b)。
R到R′同态,记为R~R′。
【环同构】σ是环R到系统R′上的一个一对一的同态映射。
R与R′同构,记为R≅R′。
若σ是R到S中的一个同态映射,则R的映象R′=σ(R)也是一个环,σ(0)就是R′的零0′,σ(-a)=-σ(a)。
若R有壹而R′不只有一个元素,则R′有壹而且σ(1)就是R′的壹1′;若a∈R有逆,则σ(a)在R′中有逆而且σ(a-1)就是σ(a)-1。
【理想】同态映射σ的核N是R的一个~.设a′是R′的任意元素,则a′的逆映象σ-1(a′)={a ∈R∣σ(a)=a′}是N的一个剩余类。
1按照剩余类的加法和乘法,R对于理想N的所有剩余类的集合R∕N是一个环,2规定σ(a)= a+N,则σ是R到R∕N上的一个同态映射,其核为N。
R∕N叫做R对于N 的剩余环3设环R同态于R′:R~R′于是R与N之间的子环与R′的子环一一对应,大环对应大环,小环对应小环,理想对应理想。
【极大理想】N ⊂ R,而R与N之间没有别的理想。
极大理想不唯一若N ⊂ R,则N是R的极大理想必要而且只要R∕N是单纯环。
【域】任意有壹的交换的单纯环。
任意域F是有壹的交换的单纯环。
设R是有壹的交换环,N是R的理想。
于是,R∕N是一个域,必要而且只要N是一个极大理想。
任意域F的特征P是零或一质数。
【最小域/素域】没有真子域的域,特征P的最小域为R (p为0或质数)。
设p为质数或等于0,特征为p的任意域F包含Rp为其最小子域。
域F上х的多项式作成的环F[х]是一个【整区】。
【多项式】1以х-α除ƒ(х)所得的余式等于ƒ(α)。
2 х-α∣ƒ(х),当且仅当α是ƒ(х)的根。
3说α是非0多项式ƒ(х)的k重根,如果(х-α)k∣ƒ(х),(х-α)k+1不整除ƒ(х)。
4若α是非常数多项式ƒ(х)的k重根,则它至少是ƒ′(х)的k-1重根。
5α是ƒ(х)的重根,当且仅当它是ƒ(х)和ƒ′(х)的公共根。
6复数域上任意非常数多项式必有根。
7实数域上,质式只能是一次式或二次式。
二次式aх2+bx+c是质式,当且仅当判别式b2-4ac<0。
设ƒ(х)= a0хn + a1хn-1 … + an 是整系数多项式,若对质数p,p不整除a0,p∣a1,…,p∣an,p2不整除an,则ƒ(х)在有理域上【不可约】。
设ƒ(х)= a0хn + a1хn-1 + … + an 是整系数多项式。
若有理数b∕c是ƒ(х)的根,其中b和c是互质的整数,则b∣an,c∣a0。
【求有理根】1.分别找a0和an的所有因子ci,bj;2.找互质对(ci,bj );3.判断ci/bj是否为根;4.判断重根。
复数α称为一个代数数,如果α是某个有理系数非0多项式的根。
若α不是任何有理系数非0多项式的根,则α称为一个超越数。
复数域中恰有n个n次单位根。
它们在乘法下作成一个n元循环群Φ1(х)=х-1 Φ2(х)=х+1Φ3(х)=х2+ x + 1Φ4(х)= x2 + 1х12-1=Φ12Φ6Φ4Φ3Φ2Φ1,х6-1= Φ6Φ3Φ2Φ1相除得х6+1 = Φ12Φ4设n不是F的特征的倍数,并设Φn(х)在F中有根。
于是,F中恰有n个n次单位根,它们在乘法下作成一个n元循环群,其ϕ(n)个生成元素恰是Φn(х)的所有的根。
F中的q-1个非0元素恰是所有q-1次单位根,而F的所有q个元素是多项式хq-х的所有的根。
F的q-1个非0元素在乘法下作成一个q-1元循环群,其ϕ(q-1)个生成元素恰是Φq-1(х)的所有的根。
【有限域】的元数必为pn的形式,其中p为其特征。
如果同构的域看作是一样的,则对任意q=pn恰有一个q元有限域,【格】部份序集(L,≤),对于任意a,b∈L,L的子集{a,b}在L中都有一个最大下界(记为inf{a,b})和一个最小上界(记为sup{a,b})。
一个序集是一个格,但是,不是所有部份序集都是。
设(L,≤)是格,S是L的子集,即S⊆L,如果(S,≤)是格,则称(S,≤)是格(L,≤)的【子格】。
设L是一个集合,×,⊕是L上两个二元代数运算,如果这两种运算对于L中元素满足:(1)交换律:a×b=b×a,a ⊕ b=b ⊕ a。
(2)结合律:a×(b×c)=(a×b)×c,a ⊕(b ⊕ c)=(a ⊕ b)⊕c。
(3)吸收律:a×(a ⊕ b)=a,a ⊕(a×b)=a。
则称此代数系统(L,×,⊕)为一个【格】。
集合L中的【部份序关系】R与其逆关系R-1,称为互相对偶的两个关系。
对任意x,y∈L,xR-1y⇔yRx。
若R是部分序关系,则R-1也是。
【格同态】(L,×,⊕)和(S,∧,∨)是个格,L到S的映射g对任意a,b∈L,有g (a×b)= g(a)∧g(b)g(a⊕b)= g(a)∨g(b)若g是L到S上的同态映射,且是一对一的,则称g是格【同构映射】。
【有界格】格(L,≤)有一个最大元素(记为1)和一个最小元素(记为0),亦即,对任意a ∈L,都有0≤a≤1,0,1称为格(L,≤)的界。
在有界格(L,×,⊕,0,1)中,一个元素b∈L,称为元素a∈L的【余元素】,如果a×b = 0,a ⊕ b = 1。
在有界格(L,×,⊕,0,1)中,任意元素a可以有余元素,也可以没有余元素;如果有余元素,则可以有一个或一个以上的余元素。
