信号检测与估值第三次作业
信号检测估计理论与识别技术习题参考答案

2-1 1[()]2E x t =,1212(,)3X t t R t t = 2-2 略。
2-3111[()]sin cos 333E x t t t=++12112212121111111(,)sin cos sin cos sin()cos()9999999X R t t t t t t t t t t =+++++++-2-4 [()]0E X t =,20(,)cos R t t w τστ+=2-5 [()]0E X t =,20(,)cos 2a R t t w ττ+= 2-6 略。
2-7 [()]0E X t =,10(,)200R t t τττ⎧=⎪+=⎨⎪≠⎩2-8 1210()()()2cos(10)(21)X X X R R R eτττττ-=+=++,2[()](0)5X E X t R ==,2(0)2X X R σ==2-9 11()()cos 22jw jw X X o G w R e d w e d τττττ∞∞---∞-∞==⎰⎰00()()()22X P w w w w w ππδδ=-++2-10 00()(()())2Y X X aG w G w w G w w =-++2-11 ())()X R u ττ=+-3-1 二元信号统计检测的贝叶斯平均代价C 为110000000100100110111111()()=()()()() ()()()()ij i i j j i C c P H P H H c P H P H H c P H P H H c P H P H H c P H P H H ===+++∑∑ 利用01()1()P H P H =-1101()1()P H H P H H =- 0010()1()P H H P H H =-得平均代价C 为[][]0011010110011011110100101110111000111011000101()1()1()() ()()()1() ()() ()()()()()()C c P H P H H c P H P H H c P H P H H c P H P H H c c c P H H P H c c c c P H H c c P H H =-⎡-⎤+-+⎣⎦+⎡-⎤⎣⎦=+-+⎡-+---⎤⎣⎦3-2 1)由于各假设j H 的先验概率()(0,1,2)j P H j =相等,所以采用最大似然准则。
信号检测与估计作业第一二三八章答案

时间:6月16日(星期一)晚上6:30-8:30 地点:六教104室(上课教室)试卷共8题,其中4题属于教材第一章内容,其余4题分别的其他章节。
请同学们对匹配滤波器,离散卡尔曼滤波,离散维纳滤波,高斯白噪声下确知信号的检测,K -L 展开,高斯白噪声信道中的单参量信号估计等内容重点关注。
1.1 (付柏成 20060150)在例1.2中,设噪声均方差电压值为σ=2v ,代价为f c =2,m c =1。
信号存在的先验概率P =0.2。
试确定贝叶斯意义下最佳门限β,并计算出相应的平均风险。
解:根据式(1-15),可以算出00.8280.21f mQc Pc ⨯Λ===⨯ 而判决门限2201ln 0.52ln 88.822βσ=+Λ=+= 根据式(1-21)可知平均风险1010Pr 0.2r 0.8R Qr r =+=+01100.2(|)0.8(|)m f c P D H c P D H =+ 而011(|)(|)D P D H p x H dx =⎰1100(|)(|)D P D H p x Hdx =⎰而2121(1)(|)exp[]22x p x H σπσ-=- 2021(|)exp[]22x p x H σπσ=-所以201121(1)(|)(|)exp[]22D D x P D H p x H dx dx σπσ-==-⎰⎰221(1)e x p []22x dx βσπσ-∞-=-⎰=17.82()()(3.91)22β-Φ=Φ=Φ 同理11210021(|)(|)exp[]22D D x P D H p x Hdx dx σπσ==-⎰⎰221e x p ()22x dx βσπσ∞=-⎰8.821()1()1(4.41)22β=-Φ=-Φ=-Φ 所以0.21(3.91)0.82[1(4.41)]R =⨯⨯Φ+⨯⨯-Φ 1.2 (关瑞东 20060155)假定加性噪声()n t 服从均值为零,方差为的正态分布。
信号检测与估计第三章

+∞
th1
⎛ N1μ − th1 ⎞ = Φ⎜ ⎟ ⎜ N 1σ ⎟ ⎝ ⎠
⎛ N1μ − N1σΦ −1 (1 − α1 ) ⎞ ⎛ N1 μ ⎞ −1 PD1 = Φ ⎜ = Φ⎜ − Φ (1 − α1 ) ⎟ ⎟ ⎜ ⎟ ⎜ ⎟ σ N σ 1 ⎝ ⎠ ⎝ ⎠
• 若采用符号检测器,其检验统计量为:
0 2,1
ARE
N1 = N2
0 2,1
渐近相对效率定义如下:
N1 ARE2,1 = lim ARE = lim H1 → H 0 H1 → H 0 N 2 N →+∞ N →+∞
N 2 →+∞
1
N 2 →+∞
1
渐近相对效率是检测器在 H1 → H 0 条件下样本数趋于无穷时 的相对效率。它是比较两种检测器性能的一种指标。
⎧ H 0 : f ( xi ) = f ( − xi ) ⎨ ⎩ H1 : f ( Asi + xi ) = f ( Asi − xi )
2)若只知道噪声分布的中位数为零,可表示为: 1 ⎧ H0 : F ( 0) = ⎪ ⎪ 2 ⎨ ⎪ H : F ( As ) = 1 1 i ⎪ ⎩ 2
定义非随机检验函数(连续型):
( ) ( ) ( )
k >0
• 混合型噪声的概率密度函数为:
⎧ ⎧ x2 ⎫ ε 1− ε ⎪ 2 x f ( x) = exp ⎨ − 2 ⎬ + exp ⎨ − 2πσ 1 2σ 2 ⎩ 2σ 1 ⎭ ⎪ σ2 ⎩ ⎫ ⎪ ⎬ ⎪ ⎭
3.2.1 衡量检测器性能的指标
1. 检测器渐近相对效率 假设二元假设检验问题有两个检测器,若它们具有相同的 虚警概率和检测概率所需的观测样本数分别为 N1 , N 2 , 则定义第2个检测器对于第1个的相对效率为:
信号检测与估计作业参考(电子科大)
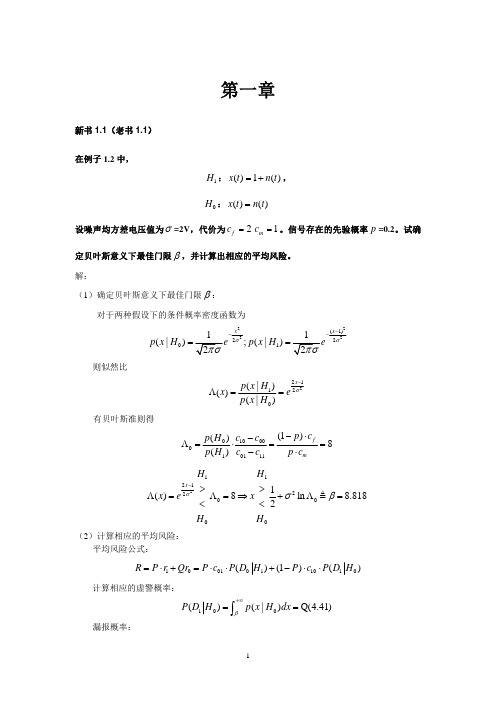
=
⎧a ⎨⎩ 0
(0 ≤ t ≤ T ) (else)
7
第二章
新书 2.4(旧书 2.1)
利用最小错误概率准则设计一接收机,对如下两个假设做出选择:
H0 : x(t) = s0 (t) + n(t) H1 : x(t) = s1(t) + n(t)
信号 s0 (t) 和 s1(t) 如下图,加性噪声是功率谱密度为 N0 / 2 的高斯白噪声。设先验概率相等,
其 中 A, B,ω1,ω2 ,ϕ 为 已 知 常 数 。 噪 声 是 功 率 谱 密 度 为 N0 / 2 的 高 斯 白 噪 声 。 信 号
B cos(ω2t + ϕ) 对接收机性能有何影响?
解:
由式(2.18)可知此时的判决门限为
∫ β
=
N0 2
ln
Λ0
+
1 2
T 0
[s12
(t
)
−
s02 (t)]dt
i =1
> <
1 M
ln Λ0
+1
β
H0
∑ 将 mx
=
1 M
M
xi 作为判决统计量与门限进行对比
i =1
6
由于高斯分布函数的线性组合仍为正态分布,则我们可以得到 mx 在两种假设下的似然
函数:
p(mx | H0 ) =
M 4π
− Mmx2
e4
,
p(mx
|
H1)
=
M − M (mx −2)2 e4
4π
新书 1.3(老书 1.3)
只用一次观测
x
来对下面两个假设做选择,
H
0
西安交大_电信学院_研究生《信号检测与估值》作业

信号检测与估值作业1.考虑下面观测样本为y 的简单二元假设检验问题:110011:()()22:(),0y y H f y rect H f y e y --⎧=⎪⎨⎪=>⎩ 其中,12121,()=0rect t if t -<<⎧⎨⎩,otherwise(a)求该假设检验的似然比检测器并确定判决域(即确定样本空间划分方法) (b)当00012,21P P P ===,时分别计算可能获得的最小错误概率解:(a )11100011,02,02:()()220,0,:(),0(),0y yy y H f y p y otherwise otherwise H f y e y p y e y --⎧⎧⎧⎧<<<<⎪⎪⎪⎪==⎨⎨⎪⎪⇒⎨⎨⎪⎪⎩⎩⎪⎪⎪⎪=>=>⎩⎩11100110100 0y 222ln 11()y >2 ()112ln 1 H H y H H H H H H H H e y p y p y y y εεεεελλεεεεε⎧>>⎪⇒⎪<<-->⎪==⎨<-⎪>⎪∞<-⎪<≤⎩><-()=化简得:0 0y 2>2H y ⎧⎪<≤⎪⎨⎪⎪⎩判为(b )()001E F MP P P P P =+-,()10F y R P p y d =⎰,()01M yR P p y d=⎰2ln 220ln 2011111112ln 2=+ln 2222424y E P y P e dy dy e λ--=+=-⎰⎰当时,()=, 2ln 420ln 4021112123ln 4=ln 4332636y E P y P e dy dy e λ--=+=-+⎰⎰当时,()=,220011110=333y E P y P e dy e λ--==-⎰,()=,当时2.考虑下面观测样本为y 的简单二元假设检验问题:110011:()()221:()2y H f y rect H f y rect y -⎧=⎪⎪⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩(a ) 求该假设检验的似然比检测器并确定判决域(即确定样本空间划分方法) (b ) 计算虚报概率F M P P 和漏报概率 解:(a )11100011:()()1(),022221:()()1,02y H f y rect p y y H f y rect y p y y -⎧=⎧⎪=<<⎪⎪⇒⎨⎨⎛⎫⎪⎪=-=<<⎩ ⎪⎪⎝⎭⎩1 111000()1y ()121H H H H p y p y εελλλεε>>=⇒=<<--()=即:1010 1<y<21 0y 1 2H H H λ⎧⎪⎪>⎨<≤⎪<⎪⎩判为(b )11000001100100100010()1111>=<0d 2()222()11=1d 102()2()11=,12()211,2F M F M F M p y P P y p y p y P y P p y p y H H p y P P λλλλλλεεεε===<>=====-=-=⎰⎰当时,,所以判为H ,,当时,,所以判为H ,,当时,,所以假设以的概率判为的概率判为则3.一个二元通信系统的表达式可以由下面的公式表示:y x n =+其中,y 是接收机观测到的样本,x 是发射的信号,n 是接收机端引入的高斯白噪声(均值为0,方差为2σ),x 取值可为-A 或+A ,分别对应假设01H H 和 (a )要求确定最小错误概率检测器的形式(b )给出先验概率分布满足1001103,,5P P P P P P ===情况下的最小错误概率检测器,并计算出相应的最小错误概率解:(a)2211022:()()())()):2 2 H y A n y A y A p y y H y A n p σσ=++⎧-+⇒=-=-⎨=-+⎩ 11122100()()=ln()1121H H H AyH H H p y y e y p y A σεεσελλεεε>>>=⇒⇒<<<---T (b )0E F M P P P P P =+0(1-) 2010010131ln 33,3442P P P P P y P A σλ=⇒==⇒==⇒T当= 22ln3222ln30123133ln 31ln 3()()()()4444242A E A P p y dy p y dy A A A Aσσσσ+∞-∞=+=-Φ-+Φ+⎰⎰010010111,122P P P P P y P λ=⇒==⇒==⇒T当=0 001011111()()()()22222E P p y dy p y dy A A +∞-∞=+=-Φ-+Φ+⎰⎰ 201001013ln35355,8852P P P P P y P A σλ=⇒==⇒==⇒T当=22322ln52301ln 5233lnln3533555()()(-)(+)8888282AE AP p y dy p y dy A A A Aσσσσ+∞-∞=+=-Φ+Φ⎰⎰ 4.接收机输出为信号电压S 和噪声电压N 之和,其二者的联合概率密度函数为:0(,), 0&0s SN f s n N N n e s αα-≤<∞≤≤=(a) 分别给出S 和N 的边缘概率密度函数()()S N f s f n 和; (b) 证明S 和N 统计独立;(c) 推导Y=S+N 的概率密度函数,并画出图形;(d) 推导()()S N f s f n 和对应假设10H H 和成立下的条件概率密度,即1()()S f y f y =0()()N f y f y =,现给定02=1N α=和,请写出最小错误概率检测器;(e) 分别计算在1001103,,23P P P P P P ===。
信号检测及估计试题-答案(不完整版)

信号检测及估计试题-答案(不完整版)一、概念:1. 匹配滤波器。
概念:所谓匹配滤波器是指输出判决时刻信噪比最大的最佳线性滤波器。
应用:在数字信号检测和雷达信号的检测中具有特别重要的意义。
在输出信噪比最大准则下设计一个线性滤波器是具有实际意义的。
2. 卡尔曼滤波工作原理及其基本公式(百度百科)首先,我们先要引入一个离散控制过程的系统。
该系统可用一个线性随机微分方程(Linear Stochastic Difference equation)来描述:X(k)=A X(k-1)+B U(k)+W(k)再加上系统的测量值:Z(k)=H X(k)+V(k)上两式子中,X(k)是k时刻的系统状态,U(k)是k时刻对系统的控制量。
A和B是系统参数,对于多模型系统,他们为矩阵。
Z(k)是k时刻的测量值,H是测量系统的参数,对于多测量系统,H为矩阵。
W(k)和V(k)分别表示过程和测量的噪声。
他们被假设成高斯白噪声(White Gaussian Noise),他们的covariance 分别是Q,R(这里我们假设他们不随系统状态变化而变化)。
对于满足上面的条件(线性随机微分系统,过程和测量都是高斯白噪声),卡尔曼滤波器是最优的信息处理器。
下面我们来用他们结合他们的covariances 来估算系统的最优化输出(类似上一节那个温度的例子)。
首先我们要利用系统的过程模型,来预测下一状态的系统。
假设现在的系统状态是k,根据系统的模型,可以基于系统的上一状态而预测出现在状态:X(k|k-1)=A X(k-1|k-1)+B U(k) (1)式(1)中,X(k|k-1)是利用上一状态预测的结果,X(k-1|k-1)是上一状态最优的结果,U(k)为现在状态的控制量,如果没有控制量,它可以为0。
到现在为止,我们的系统结果已经更新了,可是,对应于X(k|k-1)的covariance还没更新。
我们用P表示covariance:P(k|k-1)=A P(k-1|k-1) A’+Q (2)式(2)中,P(k|k-1)是X(k|k-1)对应的covariance,P(k-1|k-1)是X(k-1|k-1)对应的covariance,A’表示A的转置矩阵,Q是系统过程的covariance。
《信号检测与估计》第三章习题解答

∞ β
f
(x
|
H
0
)dx
+
P(H1
)C01
β −∞
f (x | H1)dx
∫ ∫ = 0.8
∞ − x2
e 8 dx +
0.4
β − (x−1)2 e 8 dx
2 2π β
2 2π −∞
3.3
只用一次观测值
x
对下面两个假设作出选择,H
0
:样本
x
为零均值,方差
σ
2 0
的高斯变量;H
1
:
样本
x
为零均值,方差 σ12 的高斯变量,且 σ12
dt
=
1 2
⎡ ⎢1 − ⎣
erf
⎜⎜⎝⎛
β 2σ
⎟⎟⎠⎞⎥⎦⎤
∫ β (q0 ) =
β −∞
∫ ∫ 1
− (x−1)2 e 2σ 2 dx = 1 −
2π σ
∞ β
1 2π σ
− (x −1)2 e 2σ 2
dx
=1−
1 2
⎜⎛ ⎜⎜⎝
2 π
∞ β −1
2σ
e−t
2
dt
⎟⎞ ⎟⎟⎠
=
1−
1 2
⎡ ⎢1 − ⎣
《信号检测与估计》习题解答
《信号检测与估计》第三章习题解答
3.1 在二元数字通信系统中,发送端等概发送 2V 和 0V 的脉冲信号,信道上迭加的噪声服从均值
为零,方差为σ 2 的正态分布,试用最大后验概率准则对接收信号进行判决。
解:由于
P(H1)
=
P(H 0
)
=
1 2
,且
测试信号分析与处理作业第三次作业第3题

% 含有频率f ,2f 和3f 的正弦波叠加原始信号Fs=8000; %采样频率8KHzf=500; %信号基频A=1;t=0:1/Fs:0.02; %产生时间序列x=A*sin(2*pi*f*t)+A*sin(4*pi*f*t)+A*sin(6*pi*f*t); %产生目标信号figure(1);subplot(2,1,1);plot(t,x);grid;title('原始信号');%FFT分析信号频谱len=512;y=fft(x,len); %对信号做len点FFT变换f1=Fs*(0:len/2-1)/len;subplot(2,1,2);plot(f1,abs(y(1:len/2)));grid;title('原始信号频谱')xlabel('频率(Hz)');ylabel('幅值');%数字滤波器设计,均采用巴特沃斯滤波器Rp=3; %通带最大衰减率为3dBRc=40; %祖代最小衰减率为40dB%IIR数字低通滤波器设计Fp=1.2*f;Fc=1.8*f;Wp=2*Fp/Fs;Wc=2*Fc/Fs;[N,Wn]=buttord(Wp,Wc,Rp,Rc);[B,A]=butter(N,Wn,'low');[H,W]=freqz(B,A,len,Fs);figuresubplot(2,1,1);plot(W,abs(H));grid;title('低通滤波器');xlabel('频率(Hz)');ylabel('幅值');xx=filter(B,A,x);yy=fft(xx,len);subplot(2,1,2);plot(f1,abs(yy(1:len/2)));grid;title('滤波后的信号频谱');xlabel('频率(Hz)');ylabel('幅值');%IIR 数字高通滤波器的设计Fp=2.6*f;Fc=2.2*f;Wc=2*Fc/Fs;[N,Wn]=buttord(Wp,Wc,Rp,Rc);[B,A]=butter(N,Wn,'high');[H,W]=freqz(B,A,len,Fs);figuresubplot(2,1,1);plot(W,abs(H));grid;title('高通滤波器');xlabel('频率(Hz)');ylabel('幅值');xx=filter(B,A,x);yy=fft(xx,len);subplot(2,1,2);plot(f1,abs(yy(1:len/2)));grid;title('滤波后的信号频谱');xlabel('频率(Hz)');ylabel('幅值'); %3.IIR 数字带通滤波器设计Fp=[1.8*f 2.2*f];Fc=[1.6*f 2.8*f];Wp=2*Fp/Fs;Wc=2*Fc/Fs;[N,Wn]=buttord(Wp,Wc,Rp,Rc);[B,A]=butter(N,Wn,'bandpass');[H,W]=freqz(B,A,len,Fs);figuresubplot(2,1,1);plot(W,abs(H));grid;title('带通滤波器');xlabel('频率(Hz)');ylabel('幅值');xx=filter(B,A,x);yy=fft(xx,len);subplot(2,1,2);plot(f1,abs(yy(1:len/2)));grid;title('滤波后的信号频谱');xlabel('频率(Hz)');ylabel('幅值');%3.IIR数字带阻滤波器设计Fp=[1.6*f 2.8*f];Fc=[1.8*f 2.2*f];Wc=2*Fc/Fs;[N,Wn]=buttord(Wp,Wc,Rp,Rc); [B,A]=butter(N,Wn,'stop'); [H,W]=freqz(B,A,len,Fs); figuresubplot(2,1,1);plot(W,abs(H));grid;title('带阻滤波器');xlabel('频率(Hz)');ylabel('幅值');xx=filter(B,A,x);yy=fft(xx,len);subplot(2,1,2);plot(f1,abs(yy(1:len/2))); grid;title('滤波后的信号频谱'); xlabel('频率(Hz)');ylabel('幅值');。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
(2)
(a) 求该假设检验的似然比检测器并确定判决域(即确定样本空间划分方法); (b) 当P0 = 1/2, P0 = 2/3, P0 = 1/3时, 分别计算可能获得的最小错误概率。 2. 考虑下面观测样本为y 的简单二元假设检验问题: ) ( −1 H0 : f0 (y ) = rect y 2 ; ( ) 1 y−1 H1 : f1 (y ) = rect , 2 2
(a) 分别给出S 和N 的边缘概率密度函数fS (s)和fN (n); (b) 证明S 和N 统计独立; (c) 推导Y = S + N 的概率密度函数, 并画出图形. (d) 假定fS (s)和fN (n)对应假设H1 和H0 成立下的条件概率密度函数, 即f1 (y ) = fS (y ), f0 (y ) = fN (y ). 现给定N0 = 2和α = 1, 请写出最小错误概率检测器. (e) 分别计算在P1 = P0 /3, P1 = P0 , P1 = 2P0 /3时的最小错误概率. 5. 一个三元通信系统的表达式可以由下面的公式来表示: y = x + n; (6)
信号检测与估值第三次作业
November 6, 2012
1. 考虑下面观测样本为y 的简单二元假设检验问题: ( ) H : f (y ) = 1 rect y − 1 ; 1 1 2 2 H0 : f0 (y ) = e−y , y > 0. 其中, rect(t) { 1, if − 1 < t < 1; 0, otherwise.
其中, y 是接收机观测到的样本, x是发射的信号, n是接收机端引入的高斯白噪声(均值为0, 方差为σ 2 ). x的取值可为−A/2, 0, 或+A, 分别对应假设H0 , H1 和H2 . H0 , H1 和H2 先验分布等概. (a) 要求确定最小错误概率检测器的形式, 画出判决域; (b) 最小错误概率. 6. 考虑下面的简单二元假设检验问题: { H1 : Y = S + N ; H0 : Y = N ; 其中S 和N 为统计独立的随机变量. 其概率密度函数分别为 { 1 2 , −1 < s < 1; fS (s) = 0: otherwise; and fN (n) = {
1 4 , −2
(7)
(8)
< n < 1; otherwise;
0:
(9)
(a) 当似然比检测器门限设置为λ = 1/4, λ = 1, λ = 2时, 分别给出对应的判决域; (b) 计算(a)中队应的虚报和检测概率; (c) 画出ROC曲线.
2
y 0.
(3)
(a) 求该假设检验的似然比检测器并确定判决域(即确定样本空间划分方法); (b) 计算虚报概率PF 和漏报概率PM . 3. 一个二元通信系统的表达式可以由下面的公式来表示: y = x + n; (4)
其中, y 是接收机观测到的样本, x是发射的信号, n是接收机端引入的高斯白噪声(均值为0, 方差为σ 2 ). x的取值可为−A 或+A, 分别对应假设H0 和H1 . (a) 要求确定最小错误概率检测器的形式; (b) 给出先验分布满足P1 = P0 /3, P0 = P1 , P1 = 5P3 /3情况下的最小错误概率检测器, 并计算相应的最小错误概率. 4. 接收机输出为信号电压S 和噪声电压N 之和. 其二者的联合概率密度函数为 fSN (s, n) = α −αs e , N0 1 0 ≤ s < ∞ & 0 ≤ n ≤ N0 . (5)
