高等数学定理证明
高等数学费马定理

高等数学中费马定理是指当n>2时,方程x^n+y^n=z^n无整数解。
这个定理是费马在阅读丢番图(Diophatus)《算术》拉丁文译本时提出的,但他没有给出证明。
随后,1678年G·W莱布尼兹证明了n=4时定理成立;1770年C·欧拉证明了n=3和4的情形;P·G狄利克雷和G·拉梅分别证明了n=5和7的情形;1884年E·E库默尔创立了理想数,从而证明了当n是介于2与100之间的奇数p(除去(p=37,59和67)时,定理成立。
1995年,安德鲁·怀尔斯等人将费马猜想证明过程发表在《数学年刊》,成功证明了这一定理。
费马大定理表述虽简单,但它的证明耗费了数代人的努力,许多数学家在证明过程中发现了许多新的数学理论,拓展了新的数学方法,证明费马大定理的过程可以算得上是一部数学史。
高等数学-中值定理证明
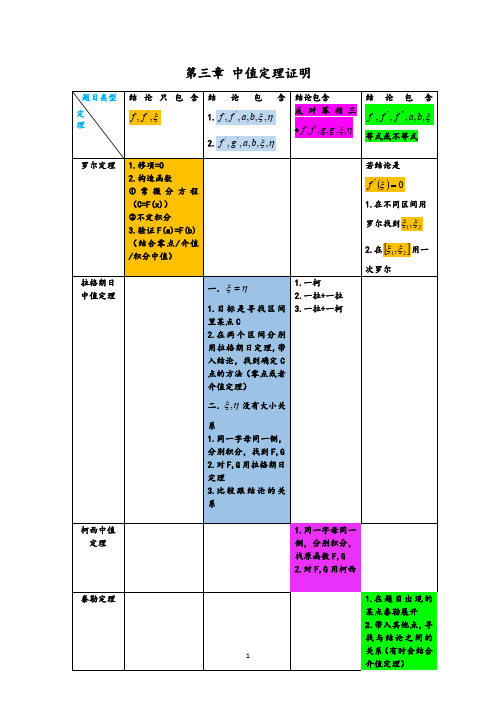
若结论是
f '' 0
1.在不同区间用
罗尔找到 1,2
2.在 1,2 用一
次罗尔
柯西中值 定理
1.同一字母同一 侧,分别积分, 找原函数 F,G 2.对 F,G 用柯西
泰勒定理
1.在 题 目 出 现 的
某点泰勒展开
2.带入其他点,寻
找与结论之间的
1
关系(有时会结合
介值定理)
1.闭区间上连续函数定理 ① ② ③ ④ 2.微分中值定理 ①
(1) 存在(0,1)内两个不同的点 , ,使得 f ' ( ) f ' () 2 .
(2)
存在(0,1)内两个不同的点 , ,使得
1 f ' ( )
1 f ' ()
2 .
(3) 存在(0,1)内两个不同的点 , ,使得 f ' ( ) f ' () 1 .
f ' ( ) (4) 存在(0,1)内两个不同的点 , 及大于零的常数 ,使得 f ' () (5) 对于任意的正整数 n,存在(0,1)内两个不同的点 , 及常数 0 ,
3
5.若 f (x) 在[0,1] 上可导,且当 x [0,1] 时有 0 f (x) 1,且 f (x) 1,证明:在 (0,1) 内有且仅有一个点 使得 f ( )
6.设 f (x) 在[0,1]上连续,在(0,1)内可导,且 f (0) = f (1) =0, f (1 ) =1。试证 2
②
③
④
3.积分中值定理 ① ②
不等式证明思路 构造函数(利用极值) 拉格朗日中值定理 函数凹凸性定义
2
1.若 f (x) 在 [a,b] 上连续,在 (a,b) 上可导, f (a) f (b) 0 ,证明: R , (a,b) 使得: f ( ) f ( ) 0
高数极限证明方法

高数极限证明方法在高等数学中,极限是一个十分重要的概念。
极限是函数趋于某个点或无穷时的一种特殊情况,它能够描述函数在该点的局部特性,如连续性、可导性等。
在证明高数极限的过程中,有一些基本的方法和原则可以被应用。
首先,我们先来看一下高数中的一些极限基本定理,它们是证明极限的基础:1.极限的唯一性定理:如果函数f(x)的极限存在,则该极限是唯一的。
也就是说,一个函数只能趋于一个极限。
2.有界收敛定理:如果一个函数在某个点a 的某个去心领域中有界且有极限,那么这个函数在该点必然有极限。
3.夹逼定理:如果对于所有的x∈X,都有g(x)≤f(x)≤h(x),并且g(x)和h(x)的极限都为L,那么f(x)的极限也为L。
4.极限的四则运算法则:如果函数f(x)和g(x)在点a处有极限,那么它们的和、差、积以及商(只要g(a)≠0)在该点也有极限,并且极限值等于对应的运算。
掌握了以上基本定理后,我们可以运用以下几种证明方法来证明高数中的极限问题:1.ε-δ方法:这是一种直接证明的方法,通过选取合适的δ,使得当0<|x-a|<δ时,相应地有|f(x) - L| <ε,其中ε为一个正数。
该方法常用于连续函数的极限证明。
2.夹逼法:当无法直接计算函数的极限时,我们可以使用夹逼法来确定极限值。
夹逼法的关键是找到两个已知函数,使得它们的极限都等于L,并且函数f(x)一直被这两个函数夹在中间。
3.断点法:当函数在某个点a处无极限时,我们可以考虑将该点变成一个极限点,并引入无穷大或无穷小,从而计算出极限。
此时,我们需要观察并分析函数在该点的性质,如左极限和右极限是否存在。
4.局部性质法:当要证明函数在某个点a处有极限时,我们可以先观察该点的局部性质,如连续性、可导性等,然后利用这些性质推导出极限。
总结一下,证明高数极限时,我们可以采用ε-δ方法来直接证明,也可以用夹逼法来确定极限值,还可以使用断点法来处理无极限的情况,最后可以利用函数的局部性质来推导极限。
高等数学定理

数学基础知识总结第一部分高数第一章函数与极限1、函数的有界性在定义域内有f(x)≥K1则函数f(x)在定义域上有下界,K1为下界;如果有f(x)≤K2,则有上界,K2称为上界。
函数f(x)在定义域内有界的充分必要条件是在定义域内既有上界又有下界。
2、函数的单调性、奇偶性、周期性(指最小正周期)3、数列的极限定理(极限的唯一性) 数列{xn}不能同时收敛于两个不同的极限。
定理(收敛数列的有界性)如果数列{xn}收敛,那么数列{xn}一定有界。
如果数列{xn}无界,那么数列{xn}一定发散;但如果数列{xn}有界,却不能断定数列{xn}一定收敛,例如数列1,-1,1,-1,(-1)n+1…该数列有界但是发散,所以数列有界是数列收敛的必要条件而不是充分条件。
定理(收敛数列与其子数列的关系)如果数列{xn}收敛于a,那么它的任一子数列也收敛于a。
●如果数列{xn}有两个子数列收敛于不同的极限,那么数列{xn}是发散的,如数列1,-1,1,-1,(-1)n +1…中子数列{x2k-1}收敛于1,{xnk}收敛于-1,{xn}却是发散的;同时一个发散的数列的子数列也有可能是收敛的。
4、函数的极限函数极限的定义中0<|x-x0|表示x≠x0,所以x→x0时f(x)有没有极限与f(x)在点x0有没有定义无关。
定理(极限的局部保号性)如果lim (x→x0)时f(x)=A,而且A>0(或A<0),就存在着点那么x0的某一去心邻域,当x在该邻域内时就有f(x) >0(或f(x) >0),反之也成立。
●函数f(x)当x→x0时极限存在的充分必要条件是左极限右极限各自存在并且相等,即f(x0-0)= f(x 0+0),若不相等则lim f(x)不存在。
●一般的说,如果lim(x→∞)f(x)=c,则直线y=c是函数y= f(x)的图形水平渐近线。
如果lim(x →x0)f(x)=∞,则直线x=x0是函数y= f(x)图形的铅直渐近线。
高等数学概念定理推论公式

高等数学概念、定理、推论、公式※ 函数及图形·和的绝对值不大于各项绝对值的和; ·差的绝对值不小于各项绝对值的差; ·乘积的绝对值等于各项绝对值的乘积;·商的绝对值等于被除数及除数的绝对值的商。
·假设自变量x 在定义域X 内每获得一确定值时,函数只有一个确定值与之对应,这种函数叫单值函数;否那么就是多值函数。
·假设函数y=f(x)当x 改变符号时函数值也只改变符号,即F(-x)=-f(x),此函数叫奇函数,奇函数对称于原点;假设x 改变符号,函数值不变,即f(-x)=f(x),即为偶函数,偶函数对称于y 轴。
·反函数的图形与直接函数(原函数)的图形对称于直线y=x※ 数列的极限及函数的极限·假如数列收敛,必然是有界的; ·有界的数列不必然都是收敛的; ·无界数列必然是发散的。
·假如0lim ()x x f x A →=,而且A >0(或A <0),那么就存在着点x 0的某一邻域,当x 在该领域内,但x ≠x 0时,f(x)>0(或f(x )<0)。
·假如f(x)≥0(或f(x)≥0),而且0lim ()x x f x A →=,那么A ≥0(或A ≤0)。
·函数f(x)当x →x0时极限存在的充分必要前提是左右极限都存在且相等。
·假如函数()f x 为无穷大,那么1()f x 为无穷小;反之亦然(()f x ≠0)。
·具有极限的函数可表示为等于其极限的一个常数及无穷小的和;反之,假如函数可表示为常数及无穷小,那么该常数就是函数的极限。
·有限个无穷小的和(代数和)也是窥小。
·有界函数与无穷小的乘积是无穷小,(常数乘以无穷小为无穷小,有限个无穷小的积是无穷小)。
·以极限不为零的函数除无穷小所得的商是无穷小。
高等数学 第3章 第一节 中值定理
(函数
即
6
,
y
5
6
ln sin x
是 y
是初等函数, 且当
x
6
ln sin x 定义域内的一部分;
,
5
6
时,cossixn
y'
sin x
x
0,
cot x.)
且ln s in
lnsin 5
ln 1 .
6
62
令 y' cos x cot x 0, sin x
得 x , 5 .
F(b) F(a)
( x) 满足罗尔定理的全部条件,且:
'(x) f '(x) f (b) f (a) F '(x)
F(b) F(a)
Y F , f Fb, f b
C•
•B
由罗尔定理,至少存在一点 ∈(a,b) ,
即:
使
f
'( )
'( ) 0,
f (b) f (a) F '( ) 0
即 1、 2、 3都是方程 f 'x 0 的根。 注意到 f ' x 0 为三次方程, 它最多有三个根。
我们已经找到它的三个实根
1、 2、 3 ,
所以这三个根就是方程
f 'x 0 的全部根。
14
例3 证明当x 0时, x ln1 x x
1 x
证 设f x ln1 x, 显然,函数 f x 在 0, x 上满足
f (b) f (a)
O a
bx
结论等价于: f f b f a
ba
或: f f b f a 0
ba
AB的方程为:
泰勒中值定理证明题

泰勒中值定理证明题泰勒中值定理是高等数学中的一项定理,包含了麦克劳林公式。
具体来说,如果函数f(x)在含有x0的某个开区间(a,b)内具有直到n+1阶的导数,那么对于任意x∈(a,b),都有:f(x)=f(x0)+f′(x0)(x−x0)+f″(x0)2!(x−x0)2+....+f(n)(x0)n!(x−x0)n+Rn(x),其中Rn(x)=f(n+1)(ξ)(n+1)!(x−x0)n+1,ξ的范围介于x0和x之间。
泰勒中值定理证明题:设函数f(x)在闭区间[-1,1]上具有三阶连续导数,且f(-1)=0,f(1)=1,f'(0)=0,证明:在开区间(-1,1)内至少存在一点ξ,使f'''(ξ)=3。
证:由于f(x)三阶可导,可考虑泰勒公式。
根据泰勒中值定理,对于任意的x∈(-1,1),存在ξ∈(-1,1),使得f(x)=f(0)+f'(0)x+(1/2)f''(ξ)x^2+[f'''(ξ)/3!]x^3。
代入已知条件,有f(1)=f(0)+f'(0)+(1/2)f''(ξ)+[f'''(ξ)/3!]。
解这个方程得到,f'''(ξ)/3!=1-f(0)-f'(0)+(1/2)f''(ξ)。
又因为f(-1)=0,所以有f(-1)=f(0)-f'(0)-(1/2)f''(ξ)+[f'''(ξ)/3!]=0。
联立上述两个方程,可以解出f'''(ξ)=3。
因此,我们证明了在开区间(-1,1)内至少存在一点ξ,使得f'''(ξ)=3。
2021考研数学高数必考的4个定理证明

2021考研数学高数必考的4个定理证明来源:文都图书高数是考研数学考察的重要科目,也是比较难的一门,其中有4个定理是高数的高频考点,我们一起来学习一下该如何运用这几个定理。
一、微分公式的证明2021年真题考了一个证明题:证明两个函数乘积的导数公式。
几乎每位同学都对这个公式怎么用比较熟悉,而对它怎么来的较为陌生。
实际上,从授课的角度,这种在2021年前从未考过的基本公式的证明,一般只会在基础阶段讲到。
如果这个阶段的考生带着急功近利的心态只关注结论怎么用,而不关心结论怎么来的,那很可能从未认真思考过该公式的证明过程,进而在考场上变得很被动。
这里给2021考研学子提个醒:要重视基础阶段的复习,那些真题中未考过的重要结论的证明,有可能考到,不要放过。
当然,该公式的证明并不难。
先考量f(x)*g(x)在点x0处的导数。
函数在一点的导数自然用导数定义实地考察,可以按照导数定义写下一个音速式子。
该音速为“0分之0”型,但无法用洛必达法则,因为分子的导数不好算是(乘积的导数公式恰好就是要证的,无法用!)。
利用数学上常用的堆砌之法,提一项,减至一项。
这个“无中生有”的项要和前后都存有联系,易于加公因子。
之后分子的四项两两接合,除以分母后考量音速,不难得出结论结果。
再由x0的任意性,便获得了f(x)*g(x)在任一点的导数公式。
类似可考虑f(x)+g(x),f(x)-g(x),f(x)/g(x)的导数公式的证明。
二、微分中值定理的证明这一部分内容比较丰富,包括费马引理、罗尔定理、拉格朗日定理、柯西定理和泰勒中值定理。
除泰勒中值定理外,其它定理要求会证。
费马定理的条件存有两个:1.f'(x0)存有2.f(x0)为f(x)的极值,结论为f'(x0)=0。
考量函数在一点的导数,用什么方法?自然想起导数定义。
我们可以按照导数定义写下f'(x0)的音速形式。
往下如何推理小说?关键必须看看第二个条件怎么用。
