等积变换经典例题
等积变形专项练习

等积变形专项练习
1。
在一个底面积是31.4平方厘米的长方体玻璃容器中,有一个底面半径是1厘米的圆锥形铝块完全浸在水中,当从水中取出铝块时,容器的水面下降了0。
2厘米。
这个圆锥形铝块高多少厘米?
2。
用半径10cm高7cm的圆柱形泥巴揉成半径一样大的圆锥形,圆锥的高是多少厘米呢?
3.一个圆柱形的水桶,内部的底面半径是20厘米,高是45厘米,里面盛有30厘米深的水。
将一个底面半径是15厘米的圆锥形铁块完全沉进水里,水不溢出,水面上升了3厘米,圆锥形铁块的高是多少?
4.有一段钢可做一个底面直径8厘米,高9厘米的圆柱形零件.如果把它改制成高是12厘米的圆锥形零件,零件的底面积是多少平方厘米?
5。
一个圆柱形容器的底面半径是4分米,高6分米,里面盛满水,把水倒在棱长是8分米的正方体容器中,水深多少分米?
6.将一个底面直径是20厘米、高是9厘米的金属圆锥,全部浸没在直径是40厘米的圆柱形水槽中且水未溢出。
水槽中的水面会升高多少厘米?
7。
把一个长2米的圆柱截去4分米后,原来的表面积就减少了25.12平方分米,原来圆柱的体积是多少立方分米?
8。
在一个底面是边长为2分米的正方形的长方形水槽中,放入一块青铜(完全浸没在水中),水面上升1分米且水未溢出.(水槽厚度忽略不计)
(1)求这块青铜的体积.
(2)如果把这块青铜铸成一个底面直径是2分米的圆柱,它的高是多少?(得数保留一位小数)
9.(拓展)在一个圆柱形储水桶里,把一段半径是5cm的圆钢全部放入水中,水面就上升9cm;把圆钢竖着拉出水面8cm长后,水面就下降4cm。
求圆钢的体积。
等积变形练习题

等积变形练习题等积变形是一种在数学中常见的概念,它涉及到图形或物体形态的变化,同时保持其面积或体积不变。
通过等积变形,我们可以研究图形之间的关系以及解决一些复杂的数学问题。
本文将介绍一些常见的等积变形练习题,帮助读者加深对等积变形的理解与应用。
1. 矩形的等积变形假设有一片固定面积的矩形,在等积变形的过程中,我们可以改变矩形的长和宽,但保持面积不变。
那么问题来了:在固定面积条件下,矩形的长和宽的关系是怎样的?解答:设矩形的长为x,宽为y,由题意可知xy=常数。
我们可以通过解方程的方法来找出x和y的关系。
将这个方程改写为y=常数/x的形式,其中常数为C。
这意味着y和x成反比例关系,当x增大时,y会减小;当x减小时,y会增大。
这样我们就找到了矩形的等积变形规律。
2. 圆的等积变形与矩形不同,圆的等积变形是指在保持圆的面积不变的情况下改变圆的半径。
现在考虑一个具体的例子:题目:一个圆的半径为r,它的面积为S。
将该圆按照一定的方式等面积地变形成一个新的圆,新的圆的半径为r'。
请问,r'与r之间的关系是怎样的?解答:圆的面积公式为S=πr²,保持面积不变意味着S=πr²=π(r')²。
将这个方程进行变形,可以得到r' = √(S/π)。
也就是说,在等积变形的过程中,圆的半径与原来的半径r之间的关系是r' = √(r²S/S'),其中S'是新圆的面积。
3. 立方体的等积变形对于一个正立方体,它的体积可以通过边长的立方来计算。
在等积变形中,我们可以改变立方体的边长,但保持体积不变。
接下来让我们看一个例子:题目:一个正立方体的边长为a,它的体积为V。
将该立方体等面积地变形成一个新的立方体,新的立方体的边长为b。
请问,b与a之间的关系是怎样的?解答:立方体的体积公式为V=a³,保持体积不变意味着a³=b³。
【小升初专项训练】04 等积变形

第5讲等积变形第一关三角形的等积变形【例1】如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为 平方厘米。
【答案】12.25【例2】如图,E、F分别是梯形ABCD两腰上的中点,已知阴影部分的面积是43c㎡,那么梯形ABCD 的面积是多少?【答案】172【例3】如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是多少平方厘米? 【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗?(两个长方形面积相等)【答案】A与B的面积相等【例5】如图,在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB,留下两个阴影部分直角三角形AED和DFC.若AD=8cm,CD=12cm,则阴影部分面积为多少?给出答案并说明你的计算依据.【答案】48【例6】如图,在直角三角形中有一个正方形,已知BD=10厘米,DC=7厘米,阴影部分的面积是多少?【答案】35平方厘米【例7】如图,梯形ABCD的面积是36,下底长是上底长的2倍,阴影三角形的面积是多少?【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大?【答案】图中甲乙的面积相等【例9】如图,在三角形ABC中,D是BC上靠近C的三等分点,E是AD中点,已知三角形ABC的面积为1,那么图中两个阴影三角形面积之和是多少?【答案】0.4【例10】已知△ABC面积为5,且BD=2DC,AE=ED,求阴影部分面积.要求写出关键的解题推理过程.【答案】2【例11】如图,将一个梯形分成四个三角形,其中两个三角形的面积分别为10与12.已知梯形的上底长度是下底的.请问:阴影部分的总面积是多少?【答案】23【例12】如图,已知梯形ABCD中,CD=10,梯形ABCD的高是4,那么阴影部分的面积是多少。
【答案】20【例13】(1)如图1,阴影部分的面积是多少?(2)如图2,一个长方形长4厘米,宽3厘米.A为长方形内的任意一点,阴影部分的面积是多少?【答案】(1)100;(2)6【例14】如图,在图中△ABE、ADF和四边形AECF面积相等.阴影部分的面积是多少?【答案】15【例15】如图,两个正方形(单位:厘米)中阴影部分的面积是多少平方厘米?【答案】8【例16】由面积为1,2,3,4的矩形拼成如图的长方形,图中阴影部分的面积为多少?【答案】【例17】如图所示,正方形ABCD的对角线BD长20厘米,BDFE是长方形.那么,五边形ABEFD的面积是多少平方厘米。
小学五年级数学思维专题训练—等积变形(含答案解析)
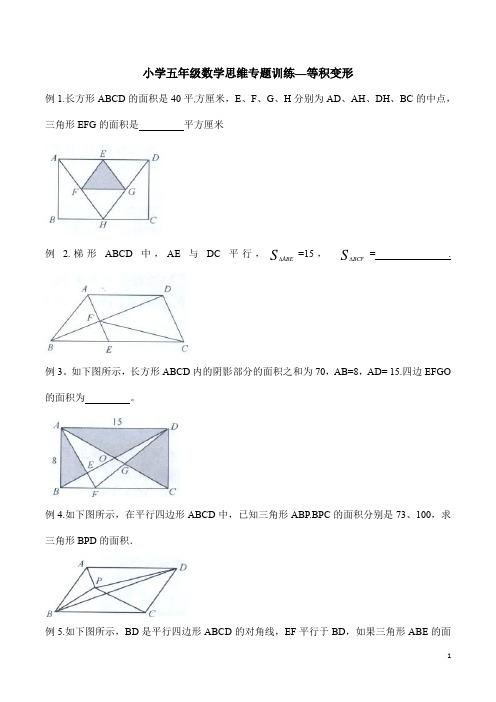
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
等积变形例题

解 在直角三角形CDH和直角三角形EKD 中,CD=DE 又∵∠EDK=180°-∠CDH-90° ∠DCH=180°-∠CDH-90° ∴ DCH与 EDK完全相等。 而ABCD是等腰梯形
K A
E
故CH=(BC-AD) ÷2 =(35-23) ÷2
23
D F
=6(厘米) ∴DK=CH=6厘米
B
35
求绿色四边形的面积。 解 连BF,则四边形BCDF为梯形。 4 6 6 ∵S黄÷S红=6÷4=1.5 ∴S白÷S红=1.5×1.5=2.25 ∴S白=S红×2.25=4 ×2.25=9(平方厘米) ∴S绿=S白+S黄-S红 =9+6-4=11(平方厘米) 答:绿色四边形ABEF的面积为11平方厘米。
S KGE=S C D S DGE=S F G P 所以 阴影部分面积= H A B 解:14÷4=3.5(厘米) 正方形BEFG的周长=14厘米, E K
FGE BGE
正方形BEFG的面积
3.5×3.5=12.25(平方厘米) 求阴影部分面积。 答:图中阴影部分面积是 12.25平方厘米。
分析与解: 分析与解:
答:丙、丁两个三角形面 积之和是甲、乙两个三角 形面积之和的1.25倍。
分析与解:
等积变形
例5
G
F
∵∠DAB=∠GAE=90° ∴ ∠GAD+ ∠EAB =360°-90 °×2 =180°
D
A C
E
∴三角形BAE绕A点顺时针旋转, 使AB与AD重合,这时,点E落 在点H,且G,A,H在一条直线上。 ∵AG=AE=AH,三角形DAH与 三角形DAG等底同高, ∴S DAH=S DAG 答:内圈三角形石板的总面积 与外圈石板的总面积一样大。
等积变形的应用——两道赛题的解法

等积变形的应用——两道赛题的解法赛题一:给定一个三角形ABC,给定它的边长a,b,c,要求把它变形成一个等腰直角三角形,且其新的三边为x,x,y。
解题思路:由等积变形定理可知,三角形ABC与新三角形ABC满足:$$\frac{a}{\sin A} = \frac{x}{\sin A'} = \frac{x}{\sin B'} = \frac{y}{\sin C'}$$解出新的三角形边长x,y的差分方程为:$$a\cdot\sin A = x\cdot\sin B = x\cdot\sin C = y\cdot\sinA'$$解得:$$x = \frac{a \cdot \sin A}{\sin B} = \frac{a \cdot \sinA}{\sin C}$$$$y = \frac{a \cdot \sin A}{\sin A'}$$赛题二:给定一个三角形ABC,给定它的边长a,b,c,要求把它变形成一个三角形,且其新的三边为x,y,z。
解题思路:由等积变形定理可知,三角形ABC与新三角形ABC满足:$$\frac{a}{\sin A} = \frac{x}{\sin A'} = \frac{y}{\sin B'} = \frac{z}{\sin C'}$$解出新的三角形边长x,y,z的差分方程为:$$a\cdot\sin A = x\cdot\sin A' = y\cdot\sin B' = z\cdot\sin C'$$解得:$$x = \frac{a \cdot \sin A}{\sin A'}$$$$y = \frac{a \cdot \sin A}{\sin B'}$$$$z = \frac{a \cdot \sin A}{\sin C'}$$。
三角形中的等积变换

【例1】用四种不同的方法,把任意一个三角形分成四个面积相 等的三角形。
A
A
A
B
C
B
C
B
C
【例2】用三种不同的方法将任意一个三角形分成三个小三角形, 使它们的面积比为1:3:4
A
A
A
C
B
C
B
C
【例3】如图,在梯形ABCD中,AC与BD是对角线,其交点O, 求证:△AOB与△COD面积相等。
A
O
D
B
C
【例4】如图,把四边形ABCD改成一个等积的三角形。
D
A
C B
【例5】如图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE 的面积为1平方厘米,求三角形ABC的面积。
A
E
D
B
C
【例6】如图,在△ABC中,BD=2AD,AG=2CG,BE=EF= FC=⅓BC,求四边形EFGD部分面积占三角形ABC面积的几分之 几?。
D
C F
A
E
B
A
D G B E F C
【例7】如图,ABCD为平行四边形,EF平行AC,如果△ADE的 面积为4平方厘米,求三角形CDF的面积。
D
C F
A
E
B
【例8】如图,四边形ABCD面积为1,且AB=AE,BC=BF, DC=CG,AD=DH,求四边形EFGH的面积。
H
C D E s1
G
s2 A
B
F
【练习】如图,三角形ABC的面积是24,D、E和F分别是。
等积变换问题

等积变换问题1、(山东烟台)如图,三个边长均为2的正方形重叠在一起,O 1、O 2是其中两个正方形的中心,则阴影部分的面积是 .2、如图,正方形ABCD 的边长为2,点E 在AB 边上.四边形EFGB 也为正方形,设△AFC 的面积为S ,则 ( )A .S=2B .S=2.4C .S=4D .S 与BE 长度有关3、(广西南宁)正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,正方形BEFG 的边长为4,则△DEK 的面积为( ) A .10 B .12 C .14 D .164.(2011重庆綦江)如图,已知A (4,a ),B (-2,-4)是一次函数y =kx +b 的图象和反比例函数xm y 的图象的交点.(1)求反比例函数和一次函数的解析式; (2)求△AOB 的面积.5、如图,矩形OABC 的两边OA ,OC 在坐标轴上,且OC =2OA ,M ,N 分别为OA ,OC 的中点,BM 与AN 交于点E ,且四边形EMON 的面积为2,6. (2011陕西,8,3分) 如图,过y 轴正半轴上的任意一点P ,作x 轴的平行线,分别与反比例函数xy x y 24=-=和的图象交于点A 和点B ,若点C 是x 轴上任意一点,连接AC 、BC ,则△ABC 的面积为 ( )A .3B .4C .5D .67. (2011河北,12,3分)根据图5—1所示的程序,得到了y 与x 的函数图象,过点M 作PQ ∥x 轴交图象于点P ,Q ,连接OP ,OQ.则以下结论 ①x <0时,x2y =,②△OPQ 的面积为定值, ③x >0时,y 随x 的增大而增大 ④MQ=2PM⑤∠POQ 可以等于90°图5—2图5—1PQM其中正确的结论是( )A .①②④B .②④⑤C .③④⑤D .②③⑤图1ABCPDEDC图3图4 CD图2BC E 8、如图1,在直角梯形ABCD 中,AD ∥BC ,∠B =∠A =90°,AD =a ,BC =b ,AB =c ,操作示例我们可以取直角梯形ABCD 的非直角腰CD 的中点P ,过点P 作PE ∥AB ,裁掉△PEC ,并将△PEC 拼接到△PFD 的位置,构成新的图形(如图2).思考发现 小明在操作后发现,该剪拼方法就是先将△PEC 绕点P 逆时针旋转180°到△PFD 的位置,易知PE 与PF 在同一条直线上.又因为在梯形ABCD 中,AD ∥BC ,∠C +∠ADP =180°,则∠FDP +∠ADP =180°,所以AD 和DF 在同一条直线上,那么构成的新图形是一个四边形,进而根据平行四边形的判定方法,可以判断出四边形ABEF 是一个平行四边形,而且还是一个特殊的平行四边形——矩形.实践探究(1)矩形ABEF 的面积是 ;(用含a ,b ,c 的式子表示) (2)类比图2的剪拼方法,请你就图3和图4的两种情形分别画出剪拼成一个平行四边形的示意图.联想拓展 小明通过探究后发现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.如图5的多边形中,AE =CD ,AE ∥CD ,能否象上面剪切方法一样沿一条直线进行剪切,拼成一个平行四边形?若能,请你在图中画出剪拼的示意图并作必要的文字说明;若不能,简要说明理由.9、(本题10分)九年级数学兴趣小组组织了以“等积变形”为的主题的课题研究. 第一学习小组发现:如图(1),点A 、点B 在直线1l 上,点C 、点D 在直线2l 上,若1l ∥2l ,则ABD ABC S S ∆∆=;反之亦成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等积变换
1、等面积图形拼接类
1、小明遇到一个问题:5个同样大小的正方形纸片排列形式如图1所示,将它们分割后拼接成一个新的正方形.他的做法是:按图2所示的方法分割后,将三角形纸片①绕AB 的中点O 旋转至三角形纸片②处,依此方法继续操作,即可拼接成一个新的正方形DEFG .
请你参考小明的做法解决下列问题:
(1)现有5个形状、大小相同的矩形纸片,排列形式如图3所示.请将其分割后拼接成
一个平行四边形.要求:在图3中画出并指明拼接成的平行四边形(画出一个..符合条件的平行四边形即可);
(2)如图4,在面积为2的平行四边形ABCD 中,点E 、F 、G 、H 分别是边AB 、 BC 、
CD 、DA 的中点,分别连结AF 、BG 、CH 、DE 得到一个新的平行四边形MNPQ . 请在图4中探究平行四边形MNPQ 面积的大小(画图..
并直接写出结果).
2、根据所给的图形解答下列问题:
(1)如图1,△ABC 中,AB=AC ,∠BAC =90°,AD ⊥BC 于D ,把△ABD 绕点A 旋转,并拼接成一个与△ABC 面积相等的正方形,请你在图1中完成这个作图;
(2)如图2,△ABC 中,AB=AC ,∠BAC =90°,请你设计一种与(1)不同的方法,将这个三角形拆分并拼接成一个与其面积相等的正方形,画出利用这个三角形得到的正方形;
(3)设计一种方法把图3中的矩形ABCD 拆分并拼接为一个与其面积相等的正方形, 请你依据此矩形画出正方形,并根据你所画的图形,证明正方形面积等于矩形ABCD 的面积的结论
.
图1
图2
图3
图
4 A
B
C
D
图3
图2
图1
C
B
A
A
B C
D
2、等分面积类问题
1、请作一条直线通过割补把下面的四边形变成面积相等的三角形
2、如图,一块矩形的铁皮ABCD 被割去一个小矩形部分DEFG ,剩下一个五边形ABCGFE ,请作一条直线把剩下的五边形分成面积相等的两部分
3、(1)请过△ABC 边BC 中点D 作一条直线平分△ABC 的面积
(2)请过△ABC 边BC 中点D 外任一点P 作一条直线平分△ABC 的面积
4、如图,梯形纸片ABCD 中,AD ∥BC 且AB DC.设AD=a,BC=b.
B
C
A
D
G E D B
C
F
A D
B C
A D
B C
A
P
A
B
C
D
A
D
C
B 过AD 中点和B
C 的中点的直线可将梯形纸片ABC
D 面积分成面积相等的两部分. 请你再设计一种方法:
只须用剪子剪一次将梯形纸片ABCD 分割成面积相等的二部分,画出设计的图形并简要说明你的分割方法.
5、如图是王大爷的一块四边形菜地,在A 处有一口井,王大爷要想从A 处引一条笔直的水渠,且这条笔直的水渠将四边形菜地分成面积相等的两部分.请你为王大爷设计一条引水渠的方案,画出图形,并简要写出作图的主要步骤.。
