投入产出表
统计师《统计工作实务》辅导:投入产出表的基本平衡关系

投⼊产出表的基本平衡关系 在投⼊产出表中有⼀些基本的总量平衡关系。
具体归纳如下: 总投⼊=总产出 中间投⼊+增加值=总投⼊ 中间使⽤+最终使⽤=总产出 增加值合计=国内⽣产总值=最终使⽤合计 需要特别指出的是,在总产出与总投⼊之间具有平衡关系,不仅⼀个经济总体的总投⼊等于其总产出,⽽且在单个部门层次上总投⼊也等于其总产出。
2. 直接消耗系数与完全消耗系数及其应⽤ 通过对投⼊产出表进⾏投⼊产出分析,可以系统反映产业之间的关联。
其基本⽅法是以第Ⅰ象限为依据,通过中间投⼊流量计算各产业间的直接消耗系数和完全消耗系数。
直接消耗系数⼜称为投⼊系数或技术系数,⼀般⽤表⽰,其定义是:每⽣产单位j产品需要消耗i产品的数量。
直接消耗系数的计算公式是: 对所有产业计算直接消耗系数,结果构成⼀个系数矩阵,通常⽤A表⽰。
直接消耗系数只反映了产业间的直接联系,却不能反映产业间联系。
需要在直接消耗系数基础上计算完全消耗系数,既反映直接联系,也反映间接联系。
单个完全消耗系数⽤b表⽰,对所有产业计算完全消耗系数,所形成的矩阵⽤B表⽰,它是依据直接消耗矩阵计算得到的,其计算公式如下: B=(I-A)-1-I 式中(I-A)-1称为列昂惕夫逆矩阵,也是⽤来分析产业联系的重要⼯具。
如果⽤X表⽰总产出向量,⽤Y表⽰最终使⽤向量,则中间使⽤矩阵为AX,根据投⼊产出表中的平衡关系可以得到: AX+Y=X 从⽽有: (I-A)-1Y=X 把上式写成差分形式,得到 (I-A)-1 ?SY=?SX 可见列昂惕夫逆矩阵度量了最终使⽤与总产出之间联系的强度,它的含义是,如果每个产业的最终使⽤都增加⼀个单位,则各产业总产出将增加的单位数。
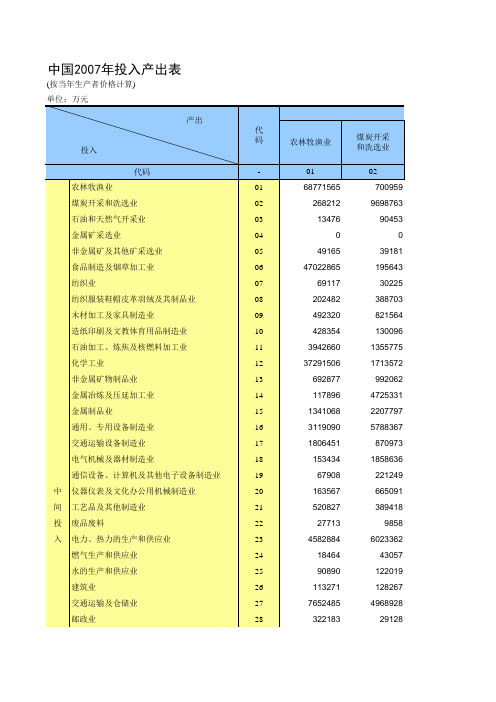
中国 42部门投入产出表
金属矿 采选业 04 68504 256257 696278 6342985 63897 150257 37717 269473 199685 127608 3768472 2879750 514886 895140 1436451 4347933 721423 944002 120793 257579 275664 44460 8289712 316644 90681 22263 2932612 11664
造纸印刷及 文教体育 用品制造业 10 5555932 784473 73112 0 0 554991 2750886 1118891 3163920 42627766 777097 20700403 411578 1897409 2269216 2009967 1227412 1069295 1531509 346966 664685 7791296 3356703 41029 470556 31394 3304644 67804
268213 1122458 1171394 2017930 138316 416766 143173 841767 129666 944730 238528 337408 158188 23442 52160456 21250239 7346723 4946838 10746273 44290073 96450530
非金属矿及 其他矿采选业 05 10190 88272 470581 0 2579576 111883 22762 169094 72528 87847 1558528 4086018 1485036 285196 354264 2215819 544602 426521 61021 105672 234257 327861 2509609 204376 60977 12714 2477216 11431
投入产出表PPT课件

.
1
在经济活动中分析投入多少财力、物力、
人力,产出多少社会财富是衡量经济效益高
低的主要标志。投入产出技术正是研究一个
经济系统各部门间的“投入”与“产出”关 系的
数学模型,该方法最早由美国著名的经济学
家瓦.列昂捷夫(W.Leontief)提出,是目前
比较成熟的经济分析方法。
.
2
一、投入产出数学模型的概念
最终需求
投入
生 产 部 门
新 创 价 值
1 2 n
工资 纯收入 合计
1 2 n 消费 累计 出口
x11 x12 x1n x 21 x 22 x 2 n
xn1 xn2
x nn
v1 v2 vn m1 m2 mn z1 z2 zn
总投入
x1 x2 xn
合计
y1 y2 yn
总 产出
x1 x2 xn
ij定理723第j部门对第i部门的完全消耗系数满足方程ijkjikijij定理724设n个部门的直接消耗系数矩阵为a完全消耗系数矩阵为b则有证明由定理723知kjikijij21例例33假设某公司三个生产部门间的报告价值型投入产出表如表74产出投入中间消耗最终需求总产出610600250152536004001840625250030506000表74求各部门间的完全消耗系数矩阵
.
8
二、直接消耗系数
定义7.2.1 第j部门生产单位价值所消耗第i部
门的价值称为第j部门对第i部门的直接消耗
系数,记作a iji,j 1 ,2 , ,n 。
由定义得
aij
xiji,
xj
j1,2,,n
(7-17)
把投入产出表中的各个中间需求 x ij 换成相应
投入产出表的结构及中国投入产出表ppt课件

一、中国式投入产出表的基本表式
中国1997年投入产出表(按当年生产者价格计算)
中间使用
最终使用
产出
物质生产部门(共101个部门)
非物质街道部门 (共23个部门)
第一产业 第二产业
第三产业
投入
(共5个部门) (共85个部门)
(共34个部门)
物质生
中 产部门
间
(101个 部门)
投
入 非物质生
产部门 (23个部
表的左下角称为第Ⅲ象限,其宾栏项目与第Ⅰ象限宾 栏项目相同,其主栏项目有固定资产折旧、劳动者 报酬、生产税净额、营业盈余等。固定资产折旧单 独作为一行列出,根据需要可归并到第Ⅰ象限或第 Ⅲ象限。第Ⅲ象限如果包括固定资产折旧,则反映 各部门增加值的构成。
• 表的右下角称为第Ⅳ象限。从理论上讲该象限是反 映最终产品的再分配的情况,实际上再分配是很复 杂的经济问题。因此,目前该象限的应用还在研究 之中。
表的右上角称为第Ⅱ象限,其主栏项目与第Ⅰ象限 主栏项目相同,其宾栏项目有最终消费、资本形成、 进出口等。在实际编表时上述这些项目还可以细分。 该象限反映不参加本期生产的最终产品的使用情况;
资金是运动的价值,资金的价值是随 时间变 化而变 化的, 是时间 的函数 ,随时 间的推 移而增 值,其 增值的 这部分 资金就 是原有 资金的 时间价 值
资金是运动的价值,资金的价值是随 时间变 化而变 化的, 是时间 的函数 ,随时 间的推 移而增 值,其 增值的 这部分 资金就 是原有 资金的 时间价 值
(五)确定部门规模的一般原则
既要坚持纯部门划分的规定,又不要使部门划分过细。
在全面衡量需要与可能后确定一个适度的规模。 所谓“需要”,是指编制投入产出表的目的:如果用于
中国投入产出表部门分类解释

中国投入产出表部门分类解释【原创版】目录一、引言二、中国投入产出表的定义与作用1.投入产出表的定义2.投入产出表的作用三、中国投入产出表部门分类详细介绍1.农业部门2.工业部门3.服务业部门四、投入产出表在国民经济中的应用五、结论正文一、引言投入产出表是一种描述国民经济各部门之间生产、消费、投资等活动关系的经济分析工具。
在我国,投入产出表被广泛应用于政策制定、产业结构调整、经济发展规划等领域。
本文将对中国投入产出表的部门分类进行详细解释,以便更好地理解其在国民经济中的作用。
二、中国投入产出表的定义与作用1.投入产出表的定义投入产出表(Input-Output Table)是一种描述国民经济各部门之间生产、消费、投资等活动关系的矩阵表。
它通过表格形式展示了各部门之间的投入来源和产出使用去向,反映了经济系统中各个环节的相互依赖关系。
2.投入产出表的作用投入产出表在国民经济中具有重要作用,主要体现在以下几个方面:(1)分析产业结构和部门间相互依赖关系:通过投入产出表,可以清晰地了解各个部门的生产、消费和投资活动,以及它们之间的相互依赖关系,为政策制定者提供有关产业结构和部门间合作关系的信息。
(2)预测和规划国民经济发展:投入产出表可以反映国民经济中各个部门的发展趋势,有助于政府部门预测未来经济发展方向,制定合理的经济发展规划和政策。
(3)分析经济波动和传导机制:投入产出表可以展示经济系统中各个环节的相互依赖关系,有助于分析经济波动的来源和传导机制,为政策制定者提供应对经济波动的有效手段。
三、中国投入产出表部门分类详细介绍1.农业部门农业部门是国民经济的基础产业,主要包括种植业、林业、畜牧业、渔业等。
农业部门的主要任务是生产农产品,为国民经济其他部门提供原材料和食品。
2.工业部门工业部门是国民经济的主导产业,主要包括采掘业、制造业、电力、燃气及水的生产和供应业等。
工业部门的主要任务是通过生产和加工,将农业部门的原材料转化为各种工业产品,为国民经济其他部门提供生产资料和消费品。
投入产出表与模型投入产出分析知识介绍

数据来源
数据主要来源于统计调查、财务报告、行业协会等渠道。
数据质量审核
对收集到的数据进行质量审核,确保数据的准确性和完整性。
数据处理和分析
对数据进行处理和分析,包括数据的筛选、整理、计算等。
编制结果展示
表格形式展示
将编制结果以表格形式展示,包 括投入产出表、直接消耗系数表、 完全消耗系数表、最终使用表和 初次投入表等。
收集各部门之间的投入产出数据,编制直接消耗系数表,反映各部门 生产过程中的直接消耗关系。
编制完全消耗系数表
根据直接消耗系数表,推算出完全消耗系数表,反映各部门之间的间 接消耗关系。
编制最终使用表和初次投入表
根据完全消耗系数表,编制最终使用表和初次投入表,反映最终使用 和初次投入情况。
数据收集与策制定提供科学依据,帮 助政府和企业制定更加合理和有效的经济政策。
决策支持
投入产出表与模型可以为决策者提供全面的经济分析 和预测,帮助决策者做出更加明智和前瞻性的决策。
THANKS
感谢观看
智能化
借助人工智能和机器学习技术,投入产出表 与模型将实现智能化分析,自动识别数据规 律和趋势,为决策提供更精准的依据。
跨行业与跨区域的应用
跨行业
随着产业融合和跨界合作的发展,投入产出表与模型将应用于更多行业,帮助不同行业 之间实现资源共享和协同发展。
跨区域
随着全球化和区域一体化的发展,投入产出表与模型将应用于更广泛的区域,促进地区 间的经济交流和合作。
通过投入产出模型分析,可以预测经 济发展趋势,为制定经济发展规划提 供支持。
环境影响评价
通过投入产出模型分析,可以评估经 济发展对环境的影响,为环境保护提 供依据。
03
oecd投入产出表中文对照

oecd投入产出表中文对照摘要:一、OECD 投入产出表简介1.OECD 的背景介绍2.投入产出表的概念和作用二、OECD 投入产出表中文对照1.表格的列名及含义2.行名及含义3.数据的具体解读三、OECD 投入产出表的应用价值1.对经济发展的分析2.对政策制定的参考作用3.对学术研究的支持四、我国与OECD 投入产出表的对比1.我国投入产出表的编制情况2.与OECD 投入产出表的差异3.启示与借鉴正文:一、OECD 投入产出表简介OECD,全称经济合作与发展组织,是一个国际性的经济组织。
它致力于研究全球经济发展趋势,为成员国提供政策建议。
投入产出表是一种描述国民经济各部门之间生产、消费和投资活动的关系的矩阵表。
通过投入产出表,我们可以了解各部门之间的相互依赖关系,进而分析经济结构和政策效果。
二、OECD 投入产出表中文对照OECD 投入产出表包含了各个成员国在一定时期内的生产、消费和投资数据。
表格的主要列名包括:部门名称、总产出、中间消费、投资、政府消费、净出口等。
行名则包括各种生产要素和最终用途。
通过中文对照,我们可以更直观地理解表格中的数据含义。
三、OECD 投入产出表的应用价值OECD 投入产出表为政策制定者、经济学家和学者提供了丰富的信息,有助于分析经济发展趋势、研究政策效果和支撑学术研究。
例如,通过分析各部门的产出和投入,我们可以了解哪些部门对经济增长的贡献较大,进而制定有利于经济发展的政策。
四、我国与OECD 投入产出表的对比我国也编制了自己的投入产出表。
与OECD 投入产出表相比,我国的表格在部门划分、数据质量和编制方法上存在一定差异。
通过对比,我们可以发现我国在投入产出表编制方面还有待改进。
投入产出表

农业
煤炭开采和洗选 石油和天然气开 业 采业 02 305197 1011979 9607 0 28957 3940 23448 129048 264976 58092 446716 918833 322616 1659288 754646 1471976 26243 287263 0 14120 817540 111284 214325 162713 03 64 186662 322143 0 2654 14028 64796 125571 39489 71140 687906 480971 123297 599256 254288 817770 12445 257564 0 10897 485014 123700 333218 41242
25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 TII VA001 VA002 VA003 VA004 TVA TI
3222616 8655 87587 497113 6024148 128033 441832 7442914 515056 4513873 88544 664564 1769 69592 1599642 830467 209908 114122 44858 0 119482762 133159686 5446504 7649132 20049338 166304661 285787423
775673 8539 35766 9714 1091612 5694 444323 469845 209304 231952 13023 151576 993 9868 64034 87844 30514 10347 61173 0 8504332 4162017 1200841 980404 1057321 7400583 15904914
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
投入产出表
Ð Ö ä ¼ ¶ Í ë È
Ò² » ú þ² ¶ ú ý² È ú ϼ º Æ Û¾ Õ É ö Ô V Ó ¼ M µ Ö º ϼ Æ × Ü² úÖ µ
× Ü ×Ö î Õ£ ¨¹ ÊÓ Ã£ ©º ϼ Æ ú ² Óà ¾ ñ « ¹¹ ² ¹ Ì× Ê ¿ â´ æ ¾ »³ ö ³ »² Ò ú ¶ þ² ú È ý² ú º ϼ Æ Ï û· Ñ û Ï· Ñ Ð Î³ É Ô ö¼ Ó Ú ¿ º ϼ Æ ö 950 4068 120 5138 2547 60 780 540 20 3947 9085 1950 23140 2100 27190 7782 80 6300 610 300 15072 42262 441 3480 931 4852 1971 2730 320 -20 5001 9853 3341 30688 3151 37180 12300 2870 7400 1150 300 24020 61200 150 1260 210 1620 4804 4714 4682 14200 790 5600 1810 8200 5744 11574 6702 24020 9085 42262 9853 61300 м Ö ä² úÆ ·¨ £û Ϻ Ä£ ©
《国民经济核算》
作者:张裕民
第三章
投入产出核算
一、投入产出表 二、直接消耗系数
三、完全消耗系数
一、投入产出表的基本原理
(一)投入产出表的概念: 中间投入(中间消耗) 1、投入 最初投入(要素投入) 中间产出(中间产品) 2、产出 最终产出(最终产品)
3.投入产出表的概念:
是根据国民经济各部门生产中的 投入来源和使用去向纵横交叉组成的 一张棋盘式平衡表,揭示了国民经济 各部门间的相互依存、相互制约的数量 关系。
2、直接消耗系数与完全消耗系数的数量关系:
ห้องสมุดไป่ตู้
完全消耗系数 = 直接消耗系数 + 各轮间接消耗系数
2、性质:
完全消耗系数 > 直接消耗系数
第三章 重点掌握
本章重点:
1,投入产出表 1)四个象限内容。 2)基本平衡关系。 2,直接消耗系数的概念及计算。
汽车生产 钢材 生铁 轮胎 橡胶 引擎 钢材
直接消耗 第一轮间接消耗 第二轮间接消耗 电 力 消 耗 完 全 消 耗
铁矿石
煤
生铁
第三轮间接消耗
(一)直接消耗系数
1、概念:
直接消耗系数又称为中间投入系数, 是两个部门间直接存在的投入产 出关系的数量表现。
或:直接消耗系数 是某部门(j部门)为生产单位产品 所消耗的各部门(i部门) 的产品和服务 的数量。
$、¥、£)。
(三)投入产出表的基本平衡关系
1.从纵向看: 中间投入 + 最初投入 = 总投入 2.从横向看: 中间使用 + 最终使用 = 总产出 3.每个部门: 总收入 = 总产出 4.全国: 最初投入总计 = 最终产品总计。 第Ⅰ象限合计 = 第Ⅱ象限合计。
二、直接消耗系数和完全消耗系数
2、直接消耗系数的计算公式:
xij aij表示直接消耗系数; 表示j部门生产时所消耗的i产品数量; Xj表示j部门的总产出。
aij
xij Xj
(i, j 1,2, n)
(二)完全消耗系数(bij)
1、概念:反映j部门生产单位最终产品,要直接和间接
消耗 i部门生产的货物或服务的数量之和。
“投入产出表”简表
产出
投入 中间投入
中间产出
最终产出
总产出
Ⅰ Ⅱ (技术经济联系)(最终产品的 (直接消耗系数)规模和结构 ) Ⅲ Ⅳ (增加值或最初 (再分配关系) 投入的构成 )
最初投入
总投入
(二)投入产出表的种类
1、按计量单位: 实物型投入产出表。(实物单位)(吨、件、台)。 价值型投入产出表。 (货币单位)( 2、按时间期限: 静 动 态投入产出表。 (期初、期末)。 态投入产出表。 (月、季、年)。
