大学物理-磁场 安培环路定律
合集下载
大学物理课件：16-5 磁场的高斯定理和安培环路定理
B2
dl2
r2
l
B2
dl2
0I
2π
d
B1
dl1
0I
2π
d
B dl 0I d d
l
2π L1
L2
0I
2π
0
第16章 稳恒磁场
8
大学
16-5 磁场的高斯定理和安培环路定理
物理
多电流情况
I1
I2
I3
B
B1
B2
B3
Bdl
l
0 (I 2
I3)
以上结果对任意形状
l
的闭合电流（伸向无限远 的电流）均成立.
第16章 稳恒磁场
2
大学
16-5 磁场的高斯定理和安培环路定理
物理
enB
s s
B
磁通量：通过某一曲 面的磁感线数为通过此曲 面的磁通量.
Φ BS cosBS
Φ B S B enS
B dS
dΦ B dS
B dΦ BdS cos
s
Φ s BdS
单位 1Wb 1T 1m2
第16章 稳恒磁场
•
•
O’
磁场磁力线：
••••••••••••••
R
为什么磁力 线画成均匀 的？
B
• • • • • • • • • • • • • •
R
A B1 B
D
B2C
作安培环路L ABCDA
B dl
L
0
L内
Ii
0
B dl L
AB
B1
dl
B dl
BC
CD B2 dl
3
大学
16-5 磁场的高斯定理和安培环路定理
大学物理安培环路定理
10-4 安培环路定理静电场的一个重要特征是电场强度E 沿任意闭合路径的积分等于零，即0d =⋅⎰l E l，那么，磁场中的磁感强度B 沿任意闭合路径的积分⎰⋅ld lB 等于多少呢？可以证明：在真空的稳恒磁场中，磁感强度B 沿任一闭合路径的积分（即B 的环流）的值，等于0μ乘以该闭合路径所包围的各电流的代数和，即∑⎰==⋅ni lI10 d il B μ （10-8）安培环路定理与静电场环路定理的比较 讨论：安培环路定理的证明如图(a)所示，有一通有电流I 的长直载流导线垂直于屏幕平面，且电流流向垂直屏幕平面向内. 在屏幕平面上取两个闭合路径1C 和2C ，其中闭合路径1C 内包围的电流为I ，而在闭合路径2C 内没有电流. 从图（b ）可以看出，由于磁感强度B 的方向总是沿着环绕直导线的圆形回路的切线方向，所以对闭合路径1C 或2C 上任意一线元l d ，磁感强度B 与l d 的点积为ϕαd cos d d Br l B ==⋅l B式中r 为载流导线至线元l d 的距离. 由第10-2节二中例1的式（2），上式可写成ϕμϕμd π2d π2d 00Ir rI==⋅l B （1）对于图（a ）的闭合回路1C ，ϕ将由0增至π2. 于是，磁感强度B 沿闭合路径1C 的环流为这就是真空中磁场的环路定理，也称安培环路定理。
它是电流与磁场之间的基本规律之一。
在式（10-8）中，若电流流向与积分回路呈右螺旋关系，电流取正值；反之则取负值。
⎰⎰===⋅1000π2π2d π2d CIIIμμϕμl B （2）可见，真空中磁感强度B 沿闭合路径的环流等于闭合路径所包围的电流乘以0μ，而与闭合路径的形状无关.然而，对于图（a ）中的闭合路径2C ，将得到不同的结果，当我们从闭合路径2C 上某一点出发，绕行一周后，角ϕ的净增量为零，即⎰=0d ϕ于是，由式（1）可得⎰=⋅20d c l B （3）比较式（2）和式（3）可以看出，它们是有差别的. 这是由于闭合路径1C 包围了电流，而闭合路径2C 却未包围电流. 于是我们可以得到普遍的安培环路定理：沿任意闭合路径的磁感强度B 的环流为⎰∑=⋅20d c I μl B式中∑I 是该闭合路径所包围电流的代数和 人物简介：安培简介安培(Andre Marie Ampere,1775-1855)，法国物理学家，对数学和化学也有贡献，他在电磁理论的建立和发展方面建树颇丰。
大学物理 安培环路定理
为可积的。 B dl
l
3）选择积分路径的取向，根据取向确定穿过回路内
电流的正负。
14
二、安培环路定理的应用
当场源分布具有高度对称性时，利用安培环 路定理计算磁感应强度。 1. 无限长载流圆柱体 已知：I、R 电流沿轴向，在截面上均匀分布
I
R
分析对称性
电流分布 轴对称 磁场分布
15
l
0 I
R
l
设闭合回路 l为 圆形回路，l与I成 右手螺旋。
5
闭合回路形状任意时：
0 I B 2r B dl L B d l cos
L
I
L
r
0I rd L 2 r 0I
P
B r
I L
磁场的环流与环路中所包 围的电流有关 。
d r
B 的方向判断如下：
对称性分析结论：
磁场沿回路切线，各点大小相等
r
dB
dB
P
dI o dI
作积分环路并计算环流
如图
rR
0
I
B dl Bdl B 2 r
利用安培环路定理求 B
R
B dl
0 I
B
r
2 rB 0 I 0 I B 2 r
r
dl
B
L
B1
1
dl1
7
L
• 推广到一般情况 I1 ~ I k —— 在环路 L 中
In
I2 I1
I k 1 ~ I n —— 在环路 L 外
则磁场环流为：
Ii
P
Ik
L
I k 1
B dl
l
3）选择积分路径的取向，根据取向确定穿过回路内
电流的正负。
14
二、安培环路定理的应用
当场源分布具有高度对称性时，利用安培环 路定理计算磁感应强度。 1. 无限长载流圆柱体 已知：I、R 电流沿轴向，在截面上均匀分布
I
R
分析对称性
电流分布 轴对称 磁场分布
15
l
0 I
R
l
设闭合回路 l为 圆形回路，l与I成 右手螺旋。
5
闭合回路形状任意时：
0 I B 2r B dl L B d l cos
L
I
L
r
0I rd L 2 r 0I
P
B r
I L
磁场的环流与环路中所包 围的电流有关 。
d r
B 的方向判断如下：
对称性分析结论：
磁场沿回路切线，各点大小相等
r
dB
dB
P
dI o dI
作积分环路并计算环流
如图
rR
0
I
B dl Bdl B 2 r
利用安培环路定理求 B
R
B dl
0 I
B
r
2 rB 0 I 0 I B 2 r
r
dl
B
L
B1
1
dl1
7
L
• 推广到一般情况 I1 ~ I k —— 在环路 L 中
In
I2 I1
I k 1 ~ I n —— 在环路 L 外
则磁场环流为：
Ii
P
Ik
L
I k 1
B dl
大学物理稳恒磁场
B2
0
r
r2 R2
I
rR
I
0I rR p r
B20R I2r rR
rp
B 0I rR 2r
B
无限长圆柱导体电流外面的磁场与电流
都集中在轴上的直线电流的磁场相同
.
R
r
无限长通电柱面
B2r 0 rR
0I rR p r I
B0 rR
rp
B 0I rR 2r
B
思考：有人说：“环路不环绕
电流时，环路上磁场必处处为
o
( D ) 20I R
B
( E ) 20I 8R
.
[A]
5.如图所示，电流由长直导线 1 经 a 点流 入电阻均匀分布的正方形线框，再由 b 点 流出，经长直导线 2 返回电源（导线 1、2 的延长线均通过 o 点）。设载流导线 1、2 和正方形线框在框中心o 点产生的磁感应 强度分别用 B1、B2、B3 表示，则 o 点的感 应强度大小
单位长度的电流）到处均匀。大小为 j
解：视为无限多平行
长直电流的场。 B
p
分析场点p的对称性
B
因为电流平面是无限大，故与电流平面等距离的 各点B的大小相等。在该平面两侧的磁场方向相反。
.
作一安培回路如图： bc和 da两边被电流平 面等分。ab和cd 与电 流平面平行,则有
L B d lB 2 lojl
(A )BR2B r. (B)BRBr. (C )2BRB r. (D )BR4Br.
.
[B]
4.两半径为R的相同导体细圆环,互相垂直放 置,且两接触点A、B连线为环的直径,现有 电流1沿AB连线方向由A端流入,再由 B端流 出,则环中心处的磁感应强度大小为:
大学物理 5.4 磁场的安培环路定理
r
l
B
例2 载流长直螺线管磁场分布
如图，均匀密绕无限长直
螺线管通有电流为I，单位
长度匝数为n）
I
解：对称性分析—— 管内垂轴
b
Ba
平面上任意一点与 B轴平行
cd b c d a
(3)磁场是有旋场 —— 电流是磁场涡旋的轴心
B dl —— 不代表磁场力的功，仅是磁场与电流的关系
L
(4)安培环路定理只适用于闭合的载流导线，对于任 意设想的一段载流导线不成立
2. 安培环路定理的应用
在静电场中，当带电体具有一定对称性时 可以利用高斯定理很方便的计算其电场分布。 在恒定磁场中，如果电流分布具有某种对称性， 也可以利用安培环路定理计算电流磁场的分布。
由 于 这 时 I 内 =0 ， 所 以 有 B=0 (在螺线环外)
l2
l1
可见，螺线环的磁场集中在
环内，环外无磁场。
对载流长直密绕螺线管，若线圈中通有电流强度为I的电
流,沿管长方向单位长度上的匝数为n，则由安培环路定理容
易求得：管内： B onI
说明
(1)积分回路绕行方向与电流方向呈右螺旋
关系
满足右螺旋关系时 Ii 0 反之 Ii 0
I
1
I
I
3
2l
I I
l
l B dl o ( I1 I2 ) l B dl o ( 2I I) oI
(2)公式中的 B 是环路上的磁感应强度，使
空间所有电流共同激发的。
L
B
LB
dr
l
B
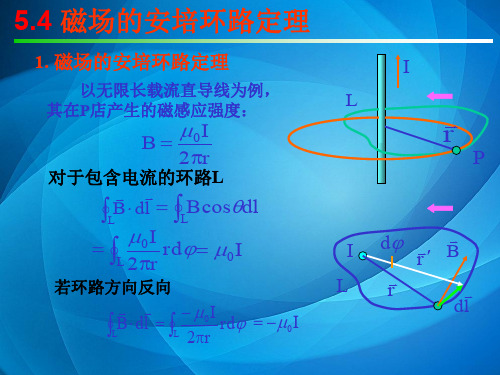
例2 载流长直螺线管磁场分布
如图，均匀密绕无限长直
螺线管通有电流为I，单位
长度匝数为n）
I
解：对称性分析—— 管内垂轴
b
Ba
平面上任意一点与 B轴平行
cd b c d a
(3)磁场是有旋场 —— 电流是磁场涡旋的轴心
B dl —— 不代表磁场力的功，仅是磁场与电流的关系
L
(4)安培环路定理只适用于闭合的载流导线，对于任 意设想的一段载流导线不成立
2. 安培环路定理的应用
在静电场中，当带电体具有一定对称性时 可以利用高斯定理很方便的计算其电场分布。 在恒定磁场中，如果电流分布具有某种对称性， 也可以利用安培环路定理计算电流磁场的分布。
由 于 这 时 I 内 =0 ， 所 以 有 B=0 (在螺线环外)
l2
l1
可见，螺线环的磁场集中在
环内，环外无磁场。
对载流长直密绕螺线管，若线圈中通有电流强度为I的电
流,沿管长方向单位长度上的匝数为n，则由安培环路定理容
易求得：管内： B onI
说明
(1)积分回路绕行方向与电流方向呈右螺旋
关系
满足右螺旋关系时 Ii 0 反之 Ii 0
I
1
I
I
3
2l
I I
l
l B dl o ( I1 I2 ) l B dl o ( 2I I) oI
(2)公式中的 B 是环路上的磁感应强度，使
空间所有电流共同激发的。
L
B
LB
dr
安培环路定理
(1)管内:取L矩形回路 abcda
边在轴上，两边与轴平行,另
aP b
两个边垂直于轴。
LB dl Bab ab Bcd cd Bab ab
e
Q
f
0I 0nI ab
d
c
∞
B内 onI 其方向与电流满足右手螺旋.
(2)管外 :
取回路efbae同理可证，无限长直螺线管外任一点的磁场为
A(rQ )
0I 2
ln
r Q
r P
A(rP )
A(rQ
)
0I 2
ln
r Q
r
-I
r P
P
两式相加,得:
A(rP )
A(rQ )
0I 2
ln
rQ rP
rP rQ
0I 2
ln
rP rP
A(rP )
A(rQ )
0I 2
ln
r P
r P
若选Q点的矢势为零,则
A(rP )
0I 2
ln
r P
r P
例2.一无限长载流圆柱导体,半径为R, 电流I均匀分布
ldr
0I 2
l
ln
rQ r
A(rP ) A(rQ )
0I 2
ln
rQ rP
+I
Q
若选Q点的矢势为零,则
A(rp
)
0I 2
ln
rQ rP
r P
注意:若选Q点在无穷远处或导线
上,磁矢势将无意义.
讨论:两根平行的载流直导线,电流大 小相等方向相反,求磁矢势.
选Q点在两直线电流之间垂线的中点处.
A(rP )
B dS 0
大学物理8-8有磁介质时的安培环路定理磁场强度
上页 下页 返回 退出
例题8-8 在均匀密绕的螺绕环内充满均匀的顺磁介 质，已知螺绕环中的传导电流为 I ，单位长度内匝 数 n ，环的横截面半径比环的平均半径小得多，磁介 质的相对磁导率和磁导率分别为 r 和 。 求环内的 磁场强度和磁感应强度。 解：在环内任取一点， 过该点作一和环同心、 r 半径为 r的圆形回路。
§8-8 有磁介质时的安培环路定理磁场强度
一、磁化强度
反映磁介质磁化程度(大小与方向)的物理量。 磁化强度：单位体积内所有分子固有磁矩的 矢量和 m 加上附加磁矩的矢量和 m分子 ，称 分子 为磁化强度，用 M 表示。 m分子 m分子 均匀磁化 M V m分子 m分子 非均匀磁化 M lim V 0 V 磁化强度的单位： A/m
上页 下页 返回 退出
0 H dl I
M ) dl I
有磁介质时的 安培环路定理
H
B
0
此式说明了介质中任一点磁场强度、 M 磁感应强度、磁化强度之间的普遍
关系，不论介质是否均匀。
实验证明：对于各向同性的介质，在磁介质 中任意一点磁化强度和磁场强度成正比。
R2
2 πr3 H d l H d l 0
即
H 0
0
I
I I
或
B0
上页 下页 返回 退出
选择进入下一节 §8-0 教学基本要求 §8-1 恒定电流 §8-2 磁感应强度 §8-3 毕奥-萨伐尔定律 §8-4 稳恒磁场的高斯定理与安培环路定理 §8-5 带电粒子在电场和磁场中的运动 §8-6 磁场对载流导线的作用 §8-7 磁场中的磁介质 §8-8 有磁介质时的安培环路定理 磁场强度 *§8-9 铁磁质
例题8-8 在均匀密绕的螺绕环内充满均匀的顺磁介 质，已知螺绕环中的传导电流为 I ，单位长度内匝 数 n ，环的横截面半径比环的平均半径小得多，磁介 质的相对磁导率和磁导率分别为 r 和 。 求环内的 磁场强度和磁感应强度。 解：在环内任取一点， 过该点作一和环同心、 r 半径为 r的圆形回路。
§8-8 有磁介质时的安培环路定理磁场强度
一、磁化强度
反映磁介质磁化程度(大小与方向)的物理量。 磁化强度：单位体积内所有分子固有磁矩的 矢量和 m 加上附加磁矩的矢量和 m分子 ，称 分子 为磁化强度，用 M 表示。 m分子 m分子 均匀磁化 M V m分子 m分子 非均匀磁化 M lim V 0 V 磁化强度的单位： A/m
上页 下页 返回 退出
0 H dl I
M ) dl I
有磁介质时的 安培环路定理
H
B
0
此式说明了介质中任一点磁场强度、 M 磁感应强度、磁化强度之间的普遍
关系，不论介质是否均匀。
实验证明：对于各向同性的介质，在磁介质 中任意一点磁化强度和磁场强度成正比。
R2
2 πr3 H d l H d l 0
即
H 0
0
I
I I
或
B0
上页 下页 返回 退出
选择进入下一节 §8-0 教学基本要求 §8-1 恒定电流 §8-2 磁感应强度 §8-3 毕奥-萨伐尔定律 §8-4 稳恒磁场的高斯定理与安培环路定理 §8-5 带电粒子在电场和磁场中的运动 §8-6 磁场对载流导线的作用 §8-7 磁场中的磁介质 §8-8 有磁介质时的安培环路定理 磁场强度 *§8-9 铁磁质
12.4 安培环路定律
§12.4 安培环路定律
1. 安培环路定理 简单探讨：
大学物理教程
讨论
I
（1）若回路L绕向与I成反右螺旋
B dl B cosdl
L L
B
O
dl
R
0 I cosdl 0 I L 2R
L
结论：L与I成右螺时，I取正，反之为负。
§12.4 安培环路定律
x
o
§12.4 安培环路定律
y
第十二章 恒定磁场
大学物理教程
解：① 利用磁感强度叠加原理分析电场对称性； 与平面等距离 各点磁感强度
大小：相等 方向：±y
dBP
x
z
P
BP
y
BA
A
o
o
§12.4 安培环路定律
I 0 大小： B 2π R 磁场 方向：与I成右螺旋
大学物理教程
I
B
取线元 dl ，则环流为：
0 I cos0dl B dl B cosdl
L L
O
dl
R
L
L
2R
d l 0 I 2π R
l
0 I
闭合路径所 包围的电流
第十二章 恒定磁场
（ r R）
B
0 I
2πr
§12.4 安培环路定律
第十二章
恒定磁场
L
（方法二：安培环路积分法） 适用性：磁场具有对称性 步骤为：
① 利用磁感强度叠加原理分析磁场对称性； ② 根据对称性选择合适的路径，计算路径
包围的电流代数和；
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Φ BS cos BS
s
一般情况 Φ s BdS
dS2
B
S 2
dS1
1
B1
dΦ1 B1 dS1 0
dΦ2 B2 dS2 0
B2
SB cosdS 0
磁场高斯定理
S B d S 0
物理意义：通过任意闭合曲面的磁通
量必等于零（故磁场是无源的）.
B B1 B2 B3
Bdl
l
0(I2 I3)
推广：
➢ 安培环路定理
n
B dl 0 Ii
i 1
n
安培环路定理
B dl 0 Ii
i 1
在真空的恒定磁场中，磁感强度 B沿任
一闭合路径的积分的值，等于 0乘以该闭合
路径所穿过的各电流的代数和.
注意
电流 I 正负的规定： I 与 L 成右螺旋
而与环路外电流无关。
3. B为环路上一点的磁感应强度，它与环路内外电流
都有关。
若
B
dl
0
并不一定说明环路上各点的 B 都为 0。
若 B dl 0 环路内并不一定无电流。
4.环路定理只适用于闭合电流或无限电流，
应用 安培环路定理的应用举例
例1
求载流螺绕环内的磁场
解 （1）对称性分析：环内B 线为同心
B dl B 2r 0 I
B 0 I 1 2r r
I
r LR
r L
分布曲线
B
0 I 2R B r
B 1 r
o
R
r
例4 无限大均匀带电(线密度为i)平面的磁场
解 如图，作安培环路
abcda，应用安培环路 定理
b
l B d l 2a B dl
2Bab 0iab B 0i
2
a
i
b
d c
B 0i
2
0i B
2
or
a
i
b
d c
四、选取环路原则
利用安培环路定理计算磁场 B ,要求磁场 具有高度的对称性 ;
目的是将:
L B d l 0 I
写成
L Bdl cos B dl 0 I
B 0 I
dl
要求环路上各点 B 大小相等，B 的方向
与环路方向一致， B // dl , cos 1
b
d
Bdl ,
cos 0
d
Bd l 0
c 螺线管外B =0；
b
Bdl Bdl
a
...............
a
bB
B外 0 dc
作闭合环路 abcda,环路 内的电流代数和为：
I n abI
B ab 0 I 0n abI B 0nI
例3：一环形载流 螺线管，匝数为
N ，内径为 R1 ， 外径为 R2 ，通有 电流 I ，求管内磁 感应强度。
时，I 为正；反之为负.
L B dl
0 (I1 I2 )
（0 I1
I
）
2
讨论：
（1）B 是否与回路L
外电流有关？
I1
I2 I3
I1
L
I1
（2）若 LB dl 0 ，是否回路L 上各处
B 0 ？是否回路 L 内无电流穿过？
1. I 为环路内的电流代数和。
2.环流 B dl 只与环路内的电流有关，
一 安培环路定理
无限长载流长直导线的磁场
B 0I
2πr
I B
I XB
电流与磁感强度成右手螺旋关系
B 0I
2π R
l
B
dl
0I dl
2π R
B dl
l
0I
I
B
dl
oR
l
设闭合回路 l 为圆形回路, l 与
I 成右螺旋
若回路绕向为逆时针
l B
dl
0I
2π
2π
0
d
0I
对任意形状的回路
B dl
B B
的方向； 的大小.
I
I
I
I
S
I
S
N
N
三 磁通量 磁场的高斯定理
S B
B ΔN ΔS
磁通场过中的某磁点感处 线垂 数直 目等B矢于量该的点单B的位数面值积.上
B
磁通量：通过
en
某曲面的磁感线数
s
s
B
B dS
B
匀强磁场中，通 过面曲 面 S的 磁 通量：
Φ B S B enS
解：在管内作环路
半径为 r ，
o R1
环路内电流代数和为
r R2
I NI
L B d l 0 I
B 2r 0NI B 0NI 2r
当 r >> ( R2 – R1) 时
o R1 r R2
N n 为沿轴向线圈密度；
2r
B 0nI 与直螺管的结论类似。
二、 磁感线
切线方向—— 疏密程度——
求管内一点的 B 。(用无
ab
限长螺线管近似。)
解：理想密绕螺线管，管
内的磁场是均匀的，管外 的磁场为 0 ；由安培环路
d
c
定律：
L B dl 0 I
r
选择如图所示的环路
b c d a
B dl ( )B dl
a
b
c
d
其中
c a
B dl B dl 0,
0I
rd
0I
d
2π r
2π
B dl l
0I
I
B
dl
oR
l d B
dl
Ir
l
I
d
B1
r1
dl1
B2 dl2
r2
l
电流在回路之外
B1
0I
2π r1
，
B2
0I
2π r2
B1
dl1
B2
dl2
0I
2π
d
B1 dl1 B2 dl2 0
l B d l 0
多电流情况
I1
I2
I3
l
B 2r 0I
B 0I
r
2r
L
将上式用于有限长直导线则得出错误结
果，算出B与无限长直电流磁感应强度
相同 ，矛盾，故安培环路定律对有限电
流不适用。
例3：圆柱形载流导体 半径为 R ，通过的电 流为 I ，电流在导体横 截面上均匀分布，求 圆柱体内、外的磁感 应强度的分布。
解：1.圆柱体内部
r < R 区域
圆，环外 B 为零.
d
R
（2）选回路
l B dl 2π RB 0NI
B 0NI
2π R
令 L 2πR
B 0 NI L
d
L
R
当 2R d 时，螺绕环内可视为均匀场 .
例2：利用安培环路定律计算载流无限长 直导线外一点的磁感应强度。
解：以电流为轴，做半径为 r 的环路
B dl B dl 0I
或 Bdl , cos 0
环路要经过所研究的场点。
五、解题方法
1.场对称性分析； 2.选取环路； 3.确定环路内电流的代数和 I ； 4.应用环路定理列方程求解。
应用环路定理求 B 要比毕萨定律简单， 但只适用于具有高度对称的场。
例5：密绕载流螺线管通 有电流为 I，线圈密度为 n，
...............B
I R
选取半径 为 r 的环路，
B dl Bdl cos
由于环路上各点 B 大小相等，方向
B // dl
0
B dl
B 2r 0r 2 I
R2
环路内电流代数和为：
I
I
R
2r 2
r2 R2
I
B
0 I 2R 2rຫໍສະໝຸດ rIR r L
2.圆柱体外一点 r > R 区域
在圆柱体外作一环路，
B dl Bdl cos