等底等高模型小学奥数
等底等高模型小学奥数
等高（等底）模型【知识点分析】1 基础知识：三角形面积=底.K高昇斯哄：三角形面枳的丸小，取决于三角瞪底和高的乘积.若底不变，高越大（小），面积越大a卜）；若高不变，底越丸（小儿面积越大（小）；2. 模型结论：①两个三角形高相等，面积比等于它们的底之比；女！■图S] * —a * b②两个三角形底相等，面积比等于它们的髙之比：特殊:等底等高的两个三角形面积相等；（注意平行线）其他常用蛀论：（1）夹在一组平行线之间的等积变形，如右上图$*=£*；反之，如果则可知宜线曲平行于CD.（2）等底等高的两个平行四边形面积相等（长方形和正方形可以看作特殊的平行四边形）；（3）三甫形罰积等于与它等底等高的平行四边珈圍积妁一半；（4）两个平行四边形高相等*面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比.3、拓展结论：拓展1:图（1）:四边形ABCD为正方形，E、F、G是各边中点，H是是AD上任意一点，贝US阴二扌S正证明：连接BH、CH,根据等高等底知：S©=S②，S云S空S⑥三S⑥，所以正图（2）：四边形ABCD为正方形，E、F、G是各边三等分点，H是是AD上任意一点、,则S阴气S正（证明方法同上）图（3）:四边形ABCD为长方形，E、F、G是各边中点，H是是AD上任意一点，则S十丄S长（证明方法同上）2拓展2：图（2）: S赵S小正，证明同上（辅助线如图）图（3）: S阴二大正，证明同上（辅助线如图）图⑷：$阴=gs中正，证明：辅助线如图，根据平行s，、RE=S住阳,所以,S阴冷S中【典型例题】W 1：如右因，E在AD上.AD至直BC・ylD = 12 ^耒，DE = 3圧米.求三角形ABC的和积是三角形EBC面积的几倍？例2:长方形ABCD的面积为36, E> F. G为各边中点，H为AD边上任意一点, 问阴影部分面积是多少？例3:（第6届走美杯5年级决春第8題）央如图，A. B、C都是正方形边的中A, ACOD比AAOB大15平方厘米。
等底等高模型小学奥数
等高（等底）模型
练一练
1.如图，E在AD上，AD垂直BC于D，AD12 厘米，DE 3 厘米．求三角形ABC的面积是三角形EBC 面积的几倍
A
E
B D C
•
2．如图所示，在平行四边形ABCD中，E为AB的中点，AF CF，三角形AFE(图中阴影部分)的面积为8 平方厘米．平行四边形ABCD的面积是多少平方厘米
D C
F
A
E B
3.如图，在长方形ABCD中，Y是BD的中点，Z是DY的中点，如果AB=24 厘米，BC8 厘米，求三角形ZCY的面积．
D C
Z Y
A B
4. 如图所示，一个面积是100 的长方形分成4 个不同的三角形．问：红色部分的面积和是多少
5.如图所示，四边形ABCD是梯形，面积是40，E是AB的中点，求阴影部分的面积.
6.如图，ABFE和CDEF都是长方形，AB的长是4 厘米，BC的长是3 厘米，那么
图中阴影部分的面积是多少平方厘米
A B
E F
D C
7.校园里有一块长方形的地长18 米，宽12 米，想种上红花、黄花和绿草.（除长方
形四个顶点外，其余各点均为各边中点）.一种设计方案如图，那么其中红花和黄花
的面积和是＿＿＿＿平方米.。
小学奥数-几何五大模型(等高模型)
模型一 三角形等高模型已经知道三角形面积的计算公式：三角形面积=底⨯高2÷从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积．如果三角形的底不变，高越大(小)，三角形面积也就越大(小)； 如果三角形的高不变，底越大(小)，三角形面积也就越大(小)；这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化．但是，当三角形的底和高同时发生变化时，三角形的面积不一定变化．比如当高变为原来的3倍，底变为原来的13，则三角形面积与原来的一样．这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化．同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状．在实际问题的研究中，我们还会常常用到以下结论： ①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比；如图 12::S S a b =baS 2S 1 DC BA③夹在一组平行线之间的等积变形，如右上图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ．④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半； ⑥两个平行四边形高相等，面积比等于它们的底之比； 两个平行四边形底相等，面积比等于它们的高之比．三角形等高模型与鸟头模型【例1】你有多少种方法将任意一个三角形分成：⑴3个面积相等的三角形；⑵4个面积相等的三角形；⑶6个面积相等的三角形。
【解析】⑴如下图，D、E是BC的三等分点，F、G分别是对应线段的中点，答案不唯一：CEDBAFCDBAGD CBA⑵如下图，答案不唯一，以下仅供参考：⑸⑷⑶⑵⑴⑶如下图，答案不唯一，以下仅供参考：【例2】如图，BD长12厘米，DC长4厘米，B、C和D在同一条直线上。
小学奥数-几何五大模型(等高模型)知识分享
小学奥数-几何五大模型(等高模型)模型一 三角形等高模型已经知道三角形面积的计算公式：三角形面积=底⨯高2÷从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积．如果三角形的底不变，高越大(小)，三角形面积也就越大(小)； 如果三角形的高不变，底越大(小)，三角形面积也就越大(小)；这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化．但是，当三角形的底和高同时发生变化时，三角形的面积不一定变化．比如当高变为原来的3倍，底变为原来的13，则三角形面积与原来的一样．这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化．同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状．在实际问题的研究中，我们还会常常用到以下结论：①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比；如图 12::S S a b =baS 2S 1 DC BA③夹在一组平行线之间的等积变形，如右上图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ．④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；三角形等高模型与鸟头模型两个平行四边形底相等，面积比等于它们的高之比．【例 1】 你有多少种方法将任意一个三角形分成：⑴ 3个面积相等的三角形；⑵ 4个面积相等的三角形；⑶6个面积相等的三角形。
【解析】 ⑴ 如下图，D 、E 是BC 的三等分点，F 、G 分别是对应线段的中点，答案不唯一：CEDBAFC DB A G D CB A⑵ 如下图，答案不唯一，以下仅供参考：⑸⑷⑶⑵⑴⑶如下图，答案不唯一，以下仅供参考：【例 2】 如图，BD 长12厘米，DC 长4厘米，B 、C 和D 在同一条直线上。
小学奥数-几何五大模型(等高模型)
模型一三角形等高模型已经知道三角形面积的计算公式：三角形面积底高2从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积.如果三角形的底不变，高越大（小），三角形面积也就越大（小）；如果三角形的高不变，底越大（小），三角形面积也就越大（小）；这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化•但是，当三角形的底和高同时1发生变化时，三角形的面积不一定变化•比如当高变为原来的3倍，底变为原来的1，则三角形面积与原来3的一样.这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化. 同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状.在实际问题的研究中，我们还会常常用到以下结论：①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如图S i :S2 a:b③夹在一组平行线之间的等积变形，如右上图S A ACD S A BCD ；反之，如果S A ACD S A BCD，则可知直线AB平行于CD •④等底等高的两个平行四边形面积相等（长方形和正方形可以看作特殊的平行四边形）；⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比.你有多少种方法将任意一个三角形分成： ⑴3个面积相等的三角形； ⑵4个面积相等的三角形； ⑶ 6个面积相等的三角形。
⑴ 如下图，D 、E 是BC 的三等分点，F 、G 分别是对应线段的中点，答案不唯一：⑵ 如下图，答案不唯一，以下仅供参考:如图，BD 长12厘米，DC 长4厘米，B 、C 和D 在同一条直线上。
⑴ 求三角形ABC 的面积是三角形 ABD 面积的多少倍？⑵求三角形ABD 的面积是三角形 ADC 面积的多少倍?因为三角形 ABD 、三角形 ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时，它们的高都是从 A 点向BC边上所作的垂线，也就是说三个三角形的高相等。
小学奥数几何五大模型
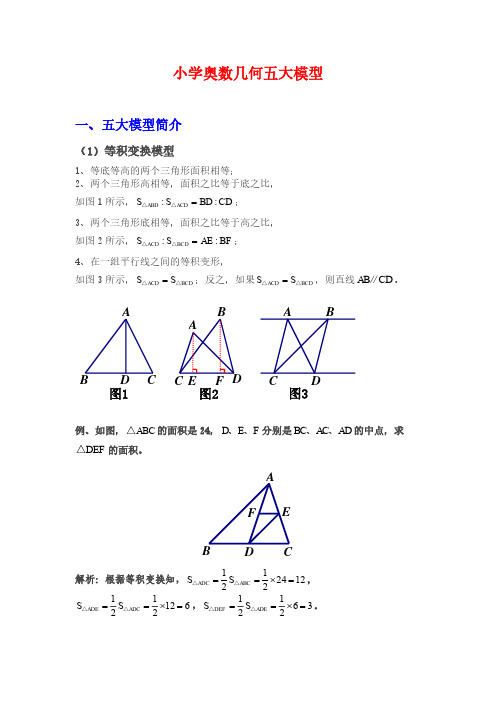
（4）相似模型1、相似三角形：形状相同、大小不相等的两个三角形相似；2、寻找相似模型的大前提是平行线：平行于三角形一边的直线和其他两边或两边延长线相交，所构成的三角形与原三角形相似。
3、相似三角形性质：①相似三角形的一切对应线段(对应高、对应边）的比等于相似比；②相似三角形周长的比等于相似比；③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类，注意这两大类中都含有DE BC ∥。
(一)金字塔模型 (二) 沙漏模型结论：因为DE BC ∥，所以ADE ABC △∽△，则①AD AE DE==；②22::ADE ABC S S AD AB =△△。
②::ABO BCO S S AE EC =△△；ED C BA E DCB A③::ACO BCO S S AF FB =△△。
二、五大模型经典例题详解 （1）等积变换模型例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点，如果正方形的边长是12，那么阴影部分的面积是多少？GFE D CBA解析：把另外三个三等分点标出之后，正方形的3条边AB BC CD 、、就被分成了相等的三段。
把点H 和这些分点、正方形的顶点连接，这样就把整个正方形分割成了9个形状各不相同的三角形，同时我们把空白部分的6个三角形按顺时针标记1～6。
这9个三角形的底边都是正方形边长的三分之一；阴影部分被分割成了其中的3个三角形。
根据等积变换模型可知，CD 边上的阴影三角形的面积与第1、2个三角形相等；BC 边上的阴影三角形与第3、4个三角形相等；AB 边上的阴影三角形与第5、6个三角形相等。
因此，阴影面积是空白面积的二分之一，是正方形面积的三分之一，即：12×12÷3=48。
例2、如图所示，Q E P M 、、、分别为直角梯形ABCD 两边AB CD 、上的点，且DQ CP ME 、、彼此平行，已知5753AD BC AE EB ====、、、，求阴影部分三角形PQM 的面积。
等底等高模型小学奥数
等高（等底）模型
练一练
1.如图，E在AD上，AD垂直BC于D，AD=12厘米，DE=3厘米．求三角形ABC的面积是三角形EBC面积的几倍？
A
E
B D C
•
2．如图所示，在平行四边形ABCD中，E为AB的中点，AF=CF，三角形AFE(图中阴影部分)的面积为8平方厘米．平行四边形ABCD的面积是多少平方厘米？
D C
F
A
E B
3.如图，在长方形ABCD中，Y是BD的中点，Z是DY的中点，如果AB=24厘米，BC=8厘米，求三角形ZCY的面积．
D C
Z Y
A B
专业整理
4. 如图所示，一个面积是100的长方形分成4个不同的三角形．问：红色部分的面积和是多少？
5.如图所示，四边形ABCD是梯形，面积是40，E是AB的中点，求阴影部分的面积.
6.如图，ABFE和CDEF都是长方形，AB的长是4厘米，BC的长是3厘米，那
么图中阴影部分的面积是多少平方厘米？
A B
E F
D C
7.校园里有一块长方形的地长18米，宽12米，想种上红花、黄花和绿草.（除长方
形四个顶点外，其余各点均为各边中点）.一种设计方案如图，那么其中红花和黄花
的面积和是＿＿＿＿平方米.。
(完整版)等底等高模型小学奥数
等高（等底）模型
练一练
1.如图，E在AD上，AD垂直BC于D，AD=12厘米，DE=3厘米．求三角形ABC的面积是三角形EBC面积的几倍？
A
E
B D C
•
2．如图所示，在平行四边形ABCD中，E为AB的中点，AF=CF，三角形AFE(图中阴影部分)的面积为8平方厘米．平行四边形ABCD的面积是多少平方厘米？
D C
F
A
E B
3.如图，在长方形ABCD中，Y是BD的中点，Z是DY的中点，如果AB=24厘米，BC=8厘米，求三角形ZCY的面积．
D C
Z Y
A B
4. 如图所示，一个面积是100的长方形分成4个不同的三角形．问：红色部分的面积和是多少？
5.如图所示，四边形ABCD是梯形，面积是40，E是AB的中点，求阴影部分的面积.
6.如图，ABFE和CDEF都是长方形，AB的长是4厘米，BC的长是3厘米，那
么图中阴影部分的面积是多少平方厘米？
A B
E F
D C
7.校园里有一块长方形的地长18米，宽12米，想种上红花、黄花和绿草.（除长方
形四个顶点外，其余各点均为各边中点）.一种设计方案如图，那么其中红花和黄花
的面积和是＿＿＿＿平方米.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
等高（等底）模型
练一练
1. 如图， E 在 AD 上， AD 垂直 BC 于 D， AD 12 厘米， DE 3 厘米．求三角形 ABC 的面积是三角形 EBC 面积的几倍？
A
E
B D C
?
2．如图所示，在平行四边形ABCD中，E为AB的中点，AF CF ，三角形AFE (图中阴影部分)的面积为8 平方厘米．平行四边形ABCD 的面积是多少平方厘米？
D
C
F
A
E B
3. 如图，在长方形 ABCD 中， Y 是 BD 的中点， Z 是 DY 的中点，如果 AB=24 厘米， BC 8 厘米，求三角形 ZCY
的面积．
D C
Z Y
A B
4. 如图所示，一个面积是100 的长方形分成4 个不同的三角形．问：红色部分的面积和是多少？
5. 如图所示，四边形ABCD 是梯形，面积是40， E 是 AB 的中点，求阴影部分的面积.
6. 如图， ABFE 和 CDEF 都是长方形， AB 的长是 4 厘米， BC 的长是 3 厘米，那么图中阴影
部分的面积是多少平方厘米？
A B
E F
D C
7.校园里有一块长方形的地长 18 米，宽 12 米，想种上红花、黄花和绿草.（除长方形四个
顶点外，其余各点均为各边中点） . 一种设计方案如图，那么其中红花和黄花的面积和是＿
＿＿＿平方米 .。