公平席位的分配
公平的席位分配等四个数学模型例子

补例2 洗衣节水问题
因为lim n
1
1 n
n
e,所以当n趋于无穷大时,(7)式分母
趋于e AW。
当n趋于无穷大时,N
的极限存在,并有
n
A
lim
n
Nn
N0
eW
(8)
(8)式说明了当水的总量一定的时候,无论你怎样洗涤,不 管次数多少,最后的结果是不可能一点污物都不残留的。
18 8 4+3+2+2+2+4=17
A7 13 23 10 7 28 18
4 2+2+2+4+4+4=18
A8 17 11 27 22 14 8 4
3+2+2+2+4+4=17
由以上表格可知该安排是合理的
作业:当7支队参加单循环赛的排球比赛时,试 合理的安排其赛程。
补例2 洗衣节水问题
问题提出: 我国淡水资源有限,节约用水势在必行。那么如何在洗衣 服中合理地用水,使得既能把衣服洗干净,又能节约用水 的问题就摆在我们的面前。一般洗衣服的过程是先将衣服 用洗涤剂浸泡,然后一次次地用水漂洗。洗衣机的运行过 程分别为加水—>漂洗—>脱水—>加水—>漂洗—>脱 水……这么一个循环过程。我们的问题是在保证一定洗涤 效果下,洗衣服分成多少次(或在洗衣机中应循环几次), 每一次的用水量是否一致,使得总的用水量最为节省?
补例2 洗衣节水问题
进一步讨论:
如何确定洗涤的次数 n 。
先引入一个清洁度 的定义。设 是洗净衣服上的污物量与
第一次浸泡后残留在衣服上的污物量之比,即 Nn N0
公平的席位分配
(i=1,2, … ,即m当) 总席位增加时, ni不应减少
“比例加惯例”方法满足 1),但不满足 2)
Q值方法满足 2), 但不满足 1)。令人遗憾!
~ 对A的相对不公平度 公平分配方案应
类似地定义 rB(n1,n2)
使 rA , rB 尽量小
将一次性的席位分配转化为动态的席位分配, 即
设A, B已分别有n1, n2 席,若增加1席,问应分给A, 还是 B
不妨设分配开始时 p1/n1> p2/n2 ,即对A不公 平
应讨论以下几种情况 初始 p1/n1> p2/n2
记 [qi]– =floor(qi) ~ 向 qi方向取整; [qi]+ =ceil(qi) ~ 向 qi方向取整.
1) [qi]– ni [qi]+ (i=1,2, … , 即ni 必取[qi]– , [qi]+ 之
m),
一
2) ni (N, p1, … , pm ) ni (N+1, p1, … , pm)
法 人数
A方 p1 B方 p2
席位 n1 n2
当p1/n1= p2/n2 时,分配公 平 若 p1/n1> p2/n2 ,对A 不公 平
p1/n1– p2/n2 ~ 对A的绝对不公平度
p1=150, n1=10, p1/n1=15
pp22=/np1210=/0n1,10–np2=2/1n02,=5
虽二者的绝对 不公平度相同
Q3
342 3 4
96.3
Q1最大,第20席给甲
第21席
Q1
1032 1112
80.4,
Q2 ,
系 Q3 同上
Q3最大,第 21席给丙系
数学论文席位的公平分配问题

数学建模论文席位的公平分配问题姓名:学号:18 15 20公平的委员分配问题摘要:1.我们首先是用惯例分配法来解决这委员分配问题的,由于方法来解决存在很大的缺陷,因此,通过组内的讨论,我们想出了Q值法来解决此问题,发现这样能作到相对公平。
我们这一组开始就考虑到了该怎样分配能作到相对公平,就这个问题,我们开始了研讨。
我们采用惯例分配法分析发现:各楼所得到的委员数A 、B 、C楼分别为:3、3、4人,而Q值法其结果为:A、B、C楼分别为:2、3、5人。
2.“取其精华,去其糟粕”我们发现Q值法能很好的解决委员分配问题,Q 值法:我们用Qi=(Pi*Pi)/[n(n+1)],其中i=A、B、C,Pi为第i楼的人数,n 为分配到的委员数,我们采用将剩下的一位委员名额分给Q值最大的一方。
通过计算得到Qa=9204.16、Qb=9240.75、Qc=9331.2比较得到:Qa>Qb>Qc,所以我们决定把剩下的一名委员分给C楼。
3.我们用惯例分配法发现有一名委员不好分配,不知道分给谁更公平些。
建议:我们的思维不能太单一了,在考虑问题方面要做到全面些,这样才会少走弯路。
(无论在哪方面都一样。
)关键字:委员分配、比例法、Q值法1.1问题的重述分配问题是日常生活中经常遇到的问题,它涉及到如何将有限的人力或其他资源以“完整的部分”分配到下属部门或各项不同任务中.分配问题涉及的内容十分广泛,例如:学校共有1000学生,235人住在A楼,333人住B楼,432人住C楼,学校要组织一个10人委员会,试用惯例分配法和Q值方法分配各楼的委员数并比较结果。
1.2问题的分析数学中通常人们用比例的方法来分配各个楼要派出几个人来组建委员会,当比例中有小数时人们有按照惯例使得各组中小数最大的组拥有更多的人数。
然而人们是怎样分配的呢?又因为没栋楼所占比例不是整数,可以会出现不公平的现象。
为了让席位分配更加公平我们不应该采用比例法,要引用不比例法更好的Q值法对其进行求解。
公平的席位分配

Q值法推广:当有m方,第i方人数 pi ,占有 ni 席位, 当总席位增加1席,计算
pi2 Qi ni (ni 1)
应将席位分给Q值最大的一方。
问题解决
先按比例计算结果将整数部分的19席分配完,有 n1 10, n2 6, n3 3 ,再用Q值法分配第20,21 席。
1032 632 342 第20席:Q1 , Q2 , Q3 , Q1最大分给甲。 1011 6 7 3 4 1032 第21席:Q1 , Q2 , Q3不变, Q3最大分给丙。 1112
公平的席位分配
问题背景
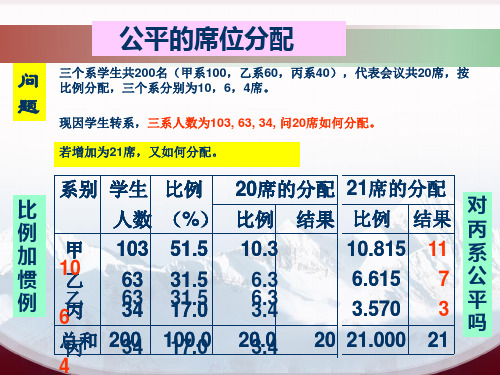
某校有3个系共200名学生,甲乙丙系各100, 60,40名。若学生代表席位设20个席位。 公平而简单的席位分配办法:按学生人数 的比例分配。 分配结果(席位):甲10;乙6;丙4。
若甲乙丙系人数分别:103、63和34,20个 席位如何分配? 若上述人数不变,增加一个席位,分配结 果如何? 这个结果对丙系太不公平,总席位增 加1席,而丙系席位却由4席减少为3席位。 找到衡量公平分配席位的指标,丙建立新 的分配方法。
练习
学校共1000名学生,235人住在A宿舍, 333人住在B宿舍,432人住在C宿舍。学生 门要组织一个10人的委员会,使用下列办 法分配各宿舍的委员数。 (1)按比例分配取整数的名额后,剩下的名 额按惯例分给小数部分较大者。 (2)用Q值法
(3)d’Hondt法:将A,B,C各宿舍的人数用 n=1,2,3等相除,其商如下
p1 p2 n1 n2 1
公平分配的原则:使得相对不公平度尽可能地小
若 rB (n1 1, n2 ) rA (n1 , n2 1) ,则席位分给A;反之分给B。 Q值法 2 2
公平的席位分配

每席代表人数: p1/ n1
不公平
Байду номын сангаас程度
例: 120:10 100:10→2 例: 1020:10 1000:10→2 改进
改进
对A相对不公平值
rA ( n1 , n 2 ) = p1 p2 − n1 n2 p2 n2 p2 p1 − n2 n1 p1 n1
绝对不公平值 基数
对B
rB ( n 1 , n 2 ) =
模型分析
总人数 p=∑pi ,总席位 n=∑ni 按人数比例 p
ni = [
i
p
n ]
则 则
pi p p < ≤ i ni +1 n n
pi Qi = n i ( n i + 1)
2
例: 120:10 100:10→2 → 0.2 例: 1020:10 1000:10→2 →0.02
目标:rA, rB 尽量小
2、确定分配方案
假设 A,B 占有 n1,n2 席 不妨设 p1/n1>p2/n2 则 p1/(n1 +1)>p2/n2 == p1/(n1 +1)<p2/n2 对A不公平值(相对)
某校 共200人 20席 调整 人数比例 20席 实际分配 21席 实际分配
甲系 100 10 103 51.3 10.3 10 10.815 11
乙系 60 6 63 31.5 6.3 6 6.615 7
丙系 40 4 34 17 3.4 4 3.57 3
产生问题:分配不公
原因 20个,丙多占0.6 21个,不充分的席位都在增加
p2 (n1 + 1) rA(n1 +1,n2)= -1 p1n2 p1/n1 )>p2/(n2 +1)
席位公平分配问题q值法的改进

席位公平分配问题q值法的改进随着社会的不断发展和进步,人们对于公平的追求也越来越强烈。
在各种社会活动和组织中,公平的分配问题一直备受关注。
席位公平分配问题作为一个重要的社会组织问题,一直以来都备受人们关注。
q值法作为目前解决席位公平分配问题的一种常用方法,然而在实际应用中却存在一些问题和不足。
如何改进q值法成为了当前亟待解决的一个问题。
1. q值法的基本原理q值法是一种基于权重的席位分配方法。
其基本原理是根据各个参与方的权重大小来确定席位的分配比例。
通常情况下,权重越大的参与方获得的席位数量也就越多。
这种方法在一定程度上确实能够体现参与方的重要性和影响力,但在实际应用中往往会出现一些问题。
2. q值法存在的问题q值法在确定权重时往往是基于主观判断的,缺乏客观的依据。
这就导致了权重的不确定性和不公平性,容易受到人为因素的影响。
q值法只是简单地依据权重来分配席位,忽略了其他可能存在的因素。
这就导致了分配结果可能并不合理和公平,无法充分考虑参与方的各种需求和意见。
再次,q值法在实际应用中往往面临的是计算复杂度较高的问题,尤其是在参与方众多、权重差异较大的情况下,很难进行准确而高效的计算。
q值法在解决席位公平分配问题时存在一些问题和不足,需要进行改进和优化。
3. q值法的改进方向为了解决q值法存在的问题,可以从以下几个方面进行改进:(1)建立客观评价体系。
可以通过建立客观的评价标准和体系来确定参与方的权重,以减少人为因素的干扰和影响,确保权重的客观和公正。
(2)综合考虑多种因素。
除了权重以外,还可以考虑其他多种因素来确定席位的分配比例,如参与方的历史贡献、实际需求等,以更全面地体现参与方的重要性和影响力。
(3)优化计算方法。
可以通过引入一些优化算法和技术,来提高席位分配的计算效率和准确性,特别是在复杂情况下的应用,能够更好地满足实际需求。
4. q值法的改进实践针对上述改进方向,可以通过实际案例和实践进行验证和应用。
公平席位的分配

公平席位的分配数学(2)班学号 0907022022 高泽标摘要:讨论公平席位分配的模型已有很多。
本文首先用比例加惯例法、Q值法、D’hondt 法对问题中名额进行了分配,再对D’hondt法的合理性进行了分析,并在Q值法对绝对尾数(绝对不公平度)的处理方式基础上,提出了相对尾数模型,并讨论了其满足Young公理的1,3,4条关键词:相对尾数 Balinsky & Young不可能定理正文1 问题复述公平的席位分配问题是一个非常有趣而重要的问题,它在政治学、管理学和对策论等领域具有广泛的应用价值。
处理这个问题的最早的方法是Hamilton法,即比例加惯例法;后来出现了Q值法;1974年M.L.Balinski和H.P.Young引入了席位分配问题的公理体系研究方法,并于1982年证明了同时满足五个公理的席位分配方法是不存在的;因此,我们只能根据实际建立在一定公平准则下成立并尽量多的满足Young公理的算法。
这里,我们需要理解并运用比例加惯例法、Q值法、D’hondt法对宿舍委员会名额进行分配,继而提出更优的公平分配席位的方法。
2 模型假设2.1 合理假设2.1.1 比例加惯例法、Q值法等分配模型均为已知;2.1.2 各个宿舍相互独立互不影响,人数保持不变;2.1.3 委员分配以各宿舍人数为唯一权重。
2.2 符号约定3 模型的建立及求解3.1按比例加惯例模型分配根据比例加惯例分配模型的原理表3.2按Q 值法模型分配首先用比例分配法对名额进行初步分配,再根据表达式 C B A i ,,=对剩下的名额进行分配表2(Q 值法分配结果):3.3 D ’hondt 模型 3.3.1 模型建立设,分别表示宿舍总人数和总分配席位数,(1,2,3i =)表示各宿舍人数,令(1,2,3,1,2,...i j ==),则得到一个数列{}ij a ,将该数列按递减顺序重新排列,得到{}()k ij a ,其中()k ij a 表示{}()k ija 中第大的项。
公平席位分配Q值法

1 问题的假设与符号定义1.1问题的假设:1.席位是以整数计量的,并且为有限个,设为N个;2.每个系别有有限个人,席位是按各集体的人员多少来分配的;3.每个系别的每个人被选举都是等可能的;4.每个单位至少应该分配到一个名额,如果某个单位,一个名额也不应该分到的话,则应将其剔除在分配之外;5.在名额分配的过程中,分配是稳定的,不受任何其他因素所干扰.1.2符号的定义:n----表示某系别的席位数(n1、n2、n3分别表示甲、乙、丙的席位数);p----表示某系别的人数(p1、p2、p3分别表示甲、乙、丙的人数);q-------表示总席位数;N-------表示总的席位人数.Q-------表示某单位的Q值.3 问题的分析通常人们都是按照人数比例来进行分配的.当比例中有小数时,人们又按照惯例将多余的席位分给比例中小数最大者.我们能得出以下结论:*公式:Npqn/4 模型建立目标:建立公平的席位分配方案.4.1 引出绝对不公平值并给出相对不公平值:设A,B 两方人数分别为21,p p ;分别占有 1n 和2n 个席位,则两方每个席位所代表的人数分别为11n p 和 22n p. 我们称 2211n p n p -为.例:10,100,1202121====n n p p则22211=-n p n p ; 又 10,1000,10202121====n n p p 则22211=-n p n p 由上例可知,用绝对不公平程度作为衡量不公平的标准,并不合理,下面我们给出相对不公平值.①若 2211n p n p > 则称 11221222211-=-n p n p n p n p n p 为对A 的相对不公平值,记为 ),(21n n r A ;②若 2211n p n p < 则称 12112111122-=-n p n p n p n p n p 为对B 的相对不公平值 ,记为 ),(21n n r B .4.2给出相对公平的席位分配方案:如果,A B 两方分别占有1n 和2n 席,利用相对不公平值A r 和B r 讨论,当总席位增加1席时,应该分配给A 还是B.不妨设1122>p n p n ,即对A 不公平,当再分配一个席位时,有以下三种情况:I .当221>+11p pn n 时,这说明即使给A 增加1席,仍然对A 不公平,所以这一席显然应给A 方.II.当221<+11p pn n 时,这说明给A 增加1席,变为对B 不公平,此时对B 的相对不公平值为:21121211-1 ++=()(,)B p n r n n p n (3)III.当221>+11p pn n 时,这说明给B 增加1席,将对A 不公平,此时对A 的相对不公平值为:12122111-1 ++=()(,)A p n r n n p n (4)因为公平分配席位的原则是使相对不公平值尽可能小,所以如果121211+<+(,)(,)B A r n n r n n (5)则这1席给A 方,反之这1席给B 方.由(3)(4)可知,(5)等价于21222211<11++()()p p n n n n (6)不难证明上述的第I 种情况221>+11p pn n 也与(6)式等价,于是我们的结论是当(6)式成立时,增加的1席应给A 方,反之给B 方.若记:2, =1,21=+()i i i i p Q i n n则增加的1席给Q 值大的一方.4.3模型内部推广:上述方法可以推广到有m 方分配席位的情况.设第i 方人数为i p ,已占有i n 个席位.当总席位增加1席时,计算:2, =1,21=+()i i i i p Q i m n n ,,则增加的1席应分配给Q 值大的一方.这种席位分配的方法称为Q 值法.5 模型求解5.1下面用Q 值法讨论甲,乙,丙系分配20个席位的问题:先按照比例将整数部分的10席分配完毕n 1=10, n 2=6, n 3=3,.再用Q 值法分配第20席和第21席;分配第20席,计算得:Q1=96.4; Q2=94.5; Q3=96.3Q1最大,于是这1席应分给甲系.分配第21席,计算得:Q1=80.4;Q2=94.5;Q3=96.3;Q3最大,于是这1席应分给丙系.5.2现象分析及结果:根据Q值分配结果与假定情况一的现象,易得出:惯例分配总席位为21时,分配不公平,以至得出总席位数N增加一个,丙的席位数反而减少了一个的错误结论.6 模型评价●我们巧用绝对值,避免了分两种情况.从而简化了运算.●改进后的Q值法席位分配方案应用性推广,分配更公平.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
公平席位的分配数学(2)班学号 0907022029 郭子龙摘要:讨论公平席位分配的模型已有很多。
本文首先用比例加惯例法、Q值法、D’hondt法对问题中名额进行了分配,再对D’hondt法的合理性进行了分析,并在Q值法对绝对尾数(绝对不公平度)的处理方式基础上,提出了相对尾数模型,并讨论了其满足Young公理的1,3,4条关键词:分配相对尾数 Balinsky & Young不可能定理正文1 问题复述公平的席位分配问题是一个非常有趣而重要的问题,它在政治学、管理学和对策论等领域具有广泛的应用价值。
处理这个问题的最早的方法是Hamilton法,即比例加惯例法;后来出现了Q值法;1974年M.L.Balinski和H.P.Young引入了席位分配问题的公理体系研究方法,并于1982年证明了同时满足五个公理的席位分配方法是不存在的;因此,我们只能根据实际建立在一定公平准则下成立并尽量多的满足Young公理的算法。
这里,我们需要理解并运用比例加惯例法、Q 值法、D’hondt法对宿舍委员会名额进行分配,继而提出更优的公平分配席位的方法。
2 模型假设2.1 合理假设1.比例加惯例法、Q值法等分配模型均为已知;2.各个宿舍相互独立互不影响,人数保持不变;3.委员分配以各宿舍人数为唯一权重。
2.2 符号约定3 模型的建立与求解3.1按比例加惯例模型分配根据比例加惯例分配模型的原理表3.2按Q 值法模型分配首先用比例分配法对名额进行初步分配,再根据表达式)1(2+=i i ii m m n Q C B A i ,,=对剩下的名额进行分配3.3 D ’hondt 模型 3.3.1 模型建立设n ,m 分别表示宿舍总人数和总分配席位数,i n (1,2,3i =)表示各宿舍人数,令iij n a j =(1,2,3,1,2,...i j ==),则得到一个数列{}ij a ,将该数列按递减顺序重新排列,得到{}()k ija ,其中()k ija表示{}()k ija 中第k 大的项。
取{}()k ija 中前m 项,则相应得到{}{}()k p ijm a i p ==(k=1,2,...,m)中的元素的个数(1,2,3p =),1m ,2m ,3m 即为按D ’hondt 模型分配的结果。
3.3.2 按D ’hondt 模型分配根据建立的D ’hondt 模型,编写MATLAB 程序求出结果(附件-程序6,附录-输入及运行结果3):3.4 相对尾数模型 3.4.1 模型准备讨论一般情况:k 个宿舍人数分别为i n ,1,2,...,i k =,总人数为1...k n n n =++,待分配的席位为m 个,理想化的分配结果是ip (1,2,...,i k =),满足1kii m p ==∑,记ii n q mn =(1,2,...,i k =)。
显然,若i q 全为整数,应有i q =i p (1,2,...,i k =),当i q 不全为整数时,需要确定同时满足下面公理的分配方案。
公理一:[][]i i i q p q -+≤≤(1,2,...,i k =),即i p取[]i q -或[]i q +之一,其中[]i q -=[]i q ,[]i q +=[]1i q +,[]i q 表示i q 的整数部分。
公理二:1212(,,,...,)(1,,,...,)i k i k p m n n n p m n n n ≤+,1,2,...,i k =,即总席位增加时,各宿舍的席位数不应该减少。
公理一显然满足Balinsky & Young 不可能定理 (见附录) 中的公理4(公平分摊性),公理二满足其的公理1(人口单调性)和公理3(名额单调性)。
令[]i i i i i n n s m m q q n n --⎡⎤=-=-⎢⎥⎣⎦,称其为对第i 个宿舍的绝对尾数值。
令[]i i i s r q -=,称其为对第i 个宿舍的相对尾数值。
3.4.2 模型建立与求解由于人数都是整数,为使分配趋于公平,需所有的i r 越小越好,所以趋于公平的分配方案应该是最大的i r 达到最小,即所有的i r 达到最小。
为方便起见,首先考虑只有两个宿舍的情形,即2k =,12n n n =+,且12n n ≠,1q 和2q 不全是整数(实际上,他们同为整数或小数)。
记i p -,i r -为总席位增加一席时的分配结果和相对尾数。
给出定理:定理:以下分配方案满足公理一,二,若12r r =,且12s s >,则取111n p m n -⎡⎤=+⎢⎥⎣⎦,22n p m n -⎡⎤=⎢⎥⎣⎦,即按比例加惯例法分配; 若12r r >,则取111n p m n -⎡⎤=+⎢⎥⎣⎦,22n p m n -⎡⎤=⎢⎥⎣⎦; 若12r r <,则取11n p m n -⎡⎤=⎢⎥⎣⎦,221n p m n -⎡⎤=+⎢⎥⎣⎦。
Balinsky & Young 不可能定理公理 1 (份额单调性) 一个州人口的增加不会导致它失去席位。
公理 2 (无偏性) 在整个时间上平均, 每个州应得到它自己应分摊的份额。
公理 3 (席位单调性) 总席位增加不会导致某个州名额减少。
公理 4 (公平分摊性) 任何州的席位数都不会偏离其比例的份额数。
公理 5 (接近份额性) 没有从一个州到另一个州的名额转让会使得这两个州都接近它们应得的份额。
按照定理,对三个宿舍的情形进行讨论。
设1r ,2r ,3r 全部为零(实际上,如果有一个为零,即是按两个宿舍分配),可以做以下分配:1)当123r r r ==时,按比例分配取整后,剩余的席位分配给绝对尾数较大的宿舍,即按比例加惯例法分配;2)当123r r r >=时,按比例分配后,若剩余一个席位,则分配给第一个宿舍,若剩余两个席位,则分配一席给第一个宿舍,另外一席分配给第二三个宿舍中绝对尾数值较大者;3)当123r r r =>时,按比例分配后,若剩余一个席位分配给第一二个宿舍中绝对尾数值较大者,若剩余两个席位,则分配给第一二宿舍各一席;4)当123r r r >>时,按比例分配后,若剩余一个席位,则分配给第一个宿舍,若剩余两个席位,则分配给第二个宿舍。
一般地,对k 个宿舍,设1r ,2r ,…,n r不全为零,且12...k r r r ≥≥≥,则当1t t r r +≠时,将剩余的1ki i n t m m n =-⎡⎤=-⎢⎥⎣⎦∑个席位分配给第一至第t 个宿舍各一席,当112t t t t r r r r -++>=>时,1ki i n t m m n =-⎡⎤=-⎢⎥⎣⎦∑ 个席位分配给第一至第1t -个宿舍及t s 和1t s +较大的宿舍各一席,当11t t t t s r r r r -++>==(1s k t <≤-)时,1ki i n t m m n =-⎡⎤=-⎢⎥⎣⎦∑ 个席位分配给第一至第1t -个宿舍及t s ,1t s +,…t s s +中较大的宿舍各一席,当1't st s t s r r r --++>=(1,'s s k t <≤-),1kii n t m mn =-⎡⎤=-⎢⎥⎣⎦∑ 个席位分配给第一至第t s-个宿舍及t s ,1t s +,…t s s +中s 个较大的所对应的宿舍各一席。
4 模型检验及结果分析席位分配的尾数模型满足Young 公理的1、3、4条,是以严格证明了的定理形式给出。
对按上述四种分配模型分配的结果列表比较。
表格中,B表示比例加惯例法,Q表示Q值法,D表示D'hondt法,R表示相对尾数法。
“比例加惯例”法用各团体人数占团体总人数的比例乘以总席位数, 取其整数位为第一次分配, 再次分配时, 则按小数位的大小分, 大的先分配, 直到席位分完。
从表4看到,当总席位数增加时,C宿舍分得的席位却减少;Q值法利用相对不公平度建立了衡量不公平程度的数量指标, 进而将席位分给最不公平的一方。
D’hondt方法将各团体的人数用正整数相除, 其商数组成一个表, 将数从大到小取, 直到取得的商数的个数等于总席位数, 统计出每个团体被取到的商数的个数, 即为该团体分得的席位数。
5 优缺点分析及改进从对模型的检验与分析可以看到,上面讨论的三个模型都有自身的不足:比例加惯例法满足公理一,却不满足公理二;Q值法满足公理二但不满足公理一;D’hondt法也不能解决对每个宿舍成员公平的大小问题;尾数法虽然满足公理一和二,但由于两个公理本身只满足Young公理体系的部分,也不尽完美。
优点:尾数模型打破Q值法的对绝对尾数的比较方法,以相对尾数来讨论,使得模型满足了Young公理体系中更多的公理,虽不尽完善,但相比之前的四种方法是很大的改进。
并且,这种对已有方法改进的思想很有启发意义。
改进:本文中只给出了尾数法对3个宿舍的名额分配程序,对不定数量宿舍的分配没能程序实现,是可以改进的。
6 模型的具体意义人生活在这个经济的社会,每个人或多或少都是一个经济人,即以自己最小的经济代价去获取自己最大的经济利益,但是经济人永无止尽的欲望与有限的资源发生了矛盾,因此人们都尽自己最大的努力使自己获得最大资源和利益。
如此,每个人都这样做,或多或少会引起其他人的不满,造成人与人之间和社会内部的矛盾,经过长久的博弈之后,人们决定让每个人都能得到一定的满足,但每个人也不能占尽全部利益!这就涉及到一个公平的问题。
我们知道绝对的公平是不存在的,那我们如何才能做到相对的公平?让每个经济人都得到满足,也满意这种资源的分配?这就是本文所要应用的具体意义。
参考文献[1]姜启源等数学建模[M](第四版)北京高等教育出版社,2010.9:278—286.[2]岳林关于Q值法的一种新定义[J]. 系统工程.1995,13(4):70—73.[3]高尚席位分配的最大熵法[J].数学的实践与认识,1996,26(2):73—75.。
