光纤光栅应变传感器实验讲义
光纤布拉格光栅传感器测量温度和应变的原理
光纤布拉格光栅传感器测量温度和应变的原理光纤布拉格光栅传感器，简称FBG传感器，这可是个神奇的东西哦！它不仅可以测量温度，还能测量应变，简直就是个万能的小助手。
今天，我就来给大家聊聊这个神奇的小家伙是怎么工作的，让我们一起揭开它的神秘面纱吧！我们来了解一下FBG传感器的基本结构。
它是由一系列周期性折射率不同的光纤组成的，这些光纤就像一根根细细的琴弦，当光线通过它们时，会发生折射现象。
而这种折射现象正是FBG传感器测量温度和应变的关键所在。
FBG传感器是如何测量温度的呢？其实，这就要靠那些神奇的光纤了。
当阳光或者光源照射到光纤上时，光纤中的原子会吸收一部分光线，使得光线在光纤内部发生反射。
而反射回来的光线经过多次反射后，最终到达了FBG传感器的检测器。
检测器会根据反射光线的强度和时间变化来计算出光纤的温度。
是不是很厉害啊！我们再来聊聊FBG传感器是如何测量应变的。
其实，这也是利用了光纤的折射现象。
当FBG传感器受到外力作用时，光纤会发生形变，从而导致折射光线的变化。
而这种变化又被检测器捕捉到，从而计算出了应变的大小。
是不是感觉FBG传感器就像一个神奇的变形金刚一样，可以感知到周围的变化呢！FBG传感器有哪些应用呢？其实，它的应用范围非常广泛。
在建筑行业中，它可以用来检测混凝土的结构变化；在医疗行业中，它可以用来监测人体的生理指标；在汽车制造行业中，它可以用来检测车身的变形情况。
只要有需要测量温度和应变的地方，FBG传感器都可以派上用场哦！当然啦，虽然FBG传感器非常神奇，但它也有一些局限性。
比如说，它的灵敏度有限，不能用来检测非常微小的应变；而且，它的精度也有一定的误差。
随着科技的发展，相信这些问题都会得到解决的。
今天关于光纤布拉格光栅传感器测量温度和应变的原理就给大家介绍到这里了。
希望对大家有所帮助哦！下次再见啦！。
光纤光栅传感器应变和温度交叉敏感问题
光纤光栅传感器应变和温度交叉敏感问题
1.2 光纤布拉格光栅原理 光纤布拉格光栅通常满足布拉格条件
式中，λB为Bragg波长，n为有效折射率，A为光栅周 期。 当作用于 光纤光栅的被测物理量(如温度、应力等)发 生变化时，会引起n和A的相应改变，从而导致λB的漂移; 反过来，通过检测λB的漂移。也可得知被测物理量的信息。 Bragg光纤光栅传感器的研究主要集中在温度和应力的准 分布式测量上。温度和应力的变化所引起的λB漂移可表示 为：
2.2 双参量矩阵法 双参量矩阵法是运用各种方法将温度 和应力对同一光波的影响分别作用于该光 波的不同参量上，然后推导出对应关系， 以实现应力和温度的区分测量。近年来， 有许多方法基于这一思想的交叉敏感问题 解决方案。如混合FBG/长周期光栅法、二 次谐波法、超结构光栅法等。
光纤光栅传感器应变和温度交叉敏感问题
在图1所示的光纤光栅传感器结构中，光源为宽谱光 源且有足够大的功率，以保证光栅反射信号良好的信噪比。 一般选用侧面发光二极管ELED的原因是其耦合进单模光 纤的光功率至少为50～100 µW。而当被测温度或压力加 在光纤光栅上时。由光纤光栅反射回的光信号可通过3 dB 光纤定向耦合器送到波长鉴别器或波长分析器，然后通过 光探测器进行光电转换，最后由计算机进行分析、储存， 并按用户规定的格式在计算机上显示出被测量的大小。 光纤光栅除了具备光纤传感器的全部优点外.还具有 在一根光纤内集成多个传感器复用的特点，并可实现多点 测量功能。
光纤光栅传感器应变和温度交叉敏感问题
2.4 温度(应力)补偿法 其实，目前研究较多的还是温度补偿 法。该方法主要通过某种方法或装置先将 温度扰动引起的波长漂移剔除掉，从而使 应变测量不受温度的影响。近年来，国内 外许多学者提出了关于FBG交叉敏感的问 题，主要考虑实现对温度、应变同时测量 的温度补偿方法。它们分为单FBG法和双 FBG法两大类。
光纤光栅应变传感的综合性实验设计
ｚ ５０ｍｉ 一 ８ Ｔ ｔ
６ ７ ． ８ Ｏ １５ ９ ７ ５ ． ２
光纤光栅 中心波 长
１ Ｏ １ ９ １ １５ ９ ７ ２ ５ ． ４ １． ３ ５ １Ｏ ６ ．５ １５ ９ ７ ４ ５． ８ １ ． ６ ５ １ ６ ２ ９ ． １５ ９ ８ ５ ５ ． ３
第２ ５卷
第 ３期
大
学
物
理
实
验
Ｖｏ ． ５ Ｎｏ ３ １２ ．
２１ ０ ２年 ６ 月
ＰＨＹＳ Ｃ Ｉ ＡＬ Ｐ ＥＸ ＥＲＩ ＭＥＮＴ ０Ｆ ＣＯＬＬＥ ＧＥ
Ｊ ｎ ２ １ ｕ．０２
文 章 编 号 ：０ ７２ ３ （ ０ ２０ —０００ １０ —９４ ２ １ ） ３０ ８ —２
光 纤光栅 应 变传 感 的综 合 性 实验 设 计 ＊
龚华平 ， 丛 ， 于梦 ， 曹 屠 董新永
（ 国计 量 学 院 ， 江 杭 州 中 浙 ３０１） １ ０ ８
摘 关 键
要： 利用光纤布拉格光栅 反射 波长对外界应变敏感 的特性 ， 测量等强度悬 臂梁产生 的应变 ， 并 词： 光纤布拉格 光栅 ； 应变传感器 ； 悬臂梁
００ ． ６１
０１４ ． ０ ｌ１Ｐ３ ＿１
０１６ ． ３
０ ７ ．１ ８
０２９ ． ２ ｉ
由此 产 生 的应 变 误差 为 １ ８ ； ． ￡ 挠度 测 量 产生 的
４ 实 验 结 果
文章 采用 光纤 光栅 对等 强度 梁产 生 的应变 进 行 测试 研 究 ， 到 的实 验结果 如 下表 １ 示 。 得 所
误 差 约 为 ０ ２ｍｍ， ． 由此 导 致 的灵 敏 度 误 差 为 ０ ０ ｍ／ ￡气流气 压 挠 动 导致 的波 长 漂 移 误 差 ．２ｐ ； （ 与前 两项 导致 的误差 可 以忽 略不计 ） 。综合 以上 因素 ， 实验误 差 的影 响很小 ， 本对 测量 结果没 有 基 影响。
光纤光栅动态应变测试实验
实验二 光纤光栅动态应变测试实验一、实验目的当简支梁受外载荷情况下，学会用光纤光栅传感器测量其表面某点的应变，加深对光纤光栅动态应变测试的理解。
在实验过程中采集数据，分析并处理数据，并做时域分析。
二、实验设备WS-ZHT2型振动综合教学实验台光纤光栅解调仪光纤光栅焊接机光纤布拉格光栅（FBG ）三、实验原理在材料力学中，由梁弯曲变形的基本公式得：zy =I M σ （1） 矩形截面，惯性矩3z b h I =12（2） 由胡克定律可知：=E σε （3）注：45号钢弹性模量E=209Gpa应力应变引起光栅布拉格波长漂移可以由下式给予描述：()Δεk ΔεPe 1λεΔλεB B =-= （4）式中，Pe 为光纤的弹光系数，εk 为应变ε引起的波长变化的灵敏度系数。
对于带有中心反射波长B λ， 的典型的石英光纤，轴向应变ε和波长漂移B Δλ有如下关系：B Δλ/B λ=0.78ε （5）说明：1nm=103pm 1pm ≈1με四、实验内容与步骤1 测量出简支梁的长宽高以及所测点在的位置，根据公式（1）、（2）、（3），给出在激励F 作用下所测点对应的应变该变量ε，即F 与ε的关系。
2 在静载荷下采集波长，求得波长的平均值0λ3 在同一频率下分别施加F1、F2、F3，分别采集所对应的波长13λλλ、2、，求出波长变化量13λλλ∆∆∆、2、（0=-λλλ∆），然后分别代入（5）式中计算得应变13εεε、2、 3 每一实验小组分别选三个频率，分别在每个频率下施加F1、F2、F3，通过采样、计算后得到应变13εεε、2、。
4 绘出时域上的应变图，进行频谱分析，观察频谱图中频率大小是否与实验中所给频率大小相同，分析时域图中应变变化与力的变化的关系，从而判断实验与理论是否吻合。
五、实验报告要求1 从理论上推导外载荷F 与应变ε之间的关系2 先在静态下求出波长平均值0λ，通过加外载荷实验得到的波长λ，算出变化量λ∆，再转化成应变ε，用EXCEL 或MATLAB 绘制时域图，并分析图形走势3 频谱分析，试着从频谱上观察振动频率，振动幅值。
光纤光栅电磁量传感器
---主讲人：马玉梅 20122531
介 绍
1. 光弹效应：当外力或振动作用于弹性体产生应变时，弹性体的折射率发生
变化，呈现双折射性质，这种有内应力的透明介质中o光和e光折射率不相
等，它与应力分布有关。这种现象即为光弹性效应。
2. 光栅周期：从一个折射率改变点到相邻一个折射率改变点的长度。
一．光纤光栅传感器测量电磁量的原理
当光栅发生应变时，产生的弹性变形将使光栅的周期改变，
光弹性效应也会使纤芯的折射率变化，相应地将引起光栅中心波
长改变。由于光栅中心波长的改变与光栅应变成良好的线性关系， 因此通过电热转换、利用电磁力、磁致伸缩材料以及电致伸缩材 料等使光纤光栅发生应变，进而便可以实现对电压、电流、磁场 等物理量的测量。
1.电磁力实现电流测量
光纤光栅电磁力调谐实验装置如图2所示，
图2(a)表示带铁芯螺线圈通电时，磁极间产
生的磁场基本上为匀强磁场。长度为 L 的刚 性细导线，沿梁的轴向被刚性地粘贴于梁的
下表面。
图2 (a) 利用电磁力测量电流方案一
(b) 利用电磁力测量电流方案二
通电后导线在稳恒磁场中受电磁力F作用，
不考虑梁和导线本身重量，光栅上考察点处 的弯矩与电流的大小成正比，粘贴在梁上的 光纤光栅产生变形，其波长漂移量与待测电
流Io 成线性关系。
当I>0 时，F 使得光栅受拉应力作用，反射 波长向长波长方向漂移; 反之，光纤光栅受
压应力作用，反射波长向短波长方向漂移；
电流强度越大，漂移量越多，因此该装置可 用来感知电流的大小[10]。
当螺线管通入电流，螺线管内产生磁场，使两块磁 铁磁化，产生栅产生拉伸应变，
光纤光栅中心波长发生移动。由于改变电流很容易 调谐光纤光栅的中心波长，这种装置可以用于电流
实验11 基于光纤布拉格光栅的应变和温度传感器实验
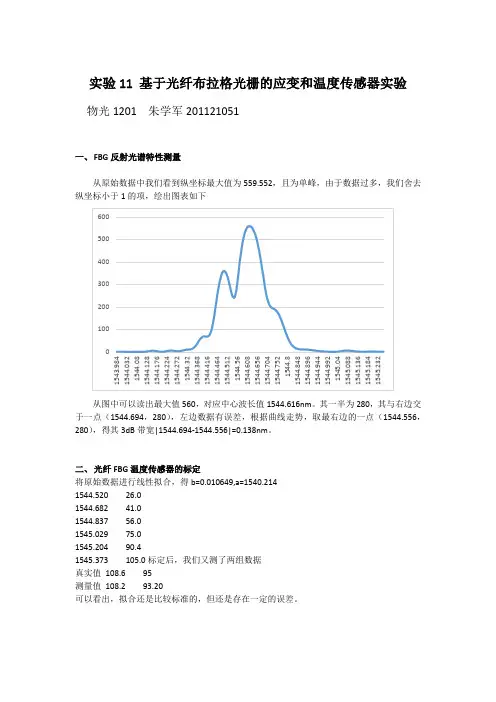
实验11基于光纤布拉格光栅的应变和温度传感器实验物光1201 朱学军201121051一、FBG反射光谱特性测量从原始数据中我们看到纵坐标最大值为559.552，且为单峰，由于数据过多，我们舍去纵坐标小于1的项，绘出图表如下从图中可以读出最大值560，对应中心波长值1544.616nm。
其一半为280，其与右边交于一点（1544.694，280），左边数据有误差，根据曲线走势，取最右边的一点（1544.556，280），得其3dB带宽|1544.694-1544.556|=0.138nm。
二、光纤FBG温度传感器的标定将原始数据进行线性拟合，得b=0.010649,a=1540.2141544.520 26.01544.682 41.01544.837 56.01545.029 75.01545.204 90.41545.373 105.0标定后，我们又测了两组数据真实值108.6 95测量值108.2 93.20可以看出，拟合还是比较标准的，但还是存在一定的误差。
三、光纤FBG应变传感器的——光纤称重传感器1564.404 01564.696 5001564.885 10001565.077 15001565.270 20001565.467 25001565.667 3000将原始数据进行线性拟合，得b=0.0000985,a=1544.615标定后，我们又测了三组数据真实值1000 2000 2500测量值1003.4082022.676 2478.746可以看出，在误差允许的范围内，拟合还是比较标准的。
四、思考题1、影响光纤FBG温度传感器的测量精度的因素有哪些？答：有操作失误、温度没有稳定就读值、光纤有损坏、系统误差等。
2、如何提高光纤FBG中心波长的计算精度？答：在最高点附近多测几组数值、整体多测几次求平均、读数时根据曲线的对称性在最高点附近两边取纵坐标相同的值再求中点。
五、心得体会通过本次实验，我了解了基于光纤布拉格光栅的应变和温度传感器的工作原理和特性，同时对传感器也有了更多的了解，测量是否精确也在一定程度上取决于标定的情况。
实验--光纤光栅传感实验
光纤光栅传感器实验一、实验目的1. 了解和掌握光纤光栅的基本特性；2. 了解和掌握光纤光栅传感器的基本结构、基本原理；3. 光纤光栅传感测量的基本方法和原理。
二、实验原理光纤光栅是近年来问世的一种特殊形式的光纤芯内波导型光栅，它具有极为丰富的频谱特性，在光纤传感、光纤通信等高新技术领域已经展示出极为重要的应用。
特别是在用于光纤传感时，由于其传感机构（光栅）在光纤内部，且它属于波长编码类型，不同于普通光纤传感的强度型，因而具有其他技术无法与之相比的一系列优异特性，如防爆、抗电干扰、抗辐射、抗腐蚀、耐高温、寿命长、可防光强变化对测量结果的影响、体积小、重量轻、灵活方便，特别能在恶劣环境下使用。
光纤光栅传感器可集信息的传感与信息的传输于一体，它极易促成光纤系统的全光纤化、微型化、集成化以及网络化等等，因此光纤光栅传感技术一经提出，便很快受到青睐，并作为一门新兴传感技术迅猛崛起。
1. 光纤光栅及其基本特性光纤光栅的基本结构如图1－1所示。
它是利用光纤材料的光折变效应，用紫外激光向光纤纤芯内由侧面写入,形成折射率周期变化的光栅结构，这种光栅称之为布喇格（Bragg ）光纤光栅。
这种折射率周期变化的Bragg 光纤光栅满足下面相位匹配条件时，入射光将被反射：Λ=eff B n 2λ (1)式中B λ 为Bragg 波长（即光栅的反射波长），为光栅周期，eff n 为光纤材料的有效折射率。
如果光纤光栅的长度为L ,由耦合波方程可以计算出反射率R 为： 附图1－1 光纤光栅示意图布喇格光纤光栅 纤芯入射光反射光光纤包层()R A A sL s sL sLr i ==+002222222()sinh cosh (/)sinh *κκβ∆图1－2 显示了两条不同反射率的布喇格光纤光栅反射谱，附图1－3为实际的一个布喇格光纤光栅反射谱和透射谱。
其峰值反射率m R 为:⎥⎥⎦⎤⎢⎢⎣⎡Λ∆=eff m n nL R 2tanh 2π (2) 反射的半值全宽度（FWHM ）,即反射谱的线宽值22⎪⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛Λ=∆eff B B n n L λλ (3) （1）式中，,eff n Λ是温度T 和轴向应变ε的函数，因此布喇格波长的相对变化量可以写成：/()(1)B a T Pe λλξε=++- (4)其中a 、ξ分别是光纤的热膨胀系数和热光系数，；Pe 是有效光弹系数，大约为0.22。
光纤光栅应变传感器实验讲义
实验 光纤布拉格光栅（FBG ）应变实验研究【实验目的】1) 了解光纤光栅传感器基本原理及FBG 应变测量的基本公式。
2) 了解飞机驾驶杆弹性元件的力学特性。
3) 学习光纤光栅应变测量的基本步骤和方法。
【实验原理】1.光纤光栅传感器的基本原理及FBG 应变测量的基本公式光纤布喇格光栅（Fiber Bragg grating, FBG ）用于传感测量技术，主要是通过外界物理量的变化对光纤光栅中心波长的调制来获取传感信息，因此它是一种波长调制型的光纤传感器。
FBG 传感原理如图1所示。
图1中，当一束入射光波进入FBG 时，根据光纤光栅模式耦合理论，当满足满足相位匹配条件时，反射光波即为FBG 的布喇格波长λB ，λB 与有效折射率n eff 和光栅周期Λ的关系为Λ2eff B n =λ （1)由式(1)可以知：n eff 与Λ的改变均会引起光纤光栅波长的改变，而且n eff 与Λ的改变与应变和温度有关。
应变和温度分别通过弹光效应与热光效应影响n eff ，通过长度改变和热膨胀效应影响周期Λ，进而使λB 发生移动。
将耦合波长λB 视为温度T 和应变ε的函数，略去高次项，则由应变和温度波动引起的光纤光栅波长的漂移可表示为Λ∆+∆Λ=∆eff eff B 22n n λ (2)Iλ透射光谱Iλ输入光谱反射光谱 波长漂移λIΛ输入光波反射光波透射光波加载物理量，如应变，温度图1 FBG 传感原理示意图由式(2)可知光纤光栅中心波长漂移量∆λ对轴向应变∆ε和环境温度变化∆T 比较敏感。
通过测量FBG 中心波长的变化，就可测量外界物理量的变化值（如应变、温度等）。
光纤光栅轴向应变测量的一般公式为()ελλe BBz1p -=∆，也是裸光纤光栅轴向应变测量的计算公式。
由上式可知，∆λBz 和ε存在线性关系，因此通过解调装置检测出布拉格波长的偏移量∆λ，就可以确定被测量ε的变化。
2. 飞机驾驶杆弹性元件的力学特性杆力传感器弹性元件采用平行梁形式，其结构如图2所示。
光纤光栅应变传感器测量应变误差分析
孙佃亮 等
之间的关系。通过理论分析，得到了横向效应所引起的测量误差，针对复杂平面应变问题，修正了测量 应变的计算公式，分析了安装角度、安装角度偏差等因素对测量精度的影响，得出：测量误差与安装角 度成近似正弦变化，随着主应变比增大，应变测量误差逐渐减小。该理论为光纤光栅在实际中的应用提 供了理论指导。
收稿日期：2019年2月25日；录用日期：2019年3月13日；发布日期：2019年3月21日
摘
*
要
光纤光栅应变传感器测量应变与实际应变并不相同，为了提高测量精度，需要研究测量应变与实际应变
通讯作者。
文章引用: 孙佃亮, 吴入军, 张晓峰, 陈田, 马雪芬. 光纤光栅应变传感器测量应变误差分析[J]. 仪器与设备, 2019, 7(1): 58-65. DOI: 10.12677/iae.2019.71009
(1)
由公式(1)可知：轴向应变与波长相对变化量成正比关系。然而，光纤光栅在实际测量时，不仅受到 如图 1 所示， 在 x 方向存在单向应变 ε x 的应变场中， 对于光纤 F2， 其承受横向作用， 设 ∆λ λ = K Bε x ， 其中 K B 为光栅的横向灵敏系数，对于光纤光栅 F1，存在： ∆λL = λ K L ε x ，其中 KL 为光栅的轴向灵敏系 数。假设 H 为横向灵敏系数与轴向灵敏系数之比，则存在公式(2)：
Open Access
1. 引言
光纤光栅应变传感器是随着通信技术的发展而发展起来的， 由于光纤光栅应变传感器同传统的机械、 电子类传感器相比，具有体积小、质量轻、抗电磁干扰等诸多优点，其在航空航天、医疗器械、土木工 程等诸多领域都得到了广泛的应用[1] [2]。 在光纤光栅应变传感器的实际应变测量时，主要利用了光纤光栅的轴向应变的灵敏性，没有考虑 光纤光栅横向效应对光纤光栅反射波长的影响，即认为光纤光栅受到的横向应变对反射波长无影响。 通过资料调研[3] [4，因此，如果 不考虑横向效应的影响，将会对光纤光栅测量结构造成一定的误差[5] [6]。苏晨辉[7]等人对表面粘贴 式光纤光栅传感器的应变传递机理进行了研究，张俊康[8]、梅钰洁[9]研究了光纤光栅传感器在螺旋管 和蒙皮中的测试技术，孙媛凯 [10]等人对光纤光栅传感器进行了实验标定，实验证明具有良好的线性 度和精度。 本文首次综合考虑了光纤光栅应变传感器横向效应、安装角度、安装角度偏差等因素对测量应变的 影响，并得到了安装角度和安装角度偏差对测量应变的关系表达式，对光纤光栅应变传感器的实际应用 具有很好的指导意义。
光纤光栅应变传感器的研制及应用
光纤光栅应变传感器的研制及应用一、本文概述光纤光栅应变传感器，作为一种新型的光纤传感器技术，近年来在多个领域展现出了广阔的应用前景。
本文将全面探讨光纤光栅应变传感器的研制过程、技术原理、性能特点以及在多个领域的应用实践。
文章首先将对光纤光栅应变传感器的基本概念进行介绍，阐述其相较于传统应变传感器的优势与特点。
随后，将详细介绍光纤光栅应变传感器的研制过程，包括其设计思路、制作工艺、封装技术等关键环节。
文章还将对光纤光栅应变传感器的性能进行全面分析，包括其灵敏度、测量范围、稳定性等关键指标。
在应用实践部分，本文将重点介绍光纤光栅应变传感器在土木工程结构健康监测、航空航天器结构应变测量、以及智能材料与结构健康监测等领域的应用案例，展示其在实际工程中的应用效果与潜力。
通过本文的阐述，旨在为读者提供光纤光栅应变传感器研制及应用方面的全面、深入的理解，为其在相关领域的研究与应用提供有益的参考与借鉴。
二、光纤光栅应变传感器的基本原理光纤光栅应变传感器是一种基于光纤光栅效应的高精度测量设备。
其基本原理是，当一束特定波长的光波在光纤中传播时，由于光纤内部的光栅结构，光波会发生反射，形成特定的光栅光谱。
当光纤受到外部应变作用时，光栅结构会发生变化，进而引起光栅光谱的波长移动。
这种波长移动与应变成线性关系，通过精确测量波长移动量，就可以推算出光纤所受的应变大小。
光纤光栅应变传感器具有灵敏度高、响应速度快、抗干扰能力强等优点，因此在工程结构健康监测、航空航天、桥梁隧道安全检测等领域有广泛的应用前景。
同时，随着光纤光栅制作技术和解调技术的不断发展，光纤光栅应变传感器的测量精度和稳定性也在不断提高，为各类复杂工程结构的安全监测提供了有力的技术支持。
三、光纤光栅应变传感器的设计与制造光纤光栅应变传感器的设计与制造是确保传感器性能稳定和精确的关键环节。
在设计阶段，我们需要充分考虑应变传感器的实际应用环境和需求，如温度、压力、湿度等环境因素，以及测量精度、响应速度、稳定性等性能要求。
光纤光栅传感实验报告
一、实验目的本次实验旨在了解光纤光栅传感技术的基本原理、工作过程以及其在实际应用中的重要性。
通过实验，掌握光纤光栅传感器的制作方法、传感特性以及传感信号的处理技术，为后续研究光纤光栅传感器在相关领域的应用打下基础。
二、实验原理光纤光栅传感器是一种基于光纤布拉格光栅（FBG）原理的新型传感器。
当外界物理量（如温度、应变、压力等）作用于光纤光栅时，光栅的布拉格波长会发生相应的变化，从而实现物理量的测量。
三、实验仪器与材料1. 光纤光栅传感器实验装置2. 光纤光谱分析仪3. 恒温水浴箱4. 拉伸机5. 氧化铝薄膜四、实验步骤1. 光纤光栅传感器的制作（1）将一根单模光纤切割成一定长度，并利用氧化铝薄膜对光纤进行腐蚀，形成光纤光栅。
（2）将制作好的光纤光栅固定在实验装置上，并进行封装。
2. 温度传感实验（1）将光纤光栅传感器放入恒温水浴箱中，分别设置不同的温度，记录光纤光谱分析仪输出的布拉格波长。
（2）分析温度与布拉格波长之间的关系，绘制温度-波长曲线。
3. 应变传感实验（1）将光纤光栅传感器连接到拉伸机上，施加不同大小的应变，记录光纤光谱分析仪输出的布拉格波长。
（2）分析应变与布拉格波长之间的关系，绘制应变-波长曲线。
五、实验结果与分析1. 温度传感实验实验结果显示，随着温度的升高，光纤光栅传感器的布拉格波长发生蓝移，且蓝移量与温度呈线性关系。
通过拟合曲线，得到温度-波长关系式：$$\Delta\lambda = aT + b$$其中，$\Delta\lambda$为布拉格波长变化量，$T$为温度，$a$和$b$为拟合参数。
2. 应变传感实验实验结果显示，随着应变的增大，光纤光栅传感器的布拉格波长发生红移，且红移量与应变呈线性关系。
通过拟合曲线，得到应变-波长关系式：$$\Delta\lambda = c\epsilon + d$$其中，$\Delta\lambda$为布拉格波长变化量，$\epsilon$为应变，$c$和$d$为拟合参数。
FBG光纤光栅的应变和温度传感特性研究与实验验证讲解
光纤光栅的应力和温度传感特性研究 (1)一光纤光栅传感器理论基础 (1)1 光纤光栅应力测量 (1)2 光纤光栅温度测量 (2)3 光纤光栅压力测量 (3)二光纤光栅传感器增敏与封装 (4)1 光纤光栅的应力增敏 (4)2 光纤光栅的温度增敏 (5)3 光纤光栅的温度减敏 (5)4 嵌入式敏化与封装 (6)5 粘敷式敏化与封装 (7)三光纤光栅传感器交叉敏感问题及其解决方法 (9)1 参考光纤光栅法 (10)2 双光栅矩阵运算法 (10)3 FBG与LPFG混合法 (11)4 不同包层直径熔接法 (12)5 啁啾光栅法 (12)光纤光栅的应力和温度传感特性研究一光纤光栅传感器理论基础1 光纤光栅应力测量由耦合模理论可知，光纤布拉格光栅(FBG)的中心反射波长为：2B eff n λ=Λ (1)式中：eff n 为导模的有效折射率，Λ为光栅的固有周期。
当波长满足布拉格条件式(1)时，入射光将被光纤光栅反射回去。
由公式(1)可知，光纤光栅的中心反射波长B λ随eff n 和Λ的改变而改变。
FBG 对于应力和温度都是很敏感的，应力通过弹光效应和光纤光栅周期Λ的变化来影响B λ，温度则是通过热光效应和热胀效应来影响B λ。
当光纤光栅仅受应力作用时，光纤光栅的折射率和周期发生变化，引起中心反射波长B λ移动，因此有：effBBeffn n λλ∆∆∆Λ=+Λ (2) 式中：eff n ∆为折射率的变化，∆Λ为光栅周期的变化。
光栅产生应力时的折射率变化：()21211112eff eff e effn n P P P n μμεε∆=---=-⎡⎤⎣⎦ (3) 式中：()21211112e eff P n P P μμ=--⎡⎤⎣⎦ (4) ε是轴向应力，μ是纤芯材料的泊松比，11P 、12P 是弹光系数，e P 是有效弹光系数。
假设光纤光栅是绝对均匀的，也就是说，光栅的周期相对变化率和光栅段的物理长度的相对变化率是一致的。
光纤光栅传感实验
光纤光栅传感实验一、实验目的1. 理解光纤光栅的制作原理；2. 掌握光纤光栅传感的原理；3. 学会使用光纤光栅传感仪软件；4. 使用光纤光栅传感仪测量温度变化对输出波长的影响；5. 使用光纤光栅传感仪测量应力变化对输出波长的影响；二、实验原理光纤光栅传感的基本原理和光纤光栅传感测量的基本原理光纤光栅受温度T 和应变ε同时影响时，光纤光栅峰值波长会发生变化，其相对变化量可以写成：Δλ/λ=(α+ξ)ΔT+（1－Pe ）ε （6）其中α、ξ分别是光纤的热膨胀系数和热光系数，其值α＝0.55×10－6，ξ＝8.3×10－6，即温度灵敏度大约是0.0136 nm /℃，（λ为1550nm ）；Pe 是有效光弹系数，大约为0.22，即应变灵敏度为0.001209 nm /με。
2.1光纤光栅温度传感器为了提高光纤光栅温度灵敏度，在光纤光栅温度传感器中，是将光纤光栅封装在温度增敏材料基座上，外部有不锈钢管保护，外面有加热装置。
如图4。
波长变化量及温度灵敏度分别为（请自行推算）：Δλ/ΔT =（(α+ξ) +（1－P ）（αj －α））λ （7）[Δλ/ΔT =αt ]αt 定义为该温度传感器的温度灵敏度，可由实验获得，大约是αt ＝0.035nm/℃。
由测量到的波长的变化量可计算出温度的变化t-t 0：2.2光纤光栅应变传感器本实验仪的光纤光栅应变传感器是一种悬臂梁应变调谐机构。
应用材料力学原理可以严格计算出光纤光栅的应变，用于模拟环境物理量使光纤光栅产生的应变。
由光纤光栅的应变又可计算出传感光栅的波长变化。
图1光纤光栅示意图出 射 光布喇格光纤光栅 纤芯入射光 反射光光纤包层光纤光栅应变传感器原理图如图5光纤光栅粘接在悬臂梁距固定端根部x 位置，螺旋测微器调节挠度，由材料力学可知，光纤光栅的应变为：3)(3l dhx l -=ε （8） 其中l 、h 、d 分别表示梁的长度、挠度和中性面至表面的距离，η＝1－PePe 是光纤有效光弹系数。
光纤光栅传感器实验指南-南昌大学.
光纤光栅传感器实验指南【原理简述】1．光纤光栅结构及传感应用光纤光栅是利用光纤材料的光折变效应，用紫外激光向光纤纤芯内由侧面写入,形成折射率周期变化的光栅结构（图1）。
当一束入射光照入光纤时，这种折射率周期变化的光纤光栅，将反射满足（1）式相位匹配条件的入射光波：Λ=eff Bn 2λ (1)式中λ B 称为Bragg 波长， Λ为光栅周期，eff n 为光纤材料的有效折射率。
如果光纤光栅的长度为L ,由耦合波方程可以计算出反射率R 为：()sLsL s sL A A R i r 22222*2sinh )2/(cosh sinh )0(0βκκ∆+==图2为一个布喇格光纤光栅反射谱和透射谱。
其峰值反射率R m 为:⎥⎥⎦⎤⎢⎢⎣⎡Λ∆=eff m n nL R 2t anh 2π (2)图2 Bragg 光纤光栅透射谱和反射谱反射的半值全宽度（FWHM ）,即反射谱的线宽值为22⎪⎪⎭⎫⎝⎛∆+⎪⎭⎫ ⎝⎛Λ=∆eff BB n n L λλ (3) 当光栅周围的应变ε或者温度T 发生变化时，将导致光栅周期Λ或纤芯折射率eff n 发生变化，从而产生光栅 Bragg 信号的波长位移 △λ，通过监测 Bragg 波长偏移情况，即可获得光栅周围的应变或者温度的变化情况，因而光纤光栅可用以如：压力、形变、位移、电流、电压、振动、速度、加速度、流量、温度等多种物理量的传感和测量。
2．光纤光栅应变传感原理图3 光纤光栅应变传感头光纤光栅粘接在悬臂梁距固定端根部x 位置，螺旋测微器调节挠度。
由材料力学可知，光纤光栅的应变为：33()l x dhl ε-=（4） 其中l 、h 、d 分别表示梁的长度、挠度和中性面至表面的距离。
挠度变化Δh 时，应变的变化量Δε及峰值波长的变化量为：h l dx l ∆-=∆3)(3ε （5） (1)e B P λλε∆=-∆ （6)Pe 是光纤有效光弹系数。
由（5）、（6）式，光纤光栅应变变化量Δε，可由波长的变化量λ∆转换计算出来，因此，光纤光栅应变传感的表达式为：()E f λ∆= （7）式（7）反映了波长变化与应变变化的函数关系，可由实验方法测出该关系。
《光纤光栅传感器》课件
远程监测
由于光纤的特性，光纤光栅 传感器可以实现远程监测， 适用于各种复杂环境。
应用领域
1 结构监测
光纤光栅传感器在桥梁、建筑等结构监测中有广泛应用。
2 油气检测
光纤光栅传感器可以用于油气管道中的泄漏检测和流量监测。
3 环境监测
光纤光栅传感器在环境监测领域中用于气体浓度、温度等参数的监测。
制备方法
工作原理
光纤光栅传感器的工作原理基于光纤中的光栅结构。当被测量物理量发生变 化时，光纤中的光栅会发生形变，从而导致光信号的改变。通过分析光信号 的变化，可以确定被测量物理量的数值。
优点
高灵敏度
光纤光栅传感器具有高灵敏 度，可以检测微小的物理量 变化。
抗干扰性强
光纤光栅传感器对外界干扰 的影响较小，具有良好的抗 干扰性能。
1
光纤制备
选择适合的光纤材料，并通过预拉伸等工艺制备光纤。
2
光栅制备
使用光刻、激光干涉等方法制备光栅结构。
3
光纤光栅组装
将光纤与光栅结构组装在一起，形成光纤光栅传感器。
实验室案例分享
实验室搭建
我们在实验室中搭建了一个光纤 光栅传感器测试平台。
传感器测试，我们验证了其性能和准确性。
《光纤光栅传感器》PPT 课件
欢迎大家来到《光纤光栅传感器》PPT课件。在本课程中，我们将介绍光纤光 栅传感器的定义、工作原理、优点、应用领域、制备方法，还会分享一些实 验室案例。让我们一起探索这一领域的知识和技术。
什么是光纤光栅传感器
光纤光栅传感器是一种利用光纤光栅结构对物理量进行测量的传感器。通过监测光纤中的光信号变化，可以获 得被测量物理量的信息。
我们还展示了一些光纤光栅传感 器在实际应用中的示例。
基于光纤光栅传感器的应变测量原理及应用
基于光纤光栅传感器的应变测量原理及应用光纤光栅传感器是一种基于光纤的传感器，可以用于测量应变、温度、压力等物理量，广泛应用于工业、民用和科学研究领域。
其中，应变测量是光纤光栅传感器的一个重要应用，下面我们将深入探讨基于光纤光栅传感器的应变测量原理及应用。
一、应变测量原理应变是表征物体形变程度的物理量。
在物体受到外力作用时，其原有的结构形态发生变化，长度或形状发生变化，这种变化称为应变。
光纤光栅传感器的测量原理是利用光纤中的光栅作为敏感元件，通过测量光纤中的光信号的变化来测量物理量。
在应变测量中，光纤光栅传感器的敏感元件是一段光纤，当光纤受到应变作用时，其长度或形状发生变化，导致光栅尺寸发生变化，从而改变了光的传播路径和波长。
通过测量光纤传输的光信号的传播路径和波长变化，可以计算出应变的大小。
二、应变测量应用基于光纤光栅传感器的应变测量可以应用于多种场合，例如力学实验、结构监测、土木工程等。
下面将重点介绍在土木工程中的应用。
1.桥梁监测桥梁是交通运输的重要组成部分，承担着极其重要的作用。
然而，由于气候、车辆荷载、地震等因素的影响，桥梁可能会出现应变和形变。
因此，桥梁的安全性和运行状态的监测是必不可少的。
光纤光栅传感器可以用于桥梁监测，通过测量桥梁的应变来判断桥梁的安全状态。
2.隧道监测隧道是重要的公共基础设施，其长期使用会产生形变，引起隧道结构的损坏和病害。
因此，隧道的监测也是必不可少的。
光纤光栅传感器可以应用于隧道监测，通过测量隧道的应变来判断隧道结构的变形情况。
3.地质灾害监测地质灾害是城市建设和农业生产过程中的重要问题。
地质灾害可能对人民生命财产造成严重的损失。
因此，地质灾害的监测也是必不可少的。
光纤光栅传感器可以应用于地质灾害监测，通过测量地质灾害发生区域的应变来判断灾害的发生情况和规模。
4.混凝土构件监测混凝土是建筑构件的常用材料。
然而，混凝土在使用过程中会受到外界环境的影响，出现应变和形变。
光纤光栅应变传感器温度补偿的解决方案ppt课件
矩阵法
矩阵法
Fig. 2 shows the respective spectra of the sensing FBG under no stress and 1500 N. It is indicated that when the sensor is stressed, the chirp bandwidth increases; meanwhile, the central wavelength moves to short wavelength,
矩阵法
利用两种不同化学聚合物分别对光纤光栅进行封 装, 其中将光栅一半封于聚胺脂甲中, 待其固化后, 再将 剩余一半光栅和甲全部封装于聚酞胺乙中, 整个光栅位 于乙的中心。封装后, 会产生两个反射峰, 且这两个峰的 压力和温度灵敏度均不相同, 从而达到压力和温度的同 时测量, 解决了测量压力时温度变化带来的不利影响。
谢 谢！
后面内容直接删除就行 资料可以编辑修改使用 资料可以编辑修改使用 资料仅供参考，实际情况实际分析
主要经营：课件设计，文档制作，网络软件设计、 图文设计制作、发布广告等 秉着以优质的服务对待每一位客户，做到让客户满 意！ 致力于合同简历、论文写作、PPT设计、计划书、 策划案、学习课件、各类模板等方方面面，打造全 网一站式需求
（2）文献内容简介： 文章提出了一种可以同时测量压力和温度嵌入式光纤布拉格光栅(FBG)传感器， 光纤光栅封装在一个锥形聚合物中，当给传感器压力时，光栅呈线性啁啾。外 加压力值和温度值可以通过测量啁啾和中央波长来获得。实验结果表明，该传 感器的应力敏感度为2.62×10-3 nm/N 和温度灵敏度为0.108 nm/℃。因为光 纤光栅受到很好的保护，且无突发的应力应变，所以传感器表现出卓越的可靠 性。 （3）文献的特色与创新点： 1. 对同一段光纤光栅的两半进行不用封装，即可以得到两个不同波长的反射 峰，通过比较两个反射峰波长的差异，初步断定中心波长的变化是由温度 还是应力应变引起的； 2. 文章采用的聚合物是一种改性丙烯酸酯胶粘剂，聚合物不仅给光纤光栅提 供了强有力的保护,也给光纤光栅提供了传感线性应变分布（有效地防止了 突发的应力应变），使得传感器更加可靠、更加实用； 3. 通过实验了解到啁啾现象只与应力应变有关，而中心波长的漂移同时受到 温度与应力应变的影响。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验 光纤布拉格光栅（FBG ）应变实验研究
【实验目的】
1) 了解光纤光栅传感器基本原理及FBG 应变测量的基本公式。
2) 了解飞机驾驶杆弹性元件的力学特性。
3) 学习光纤光栅应变测量的基本步骤和方法。
【实验原理】
1.光纤光栅传感器的基本原理及FBG 应变测量的基本公式
光纤布喇格光栅（Fiber Bragg grating, FBG ）用于传感测量技术，主要是通过外界物理量的变化对光纤光栅中心波长的调制来获取传感信息，因此它是一种波长调制型的光纤传感器。
FBG 传感原理如图1所示。
图1中，当一束入射光波进入FBG 时，根据光纤光栅模式耦合理论，当满足满足相位
匹配条件时，反射光波即为FBG 的布喇格波长λB ，λB 与有效折射率n eff 和光栅周期Λ的关系为
Λ2eff B n =λ （1)
由式(1)可以知：n eff 与Λ的改变均会引起光纤光栅波长的改变，而且n eff 与Λ的改变与应变和温度有关。
应变和温度分别通过弹光效应与热光效应影响n eff ，通过长度改变和热膨胀效应影响周期Λ，进而使λB 发生移动。
将耦合波长λB 视为温度T 和应变ε的函数，略去高次项，则由应变和温度波动引起的光纤光栅波长的漂移可表示为
Λ
∆+∆Λ=∆eff eff B 22n n λ (2)
I
λ
透射光谱
I
λ
输入光谱
反射光谱 波长漂移
λ
I
Λ
输入光波
反射光波
透射光波
加载物理量，如应变，温度
图1 FBG 传感原理示意图
由式(2)可知光纤光栅中心波长漂移量∆λ对轴向应变∆ε和环境温度变化∆T 比较敏感。
通过测量FBG 中心波长的变化，就可测量外界物理量的变化值（如应变、温度等）。
光纤光栅轴向应变测量的一般公式为
()ελλe B
Bz
1p -=∆，也是裸光纤光栅轴向应变测量的计
算公式。
由上式可知，∆λBz 和ε存在线性关系，因此通过解调装置检测出布拉格波长的偏移量∆λ，就可以确定被测量ε的变化。
2. 飞机驾驶杆弹性元件的力学特性
杆力传感器弹性元件采用平行梁形式，其结构如图2所示。
弹性元件由互相交叉90°的两对关联平行梁组成一个测力悬杆，其中一组感受纵向作用力，另一组感受横向作用力，上下部分连为一体，增加了梁的刚度，提高了梁的固有频率并具有良好的散热条件。
对其中每一方向作用力，由于其侧向刚度大，于是侧向负载能力强，与施加力平行的一对平行梁轴向应变可以忽略不计，外加力主要使与作用方向垂直的一对平行梁变形。
杆力传感器弹性元件为方框平行梁结构，为便于分析和简化计算，将方框平行梁简化为
一超静定刚架，力学模型如图3 (a)所示。
因为刚架计算通常忽略轴力对变形的影响，力学模型又可进一步简化为一个反对称载
荷作用的刚架，简化后的力学模型如图3 (b)所示，其中P=1/2P 0。
将受反对称载荷作用的刚架沿水平对称轴截开，这时垂直梁的截面上有三对内力力，即一对剪力X 、一对轴力N 、一对弯矩M ，多余约束力如图3 (c)所示。
根据结构力学反对称结构对称的外力为零的理论，
图2 弹性元件结构简图
x y z
(纵向)
(横向)
纵向力F
横向力F
图3 简化后的模型
(a) 超静定刚架结构 载荷P 0
a
L
b
h
(c) 多余未知力图
载荷P 载荷P
X
M N (b) 简化后力学模型
载荷P 载荷P
a L
A
B
C
D
因轴力N 、弯矩M 都是对称的，所以对称内力抵消，可以忽略。
只有反对称的剪切力X 存在。
为解除原结构中的多余应力使之成为静定结构，截断了垂直梁，超静定次数为1。
选取图3 (c)结构为基本系，利用弹性系统求解位移的图形互乘法，计算基本系的柔度系数δ11和自由项∆1p
23
1211122EI a EI La +
=δ (3)
1214EI PaL p
=
∆ (4)
将11和1p 带入力法正则方程式1=X 11+1p=0中，并令垂直梁与平行梁的刚度比为I2L/I1a =K ，则可以计算剪切力X 为
a PL
K K X p
216611
1⋅
+-
=∆-
=δ (5)
上下两个平行梁的弯矩可以表示为
41662D C PL K K X a M M ⋅+-==
= (6)
41626241662B A PL
K K PL PL K K X a M M ⋅++=+⋅+-==
= (7)
由公式(4)、(5)可以知道，当刚度比K 值不大时，平行梁上弯矩的零点，在靠近加载点一侧；当刚度比K 值很大时，平行梁上弯矩的零点趋于中点，即：MA=MB=PL/4，MC=MD=-PL/4。
工程应用中，K 值很大，我们可以认为平行梁弯矩零点就在其中点处。
正是由于弹性元件平行梁的这种受力弯曲结构，光纤光栅两点的粘贴位置应位于平行梁的上半部分或者下半部分，否则由于两边应变方向相反，会出现光纤光栅应变抵消的现象，影响传感器的灵敏度。
当弹性元件平行梁的C 、D 两端为自由端时，外力载荷作用下，平行梁上的弯矩MA=MB=PL/2，MC=MD=0；而实际情况C 、D 两端不是自由的，平行梁除了受外加载荷力外，还受一未知剪力X 作用，使得平行梁的弯矩发生变化，平行梁中点处的弯矩为零，两端弯矩最大且大小相等方向相反。
根据这种情况，可以仅把平行梁的一半看做是一个矩形悬臂梁，按照悬臂梁的结构进行计算，只是悬臂梁的长度应为平行梁长度的一半。
图3 (c)每一个梁都可以看做是矩形悬臂梁结构，对于光纤光栅式驾驶杆力传感器，我们可以根据矩形悬臂梁的应变情况分析，只是由于弹性元件应变的特殊情况，需要对光纤光栅选择特殊的粘贴位置（以弹性元件平行梁中线为基准，粘贴在中线上半部或下半部）。
对于如图4所示的矩形悬臂梁来说，有I =(1/12)bh 2，为o 点处悬臂梁截面的惯性矩，M(z)=P(L -z)为考察点z 处截面弯矩。
由挠度曲线的基本微分方程的两次积分后得到
2
1326121C z C z z EI
P
++⎪⎭⎫
⎝⎛-=
ν (8)
其积分常数C 1可以根据支撑处梁的斜度为零这一边界条件来求得，将ν (0)=0带入式(8)，可解得C 1=0；同理，由悬臂梁固定挠度的边界条件ν(0)=0，可以解得C 2=0。
因而可将悬臂梁的挠度曲线方程简化为
⎪
⎭⎫ ⎝⎛-=
32612
1z z EI
P ν (9) 沿梁轴向距固定端z 处的应变与弯矩M 之间有如下关系
EI M x z 0
=
ε (10)
式中，x 0为考察点距中性面的距离，对于图1所示的矩形悬臂梁结构，x 0=h /2。
将式(5)带入式(9)，可以得到自由端挠度υ与考察点z 处的应变εz 的关系为
3
1
12)(3L h z L z νε-=
(11)
对于飞机驾驶杆弹性元件的平行梁结构，当为弹性元件加载力P 时，平行梁沿z 轴向的应变关系式为
图4 矩形悬臂梁结构示意图
h 1
L 1
ν
z
y
x
b
z 0
3.
)2(6L h z L νε-=
(12)
把式（12)带入
()ελλe B
Bz
1p -=∆可以得到
()3e B B 26)
1(L h z L p ν
λλ--=∆ (13)
其中p e =n 2[ρ12-υ(ρ11-ρ12)]/2。
由式(13)可以知道，理论上光纤光栅中心波长漂移量∆λB 与弹性元件自由端的位移量（表征为所加载荷大小）成简单的线性关系，每单位载荷中心波长的漂移量即为传感器的灵敏度。
【实验仪器】
光纤光栅解调仪、宽带光源、光纤耦合器、杆力传感器弹性元件。
贴片式光纤光栅等。
【实验内容】
1) 首先要求同学们把仪器说明书通读一遍，没有读懂以前严禁乱调仪器。
2) 在特定的实验温度环境下，0-10kg 加载砝码，记录光纤光栅中心波长漂移量。
3) 利用origin 画图，得到光纤光栅中心波长与加载力（F=mg,g 取10）之间的线性关
系。