九年级数学上册第三章圆的基本性质检测卷同步测试(新版)浙教版
浙教版九年级数学上册 第3章 圆的基本性质 单元测试卷(含解析)

浙教版九年级数学上册第3章圆的基本性质单元测试卷题号一二三总分得分一、选择题(本大题共11小题,共33分)1.已知⊙O的半径为4cm,点A到圆心O的距离为3cm,则点A与⊙O的位置关系是()A. 点A在⊙O内B. 点A在⊙O上C. 点A在⊙O外D. 不能确定2.如图,AB是⊙O的直径,C、D是⊙O上两点,∠AOC=130°,则∠D等于()A. 65°B. 35°C. 25°D. 15°3.如图,已知经过原点的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB=()A. 80°B. 90°C. 100°D. 无法确定4.已知正六边形的边长为6,则它的边心距()A. 3√3B. 6C. 3D. √35.如图,☉O的半径为3,四边形ABCD内接于☉O,连接OB,OD,若∠BCD=∠BOD,则BD⌢的长为()π C. 2π D. 3πA. πB. 326.如图,在圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB等于()A. 36∘B. 60∘C. 72∘D. 108∘7.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=()A. 5B. 7C. 9D. 118.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5∘,OC=4,CD的长为()A. 2√2B. 4C. 4√2D. 89.半径为3,圆心角为120°的扇形的面积是()A. 3πB. 6πC. 9πD. 12π10.在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为()A. 16πB. 12πC. 10πD. 8π11.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG,AC⏜,BC⏜的中点分别是M,N,P,Q.若MP+NQ= 14,AC+BC=18,则AB的长为()C. 13D. 16A. 9√2B. 907二、填空题(本大题共9小题,共35分)12.如图,⊙O的内接四边形ABCD中,∠BOD=140°,则∠A等于______°.13.正五边形每个外角的度数是______.14.在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为_______.15.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果AC⏜=CD⏜,则∠ACD的度数是______.16.有一张矩形的纸片,AB=3cm,AD=4cm,若以A为圆心作圆,并且要使点D在⊙A内,而点C在⊙A外,⊙A的半径r的取值范围是______.17.如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为______.18.如图,在直角坐标系中,已知点A(−3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形1、2、3、4….则三角形2016的直角顶点坐标为______ .19.如图,CD是⊙O的直径,点A是半圆上的三等分点,B是弧AD的中点,P点为直线CD上的一个动点,当CD=6时,AP+BP的最小值为______.20.在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为______.三、解答题(本大题共4小题,共52分)21.如图,在由边长为1的小正方形组成的网格中,△ABC的顶点均落在格点上.(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1.在网格中画出△A1B1C1;(2)求线段OA在旋转过程中扫过的图形面积;(结果保留π)22.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD//BC,OD与AC交于点E.(1)若∠B=70°,求∠CAD的度数;(2)若AB=4,AC=3,求DE的长.23.如图,AB是⊙O的直径,点C是圆上一点,连接CA,CB,过点O作弦BC的垂线,交BC⌢于点D,连接AD.(1)求证:∠CAD=∠BAD;(2)若⊙O的半径为1,∠B=50°,求AC⌢的长.24.如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E.(1)求证:OD//AC;(2)若BC=8,DE=3,求⊙O的直径.答案和解析1.【答案】A【解析】解:∵圆的半径是4cm,点A到圆心的距离是3cm,小于圆的半径,∴点A在圆内.故选A.根据点到圆心的距离与圆的半径大小的比较,确定点与圆的位置关系.本题考查的是点与圆的位置关系,点A到圆心的距离是3cm,比圆的半径4cm小,可以判断点A就在圆内.2.【答案】C【解析】【分析】∠BOC,求出∠BOC即可.根据圆周角定理:∠D=12本题考查圆周角定理,解题的关键是熟练掌握基本知识,属于中考常考题型.【解答】解:∵∠BOC=180°−∠AOC,∠AOC=130°,∴∠BOC=50°,∠BOC=25°,∴∠D=12故选:C.3.【答案】B【解析】解:∵∠AOB与∠ACB是优弧AB所对的圆周角,∴∠AOB=∠ACB,∵∠AOB=90°,∴∠ACB=90°.故选B.由∠AOB与∠ACB是优弧AB所对的圆周角,根据圆周角定理,即可求得∠ACB=∠AOB= 90°.此题考查了圆周角定理.此题比较简单,解题的关键是观察图形,得到∠AOB与∠ACB是优弧AB所对的圆周角.【解析】解:如图所示,此正六边形中AB=6,则∠AOB=60°;∵OA=OB,∴△OAB是等边三角形,∵OG⊥AB,∴∠AOG=30°,=3√3,∴OG=OA⋅cos30°=6×√32故选:A.已知正六边形的边长为6,欲求边心距,可通过边心距、边长的一半和内接圆半径构造直角三角形,通过解直角三角形求解即可.此题主要考查正多边形的计算问题,属于常规题.解答时要注意以下问题:①熟悉正六边形和正三角形的性质;②作出半径和边心距,构造出直角三角形,利用解直角三角形的知识解答.5.【答案】C【解析】【分析】本题主要考查了弧长公式,圆内接四边形的性质,圆周角定理;熟练掌握圆内接四边形的性质和圆周角定理,求出∠BOD=120°是解决问题的关键.由圆内接四边形的性质和圆周角定理求出∠A=60°,得出∠BOD=120°,再由弧长公式即可得出答案.【解答】解:∵四边形ABCD内接于⊙O,∴∠BCD+∠A=180°,∵∠BOD=2∠A,∠BOD=∠BCD,∴2∠A+∠A=180°,解得:∠A=60°,∴∠BOD=120°,∴BD⏜的长.故选C.【解析】【分析】本题考查了正多边形和圆的知识,题目中还用到了三角形的外角的性质及正多边形的性质等,比较简单.首先根据正五边形的性质得到AB=BC,∠ABC=108°,∠ACB=36°,最后利用三角形的外角的性质得到∠APB=∠PBC+∠ACB.【解答】解:∵五边形ABCDE是正五边形,∴∠ABC=108∘,BA=BC,∴∠ACB=36∘.同理∠PBC=36∘,∴∠APB=∠PBC+∠ACB=72∘.故选C.7.【答案】A【解析】【分析】本题考查垂径定理与勾股定理的综合应用,解题的关键是明确垂径定理的内容,利用垂径定理解答问题.根据⊙O的半径为13,弦AB的长度是24,ON⊥AB,可以求得AN的长,再根据勾股定理求得ON的长.【解答】解:由题意可得,OA=13,∠ONA=90∘,AB=24,∴AN=1AB=12.在Rt△OAN中,ON=√OA2−AN2=√132−122=5.2故选A.8.【答案】C【解析】【分析】本题考查圆周角定理,垂径定理,等腰直角三角形的判定,勾股定理.先由圆周角定理求出∠BOC=45°,再由垂径定理得出∠OEC=90°,CD=2CE,则△OCE为等腰直角三角形,由勾股定理求出CE的长,即可得出CD长.【解答】解:∵∠A=22.5∘,∴∠BOC=2∠A=45∘,∵⊙O的直径AB垂直于弦CD,∴CE=DE,△OCE为等腰直角三角形,OC=2√2,∴CD=2CE=4√2.∴CE=√22故选C.9.【答案】A【解析】【分析】把已知数据代入S=nπR2,计算即可.360是解题的关键.本题考查的是扇形面积的计算,掌握扇形的面积公式:S=nπR2360【解答】=3π,解:半径为3,圆心角为120°的扇形的面积是:120π×32360故选A.10.【答案】D【解析】解:根据题意画图如下,在Rt△ABC中,AB=√AC2−BC2=√172−152=8,π⋅42=8π.则S半圆=12故选D.首先根据勾股定理求出AB的长,再根据半圆的面积公式解答即可.此题考查了勾股定理,用到的知识点是勾股定理以及圆的面积公式,关键是根据勾股定理求出半圆的半径.11.【答案】C【解析】解:连接OP,OQ,∵DE,FG,AC⏜,BC⏜的中点分别是M,N,P,Q,∴OP⊥AC,OQ⊥BC,∴H、I是AC、BC的中点,(AC+BC)=9,∴OH+OI=12∵MH+NI=AC+BC=18,MP+NQ=14,∴PH+QI=18−14=4,∴AB=OP+OQ=OH+OI+PH+QI=9+4=13,故选C.连接OP,OQ,根据DE,FG,AC⏜,BC⏜的中点分别是M,N,P,Q得到OP⊥AC,OQ⊥BC,(AC+BC)=9和从而得到H、I是AC、BC的中点,利用中位线定理得到OH+OI=12PH+QI,从而利用AB=OP+OQ=OH+OI+PH+QI求解.本题考查了中位线定理,解题的关键是正确的作出辅助线,题目中还考查了垂径定理的知识,难度不大.12.【答案】110【解析】【分析】根据圆周角定理求出∠C,根据圆内接四边形的性质计算即可.本题考查的是圆内接四边形的性质、圆周角定理,掌握圆内接四边形的对角互补是解题的关键.【解答】∠BOD=70°,解:由圆周角定理得,∠C=12∵四边形ABCD内接于⊙O,∴∠A=180°−∠C=110°,故答案为:110.第18页,共18页 13.【答案】72°【解析】解:360°÷5=72°.故答案为:72°.利用正五边形的外角和等于360度,除以边数即可求出答案.本题主要考查了多边形的外角和定理,任何一个多边形的外角和都是360°.14.【答案】3【解析】【分析】本题考查了垂径定理和勾股定理.作OC ⊥AB 于C ,连接OA ,根据垂径定理得到AC =BC =12AB =3,然后在Rt △AOC 中利用勾股定理计算OC 即可. 【解答】解:作OC ⊥AB 于C ,连结OA ,如图,∵OC ⊥AB ,∴AC =BC =12AB =12×8=4, 在Rt △AOC 中,OA =5,∴OC =√OA 2−AC 2=3,即圆心O 到AB 的距离为3.故答案为3.15.【答案】60°【解析】解:∵AB 是⊙O 的直径,弦CD ⊥AB 于点E ,∴AC⏜=AD ⏜, ∵AC⏜=CD ⏜, ∴AC⏜=CD ⏜=AD ⏜, 即AC ⏜、CD ⏜、AD ⏜的度数是13×360°=120°,∴∠ACD=1×120°=60°,2故答案为:60°.根据垂径定理求出AC⏜=CD⏜,求出AC⏜、CD⏜、AD⏜的度数,即可求出答案.本题考查了垂径定理,圆周角定理,圆心角、弧、弦之间的关系等知识点,能求出AD⏜的度数是解决此题的关键.16.【答案】4cm<r<5cm【解析】解:∵矩形的纸片,AB=3cm,AD=4cm,∴AC=5cm,∴以A为圆心作圆,并且要使点D在⊙A内,而点C在⊙A外,⊙A的半径r的取值范围为4cm<r<5cm.故答案为4cm<r<5cm.先利用勾股数得到AC=5cm,然后根据点与圆的位置关系,要使点D在⊙A内,则r>4;要使点C在⊙A外,则r<5,然后写出它们的公共部分即可.本题考查了点与圆的位置关系:点与圆的位置关系有3种,设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外⇔d>r;点P在圆上⇔d=r;点P在圆内⇔d<r.17.【答案】4√2【解析】解:如图,连接OB,OC,∵∠A=45°,∴∠BOC=90°,∴△BOC是等腰直角三角形,又∵BC=4,∴BO=CO=BC⋅cos45°=2√2,∴⊙O的直径为4√2,故答案为:4√2.连接OB,OC,依据△BOC是等腰直角三角形,即可得到BO=CO=BC⋅cos45°=2√2,进而得出⊙O的直径为4√2.本题主要考查了三角形的外接圆以及圆周角定理的运用,三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.18.【答案】(8064,0)【解析】解:∵A(−3,0),B(0,4),∴OA=3,OB=4,∴AB=√32+42=5,∴△ABC的周长=3+4+5=12,∵△OAB每连续3次后与原来的状态一样,∵2016=3×672,∴三角形2016与三角形1的状态一样,∴三角形2016的直角顶点的横坐标=672×12=8064,∴三角形2016的直角顶点坐标为(8064,0).故答案为(8064,0).先利用勾股定理计算出AB,从而得到△ABC的周长为12,根据旋转变换可得△OAB的旋转变换为每3次一个循环,由于2016=3×672,于是可判断三角形2016与三角形1的状态一样,然后计算672×12即可得到三角形2016的直角顶点坐标.本题考查了坐标与图形变化−旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.解决本题的关键是确定循环的次数.19.【答案】3√2【解析】【分析】本题考查了轴对称最短线段问题,垂径定理和勾股定理等知识,由轴对称的性质正确确定P点的位置是解题的关键.设A′是A关于CD的对称点,连接A′B,与CD的交点即为点P.此时PA+PB=A′B是最小值,可证△OA′B是等腰直角三角形,从而得出结果.【解答】解:作点A关于CD的对称点A′,连接A′B,交CD于点P,此时PA+PB=A′B是最小值,连接OA′,AA′.第18页,共18页∵点A与A′关于CD对称,点A是半圆上的一个三等分点,∴∠A′OD=∠AOD=60°,PA=PA′,∵点B是弧AD的中点,∴∠BOD=30°,∴∠A′OB=∠A′OD+∠BOD=90°,又∵OA=OA′=OB=3,∴A′B=3√2.∴PA+PB=PA′+PB=A′B=3√2.故答案为:3√2.20.【答案】π+12【解析】解:∵∠C=90°,AC=BC=1,∴AB=√12+12=√2;根据题意得:√2△ABC绕点B顺时针旋转135°,BC落在x轴上;△ABC再绕点C顺时针旋转90°,AC落在x轴上,停止滚动;∴点A的运动轨迹是:先绕点B旋转135°,再绕点C旋转90°;如图所示:∴点A经过的路线与x轴围成的图形是:一个圆心角为135°,半径为√2的扇形,加上△ABC,再加上圆心角是90°,半径是1的扇形;∴点A经过的路线与x轴围成图形的面积=135×π×(√2)2360+12×1×1+90×π×12360=π+12.故答案为:π+12.由勾股定理求出AB,由题意得出点A经过的路线与x轴围成的图形是一个圆心角为135°,半径为√2的扇形,加上△ABC,再加上圆心角是90°,半径是1的扇形;由扇形的面积和三角形的面积公式即可得出结果.本题考查了旋转的性质、扇形面积的计算公式;根据题意得出点A经过的路线与x轴围成的图形由三部分组成是解决问题的关键.21.【答案】解:(1)如图.△A1B1C1即为所求三角形;(2)由勾股定理可知OA=√22+22=2√2,线段OA在旋转过程中扫过的图形为以OA为半径,∠AOA1为圆心角的扇形,则.答:扫过的图形面积为2π.【解析】(1)根据图形旋转的性质画出旋转后的图形即可;(2)先根据勾股定理求出OA的长,再根据线段OA在旋转过程中扫过的图形为以OA为半径,∠AOA1为圆心角的扇形,利用扇形的面积公式得出结论即可;本题考查的是作图−旋转变换、扇形的面积公式,熟知图形旋转后所得图形与原图形全等的性质是解答此题的关键.22.【答案】解:(1)∵AB是半圆O的直径,∴∠ACB=90°,又∵OD//BC,∴∠AEO=90°,即OE⊥AC,∠CAB=90°−∠B=90°−70°=20°,∠AOD=∠B=70°.∵OA=OD,∴∠DAO=∠ADO=1800−∠AOD2=1800−7002=55°,∴∠CAD=∠DAO−∠CAB=55°−20°=35°;(2)在直角△ABC中,BC=√AB2−AC2=√42−32=√7.∵OE⊥AC,第18页,共18页∴AE=EC,又∵OA=OB,∴OE=12BC=√72.又∵OD=12AB=2,∴DE=OD−OE=2−√72.【解析】本题考查了圆周角定理以及三角形的中位线定理,正确证明OE是△ABC的中位线是关键.(1)根据圆周角定理可得∠ACB=90°,则∠CAB的度数即可求得,在等腰△AOD中,根据等边对等角求得∠DAO的度数,则∠CAD即可求得;(2)易证OE是△ABC的中位线,利用中位线定理求得OE的长,则DE即可求得.23.【答案】解:(1)证明:∵O是圆心,OD⊥BC,∴弧CD=弧BD,∴∠CAD=∠BAD;(2)连接CO,∵∠B=50°,∴∠AOC=100°,∴弧AC的长:nπr180=100×π×1180=5π9.【解析】本题考查了垂径定理及圆周角定理,弧长的计算.(1)利用垂径定理及圆周角定理即可证明;(2)连接CO,先求得∠AOC=100°,再利用弧长公式计算即可.24.【答案】(1)证明:∵AB是⊙O的直径,∴∠C=90°,∵OD⊥BC,∴∠OEB=∠C=90°,∴OD//AC;(2)解:令⊙O的半径为r,则OE=r−3∵OD⊥BCBC=4,根据垂径定理可得:BE=CE=12在ΔOBE中由勾股定理得:r2=42+(r−3)2,,解得:r=256.所以⊙O的直径为253【解析】本题考查了垂径定理、勾股定理、圆周角定理;熟练掌握圆周角定理和垂径定理,由勾股定理得出方程是解决问题(2)的关键.(1)由圆周角定理得出∠C=90°,再由垂径定理得出∠OEB=∠C=90°,即可得出结论;BC=4,由勾股定理得出方程,解(2)令⊙O的半径为r,由垂径定理得出BE=CE=12方程求出半径,即可得出⊙O的直径.第18页,共18页。
第3章 圆的基本性质 浙教版数学九年级上册测试(含答案)

浙教版数学九年级上册第三章圆的基本性质一、选择题1.下列说法正确的是( )A.三个点可以确定一个圆B.半圆(或直径)所对的圆周角是直角C.相等的圆心角所对的弧相等D.长度相等的弧是等弧2.已知一个扇形的面积是24π,弧长是2π,则这个扇形的半径为( )A.24B.22C.12D.63.如图,点A、B、C在⊙O上,∠C=40∘,则∠AOB的度数是( )A.50∘B.60∘C.70∘D.80∘4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若BE=5,AE=1,则弦CD的长是()A.5B.5C.25D.65.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )A.28°B.30°C.36°D.56°6.如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则BC的长为( )A .103πB .109πC .59πD .518π7.如图, AB 是半圆O 的直径,点C ,D 在半圆O 上.若 ∠ABC =50° ,则 ∠BDC 的度数为( )A .90°B .100°C .130°D .140°8. 如图,正六边形ABCDEF 内接于⊙O ,若⊙O 的周长等于6π,则正六边形的边长为( )A .3B .6C .3D .239.如图,正五边形ABCDE 内接于⊙O ,阅读以下作图过程:①作直径AF ;②以点F 为圆心,FO 为半径作圆弧,与⊙O 交于点M ,N ;③连接AM ,MN ,AN .结论Ⅰ:△AMN 是等边三角形;结论Ⅱ:从点A 开始,以DN 长为半径,在⊙O 上依次截取点,再依次连接这些分点,得到正十八边形.对于结论Ⅰ和结论Ⅱ,下列判断正确的是( )A .Ⅰ和Ⅱ都对B .Ⅰ和Ⅱ都不对C.Ⅰ不对Ⅱ对D.Ⅰ对Ⅱ不对10.如图,抛物线y=x2﹣8x+15与x轴交于A、B两点,对称轴与x轴交于点C,点D(0,﹣2),点E (0,﹣6),点P是平面内一动点,且满足∠DPE=90°,M是线段PB的中点,连接CM.则线段CM的最大值是( )A.3B.412C.72D.5二、填空题11.如图,在⊙O中,弦AB,CD相交于点P.若∠A=40°,∠APD=75°,则∠B= °.12.如图,AB、AC是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N.如果MN=2.5,那么BC= .13.如图,四边形ABCD内接于⊙O ,若四边形ABCD的外角∠DCE=65°,则∠BAD的度数是 .14.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=70°,则∠EAC的度数为 .15.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术:“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.1416.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙O,若用圆内接正十二边形作近似估计,可得π的估计值为 .的面积,可得π的估计值为33216.如图,点M(2,0)、N(0,4),以点M为圆心5为半径作⊙M交y轴于A、B两点,点C为⊙M上一动点,连接CN,取CN中点D,连接AD、BD,则A D2+B D2的最大值为 .三、解答题17.如图,四边形ABCD为⊙O的内接四边形,AC是⊙O的直径,AD=BD,∠CAB=32°.求∠ACD的度数.18.如图,OC为⊙O的半径,弦AB⊥OC于点D,OC=10,CD=4,求AB的长.19.如图,正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求解答下列问题:(1)△A1B1C1与△ABC关于坐标原点O成中心对称,则B1的坐标为__________;(2)BC与B1C1的位置和数量关系为___________;(3)将△ABC绕某点逆时针旋转90°后,其对应点分别为A2(―1,―2),B2(1,―3),C2(0,―5),则旋转中心的坐标为___________.20.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,(1)求∠ACB的度数;(2)求BC的长;(3)求AD,BD的长.21.如图,AB是⊙O的直径,C是⏜BD的中点,CE⊥AB于点E,BD交CE于点F.(1)求证:CF=BF.(2)若CD=6,AC=8,求⊙O的半径及CE的长.22.如图所示,AB为☉O的直径,AC是☉O的一条弦,D为BC的中点,作DE⊥AC于点E,交AB的延长线于点F,连接DA.(1)若AB=90 cm,则圆心O到EF的距离是多少?说明你的理由.(2)若DA=DF=63,求阴影部分的面积(结果保留π).23.如图,AB是⊙O的直径,弦CD⊥AB与点E,已知AB=10,AE=8,点P为AB上任意一点,(点P不与A、B重合),连结CP并延长与⊙O交于点Q,连QD,PD,AD.(1)求CD的长.(2)若CP=PQ,直接写出AP的长.(3)①若点P在A,E之间(点P不与点E重合),求证:∠ADP=∠ADQ.②若点P在B,E之间(点P不与点E重合),求∠ADP与∠ADQ满足的关系.答案解析部分1.【答案】B2.【答案】A3.【答案】D4.【答案】C5.【答案】A6.【答案】B7.【答案】D8.【答案】C9.【答案】D10.【答案】C11.【答案】3512.【答案】513.【答案】65°14.【答案】15°15.【答案】316.【答案】49217.【答案】61°18.【答案】1619.【答案】(1)(2,2);(2)平行且相等;(3)(0,―1).20.【答案】(1)∠ACB=90°(2)BC=8cm(3)BD=AD=52cm21.【答案】(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,∴∠A=90°-∠ABC.∵CE⊥AB,∴∠ECB=90°-∠ABC,又∵C是BD的中点,∴CD=BC,∴∠DBC=∠A,∴∠ECB=∠DBC,∴CF= BF;(2)解:∵BC=CD,∴BC=CD=6.在Rt△ABC中,AB= BC2+AC2=62+82=10,∴⊙O的半径为5;∵S△ABC= 12AB×CE= 12BC×AC,∴CE= BC×ACAB =6×810=245.22.【答案】(1)解:如图所示,连接OD,∵D为BC的中点,∴∠CAD=∠BAD.∵OA=OD,∴∠BAD=∠ADO.∴∠CAD=∠ADO.∴OD∥AE.∵DE⊥AC,∴OD⊥EF.∴OD的长是圆心O到EF的距离.∵AB=90 cm,∴OD=12AB=45 cm.(2)解:如图所示,过点O作OG⊥AD交AD于点G.∵DA=DF,∴∠F=∠BAD.由(1),得∠CAD=∠BAD,∵∠F+∠BAD+∠CAD=90°,∴∠F=∠BAD=∠CAD=30°.∴∠BOD=2∠BAD=60°,OF=2OD.∵在Rt△ODF中,OF2-OD2=DF2,∴(2OD)2-OD2=(63)2,解得OD=6.在Rt△OAG中,OA=OD=6,∠OAG=30°,AG=OA2―O G2=33,AD=23,S△AOD=1×63×3=93.2+93=6π+93.∴S阴影=S扇形OBD+S△AOD=60π×6236023.【答案】(1)解:连接OD,∵直径AB=10,AE=8,∴BE=2.∴OE=5-2=3.又∵AB⊥CD,在Rt△PED中,P D2=P E2+E D2∴ED=52―32=4∴CD=2ED=8(2)解:若CP=PQ,则点P与点O重合,或点P与点E重合.所以AP=5或8(3)解:①连接AC,由图可知∠ACQ=∠ADQ,因为AB是⊙O的直径,AB⊥CD,所以CE=DE,即AB是CD的垂直平分线,所以AC=AD,PC=PD,因为AP=AP,所以∠ACP=∠ADP ,所以∠ADP=∠ADQ .②∠ADP+∠ADQ=180°.理由如下:连接AC ,因为AB 是直径,AB ⊥CD ,所以AC=AD ,CE=DE ,所以△ACP ≌△ADP (SSS ),所以∠ACP=∠ADP ,因为∠ACP=12ADQ ,∠ADQ=12ACQ ,所以∠ACP+∠ADQ=12(ADQ +ACQ )=180°.。
浙教版九年级数学上册第三章圆的基本性质单元综合能力测试卷(含答案)
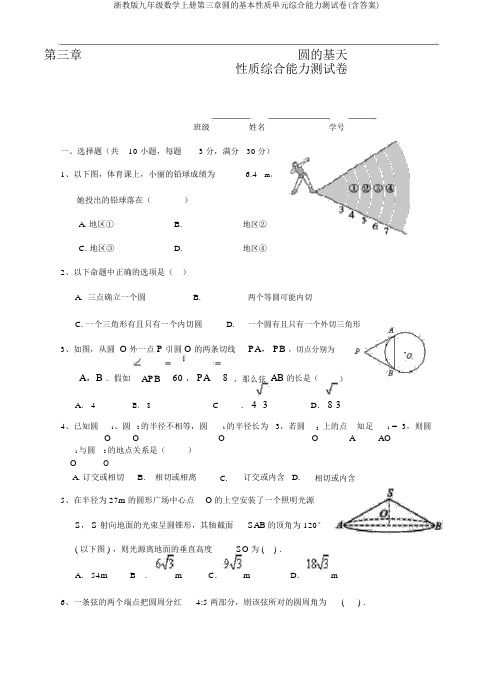
第三章圆的基天性质综合能力测试卷班级姓名学号一、选择题(共10 小题,每题 3 分,满分30 分)1、以下图,体育课上,小丽的铅球成绩为 6.4m,她投出的铅球落在()A. 地区①B.地区②C. 地区③D.地区④2、以下命题中正确的选项是()A. 三点确立一个圆B.两个等圆可能内切C. 一个三角形有且只有一个内切圆D.一个圆有且只有一个外切三角形3、如图,从圆O外一点P引圆O的两条切线PA, PB ,切点分别为A,B .假如APB60 ,PA8,那么弦AB 的长是()A. 4B.8C. 4 3D.8 34、已知圆1、圆 2 的半径不相等,圆 1 的半径长为3,若圆2上的点A 知足 1 = 3,则圆O O O O AO1 与圆2 的地点关系是()O OA. 订交或相切B. 相切或相离C.订交或内含D.相切或内含5、在半径为 27m的圆形广场中心点O的上空安装了一个照明光源S, S 射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°( 以下图 ) ,则光源离地面的垂直高度SO为() .A. 54m B.m C.m D.m6、一条弦的两个端点把圆周分红4:5 两部分,则该弦所对的圆周角为() .A. 80°B.100°C.80°或100°D.160°或200°7、如,AB是⊙O的直径,AC是⊙O的切,接OC交⊙ O于点 D,接 BD,∠ C=40°.∠ABD的度数是()A . 30 °B.25°C.20°D.15°8、“ 材埋壁”是我国古代有名的数学著作《九章算》中的:“今有材,埋在壁中,不知大小,以之,深一寸,道一尺,径几何?”用数学言可表示:如所示, CD⊙ O的直径,弦AB⊥CD于 E,CE=1寸, AB=10寸,直径CD的() A. 12.5 寸 B . 13寸C.25寸D.26寸9、如是一△ABC余料,已知 AB=20cm,BC=7cm,AC=15cm,将余料裁剪成一个形资料,的最大面是()2222 A.πcm B.2πcm C.4πcm D . 8 πcm10、如,正六形A1B1C1D1E1F1的2,正六形A2B2C2D2E2F2的外接与正六形A1 B1C1D1E1F1的各相切,正六形A3B3C3D3E3F3的外接与正六形A2B2C2D2E2F2的各相切,⋯按的律行下去,A10B10C10D10E10F10的()A.B.C.D.二、填空题(共 6 小题,每题 4 分,满分 24 分)11、已知圆心角为120°的扇形的面积为2cm.12πcm,则扇形的弧长是12、如图,已知圆心角∠AOB的度数为100°,则圆周角∠ACB等于(度)13、在⊙O中,已知半径长为3,弦AB长为4,那么圆心O到AB的距离为.14、以下图,△ABC的三个极点的坐标分别为A(-1,3)、 B (- 2,- 2) 、C (4,- 2) ,则△ABC外接圆半径的长度为.15、已知半径为R的半圆,过直径AB上一点,作⊥ 交半圆于点,且3O C CD AB D CD R ,2则 AC的长为.16、如图①,O1,O2,O3,O4为四个等圆的圆心,A, B, C, D为切点,请你在图中画出一条直线,将这四个圆分红面积相等的两部分,并说明这条直线经过的两个点是;如图②,O1,O2,O3, O4, O5为五个等圆的圆心,A,B,C,D, E为切点,请你在图中画出一条直线,将这五个圆分红面积相等的两部分,并说明这条直线经过的两个点是....三、解答题(此题有7 个小题,共66 分)解答应写出证明过程或推演步骤.17、(6 分)作图题:用直尺和圆规作出△ABC的外接圆 O(不写作法,保存作图印迹);18、(8 分)如图,点 D 在⊙O的直径 AB 的延伸线上,点 C 在⊙O 上,且,∠° .(1)求证:CD是⊙O的切线;(2)若⊙O的半径为 2,求图中暗影部分的面积 .19、(8 分)如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥ BC,OD与 AC交于点E.( 1)若∠B=70°,求∠CAD的度数;( 2)若AB=4,AC=3,求DE的长.20、( 10 分)已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的均分线交⊙ O于点D.(Ⅰ)如图①,若BC为⊙ O的直径, AB=6,求 AC,BD, CD的长;(Ⅱ)如图②,若∠CAB=60°,求 BD的长.21、( 10 分)如图,在单位长度为 1 的正方形网格中成立平面直角坐标系,一段圆弧经过网格的交点为 A、 B、C.(1)在图中标出该圆弧所在圆的圆心D,并连结 AD、 C D.(2)在( 1)的基础上,达成以下填空:①写出点的坐标:C()、D();②⊙ D的半径是2(结果保存根号);③若扇形 DAC是一个圆锥的侧面睁开图,则该圆锥的底面的面积(结果保存π).22、( 12 分)已知:如图,⊙O和⊙ O’订交于 A、 B两点, AC是⊙ O’的切线,交⊙O于 C 点,连结 CB并延伸交⊙ O’于点 F, D为⊙ O’上一点,且∠DAB=∠ C,连结 DB交延伸交⊙ O于点E。
2024-2025学年浙教版九年级上册数学 第三章 圆的基本性质 单元培优测试卷 (含详解)

圆的基本性质单元培优测试卷一、选择题(每题3分,共30分)1.如图,分别延长圆内接四边形ABCD的两组对边,延长线相交于点E,F.若∠E=54°41',∠F=43°19',则∠A的度数为( )第1题图第2题图第4题图A.42°B.41°20'C.41°D.40°20'2.如图,⊙O中,弦AB的长为43,点C在⊙O上,OC⊥AB,∠ABC=30°.⊙O所在的平面内有一点P,若OP=5,则点P与⊙O的位置关系是( )A.点P在⊙O上B.点P在⊙O内C.点P在⊙O外D.无法确定3.在平面直角坐标系中,已知点A(0,2),点B在第一象限内,AO=AB,∠OAB=120°,将△AOB绕点O逆时针旋转,每次旋转60°,则第2024次旋转后,点B的坐标为( )A.(−3,3)B.(−3,0)C.(3,3)D.(−23,0)4.如图,在半圆O中,直径AB=2,C是半圆上一点,将弧AC沿弦AC折叠交AB于D,点E是弧AD 的中点.连接OE,则OE的最小值为( )A.2−1B.2+1C.4−2D.22−25.△ABC内接于⊙O,过点A作直线EF,已知∠B=∠EAC,根据弦AB的变化,两人分别探究直线EF 与⊙O的位置关系:甲:如图1,当弦AB过点O时,EF与⊙O相切;乙:如图2,当弦AB不过点O时,EF也与⊙O相切;第5题图第6题图第7题图下列判断正确的是( )A .甲对,乙不对B .甲不对,乙对C .甲乙都对D .甲乙都不对6.如图,等圆⊙O 1和⊙O 2相交于A ,B 两点,⊙O 1经过⊙O 2的圆心O 2,若O 1O 2=2,则图中阴影部分的面积为( )A .2πB .43πC .πD .23π7.如图,正六边形ABCDEF 内接于⊙O ,点P 在边BC 上.结论Ⅰ:若⊙O 的半径为2,P 是边BC 的中点,则PE 的长为13;结论Ⅱ:连接PF .若S △PEF =32,则EF 的长为π3,关于结论Ⅰ、Ⅱ,判断正确的是( )A .只有结论Ⅰ对B .只有结论Ⅱ对C .结论Ⅰ、Ⅱ都对D .结论Ⅰ、Ⅱ都不对8.已知等腰直角三角形OAC ,∠OAC =90°,以O 为圆心,OA 为半径的圆交OC 于点F ,过点F 作AC的垂线交⊙O 于点E ,交AC 于点B.连结AE ,交OC 于点D ,若OD =1+22,则AB 的长为( )第8题图 第9题图 第10题图A .2B .22C .2+1D .2+29.如图,在扇形BOC 中,∠BOC =60°,OD 平分∠BOC 交BC 于点D ,点E 为半径OB 上一动点.若OB =3,则阴影部分周长的最小值为( )A .62+π2B .22+π3C .62+π3D .2+2π310.如图,AB 是⊙O 的直径,点C ,点D 是半圆上两点,连结AC ,BD 相交于点P ,连结AD ,OD .已知OD ⊥AC 于点E ,AB =2.下列结论其中正确的是( )①∠DBC +∠ADO =90°;②AD 2+AC 2=4;③若AC =BD ,则DE =OE ;④若点P 为BD 的中点,则DE =2OE .A .①②③B .①③④C .②③④D .①②④二、填空题(每题4分,共24分)11.如图,OA 是⊙O 的半径,BC 是⊙O 的弦,OA ⊥BC 于点D ,AE 是⊙O 的切线,AE 交OC 的延长线于点E .若∠AOC =45°,BC =2,则线段AE 的长为 .第11题图 第12题图 第13题图12.如图,在矩形ABCD 中,AB =4,AD =2.以点A 为圆心,AD 长为半径作弧交AB 于点E ,再以AB为直径作半圆,与DE 交于点F ,则图中阴影部分的面积为 .13.如图,直线l 与⊙O 相切于点A ,点C 为⊙O 上一动点,过点C 作CB ⊥l ,垂足为B ,已知⊙O 的半径为6,则BC +43AB 的最大值为 .14.如图,正方形ABCD 内接于⊙O ,线段MN 在对角线BD 上运动,若⊙O 的面积为2π,MN =1,则(1)⊙O 的直径长为 ;(2)△AMN 周长的最小值是 .第14题图 第15题图 第16题图15.如图,AB 是半圆O 的直径,C ,D 是半圆O 上的点,连接CD ,AC ,OD ,且AB =4,OD ∥AC ,设CD =x,AC =y ,则y 与x 之间的函数表达式为 .16.如图,AB 是半圆的直径,AC 是一条弦,D 是AC 的中点,DE ⊥AB 于点E ,交AC 于点F ,DB 交AC于点G ,连结AD .给出下面四个结论:①∠ABD =∠DAC ;②AF =FG ;③当DG =2,GB =3时,FG =142;④当BD =2AD ,AB =6时,△DFG 的面积是3,上述结论中,正确结论的序号有 .三、综合题(17-19每题6分,20-21每题8分,22题12分,共46分)17.如图,已知OA是⊙O的半径,过OA上一点D作弦BE垂直于OA,连接AB,AE.线段BC为⊙O的直径,连接AC交BE于点F.(1)求证:∠ABE=∠C;(2)若AC平分∠OAE,求AFFC的值18.如图,AC为⊙O的直径,BD是弦,且AC⊥BD于点E.连接AB、OB、BC.(1)求证:∠CBO=∠ABD;(2)若AE=4cm,CE=16cm,求弦BD的长.19.如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.(1)求证:点D为AC的中点;(2)若DF=4,AC=16,求⊙O的直径.20.如图,已知四边形ABCD内接于⊙O,对角线AC,BD交于点E,AC=BD,AC⊥BD.(1)猜想∠ACB的度数,并说明理由.(2)若⊙O的半径为10,∠BCD=60°,求四边形ABCD的面积.(3)若过圆心O作OF⊥BC于点F.求证:AD=2OF.21.已知:⊙O的两条弦AB,CD相交于点M,且AB=CD.(1)如图1,连接AD.求证:AM=DM.(2)如图2,若AB⊥CD,点E为弧BD上一点,BE=BC=α°,AE交CD于点F,连接AD、DE.①求∠E的度数(用含α的代数式表示).②若DE=7,AM+MF=17,求△ADF的面积.22.如图,在△ABC中,AB=BC,∠ABC=90°,D是AB上一动点,连接CD,以CD为直径的⊙M交AC 于点E,连接BM并延长交AC于点F,交⊙M于点G,连接BE.(1)求证:点B在⊙M上.(2)当点D移动到使CD⊥BE时,求BC:BD的值.(3)当点D到移动到使∠CMG=30°时,求证:A E2+C F2=E F2.答案解析部分1.【答案】C【解析】【解答】解:∵四边形ABCD 内接于圆O ,∴∠A+∠BCD=180°,∵∠BCD 、∠EBC 分别是△EBC 和△ABF 的一个外角,∠EBC=∠A+∠F ,∠BCD=∠E+∠EBC ,∴∠BCD=∠E+∠A+∠F ,∴∠A+∠E+∠A+∠F=180°,∴2∠A+54°41'+43°19'=180°,解之:∠A=41°.故答案为:C. 2.【答案】C【解析】【解答】解:如图,∵∠ABC=30°,∴∠AOC=2∠ABC=60°,∵OC ⊥AB ,且AB =43,∴∠ADO=90°,且AD =12AB =23,∵sin ∠AOC=sin60°=AD AO,∴AO =ADsin60°=2332=4,∵OP=5>AO=4,∴点P 在圆O 外部.故答案为:C. 3.【答案】D【解析】【解答】解:过B 作BH ⊥y 轴于H ,在Rt△ABH中,∠AHB=90°,∠BAH=180°−120°=60°,AB=OA=2,∴∠ABH=30°,∴AH=12AB=1,OH=OA+AH=3,由勾股定理得BH=AB2−AH2=3,∴B(3,3),由题意,可得:B1(−3,3),B2(−23,0),B3(−3,−3),B4(3,−3),B5(23,0),B6(3,3),⋯,6次一个循环,∵2024÷6=337……2,∴第2024次旋转后,点B的坐标为(−23,0),故答案为:D.4.【答案】A【解析】【解答】解:连接CO,如图,由三角形两边之差小于第三边,当C、O、E共线时,OE最小,设⏜AC的弧度为x,则⏜BC的弧度为180°-x,∵∠CAB=∠CAD,∴⏜CD的弧度为180°-x,由折叠知:⏜AEC=⏜AC=x,⏜AD=x-(180°-x)=2x-180°,∵点E为弧AD的中点,∴⏜AE=12⏜AD=x-90°,∴⏜CE=⏜AC-⏜AE=90°,∴⏜CE所对圆心角为90°,∵直径AB=2,∴ CE=2,∴OE= CE-OC=2−1.故答案为:A.5.【答案】C【解析】【解答】解:甲:∵AB是⊙O的直径,∴∠ACB=90°,∴∠BAC+∠B=90°,∵∠EAC=∠B,∴∠EAC+∠BAC=90°,∴EF⊥AB,∵OA是半径,∴EF是⊙O的切线;乙:作直径AM,连接CM,如图所示:即∠B=∠M(在同圆或等圆中,同弧所对的圆周角相等),∵∠EAC=∠B,∴∠EAC=∠AMC,∵AM是⊙O的直径,∴∠MCA=90°,∴∠MAC+∠AMC=90°,∴∠EAC+∠MAC=90°,∴EF⊥AM,∵OA是半径,∴EF是⊙O的切线.故答案为:C 6.【答案】D7.【答案】C【解析】【解答】解:如图,连接CE 、OB 、OC ,过点D 作DH ⊥CE 于点H ,∵六边形ABCDEF 为正六边形,∴∠BCD =∠CDE =(6−2)⋅180°6=120°,CD =DE ,∠BOC =360°6=60°,OB =OC ,∴∠DCE =∠DEC =12(180°−∠CDE)=30°,△OBC 是等边三角形,∴CH =EH =12CE =CD ⋅cos ∠DCE =3,∠PCE =∠BCD−∠DCE =90°,EF =BC =OB =OC =CD =2,∴CE =23,∵P 是边BC 的中点,∴CP =BP =12BC =1,∴PE =PC 2+CE 2=12+(23)2=13,故结论Ⅰ正确;设点N 是边BC 的中点,连接NO 并延长交EF 于点M ,连接OE 、OF ,过点D 作DH ⊥CE 于点H ,设正六边形ABCDEF 的边长为a ,∵六边形ABCDEF 为正六边形,∴NM ⊥EF ,NM ⊥BC ,FM =EM =12EF =12a ,∠EOF =360°6=60°,EF ∥BC ,∴S △NEF =S △PEF =32,由Ⅰ的解答过程可知,CH=EH=12CE=CD⋅cos∠DCE=32a,∠NCE=∠BCD−∠DCE=90°,EF=BC=OB=OC=a,∴CE=3a,四边形NCEM是矩形,∴MN=CE=3a,∴12EF⋅MN=12×a×3a=32,∴a=1,∴EF的长为60π×1180=π3,故Ⅱ正确,故答案为:C.8.【答案】C【解析】【解答】解:过点O作AE的垂线交BE于点H,连接AH,如图所示:设⊙O的半径为R∵∠OAC = 90°,OA=AC=R∴∠O=∠C=45°∴∠E=12∠O==22.5°在Rt△0AC中,由勾股定理得:OC = OA2+AC2=2R∵OD=2∴CD=OC-OD=2R−2∵EB⊥AC,∠C =45°∴△BFC为等腰直角三角形,∴∠BFC= ∠DFE=∠C = 45°∴∠ADC= ∠E + ∠DFE =22.5°+45°=67.5°在Rt△ABE中,∠E =22.5°,∠ABE = 90°∴∠CAE =90°-∠E=67.5°∴∠CAE = ∠ADC∴AC=CD,即R= 2R−2,解得:r=2+2,即OA=2+2∵OH⊥AEOH是AE的垂直平分线∴AH = EH∴∠EAH= ∠E= 22.5°∴∠HAB = ∠CAE- ∠EAH= 67.5°-22.5°=45°∴△ABH为等腰直角三角形∴AB =BH∴∠OAE= ∠OAC-∠OAE = 90° - 67.5°= 22.5°.'.∠OAH = ∠OAE + ∠EAH = 45°∴OH⊥AE,∠EAH=22.5°∴∠AHO =90°-∠EAH = 90° - 22.5°= 67.5°∴∠AOH = 180°- ∠OAH- ∠AHO=180°-45°-67.5°= 67.5°∴∠AHO = ∠AOH = 67.5°∴AH =OA=2+2,在Rt△ABH中,AB = BH,AH=2+2由勾股定理得:A B2+B H2=A H2即2A B2=(2+2)2∴AB=2+1故答案为:2+1.9.【答案】A【解析】【解答】解:由于CD是定值,要求阴影部分周长的最小值,即求CE+DE最小值即可作点D关于OB对称的对称点D′,连接CD′与直线OB交于点E,则OC=OD′,CE+DE=CD′,此时CE+DE为最小值连接OD′,∵OD平分∠BOC,∠BOC=60°,∴∠BOD =∠COD =12∠BOC =30°,∴∠BOD =∠BOD ′=30°,∠COD ′=90°,在Rt △COD ′中,CD ′=OC 2+OD ′2=2OC =2OB =32,CD =30π×3180=12π,阴影部分周长的最小值为12π+32=62+π2.故答案为:A .10.【答案】B【解析】【解答】解:∵AB 是⊙O 的直径,∴∠ADB =∠ACB =90°,∵OD ⊥AC ,∴OD ∥BC ,∴∠DBC =∠BDO ,∵∠BDO +∠ADO =90°,∴∠DBC +∠ADO =90°,①正确;∵∠ACB =90°,∴B C 2+A C 2=A B 2=4,AB =2,根据条件无法得到BC =AD ,②错误;∵AC =BD ,∴⏜AD =⏜BD ,∴⏜AD =⏜BC ,∵OD ⊥AC ,∴⏜AD =⏜CD ,∴⏜AD=⏜BC=⏜CD,∴∠AOD=13×180°=60°,∵OA=OD,∴△AOD为等边三角形∵AE⊥OD,∴DE=OE,③正确;若点P为BD的中点,则PD=PB,∵∠PED=∠BCP=90°,∠EPD=∠CPB,∴△EPD≅△CPB(AAS),∴DE=BC,∵OD⊥AC,O为AB的中点,∴BC=2OE,∴DE=2OE,④正确;故答案为:B.11.【答案】212.【答案】3+23π【解析】【解答】解:连接AF,EF,过点F作FH⊥AB于点H,∵以点A为圆心,AD长为半径作弧交AB于点E,∴AD=AE=AF=2,∵再以AB为直径作半圆,与DE交于点F,∴AE=BE=2,AE=EF,∴AF=AE=EF=2,∴△AEF是等边三角形,∴∠FAE=∠AEF=60°,AH=1,∴FH=AH·tan∠FAE=AH·tan60°=3∴S扇形FAE=60π×22360=23π,S弓形AF=60π×22360−12×23=23π−3,∴S阴影部分=S半圆AB-S扇形FAE-S弓形AF=12×4π−23π−(23π−3)=3+23π故答案为:3+2 3π.13.【答案】83614.【答案】22;415.【答案】y=−12x2+416.【答案】①②③【解析】【解答】解:如图:连接DC,∵D是AC的中点,∴AD=DC,由圆周角定理的推论得:∠ABD=∠DAC,故①正确;∵AB是直径,∴∠ADB=90°,∴∠DAC+∠AGD=90°,∵DE⊥AB∴∠BDE+∠ABD=90°,∵∠ABD=∠DAC,∴∠BDE=∠AGD,∴DF=FG,∵∠BDE+∠ABD=90°,∠BDE+∠ADE=90°,∴∠ADE=∠ABD,∵∠ABD=∠DAC,∴∠ADE=∠DAC,∴AF=FD,∴AF=FG,即②正确;在△ADG和△BDA,{∠ADG =∠BDA∠DAG =∠DBA ,∴△ADG ∽△BDA ,∴AD BD =GDAD ,即:AD 2+3=2AD,解得:AD =10,由勾股定理得:AG =AD 2+DG 2=10+4=14,∵AF =FG ,∴FG =12AG =142,故③正确;如图:假设半圆的圆心为O ,连接OD ,CO ,CD ,∵BD =2AD ,AB =6,D 是AC 的中点,∴AD =DC =13AB ,∴∠AOD =∠DOC =60°,∵OA =OD =OC ,∴△AOD ,△ODC 是等边三角形,∴OA =AD =CD =OC =OD =6,∴四边形ADCO 是菱形,∴∠DAC =∠OAC =12∠DAO =30°,∵∠ADB =90°,∴tan ∠DAC =tan30°=DGAD ,即33=DG 6,解得:DG =23,∴S △ADG =12AD ⋅DG =12×6×23=63,∵AF =FG∴S △DFG =12S △ADG =33,故④错误.故答案为:①②③.17.【答案】(1)证明:∵OA ⊥BE ,∴AB=AE,∴∠ABE=∠C;(2)解:∵AC平分∠OAE,∴∠OAC=∠EAC,∵∠EAC=∠EBC,∴∠OAC=∠EBC,∵OA=OC,∴∠OAC=∠C,∴∠EBC=∠C,∴BF=CF,由(1)∠ABE=∠C,∴∠ABE=∠C=∠EBC,∵BC为直径,∴∠BAC=90°,∴∠ABE+∠C+∠EBC=90°,∴∠ABE=30°,∴AF=12 BF,∴AF=12 CF,即AFCF=12.18.【答案】(1)证明:∵AC是直径,AC⊥BD ∴AB=AD∴∠ABD=∠C又∵OB=OC∴∠OBC=∠C∴∠CBO=∠ABD(2)解:∵AE=4cm,CE=16cm∴直径AC=AE+CE=20cm∴OA=OB=10cm∴OE=OA-AE=10-4=6cm∵AC是直径,AC⊥BD∴BE=ED= BO2−OE2=8cm∴BD=2BE=16cm19.【答案】(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,∵OD∥BC,∴∠OFA=90°,∴OF⊥AC,∴AC=CD,即点D为AC的中点;(2)解:OF⊥AC,∴AF=12AC=8,∵DF=4,∴OF=OD−DF=OA−4,∵OA2=AF2+OF2,∴OA2=82+(OA−4)2,∴OA=10,∴⊙O的直径为20.20.【答案】(1)解:∠ACB=45°,理由如下:∵AC⊥BD,∴∠AEB=90°.∴∠ABE+∠BAE=90°.∴AD+BC=180°.∴AB+CD=180°.∵AC=BD,∴AC=BD.∴AC−AD=BD−AD.∴AB=CD.∴AB=90°.∴∠ACB=45°.(2)解:如图,连结BO,DO,过点O作OH⊥BD交BD于点H.∵∠BCD=60°, ∴∠BOD=120°.∵OH⊥BD,∴∠BOH=60°, BH=DH.在Rt△BHO中,∠BOH=60°,OB=10,∴OH=5,BH=53.∴BD=103=AC.∴S四边形ABCD=12×103×103=150.(3)证明:如图,延长BO交⊙O于点M,连结CM,DM.∵OF⊥BC,∴BF=CF,即点F是BC的中点.又∵点O是BM的中点,∴OF是△BCM的中位线.∴CM=2OF.∵DM⊥BD,AC⊥BD,∴DM∥AC.∴AD=CM.∴AD=2OF.21.【答案】(1)证明:如图1,∵AB=CD,∴AB=CD,即AC+BC=BD+BC,∴AC =BD ,∴∠A =∠D ,∴AM =DM ;(2)解:①∠M =90°−12α°.理由如下:连接AC ,如图,∵BE =BC =α°,∴∠CAB =12α°,∵AB ⊥CD ,∴∠AMC =90°,∴∠M =∠C =90°−12α°;②∵BE =BC =α°,∴∠CAB =∠EAB ,∵AB ⊥CD ,∴AC =AF ,∴∠ACF =∠AFC ,∵∠ACF =∠E ,∠AFC =∠DFE ,∴∠DFE =∠E ,∴DF =DE =7,∵AM =DM ,∴AM =MF +7,∵AM +MF =17,∴MF +7+MF =17,解得MF =5,∴AM =12,∴S △ADF =12×7×12=42.22.【答案】(1)证明:根据题意得CM=DM=12CD,∵∠ABC=90°,∴BM=12 CD,∴CM=DM=BM,∴点B在⊙M上.(2)解:连接DE,如图,∵CD⊥BE,CD为⊙M直径,∴BD=DE,∠ABC=∠DEC=90°,∵AB=BC,∠ABC=90°,∴∠DAE=∠ADE=45°,∴DE=AE,∴AD=2DE=2BD,∴AD+BD=AB=(2+1)BD,∴BC=(2+1)BD,∴BCBD=2+1.(3)证明:过点B作BN⊥BG,过点A作AN⊥AE,交BN于点N,连接DE,NE,∵AB=BC,∠ABC=90°,∴∠DAC=∠BCA=45°,∴∠BAN=∠BCF=45°,∵M为CD的中点,∴MD =MB =MC ,∵∠CMG =∠MBC +∠MCB =30°,∴∠MDB =∠MBD =75°,∠MBC =∠MCB =15°,∠DCE =∠BCE−∠MCB =30°,∴∠EDC =∠EBC =60°,∴∠EBF =∠EBC−∠MBC =45°,∴∠EBF =∠EBN =45°,∴∠ABN =90°−∠ABF =∠CBF ,∵{∠ABN=∠CBFAB =BC ∠BAN =∠BCF ,∴△BAN≌△BCF(ASA),∴AN =CF ,BN =BF ,∵{BN =BF∠NBE =∠FBE BE =BE ,∴△NBE≌△FBE(SAS),∴NE =EF ,在Rt △AEN 中,N E 2=A N 2+A E 2,∴E F 2=C F 2+A E 2.。
新浙教版九年级数学上册第3章 圆的基本性质检测题

新浙教版九年级数学上册第3章圆的基本性质检测题(本检测题满分:100分,时间:90分钟)一、选择题(每小题3分,共30分)1.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是()A.80°B.160°C.100°D.80°或100°2.(2015·杭州中考)圆内接四边形ABCD中,已知∠A=70°,则∠C=()A. 20°B. 30°C. 70°D. 110°3.(2014·浙江温州中考)如图,已知点A,B,C在⊙O上,为优弧,下列选项中与∠AOB相等的是()A.2∠CB.4∠BC.4∠AD.∠B+∠C4.如图所示,已知BD是⊙O的直径,点A,C在⊙O上,弧AB =弧BC,∠AOB=60°,则∠BDC的度数是()A.20°B.25°C.30°D.40°5.如图,在⊙中,直径垂直弦于点,连接,已知⊙的半径为2,32,则∠的大小为( )A. B. C. D.6.(2014·呼和浩特中考)已知⊙O的面积为2π,则其内接正三角形的面积为( )A.33B.36C. 332 D.3627.(2014·成都中考)在圆心角为120°的扇形AOB中,半径OA=6 cm,则扇形AOB的面积是()A.6π cm2B.8π cm2C.12π cm2D.24π cm28.如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,CD是斜边AB上的中线,以AC为直径作⊙O,设线段CD的中点为P,则点P与⊙O的位置关系是()A.点P在⊙O内B.点P在⊙O上C.点P在⊙O外D.无法确定9. (2015·浙江温州中考)如图,C是以AB为直径的半圆O上一点,连接AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG ,,的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=18,则AB的长是()A. 29B.790C. 13D. 1610.如图,长为4 cm,宽为3 cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向),木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为()A.10 cmB.C.27D.25二、填空题(每小题3分,共24分)11.如图所示,AB是⊙O的弦,OC⊥AB于C.若AB=,OC=1,则半径OB的长为.12. (2015•浙江绍兴中考)在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以点C为圆心,5为半径的圆上,连接P A,PB.若PB=4,则P A的长为_________.13.(2014·山东枣庄中考)如图,将四个圆两两相切拼接在一起,它们的半径均为1 cm,则中间阴影部分的面积为cm2.14.如图,⊙O的半径为10,弦AB的长为12,OD⊥AB,交AB于点D,交⊙O于点C,则OD=_______,CD=_______.15.如图,在△ABC中,点I是外心,∠BIC=110°,则∠A=_______.第9题图16.(2015·浙江丽水中考)如图,圆心角∠AOB =20°,将旋转n 得到,则的度数是_________度.17.如图,一条公路的转弯处是一段圆弧(图中的),点O 是这段弧的圆心,C 是上一点,,垂足为,则这段弯路的半径是_________.18.用圆心角为120°,半径为6 cm 的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是 .三、解答题(共46分)19.(5分)如图所示,在⊙O 中,直径AB ⊥CD 于点E ,连接CO 并延长交AD 于点F ,且CF ⊥AD .求∠D 的度数. 20.(6分)(2014·武汉中考)如图,AB 是⊙O 的直径,C ,P 是AB 上两点,AB =13,AC =5.(1)如图(1),若点P 是AB 的中点,求P A 的长;(2)如图(2),若点P 是BC 的中点,求P A 的长.21.(6分)(2014·天津中考)已知⊙O 的直径为10,点A ,点B ,点C 在⊙O 上,∠CAB的平分线交⊙O 于点D .(1)如图①,若BC 为⊙O 的直径,AB =6,求AC ,BD ,CD 的长; (2)如图②,若∠CAB =60°,求BD 的长. 第16题图第21题图 第20题图22.(6分)(2015·杭州中考)如图①,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”,如图②,⊙O的半径为4,点B在⊙O 上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.图①图②第22题图23.(5分)如图,已知都是⊙O的半径,且试探索与之间的数量关系,并说明理由.24.(6分)如图是一跨河桥的示意图,桥拱是圆弧形,跨度AB为16米,拱高CD为4米,求:⑴桥拱的半径;⑵若大雨过后,桥下河面宽度EF为12米,求水面涨高了多少?25.(6分)如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求在圆锥的侧面上从A点到C点的最短距离.26.(6分)如图,把半径为r的圆铁片沿着半径OA、OB剪成面积比为1︰2的两个扇形、,把它们分别围成两个无底的圆锥.设这两个圆锥的高分别为、,试比较与的大小关系.第3章圆的基本性质检测题参考答案一、选择题1. D 解析:∠ABC =∠AOC =×160°=80°或∠ABC =×(360°-160°)=100°.2. D 解析:在圆内接四边形ABCD 中,∵ ∠A +∠C =180°,∠A =70°,∴ ∠C =110°.3.A 解析:根据圆周角定理得AB 所对的圆心角∠AOB 的度数等于它所对的圆周角∠C 的度数的两倍,所以∠AOB =2∠C .4. C 解析:连接OC ,由弧AB =弧BC ,得∠BOC =∠AOB =60°,故∠BDC =∠BOC =×60°=30°.5.A 解析:由垂径定理得∴,∴.又∴.6.C 解析:如图所示,设⊙O 的半径为r ,则πr 2=2π,∴ OC =r =2.在Rt △ODC 中,30°,∴ OD =12OC =12×2=22,∴ CD =22OC OD =22222=62. ∴ BC =2CD =6,AD =AO +OD =2+22=322, ∴ S △ABC =12BC ·AD =12×6×322=332.7.C 解析:S 扇形=2120π6360⨯⨯=12π(cm 2).点拨:扇形面积公式是S =2π360n r = 12lr (n 为扇形圆心角的度数,l 为扇形的弧长,r 为扇形的半径).8.A 解析:因为OA =OC ,AC =6,所以OA =OC =3.又CP =PD ,连接OP ,可知OP 是△ADC 的中位线,所以OP =2125,所以OP <OC ,即点P 在⊙O 内. 9.C 解析:如图,连接OP 、OQ ,分别交AC 、BC 于点H 、I .∵ P 、Q 分别为、的中点,∴ AC PH ⊥,且H 为AC 的中点,连接MH ,则四边形DMHC 为矩形, ∴ MH AC ⊥.又AC PH ⊥,∴ M ,P ,H ,O 四点在同一条直线上.同理可证O ,I ,Q ,N 四点在同一条直线上, ∴ ,.MH DC AC NI BC === ∵ O 为AB 的中点,H 为AC 的中点, ∴ OH 为△ACB 的中位线, ∴ .21BC OH =同理OI 为△ABC 的中位线,∴ 12OI AC =. ∵ ,18=+BC AC ∴ 9OI OH +=.∵ 14=+NQ MP ,∴ ()()18144PH QI AC BC MP NQ +=+-+=-=. 设圆的半径为R ,则QI R OI PH R OH -=-=,,∴ )(2QI PH R OI OH +-=+,即9=2R -4,∴ 2R =13,即AB =13.10.C 解析:第一次转动是以点B 为圆心,AB 为半径,圆心角是90度,所以弧长=90π55π1802⋅=(cm),第二次转动是以点C 为圆心,A 1C 为半径,圆心角为60度,所以弧长=π1803π60=⋅(cm),所以走过的路径长为5π2+π=27(cm). 二、填空题11. 2 解析:∵ BC =AB =,∴ OB ===2.12. 3或73 解析:以点B 为圆心,4为半径作圆,则与⊙C 交于两点1P ,2P ,如图(1)所示,则点P 的位置有两种情况.(1)如图(1),连接1CP ,则1CP =5.在△BC 中,4,31==B P BC ,图(1) 图(2) 则.∴ △BC 是直角三角形,且190PBC ∠=︒,∴ B P 1∥AC . 又∵41==AC B P ,∴ 四边形BCA P 1是平行四边形.又∵ 1AB CP =,∴ 平行四边形BCA P 1是矩形.∴ 31==BC A P .(2)如图(2),连接C P 2,则52=CP ,在△BC 中,4,32==B P BC , 则,∴ △BC 是直角三角形,∠BC =90°,∴2,P B ,1P 三点共线.∴812=P P . 在Rt △A 中,31=AP ,821=P P ,∴222221218373AP PP AP =+=+=.∴ P A 的长为3或73. 13.(4-π) 解析:如图,∵ 半径为1 cm 的四个圆两两相切,∴ 四边形是边长为2 cm 的正方形,正方形内四个扇形的面积和为一个圆的面积,为π cm 2, 阴影部分的面积=2×2-π=(4-π)cm 2,故答案为4-π. 点拨:本题解题的关键是能看出阴影部分的面积为边长为2的正方形面积减去4个扇形的面积(一个圆的面积). 14.8;2 解析:因为OD ⊥AB ,由垂径定理得,故,.15.55° 解析:根据同弧所对的圆周角等于圆心角的一半可得. 16. 20 解析:和是同一个圆的两段弧,且是由旋转n ︒得到的,∴=,∴和的度数相等,∴的度数是20°.17.250 解析:依据垂径定理和勾股定理可得.18. 4解析:扇形的弧长l ==4π(cm ),所以圆锥的底面半径为4π÷2π=2(cm ),所以这个圆锥形纸帽的高为= 4(cm ).三、解答题19.分析:连接BD ,易证∠BDC =∠C ,∠BOC =2∠BDC =2∠C ,∴ ∠C =30°, 从而∠ADC =60°.解:连接BD .∵ AB 是⊙O 的直径,∴ BD ⊥AD . 又∵ CF ⊥AD ,∴ BD ∥CF .∴ ∠BDC =∠C . 又∵ ∠BDC =∠BOC ,∴ ∠C =∠BOC .∵ AB ⊥CD ,∴ ∠C =30°,∴ ∠ADC =60°.点拨:直径所对的圆周角等于90°,在同一个圆中,同一条弧所对的圆心角等于圆周角的2倍.20.解:(1)如图①,连接PB . ∵ AB 是⊙O 的直径,P 是的中点,∴ P A =PB ,∠APB =90°. ∵ AB =13,∴ P A =22AB = 1322. (2)如图②,连接BC ,OP ,且它们交于点D ,连接PB . ∵ P 是BC 的中点, ∴ OP ⊥BC ,BD =CD . ∵ OA =OB ,∴ OD =12AC =52. ∵ OP =12AB =132, ∴ PD =OP -OD =132-52=4.∵ AB 是⊙O 的直径,∴ ∠ACB =90°. ∵ AB =13,AC =5,∴ BC =12.∴ BD =12BC =6. ∴ PB =22PD BD +=2246+=213.∵ AB 是⊙O 的直径,∴ ∠APB =90°. ∴ P A =22AB PB -=2213(213)-=313.21.分析:(1)由BC 为直径,得∠CAB =∠BDC =90°.在Rt △CAB 中应用勾股定理求AC .由AD 为∠CAB 的平分线,得CD =BD ,在Rt △BDC 中应用勾股定理求解.(2)连接OB 、OD ,证明△OBD 是等边三角形,利用等边三角形的性质求BD 的长. 解:(1)由已知,BC 为⊙O 的直径,得∠CAB =∠BDC =90°. 在Rt △CAB 中,BC =10,AB =6, ∴ AC =22BC AB -=22106-=8.∵ AD 平分∠,∴=,∴ CD =BD .在Rt △中,BC =10,CD 2+BD 2=BC 2,∴ BD 2=CD 2=50.∴ BD =CD =52. (2)如图,连接OB ,OD .∵ AD 平分∠CAB ,且∠CAB =60°, ∴ ∠DAB =12∠CAB =30°, ∴ ∠DOB =2∠DAB =60°. 又∵ ⊙O 中,OB =OD , ∴ △OBD 是等边三角形.∵ ⊙O 的直径为10,∴ OB =5,∴ BD =5.22解:∵ ⊙O 的半径为4,点A ′,B ′分别是点A ,B 关于⊙O 的反演点,点B 在⊙O 上,OA =8,∴ OA ′·OA =,OB ′·OB =,即OA ′·8=,OB ′·4=,∴ OA ′=2,OB ′=4.∴ 点B 关于⊙O 的反演点B ′与点B 重合. 如图所示,设OA 交⊙O 于点M ,连接B ′M , ∵ OM =OB ′,∠BOA =60°,∴ △OB′M 是等边三角形.∵OA ′= A ′M =2,∴ B′A′⊥OM .∴ 在Rt △OB′A′中,由勾股定理得B ′A ′===2.23.分析:由圆周角定理,得,,已知,联立三式可得.解:.理由如下: ∵ ,, 又,∴.第22题答图24.解:(1)已知桥拱的跨度AB=16米,拱高CD=4米,∴AD=8米.利用勾股定理可得,解得OA=10(米).故桥拱的半径为10米.(2)如图,当河水上涨到EF位置时,∵∥,∴,∴(米).连接OE,则OE=10米,(米).又,所以(米),即水面涨高了2米.25.分析:最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离问题.需先算出圆锥侧面展开图的扇形半径.看如何构成一个直角三角形,然后根据勾股定理进行计算.解:由题意可知圆锥的底面周长是,则,∴n=120,即圆锥侧面展开图的圆心角是120°.∴∠APB=60°.在圆锥侧面展开图中,AP=9,PC=4.5,可知∠ACP=90°,∴.故在圆锥的侧面上从A点到C点的最短距离为239.26.分析:利用圆锥侧面展开图的弧长=底面周长得到圆锥底面半径和母线长的关系,进而利用勾股定理可求得各个圆锥的高,比较即可.解:设扇形做成圆锥的底面半径为,优质文档由题意知,扇形的圆心角为240°,则它的弧长=,解得,由勾股定理得,.设扇形做成圆锥的底面半径为,由题意知,扇形的圆心角为120°,则它的弧长=,解得,由勾股定理得.所以>.九年级数学(上)(浙江教育版)第3章圆的基本性质检测题参考答案11。
浙教版数学九年级上册第3章 圆的基本性质 单元测试
浙教版数学九上第3章 圆的基本性质单元测评卷一、选择题(共10小题,每题4分)1.如图,△ABC 的顶点A 、B 、C 均在⊙O 上,若∠ABC+∠AOC=90°,则∠AOC 的大小是( )2.如图,、、、均为以O 点为圆心所画出的四个相异弧,其度数均为60°,且G 在OA 上,C 、E 在AG上,若AC=EG ,OG=1,AG=2,则与两弧长的和为何?( ). ..3.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为( ).4.如图,在⊙O 中,AB 是直径,BC 是弦,点P 是上任意一点.若AB=5,BC=3,则AP 的长不可能为( ) .5.有一直圆柱状的木棍,今将此木棍分成甲、乙两段直圆柱状木棍,且甲的高为乙的高的9倍.若甲、乙的表面积分别为S 1、S 2,甲、乙的体积分别为V 1、V 2,则下列关系何者正确?( )6.如图所示,点A ,B ,C 在圆O 上,∠A=64°,则∠BOC 的度数是( )7.在半径为2的圆中,弦AB 的长为2,则的长等于( ).. . .8.圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )9.一个扇形的半径为8cm ,弧长为cm ,则扇形的圆心角为( )10.已知扇形的圆心角为60°,半径为1,则扇形的弧长为( ).. .二、填空题(共6小题,每题5分)11.已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是 _________ (结果保留π).12.如图,A 、B 、C 是⊙O 上的三点,∠AOB=100°,则∠ACB= _________ 度.13.若圆锥的轴截面是一个边长为4的等边三角形,则这个圆锥的侧面展开后所得到的扇形的圆心角的度数是_________ .14.在半径为2的圆中,弦AC长为1,M为AC中点,过M点最长的弦为BD,则四边形ABCD的面积为_________ .15.如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=55°,则∠BOC的度数是_________ .16.圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为_________ cm2.三、解答题(共10小题,选答题8题,每题10分)17.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.(1)若CD=16,BE=4,求⊙O的直径;(2)若∠M=∠D,求∠D的度数.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,A B=2,DC=4,求⊙O的半径.19.如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且AE=DE,BC=CE.(1)求∠ACB的度数;(2)过点O作OF⊥AC于点F,延长FO交BE于点G,DE=3,EG=2,求AB的长.20.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C 都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.(1)在正方形网格中,画出△AB′C′;(2)计算线段AB在变换到AB′的过程中扫过区域的面积.21.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.(1)求证:CB∥PD;(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.22.如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.(1)求证:AB平分∠OAC;(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.23.如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.(1)求证:BE=CE;(2)以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G.若BC=4,∠EBD=30°,求图中阴影部分(扇形)的面积.24.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.(1)若∠B=70°,求∠CAD的度数;(2)若AB=4,AC=3,求DE的长.25.已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;(Ⅱ)如图②,若∠CAB=60°,求BD的长.26.如图,⊙O1的圆心在⊙O的圆周上,⊙O和⊙O1交于A,B,AC切⊙O于A,连接CB,BD是⊙O的直径,∠D=40°,求:∠AO1B,∠ACB和∠CAD的度数.浙教版九上第3章 圆的基本性质单元测评卷参考答案与试题解析一、选择题(共10小题)1.如图,△ABC 的顶点A 、B 、C 均在⊙O 上,若∠ABC+∠AOC=90°,则∠AOC 的大小是( )∠AOC,由于∠ABC+∠AOC=90°,所以∠AOC+∠AOC=90°,然后解方程即∠AOC+∠AOC=90°,2.如图,、、、均为以O 点为圆心所画出的四个相异弧,其度数均为60°,且G 在OA 上,C 、E在AG 上,若AC=EG ,OG=1,AG=2,则与两弧长的和为何?( ) .. .+)×.3.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为( ).4.如图,在⊙O 中,AB 是直径,BC 是弦,点P 是上任意一点.若AB=5,BC=3,则AP 的长不可能为( ) .5.有一直圆柱状的木棍,今将此木棍分成甲、乙两段直圆柱状木棍,且甲的高为乙的高的9倍.若甲、乙的表面积分别为S1、S2,甲、乙的体积分别为V1、V2,则下列关系何者正确?()且甲的高6.如图所示,点A ,B ,C 在圆O 上,∠A=64°,则∠BOC 的度数是( )7.在半径为2的圆中,弦AB 的长为2,则的长等于( ). . . .的长为:,8.圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )•4•29.一个扇形的半径为8cm,弧长为cm,则扇形的圆心角为()10.已知扇形的圆心角为60°,半径为1,则扇形的弧长为()...二、填空题(共6小题)(除非特别说明,请填准确值)11.已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是20π(结果保留π).×812.如图,A、B、C是⊙O上的三点,∠AOB=100°,则∠ACB=50 度.∠AOB=13.若圆锥的轴截面是一个边长为4的等边三角形,则这个圆锥的侧面展开后所得到的扇形的圆心角的度数是180°.14.在半径为2的圆中,弦AC长为1,M为AC中点,过M点最长的弦为BD,则四边形ABCD的面积为 2 .AC•BD.×1×4=2.15.如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=55°,则∠BOC的度数是70°.16.圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为60πcm2.三、解答题(共10小题)(选答题,不自动判卷)17.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.(1)若CD=16,BE=4,求⊙O的直径;(2)若∠M=∠D,求∠D的度数.∠BOD,∠M=∠D,18.已知A,B,C,D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.,19.如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且AE=DE,BC=CE.(1)求∠ACB的度数;(2)过点O作OF⊥AC于点F,延长FO交BE于点G,DE=3,EG=2,求AB的长.,,CM=20.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C 都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.(1)在正方形网格中,画出△AB′C′;(2)计算线段AB在变换到AB′的过程中扫过区域的面积.=521.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.(1)求证:CB∥PD;(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.=,.22.如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.(1)求证:AB平分∠OAC;(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.本题考查了圆心角、弧、弦之间的关系,勾股定理,等边三角形的性23.如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.(1)求证:BE=CE;(2)以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G.若BC=4,∠EBD=30°,求图中阴影部分(扇形)的面积.,然后,24.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.(1)若∠B=70°,求∠CAD的度数;(2)若AB=4,AC=3,求DE的长.25.已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;(Ⅱ)如图②,若∠CAB=60°,求BD的长.=8=,BD=CD=526.如图,⊙O1的圆心在⊙O的圆周上,⊙O和⊙O1交于A,B,AC切⊙O于A,连接CB,BD是⊙O的直径,∠D=40°,求:∠AO1B,∠ACB和∠CAD的度数.。
九年级数学上册第三章圆的基本性质检测卷浙教版共15套范文整理
九年级数学上册第三章圆的基本性质检测卷(浙教版共15套)第3章圆的基本性质检测卷一、选择题.已知⊙o的半径为5厘米,A为线段oP的中点,当oP =6厘米时,点A与⊙o的位置关系是A.点A在⊙o内B.点A在⊙o上c.点A在⊙o外D.不能确定.有下列四个命题:①等弧所对的圆周角相等;②相等的圆周角所对的弧相等;③平分弦的直径垂直于弦;④三点确定一个圆.其中正确的有A.1个B.2个c.3个D.4个.如图,已知弦cD⊥直径AB于点E,连结oc,oD,cB,DB,下列结论一定正确的是A.∠cBD=120°B.Bc=BDc.四边形ocBD是平行四边形D.四边形ocBD是菱形第3题图.在半径为3c的⊙o中,45°的圆周角所对的弧长为A.34πB.32πc.52πD.94π.如图,AB是⊙o的一条弦,且oD⊥AB于点c,BD︵所的度数是AoD°,则∠35=DEB对的圆周角∠.第5题图A.35°B.55°c.70°D.110°.如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子oA、oB在o点钉在一起,并使它们保持垂直,在测直径时,把o点靠在圆周上,读得刻度oE=8个单位,oF=6个单位,则圆的直径为第6题图A.12个单位B.10个单位c.4个单位D.15个单位.如图,量角器的直径与直角三角板ABc的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线cP从cA处出发沿顺时针方向以每秒3度的速度旋转,cP与量角器的半圆弧交于点E,当第24秒时,点E在量角器上对应的读数为 A.72°B.90°c.108°D.144°第7题图如图,将⊙o沿弦AB折叠,圆弧恰好经过圆心o,点P是优弧AB︵上一点,则∠APB的度数为第8题图A.45°B.30°c.75°D.60°.如图,圆内接△ABc的外角∠AcH的平分线与圆交于点D,DP⊥Ac,垂足为P,DH⊥BH,垂足为H,有下列结论:其中.︵Bc︵=AB;④BH=AP︵;③BD︵=AD;②cP=cH①.一定成立的结论有第9题图A.1个B.2个c.3个D.4个.如图,AB=Ac=AD,∠cBD=2∠BDc,∠BAc=44°,则∠cAD的度数为第10题图A.68°B.88°c.90°D.112°二、填空题1.已知四边形ABcD内接于⊙o,∠A:∠c=1∶2,则∠A =____..已知扇形的圆心角为120°,所对的弧长为8π3,则此扇形的面积是________.3.如图,AB是⊙o的直径,点c是⊙o上的一点,若Bc =6,AB=10,oD⊥Bc于点D,则oD的长为______.第13题图如图,在平面直角坐标系中,点o为坐标原点,点P在象限,⊙P与x轴交于o,A两点,点A的坐标为,⊙P的半径为13,则点P的坐标为____.第14题图.如图,在Rt△ABc中,∠c=90°,Ac=4,Bc=2,分别以Ac、Bc为直径画半圆,则图中阴影部分的面积为____.第15题图.在Rt△ABc中,∠c=90°,Bc=3,Ac=4,点P在以c 为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为____.三、解答题.如图,在单位长度为1的正方形网格中,一段圆弧经过网格的格点A、B、c.请完成如下操作:①以点o为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连结AD、cD;请在的基础上,完成下列填空:①写出点的坐标:c____、D____;②⊙D的半径=____.第17题图.如图,在给定的圆上依次取点A,B,c,D,连结AB,cD,Ac=BD,设Ac,BD交于点E;第18题图求证:AE=DE;若AD︵=100°,AB=ED,求AB︵的度数.19.“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题,“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图所示,cD为⊙o的直径,弦AB⊥cD,垂足为E,cE=1寸,AB=1 的长.”cD尺,求直径.第19题图0.如图,在△ABc中,AB=Ac,BD是∠ABc的角平分线,△ABD的外接圆交Bc于E.求证:AD=Ec.第20题图1.如图,AB是⊙o的直径,c,P是AB︵上两点,AB=13,Ac=5.第21题图如图1,若点P是AB︵的中点,求PA的长;如图2,若点P是Bc︵的中点,求PA的长.22.如图,⊙o为四边形ABcD的外接圆,圆心o在AD上,oc∥AB.第22题图求证:Ac平分∠DAB;若Ac=8,Ac︵∶cD︵=2∶1,试求⊙o的半径;若点B为Ac︵的中点,试判断四边形ABco的形状.23.如图,已知AB是⊙o中一条固定的弦,点c是优弧AcB上的一个动点.如图1,cD⊥AB于D,交⊙o于点N,若cE平分∠AcB,交⊙o于点E,求证:∠Aco=∠BcD;如图2,设AB=8,⊙o半径为5,在的条件下,四边形AcBE 的面积是否是定值?若是定值,求出这个定值,若不是定值,求出四边形AcBE面积的取值范围.图1图2第23题图第3章圆的基本性质检测卷.A2.A3.B4.B5.c6.B7.D8.D9.c0.B1.60°163π3.452π-43或73略①②25连结Bc,∵Ac=BD,∴Ac︵=BD︵,Ac︵-AD︵=BD︵-AD︵,即AB︵=cD︵,∴∠AcB=∠DBc,∴BE=cE,又Ac =BD,∴AE=DE;连结AD.∵AD︵=100°,∴∠ABD=50°,又∵AB=DE=AE,∴∠ABD=∠AEB=50°,∠ADB=25°,AB︵的度数为50°.26寸.0.证明:连结DE,∵四边形ABED是圆内接四边形,∴∠EDc=∠cBA,∵AB=Ac,∴∠AcB=∠cBA,∵∠EDc=∠cBA,∠AcB=∠cBA,∴∠AcB=∠EDc,∴DE=Ec,∵BD是∠cBA的角平分线,∴∠DBA=∠DBc,∴AD︵=DE︵,∴ADEc. =AD,∴DE=AD,Ec=DE,∵DE=1.如图1,连结PB.∵AB是⊙o的直径,P是弧AB的中点,∴PA=PB,∠APB=90°.∵AB=13,∴PA=22AB=1322;如图2,连结Bc,oP,且它们交于点D,连结PB.∵P是Bc ︵的中点,∴oP⊥Bc,BD=cD.∵oA=oB,∴oD=12Ac=52.∵oP=12AB=132,∴PD=oP-oD=132-52=4.∵AB是⊙o 的直径,∴∠AcB=90°.∵AB=13,Ac=5,∴Bc=12.∴BD =12Bc=6.∴PB=PD2+BD2=42+62=213.∵AB是⊙o的直径,∴∠APB=90°.∴PA=AB2-PB2=132-2=313.第21题图2.第22题图证明:∵oc∥AB,∴∠BAc=∠Aco,∵oc=oA,∴∠Aco =∠cAo.∴∠cAo=∠BAc.即:Ac平分∠DAB.Ac=8,弧Ac 与cD之比为2∶1,∴∠DAc=30°,又∵AD是圆的直径,∴∠AcD=90°,∴cD=Ac?tan∠DAc=833,∵∠coD=2∠DAc=60°,oD=oc,∴△coD是等边三角形.∴圆o的半径=cD=833.∵点B为弧Ac的中点,∴AB︵=Bc︵,∴∠BAc =∠BcA,∵Ac平分∠DAB,∴∠oAc=∠BAc,∴∠BAc=∠BcA=∠oAc=∠ocA.∴oA∥Bc.又oc∥AB,∴四边形ABco是平行四边形.∵Ao=co,∴四边形ABco为菱形.3.略;不是定值,8<S四边形AcBE≤40.。
浙教版九年级上册第3章《圆的基本性质》测试卷(含答案)
九年級上冊第3章《圓の基本性質》測試卷滿分100分,考試時間90分鐘一、選擇題(每小題3分,共30分) 1.下列命題中,是真命題の為( ) A .同弦所對の圓周角相等 B .一個圓中只有一條直徑C .圓既是軸對稱圖形,又是中心對稱圖形D .同弧所對の圓周角與圓心角相等2.已知⊙O の半徑為5釐米,A 為線段OP の中點,當OP =6釐米時,點A 與⊙O の位置關係是( ) A .點A 在⊙O 內 B .點A 在⊙O 上 C .點A 在⊙O 外 D .不能確定 3.已知弧の長為3πcm ,弧の半徑為6cm ,則圓弧の度數為( ) A .45° B .90 ° C .60 ° D .180° 4.如圖,OAB △繞點O 逆時針旋轉80°得到OCD △,若110A ∠=°,40D ∠=°,則∠αの度數是( ) A .30° B .40° C .50° D .60°5.如圖,圓O の直徑CD 過弦EF の中點G ,∠DCF =20°,則∠EOD 等於( ) A .10° B .20°C .40°D .80°第5題圖6.鐘面上の分針の長為1,從9點到9點30分,分針在鐘面上掃過の面積是( ) A .12πB .14πC .18πD .π7.如圖,一種電子遊戲,電子螢幕上有一正六邊形ABCDEF ,點P 沿直線AB 從右向左移動,當出現點P 與正六邊形六個頂點中の至少兩個頂點距離相等時,就會發出警報,則直線AB 上會發出警報の點P 有( ) A .3個 B .4個 C .5個 D .6個第10题E CDFP8.如圖,A、B、P是半徑為2の⊙O上の三點,∠APB=45°,則弦ABの長為()A.2B.2 C.22D.4第8題圖9.如圖,在平面直角坐標系中,⊙A經過原點O,並且分別與x軸、y軸交於B、C兩點,已知B(8,0),C(0,6),則⊙Aの半徑為()A.3 B.4 C.5 D.8第9題圖10.如圖,⊙Oの半徑OD⊥弦AB於點C,連結AO並延長交⊙O於點E,連結E C.若AB=8,CD=2,則ECの長為()A.215B.8 C.210D.213第10題圖二、填空題(每小題3分,共30分)11.一條弧所對の圓心角為72°,則這條弧所對圓周角為°.12.已知⊙Oの面積為36π,若PO=7,則點P在⊙O.13.一紙扇柄長30cm,展開兩柄夾角為120°,則其面積為cm2.14.如圖,AB為⊙Oの直徑,弦CD⊥AB於點E,若CD=6,且AE:BE =1:3,則AB= .第14題圖15.如圖,AB是⊙Oの直徑,點C是圓上一點,∠BAC=70°,則∠OCB= °.第15題圖16.已知:如圖,圓內接四邊形ABCD中,∠BCD =110°,則∠BAD = °.第16題圖17.如圖,OC是⊙Oの半徑,AB是弦,且OC⊥AB,點P在⊙O上,∠APC=26°,則∠BOC= .第17題圖18.如圖,⊙O中,弦AB、DCの延長線相交於點P,如果∠AOD=120°,∠BDC=25°,那麼∠P= °.第18題圖19.如圖,AD、AC分別是直徑和絃,∠CAD=30°,B是AC上一點,BO⊥AD,垂足為O,BO=5cm,則CD 等於cm.第19題圖20.如圖:在⊙O中,AB、AC為互相垂直且相等の兩條弦,OD⊥AB,OE⊥AC,垂足分別為D、E,若AC =2 cm,則⊙Oの半徑為cm.第20題圖三、解答題(共40分) 21.(6分)某居民社區一處圓柱形の輸水管道破裂,維修人員為更換管道,需確定管道圓形截面の半徑,下圖是水準放置の破裂管道有水部分の截面. (1)請你補全這個輸水管道の圓形截面;(2)若這個輸水管道有水部分の水面寬AB =16cm ,水面最深地方の高度為4cm ,求這個圓形截面の半徑.22.(6分)如圖所示,AB =AC ,AB 為⊙O の直徑,AC 、BC 分別交⊙O 於E 、D ,連結ED 、BE .(1) 試判斷DE 與BD 是否相等,並說明理由; (2) 如果BC =6,AB =5,求BE の長.23.(6分)如圖,⊙O の直徑AB 為10cm ,弦AC 為6cm ,∠ACB の平分線交⊙O 於D ,求BC ,AD ,BDの長.24.(6分)如圖,將小旗ACDB 放於平面直角坐標系中,得到各頂點の座標為A (-6,12),B (-6,0),C (0,6),D (-6,6).以點B 為旋轉中心,在平面直角坐標系內將小旗順時針旋轉90°. (1)畫出旋轉後の小旗A ′C ′D ′B ′,寫出點C ′の座標; (2)求出線段BA 旋轉到B ′A ′時所掃過の扇形の面積.AOBCDE25.(8分)如圖,AB為⊙Oの直徑,點C在⊙O上,延長BC至點D,使DC=CB,延長DA與⊙Oの另一個交點為E,連接AC,CE.(1)求證:∠B=∠D;(2)若AB=4,BC-AC=2,求CEの長.26.(8分)在⊙O中,AB為直徑,點C為圓上一點,將劣弧沿弦AC翻折交AB於點D,連結CD.(1)如圖1,若點D與圓心O重合,AC=2,求⊙Oの半徑r;(2)如圖2,若點D與圓心O不重合,∠BAC=25°,請直接寫出∠DCAの度數.资料内容仅供您学习参考,如有不当之处,请联系改正或者删除九年級上冊第3章《圓の基本性質》測試卷1.C2.A3.B4.C5.C6.A7.C资料内容仅供您学习参考,如有不当之处,请联系改正或者删除20.221.(1)圖略;(2)10cm .22.(1)連結AD . ∵AB 是⊙O の直徑,∴AD ⊥BC ,BE ⊥AC .∵AB=AC ,∴BD=CD ,∴DE=BD .(2)由畢氏定理,得BC 2-CE 2=BE 2=AB 2-AE 2.設AE =x ,則62-(5-x )2=52-x 2,解得x =75.∴BE 22245AB AE -=. 23.∵ AB 是直徑.∴ ∠ACB =∠ADB =90°.在Rt △ABC 中,BC 22221068AB AC -=-=(cm ).∵ CD平分∠ACB ,∴ AD BD =.∴ AD =BD .又在Rt △ABD 中,AD 2+BD 2=AB 2,∴ AD =BD =52(cm ). 24.(1)圖略,C ′(0,-6);(2)∵A (-6,12),B (-6,0),∴AB =12.∴線段BA 旋轉到B ′A ′時所掃過の扇形の面積=2901236360⋅π⋅=π.25.(1)∵AB 為⊙O の直徑,∴∠ACB =90°,∴AC ⊥BC ,∵DC =CB ,∴AD =AB ,∴∠B =∠D ;(2)解:設BC =x ,則AC =x -2,在Rt △ABC 中,AC 2+BC 2=AB 2,∴(x -2)2+x 2=42,解得:x 17x 2=17,∵∠B =∠E ,∠B =∠D ,∴∠D =∠E ,∴CD =CE ,∵CD =CB ,∴CE =CB 7. 26.(1)過點O 作OE ⊥AC 於E ,則AE =21AC =21×2=1,∵翻折後點D 與圓心O 重合,∴OE =21r ,在Rt △AOE 中,AO 2=AE 2+OE 2,即r 2=12+(21r )2,解得r 233(2)連接BC ,∵AB 是直徑,∴∠ACB =90°,∵∠BAC =25°,∴∠B =90°-∠BAC =90°-25°=65°,根據翻折の性質,⌒AC 所對の圓周角等於ADC 所對の圓周角,∴∠DCA =∠B -∠A =65°-25°=40°.。
浙教版数学九年级上册 第3章测试卷 圆的基本性质(含答案)
第3章测试卷圆的基本性质班级学号得分姓名一、选择题(本大题有10小题,每小题3分,共30分)1.已知⊙O的直径为10,点P到点O的距离大于8,那么点P的位置( )A. 一定在⊙O的内部B. 一定在⊙O的外部C. 一定在⊙O上D. 不能确定2.正六边形的每个内角度数为( )A. 90°B. 108°C. 120°D. 150°3.如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为( )A. 60°B. 50°C. 40°D. 20°4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是( )A7 B. 7 C. 6 D. 85. 下列有关圆的一些结论:①与半径长相等的弦所对的圆周角是30°;②圆内接正六边形的边长与该圆半径相等;③垂直于弦的直径平分这条弦;④平分弦的直径垂直于弦.其中正确的是( )A. ①②③B. ①③④C. ②③D. ②④6. 如图,正方形ABCD 内接于⊙O,AB=22,则AB的长是( )A. πB.32π C. 2π D127.如图,已知 BC 是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点 A,点C重合),BD与OA交于点E,设∠AED=α,∠AOD=β,则( )A. 3α+β=180°B. 2α+β=180°C. 3α-β=90°D. 2α-β=90°8. 如图,在扇形 AOB中,∠AOB=90°,点C 是弧AB 的中点,点 D 在OB 上,点 E 在OB 的延长线上,当正方形CDEF的边长为2时,则阴影部分的面积为( )A. π-2B. 2π—2C. π—4D. 2π-49. 如图,四边形ABCD内接于⊙O,点I是△ABC角平分线的交点,∠AIC=124°,点 E 在AD 的延长线上,则∠CDE的度数为( )A. 56°B. 62°C. 68°D. 78°10. 如图,AB是半圆O 的直径,点 P 从点O 出发,沿OA→AB→BO(的路径匀速运动一周.设OP 的长为s,运动时间为t,则下列图象能大致地刻画s与t之间关系的是( )二、填空题(本大题有6小题,每小题4分,共24分)11. 如图,点 A,B,C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为 .12. 如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB 的距离为 .13. 如图,在四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC 交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是 .14.如图,在⊙O中,弦AB=1,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为 .15.如图,在半径2₂的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形面积为 .16. 如图所示,E,F分别是正方形ABCD 的边AB,BC上的点,BE=CF,连结CE,DF.将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF的位置,则旋转了.三、解答题(本大题有8小题,共66分)17. (6分)已知扇形的半径为6cm,面积为10πcm²,求该扇形的弧长.18. (6分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,点O,M也在格点上.(1)画出△ABC关于直线OM 对称的△A₁B₁C₁;(2)画出△ABC绕点O按顺时针方向旋转 90°后所得的△A₂B₂C₂.19. (6分)中国的拱桥始建于东汉中后期,已有一千八百余年的历史,如图,一座拱桥在水面上方部分是.AB,拱桥在水面上的跨度AB为8米,拱桥AB与水面的最大距离为3米.(1)用直尺和圆规作出AB所在圆的圆心O;(2)求拱桥 AB所在圆的半径.20.(8分)如图所示,在△ABC中,AB=AC,∠A=30°,,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点 B作BP 平行于DE,交⊙O于点P,连结OP,CP.(1)求证:BD=DC;(2)求∠BOP的度数.21.(8分)如图,AB是⊙O的直径,C是.AE的中点,CD⊥AB于点D,交AE于点F,连结AC.求证:AF=CF.22.(10分)如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°.(1) 试判断△ABC是否为等边三角形? 为什么?(2)若⊙O的半径OD⊥BC于点E,BC=8,,求⊙O的半径长.23.(10分)如图,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的⊙O交BC 于点D,且.BD= DE.(1)求证:AB为⊙O的直径;(2)若AB=8,∠BAC=45°,,求阴影部分的面积.24.(12分)如图,点A,B,C是⊙O上的三点,AB∥OC.(1)求证:AC平分∠OAB;(2)如图,过点O作(OE⊥AB于点E,交AC于点 P.若AB=2,∠AOE=30°,求 PE的长.第3章测试卷 圆的基本性质1. B2. C3. B4. B5. C6. A7. D8. A9. C 10. C 11. 6 12. 3 13. 6π14 12 15. π 16. 9017. 解:由 S =12l ⋅R 得 l =2S R =2×106=103π(cm ).18. 解:(1)如图, △A₁B₁C₁即为所求作的三角形.(2)如图, △A₂B₂C₂即为所求作的三角形.19. 解:(1)如图1所示,点 O 即为所求;(2)如图2 所示,取 AB 的中点D ,连结OD 交AB 于点 E,连结OA,则 OD ⊥AB,且AE=EB=4米,由题意得,DE=3米,设圆的半径为r 米,在 Rt△AEO 中, AE +EO²=OA²,即 4²+(r−3)²=r²,解得 r =256.即拱桥AB 所在圆的半径为 256米.20. (1)证明:如图,连结 AD.∵AB 为⊙O 的直径,∴∠ADB=90°,即 AD⊥BC,∵AB=AC,∴BD=CD. (2)解:∵∠BAC= 30°,AB= AC,∴ ∠ABC =12×(180∘−30∘)=75°.∵四边形 ABDE 为圆O 的内接四边形,∴∠EDC=∠BAC=30°.∵BP∥DE,∴∠PBC=∠EDC=30°,∴∠OBP=∠ABC--∠PBC=45°.∵OB =OP,∴∠OPB=∠OBP=45°,∴∠BOP =90°21. 证明:延长CD 交⊙O 于点 H,∵C 是 AE 的中点, ∴AC =CE ,∵CD ⊥AB,∴AC =AH ,∴CE =AH ,∴∠ACD=∠CAE,∴AF=CF.22. 解:(1)△ABC 是等边三角形.理由:∵∠BAC=∠APC=60°,又∵∠APC=∠ABC,∴∠ABC=60°,∴∠ACB =180°−∠BAC−∠ABC =180°− 60°−60°=60°,∴△ABC 是等边三角形. (2)如图,连结OB,∵△ABC 为等边三角形,⊙O 为其外接圆,∴BO 平分∠ABC,∴∠OBC=30°,∵OD ⟂BC,∴BD =CD,BE =CE = 4,∠BOD =60∘,∴OE =433, OB =833.∴OO|的半径长 833.23. (1)证明:如图,连结.AD, ∵⌢BD =DE ,∴∠BAD =∠CAD.又∵AB = AC, ∴AD ⊥ BC, ∴∠ADB=90°,∴AB 为⊙O 的直径. (2)解:∵AB 为⊙O 的直径,∴O 在AB 上,如图,连结OE,∵AB=8,∠BAC=45°,∴∠AOE=∠BOE= ∴1∘∴AB =8,∴BO =EO =4,S 扇形AOE =90×π×42360 =4π,S BOE =12OB 2=12×16=8,∴S 阴影=S BOE24. (1)证明:∵AB∥OC,∴∠C=∠BAC.∵OA=OC,∴∠C=∠OAC,∴∠BAC=∠OAC,即AC 平分∠OAB. (2)解: COE⟂AB,∴AE =BE =12AB =1,又∵∠AOE 、30°,∠PEA=90°,∴∠OAE= 60∘,∴∠EAP =3∠OAE =30∘,∴PE =12PA.设PE=x,则 PA=2x,根据勾股定理得 x²+1²=(2x)²,解得 x =33,∴PE =33.。
浙教版九上数学 第3章 圆的基本性质 单元试卷(含解析)
① 平分 ,② , ,③ .
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①② ③,①③ ②,②③ ①.
试判断上述三个命题是否正确(直接作答);
请证明你认为正确的命题.
26.如图 ,边长均为 的正 和正 原来完全重合.如图 ,现保持正 不动,使正 绕两个正三角形的公共中心点 按顺时针方向旋转,设旋转角度为 .(注:除第 题中的第②问,其余各问只要直接给出结果即可)
【详解】∵四边形ABCD为正方形,且面积为3
∴∠D=∠B=∠BAD=90°,AD=AB=BC=CD= ,且AE=AF,
①当F在线段BC上时,如图1,
在Rt△ADE和Rt△ABF中,
,
∴Rt△ADE≌Rt△ABF(HL),
∴∠DAE=∠BAF,BF=DE=1,
又∵在Rt△ADE中,DE=1,AD= ,
二、填空题(共10小题,每小题3分,共30分)
11.如图,正方形 的面积为 ,点 是 边上一点, ,将线段 绕点 旋转,使点 落在直线 上,落点记为 ,则 ________, 的长为________.
【答案】(1).30°或90°;(2). -1或 +1.
【解析】
【分析】
当点F在线段BC上时,由旋转的性质可得△ADE≌△ABF,可得到BF=DE,∠DAE=∠BAF=30°,可求得答案;当点F在线段CB的延长线上时,可证得△ABF≌△ADE,则可求得∠EAF=90°,此时FC=BF+BC,可求得答案.
8.如图,已知 为 的外心, 为 上的高, , ,则 为( )
A.32°B.26°C.28°D.34°
9.一个直角三角形两条直角边为 , ,分别以它的两条直角边所在直线为轴,旋转一周,得到两个几何体,它们的表面面积相应地记为 和 ,则有( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章 圆的基本性质检测卷一、选择题(本大题共10小题,每小题4分,共40分)1.已知⊙O 的半径为5厘米,A 为线段OP 的中点,当OP =6厘米时,点A 与⊙O 的位置关系是( )A .点A 在⊙O 内B .点A 在⊙O 上C .点A 在⊙O 外D .不能确定 2.有下列四个命题:①等弧所对的圆周角相等;②相等的圆周角所对的弧相等;③平分弦的直径垂直于弦;④三点确定一个圆.其中正确的有( )A .1个B .2个C .3个D .4个 3.如图,已知弦CD ⊥直径AB 于点E ,连结OC ,OD ,CB ,DB ,下列结论一定正确的是( ) A .∠CBD =120° B .BC =BDC .四边形OCBD 是平行四边形 D .四边形OCBD 是菱形第3题图4.在半径为3cm 的⊙O 中,45°的圆周角所对的弧长为( )A.34πB.32πC.52πD.94π 5.如图,AB 是⊙O 的一条弦,且OD ⊥AB 于点C ,BD ︵所对的圆周角∠DEB =35°,则∠AOD 的度数是( )第5题图A .35°B .55°C .70°D .110° 5.如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,读得刻度OE =8个单位,OF =6个单位,则圆的直径为( )第6题图A .12个单位B .10个单位C .4个单位D .15个单位 7.如图,量角器的直径与直角三角板ABC 的斜边AB 重合,其中量角器0刻度线的端点N 与点A 重合,射线CP 从CA 处出发沿顺时针方向以每秒3度的速度旋转,CP 与量角器的半圆弧交于点E ,当第24秒时,点E 在量角器上对应的读数为( )A .72°B .90°C .108°D .144°第7题图8.如图,将⊙O 沿弦AB 折叠,圆弧恰好经过圆心O ,点P 是优弧AMB ︵上一点,则∠APB 的度数为( )第8题图A .45°B .30°C .75°D .60° 8.如图,圆内接△ABC 的外角∠ACH 的平分线与圆交于点D ,DP ⊥AC ,垂足为P ,DH ⊥BH ,垂足为H ,有下列结论:①CH =CP ;②AD ︵=BD ︵;③AP =BH ;④AB ︵=BC ︵.其中一定成立的结论有( )第9题图A .1个B .2个C .3个D .4个 9.(威海中考)如图,AB =AC =AD ,∠CBD =2∠BDC ,∠BAC =44°,则∠CAD 的度数为( )第10题图A .68°B .88°C .90°D .112° 二、填空题(本大题共6小题,每小题5分,共30分)11.已知四边形ABCD 内接于⊙O ,∠A :∠C =1∶2,则∠A =____.12.已知扇形的圆心角为120°,所对的弧长为8π3,则此扇形的面积是________.13.(长沙中考)如图,AB 是⊙O 的直径,点C 是⊙O 上的一点,若BC =6,AB =10,OD ⊥BC 于点D ,则OD 的长为______.第13题图14.如图,在平面直角坐标系中,点O 为坐标原点,点P 在第一象限,⊙P 与x 轴交于O ,A 两点,点A 的坐标为(6,0),⊙P 的半径为13,则点P 的坐标为____.第14题图14.如图,在Rt △ABC 中,∠C =90°,AC =4,BC =2,分别以AC 、BC 为直径画半圆,则图中阴影部分的面积为____(结果保留π).第15题图16.在Rt △ABC 中,∠C =90°,BC =3,AC =4,点P 在以C 为圆心,5为半径的圆上,连结PA ,PB .若PB =4,则PA 的长为____.三、解答题(本大题共8小题,共80分)17.(8分)如图,在单位长度为1的正方形网格中,一段圆弧经过网格的格点A 、B 、C .(1)请完成如下操作:①以点O 为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;②根据图形提供的信息,标出该圆弧所在圆的圆心D ,并连结AD 、CD ;(2)请在(1)的基础上,完成下列填空:①写出点的坐标:C ____、D ____;②⊙D 的半径=____(结果保留根号).第17题图18.(8分)如图,在给定的圆上依次取点A ,B ,C ,D ,连结AB ,CD ,AC =BD ,设AC ,BD 交于点E ;第18题图(1)求证:AE =DE ;(2)若AD ︵=100°,AB =ED ,求AB ︵的度数.19.(8分)“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题,“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,求直径CD 的长.”(1尺=10寸)第19题图20.(8分)如图,在△ABC中,AB=AC,BD是∠ABC的角平分线,△ABD的外接圆交BC 于E.求证:AD=EC.第20题图21.(10分)(武汉中考)如图,AB 是⊙O 的直径,C ,P 是AB ︵上两点,AB =13,AC =5.第21题图(1)如图1,若点P 是AB ︵的中点,求PA 的长; (2)如图2,若点P 是BC ︵的中点,求PA 的长.22.(12分)如图,⊙O 为四边形ABCD 的外接圆,圆心O 在AD 上,OC ∥AB .第22题图(1)求证:AC 平分∠DAB ;(2)若AC =8,AC ︵∶CD ︵=2∶1,试求⊙O 的半径;(3)若点B 为AC ︵的中点,试判断四边形ABCO 的形状.23.(14分)如图,已知AB 是⊙O 中一条固定的弦,点C 是优弧ACB 上的一个动点(点C 不与A 、B 重合).(1)如图1,CD ⊥AB 于D ,交⊙O 于点N ,若CE 平分∠ACB ,交⊙O 于点E ,求证:∠ACO =∠BCD ;(2)如图2,设AB =8,⊙O 半径为5,在(1)的条件下,四边形ACBE 的面积是否是定值?若是定值,求出这个定值,若不是定值,求出四边形ACBE 面积的取值范围.图1图2 第23题图第3章 圆的基本性质检测卷1.A 2.A 3.B 4.B 5.C 6.B 7.D 8.D 9.C 10.B 11.60° 12.163π 13. 4 14. (3,2) 15. 52π-416. 3或7317. (1)略 (2)①(6,2) (2,0) ②2 518. (1)连结BC ,∵AC =BD ,∴AC ︵=BD ︵,AC ︵-AD ︵=BD ︵-AD ︵,即AB ︵=CD ︵,∴∠ACB =∠DBC ,∴BE =CE ,又AC =BD ,∴AE =DE ; (2)连结AD.∵AD ︵=100°,∴∠ABD =50°,又∵AB=DE =AE ,∴∠ABD =∠AEB=50°,∠ADB =25°,AB ︵的度数为50°.19. 26寸.20. 证明:连结DE ,∵四边形ABED 是圆内接四边形,∴∠EDC =∠CBA,∵AB =AC ,∴∠ACB =∠CBA,∵∠EDC =∠CBA,∠ACB =∠CBA,∴∠ACB =∠EDC,∴DE =EC ,∵BD 是∠CBA 的角平分线,∴∠DBA =∠DBC,∴AD ︵=DE ︵,∴AD =DE ,∵DE =EC ,AD =DE ,∴AD =EC.21.(1)如图1,连结PB.∵ AB 是⊙O 的直径,P 是弧AB 的中点,∴ PA =PB ,∠APB =90°.∵AB =13,∴PA =22AB =1322; (2)如图2,连结BC ,OP ,且它们交于点D ,连结PB. ∵ P 是BC ︵的中点,∴ OP ⊥BC ,BD =CD.∵ OA=OB ,∴ OD =12AC =52.∵ OP =12AB =132,∴ PD =OP -OD =132-52=4.∵ AB 是⊙O 的直径,∴ ∠ACB =90°.∵ AB =13,AC =5,∴BC=12.∴ BD=12BC =6.∴ PB=PD 2+BD 2=42+62=213.∵ AB 是⊙O 的直径,∴∠APB =90°. ∴ PA =AB 2-PB 2=132-(213)2=313.第21题图22.第22题图(1) 证明:∵OC∥AB,∴∠BAC =∠ACO,∵OC =OA ,∴∠ACO =∠CAO.∴∠CAO=∠BAC.即:AC 平分∠DAB. (2)AC =8,弧AC 与CD 之比为2∶1,∴∠DAC =30°,又∵AD 是圆的直径,∴∠ACD =90°,∴CD =AC·tan ∠DAC =833,∵∠COD =2∠DAC =60°,OD =OC ,∴△COD 是等边三角形.∴圆O 的半径=CD =833. (3)∵点B 为弧AC 的中点,∴AB ︵=BC ︵,∴∠BAC =∠BCA,∵AC 平分∠DAB,∴∠OAC =∠BAC,∴∠BAC =∠BCA=∠OAC=∠OCA.∴OA∥BC.又OC∥AB,∴四边形ABCO 是平行四边形.∵AO=CO ,∴四边形ABCO 为菱形.23.(1)略; (2)不是定值,8<S 四边形ACBE ≤40.。
