电磁感应的综合应用(能量问题、动量问题、杆+导轨模型)(教师版)
电磁感应中的“杆+导轨”类问题(3大模型)(解析版)
电磁感应中的“杆＋导轨”类问题(3大模型)电磁感应“杆＋导轨”模型的实质是不同形式的能量的转化过程，处理这类问题要从功和能的观点入手，弄清导体棒切割磁感线过程中的能量转化关系，现从力学、图像、能量三种观点出发，分角度讨论如下：模型一 单杆＋电阻＋导轨模型[初建模型][母题] 如图所示，相距为L 的两条足够长的光滑平行金属导轨MN 、PQ 与水平面的夹角为θ，N 、Q 两点间接有阻值为R 的电阻。
整个装置处于磁感应强度为B 的匀强磁场中，磁场方向垂直导轨平面向下。
将质量为m 、阻值也为R 的金属杆cd 垂直放在导轨上，杆cd 由静止释放，下滑距离x 时达到最大速度。
重力加速度为g ，导轨电阻不计，杆与导轨接触良好。
求：(1)杆cd 下滑的最大加速度和最大速度； (2)上述过程中，杆上产生的热量。
[解析] (1)设杆cd 下滑到某位置时速度为v ，则杆产生的感应电动势E ＝BL v ，回路中的感应电流I ＝ER ＋R杆所受的安培力F ＝BIL 根据牛顿第二定律有mg sin θ－B 2L 2v2R＝ma当速度v ＝0时，杆的加速度最大，最大加速度a ＝g sin θ，方向沿导轨平面向下当杆的加速度a ＝0时，速度最大，最大速度v m ＝2mgR sin θB 2L 2，方向沿导轨平面向下。
(2)杆cd 从开始运动到达到最大速度过程中，根据能量守恒定律得mgx sin θ＝Q 总＋12m v m 2又Q 杆＝12Q 总，所以Q 杆＝12mgx sin θ－m 3g 2R 2sin 2θB 4L 4。
[答案] (1)g sin θ，方向沿导轨平面向下 2mgR sin θB 2L 2，方向沿导轨平面向下 (2)12mgx sin θ－m 3g 2R 2sin 2θB 4L 4[内化模型]单杆＋电阻＋导轨四种题型剖析开始时a ＝g sin α，B L[变式] 此题若已知金属杆与导轨之间的动摩擦因数为μ。
现用沿导轨平面向上的恒定外力F 作用在金属杆cd 上，使cd 由静止开始沿导轨向上运动，求cd 的最大加速度和最大速度。
模型25电磁感应中导轨和能量问题(教师版含解析)-备战2021年高考物理模型专题突破
25电磁感应中导轨和能量问题1．如图所示，在一匀强磁场中有一U形导线框abcd，线框处于水平面内，磁场与线框平面垂直，R为一电阻，ef为垂直于ab的一根导体杆，它可在ab、cd上无摩擦地滑动。
杆ef及线框中导线的电阻都可不计。
开始时，给ef一个向右的初速度，则( )A．ef将减速向右运动，但不是匀减速B．ef将匀减速向右运动，最后停止C．ef将匀速向右运动D．ef将往返运动【答案】A【详解】ef向右运动，切割磁感线，产生感应电动势和感应电流，会受到向左的安培力而做减速运动，直到停止，但不是匀减速，由22B L vF BIL ma===R知，ef做的是加速度减小的减速运动，故A正确，BCD正确。
故选A。
2．(2020·和县第二中学高二月考)如图所示，一粗糙的平行金属轨道平面与水平面成θ角，两轨道上端用一电阻R相连，该装置处于匀强磁场中，磁场方向垂直于轨道平面向上。
质量为m的金属杆ab以初速度v0从轨道底端向上滑行，滑行到某高度h后又返回到底端。
若运动过程中金属杆始终保持与导轨垂直且接触良好，轨道与金属杆的电阻均忽略不计。
则下列说法正确的是( )A．金属杆ab上滑过程与下滑过程通过电阻R的电量一样多B．金属杆ab上滑过程与下滑过程产生的焦耳热一定相等C．金属杆ab在整个过程中损失的机械能等于装置产生的焦耳热D ．金属杆ab 上滑过程中克服安培力与摩擦力做功之和等于2012mv 【答案】A【详解】A ．根据 E q It t R R∆Φ=== 上滑过程和下滑过程磁通量的变化量相等，则通过电阻R 的电量相等，A 正确；B ．经过同一位置时：下滑的速度小于上滑的速度，下滑时棒受到的安培力小于上滑所受的安培力，则下滑过程安培力的平均值小于上滑过程安培力的平均值，所以上滑导体棒克服安培力做功大于下滑过程克服安培力做功，故上滑过程中电阻R 产生的热量大于下滑过程中产生的热量，上滑过程与下滑过程电磁感应而产生的焦耳热不相等，B 错误；C ．根据能量守恒定律可知金属杆ab 在整个过程中损失的机械能等于装置产生的焦耳热和因摩擦产生的热，C 错误；D ．金属杆ab 上滑过程中受到重力、安培力、摩擦力作用，这些力都做功负功，根据动能定理得知：ab 棒克服重力、安培力与摩擦力所做功之和等于2012mv ，D 错误。
电磁感应规律的综合应用(解析版)-2023年高考物理压轴题专项训练(新高考专用)
压轴题07电磁感应规律的综合应用目录一，考向分析 (1)二．题型及要领归纳 (2)热点题型一以动生电动势为基综合考查导体棒运动的问题 (2)热点题型二以感生电动势为基综合考查导体棒运动的问题 (9)热点题型三以等间距双导体棒模型考动量能量问题 (16)热点题型四以不等间距双导体棒模型考动量定理与电磁规律的综合问题 (21)热点题型五以棒＋电容器模型考查力电综合问题 (27)三．压轴题速练 (33)一，考向分析1.本专题是运动学、动力学、恒定电流、电磁感应和能量等知识的综合应用，高考既以选择题的形式命题，也以计算题的形式命题。
2.学好本专题，可以极大地培养同学们数形结合的推理能力和电路分析能力，针对性的专题强化，可以提升同学们解决数形结合、利用动力学和功能关系解决电磁感应问题的信心。
3.用到的知识有：左手定则、安培定则、右手定则、楞次定律、法拉第电磁感应定律、闭合电路欧姆定律、平衡条件、牛顿运动定律、函数图像、动能定理和能量守恒定律等。
电磁感应综合试题往往与导轨滑杆等模型结合，考查内容主要集中在电磁感应与力学中力的平衡、力与运动、动量与能量的关系上,有时也能与电磁感应的相关图像问题相结合。
通常还与电路等知识综合成难度较大的试题，与现代科技结合密切,对理论联系实际的能力要求较高。
4.电磁感应现象中的电源与电路(1)产生感应电动势的那部分导体相当于电源。
(2)在电源内部电流由负极流向正极。
(3)电源两端的电压为路端电压。
5.电荷量的求解电荷量q＝IΔt，其中I必须是电流的平均值。
由E＝n ΔΦΔt、I＝ER总、q＝IΔt联立可得q＝n ΔΦR总，与时间无关。
6.求解焦耳热Q的三种方法(1)焦耳定律：Q＝I2Rt，适用于电流、电阻不变。
(2)功能关系：Q＝W克服安培力，电流变不变都适用。
(3)能量转化：Q＝ΔE(其他能的减少量)，电流变不变都适用。
7.用到的物理规律匀变速直线运动的规律、牛顿运动定律、动能定理、能量守恒定律等。
2020年高考物理压轴题专练附解答：电磁感应的综合应用(能量问题、动量问题、杆 导轨模型)
电磁感应的综合应用（能量问题、动量问题、杆+导轨模型）考点一: 电磁感应中的能量问题1.能量转化及焦耳热的求法(1)能量转化(2)求解焦耳热Q的三种方法2.解题的一般步骤(1)确定研究对象(导体棒或回路);(2)弄清电磁感应过程中,哪些力做功,哪些形式的能量相互转化;(3)根据功能关系或能量守恒定律列式求解.3.方法技巧求解电能应分清两类情况(1)若回路中电流恒定,可以利用电路结构及W=UIt或Q=I2Rt直接进行计算.(2)若电流变化,则①利用安培力做的功求解:电磁感应中产生的电能等于克服安培力所做的功;②利用能量守恒求解:若只有电能与机械能的转化,则机械能的减少量等于产生的电能.③利用功能关系求解:若除重力、安培力做功外,还有其他力做功,则其他力做功等于增加的机械能和电能.学科#网考点二电磁感应中的动量问题电磁感应问题往往涉及牛顿定律、动量守恒、能量守恒、电路的分析和计算等许多方面的物理知识,试题常见的形式是导体棒切割磁感线,产生感应电流,从而使导体棒受到安培力作用.导体棒运动的形式有匀速、匀变速和非匀变速3种,对前两种情况,容易想到用牛顿定律求解,对后一种情况一般要用能量守恒和动量守恒定律求解,但当安培力变化,且又涉及位移、速度、电荷量等问题时,用动量定理求解往往能巧妙解决.方法技巧动量在电磁感应中的应用技巧(1)在电磁感应中,动量定理应用于单杆切割磁感线运动,可求解变力的时间、速度、位移和电荷量.①求电荷量或速度:B错误!未找到引用源。
lΔt=mv2-mv1,q=错误!未找到引用源。
t.③求位移:-BIlΔt=-错误!未找到引用源。
22B l v tR总=0-mv0,即-错误!未找到引用源。
x=m(0-v0).(2)电磁感应中对于双杆切割磁感线运动,若双杆系统所受合外力为零,运用动量守恒定律结合能量守恒定律可求解与能量有关的问题.考点三：电磁感应中的“杆+导轨”模型模型概述“导轨+杆”模型是电磁感应问题在高考命题中的“基本道具”,也是高考的热点,考查的知识点多,题目的综合性强,物理情景变化空间大,是我们复习中的难点.“导轨+杆”模型又分为“单杆”型和“双杆”型;导轨放置方式可分为水平、竖直和倾斜;杆的运动状态可分为匀速运动、匀变速运动、非匀变速运动或转动等;磁场的状态可分为恒定不变、均匀变化和非均匀变化等等,情景复杂,形式多变常见类型单杆水平式(导轨光滑)设运动过程中某时刻棒的速度为v,加速度为a=错误!未找到引用源。
电磁感应的综合应用(能量问题、动量问题、杆+导轨模型)(学生版)
6
2．(10 分)【加试题】（2017 年 4 月浙江选考）间距为 l 的两平行金属导轨由水平部分和倾 斜部分平滑连接而成，如图 所示。倾角为θ的导轨处于大小为 B1 方向垂直导轨平面向上的 匀强磁场区间 I 中。 水平导轨上的无磁场区间静止放置—质量为 3m 的“联动双杆”（由两根 长为 l 的金属杆 cd 和 ef 用长度为 L 的刚性绝缘杆连接构成），在“联动双杆”右侧存在大小 为 B2、方向垂直导轨平面向上的匀强磁场区间 II，其长度大于 L。质量为 m、长为 l 的金属 杆 ab 从倾斜导 轨上端释放，达到匀速后进入水平导轨（无能量损失），杆以与“联动双杆” 发生碰撞，碰后杆 ab 和 cd 合在一起形成“联动三杆'。“联动三杆”继续沿水平导轨进人磁场 区间 II 并从 中滑出。运动过程中，杆 ab、cd 和 ef 与导轨始终接触良好，且保持与导轨垂 直。 已知杆 ab、cd 和 ef 电阻均为 R=0.02Ω，m=0.1kg，l=0.5m，L=0.3m，θ=30°，B1=0.1T， B2=0.2T。不计摩擦阻力和导轨电阻，忽略磁场边界效应。求
I=
Q t
=CBL
v t
=CBLa,安培力
F
安
=BIL=CB2L2a,F-F
安=ma,a=
m
F B 2 L2C
,所
以杆做匀加速运动
5
电磁感应与动量结合问题
高考真题 1．（2018 高考天津理综）真空管道超高速列车的动力系统是一种将电能直接转换成平动动 能的装置。图 1 是某种动力系统的简化模型，图中粗实线表示固定在水平面上间距为 l 的两 条平行光滑金属导轨，电阻忽略不计，ab 和 cd 是两根与导轨垂直，长度均为 l，电阻均为 R 的金属棒，通过绝缘材料固定在列车底部，并与导轨良好接触，其间距也为 l，列车的总质 量为 m。列车启动前，ab、cd 处于磁感应强度为 B 的匀强磁场中，磁场方向垂直于导轨平 面向下，如图 1 所示，为使列车启动，需在 M、N 间连接电动势为 E 的直流电源，电源内 阻及导线电阻忽略不计，列车启动后电源自动关闭。
电磁感应动力学、能量、动量-高二物理课件(人教版2019选择性必修第二册)
考法(三) 斜面上的动力学问题
3.（多选）如图所示，平，相距L＝0.4m，导轨所在平面与水平面的夹角为30°，
其电阻不计。把完全相同的两金属棒(长度均为0.4 m)ab、cd分别垂直于导轨放置，
并使棒的两端都与导轨良好接触。已知两金属棒的质量均为m＝0.1 kg、电阻均为
R＝0.2Ω，整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度为B＝0.5
(1)金属棒运动的最大速率v；(2)金属棒在磁场中速度为V/2 时的加速度大小；(3)金属棒在磁场区域运动过程中，电阻 R上产生的焦耳热。
提能点(三) 电磁感应中的能量与动量问题
1．导体棒在磁场中做非匀变速运动的问题中，应用动量定理 可以解决牛顿运动定律不易解答的问题。
2．在相互平行的光滑水平轨道间的双导体棒做切割磁感线运动 时，由于这两根导体棒所受的安培力等大反向，若不受其他外力， 两导体棒的总动量守恒，解决此类问题应用动量守恒定律解答往 往比较便捷。
电磁感应中的动力学临界问题的分析思路
(1)解决这类问题的关键是通过受力情况和运动状态的分析，寻找过程中 的临界状态，如速度、加速度为最大值或最小值的条件。
[针对训练]
1．(2021·运城模拟)(多选)电磁轨道炮利用电流和磁场的作用使炮弹获得超高速 度，其原理示意图如图所示。两根固定于水平面内的光滑平行金属导轨间距为L， 导轨间存在垂直于导轨平面向里、磁感应强度大小为B的匀强磁场，导轨电阻不计。 炮弹可视为一质量为m、电阻为R的金属棒MN，垂直放在两导轨间处于静止状态， 并与导轨良好接触。首先将开关S接1，使电容器完全充电。然后将开关S接至2, MN达到最大速度vm后离开导轨。这个过程中( BD )
祝同学们学习愉快
电磁感应中的“单杆＋电容””模型
电磁感应中的“杆 导轨”类问题(3大模型)解题技巧
辅导23：电磁感应中的“杆＋导轨”类问题(3大模型)解题技巧电磁感应中的杆＋导轨模型的实质是不同形式的能量的转化过程，处理这类问题要从功和能的观点入手，弄清导体棒切割磁感线过程中的能量转化关系，现从力学、图像、能量三种观点出发，分角度讨论如下：类型一：单杆+电阻+导轨模型类【初建模型】【例题1】(2017·淮安模拟)如图所示，相距为L 的两条足够长的光滑平行金属导轨MN 、PQ 与水平面的夹角为θ，N 、Q 两点间接有阻值为R 的电阻。
整个装置处于磁感应强度为B 的匀强磁场中，磁场方向垂直导轨平面向下。
将质量为m 、阻值也为R 的金属杆cd 垂直放在导轨上，杆cd 由静止释放，下滑距离x 时达到最大速度。
重力加速度为g ，导轨电阻不计，杆与导轨接触良好。
求：(1)杆cd 下滑的最大加速度和最大速度； (2)上述过程中，杆上产生的热量。
【思路点拨】：【答案】：(1)g sin θ，方向沿导轨平面向下；2mgR sin θB 2L 2，方向沿导轨平面向下；(2)12mgx sin θ－m 3g 2R 2sin 2θB 4L 4【解析】：(1)设杆cd 下滑到某位置时速度为v ，则杆产生的感应电动势E ＝BLv 回路中的感应电流I ＝ER ＋R杆所受的安培力F ＝BIL根据牛顿第二定律有mg sin θ－B 2L 2v2R ＝ma当速度v ＝0时，杆的加速度最大，最大加速度a ＝g sin θ，方向沿导轨平面向下 当杆的加速度a ＝0时，速度最大，最大速度v m ＝2mgR sin θB 2L 2，方向沿导轨平面向下。
(2)杆cd 从开始运动到达到最大速度过程中，根据能量守恒定律得mgx sin θ＝Q 总＋12mv m 2又Q杆＝12Q总，所以Q杆＝12mgx sin θ－m3g2R2sin2θB4L4。
【内化模型】单杆+电阻+导轨四种题型剖析【变式】：此题若已知金属杆与导轨之间的动摩擦因数为μ。
(含答案)应用动力学和能量观点解决电磁感应中的“导轨杆”模型问题.docx
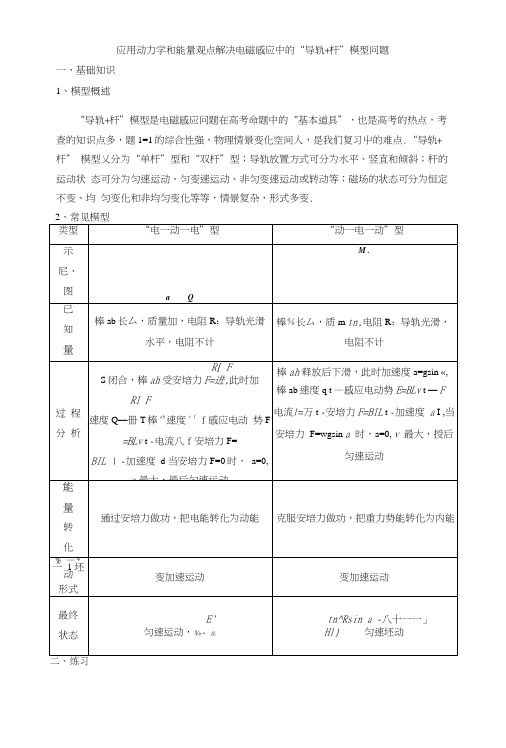
应用动力学和能量观点解决电磁感应中的“导轨+杆”模型问题一、基础知识1、模型概述“导轨+杆”模型是电磁感应问题在高考命题中的“基本道具”，也是高考的热点，考查的知识点多，题1=1的综合性强，物理情景变化空间人，是我们复习屮的难点.“导轨+杆” 模型乂分为“单杆”型和“双杆”型；导轨放置方式可分为水平、竖直和倾斜；杆的运动状态可分为匀速运动、匀变速运动、非匀变速运动或转动等；磁场的状态可分为恒定不变、均匀变化和非均匀变化等等，情景复杂，形式多变.2、常见模型二、练习解析 ⑴设卬在磁场区域"cd 内运动时间为d 乙从开始运动到〃位置的时间为/2, 则由运动学公式得1 21 八2 L =〒2gsin 〃・斤，L=㊁gsin 0・£解得旷pi 爲’/2=需£（i 分）因为“勺2,所以甲离开磁场时，乙还没有进入磁场.（1分）设乙进入磁场时的速度为可，乙屮产牛的感应电动势为E ］,回路屮的电流为厶，贝IJ 如嶄=mgLsin 0（］分）E\=BdsQ 分） Zi=Ei/2R （l 分） mgsin O=BJ {d （\ 分）解得2鬱需9分）（2）从释放金属杆开始计时，设经过时间/,甲的速度为“，甲中产牛的感应电动势为E,回路中的电流为/,外力为F,则1、如图弄示,两根足够长、电阻• * • % I•• »«^ZW«I4 I ・♦ Jtf-rr-W •- V ,I与水平面夹角为趴导轨平面内的矩形区域血cd• • • • • • ••••■• • • •• ••• ••••・M • ••••••• • •••垂首干斜面向卜•血与cd ・间相原为・令爆杆• • • • • • ■ 9■•■•••• • • • •明确电路结构，挖掘隐含梅抿荐族状杰犒牢税图6・甲、乙的阻值相同，质址均为九甲杆锂雹场区域的上边界血处，乙杆上方与甲相更［处，甲、乙两杆都与导轨垂直II 接触KI 好•由静止样放两杆的同 时，在甲杆上施加一个垂直于杆平行丁•导轨的外力F,使甲杆在冇磁场的矩形区域 内向下做匀期速直线运动，加速度大小炉2gsin0,甲离开磁场时撤去化乙杆 进人磁场后恰好做匀速运动，然后离开磁场・（1）求毎根金属杆的电E/?fl 多大?（2）从释放金居杆开始计时，求外力F 随时间t 的变化关系式，并说明F 的方向.（3）若整个过程中，乙金届杆共产生热昴Q,求外力F 对甲金届杆做的功W 是多少?⑤岀于甲、乙秀杆串联，产生的史 只有甲杆在磁场中运动的过程，刑 功和重力做功使两杆的内能和甲*• • • • • • • • • • ■ • • • • ■■■增加.甲杆离开磁场后，乙杆;切 勞能转化为两杆的内能.②说明乙杆受力平衡「应远期断i 磁场时甲杆是否离开磁场.③先分析两杆在导轨上各自运动」时间，可輛用乙杆在磁场中的匀殳析求解电阻R. ④用牛顿第二定律、法拉第电磁总X.・• • •• ..合电路知识求解.①可如甲般外为卩平行寻編卸 变力.v=at（\分）E=Bdv（\分）I=E/2R（］分）F+wgsin O~BId=nia （\ 分） <7=2gsin 6联立以上各式解得方向垂直于杆平行于导轨向下.(1分)(3)甲在磁场运动过程中，乙没冇进入磁场，设甲离开磁场时速度为％,甲、乙产生的热量相同，均设为0,则vl=2aL(\ 分)W+〃?g 厶sin 0=2Q]+苏就（2 分）解得 W=20x+mgLsmO乙在磁场运动过程中,甲、乙产生相同的热量,均设为g ，贝IJ 2@=吨厶sin 0(2分) 根据题意有0=01+0(1分) 解得"=20(1分)gsin 0(2) F=〃7gsin&+〃gsin0、^^^2(OW/W 寸瓷 命 方向垂直于杆平行于导轨向下 (3) 202、如图甲所示，足够长的光滑平行金属导轨MM P0竖直放置，其宽度厶=1 m, 一匀强 磁场垂直穿过导轨平面，导轨的上端M 与P 之间连接阻值为/?=0.40 Q 的电阻，质量 为加=0.01 kg 、电阻为厂=0.30 Q 的金属棒ah 紧贴在导轨上•现使金属林ab [Il 静止开 始下滑，下滑过程中弘始终保持水平，且与导轨接触良好，其下滑距离x 与时间/的 关系如图乙所示，图彖中的04段为曲线，M 段为直线，导轨电阻不计，g=10m/s 1 2 3(忽 略〃棒运动过程中对原磁场的影响)，求：解析(1)金属棒在段匀速运动，山题中图象乙得:1 磁感应强度B 的大小；2 金属棒ab 在开始运动的1.5 s 内，通过电阻尺的电荷量;3 金属棒〃在开始运动的1.5 s 内，电阻上产牛的热量. 答案(1)0.1 T (2)0.67 C (3)0.26 JF=wgsin 0+加gsin 0怦.gw0=石=7 m/sBLumg=BIL解得3 = 0.1 T⑵q="F △/— A01 ={R+r)\t\S△°F解得：g = 0.67 C1 2 (3)Q=〃?gx_ 尹矿解得 2=0.455 J 从而0?=专屈=0.26 J3、如图所示，足够长的光滑平行金属导轨cd 和前水平放置，在其左端连接倾角为〃=37。
电磁感应的综合应用(能量问题、动量问题、杆+导轨模型)(教师版)
电磁感应的综合应用命题点一 电磁感应中的动量和能量的应用 （一）电磁感应中的能量问题 1.求解电能应分清两类情况(1)若回路中电流恒定，可以利用电路结构及UIt W =或t 2R I Q =直接进行计算. (2)若电流变化，则①利用安培力做功求解：电磁感应中产生的电能等于克服安培力所做的功；②利用能量守恒求解：若只有电能与机械能的转化，则减少的机械能等于产生的电能. 2.电磁感应现象中的能量转化3.求解焦耳热Q 的三种方法（二）动量定理在电磁感应问题中的运用 研究对象：切割磁感线的单棒（或矩形框） 规律：动量定理、电流定义式（三）动量守恒定律在电磁感应问题中的运用研究对象：切割磁感线的双棒（等长）规律：(1)动量守恒定律(2)能量转化规律系统机械能的减小量等于内能的增加量. （类似于完全非弹性碰撞）等距双棒特点分析1．电路特点刚开始棒2相当于电源;棒1受安培力而加速起动,运动后产生反电动势.1 22．电流特点3．两棒的运动情况特点棒1做加速度减小的加速运动棒2做加速度减小的减速运动最终两棒具有共同速度（四）电磁感应中的“杆+导轨”模型常见类型单杆水平式(导轨光滑)设运动过程中某时刻棒的速度为v,加速度为a=Fm-22B L vmR,a,v同向,随v的增加,a减小,当a=0时,v最大,I=BLvR恒定单杆倾斜式(导轨光滑)杆释放后下滑,开始时a=gsin α,速度v↑→E=BLv↑→I=ER↑→F=BIL↑→a↓,当F=mgsin α时,a=0,v最大双杆切割式(导轨光滑)杆MN做变减速运动,杆PQ做变加速运动,稳定时,两杆的加速度均为零,以相等的速度匀速运动.对系统动量守恒,对其中某杆适用动量定理学科&网光滑不等距导轨杆MN做变减速运动,杆PQ做变加速运动,稳定时,两杆的加速度均为零,两杆以不同的速度做匀速运动含“源”水平光滑导轨(v0=0)S闭合,ab杆受安培力F=BLEr,此时a=BLEmr,速度v↑⇒E感=BLv↑⇒I↓⇒F=BIL↓⇒加速度a↓,当E感=E时,v最大,且v m=EBL含“容”水平光滑导轨(v0=0)拉力F恒定,开始时a=Fm,速度v↑⇒E=BLv↑,经过Δt速度为v+Δv,此时E′=BL(v+Δv),电容器增加的电荷量ΔQ=CΔU=C(E′-E)=CBLΔv,电流I=Qt∆∆=CBL vt∆∆=CBLa,安培力F安=BIL=CB2L2a,F-F安=ma,a=22Fm B L C+,所以杆做匀加速运动vvtOv注:在以上模型中,受到的外力F 可以是拉力或重力,也可以是它们的合力或分力,例如导体棒沿光滑平行倾斜导轨下滑,无重力之外的外力时,重力的下滑分力将成为合外力.电磁感应与动量结合问题高考真题1．（2018高考天津理综）真空管道超高速列车的动力系统是一种将电能直接转换成平动动能的装置。
电磁感应与动力学、能量、动量的综合应用(单轨、双轨、线框、圆盘、变磁场)(解析版) 高考物理
电磁感应与动力学、能量、动量的综合应用（单轨、双轨、线框、圆盘、变磁场）60分钟电磁感应与动力学、能量、动量的综合应用（单轨、双轨、A．线框穿出磁场I的过程中和进入磁场II的过程中，线框中产生的感应电流方向反A．通过金属棒的电流不变B．感应电流方向为顺时针方向C．A、C两点的电势始终有D．整个过程中通过金属棒的电荷量为A．若圆盘转动的角速度恒定，则电流大小恒定B．若从上往下看，圆盘顺时针转动，则电流沿C．若圆盘转动方向不变，角速度大小发生变化，则电流方向可能发生变化D．若圆盘转动的角速度变为原来的【答案】AA ．0~t 0时间内，回路中的感应电动势为200B L t B ．0~t 0时间内，施加在N 杆上的拉力F 随时间t 变化的关系为0mg F t t =×C ．重物下落的最大速度为2203mgR B L D ．从t =0时刻到重物达到最大速度的过程中，回路产生的焦耳热为32mgx -A ．重物的速度大小为24mgRB B ．导体棒ab 受到的安培力大小为C ．Oa 进出磁场一次，通过其某横截面的电荷量为D ．图示时刻，导体棒上从重物重力势能转化为回路的电能，根据能量守恒，重力的功率等于回路电功率，有解得A．线框在磁场B．线框ab边刚穿出磁场C．线框ab边在磁场D．线框ab边在磁场【答案】BCA．导体棒上a、b两点的电压为A．金属线框从刚进入左磁场区域到最终停止的过程中一直做匀减速直线运动B．金属线框通过两个磁场区域过程中产生的焦耳热为C．金属线框进入左侧磁场区域过程中，通过金属线框的电荷量为A．金属棒的速度为0v时，金属棒的加速度大小为B．金属棒能获得的最大速度为C．弹射过程中，流过金属棒的电荷量为A．0t时导体棒1的速度大小为12m/s0t:时间内，导体棒1沿导轨下滑的距离为B．0A ．金属棒刚进入磁场时的速度大小为02vB ．匀强磁场的磁感应强度大小为032mv R LA．运动过程中导体棒a、b组成的系统动量守恒B．导体棒a、b运动稳定后的速度之比为C．从开始到运动稳定的过程中，通过导体棒A ．导棒a 开始运动时的加速度大小为B ．导棒a 刚要滑离宽导轨时速度大小为C ．导棒b 最终的速度大小为019vA．导体棒和导轨之间的动摩擦因数为B．导体棒匀速运动阶段电阻R的发热功率为C．若将电阻R减小，其他保持不变，则导体棒可能以某个更大的速度匀速运动导体棒匀速运动时，回路的感应电流则电阻R的发热功率由平衡条件【答案】（1）4m/s；（2）7.6C；（3）0.4m【详解】（1）当金属棒ab所受合力为零时，棒的速度最大，对所以金属棒ab运动的最大速度v m【答案】（1）2g；（2）122B B ；（3）32244244mgx m g R B L -【详解】（1）a 刚开始运动时有最大加速度，即【答案】(1)22B L vg mR+【详解】(1)导体棒以初速度向上做减速运动，此时的安培力也是最大，故此时加速度最大，则有【答案】（1）4V ，电流由D 流向C ，电流由D 流向22rad /s w £；（3）1.5m /s【详解】（1）假设金属棒ab 静止，对金属棒CD ，由法拉第电磁感应定律有12E B =根据闭合电路欧姆定律，有E =解得。
高考物理电磁感应关于能量、电量、力学、杆、导轨等汇总分析
导体棒切割磁感线问题分类解析杨中甫电磁感应中，“导体棒”切割磁感线问题是高考常见命题。
解此类型问题的一般思路是：先解决电学问题，再解决力学问题，即先由法拉第电磁感应定律求感应电动势，然后根据欧姆定律求感应电流，求出安培力，再往后就是按力学问题的处理方法，如进行受力情况分析、运动情况分析及功能关系分析等。
导体棒切割磁感线的运动一般有以下几种情况：匀速运动、在恒力作用下的运动、恒功率运动等，现分别举例分析。
一、导体棒匀速运动导体棒匀速切割磁感线处于平衡状态，安培力和外力等大、反向，给出速度可以求外力的大小，或者给出外力求出速度，也可以求出功、功率、电流强度等，外力的功率和电功率相等。
例1. 如图1所示，在一磁感应强度B ＝0.5T 的匀强磁场中，垂直于磁场方向水平放置着两根相距为h ＝0.1m 的平行金属导轨MN 和PQ ，导轨电阻忽略不计，在两根导轨的端点N 、Q 之间连接一阻值R ＝0.3Ω的电阻。
导轨上跨放着一根长为L ＝0.2m ，每米长电阻r ＝2.0Ω/m 的金属棒ab ，金属棒与导轨正交放置，交点为c 、d ，当金属棒在水平拉力作用于以速度v ＝4.0m/s 向左做匀速运动时，试求：图1（1）电阻R 中的电流强度大小和方向；（2）使金属棒做匀速运动的拉力； （3）金属棒ab 两端点间的电势差； （4）回路中的发热功率。
解析：金属棒向左匀速运动时，等效电路如图2所示。
在闭合回路中，金属棒cd 部分相当于电源，内阻r cd ＝hr ，电动势E cd ＝Bhv 。
图2（1）根据欧姆定律，R 中的电流强度为I E R r Bhv R hrcd cd=+=+=0.4A ，方向从N 经R 到Q 。
（2）使金属棒匀速运动的外力与安培力是一对平衡力，方向向左，大小为F ＝F 安＝BIh ＝0.02N 。
（3）金属棒ab 两端的电势差等于U ac 、U cd 与U db 三者之和，由于U cd ＝E cd －Ir cd ，所以U ab ＝E ab －Ir cd ＝BLv －Ir cd ＝0.32V 。
高中物理高考物理一轮复习单元综合专题十电磁感应中的“杆_轨”模型课件新人教版201908021252
运动条件
运动情况分析
F＝B2LR2v0 合力为零，做匀速运动
F 为恒力
F>B2LR2v0
v↑⇒BLv↑⇒I↑⇒BIL↑⇒a↓⇒ a＝0，匀速运动．
F<B2LR2v0
v↓ ⇒ BLv↓ ⇒ I↓ ⇒ BIL↓ ⇒ a↓ ⇒a＝0，匀速运动
F 随时间 t 按一定线性规 要使棒做匀加速运动，由牛顿第二
律变化
①作用于 ab 的恒力(F)的功率： P＝Fv＝0.6×7.5 W＝4.5 W ②电阻(R＋r)产生焦耳热的功率： P′＝I′2(R＋r)＝1.52×(0.8＋0.2) W＝2.25 W
③逆时针方向的电流 I′，从电池的正极流入，负极流出，电 池处于“充电”状态，吸收能量，以化学能的形式储存起来．电 池吸收能量的功率：P″＝I′E＝1.5×1.5 W＝2.25 W.
单元综合专题
(十)电磁感应中的“杆—轨”模型
专题综述
电磁感应中的“杆—轨”运动模型，是导体切割磁感线运动 过程中动力学与电磁学知识的综合应用，此类问题是高考命题的 重点，主要类型有：“单杆”模型、“单杆＋电源”模型、“单杆 ＋电容”模型、“双杆”模型．
题型透析
电磁感应中的“单杆”模型 【基本模型】如图，金属导轨水平光滑，导轨间距为 L，导 体棒的质量为 m，回路总电阻为 R.导体棒在水平力 F 的作用下 运动，进入磁场时的速度为 v0，导体棒在磁场中的运动情况分析 如下：
定律：F＝ma＋B2L2（Rv0＋at）
例 1 (2018·济南模拟 )如 图所示， 光滑的
“ ”形金属导体框竖直放置，质量为 m 的金 属棒 MN 与框架接触良好．磁感应强度分别为 B1、 B2 的有界匀强磁场方向相反，但均垂直于框架平 面，分别处在 abcd 和 cdef 区域．现从图示位置由静止释放金属 棒 MN，当金属棒进入磁场 B1 区域后，恰好做匀速运动．以下 说法中不正确的有( )
电磁感应中的双杆双动导轨滑轨能量动量问题大综合
电磁感应中的双杆双动导轨滑轨能量动量问题大综合————————————————————————————————作者：————————————————————————————————日期：问题3：电磁感应中的“双杆问题”电磁感应中“双杆问题”是学科内部综合的问题，涉及到电磁感应、安培力、牛顿运动定律和动量定理、动量守恒定律及能量守恒定律等。
要求学生综合上述知识，认识题目所给的物理情景，找出物理量之间的关系，因此是较难的一类问题，也是近几年高考考察的热点。
下面对“双杆”类问题进行分类例析1.“双杆”向相反方向做匀速运动当两杆分别向相反方向运动时，相当于两个电池正向串联。
[例5] 两根相距d=0.20m的平行金属长导轨固定在同一水平面内，并处于竖直方向的匀强磁场中，磁场的磁感应强度B=0.2T，导轨上面横放着两条金属细杆，构成矩形回路，每条金属细杆的电阻为r=0.25Ω，回路中其余部分的电阻可不计。
已知两金属细杆在平行于导轨的拉力的作用下沿导轨朝相反方向匀速平移，速度大小都是v=5.0m/s，如图所示，不计导轨上的摩擦。
（1）求作用于每条金属细杆的拉力的大小。
（2）求两金属细杆在间距增加0.40m的滑动过程中共产生的热量。
解析：（1）当两金属杆都以速度v匀速滑动时，每条金属杆中产生的感应电动势分别为：E1=E2=Bdv由闭合电路的欧姆定律，回路中的电流强度大小为：因拉力与安培力平衡，作用于每根金属杆的拉力的大小为F1=F2=IBd。
由以上各式并代入数据得N（2）设两金属杆之间增加的距离为△L，则两金属杆共产生的热量为，代入数据得Q=1.28×10-2J。
2.“双杆”同向运动，但一杆加速另一杆减速当两杆分别沿相同方向运动时，相当于两个电池反向串联。
[例6] 两根足够长的固定的平行金属导轨位于同一水平面内，两导轨间的距离为L。
导轨上面横放着两根导体棒ab和cd，构成矩形回路，如图所示。
两根导体棒的质量皆为m，电阻皆为R，回路中其余部分的电阻可不计。
应用动力学和能量观点解决电磁感应中的“导轨+杆”模型问题
简单物理 2014年3月第1页光滑导轨运动过程收尾状态v=0匀速匀速无电阻时匀速匀加速应用动力学和能量观点解决电磁感应中的“导轨＋杆”模型问题RvRFtvtvCvCFtvtvvvttv Fxv1．模型概述“导轨＋杆”模型是电磁感应问题在高考命题中的“基本道具”，也是高考的热点，考查的知识点多，题目的综合性强，物理情景变化空间大，是我们复习中的难点．“导轨＋杆”模型又分为“单杆”型和“双杆”型；导轨放置方式可分为水平、竖直和倾斜；杆的运动状态可分为匀速运动、匀变速运动、非匀变速运动或转动等；磁场的状态可分为恒定不变、均匀变化和非均匀变化等等，情景复杂，形式多变．2．常见模型类型“电—动—电”型“动—电—动”型示意图已知量棒ab长L，质量m，电阻R；导轨光滑水平，电阻不计棒ab长L，质量m，电阻R；导轨光滑，电阻不计过程分析S闭合，棒ab受安培力F＝BLER，此时加速度a＝BLEmR，棒ab速度v↑→感应电动势E′＝BLv↑→电流I↓→安培力F＝BIL↓→加速度a↓，当安培力F＝0时，a＝0，v最大，最后匀速运动棒ab释放后下滑，此时加速度a＝g sin α，棒ab速度v↑→感应电动势E＝BLv↑→电流I＝ER↑→安培力F＝BIL↑→加速度a↓，当安培力F＝mg sin α时，a＝0，v最大，最后匀速运动能量转化通过安培力做功，把电能转化为动能克服安培力做功，把重力势能转化为内能运动形式变加速运动变加速运动最终状态匀速运动，v m＝E′BL匀速运动v m＝mgR sin αB2L2解析 (1)设甲在磁场区域abcd 内运动时间为t 1，乙从开始运动到ab 位置的时间为t 2， 则由运动学公式得L ＝12·2g sin θ·t 21，L ＝12g sin θ·t 22解得t 1＝ L g sin θ，t 2＝ 2Lg sin θ (1分)因为t 1<t 2，所以甲离开磁场时，乙还没有进入磁场． (1分) 设乙进入磁场时的速度为v 1，乙中产生的感应电动势为E 1，回路中的电流为I 1，则12mv 21＝mgL sin θ (1分) E 1＝Bdv 1 (1分) I 1＝E 1/2R (1分) mg sin θ＝BI 1d (1分)解得R ＝B 2d 22m 2Lg sin θ (1分)(2)从释放金属杆开始计时，设经过时间t ，甲的速度为v ，甲中产生的感应电动势为E ， 回路中的电流为I ，外力为F ，则v ＝at (1分) E ＝Bdv (1分) I ＝E /2R (1分) F ＋mg sin θ－BId ＝ma (1分) a ＝2g sin θ 联立以上各式解得 F ＝mg sin θ＋mg sin θ2g sin θL·t (0≤t ≤ Lg sin θ) (1分) 方向垂直于杆平行于导轨向下． (1分) (3)甲在磁场运动过程中，乙没有进入磁场，设甲离开磁场时速度为v 0，甲、乙产生的热 量相同，均设为Q 1，则v 20＝2aL (1分)W ＋mgL sin θ＝2Q 1＋12mv 20 (2分)解得W ＝2Q 1＋mgL sin θ乙在磁场运动过程中，甲、乙产生相同的热量，均设为Q 2，则2Q 2＝mgL sin θ(2分)根据题意有Q ＝Q 1＋Q 2 (1分) 解得W ＝2Q (1分)答案 (1)B 2d 22m 2Lg sin θ(2)F ＝mg sin θ＋mg sin θ 2g sin θL ·t (0≤t ≤ Lg sin θ)，方向垂直于杆平行于导轨向下(3)2Q突破训练3 如图7甲所示，足够长的光滑平行金属导轨MN 、PQ 竖直放置，其宽度L ＝1 m ，一匀强磁场垂直穿过导轨平面，导轨的上端M 与P 之间连接阻值为R ＝0.40 Ω的电阻，质量为m ＝0.01 kg 、电阻为r ＝0.30 Ω的金属棒ab 紧贴在导轨上．现使金属棒ab 由静止开始下滑，下滑过程中ab 始终保持水平，且与导轨接触良好，其下滑距离s 与时间t的关系如图乙所示，图象中的OA 段为曲线，AB 段为直线，导轨电阻不计，g ＝10 m/s 2(忽略ab 棒运动过程中对原磁场的影响)，求：甲 乙图7(1)磁感应强度B 的大小；(2)金属棒ab 在开始运动的1.5 s 内，通过电阻R 的电荷量； (3)金属棒ab 在开始运动的1.5 s 内，电阻R 上产生的热量． 答案 (1)0.1 T (2)0.67 C (3)0.26 J解析 (1)金属棒在AB 段匀速运动，由题中图象乙得：v ＝ΔsΔt ＝7 m/s I ＝BLv r ＋R ，mg ＝BIL 解得B ＝0.1 T (2)q ＝I Δt I ＝ΔΦR ＋r Δt ΔΦ＝ΔS Δt B解得：q ＝0.67 C(3)Q ＝mgs －12mv 2解得Q ＝0.455 J从而Q R ＝Rr ＋R Q ＝0.26 J高考题组1． (2012·山东理综·20)如图8所示，相距为L 的两条足够长的光滑平行金属导轨与水平面的夹角为θ，上端接有定值电阻R ，匀强 磁场垂直于导轨平面，磁感应强度为B .将质量为m 的导体棒由 静止释放，当速度达到v 时开始匀速运动，此时对导体棒施加 一平行于导轨向下的拉力，并保持拉力的功率恒为P ，导体棒最终以2v 的速度匀速运动．导体棒始终与导轨垂直且接触良好， 图8 不计导轨和导体棒的电阻，重力加速度为g .下列选项正确的是 ( ) A ．P ＝2mgv sin θ B ．P ＝3mgv sin θC ．当导体棒速度达到v 2时加速度大小为g2sin θD ．在速度达到2v 以后匀速运动的过程中，R 上产生的焦耳热等于拉力所做的功 答案 AC解析 根据I ＝E R ＝BLvR ，导体棒由静止释放，速度达到v 时，回路中的电流为I ，则根据共点力的平衡条件，有mg sin θ＝BIL .对导体棒施加一平行于导轨向下的拉力，使其以2v 的速度匀速运动时，则回路中的电流为2I ，则根据平衡条件，有F ＋mg sin θ＝B ·2IL ，所以拉力F ＝mg sin θ，拉力的功率P ＝F ×2v ＝2mgv sin θ，故选项A 正确，选项B 错误；当导体棒的速度达到v 2时，回路中的电流为I 2，根据牛顿第二定律，得mg sin θ－B I 2L ＝ma ，解得a ＝g2sin θ，选项C 正确；当导体棒以2v 的速度匀速运动时，根据能量守恒定律知，重力和拉力所做的功之和等于R 上产生的焦耳热，故选项D 错误．2． (2012·江苏单科·13)某兴趣小组设计了一种发电装置，如图9所示．在磁极和圆柱状铁芯之间形成的两磁场区域的圆心角α均为49π，磁场均沿半径方向．匝数为N 的矩形线圈abcd 的边长ab ＝cd ＝l 、bc ＝ad ＝2l .线圈以角速度ω绕中心轴匀速转动，bc 边和ad 边同时进入磁场．在磁场中，两条边所经过处的磁感应强度大小均为B 、方向始终与两边的运动方向垂直．线圈的总电阻为r ，外接电阻为R .求：图9(1)线圈切割磁感线时，感应电动势的大小E m ； (2)线圈切割磁感线时，bc 边所受安培力的大小F ； (3)外接电阻上电流的有效值I .答案 (1)2NBl 2ω (2)4N 2B 2l 3ωr ＋R (3)4NBl 2ω3 r ＋R解析 (1)bc 、ad 边的运动速度v ＝ωl2感应电动势E m ＝4NBlv 解得E m ＝2NBl 2ω(2)电流I m ＝E mr ＋R安培力F ＝2NBI m l解得F ＝4N 2B 2l 3ωr ＋R(3)一个周期内，通电时间t ＝49TR 上消耗的电能W ＝I 2m Rt 且W ＝I 2RT解得I ＝4NBl 2ω3 r ＋R .模拟题组3． 如图10，两根足够长光滑平行金属导轨PP ′、QQ ′倾斜放置，匀强磁场垂直于导轨平面，导轨的上端与水平放置的 两金属板M 、N 相连，板间距离足够大，板间有一带电微粒，金属棒ab 水平跨放在导轨上，下滑过程中与导轨接触良好． 图10 现同时由静止释放带电微粒和金属棒ab ，则 ( ) A ．金属棒ab 最终可能匀速下滑 B ．金属棒ab 一直加速下滑C ．金属棒ab 下滑过程中M 板电势高于N 板电势D ．带电微粒不可能先向N 板运动后向M 板运动 答案 BC解析 金属棒沿光滑导轨加速下滑，棒中有感应电动势而对金属板M 、N 充电，充电电 流通过金属棒时金属棒受安培力作用，只有金属棒速度增大时才有充电电流，因此总有 mg sin θ－BIl >0，金属棒将一直加速下滑，A 错，B 对；由右手定则可知，金属棒a 端(即 M 板)电势高，C 对；若微粒带负电，则电场力向上，与重力反向，开始时电场力为0， 微粒向下加速，当电场力增大到大于重力时，微粒的加速度向上，可能向N 板减速运动 到零后再向M 板运动，D 错．4． 如图11所示，足够长的光滑平行金属导轨cd 和ef 水平放置，在其左端连接倾角为θ＝37°的光滑金属导轨ge 、hc ，导轨间距均为L ＝1 m ，在水平导轨和倾斜导轨上，各放一根与导轨垂直的金属杆，金属杆与导轨接触良好．金属杆a 、b 质量均为m ＝0.1 kg ，电阻R a ＝2 Ω、R b ＝3 Ω，其余电阻不计．在水平导轨和斜面导轨区域分别有竖直向上和竖直向下的匀强磁场B 1、B 2，且B 1＝B 2＝0.5 T ．已知从t ＝0时刻起，杆a 在外力F 1作用下由静止开始水平向右运动，杆b 在水平向右的外力F 2作用下始终保持静止状态，且F 2＝0.75＋0.2t (N)．(sin 37°＝0.6，cos 37°＝0.8，g 取10 m/s 2)图11简单物理2014年3月第 PAGE \* MERGEFORMAT 7 页(1)通过计算判断杆a的运动情况；(2)从t＝0时刻起，求1 s内通过杆b的电荷量；(3)若t＝0时刻起，2 s内作用在杆a上的外力F1做功为13.2 J，则这段时间内杆b上产生的热量为多少？答案(1)以4 m/s2的加速度做匀加速运动(2)0.2 C(3)6 J解析(1)因为杆b静止，所以有F2－B2IL＝mg tan 37°而F2＝0.75＋0.2t(N)解得I＝0.4t (A)整个电路中的电动势由杆a运动产生，故E＝I(R a＋R b)E＝B1Lv解得v＝4t所以，杆a做加速度为a＝4 m/s2的匀加速运动．(2)杆a在1 s内运动的距离d＝ eq \f(1,2) at2＝2 mq＝ eq \x\to(I) Δteq \x\to(I) ＝ eq \f(E,R a＋R b)E＝ eq \f(ΔΦ,Δt) ＝ eq \f(B1Ld,Δt)q＝ eq \f(ΔΦ,R a＋R b) ＝ eq \f(B1Ld,R a＋R b) ＝0.2 C即1 s内通过杆b的电荷量为0.2 C(3)设整个电路中产生的热量为Q，由能量守恒定律得W1－Q＝ eq \f(1,2) mv EMBED Equation.3v1＝at＝8 m/s解得Q＝10 J从而Q b＝ eq \f(R b,R a＋R b) Q＝6 J。
高中物理选择性必修第二册教学课件《电磁感应定律的应用(能量、动量、双杆)》
02
电磁感应中的“双杆”模型
分 类 五 ： 动 量 守 恒 和 功 能 关 系 的综 合应用
1.题型简述
（1）如果相互平行的水平轨道间有双导体棒做切割磁感线运动，当这
两根导体棒所受的安培力等大反向，且不受其他外力，两导体棒的总动
量守恒，可用动量守恒定律求解导体棒的共速问题.
2.方法技巧
解决此类问题时通常将两棒视为一个整体，于是相互作用的安培力是系
(1)导体棒b中产生的内能；
(2)导体棒a、b间的最小距离.
()
() −
电磁感应中的双杆模型总结(无外力）
光滑平行等距导轨
情景图
光滑平行不等距导轨
质量m1=m2
质量m1=m2
电阻r1=r2
电阻r1=r2
长度L1=L2
长度L1=2L2
运动
分析
稳定条件
能量分析
虚线MN右侧区域存在磁感应强度为B、方向竖直向下的匀强磁场.质量均为m、
长度均为L、电阻均为R的导体棒a、b，垂直导轨放置且保持与导轨接触良好.
开始导体棒b静止于与MN相距为x0处，导体棒a以水平速度v0从MN处进入磁场.
不计导轨电阻，忽略因电流变化产生的电磁辐射，运动过程中导体棒a、b没有
发生碰撞.求：
Rr
ab棒做加速度减小
的加速运动，达到最大
速度后作匀速运动。
1 2
（3） Fx W安 = mvm 0
2
Q = W安
1 F (R r)
Q = Fx m
2 B 2 L2
F (R r)
B 2 L2 v
ma 0时 vm =
专题13 电磁感应中的单杆、双杆和导体框问题(讲义)原卷版-【高频考点解密】2024年高考物理二轮
专题13电磁感应中的单杆、双杆、导线框问题01专题网络.思维脑图 (1)02考情分析.解密高考 (2)03高频考点.以考定法 (2) (2) (5) (7)考向1：导体棒平动切割磁感应线的综合问题 (7)考向2：导体棒旋转切割磁感应线的综合问题 (8)考向3：线框进出磁场类问题的综合应用 (9)考向4：双杆在导轨上运动的综合应用 (10)04核心素养.难点突破 (11)05创新好题.轻松练 (16)新情境1：航空航天类 (16)新情境2：航洋科技类 (18)新情境3：生产生活相关类 (19)一、电磁感应中的单杆模型1．单杆模型的常见情况质量为m、电阻不计的单杆ab以一定初速度v0在光滑水平轨道上滑动，两平行导轨间距为L 轨道水平光滑，单杆ab质量为m，电阻不计，两平行导轨间距为L轨道水平光滑，单杆ab质量为m，电阻不计，两平行导轨间距为L，拉力F恒定轨道水平光滑，单杆ab质量为m，电阻不计，两平行导轨间距为L，拉力F恒定F 做的功一部分转化2．在电磁感应中，动量定理应用于单杆切割磁感线运动，可求解变力的时间、速度、位移和电荷量。
(1)求电荷量或速度：B I LΔt ＝mv 2－mv 1，q ＝I Δt 。
(2)求位移：－B 2L 2v ΔtR 总＝0－mv 0，x ＝v̅Δt 。
(3)求时间：⇒－B I LΔt ＋F 其他·Δt ＝mv 2－mv 1，即－BLq ＋F 其他·Δt ＝mv 2－mv 1 已知电荷量q ，F 其他为恒力，可求出变加速运动的时间。
⇒－B 2L 2v ΔtR 总＋F 其他·Δt ＝mv 2－mv 1，v̅Δt ＝x已知位移x ，F 其他为恒力，也可求出变加速运动的时间。
二、电磁感应中的双杆模型1．双杆模型的常见情况(1)初速度不为零，不受其他水平外力的作用质量m b＝m a；电阻r b＝r a；长度L b＝L a质量m b＝m a；电阻r b＝r a；长度L b＝2L a杆b受安培力做变减速运动，杆a受安培力能量质量m b＝m a；电阻r b＝r a；长度L b＝L a摩擦力F fb＝F fa；质量m b＝m a；电阻r b＝r a；长度L b＝L a 开始时，两杆受安培力做变加速运动；开始时，若F<F≤2F，则a杆先变加速后匀速运动；b杆F做的功转化为两杆的动能和内能：F做的功转化为两杆的动能和内能(包括电热和摩擦热)：进行解决。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
动力学、动量和能量观点在电学中的应用命题点一电磁感应中的动量和能量的应用（一）电磁感应中的能量问题1.求解电能应分清两类情况(1)若回路中电流恒定，可以利用电路结构及UIt W =或t 2R I Q =直接进行计算.(2)若电流变化，则①利用安培力做功求解：电磁感应中产生的电能等于克服安培力所做的功；②利用能量守恒求解：若只有电能与机械能的转化，则减少的机械能等于产生的电能.2.电磁感应现象中的能量转化3.求解焦耳热Q 的三种方法（二）动量定理在电磁感应问题中的运用研究对象：切割磁感线的单棒（或矩形框）规律：动量定理、电流定义式B IL t P mv mv -⋅∆=∆=-0mv mv p q BL BL-∆==tq I ∆=（三）动量守恒定律在电磁感应问题中的运用研究对象：切割磁感线的双棒（等长）规律：(1)动量守恒定律(2)能量转化规律系统机械能的减小量等于内能的增加量.（类似于完全非弹性碰撞）等距双棒特点分析1．电路特点刚开始棒2相当于电源;棒1受安培力而加速起动,运动后产生反电动势.2．电流特点3．两棒的运动情况特点棒1做加速度减小的加速运动棒2做加速度减小的减速运动最终两棒具有共同速度12v0v共tO v（四）电磁感应中的“杆+导轨”模型（1）单杆模型(光滑平行导轨)基本类型发电式充电式阻尼式图示运动过程力学分析单杆受外力F 和F 安,v ↑⇒F 安↑⇒a ↓,直至a=0,F=F 安,v恒定,单杆匀速运动,I 恒定.不计任何电阻时,单杆匀加速运动,I 恒定,ΔQ=CBL Δv,I=CBLa,F-BIL=ma.单杆只受安培力F 安,则v ↓⇒F 安↓⇒a ↓,单杆最后静止,I=0.注:在以上模型中,受到的外力F 可以是拉力或重力,也可以是它们的合力或分力,例如导体棒沿光滑平行倾斜导轨下滑,无重力之外的外力时,重力的下滑分力将成为合外力.常见类型单杆水平式(导轨光滑)设运动过程中某时刻棒的速度为v,加速度为a=Fm-22B L vmR,a,v同向,随v的增加,a减小,当a=0时,v最大,I=BLvR恒定单杆倾斜式(导轨光滑)杆释放后下滑,开始时a=gsinα,速度v↑→E=BLv↑→I=ER↑→F=BIL↑→a↓,当F=mgsinα时,a=0,v最大双杆切割式(导轨光滑)杆MN做变减速运动,杆PQ做变加速运动,稳定时,两杆的加速度均为零,以相等的速度匀速运动.对系统动量守恒,对其中某杆适用动量定理学科&网光滑不等距导轨杆MN做变减速运动,杆PQ做变加速运动,稳定时,两杆的加速度均为零,两杆以不同的速度做匀速运动含“源”水平光滑导轨(v0=0)S闭合,ab杆受安培力F=BLEr,此时a=BLEmr,速度v↑⇒E感=BLv↑⇒I↓⇒F=BIL↓⇒加速度a↓,当E感=E时,v最大,且v m=EBL含“容”水平光滑导轨(v0=0)拉力F恒定,开始时a=Fm,速度v↑⇒E=BLv↑,经过Δt速度为v+Δv,此时E′=BL(v+Δv),电容器增加的电荷量ΔQ=CΔU=C(E′-E)=CBLΔv,电流I=Qt∆∆=CBL vt∆∆=CBLa,安培力F安=BIL=CB2L2a,F-F安=ma,a=22Fm B L C+,所以杆做匀加速运动电磁感应与动量结合问题高考真题1．（2018高考天津理综）真空管道超高速列车的动力系统是一种将电能直接转换成平动动能的装置。
图1是某种动力系统的简化模型，图中粗实线表示固定在水平面上间距为l 的两条平行光滑金属导轨，电阻忽略不计，ab 和cd 是两根与导轨垂直，长度均为l ，电阻均为R 的金属棒，通过绝缘材料固定在列车底部，并与导轨良好接触，其间距也为l ，列车的总质量为m 。
列车启动前，ab 、cd 处于磁感应强度为B 的匀强磁场中，磁场方向垂直于导轨平面向下，如图1所示，为使列车启动，需在M 、N 间连接电动势为E 的直流电源，电源内阻及导线电阻忽略不计，列车启动后电源自动关闭。
（1）要使列车向右运行，启动时图1中M 、N 哪个接电源正极，并简要说明理由；（2）求刚接通电源时列车加速度a 的大小；（3）列车减速时，需在前方设置如图2所示的一系列磁感应强度为B 的匀强磁场区域，磁场宽度和相邻磁场间距均大于l 。
若某时刻列车的速度为0v ，此时ab 、cd 均在无磁场区域，试讨论：要使列车停下来，前方至少需要多少块这样的有界磁场？【解析】本题考查线框在匀强磁场中的切割磁感线运动。
（1）M 接电源正极，列车要向右运动，安培力方向应向右，根据左手定则，接通电源后，金属棒中电流方向由a 到b ，由c 到d ，故M 接电源正极。
（2启动时ab 、cd 并联，设回路总电阻为R 总，由电阻的串并联知识得2RR =总①；设回路总电阻为I ，根据闭合电路欧姆定律有E I R =总②设两根金属棒所受安培力之和为F ，有F =BIl ③根据牛顿第二定律有F =ma ④，联立①②③④式得2BEla mR=⑤（3）设列车减速时，cd 进入磁场后经t ∆时间ab 恰好进入磁场，此过程中穿过两金属棒与导轨所围回路的磁通量的变化为∆Φ，平均感应电动势为1E ，由法拉第电磁感应定律有1E t∆Φ=∆⑥，其中2Bl ∆Φ=⑦；设回路中平均电流为'I ，由闭合电路欧姆定律有1'2E I R=⑧设cd 受到的平均安培力为'F ，有''F I lB =⑨以向右为正方向，设t ∆时间内cd 受安培力冲量为I 冲，有'I F t =-∆冲⑩同理可知，回路出磁场时ab 受安培力冲量仍为上述值，设回路进出一块有界磁场区域安培力冲量为0I ，有02I I =冲⑪设列车停下来受到的总冲量为I 总，由动量定理有00I mv =-总⑫联立⑥⑦⑧⑨⑩⑪⑫式得0220=I mv R I B l总⑬讨论：若0I I 总恰好为整数，设其为n ，则需设置n 块有界磁场，若0I I 总不是整数，设0I I 总的整数部分为N ，则需设置N +1块有界磁场。
⑭．2．(10分)【加试题】（2017年4月浙江选考）间距为l 的两平行金属导轨由水平部分和倾斜部分平滑连接而成，如图所示。
倾角为θ的导轨处于大小为B 1方向垂直导轨平面向上的匀强磁场区间I 中。
水平导轨上的无磁场区间静止放置—质量为3m 的“联动双杆”（由两根长为l 的金属杆cd 和ef 用长度为L 的刚性绝缘杆连接构成），在“联动双杆”右侧存在大小为B 2、方向垂直导轨平面向上的匀强磁场区间II ，其长度大于L 。
质量为m 、长为l 的金属杆ab 从倾斜导轨上端释放，达到匀速后进入水平导轨（无能量损失），杆以与“联动双杆”发生碰撞，碰后杆ab 和cd 合在一起形成“联动三杆'。
“联动三杆”继续沿水平导轨进人磁场区间II 并从中滑出。
运动过程中，杆ab 、cd 和ef 与导轨始终接触良好，且保持与导轨垂直。
已知杆ab 、cd 和ef 电阻均为R =0.02Ω，m =0.1kg ，l =0.5m ，L =0.3m ，θ=30°，B 1=0.1T ，B 2=0.2T 。
不计摩擦阻力和导轨电阻，忽略磁场边界效应。
求（1）杆ab 在倾斜导轨上匀速运动时的速度v 0；（2）“联动三杆”进人磁场区间II 前的速度大小v 1；（3）“联动三杆”滑过磁场区间II 产生的焦耳热Q 。
【参考答案】(1)=6m/s (2)v’=1.5m/s (3)0.25J【考点】本题主要考察知识点：电磁感应与动量守恒定律综合应用【名师解析】将杆ab 在倾斜导轨上运动所受的力沿着斜面和垂直斜面正交分解，匀速运动时重力沿斜面方向的分力与安培力平衡(1)感应电动势：E=B 1lv 0电流：I=1.5E R安培力:F=B 1Il杆ab 在倾斜导轨上匀速运动,由平衡条件，F=mg sin θ联立解得：v 0==6m/s 。
（2）由动量守恒定律，m v 0=4mv解得：v=1.5m/s（3）进入B2磁场区域，设速度变化△v,根据动量定理有：B 2Il △t=-4m △v I △t=△q ，I=E/(1.5R)，E=t∆Φ∆，△Ф=B 2Ll 联立解得：△v =2226B Ll mR=-0.25m/s 。
出B2磁场后“联动三杆”的速度为：v’=v+2△v =1.5m/s+2（-0.25m/s ）=1.0m/s “联动三杆”滑过磁场区间II 产生的焦耳热Q =12×4m(v 2-v’2)=0.25J 。
3．（2018年4月浙江选考）如图所示，在竖直平面内建立xOy 坐标系，在0≤x ≤0.65m 、y ≤0.40m 范围内存在一具有理想边界，方向垂直纸面向内的匀强磁场区域。
一边长l =0.10m 、质量m =0.02kg 、电阻R =0.40Ω的匀质正方形刚性导线框abcd 处于图示位置，其中心的坐标为（0，0.65m ）。
现将线框以初速度v 0=2.0m/s 水平向右抛出，线框在进入磁场过程中速度保持不变，然后在磁场中运动，最后从磁场右边界离开磁场区域，完成运动全过程。
线框在全过程中始终处于xOy 平面内，其ab 边与x 轴保持平行，空气阻力不计。
求：（1）磁感应强度B 的大小；（2）线框在全过程中产生的焦耳热Q ；（3）在全过程中，cb 两端的电势差U cb 与线框中心位置的x 坐标的函数关系。
【解析】：本题考查线框在匀强磁场中的切割磁感线运动。
（1）线框做平抛运动，当ab 边与磁场上边界接触时，竖直方向分速度v y 20.650.402l g ⎛⎫--⎪⎝⎭=2m/s.由于水平速度与竖直速度数值相等，所以线框进入磁场区域的速度方向与水平方向成45°角。
题述线框匀速进入磁场区域，线框受力平衡，mg=BIl ，线框ad 边和cd 边切割磁感线产生的感应电动势抵消，只需考虑ab 边切割磁感线产生感应电动势，E=Blv y ，线框中电流，I=E/R ，联立解得：B =2T 。
（2）线框全部进入磁场区域后，磁通量不变，不产生感应电流，在水平方向做匀速运动，在竖直方向做加速度为g 的匀加速直线运动。
从磁场右边界离开磁场区域过程中，上下两边产生的感应电动势抵消，只需考虑左侧边切割磁感线产生的感应电动势。
由i=e/R ，e=t∆Φ∆，q=i △t ，△Ф=Bl 2，联立解得q=Bl 2/R 。
在水平方向，由动量定理，-Bil △t=m △v ，设线框出来磁场区域的水平速度为v ，方程两侧求和，注意到Σi △t =q ，Σm △v=v-v 0，得：Blq=m (v 0-v )，代入相关数据解得：v =1.5m/s根据能量守恒定律，线框在全过程中产生的焦耳热Q=mgl+12mv 02-12mv 2，代入相关数据解得：Q =0.0375J 。