《精品》2017-2019三年高考真题专题16算法初步-数学(文)分项汇编(解析版)
(25套)2019高考数学三年高考适合全国真题分项版汇总.docx

(25套)2019高考数学三年高考真题分项版汇总岂专题01集合和常用逻辑用语一三年高考(2015-2017 )数字(文)真题分项版解析(原卷版).doc幽专题02函数一三年高考(2016-2018 )数学(文)真题分项版解析(原卷版).doc凶专题03导数的几何意义与运算一三年高考(2016-2018 )数学(文)真题分项版解析(原卷版).doc回专题04导数与函数的单调性一三年高考(2016-2018 )数字(文)真题分项版解析(原卷版).doc回专题06导数与函数的零点等综合问题一三年高考(2016-2018 )数学(文)真题分项版解析(原卷版).doc 电专题07三角函数一三年高考(2016-2018 )数学(文)真题分项版解析(原卷版).doc也专题08三角"三年高考(2016-2018 )数学(文)真题分项版解析(原卷版).doc也专题09平面向量一三年高考(2016-2018)数学(文)真题分项版解析(原卷版).doc亠专题10 裁数列許比数列一三年高考(2016-2018 )数学(文)頁题分析(原卷版).doc"专题11数列通项公式与求和一三年高考(2016-2018 )数学(文)真题分项版解析(原卷版).doc电专题12不等式一三年高考(2016-2018 )数学(文)真題分项版解析(原卷版).doc场专题13直线与圍一三年高考(2016-2018)数学(文)真題分项版解析(原卷版).doc场专题14椭圆及冥相关的综合问题一三年高考(2016-2018 )数学(文)頁題分项版解析(原卷版).doc电专题15双曲线一三年高考(2016-2018 )数学(文)真題分项版解析(原卷版).doc场专题16抛物线一三年高考(2016-2018 )数学(文)真題分项版解析(原卷版).doc3专题17立休几何中线面位置关系一三年高考(2016-2018)数学(文)真題分项版解析(原卷版).doc 呵专题18立休几何中一三年高考(2016-2018 )数学(文)真题分项版解析(原卷版).doc3专题19立休几何中休积与表面积一三年高考(2016-2018)数学(文)真題分项版解析(原卷版).doc电专题20概率一三年高考(2016-2018 )数学(文)真題分项版解析(原卷版).doc岂专题21统计一三年高考(2016-2018 )数学(文)真題分项版解析(原卷版).doc岂专题22算法一三年高考(2016-2018 )数学(文)真题分项版解析(原卷版).doc岂专题23复数一三年高考(2016-2018 )数学(文)真题分项版解析(原卷版).doc岂专题24推理与证明一三年高考(2016-2018 )数学(文)真题分项版解析(原卷版).doc巴]专题25选修部分一三年高考(2016-2018 )数学(文)真題分项版解析(原卷版).doc第一章集合与常用逻辑用语[2018年咼考试题】1. [2018课标1,文1】己知集合A={A|X<2},B二{兄3-2兀>0},则A.A B二{朮<寸》B. A 8=0C. A jx|x<|jD. A B=R2. 【2018 课标II,文1】设集合A = {1,2,3}, B = {2,3,4}则 A B =A. {1,2,3,4}B. {1,2,3}C. {2,3,4}D. {1,3,4}3. [2018课标3,文1】已知集合A二{1,2,3,4}, B二{2,4,6,8},则A B中元素的个数为( )A. 1B. 2C. 3D. 44. [2018 天津,文1】设集合A = {1,2,6},B = {2,4},C = {1,2,3,4},则(A B) C(A) {2) (B) {1,2,4} (C) {1,2,4,6} (D) {1,2,3,4,6}5. [2018 北京,文1】已知 = 集合A = {x\x<-2^x>2} f则0A =(A) (-2,2)(B) (―—2) (2,+<x))(C) [-2,2](D) (YO,—2] [2, +co)6. [2018浙江,1】已知P二= {x|-l<x<l}, 2 = {0<x<2},则P\JQ =A. (—1,2)B. (0,1)C. (-1,0)D. (1,2)7. [2018 天津,文2】设xeR ,贝9 “ 2 —兀》0 ” 是x —1 1 ” 的(A)充分而不必要条件(B)必要而不充分条件(C)充要条件(D)既不充分也不必要条件8. [2018 111 东,文1】设集合M = {x||x-1| < 1}, AT = {x|x < 2},则M N =A.(-l,l)B. (-1,2)C.(0,2)D. (1,2)9. [2018山东,文5】已知命题p:F-x + lnO;命题q:若a2 </?2 JiJ a<h.下列命题为真命题的是A. /? A <7B. /? A—C.—ip A qD.-i/? A—10. 【2018北京,文13】能够说明“设G, b, c是任意实数.若a>b>c,则xb>c“是假命题的一组整数a,b,c的值依次为_______________________________ .11. (2018江苏,1】已知集合4 = {1,2}, B = {a,/+3},若A 〃 = {?则实数d的值为_________ .12.12018江苏,1】已知集合A = {1,2}, B={Q,/+3},若A B = 则实数a的值为_____________ .第二章函数[2018年高考试题】sin1. [2018课标「文8】函数——的部分图像大致为1 一COSX3. [2018浙江,5】若函数Xx)=/+ ax+b 在区间[0,4.与G 有关,且与方有关 B.与d 有关,但与方无关C.与a 无关,且与b 无关D.与d 无关,但与/?有关4.【2018北京,文5】已知函数/U) = 3r -(|)\则/(兀)(A) 是偶函数,且在R 上是增函数 (B) 是奇函数,且在R 上是增函数2.的部分图像大致为( 1]上的最大值是M,最小值是加,则Mcin Y[2018课标3,文7】函数y = l + x +巴二)(C) 是偶函数,且在R 上是减两数 (D) 是奇函数,且在R 上是增函数5.【2018北京,文8】根据有关资料,围棋状态空间复杂度的上限M 约为3⑹,而可观测 宇宙屮普通物质的原子总数"约为1O 80.则下列各数中与理■最接近的是N(参考数据:lg3=0.48)(B) IO 53 (D) 10937. 【2018天津,文6 ]已知奇函数/(x)在R 上是增函数•若Cl = -/(log 2 -),/? = /(log 2 4」),c = /(20-8),则 a,b,c 的大小关系为(A) a <h < c (B) h <a <c (C) c <b < a (D) c < a <b 8. [2018课标II,文8】函数/(x) = ln(x 2-2x-8)的单调递增区间是 A. (-co,-2) B. (-oo,-l) C. (1,-boo) D. (4,+oo)9. [2018课标1,文9】己知函数/(x) = lnx + ln(2-x),则C. 3-/U)的图像关于直线戸1对称D. y= f(x)的图像关于点(1, 0)对称10. [2018山东,文10]若函数eV(x)(e=2.71828 ,是自然对数的底数)在/(兀)的定义域上单调递增,则称函数/(X )具有M 性质,下列函数屮具有M 性质的是A. /(x) = 2~vB. /(x) = x 2C. /(x) = 3"vD. /(x) = cosx| x\ + 2^c< 111. [2018天津,文8]已知函数f(x) = \2设owR ,若关于X 的不等式X H --- , X 1 •. 兀Xf(x)>\-+a\^R 上恒成立,则d 的取值范围是(A) 1033 (C) IO 736. [2018山东,文9】设/(x) =y[x,O<X<\2(x-l),x> 1 ,若于⑷= /(a+l),则/卫丿A. 2B. 4C. 6D.A. /⑴在((),2)单调递增B. /(兀)在(0, 2)单调递减(A) [-2,21 (B) [-2A/3,2] (C) [-2,2^3] (D) [-273,2^3]12. [2018课标II,文14]已知函数/(x)是定义在R上的奇函数,当xe(-oo,0)时,/(x) = 2x3 + x2,则,/'(2) = _________ •13. 【2018北京,文门】已知兀\(), y>0f且兀+)=1,则_? +),2的取值范围是 ___________ .兀 + ] Y v 0 114. [2018课标3,文16】设函数f(x) = 9~ '则满足f(x) + f(x——)>1的兀的取值2 爲x>0, 2范围是 _________ •15 [2018山东,文14】己知人兀)是定义在R上的偶函数,且几汁4)=心・2).若当"[-3,0]时,/'(兀)=6:则./(9⑼二_.16. [2018江苏,11】已知函数f(x) = x3-2x + e x-丄,其中e是自然对数的底数.若e A/(Q -1) + /(2/)w o,则实数a的取值范围是________ .2 门1712018江苏,14】设/(兀)是定义在R且周期为1的函数,在区间[0,1)上,/(兀)=厂英中集合D = «x\x = -~ ,n G N* »,则方程f(x)-\gx = O的解的个数是_______ .n[2017, 2016, 2014 高考题】1. 【2017高考新课标1文数】若d>b>0,0vcvl,则()(A) log a c<log/?c (B) log^vlogrb (C) d<b c (D) c a>c b2. [2014高考北京文第2题】下列函数中,定义域是尺且为增函数的是( )A.y = e~xB. y = x3C. y = \nxD.y= x3. [2014高考北京文第8题】加工爆米花时,爆开月.不糊的粒数占加工总粒数的百分比称为“可食用率” •在特定条件下,可食用率卩与加工吋间/(单位:分钟)满足的函数关系p = at2^bt + c (。
2017-2019年高考真题数学(文)分项汇编_专题16 算法初步
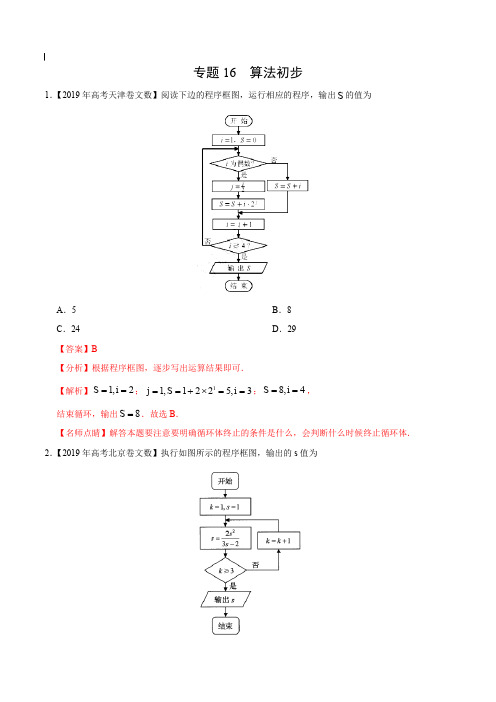
专题16 算法初步1.【2019年高考天津卷文数】阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .29【答案】B【分析】根据程序框图,逐步写出运算结果即可.【解析】1,2S i ==;11,1225,3j S i ==+⨯==;8,4S i ==,结束循环,输出8S =.故选B .【名师点睛】解答本题要注意要明确循环体终止的条件是什么,会判断什么时候终止循环体. 2.【2019年高考北京卷文数】执行如图所示的程序框图,输出的s 值为A .1B .2C .3D .4【答案】B【分析】根据程序框图中的条件逐次运算即可. 【解析】初始:1s =,1k =,运行第一次,2212312s ⨯==⨯-,2k =,运行第二次,2222322s ⨯==⨯-,3k =,运行第三次,2222322s ⨯==⨯-,结束循环,输出2s =,故选B .【名师点睛】本题考查程序框图,属于容易题,注重基础知识、基本运算能力的考查.3.【2019年高考全国Ⅰ卷文数】如图是求112122++的程序框图,图中空白框中应填入A .12A A =+ B .12A A =+C .112A A=+D .112A A=+【答案】A【分析】本题主要考查算法中的程序框图,渗透阅读、分析与解决问题等素养,认真分析式子结构特征与程序框图结构,即可找出作出选择.【解析】初始:1,122A k ==≤,因为第一次应该计算1122+=12A +,1k k =+=2; 执行第2次,22k =≤,因为第二次应该计算112122++=12A +,1k k =+=3, 结束循环,故循环体为12A A=+,故选A .【秒杀速解】认真观察计算式子的结构特点,可知循环体为12A A=+.4.【2019年高考全国Ⅲ卷文数】执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于A .4122- B .5122-C .6122-D .7122-【答案】C【分析】根据程序框图,结合循环关系进行运算,可得结果. 【解析】输入的ε为0.01,11,01,0.01?2x s x ==+=<不满足条件; 1101,0.01?24s x =++=<不满足条件;⋅⋅⋅611101,0.00781250.01?22128S x =++++==<满足条件,结束循环;输出676111112(1)22222S =+++=⨯-=-,故选C .【名师点睛】解答本题关键是利用循环运算,根据计算精确度确定数据分析.5.【2018年高考全国Ⅱ卷文数】为计算11111123499100S =-+-++-,设计了下面的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+【答案】B 【解析】由11111123499100S =-+-++-得程序框图先对奇数项累加,偶数项累加,最后再相减.因此在空白框中应填入,故选B .6.【2018年高考北京卷文数】执行如图所示的程序框图,输出的s 值为A.12B.56C.76D.712【答案】B【解析】执行循环前:k=1,S=1.在执行第一次循环时,S=1–1122=.由于k=2≤3,所以执行下一次循环.S=115236+=,k=3,直接输出S=56,故选B.7.【2018年高考天津卷文数】阅读如图的程序框图,运行相应的程序,若输入N的值为20,则输出T 的值为A.1 B.2C.3 D.4【答案】B【解析】若输入N=20,则i=2,T=0,202Ni==10是整数,满足条件.T=0+1=1,i=2+1=3,i≥5不成立,循环,203Ni=不是整数,不满足条件,i=3+1=4,i≥5不成立,循环,204Ni==5是整数,满足条件,T=1+1=2,i=4+1=5,i≥5成立,输出T=2,故选B.8.【2017年高考全国Ⅱ卷文数】执行下面的程序框图,如果输入的1a=-,则输出的S=A .2B .3C .4D .5【答案】B【解析】阅读流程图,初始化数值1,1,0a k S =-==. 循环结果执行如下:第一次:011,1,2S a k =-=-==;第二次:121,1,3S a k =-+==-=;第三次:132,1,4S a k =-=-==; 第四次:242,1,5S a k =-+==-=;第五次:253,1,6S a k =-=-==; 第六次:363,1,7S a k =-+==-=;结束循环,输出3S =.故选B.【名师点睛】算法与流程图的考查,侧重于对流程图循环结构的考查.求解时,先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,如:是求和还是求项.9.【2017年高考全国Ⅰ卷文数】下面程序框图是为了求出满足321000n n ->的最小偶数n ,A .A >1000和n =n +1B .A >1000和n =n +2C .A ≤1000和n =n +1D .A ≤1000和n =n +2【答案】D【解析】由题意,因为321000n n ->,且框图中在“否”时输出,所以判定框内不能输入1000A >,故填1000A ≤,又要求n 为偶数且初始值为0,所以矩形框内填2n n =+,故选D.【名师点睛】解决此类问题的关键是读懂程序框图,明确顺序结构、条件结构、循环结构的真正含义.本题巧妙地设置了两个空格需要填写,所以需要抓住循环的重点,偶数该如何增量,判断框内如何进行判断可以根据选项排除.10.【2017年高考全国Ⅲ卷文数】执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .2【答案】D【解析】阅读程序框图,程序运行如下:首先初始化数值:1,100,0t M S ===,然后进入循环体:此时应满足t N ≤,执行循环语句:100,10,1210MS S M M t t =+==-=-=+=; 此时应满足t N ≤,执行循环语句:90,1,1310MS S M M t t =+==-==+=; 此时满足91S <,可以跳出循环,则输入的正整数N 的最小值为2. 故选D .【名师点睛】对算法与程序框图的考查,侧重于对程序框图中循环结构的考查.先明晰算法及程序框图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环的起始条件、循环次数、循环的终止条件,更要通过循环规律,明确程序框图研究的数学问题,是求和还是求项. 11.【2017年高考北京卷文数】执行如图所示的程序框图,输出的s 值为A .2B .32 C .53D .85【答案】C【解析】0k =时,03<成立,第一次进入循环:111,21k s +===; 13<成立,第二次进入循环:2132,22k s +===; 23<成立,第三次进入循环:31523,332k s +===, 33<不成立,此时输出53s =,故选C .【名师点睛】解决此类型问题时要注意:第一,要明确是当型循环结构,还是直到型循环结构,并根据各自的特点执行循环体;第二,要明确图中的累计变量,明确每一次执行循环体前和执行循环体后,变量的值发生的变化; 第三,要明确循环体终止的条件是什么,会判断什么时候终止循环体,争取写出每一个循环,这样避免出错.12.【2017年高考天津卷文数】阅读下面的程序框图,运行相应的程序,若输入N 的值为24,则输出N 的值为A .0B .1C .2D .3【答案】C【解析】初始:24N =,进入循环后N 的值依次为8,7,6,2N N N N ====,输出2N =,故选C .【名师点睛】识别算法框图和完善算法框图是近几年高考的重点和热点.对于此类问题: ①要明确算法框图中的顺序结构、条件结构和循环结构; ②要识别运行算法框图,理解框图解决的问题;③按照框图的要求一步一步进行循环,直到跳出循环体输出结果.近几年框图问题考查很活,常把框图的考查与函数、数列等知识相结合.13.【2019年高考江苏卷】下图是一个算法流程图,则输出的S 的值是______________.【答案】5【分析】结合所给的流程图运行程序确定输出的值即可. 【解析】执行第一次,1,1422x S S x =+==≥不成立,继续循环,12x x =+=; 执行第二次,3,2422x S S x =+==≥不成立,继续循环,13x x =+=; 执行第三次,3,342xS S x =+==≥不成立,继续循环,14x x =+=;执行第四次,5,442xS S x =+==≥成立,输出 5.S =【名师点睛】识别、运行程序框图和完善程序框图的思路: (1)要明确程序框图的顺序结构、条件结构和循环结构; (2)要识别、运行程序框图,理解框图所解决的实际问题; (3)按照题目的要求完成解答并验证.14.【2018年高考江苏卷】一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为______________.【答案】8【解析】由伪代码可得3,2;5,4;7,8I S I S I S ======,因为76>,所以结束循环,输出8.S =15.【2017年高考江苏卷】如图是一个算法流程图,若输入x 的值为116,则输出y 的值是______________.【答案】2- 【解析】由题意得212log 216y =+=-,故答案为2-. 【名师点睛】算法与流程图的考查,侧重于对流程图循环结构、条件结构和伪代码的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环的初始条件、循环次数、循环的终止条件,要通过循环规律,明确流程图研究的数学问题,是求和还是求项.。
三年高考:数学(理)真题分项版解析—— 专题16 选修部分

三年高考(2019-2019)数学(理)试题分项版解析第十六章 选修部分一、选择题1. 【2019,安徽理4】以平面直角坐标系的原点为极点,x 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线l 的参数方程是13x t y t =+⎧⎨=-⎩(t 为参数),圆C 的极坐标方程是θρcos 4=,则直线l 被圆C 截得的弦长为( )A .14B .142C .2D .22 【答案】D .考点:1.极坐标方程、参数方程与平面直角方程之间的转化;2.圆中弦长的求解. 【名师点睛】对于极坐标与参数方程的问题,考生要把握好如何将极坐标方程转化成普通方程,抓住核心:222,cos ,sin x y x y ρρθρθ=+==,普通方程转化成极坐标方程,抓住核心:222,tan yx y xρθ+==.另外,求圆中弦长问题,只需要找出直角三角形(三边为半径、圆心到弦的距离、半弦)的勾股定理关系即可.2. 【2019高考北京理第3题】曲线1cos 2sin x y θθ=-+⎧⎨=+⎩,(θ为参数)的对称中心( )A .在直线2y x =上B .在直线2y x =-上C .在直线1y x =-上D .在直线1y x =+上【答案】B 【解析】试题分析:参数方程⎩⎨⎧+=+-=θθsin 2cos 1y x 所表示的曲线为圆心在)2,1(-,半径为1的圆,其对称中心为)2,1(-,逐个代入选项可知,点)2,1(-满足x y 2-=,故选B. 考点:圆的参数方程,圆的对称性,点与直线的位置关系,容易题.名师点睛:本题考查参数方程,本题属于基础题,参数方程主要考查互化问题,本题是参数方程化为普通方程,利用平方关系消去参数化为普通方程,把参数方程化为普通方程需要注意的是变量的取值范围;另一种是把普通方程化为参数方程.3. 【2019湖北卷10】已知函数)(x f 是定义在R 上的奇函数,当0≥x 时,)3|2||(|21)(222a a x a x x f --+-=,若R ∈∀x ,)()1(x f x f ≤-,则实数a 的取值范围为( )A.]61,61[-B.]66,66[-C. ]31,31[- D. ]33,33[- 【答案】B考点:函数的奇函数的性质、分段函数、最值及恒成立,难度中等.【名师点睛】将含绝对值的函数、函数的奇偶性、分段函数和不等式等内容联系在一起,凸显了知识之间的联系性、综合性,体现了函数思想、转化与化归的数学思想在函数问题中的应用,能较好的考查学生的作图能力和综合能力.其解题的关键是正确地画出分段函数的图像并通过函数图像建立不等关系.二、填空题1.【2019高考安徽,理12】在极坐标中,圆8sin ρθ=上的点到直线()3R πθρ=∈距离的最大值是 . 【答案】6【考点定位】1.极坐标方程与普通方程的转化;2.圆上的点到直线的距离.【名师点睛】对于极坐标与参数方程的问题,考生要把握好如何将极坐标方程转化成普通方程,抓住核心:222,cos ,sin x y x y ρρθρθ=+==,普通方程转化成极坐标方程,抓住核心:222,tan yx y xρθ+==.圆上的点到直线的距离最大值或最小值,要考虑到圆的半径加上(或减去)圆心到直线的距离.2. 【2019高考广东卷.理.14】 (坐标系与参数方程选做题)在极坐标系中,曲线1C 和2C 的方程分别为2sin cos ρθθ=和sin 1ρθ=,以极点为平面直角坐标系的原点,极轴为x 轴正半轴,建立平面直角坐标系,则曲线1C 和2C 交点的直角坐标为_________. 【答案】()1,1.【解析】曲线1C 的极坐标方程为()2sin cos ρθρθ=,化为普通方程得2y x =,曲线2C 的普通方程为1y =,联立曲线1C 和2C 的方程得21y x y ⎧=⎨=⎩,解得11x y =⎧⎨=⎩,因此曲线1C 和2C 交点的直角坐标为()1,1.【考点定位】本题考查极坐标与参数方程的相互转化以及曲线的交点坐标求解,属于中等题. 【名师点晴】本题主要考查的是极坐标方程化为直角坐标方程和两曲线的交点,属于中等题.解决此类问题的关键是极坐标方程转化为平面直角坐标系方程,并把几何问题代数化.3. 【2019高考广东卷.理.15】 (几何证明选讲选做题)如图3,在平行四边形ABCD 中,点E 在AB 上且AE EB 2=,AC 与DE 交于点F ,则=∆∆的面积的面积AEF CDF .图3FEDCBA【答案】9【解析】由于四边形ABCD 为平行四边形,则//AB CD ,因此CDF AEF ∆∆,由于2EB AE =,所以1133AE AB CD ==,因此3CD AE=,故2239CDF CD AEF AE ∆⎛⎫=== ⎪∆⎝⎭的面积的面积.【考点定位】本题考查相似三角形性质的应用,属于中等题.【名师点晴】本题主要考查的是相似三角形的性质定理,属于中等题.解题时一定要抓住重要字眼“面积”,否则很容易出现错误.解本题需要掌握的知识点是相似三角形的性质定理,即相似三角形面积的比、外接圆的面积比都等于相似比的平方.4. 【2019年高考北京理数】在极坐标系中,直线cos sin 10ρθθ--=与圆2cos ρθ=交于A ,B 两点,则||AB =______.【答案】2 【解析】试题分析:分别将直线方程和圆方程化为直角坐标方程:直线为10x -=过圆22(1)1x y -+=圆心,因此2AB =,故填:2.考点:极坐标方程与直角方程的互相转化.【名师点睛】将极坐标或极坐标方程转化为直角坐标或直角坐标方程,直接利用公式θρθρsin ,cos ==y x 即可.将直角坐标或直角坐标方程转化为极坐标或极坐标方程,要灵活运用x =θρθρsin ,cos ==y x 以及22y x +=ρ,)0(tan ≠=x xyθ,同时要掌握必要的技巧.5.【2019高考广东,理14】(坐标系与参数方程选做题)已知直线l 的极坐标方程为24sin(2=-)πθρ,点A 的极坐标为74A π⎛⎫ ⎪⎝⎭,则点A 到直线l 的距离为 .【答案】2. 【解析】依题直线l:2sin 4πρθ⎛⎫-= ⎪⎝⎭74A π⎛⎫ ⎪⎝⎭可化为l :10x y -+=和()2,2A -,所以点A 与直线l 的距离为2d==,故应填入2.【考点定位】极坐标方程化为普通方程,极坐标化平面直角坐标,点到直线的距离,转化与化归思想.【名师点睛】本题主要考查正弦两角差公式,极坐标方程化为普通方程,极坐标化平面直角坐标,点到直线的距离,转化与化归思想的应用和运算求解能力,属于容易题,解答此题在于准确把极坐标问题转化为平面直角坐标问题,利用平面几何点到直线的公式求解.6. 【2019高考天津理数】如图,AB 是圆的直径,弦CD 与AB 相交于点E ,BE=2AE =2,BD =ED ,则线段CE 的长为__________.考点:相交弦定理【名师点睛】1.解决与圆有关的成比例线段问题的两种思路(1)直接应用相交弦、切割线定理及其推论;(2)当比例式(等积式)中的线段分别在两个三角形中时,可转化为证明三角形相似,一般思路为“相似三角形→比例式→等积式”.在证明中有时还要借助中间比来代换,解题时应灵活把握.2.应用相交弦定理、切割线定理要抓住几个关键内容:如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等.7. 【2019高考广东,理15】(几何证明选讲选作题)如图1,已知AB 是圆O 的直径,4AB =,EC 是圆O 的切线,切点为C ,1BC =,过圆心O 做BC 的平行线,分别交EC 和AC 于点D 和点P ,则OD = .【答案】8.【解析】如下图所示,连接OC ,因为//OD BC ,又B C A C ⊥,所以OP AC ⊥,又O 为AB 线段的中点,所以1122OP BC ==,在R t O C D ∆中,122OC AB ==,由直角三角形的射影定理可得2OC OP OD =⋅即222812OC OD OP===,故应填入8.【考点定位】直线与圆的位置关系,直角三角形的射影定理.【名师点睛】本题主要考查直线与圆的位置关系,直角三角形的射影定理运用,属于中档题,解答平面几何问题关键在于认真审题分析图形中的线段关系,适当作出辅助线段,此题连接OC ,则容易得到Rt OCD ∆,并利用直角三角形的射影定理求得线段OD 的值.8. 【 2019湖南11】在平面直角坐标系中,倾斜角为4π的直线l 与曲线2cos 1sin x C y αα=+⎧⎨=+⎩:,(α为参数)交于A 、B 两点,且2AB =,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,则直线l 的极坐标方程是________. 【答案】()cos sin 1ρθθ-=【考点定位】极坐标 参数方程【名师点睛】本题主要考查了只需的极坐标方程,解决问题的关键是根据所给直线与圆几何关系求解得到直线方程,根据极坐标定义写出对应的极坐标方程即可,难度不大,属于基础题目.9. 【 2019湖南12】如图3,已知AB ,BC 是O 的两条弦,AO BC ⊥,AB =BC =O 的半径等于________.图 3【答案】32【解析】设线段AO 交BC 于点D 延长AO 交圆与另外一点E ,因为AO BC ⊥且AO 为圆半径,所以BD DC ==由三角形ABD 的勾股定理可得1AD =,由双割线定理可得2BD DC AD DE DE =⇒=,则直径332AE r =⇒=,故填32.E【考点定位】勾股定理 双割线定理【名师点睛】本题主要考查了平面几何选讲部分的勾股定理、双割线定理,解决问题的关键是根据所给几何关系运用勾股定理、双割线定理进行推理计算即可得到所求圆的半径.10. 【 2019湖南13】若关于x 的不等式23ax -<的解集为5133x x ⎧⎫-<<⎨⎬⎩⎭,则a =________.【答案】3-【解析】因为等式23ax -<的解集为5133x x ⎧⎫-<<⎨⎬⎩⎭,所以51,33-为方程23ax -=的根,即52331233a a ⎧--=⎪⎪⎨⎪-=⎪⎩3a ⇒=-,故填3-. 【考点定位】绝对值不等式 绝对值方程【名师点睛】本题主要考查了绝对值不等式,解决问题的关键是根据不等式的解集结合不等式对应的绝对值方程联立方程求解即可得到a 值,属于绝对值不等式部分的常考题目,属于基础题目.11. 【2019高考陕西版理第15题】(几何证明选做题)如图,ABC ∆中,6=BC ,以BC为直径的半圆分别交AC AB ,于点F E ,,若AE AC 2=,则EF =_______.【答案】3 【解析】试题分析:由四边形BCFE 为圆内接四边形AEF C ⇒∠=∠,AFE B ∠=∠AEF ACB ⇒∆∆⇒12AE EF AC BC ==,又因为6BC =,所以3EF =,故答案为3. 考点:几何证明;三角形相似.【名师点晴】本题主要考查的是几何证明,属于容易题.此类问题一般都综合了有关圆的相关定理,同时又考察相似三角形有关定理,但难度一般都不大,解题注意整合已知条件,严密推理. 凡是题目中涉及长度的,通常会使用到相似三角形、全等三角形、正弦定理、余弦定理等基础知识.12. 【2019高考陕西版理第15题】(坐标系与参数方程选做题)在极坐标系中,点)6,2(π到直线1)6sin(=-πθρ的距离是_______.【答案】1考点:极坐标方程;点到直线距离.【名师点晴】本题主要考查的是极坐标系与参数方程,属于容易题.此类问题一般主要是极坐标与直角坐标的互化,参数方程与普通方程的互化,解题时主要是熟记有关互化公式,有的题目会考察到其中参数实际的几何意义13. 【2019高考重庆理第14题】过圆外一点P 作圆的切线PA (A 为切点),再作割线PBC分别交圆于B 、C , 若6=PA ,AC =8,BC =9,则AB =________. 【答案】4 【解析】 试题分析:由切割线定理得:2PA PB PC =⋅,设PB x =,则||9PC x =+所以,()369,x x =+即29360x x +-=,解得:12x =-(舍去),或3x =又由是圆的切线,所以ACP BAP ∠=∠,所以ACP BAP ∆∆、||||||PA AB AC PC ∴=,所以86412AB ⨯== 所以答案应填:4.考点:1、切割线定理;2、三角形相似.【名师点睛】本题考查三角形外接圆直径的证明,相交弦定理,切割线定理,解题时要认真审题,注意圆的性质的灵活运用.14. 【2019高考重庆理第15题】已知直线l 的参数方程为⎩⎨⎧+=+=ty tx 32(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为()2sin 4cos 00,02ρθθρθπ-=≥≤<,则直线l 与曲线C 的公共点的极径=ρ________.考点:参数方程与极坐标.【名师点睛】本题考查参数方程,及坐标方程的运用,两点间的距离公式,属于基础题,正确将参数方程化为普通方程,将极坐标方程化为直角坐标方程是解决问题的关键.15. 【2019高考重庆,理14】如图,圆O 的弦AB ,CD 相交于点E ,过点A 作圆O 的切线与DC 的延长线交于点P ,若PA =6,AE =9,PC =3,CE :ED =2:1,则BE =_______.题(14)图【答案】2【解析】首先由切割线定理得2PA PC PD =⋅,因此26123PD ==,9CD PD PC =-=,又:2:1CE ED =,因此6,3CE ED ==,再相交弦定理有AE EB CE ED ⋅=⋅,所以6329CE ED BE AE ⋅⨯===. 【考点定位】相交弦定理,切割线定理.【名师点晴】平面几何问题主要涉及三角形全等,三角形相似,四点共圆,圆中的有关比例线段(相关定理)等知识,本题中有圆的切线,圆的割线,圆的相交弦,由圆的切割线定理和相交弦定理就可以得到题中有关线段的关系.16. 【2019高考重庆,理15】已知直线l 的参数方程为11x ty t=-+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立坐标系,曲线C 的极坐标方程为235cos 24(0,)44ππρθρθ=><<,则直线l 与曲线C 的交点的极坐标为_______. 【答案】(2,)π【解析】直线l 的普通方程为2y x =+,由2c o s24ρθ=得222(cos sin )4ρθθ-=,直角坐标方程为224x y -=,把2y x =+代入双曲线方程解得2x =-,因此交点.为(2,0)-,其极坐标为(2,)π.【考点定位】参数方程与普通方程的互化,极坐标方程与直角坐标方程的互化.【名师点晴】参数方程主要通过代入法或者已知恒等式(如22cos sin 1αα+=等三角恒等式)消去参数化为普通方程,通过选取相应的参数可以把普通方程化为参数方程,利用关系式cos sin x y ρθρθ=⎧⎨=⎩,222tan x y y xρθ⎧+=⎪⎨=⎪⎩等可以把极坐标方程与直角坐标方程互化,本题这类问题一般我们可以先把曲线方程化为直角坐标方程,用直角坐标方程解决相应问题.17. 【2019高考重庆,理16】若函数()12f x x x a =++-的最小值为5,则实数a =_______.【答案】4a =或6a =-【考点定位】绝对值的性质,分段函数.【名师点晴】与绝对值有关的问题,我们可以根据绝对值的定义去掉绝对值符号,把问题转化为不含绝对值的式子(函数、不等式等),本题中可利用绝对值定义把函数化为分段函数,再利用函数的单调性求得函数的最小值,令此最小值为5,求得a 的值.18.【2019高考北京理第9题】在极坐标系中,点π2,6⎛⎫⎪⎝⎭到直线ρsin θ=2的距离等于__________.【答案】1 【解析】试题分析:在极坐标系中,点π2,6⎛⎫⎪⎝⎭对应直角坐标系中坐标为,1),直线ρsin θ=2对应直角坐标系中的方程为y =2,所以点到直线的距离为1. 考点:极坐标方程与直角坐标方程的互化.【名师点睛】本题考查极坐标基础知识,要求学生使用互化公式熟练进行点的坐标转化及曲线方程的转化,然后利用点到直线距离公式求出距离,本题属于基础题,先把点的极坐标化为直角坐标,再把直线的极坐标方程化为直角坐标方程,最后求点到直线的距离.19.【2019高考北京,理11】在极坐标系中,点π23⎛⎫ ⎪⎝⎭‚到直线()cos 6ρθθ=的距离为 .【答案】1【解析】先把点(2,)3π极坐标化为直角坐标,再把直线的极坐标方程()cos 6ρθθ+=化为直角坐标方程60x +-=,利用点到直线距离公式1d ==.考点定位:本题考点为极坐标方程与直角坐标方程的互化及求点到直线距离,要求学生熟练使用极坐标与直角坐标互化公式进行点的坐标转化及曲线方程的转化,熟练使用三个距离公式,包括两点间的距离、点到直线的距离、两条平行线的距离.【名师点睛】本题考查极坐标基础知识,要求学生使用互化公式熟练进行点的坐标转化及曲线方程的转化,然后利用点到直线距离公式求出距离,本题属于基础题,先把点的极坐标化为直角坐标,再把直线的极坐标方程化为直角坐标方程,最后求点到直线的距离.20. 【2019年普通高等学校招生全国统一考试湖北卷15】(选修4-1:几何证明选讲)如图,P 为⊙O 的两条切线,切点分别为B A ,,过PA 的中点Q 作割线交⊙O 于D C ,两点,若,3,1==CD QC 则=PB .【答案】4 【解析】试题分析:由切割线定理得4)31(12=+⨯=⋅=QD QC QA ,所以2=QA ,所以4==PA PB .考点:圆的切线长定理,切割线定理,容易题.几何证明选讲一般考查圆的性质等简单的知识,主要以填空题的形式出现,难度一般较小.【名师点睛】本题考查圆的切线长定理、切割线定理,夯实基础,注重基础知识的运用,其难度虽不大,但充分体现了数学学科知识间的内在联系,能较好的考查学生对基本知识的识记能力和灵活运用能力.其解题的关键是合理地运用切割线定理.21. 【2019年普通高等学校招生全国统一考试湖北卷16】(选修4-4:坐标系与参数方程)已知曲线1C 的参数方程是⎪⎩⎪⎨⎧==33t y tx ()为参数t ,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程是2=ρ,则1C 与2C 交点的直角坐标为 . 【答案】)1,3( 【解析】试题分析:由⎪⎩⎪⎨⎧==33t y tx 消去t 得)0,0(322≥≥=y x y x ,由2=ρ得422=+y x ,解方程组⎪⎩⎪⎨⎧==+222234yx y x 得1C 与2C 的交点坐标为)1,3(. 考点:参数方程、极坐标方程与平面直角坐标方程的转化,曲线的交点,容易题.极坐标方程、参数方程与直角坐标方程互化,主要以填空题的形式出现,难度一般较小.【名师点睛】以圆的极坐标方程和直线的参数方程为载体,重点考查了极坐标与直角坐标的转化、直线与圆的位置关系等内容,渗透着化归与转化的数学思想,能较好的考查学生基础知识的识记能力、综合运用能力.22. 【2019高考湖北,理15】(选修4-1:几何证明选讲)如图,PA 是圆的切线,A 为切点,PBC 是圆的割线,且3BC PB =,则ABAC=.【答案】21 【解析】因为PA 是圆的切线,A 为切点,PBC 是圆的割线, 由切割线定理知,)(2BC PB PB PC PB PA +=⋅=,因为3BC PB =, 所以224PB PA =,即PB PA 2=, 由PAB ∆∽PCA ∆,所以21==PA PB AC AB . 【考点定位】圆的切线、割线,切割线定理,三角形相似.【名师点睛】判定两个三角形相似要注意结合图形的性质特点灵活选择判定定理.在一个题目中,相似三角形的判定定理和性质定理可能多次用到.23. 【2019高考湖北,理16】在直角坐标系xoy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系. 已知直线l 的极坐标方程为(sin 3cos )0ρθθ-=,曲线C 的参数方程为1,1x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩( t 为参数) ,l 与C 相交于A ,B 两点,则||AB = . 【答案】52【考点定位】极坐标方程、参数方程与普通方程的转化,两点间的距离.【名师点睛】化参数方程为普通方程时,未注意到普通方程与参数方程的等价性而出错.24. 【2019上海,理7】已知曲线C 的极坐标方程为1)sin 4cos 3(=-θθp ,则C 与极轴的交点到极点的距离是 . 【答案】13【解析】令0θ=,则(3cos0sin 0)1ρ-=,13ρ=,所以所求距离为13. 【考点】极坐标.【名师点睛】设M 是平面内一点,极点O 与点M 的距离|OM |叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角θ叫做点M 的极角,记为θ.有序数对(ρ,θ)叫做点M 的极坐标,记为M (ρ,θ).25.【2019高考陕西版理第15题】(不等式选做题)设R n m b a ∈,,,,且5,522=+=+nb ma b a ,则22n m +的最小值为______.【解析】试题分析:由柯西不等式得:22222()()()a b m n ma nb ++≥+,所以2225()5m n +≥,得225m n +≥≥.考点:柯西不等式.【名师点晴】本题主要考查的是柯西不等式,属于容易题,解题时关键是充分利用已知条件225,5a b ma nb +=+=,结合柯西不等式可得22222()()()a b m n ma nb ++≥+,则问题可解三、解答题1.【2019江苏,理21A 】[选修4-1:几何证明选讲]如图,AB 是圆O 的直径,CD 是圆O 上位于AB 异侧的两点,证明OCB D ∠=∠【答案】见解析.【解析】由题意,D B ∠=∠,又∵OC OB =,∴OCB B ∠=∠,∴OCB D ∠=∠. 【考点定位】圆周角定理. 【名师点晴】(1)圆周角定理圆上一条弧所对的圆周角等于它所对的圆心角的一半. (2)圆心角定理圆心角的度数等于它所对弧的度数.推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等. 推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.2. 【2019江苏,理21B 】[选修4-2:矩阵与变换]已知矩阵1211,121A B x -⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦,向量2a y ⎡⎤=⎢⎥⎣⎦,,x y 是实数,若Aa Ba =,求x y +的值. 【答案】72. ABDCO【解析】由题意得22224y y xy y -+=+⎧⎨+=-⎩,解得124x y ⎧=-⎪⎨⎪=⎩.∴72x y +=.【考点定位】矩阵的运算.【名师点晴】求特征值和特征向量的方法 (1)矩阵a b c d ⎡⎤A =⎢⎥⎣⎦的特征值λ满足()0()()0abf a d bc cd λλλλλ--==⇒---=--,属于λ的特征向量x y α⎡⎤=⎢⎥⎣⎦满足x x A y y λ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦. (2)求特征向量和特征值的步骤: ①解()0abfcdλλλ--==--得特征值;②解()0()0a x by cx d y λλ--=⎧⎨-+-=⎩,取x =1或y =1,写出相应的向量.7. 【2019江苏,理21C 】[选修4-4:坐标系与参数方程]在平面直角坐标系xoy 中,已知直线l的参数方程1222x ty t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数),直线l 与抛物线24y x =相交于AB 两点,求线段AB 的长【答案】【解析】直线l 的普通方程为1(2)0x y -+-=,即3y x =-,与抛物线方程联立方程组解得111,2,x y =⎧⎨=⎩229,6x y =⎧⎨=-⎩,∴AB ==. 【考点定位】直线的参数方程.【名师点晴】1.运用互化公式:222,sin ,cos x y y x ρρθρθ=+==将极坐标化为直角坐标;2.直角坐标方程与极坐标方程的互化,关键要掌握好互化公式,研究极坐标系下图形的性质,可转化直角坐标系的情境进行.3. 【2019江苏,理21D 】[选修4-5:不等式选讲]已知0,0x y >>,证明22(1)(1)9x y x y xy ++++≥ 【答案】见解析.【解析】∵0,0x y >>,∴21x y ++≥21x y ++≥∴22(1)(1)9x y x y xy ++++≥=. 【考点定位】算术平均值-几何平均不等式. 【名师点晴】两个常用基本不等式(1)柯西不等式:设a 1,a 2,…,a n ,b 1,b 2,…,b n 为实数,则(a 21+a 22+…+a 2n )(b 21+b 22+…+b 2n )≥(a 1b 1+a 2b 2+…+a n b n )2,当且仅当b i =0或存在一个数k ,使a i =kb i (i =1,2,…,n )时,等号成立.(2)平均值不等式:如果a 1,a 2,…,a n 为n 个正数,则a 1+a 2+…+a n n ≥n a 1a 2…a n ,当且仅当a 1=a 2=…=a n时,等号成立.4. 【2019江苏,理23】已知函数0sin ()(0)xf x x x=>,设()n f x 为1()n f x -的导数,*n N ∈ (1)求122()()222f f πππ+的值;(2)证明:对任意*n N ∈,等式1()()4442n n nf f πππ-+=都成立. 【答案】(1)1-;(2)证明见解析.【解析】(1)由已知102sin cos sin ()'()()'x x x f x f x x x x===-, 21223cos sin sin 2cos 2sin ()'()()'x x x x xf x f x x x x x x==-=--+, 所以124()2f ππ=-,23216()2f πππ=-+,故122()()222f f πππ+1=-.(2)由(1)得01()()cos sin()2f x xf x x x π+==+,两边求导可得122()()cos()sin sin()2f x xf x x x x ππ+=+=-=+,类似可得2333()()sin()2f x xf x x π+=+, 下面我们用数学归纳法证明1()()sin()2n n n nf x xf x x π-+=+对一切*n N ∈都成立,【考点定位】复合函数的导数,数学归纳法.【名师点晴】用数学归纳法证明一个与正整数有关的命题时,其步骤为: ①归纳奠基:证明当取第一个自然数0n 时命题成立;②归纳递推:假设n k =,(k N *∈,0k n ≥)时,命题成立,证明当1n k =+时,命题成立; ③由①②得出结论.5. 【2019江苏高考,21】A (选修4—1:几何证明选讲)如图,在ABC ∆中,AC AB =,ABC ∆的外接圆圆O 的弦AE 交BC 于点D求证:ABD ∆∽AEB ∆【答案】详见解析 【解析】试题分析:利用等弦对等角,同弧对等角,得到ABD E ∠=∠,又公共角BAE ∠,所以两三角形相似试题解析:因为C AB =A ,所以D C ∠AB =∠. 又因为C ∠=∠E ,所以D ∠AB =∠E , 又∠BAE 为公共角,可知D ∆AB ∽∆AEB . 【考点定位】相似三角形【名师点晴】1.判定两个三角形相似的常规思路(1)先找两对对应角相等;(2)若只能找到一对对应角相等,则判断相等的角的两夹边是否对应成比例;(3)若找不到角相等,就判断三边是否对应成比例,否则考虑平行线分线段成比例定理及相似三角形的“传递性”. 2.借助图形判断三角形相似的方法(1)有平行线的可围绕平行线找相似;(2)有公共角或相等角的可围绕角做文章,再找其他相等的角或对应边成比例;(3)有公共边的可将图形旋转,观察其特征,找出相等的角或成比例的对应边. B (选修4—2:矩阵与变换)已知R y x ∈,,向量⎥⎦⎤⎢⎣⎡-=11α是矩阵⎢⎣⎡⎥⎦⎤=01y x A 的属性特征值2-的一个特征向量,矩阵A 以及它的另一个特征值.【答案】1120-⎡⎤A =⎢⎥⎣⎦,另一个特征值为1. 【解析】试题分析:由矩阵特征值与特征向量可列出关于x,y 的方程组,再根据特征多项式求出矩阵另一个特征值A(第21——A 题)试题解析:由已知,得2ααA =-,即1112012x x y y --⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦, 则122x y -=-⎧⎨=⎩,即12x y =-⎧⎨=⎩,所以矩阵1120-⎡⎤A =⎢⎥⎣⎦. 从而矩阵A 的特征多项式()()()21fλλλ=+-,所以矩阵A 的另一个特征值为1.【考点定位】矩阵运算,特征值与特征向量 【名师点晴】求特征值和特征向量的方法 (1)矩阵a b c d ⎡⎤A =⎢⎥⎣⎦的特征值λ满足()0()()0abf a d bc cd λλλλλ--==⇒---=--,属于λ的特征向量x y α⎡⎤=⎢⎥⎣⎦满足x x A y y λ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦. (2)求特征向量和特征值的步骤: ①解()0abfcdλλλ--==--得特征值;②解()0()0a x by cx d y λλ--=⎧⎨-+-=⎩,取x =1或y =1,写出相应的向量.C (选修4—4:坐标系与参数方程)已知圆C 的极坐标方程为2sin()404πρθ+--=,求圆C 的半径.【解析】试题分析:先根据222,sin ,cos x y y x ρρθρθ=+==将圆C 的极坐标方程化成直角坐标方程,再根据圆的标准方程得到其半径.试题解析:以极坐标系的极点为平面直角坐标系的原点O ,以极轴为x 轴的正半轴,建立直角坐标系x y O .圆C 的极坐标方程为240ρθθ⎫+-=⎪⎪⎝⎭,化简,得22sin 2cos 40ρρθρθ+--=.则圆C 的直角坐标方程为222240x y x y +-+-=,即()()22116x y -++=,所以圆C . 【考点定位】圆的极坐标方程,极坐标与之间坐标互化【名师点晴】1.运用互化公式:222,sin ,cos x y y x ρρθρθ=+==将极坐标化为直角坐标;2.直角坐标方程与极坐标方程的互化,关键要掌握好互化公式,研究极坐标系下图形的性质,可转化直角坐标系的情境进行. D (选修4—5:不等式选讲) 解不等式|23|3x x ++≥【答案】153x x x ⎧⎫≤-≥-⎨⎬⎩⎭或【考点定位】含绝对值不等式的解法【名师点晴】①利用绝对值不等式的几何意义求解,体现了数形结合的思想; ②利用“零点分段法”求解,体现了分类讨论的思想;③通过构造函数,利用函数的图象求解,体现了函数与方程的思想.6. 【2019高考陕西,理22】(本小题满分10分)选修4-1:几何证明选讲如图,AB 切O 于点B ,直线D A 交O 于D ,E 两点,C D B ⊥E ,垂足为C .(I )证明:C D D ∠B =∠BA ;(II )若D 3DC A =,C B =O 的直径.【答案】(I )证明见解析;(II )3. 【解析】故D D 3E =AE -A =,即圆O 的直径为3.考点:1、直径所对的圆周角;2、弦切角定理;3、切割线定理.【名师点晴】本题主要考查的是直径所对的圆周角、弦切角定理和切割线定理,属于容易题.解题时一定要注意灵活运用圆的性质,否则很容易出现错误.凡是题目中涉及长度的,通常会使用到相似三角形、全等三角形、正弦定理、余弦定理等基础知识.7. 【2019高考陕西,理23】选修4-4:坐标系与参数方程在直角坐标系x y O 中,直线l的参数方程为1322x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数).以原点为极点,x 轴正半轴为极轴建立极坐标系,C的极坐标方程为ρθ=.(I )写出C 的直角坐标方程;(II )P 为直线l 上一动点,当P 到圆心C 的距离最小时,求P 的直角坐标.【答案】(I )(223x y +-=;(II )()3,0.【解析】试题分析:(I )先将ρθ=两边同乘以ρ可得2s i nρθ=,再利用222x y ρ=+,sin x ρθ=可得C 的直角坐标方程;(II )先设P 的坐标,则C P =,再利用二次函数的性质可得C P 的最小值,进而可得P 的直角坐标.试题解析:(I )由ρθ=,得2sin ρθ=,从而有22+x y =,所以(22+3x y -=.(II)设1(32P +,又,则|PC |== 故当0t =时,C P 取最小值,此时P 点的直角坐标为()3,0.考点:1、极坐标方程化为直角坐标方程;2、参数的几何意义;3、二次函数的性质. 【名师点晴】本题主要考查的是极坐标方程化为直角坐标方程、参数的几何意义和二次函数的性质,属于容易题.解决此类问题的关键是极坐标方程或参数方程转化为平面直角坐标系方程,并把几何问题代数化.8. 【2019高考陕西,理24】(本小题满分10分)选修4-5:不等式选讲已知关于x 的不等式x a b +<的解集为{}24x x <<. (I )求实数a ,b 的值;(II + 【答案】(I )3a =-,1b =;(II )4. 【解析】试题分析:(I )先由x a b +<可得b a x b a --<<-,再利用关于x 的不等式x a b +<的解集为{}24x x <<可得a ,b 的值;(II ,试题解析:(I )由||x a b +<,得b a x b a --<<-。
2017-2019年高考真题数学(文)分项汇编_专题10 解三角形

专题10 解三角形1.【2019年高考全国Ⅰ卷文数】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a sin A −b sin B =4c sin C ,cos A =14-,则b c= A .6 B .5 C .4D .3【答案】A【解析】由已知及正弦定理可得2224a b c -=,由余弦定理推论可得2222214131cos ,,,422424b c a c c c A bc bc b +---==∴=-∴=3462b c ∴=⨯=,故选A . 【名师点睛】本题考查正弦定理及余弦定理推论的应用.先利用余弦定理推论得出a ,b ,c 关系,再结合正弦定理边角互换列出方程,解出结果.2.【2019年高考北京卷文数】如图,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,APB ∠是锐角,大小为β.图中阴影区域的面积的最大值为A .4β+4cos βB .4β+4sin βC .2β+2cos βD .2β+2sin β【答案】B【解析】设圆心为O ,如图1,连接OA ,OB ,AB ,OP ,则22AOB APB ∠=∠=β,所以22242OABS ⨯==扇形ββ,因为ABP AOB OAB S S S S =+-△△阴影扇形,且AOB OAB S S △扇形,都已确定, 所以当ABP S △最大时,阴影部分面积最大.观察图象可知,当P 为弧AB 的中点时(如图2),阴影部分的面积S 取最大值,此时∠BOP =∠AOP =π−β,面积S 的最大值为ABP AOB OAB S S S S =+-△△阴影扇形=4β+S △POB + S △POA =4β+12|OP ||OB |sin (π−β)+12|OP ||OA |sin (π−β)=4β+2sin β+2sin β=4β+4 sin β,故选B. 【名师点睛】本题主要考查阅读理解能力、数学应用意识、数形结合思想及数学式子变形和运算求解能力,有一定的难度.关键是观察分析区域面积最大时的状态,并将面积用边角等表示.3.【2018年高考全国Ⅲ文数】ABC △的内角A ,B ,C 的对边分别为a ,b ,c .若ABC △的面积为2224a b c +-,则C =A .2πB .3π C .4πD .6π【答案】C【解析】由题可知2221sin 24ABCa b c S ab C +-==△,所以2222sinC a b c ab +-=, 由余弦定理2222cos a b c ab C +-=,得sin cos C C =,因为()0,πC ∈,所以π4C =, 故选C.【名师点睛】本题主要考查余弦定理与三角形的面积公式在解三角形中的应用,考查考生的运算求解能力,考查的核心素养是数学运算.解三角形的题型一般有两类:一是边角关系的转化,考生需对所给的边角关系进行恒等变形;二是有几何背景的题型,难点在于涉及两个或两个以上的三角形,解决此类问题可利用正、余弦定理进行求解,同时要重视三角函数的知识在解三角形中的运用.4.【2018年高考全国Ⅱ文数】在ABC △中,cos2C =,1BC =,5AC =,则AB =A . BCD .【答案】A【解析】因为cos2C =cos C =22cos 2C −1=2×2−1=35-.于是,在△ABC 中,由余弦定理得AB 2=AC 2+BC 2−2AC ×BC ×cos C =52+12−2×5×1×(35-)=32,所以AB =故选A.【名师点睛】本题主要考查二倍角公式、余弦定理,考查考生的运算求解力,考查的数学核心素养是数学运算.解三角形是近几年高考中的高频者点,将解三角形与其他知识巧妙地融合在一起,既体现了试题设计的亮点,又体现了对所学知识的交汇考查.5.【2017年高考全国Ⅰ文数】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知sin sin (sin cos )0B A C C +-=,a =2,c ,则C =A .π12B .π6 C .π4D .π3【答案】B【解析】由题意sin()sin (sin cos )0A C A C C ++-=得sin cos cos sin sin sin sin cos 0A C A C A C A C ++-=,即πsin (sin cos )sin()04C A A C A +=+=,所以3π4A =.由正弦定理sin sin a c A C =得23πsin sin 4C =,即1sin 2C =, 因为c <a ,所以C<A , 所以π6C =,故选B . 【名师点睛】在解有关三角形的题目时,要有意识地考虑用哪个定理更合适,或是两个定理都要用,要抓住能够利用某个定理的信息.一般地,如果式子中含有角的余弦或边的二次式时,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.6.【2019年高考全国Ⅱ卷文数】ABC △的内角A ,B ,C 的对边分别为a ,b ,c .已知b sin A +a cos B =0,则B =___________. 【答案】3π4【解析】由正弦定理,得sin sin sin cos 0B A A B +=.(0,),(0,)A B ∈π∈π,sin 0,A ∴≠∴sin cos 0B B +=,即tan 1B =-,3.4B π∴=【名师点睛】本题考查利用正弦定理转化三角恒等式,渗透了逻辑推理和数学运算素养.采取定理法,利用转化与化归思想解题.本题容易忽视三角形内角的范围致误,三角形内角均在(0,π)范围内,化边为角,结合三角函数的恒等变化求角.7.【2019年高考浙江卷】在ABC △中,90ABC ∠=︒,4AB =,3BC =,点D 在线段AC 上,若45BDC ∠=︒,则BD =___________,cos ABD ∠=___________.【解析】如图,在ABD △中,由正弦定理有:sin sin AB BD ADB BAC =∠∠,而3π4,4AB ADB =∠=,5AC ,34sin ,cos 55BC AB BAC BAC AC AC ∠==∠==,所以BD =ππcos cos()cos cos sin sin 4410ABD BDC BAC BAC BAC ∠=∠-∠=∠+∠=.【名师点睛】本题主要考查解三角形问题,即正弦定理、三角恒等变换、数形结合思想及函数方程思想.在ABD △中应用正弦定理,建立方程,进而得解.解答解三角形问题,要注意充分利用图形特征.8.【2018年高考北京卷文数】若ABC △)222a c b +-,且∠C 为钝角,则∠B =_________;ca的取值范围是_________.【答案】60︒,()2,+∞【解析】)2221sin 2ABC S a c b ac B =+-=△,2222a c b ac +-∴=,即cos B =,sin πcos 3B B B ∴=∠=,则2π1sin cos sin sin 1132sin sin sin tan 2A A Ac C a A A A A ⎛⎫⎛⎫---⋅ ⎪ ⎪⎝⎭⎝⎭====+, C ∠为钝角,ππ,036B A ∠=∴<∠<,)1tan ,tan A A ⎛∴∈∈+∞ ⎝⎭,故()2,ca∈+∞.故答案为60︒,()2,+∞.【名师点睛】此题考查解三角形的综合应用,能够根据题干给出的信息选用合适的余弦定理公式是解题的第一个关键;根据三角形内角πA B C ++=的隐含条件,结合诱导公式及正弦定理,将问题转化为求解含A ∠的表达式的最值问题是解题的第二个关键.9.【2018年高考浙江卷】在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c.若a =b =2,A =60°,则sin B =___________,c =___________.,3 【解析】由正弦定理得sin sin a A b B =,所以πsin sin ,37B == 由余弦定理得22222cos ,742,3a b c bc A c c c =+-∴=+-∴=(负值舍去).【名师点睛】解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化为边和角之间的关系,从而达到解决问题的目的.解答本题时,根据正弦定理得sin B ,根据余弦定理解出c .10.【2018年高考全国Ⅰ文数】ABC △的内角A B C ,,的对边分别为a b c ,,,已知sin sin 4sin sin b C c B a B C +=,2228b c a +-=,则△ABC 的面积为________.【解析】根据题意,由sin sin 4sin sin b C c B a B C +=,结合正弦定理可得sin sin sin sin B C C B +4sin sin sin A B C =,即1sin 2A =,由2228b c a +-=,结合余弦定理可得2cos 8bc A =,所以A 为锐角,且cos A =,从而求得3bc =,所以ABC △的面积为111sin 22323S bc A ==⨯=,. 【名师点睛】本题主要考查正、余弦定理的应用与三角形的面积公式,考查考生的化归与转化能力、运算求解能力,考查的数学核心素养是数学运算.解答本题时,利用正弦定理,通过sin sin b C c B +=4sin sin a B C ,可以求出1sin 2A =,再利用余弦定理求出bc =,然后利用三角形的面积公式求解即可.11.【2018年高考江苏卷】在ABC △中,角,,A B C 所对的边分别为,,a b c ,120ABC ∠=︒,ABC ∠的平分线交AC 于点D ,且1BD =,则4a c +的最小值为 ▲ . 【答案】9【解析】由题意可知,ABC ABD BCD S S S =+△△△,由角平分线的性质和三角形的面积公式得111sin1201sin 601sin 60222ac a c ︒=⨯⨯︒+⨯⨯︒,化简得ac a c =+,即111a c+=,因此1144(4)()559c a a c a c a c a c +=++=++≥+=,当且仅当23c a ==时取等号,则4a c +的最小值为9.【名师点睛】本题主要考查三角形的面积公式、基本不等式,考查分析问题、解决问题的能力,考查的核心素养是数学运算.应用基本不等式求解最值时,要注意对条件“一正、二定、三相等”进行检验,尤其是等号成立的条件.12.【2017年高考全国Ⅱ卷文数】ABC △的内角,,A B C 的对边分别为,,a b c ,若2cos cos cos b B a C c A =+,则B =.【答案】π3【解析】由正弦定理可得1π2sin cos sin cos sin cos sin()sin cos 23B B AC C A A C B B B =+=+=⇒=⇒=. 故答案为π3. 【名师点睛】解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向. 第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化. 第三步:求结果.13.【2017年高考全国Ⅲ卷文数】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知C =60°,b,c =3,则A =_________. 【答案】75°【解析】由正弦定理sin sin b c B C=,得sin 2sin 32b C Bc ===,结合b c <可得45B =,则18075A B C =--=.【名师点睛】解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理,结合已知条件灵活转化为边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向. 第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化. 第三步:求结果.14.【2017年高考浙江卷】已知△ABC ,AB =AC =4,BC =2. 点D 为AB 延长线上一点,BD =2,连结CD ,则△BDC 的面积是______,cos ∠BDC =_______.【答案】,24【解析】取BC 中点E ,由题意:AE BC ⊥,△ABE 中,1cos 4BE ABC AB ∠==,∴1cos ,sin 4DBC DBC ∠=-∠==∴1sin 22△BCD S BD BC DBC =⨯⨯⨯∠=. ∵2ABC BDC ∠=∠,∴21cos cos 22cos 14ABC BDC BDC ∠=∠=∠-=,解得cos 4BDC ∠=或cos 4BDC ∠=-(舍去).综上可得,△BCD ,cos BDC ∠=. 【名师点睛】利用正、余弦定理解决实际问题的一般思路:(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可以利用正弦定理或余弦定理求解;(2)实际问题经抽象概括后,已知量与未知量涉及两个或两个以上三角形,这时需作出这些三角形,先解够条件的三角形,再逐步解其他三角形,有时需要设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要的解.15.【2019年高考全国Ⅲ卷文数】ABC △的内角A 、B 、C 的对边分别为a 、b 、c .已知sin sin 2A Ca b A +=.(1)求B ;(2)若△ABC 为锐角三角形,且c =1,求△ABC 面积的取值范围.【答案】(1)B =60°;(2)()82. 【解析】(1)由题设及正弦定理得sin sinsin sin 2A CA B A +=. 因为sin A ≠0,所以sinsin 2A CB +=. 由180A BC ︒++=,可得sincos 22A C B +=,故cos 2sin cos 222B B B=. 因为cos02B ≠,故1sin 22B =,因此B =60°.(2)由题设及(1)知△ABC的面积4ABC S a =△. 由正弦定理得()sin 120sin 1sin sin 2tan 2C c A a C C C ︒-===+.由于△ABC 为锐角三角形,故0°<A <90°,0°<C <90°,由(1)知A +C =120°,所以30°<C <90°,故122a <<,ABC S <<△. 因此,△ABC面积的取值范围是82⎛⎝⎭. 【名师点睛】这道题考查了三角函数的基础知识,以及正弦定理的使用(此题也可以用余弦定理求解),最后考查V ABC 是锐角三角形这个条件的利用,考查的很全面,是一道很好的考题. 16.【2019年高考北京卷文数】在△ABC 中,a =3,–2b c =,cos B =12-. (1)求b ,c 的值; (2)求sin (B +C )的值. 【答案】(1)7b =,5c =;(2)14. 【解析】(1)由余弦定理2222cos b a c ac B =+-,得2221323()2b c c =+-⨯⨯⨯-.因为2b c =+,所以2221(2)323()2c c c +=+-⨯⨯⨯-. 解得5c =. 所以7b =. (2)由1cos 2B =-得sin 2B =.由正弦定理得sin sin 14a A Bb ==. 在ABC △中,B C A +=π-.所以sin()sin 14B C A +==. 【名师点睛】本题主要考查余弦定理、正弦定理的应用,两角差的正弦公式的应用等知识,意在考查学生的转化能力和计算求解能力.17.【2019年高考天津卷文数】在ABC △中,内角,,A B C 所对的边分别为,,a b c .已知2b c a +=,3sin 4sin c B a C =.(1)求cos B 的值; (2)求sin 26πB ⎛⎫+⎪⎝⎭的值. 【答案】(1)14-;(2)【解析】(1)在ABC △中,由正弦定理sin sin b cB C=,得sin sin b C c B =, 又由3sin 4sin c B a C =,得3sin 4sin b C a C =,即34b a =.又因为2b c a +=,得到43b a =,23c a =. 由余弦定理可得222222416199cos 22423a a a a cb B ac a a +-+-===-⋅⋅. (2)由(1)可得sin 4B ==,从而sin 22sin cos 8B B B ==-,227cos 2cos sin 8B B B =-=-,故717sin 2sin 2cos cos 2sin 666828216B B B πππ⎛⎫+=+=--⨯=-⎪⎝⎭. 【名师点睛】本小题主要考查同角三角函数的基本关系,两角和的正弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识.考查运算求解能力.18.【2019年高考江苏卷】在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .(1)若a =3c ,b,cos B =23,求c 的值; (2)若sin cos 2A B a b =,求sin()2B π+的值.【答案】(1)3c =;(2)5.【解析】(1)因为23,3a cb B ===,由余弦定理222cos 2a c b B ac +-=,得2222(3)323c c c c+-=⨯⨯,即213c =.所以3c =. (2)因为sin cos 2A Ba b =, 由正弦定理sin sin a b A B =,得cos sin 2B Bb b=,所以cos 2sin B B =. 从而22cos (2sin )B B =,即()22cos 41cos B B =-,故24cos 5B =.因为sin 0B >,所以cos 2sin 0B B =>,从而cos B =.因此πsin cos 25B B ⎛⎫+== ⎪⎝⎭【名师点睛】本小题主要考查正弦定理、余弦定理、同角三角函数关系、诱导公式等基础知识,考查运算求解能力.19.【2019年高考江苏卷】如图,一个湖的边界是圆心为O 的圆,湖的一侧有一条直线型公路l ,湖上有桥AB (AB 是圆O 的直径).规划在公路l 上选两个点P 、Q ,并修建两段直线型道路PB 、QA .规划要求:线段PB 、QA 上的所有点到点O 的距离均不小于圆....O 的半径.已知点A 、B 到直线l 的距离分别为AC 和BD (C 、D 为垂足),测得AB =10,AC =6,BD =12(单位:百米). (1)若道路PB 与桥AB 垂直,求道路PB 的长;(2)在规划要求下,P 和Q 中能否有一个点选在D 处?并说明理由;(3)在规划要求下,若道路PB 和QA 的长度均为d (单位:百米).求当d 最小时,P 、Q 两点间的距离.【答案】(1)15(百米);(2)见解析;(3)17+. 【解析】解法一:(1)过A 作AE BD ⊥,垂足为E .由已知条件得,四边形ACDE 为矩形,6, 8DE BE AC AE CD =====.' 因为PB ⊥AB ,所以84cos sin 105PBD ABE ∠=∠==. 所以12154cos 5BD PB PBD ===∠. 因此道路PB 的长为15(百米).(2)①若P 在D 处,由(1)可得E 在圆上,则线段BE 上的点(除B ,E )到点O 的距离均小于圆O 的半径,所以P 选在D 处不满足规划要求.②若Q 在D 处,连结AD ,由(1)知10AD ==,从而2227cos 0225AD AB BD BAD AD AB +-∠==>⋅,所以∠BAD 为锐角.所以线段AD 上存在点到点O 的距离小于圆O 的半径. 因此,Q 选在D 处也不满足规划要求. 综上,P 和Q 均不能选在D 处. (3)先讨论点P 的位置.当∠OBP <90°时,线段PB 上存在点到点O 的距离小于圆O 的半径,点P 不符合规划要求;当∠OBP ≥90°时,对线段PB 上任意一点F ,OF ≥OB ,即线段PB 上所有点到点O 的距离均不小于圆O 的半径,点P 符合规划要求.设1P 为l 上一点,且1PB AB ⊥,由(1)知,1P B =15, 此时11113sin cos 1595PD PB PBD PB EBA =∠=∠=⨯=;当∠OBP >90°时,在1PPB △中,115PB PB >=. 由上可知,d ≥15. 再讨论点Q 的位置.由(2)知,要使得QA ≥15,点Q 只有位于点C 的右侧,才能符合规划要求.当QA =15时,1CQ =此时,线段QA 上所有点到点O 的距离均不小于圆O 的半径.综上,当PB ⊥AB ,点Q 位于点C 右侧,且CQ =时,d 最小,此时P ,Q 两点间的距离PQ =PD +CD +CQ =17+因此,d 最小时,P ,Q 两点间的距离为17+. 解法二:(1)如图,过O 作OH ⊥l ,垂足为H.以O 为坐标原点,直线OH 为y 轴,建立平面直角坐标系.因为BD =12,AC =6,所以OH =9,直线l 的方程为y =9,点A ,B 的纵坐标分别为3,−3.因为AB 为圆O 的直径,AB =10,所以圆O 的方程为x 2+y 2=25.从而A (4,3),B (−4,−3),直线AB 的斜率为34. 因为PB ⊥AB ,所以直线PB 的斜率为43-, 直线PB 的方程为42533y x =--.所以P (−13,9),15PB ==. 因此道路PB 的长为15(百米).(2)①若P 在D 处,取线段BD 上一点E (−4,0),则EO =4<5,所以P 选在D 处不满足规划要求. ②若Q 在D 处,连结AD ,由(1)知D (−4,9),又A (4,3), 所以线段AD :36(44)4y x x =-+-剟.在线段AD 上取点M (3,154),因为5OM =<=, 所以线段AD 上存在点到点O 的距离小于圆O 的半径. 因此Q 选在D 处也不满足规划要求. 综上,P 和Q 均不能选在D 处. (3)先讨论点P 的位置.当∠OBP <90°时,线段PB 上存在点到点O 的距离小于圆O 的半径,点P 不符合规划要求;当∠OBP ≥90°时,对线段PB 上任意一点F ,OF ≥OB ,即线段PB 上所有点到点O 的距离均不小于圆O 的半径,点P 符合规划要求.设1P 为l 上一点,且1PB AB ⊥,由(1)知,1P B =15,此时1P (−13,9); 当∠OBP >90°时,在1PPB △中,115PB PB >=. 由上可知,d ≥15. 再讨论点Q 的位置.由(2)知,要使得QA≥15,点Q 只有位于点C 的右侧,才能符合规划要求.当QA =15时,设Q (a ,9),由15(4)AQ a ==>,得a =4+Q (4+9),此时,线段QA 上所有点到点O 的距离均不小于圆O 的半径.综上,当P (−13,9),Q (4+9)时,d 最小,此时P ,Q 两点间的距离4(13)17PQ =+-=+.因此,d 最小时,P ,Q 两点间的距离为17+.【名师点睛】本小题主要考查三角函数的应用、解方程、直线与圆等基础知识,考查直观想象和数学建模及运用数学知识分析和解决实际问题的能力.20.【2018年高考天津卷文数】在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知b sin A =a cos(B –π6). (1)求角B 的大小;(2)设a =2,c =3,求b 和sin(2A –B )的值.【答案】(1)π3;(2)b ;sin(2A –B )=14【解析】(1)在△ABC 中,由正弦定理sin sin a bA B=,可得sin sin b A a B =,又由πsin cos()6b A a B =-,得πsin cos()6a B a B =-,即πsin cos()6B B =-,可得tan B = 又因为(0π)B ∈,,可得B =π3. (2)在△ABC 中,由余弦定理及a =2,c =3,B =π3,有2222cos 7b a c ac B =+-=,故b. 由πsin cos()6b A a B =-,可得sin A =因为a <c,故cos A =.因此sin 22sin cos A A A ==21cos 22cos 17A A =-=. 所以,sin(2)sin 2cos cos 2sin A B A B A B -=-=11727214⨯-⨯= 【名师点睛】本小题主要考查同角三角函数的基本关系,两角差的正弦与余弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识,考查运算求解能力.在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注意公式变式的应用.解决三角形问题时,注意角的限制范围.21.【2017年高考天津卷文数】在ABC △中,内角,,A B C 所对的边分别为,,a b c .已知sin 4sin a A b B =,222)ac a b c =--.(1)求cos A 的值; (2)求sin(2)B A -的值.【答案】(1)5-2)5-. 【解析】(1)由sin 4sin a A b B =及sin sin a bA B=,得2a b =.由222)ac a b c =--及余弦定理,得2225cos 2acb c aA bcac -+-=== (2)由(1)可得sin A =,代入sin 4sin a A b B =,得sin sin 4a A B b ==.由(1)知A 为钝角,所以cos 5B ==. 于是4sin 22sin cos 5B B B ==,23cos 212sin 5B B =-=,故43sin(2)sin 2cos cos 2sin (55555B A B A B A -=-=⨯--⨯=-. 【名师点睛】利用正弦定理进行“边转角”可寻求角的关系,利用“角转边”可寻求边的关系,利用余弦定理借助三边关系可求角,利用两角和差的三角公式及二倍角公式可求三角函数值.利用正、余弦定理解三角形是高考的高频考点,常与三角形内角和定理、三角形面积公式等相结合,利用正、余弦定理进行解题.解答本题时,(1)首先根据正弦定理sin sin a bA B=得到2a b =,再根据余弦定理即可求得cos A 的值;(2)根据(1)的结论和条件,由cos A 求得sin A ,然后根据sin 4sin a A b B =求得sin B ,再求cos B ,然后由二倍角公式求sin 2,cos 2B B ,最后代入sin(2)B A -的展开式即可.22.【2017年高考山东卷文数】在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,已知b =3,6AB AC ⋅=-,3ABC S =△,求A 和a .【答案】3=π,4A a 【解析】因为6AB AC ⋅=-,所以cos 6bc A =-, 又3ABC S =△,所以sin 6bc A =, 因此tan 1A =-,又0πA <<, 所以3π4A =,又3b =,所以c =由余弦定理2222cos a b c bc A =+-,得29823(a =+-⨯⨯,所以a =【名师点睛】正、余弦定理是应用极为广泛的两个定理,它将三角形的边和角有机地联系起来,从而使三角与几何产生联系,为求与三角形有关的量(如面积、外接圆、内切圆半径和面积等)提供了理论依据,也是判断三角形形状、证明三角形中有关等式的重要依据.其主要方法有:化角法,化边法,面积法,运用初等几何法.注意体会其中蕴涵的函数与方程思想、等价转化思想及分类讨论思想. 23.【2017年高考江苏卷】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm ,容器Ⅰ的底面对角线AC 的长为,容器Ⅱ的两底面对角线EG ,11E G 的长分别为14cm 和62cm .分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm .现有一根玻璃棒l ,其长度为40cm .(容器厚度、玻璃棒粗细均忽略不计)(1)将l 放在容器Ⅰ中,l 的一端置于点A 处,另一端置于侧棱1CC 上,求l 没入水中部分的长度; (2)将l 放在容器Ⅱ中,l 的一端置于点E 处,另一端置于侧棱1GG 上,求l 没入水中部分的长度.【答案】(1)16cm(如果将“没入水中部分”理解为“水面以上部分”,则结果为24cm);(2)20cm(如果将“没入水中部分”理解为“水面以上部分”,则结果为20cm).【解析】(1)由正棱柱的定义,1CC ⊥平面ABCD ,所以平面11A ACC ⊥平面ABCD ,1CC AC ⊥. 记玻璃棒的另一端落在1CC 上点M 处.因为40AC AM ==,所以30MC ==,从而3sin 4MAC =∠, 记AM 与水面的交点为1P ,过1P 作P 1Q 1⊥AC ,Q 1为垂足, 则P 1Q 1⊥平面ABCD ,故P 1Q 1=12,从而AP 1=1116sin P MACQ =∠.答:玻璃棒l 没入水中部分的长度为16cm .(如果将“没入水中部分”理解为“水面以上部分”,则结果为24cm)(2)如图,O ,O 1是正棱台的两底面中心.由正棱台的定义,OO 1⊥平面EFGH ,所以平面E 1EGG 1⊥平面EFGH ,O 1O ⊥EG . 同理,平面E 1EGG 1⊥平面E 1F 1G 1H 1,O 1O ⊥E 1G 1. 记玻璃棒的另一端落在GG 1上点N 处.过G 作GK ⊥E 1G 1,K 为垂足,则GK =OO 1=32. 因为EG = 14,E 1G 1= 62,所以KG 1=6214242-=,从而140GG ===. 设1,,EGG ENG αβ==∠∠则114sin sin()cos 25KGG KGG απ=+==∠∠.因为2απ<<π,所以3cos 5α=-.在ENG △中,由正弦定理可得4014sin sin αβ=,解得7sin 25β=. 因为02βπ<<,所以24cos 25β=. 于是42473sin sin()sin()sin co 3s cos sin ()5252555NEG αβαβαβαβ=π--=+=+=⨯+-⨯=∠.记EN 与水面的交点为P 2,过P 2作P 2Q 2⊥EG ,Q 2为垂足,则P 2Q 2⊥平面EFGH , 故P 2Q 2=12,从而EP 2=2220sin P NEGQ =∠.答:玻璃棒l 没入水中部分的长度为20cm .(如果将“没入水中部分”理解为“水面以上部分”,则结果为20cm)【名师点睛】解答本题时,(1)转化为直角三角形ACM 中,利用相似性质求解AP 1;(2)转化到三角形EGN 中,先利用直角梯形性质求角1EGG ∠,再利用正弦定理求角ENG ∠,最后根据直角三角形求高,即为l 没入水中部分的长度.解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向;第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化;第三步:求结果.。
专题16 语言文字运用(病句类)-高考语文真题分项汇编 (全国通用)(学生卷)

专题16 语言文字运用(病句类)【2023年】(2022·全国甲卷)阅读下面的文字,完成下面小题。
能否将珍贵的文物置于掌中观赏品味?能否步入千年墓穴一探究竟?能否与未曾展出的国宝亲密接触?……与过去相比,今天的博物馆已经发生了①_______________的变化。
有了科技的助力,这些往日因时空限制而②_______________的事情都已成为现实。
“博物馆+高科技”让那些沉睡千年的古物“活”在了今人面前,为越来越多的人带来不一样的观展体验,让他们可以去那些原本“去不了”的地方,看那些本来“看不到的事物”。
故宫博物院举办的那场名为《清明上河图3.0》的高科技互动展演艺术,用现代超高清数字技术完美融合古代绘画艺术。
观众们沿着张择端的笔触走进繁华的北宋都城汴梁,穿梭于楼台之间,泛舟于汴河之上,观两岸人来人往,看水鸟掠过船篷。
沉浸其中,确有一种③______________的情趣。
在2016年的纪念殷墟妇好墓考古发掘四十周年特展上,首都博物馆利用虚拟技术带领观众“回到”妇好墓的考古发掘现场,上下6层、深达7.5米的妇好墓葬④_______________。
此外还有一些博物馆利用虚拟技术,以数字化方式展现文物全貌。
观众只需在屏幕上滑动手指,就可近距离、全角度现赏文物,将静置于展柜中、封存进仓库里、消散在过往中的历史“托在手上”,全方位观察岁月留下的每一处细痕。
18.文中画横线的句子有语病,请进行修改,使语言表达准确流畅。
可少量增删词语,不得改变原意。
(2022·全国乙卷)阅读下面的文字,完成下面小题。
近日,眼科门诊一连来了几名特殊患者,都是晚上熬夜看手机,第二天早上看不见东西了,这种疾病被称为“眼中风”。
“中风”一词原指脑中风,包括缺血性和出血性脑中风,近几年被引入眼科。
临床上,眼科医生把视网膜动脉阻塞这类缺血性眼病和视网膜静脉阻塞这类出血性眼病统称为“眼中风”。
“眼中风”是眼科临床急症之一,不及时治疗会导致严重的视力损害。
2017年-2019年高考文科数学全国卷三真题试卷与答案(新课标)

绝密★ 启用前2017 年普通高等学校招生全国统一考试(新课标Ⅲ)文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4} , B={2,4,6,8} ,则 A B 中元素的个数为A .1B.2C. 3D.42.复平面内表示复数z=i(–2+i)的点位于A .第一象限B.第二象限C.第三象限D.第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014 年 1 月至 2016 年 12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8 月D .各年 1 月至 6 月的月接待游客量相对于7 月至 12 月,波动性更小,变化比较平稳4.已知sincos4=,则 sin 237 B .2 2 7 A .9C .D .9993x 2 y6 05.设 x , y 满足约束条件x 0 ,则 z=x-y 的取值范围是yA .[ – 3,0]B . [ – 3,2]C . [0,2]D . [0,3]16.函数 f(x)= sin(x+)+cos( x-)的最大值为536A .6B . 1C .3D .15557.函数 y=1+x+sin x的部分图像大致为x 2A .B .C .D .8.执行下面的程序框图,为使输出S 的值小于 91,则输入的正整数 N 的最小值为A .5B .4C . 3D .29.已知圆柱的高为 1,它的两个底面的圆周在直径为2 的同一个球的球面上,则该圆柱的体积为A .πB .3πC .ππ42D .410.在正方体ABCDA 1B 1C 1D 1中,E 为棱CD 的中点,则A .A 1E ⊥DC 1B .A 1E ⊥BDC .A 1E ⊥BC 1D .A 1E ⊥ACx 2 y 2 1 ,(a>b>0)的左、右顶点分别为 12 1 2为直径的圆与直线b 2a 2bx ay 2ab0 相切,则C 的离心率为6B .3C .21A .33D .3312.已知函数f ( x)x 2 2x a(e x 1 ex 1) 有唯一零点,则 a=1B .1C .1D . 1A .322二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
2017-2019高考数学(文科)试卷及答案
2017年广东省高考数学试卷(文科)(全国新课标Ⅰ)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={x|x<2},B={x|3﹣2x>0},则()A.A∩B={x|x<} B.A∩B=∅ C.A∪B={x|x<} D.A∪B=R2.(5分)为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别是x1,x2,…,x n,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是()A.x1,x2,…,x n的平均数B.x1,x2,…,x n的标准差C.x1,x2,…,x n的最大值D.x1,x2,…,x n的中位数3.(5分)下列各式的运算结果为纯虚数的是()A.i(1+i)2B.i2(1﹣i)C.(1+i)2D.i(1+i)4.(5分)如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是()A.B.C.D.5.(5分)已知F是双曲线C:x2﹣=1的右焦点,P是C上一点,且PF 与x轴垂直,点A的坐标是(1,3),则△APF的面积为()A.B.C.D.6.(5分)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()A.B.C.D.7.(5分)设x,y满足约束条件,则z=x+y的最大值为()A.0 B.1 C.2 D.38.(5分)函数y=的部分图象大致为()A.B.C.D.9.(5分)已知函数f(x)=lnx+ln(2﹣x),则()A.f(x)在(0,2)单调递增B.f(x)在(0,2)单调递减C.y=f(x)的图象关于直线x=1对称D.y=f(x)的图象关于点(1,0)对称10.(5分)如图程序框图是为了求出满足3n﹣2n>1000的最小偶数n,那么在和两个空白框中,可以分别填入()A.A>1000和n=n+1 B.A>1000和n=n+2C.A≤1000和n=n+1 D.A≤1000和n=n+211.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知sinB+sinA (sinC﹣cosC)=0,a=2,c=,则C=()A.B.C.D.12.(5分)设A,B是椭圆C:+=1长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是()A.(0,1]∪[9,+∞)B.(0,]∪[9,+∞)C.(0,1]∪[4,+∞)D.(0,]∪[4,+∞)二、填空题:本题共4小题,每小题5分,共20分。
(2017-2019)高考文数真题分类汇编专题16 算法初步(学生版)
专题16 算法初步1.【2019年高考天津卷文数】阅读下边的程序框图,运行相应的程序,输出S的值为A.5B.8C.24D.292.【2019年高考北京卷文数】执行如图所示的程序框图,输出的s值为A.1B.2C.3D.43.【2019年高考全国Ⅰ卷文数】如图是求112122++的程序框图,图中空白框中应填入A .12A A =+B .12A A =+C .112A A=+D .112A A=+4.【2019年高考全国Ⅲ卷文数】执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于A .4122-B .5122-C .6122-D .7122-5.【2018年高考全国Ⅱ卷文数】为计算11111123499100S =-+-++-L ,设计了下面的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+6.【2018年高考北京卷文数】执行如图所示的程序框图,输出的s 值为A .12 B .56 C .76D .7127.【2018年高考天津卷文数】阅读如图的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为A.1B.2C.3D.4a=-,则输出的S= 8.【2017年高考全国Ⅱ卷文数】执行下面的程序框图,如果输入的1A .2B .3C .4D .59.【2017年高考全国Ⅰ卷文数】下面程序框图是为了求出满足321000n n ->的最小偶数n ,那么在和两个空白框中,可以分别填入A .A >1000和n =n +1B .A >1000和n =n +2C .A ≤1000和n =n +1D .A ≤1000和n =n +210.【2017年高考全国Ⅲ卷文数】执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .211.【2017年高考北京卷文数】执行如图所示的程序框图,输出的s值为A.2B.3 2C.53D.8512.【2017年高考天津卷文数】阅读下面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为A.0B.1C.2D.313.【2019年高考江苏卷】下图是一个算法流程图,则输出的S的值是______________.14.【2018年高考江苏卷】一个算法的伪代码如图所示,执行此算法,最后输出的S的值为______________.15.【2017年高考江苏卷】如图是一个算法流程图,若输入的值为116,则输出y的值是______________.。
算法初步-2019年高考真题和模拟题分项汇编数学(文)+Word版含解析
专题 算法初步1.【2019年高考天津卷文数】阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .29【答案】B【分析】根据程序框图,逐步写出运算结果即可.【解析】1,2S i ==;11,1225,3j S i ==+⨯==;8,4S i ==,结束循环,输出8S =.故选B .【名师点睛】解答本题要注意要明确循环体终止的条件是什么,会判断什么时候终止循环体. 2.【2019年高考北京卷文数】执行如图所示的程序框图,输出的s 值为A .1B .2C .3D .4【答案】B【分析】根据程序框图中的条件逐次运算即可. 【解析】初始:1s =,1k =,运行第一次,2212312s ⨯==⨯-,2k =,运行第二次,2222322s ⨯==⨯-,3k =,运行第三次,2222322s ⨯==⨯-,结束循环,输出2s =,故选B .【名师点睛】本题考查程序框图,属于容易题,注重基础知识、基本运算能力的考查.3.【2019年高考全国Ⅰ卷文数】如图是求112122++的程序框图,图中空白框中应填入A .12A A =+B .12A A=+C .112A A=+D .112A A=+【答案】A【分析】本题主要考查算法中的程序框图,渗透阅读、分析与解决问题等素养,认真分析式子结构特征与程序框图结构,即可找出作出选择.【解析】初始:1,122A k ==≤,因为第一次应该计算1122+=12A +,1k k =+=2; 执行第2次,22k =≤,因为第二次应该计算112122++=12A +,1k k =+=3,结束循环,故循环体为12A A=+,故选A .【秒杀速解】认真观察计算式子的结构特点,可知循环体为12A A=+.4.【2019年高考全国Ⅲ卷文数】执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于A .4122- B .5122-C .6122-D .7122-【答案】C【分析】根据程序框图,结合循环关系进行运算,可得结果. 【解析】输入的ε为0.01,11,01,0.01?2x s x ==+=<不满足条件; 1101,0.01?24s x =++=<不满足条件;⋅⋅⋅611101,0.00781250.01?22128S x =++++==<满足条件,结束循环;输出676111112(1)22222S =+++=⨯-=-,故选C .【名师点睛】解答本题关键是利用循环运算,根据计算精确度确定数据分析.5.【2019年高考江苏卷】下图是一个算法流程图,则输出的S 的值是______________.【答案】5【分析】结合所给的流程图运行程序确定输出的值即可. 【解析】执行第一次,1,1422x S S x =+==≥不成立,继续循环,12x x =+=; 执行第二次,3,2422x S S x =+==≥不成立,继续循环,13x x =+=; 执行第三次,3,342xS S x =+==≥不成立,继续循环,14x x =+=;执行第四次,5,442xS S x =+==≥成立,输出 5.S =【名师点睛】识别、运行程序框图和完善程序框图的思路:(1)要明确程序框图的顺序结构、条件结构和循环结构;(2)要识别、运行程序框图,理解框图所解决的实际问题;(3)按照题目的要求完成解答并验证.6.【天津市和平区2018-2019学年度第二学期高三年级第三次质量调查】在如图所示的计算1592017++++L 的程序框图中,判断框内应填入的条件是A .2017?i ≤B .2017?i <C .2013?i <D .2021?i ≤【答案】A【解析】由题意结合流程图可知当2017i =时,程序应执行S S i =+,42021i i =+=, 再次进入判断框时应该跳出循环,输出S 的值;结合所给的选项可知判断框内应填入的条件是2017?i ≤.故选A .7.【吉林省长春市北京师范大学长春市附属中学2019届高三第四次模拟考试】根据如图所示的程序框图,当输入的x 值为3时,输出的y 值等于A .1B .eC .1e -D .2e -【答案】C【解析】由题3x =,231x x =-=-,此时0x >,继续运行,1210x =-=-<,程序运行结束,得1e y -=,故选C .8.【西南名校联盟重庆市第八中学2019届高三5月高考适应性月考卷(六)】执行如图所示的程序框图,则输出的值为A .4B .5【答案】C【解析】由题可得3,27,315,431,563,6S i S i S i S i S i ==→==→==→==→==, 此时结束循环,输出6i =,故选C .9.【山东省济宁市2019届高三二模】阅读如图所示的程序框图,运行相应的程序,输出的S 的值等于A .30B .31C .62D .63【答案】B【解析】由流程图可知该算法的功能为计算123412222S =++++的值,即输出的值为512341(12)122223112S ⨯-=++++==-.故选B .10.【辽宁省大连市2019届高三第二次模拟考试】执行如图所示的程序框图,若输出结果为1,则可输入的实数x 值的个数为A .1B .2【答案】B【分析】根据程序框图的含义,得到分段函数221,2log ,2x x y x x ⎧-≤⎪=⎨>⎪⎩,分段解出关于x 的方程,即可得到可输入的实数x 值的个数.【解析】根据题意,该框图的含义是:当2x ≤时,得到函数21y x =-;当2x >时,得到函数2log y x =, 因此,若输出的结果为1时,若2x ≤,得到211x -=,解得x = 若2x >,得到2log 1x =,无解,因此,可输入的实数x的值可能为,共有2个.故选B .11.【江西省新八校2019届高三第二次联考】如图所示的程序框图所实现的功能是A .输入a 的值,计算2021(1)31a -⨯+的值 B .输入a 的值,计算2020(1)31a -⨯+的值 C .输入a 的值,计算2019(1)31a -⨯+的值 D .输入a 的值,计算2018(1)31a -⨯+的值【答案】B【解析】由程序框图,可知1a a =,132n n a a +=-,由i 的初值为1,末值为2019, 可知,此递推公式共执行了201912020+=次,又由132n n a a +=-,得113(1)n n a a +-=-,得11(1)3n n a a --=-⨯即1(1)31n n a a -=-⨯+,故2021120202021(1)31(1)31a a a -=-⨯+=-⨯+,故选B . 12.【山西省2019届高三考前适应性训练(二模)】执行如图所示的程序框图,则输出x 的值为A .2-B .13- C .12D .3【答案】A【分析】根据程序框图进行模拟运算得到x 的值具备周期性,利用周期性的性质进行求解即可.【解析】∵12x =,∴当1i =时,13x =-;2i =时,2x =-; 3i =时,3x =,4i =时,12x =,即x 的值周期性出现,周期数为4,∵201850442=⨯+,则输出x 的值为2-,故选A .【名师点睛】本题主要考查程序框图的识别和判断,结合条件判断x 的值具备周期性是解决本题的关键,属于中档题.13.【青海省西宁市第四高级中学、第五中学、第十四中学三校2019届高三4月联考】若某程序框图如图所示,则该程序运行后输出的值是A .5B .4C .3D .2【答案】B【分析】模拟执行循环结构的程序得到n 与i 的值,计算得到2n =时满足判断框的条件,退出循环,输出结果,即可得到答案.【解析】模拟执行循环结构的程序框图, 可得:6,1n i ==, 第1次循环:3,2n i ==; 第2次循环:4,3n i ==; 第3次循环:2,4n i ==,此时满足判断框的条件,输出4i =.故选B .【名师点睛】本题主要考查了循环结构的程序框图的应用,其中解答中根据给定的程序框图,根据判断框的条件推出循环,逐项准确计算输出结果是解答的关键,着重考查了考生的运算与求解能力,属于基础题.14.【江苏省七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019届高三第三次调研】下图是一个算法流程图.若输出 的值为4,则输入x 的值为______________.【答案】1-【解析】当1x ≤时,由流程图得3y x =-, 令34y x =-=,解得1x =-,满足题意. 当1x >时,由流程图得3y x =+, 令34y x =+=,解得1x =,不满足题意. 故输入x 的值为1-.15.【北京市人大附中2019届高三高考信息卷(三)】执行如图所示的程序框图,若输入x 值满足24x -<≤,则输出y 值的取值范围是______________.【答案】[3,2]-【解析】根据输入x 值满足24x -<≤,利用函数的定义域,分成两部分:即22x <<﹣和24x ≤≤,当22x <<﹣时,执行23y x =- 的关系式,故31y -≤<, 当24x ≤≤时,执行2log y x =的关系式,故12y ≤≤. 综上所述:[3,2]y ∈-,故输出y 值的取值范围是[3,2]-.。
《精品》2017-2019三年高考真题数学(理)分项汇编专题01集合与常用逻辑用语(原卷版)
专题01集合与常用逻辑用语1.【2019年高考全国Ⅰ卷理数】已知集合M {x|4x 2},N {x|x2x 60},则M N= A.{x 4x3B.{x 4x 2C.{x 2x2D.{x2x 32.【2019年高考全国Ⅱ卷理数】设集合A={x|x2–5x+6>0},B={x|x–1<0},则A∩B= A.(–∞,1)C.(–3,–1)B.(–2,1)D.(3,+∞)3.【2019年高考全国Ⅲ卷理数】已知集合A {1,0,1,2},B {x|x21},则A B A.C.1,0,11,1B.D.0,10,1,24.【2019年高考天津理数】设集合A {1,1,2,3,5},B {2,3,4},C {x R|1x 3},则(A C)B A.C.21,2,3B.D.2,31,2,3,45.【2019年高考浙江】已知全集U 1,0,1,2,3,集合A 0,1,2,B 1,0,1,则(UA)B=A.C.11,2,3B.D.0,11,0,1,36.【2019年高考浙江】若a>0,b>0,则“a+b≤4”是“ab≤4”的A.充分不必要条件C.充分必要条件B.必要不充分条件D.既不充分也不必要条件7.【2019年高考天津理数】设x R,则“x25x 0”是“|x 1|1”的A.充分而不必要条件C.充要条件B.必要而不充分条件D.既不充分也不必要条件8.【2019年高考全国Ⅱ卷理数】设α,β为两个平面,则α∥β的充要条件是A.α内有无数条直线与β平行C.α,β平行于同一条直线B.α内有两条相交直线与β平行D.α,β垂直于同一平面19.【2019年高考北京理数】设点A,B,C不共线,则“AB与AC的夹角为锐角”是“|AB AC ||B C|的”A.充分而不必要条件C.充分必要条件B.必要而不充分条件D.既不充分也不必要条件10.【2018年高考浙江】已知全集U={1,2,3,4,5},A={1,3},则ðA=UA.C.{2,4,5}11.【2018年高考全国Ⅰ卷理数】已知集合B.{1,3}D.{1,2,3,4,5}Axx 2x 20,则ðARA.C.x 1x 2x|x1x|x 2B.D.x 1x 2x|x 1x|x 212.【2018年高考全国Ⅲ卷理数】已知集合A x|x 1≥0,B 0,1,2,则A B A.0C.1,2B.1D.0,1,213.【2018年高考天津理数】设全集为R,集合A {x0x 2},B {x x 1},则A I (ðB)R A.{x0x 1}B.{x0x 1}C.{x1x 2}D.{x0x 2}14.【2018年高考全国Ⅱ卷理数】已知集合A x,y x2y2≤3,x Z,y Z,则A中元素的个数为A.9C.5B.8D.415.【2018年高考北京理数】已知集合A={x||x|<2},B={–2,0,1,2},则AA.{0,1} B.{–1,0,1}B=C.{–2,0,1,2}D.{–1,0,1,2}16.【2018年高考浙江】已知平面α,直线m,n满足m α,n α,则“m∥n”是“m∥α”的A.充分不必要条件C.充分必要条件B.必要不充分条件D.既不充分也不必要条件217.【2018年高考天津理数】设x R,则“|x 11|22”是“x31”的A.充分而不必要条件C.充要条件B.必要而不充分条件D.既不充分也不必要条件18.【2018年高考北京理数】设a,b均为单位向量,则“a 3b 3a b”是“a⊥b”的A.充分而不必要条件C.充分必要条件B.必要而不充分条件D.既不充分也不必要条件19.【2017年高考全国Ⅰ卷理数】已知集合A={x|x<1},B={x|3x 1},则A.C.AAB {x|x 0}B {x|x 1}B.D.AAB RB20.【2017年高考全国Ⅱ卷理数】设集合A 1,2,4,B xx 24x m 0.若A B1,则BA.C.1,31,3B.D.1,01,521.【2017年高考全国Ⅲ卷理数】已知集合A=的个数为A.3C.1(x,y│)x2y21,B=B.2D.0(x,y│)y x,则A B中元素22.【2017年高考北京理数】若集合A={x|–2<x<1},B={x|x<–1或x>3},则A B=A.{x|–2<x<–1}C.{x|–1<x<1}23.【2017年高考浙江】已知集合P {x|1x 1} A.(1,2)C.(1,0)B.{x|–2<x<3}D.{x|1<x<3},Q {0x 2}B.(0,1)D.(1,2),那么P Q24.【2017年高考天津理数】设集合A {1,2,6},B {2,4},C {x R|1x 5},则(A B) C A.{2}B.{1,2,4}C.{1,2,4,6}D.{x R|1x 5}325.【2017 年高考山东理数】设函数y 4x2的定义域为A,函数y ln(1x)的定义域为B,则A B= A.(1,2)B.(1,2]C.(-2,1)D.[-2,1)26.【2017年高考浙江】已知等差数列{a }的公差为d,前n项和为S,则“d>0”是“S+S>2S”的n n465A.充分不必要条件C.充分必要条件B.必要不充分条件D.既不充分也不必要条件27.【2017年高考北京理数】设m,n为非零向量,则“存在负数,使得m n”是“m n<0”的A.充分而不必要条件C.充分必要条件B.必要而不充分条件D.既不充分也不必要条件28.【2017年高考山东理数】已知命题p:x 0,ln(x 1)0;命题q:若a>b,则a b,下列命题为真命题的是A.C.p qp qB.D.p qp q29.【2017年高考全国Ⅰ卷理数】设有下面四个命题p 1:若复数z满足1zR,则z R;p2:若复数z满足z2R,则z R;p 3:若复数z,z12满足z z R12,则z z12;p4:若复数z R,则z R.其中的真命题为A.p,p13B.p,p14C.p, p23D.p,p2430.【2019年高考江苏】已知集合A {1,0,1,6},B {x| x 0,x R},则A B ▲. 31.【2018年高考江苏】已知集合,,那么________.32.【2017年高考江苏】已知集合A {1,2},B {a,a23},若A B {1},则实数a的值为▲.33.【2018年高考北京理数】能说明“若f(x)>f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是__________.2245。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题16 算法初步1.【2019年高考天津卷文数】阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .29【答案】B【分析】根据程序框图,逐步写出运算结果即可.【解析】1,2S i ==;11,1225,3j S i ==+⨯==;8,4S i ==,结束循环,输出8S =.故选B .【名师点睛】解答本题要注意要明确循环体终止的条件是什么,会判断什么时候终止循环体. 2.【2019年高考北京卷文数】执行如图所示的程序框图,输出的s 值为A .1B .2C .3D .4【答案】B【分析】根据程序框图中的条件逐次运算即可. 【解析】初始:1s =,1k =,运行第一次,2212312s ⨯==⨯-,2k =,运行第二次,2222322s ⨯==⨯-,3k =,运行第三次,2222322s ⨯==⨯-,结束循环,输出2s =,故选B .【名师点睛】本题考查程序框图,属于容易题,注重基础知识、基本运算能力的考查.3.【2019年高考全国Ⅰ卷文数】如图是求112122++的程序框图,图中空白框中应填入A .12A A =+ B .12A A =+C .112A A=+D .112A A=+【答案】A【分析】本题主要考查算法中的程序框图,渗透阅读、分析与解决问题等素养,认真分析式子结构特征与程序框图结构,即可找出作出选择.【解析】初始:1,122A k ==≤,因为第一次应该计算1122+=12A +,1k k =+=2; 执行第2次,22k =≤,因为第二次应该计算112122++=12A +,1k k =+=3, 结束循环,故循环体为12A A=+,故选A .【秒杀速解】认真观察计算式子的结构特点,可知循环体为12A A=+.4.【2019年高考全国Ⅲ卷文数】执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于A .4122- B .5122-C .6122-D .7122-【答案】C【分析】根据程序框图,结合循环关系进行运算,可得结果. 【解析】输入的ε为0.01,11,01,0.01?2x s x ==+=<不满足条件; 1101,0.01?24s x =++=<不满足条件;⋅⋅⋅611101,0.00781250.01?22128S x =++++==<满足条件,结束循环;输出676111112(1)22222S =+++=⨯-=-,故选C .【名师点睛】解答本题关键是利用循环运算,根据计算精确度确定数据分析.5.【2018年高考全国Ⅱ卷文数】为计算11111123499100S =-+-++-,设计了下面的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+【答案】B 【解析】由11111123499100S =-+-++-得程序框图先对奇数项累加,偶数项累加,最后再相减.因此在空白框中应填入 ,故选B .6.【2018年高考北京卷文数】执行如图所示的程序框图,输出的s 值为A.12B.56C.76D.712【答案】B【解析】执行循环前:k=1,S=1.在执行第一次循环时,S=1–1122=.由于k=2≤3,所以执行下一次循环.S=115236+=,k=3,直接输出S=56,故选B.7.【2018年高考天津卷文数】阅读如图的程序框图,运行相应的程序,若输入N的值为20,则输出T 的值为A.1 B.2C.3 D.4【答案】B【解析】若输入N=20,则i=2,T=0,202Ni==10是整数,满足条件.T=0+1=1,i=2+1=3,i≥5不成立,循环,203Ni=不是整数,不满足条件,i=3+1=4,i≥5不成立,循环,204Ni==5是整数,满足条件,T=1+1=2,i=4+1=5,i≥5成立,输出T=2,故选B.8.【2017年高考全国Ⅱ卷文数】执行下面的程序框图,如果输入的1a=-,则输出的S=A .2B .3C .4D .5【答案】B【解析】阅读流程图,初始化数值1,1,0a k S =-==. 循环结果执行如下:第一次:011,1,2S a k =-=-==;第二次:121,1,3S a k =-+==-=;第三次:132,1,4S a k =-=-==; 第四次:242,1,5S a k =-+==-=;第五次:253,1,6S a k =-=-==; 第六次:363,1,7S a k =-+==-=;结束循环,输出3S =.故选B.【名师点睛】算法与流程图的考查,侧重于对流程图循环结构的考查.求解时,先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,如:是求和还是求项.9.【2017年高考全国Ⅰ卷文数】下面程序框图是为了求出满足321000n n ->的最小偶数n ,A .A >1000和n =n +1B .A >1000和n =n +2C .A ≤1000和n =n +1D .A ≤1000和n =n +2【答案】D【解析】由题意,因为321000n n ->,且框图中在“否”时输出,所以判定框内不能输入1000A >,故填1000A ≤,又要求n 为偶数且初始值为0,所以矩形框内填2n n =+,故选D.【名师点睛】解决此类问题的关键是读懂程序框图,明确顺序结构、条件结构、循环结构的真正含义.本题巧妙地设置了两个空格需要填写,所以需要抓住循环的重点,偶数该如何增量,判断框内如何进行判断可以根据选项排除.10.【2017年高考全国Ⅲ卷文数】执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .2【答案】D【解析】阅读程序框图,程序运行如下:首先初始化数值:1,100,0t M S ===,然后进入循环体:此时应满足t N ≤,执行循环语句:100,10,1210MS S M M t t =+==-=-=+=; 此时应满足t N ≤,执行循环语句:90,1,1310MS S M M t t =+==-==+=; 此时满足91S <,可以跳出循环,则输入的正整数N 的最小值为2. 故选D .【名师点睛】对算法与程序框图的考查,侧重于对程序框图中循环结构的考查.先明晰算法及程序框图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环的起始条件、循环次数、循环的终止条件,更要通过循环规律,明确程序框图研究的数学问题,是求和还是求项. 11.【2017年高考北京卷文数】执行如图所示的程序框图,输出的s 值为A .2B .32 C .53D .85【答案】C【解析】0k =时,03<成立,第一次进入循环:111,21k s +===; 13<成立,第二次进入循环:2132,22k s +===; 23<成立,第三次进入循环:31523,332k s +===, 33<不成立,此时输出53s =,故选C .【名师点睛】解决此类型问题时要注意:第一,要明确是当型循环结构,还是直到型循环结构,并根据各自的特点执行循环体;第二,要明确图中的累计变量,明确每一次执行循环体前和执行循环体后,变量的值发生的变化; 第三,要明确循环体终止的条件是什么,会判断什么时候终止循环体,争取写出每一个循环,这样避免出错.12.【2017年高考天津卷文数】阅读下面的程序框图,运行相应的程序,若输入N 的值为24,则输出N 的值为A .0B .1C .2D .3【答案】C【解析】初始:24N =,进入循环后N 的值依次为8,7,6,2N N N N ====,输出2N =,故选C .【名师点睛】识别算法框图和完善算法框图是近几年高考的重点和热点.对于此类问题: ①要明确算法框图中的顺序结构、条件结构和循环结构; ②要识别运行算法框图,理解框图解决的问题;③按照框图的要求一步一步进行循环,直到跳出循环体输出结果.近几年框图问题考查很活,常把框图的考查与函数、数列等知识相结合.13.【2019年高考江苏卷】下图是一个算法流程图,则输出的S 的值是______________.【答案】5【分析】结合所给的流程图运行程序确定输出的值即可. 【解析】执行第一次,1,1422x S S x =+==≥不成立,继续循环,12x x =+=; 执行第二次,3,2422x S S x =+==≥不成立,继续循环,13x x =+=; 执行第三次,3,342xS S x =+==≥不成立,继续循环,14x x =+=;执行第四次,5,442xS S x =+==≥成立,输出 5.S =【名师点睛】识别、运行程序框图和完善程序框图的思路: (1)要明确程序框图的顺序结构、条件结构和循环结构; (2)要识别、运行程序框图,理解框图所解决的实际问题; (3)按照题目的要求完成解答并验证.11 14.【2018年高考江苏卷】一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为______________.【答案】8【解析】由伪代码可得3,2;5,4;7,8I S I S I S ======,因为76>,所以结束循环,输出8.S =15.【2017年高考江苏卷】如图是一个算法流程图,若输入x 的值为116,则输出y 的值是______________.【答案】2- 【解析】由题意得212log 216y =+=-,故答案为2-. 【名师点睛】算法与流程图的考查,侧重于对流程图循环结构、条件结构和伪代码的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环的初始条件、循环次数、循环的终止条件,要通过循环规律,明确流程图研究的数学问题,是求和还是求项.。
