实变函数论考试试题及答案
实变函数本科试题及答案

实变函数本科试题及答案一、选择题(每题3分,共30分)1. 实数集R上的开区间(a, b)是一个开集,这是因为它满足:A. 任意点的邻域性质B. 包含所有有理数C. 包含所有整数D. 包含所有实数答案:A2. 下列哪个选项不是实数集R的子集?A. 空集B. (0, 1)C. 整数集ZD. 实数集R本身答案:C3. 一个函数在某点连续的充要条件是:A. 在该点导数存在B. 该点的左极限等于右极限C. 在该点的极限存在且等于函数值D. 在该点的振幅为零答案:C4. Lebesgue可测集的定义是基于:A. 开区间B. 闭区间C. 开集D. 半开半闭区间答案:A5. 如果一个实值函数在区间[a, b]上单调增加且有界,则根据Weierstrass定理,该函数必定:A. 有最大值和最小值B. 仅在有限点处不连续C. 仅在至多可数点处不连续D. 在区间[a, b]上连续答案:A6. 一个函数在某点的导数为0,这意味着该点是函数的:A. 驻点B. 极值点C. 拐点D. 渐近点答案:A7. 集合的外测度是:A. 集合所有开覆盖的体积的上确界B. 集合所有闭覆盖的体积的下确界C. 集合所有开覆盖的体积的下确界D. 集合所有闭覆盖的体积的上确界答案:A8. 如果一个函数在区间[a, b]上可积,则它的积分值:A. 必须为正B. 必须为负C. 可以是任意实数D. 必须为零答案:C9. 一个函数在某区间上一致连续的定义是:A. 该区间内任意两点的函数值之差的绝对值有界B. 该区间内任意两点的函数值之差的绝对值无界C. 函数在该区间的任意子区间上连续D. 函数在该区间的端点处的极限存在答案:A10. 根据Riemann积分的定义,如果一个函数在区间[a, b]上的积分存在,则:A. 该函数在该区间上必定连续B. 该函数在该区间上必定有界C. 该函数在该区间上必定单调增加D. 该函数在该区间上必定一致连续答案:B二、填空题(每题4分,共20分)11. 如果函数f(x)在点x=c处的左极限为L,则记为______。
实变函数测试题与答案范本

实变函数测试题与答案范本一、选择题1. 下列函数中,是实变函数的是:A. f(x) = √(x^2 - 1)B. f(x) = log(x)C. f(x) = cos(x)D. f(x) = 1/x答案:C. f(x) = cos(x)2. 设函数 f(x) 的定义域为 (-∞, 4],则下列函数定义中错误的是:A. f(x) = x^2B. f(x) = √(4 - x)C. f(x) = 1/(x - 3)D. f(x) = 2^x答案:C. f(x) = 1/(x - 3)3. 函数 f(x) = |x - 2| 的图像在 x = 2 处是否存在间断点?A. 存在间断点B. 不存在间断点答案:B. 不存在间断点二、计算题1. 求函数 f(x) = x^3 + 2x^2 - x 的零点。
解答:将 f(x) = 0,得到方程 x^3 + 2x^2 - x = 0。
对该方程进行因式分解得:x(x + 1)(x - 1) = 0。
解得 x = 0,x = -1,x = 1 为函数 f(x) 的零点。
2. 计算函数 f(x) = log(x^2 + 3x) 的导数。
解答:对 f(x) = log(x^2 + 3x) 进行求导。
使用链式法则,有 f'(x) = [1/(x^2 + 3x)] * (2x + 3)。
化简得到:f'(x) = (2x + 3)/(x^2 + 3x)。
三、证明题证明:若函数 f(x) 在区间 [a, b] 上连续且单调递增,那么 f(x) 在 [a, b] 上存在唯一的反函数。
解答:首先证明 f(x) 在 [a, b] 上是单射。
假设存在x1 ≠ x2,但 f(x1) = f(x2)。
由于 f(x) 在 [a, b] 上单调递增,可推出x1 ≠ x2,矛盾。
因此,f(x)在 [a, b] 上是单射。
接下来证明 f(x) 在 [a, b] 上是满射。
由于 f(x) 在 [a, b] 上连续,根据介值定理,f(x) 在 [a, b] 上取得最大值 M 和最小值 m。
(完整版)实变函数试题库1及参考答案

实变函数试题库及参考答案(1) 本科一、填空题1.设,A B 为集合,则()\A B B U A B U (用描述集合间关系的符号填写) 2.设A 是B 的子集,则A B (用描述集合间关系的符号填写) 3.如果E 中聚点都属于E ,则称E 是 4.有限个开集的交是5.设1E 、2E 是可测集,则()12m E E U 12mE mE +(用描述集合间关系的符号填写) 6.设nE ⊂¡是可数集,则*m E 07.设()f x 是定义在可测集E 上的实函数,如果1a ∀∈¡,()E x f x a ⎡⎤≥⎣⎦是 ,则称()f x 在E 上可测8.可测函数列的上极限也是 函数9.设()()n f x f x ⇒,()()n g x g x ⇒,则()()n n f x g x +⇒ 10.设()f x 在E 上L 可积,则()f x 在E 上 二、选择题1.下列集合关系成立的是( )A ()\B A A =∅I B ()\A B A =∅IC ()\A B B A =UD ()\B A A B =U2.若nR E ⊂是开集,则( )A E E '⊂B 0E E =C E E =DE E '=3.设(){}n f x 是E 上一列非负可测函数,则( )A ()()lim lim n n E En n f x dx f x dx →∞→∞≤⎰⎰ B ()()lim lim n n E E n n f x dx f x dx →∞→∞≤⎰⎰C ()()lim lim n n E En n f x dx f x dx →∞→∞≤⎰⎰ D ()()lim lim n n EE n n f x dx f x →∞→∞≤⎰⎰三、多项选择题(每题至少有两个以上的正确答案) 1.设[]{}0,1E =中无理数,则( )A E 是不可数集B E 是闭集C E 中没有内点D 1mE =2.设nE ⊂¡是无限集,则( )A E 可以和自身的某个真子集对等B E a ≥(a 为自然数集的基数)C E '≠∅D *0mE >3.设()f x 是E 上的可测函数,则( )A 函数()f x 在E 上可测B ()f x 在E 的可测子集上可测C ()f x 是有界的D ()f x 是简单函数的极限4.设()f x 是[],a b 上的有界函数,且黎曼可积,则( )A ()f x 在[],a b 上可测B ()f x 在[],a b 上L 可积C ()f x 在[],a b 上几乎处处连续D ()f x 在[],a b 上几乎处处等于某个连续函数四、判断题1. 可数个闭集的并是闭集. ( )2. 可数个可测集的并是可测集. ( )3. 相等的集合是对等的. ( )4. 称()(),f x g x 在E 上几乎处处相等是指使()()f x g x ≠的x 全体是可测集. ( ) 五、定义题1. 简述无限集中有基数最小的集合,但没有最大的集合.2. 简述点集的边界点,聚点和内点的关系.3. 简单函数、可测函数与连续函数有什么关系?4. [],a b 上单调函数与有界变差函数有什么关系?六、计算题1. 设()[]230,1\xx E f x xx E⎧∈⎪=⎨∈⎪⎩,其中E 为[]0,1中有理数集,求()[]0,1f x dx ⎰.2. 设{}n r 为[]0,1中全体有理数,(){}[]{}12121,,00,1\,,n n n x r r r f x x r r r ∈⎧⎪=⎨∈⎪⎩L L ,求()[]0,1lim n n f x dx →∞⎰.七、证明题1.证明集合等式:(\)A B B A B =U U2.设E 是[0,1]中的无理数集,则E 是可测集,且1mE =3.设(),()f x g x 是E 上的可测函数,则[|()()]E x f x g x >是可测集4.设()f x 是E 上的可测函数,则对任何常数0a >,有1[|()|]|()|E mE x f x a f x dx a≥≤⎰5.设()f x 是E 上的L -可积函数,{}n E 是E 的一列可测子集,且lim 0n n mE →∞=,则lim ()0nE n f x dx →∞=⎰实变函数试题库及参考答案(1) 本科一、填空题1.=2.≤3.闭集4.开集5.≤6.=7.可测集8.可测9.()()f x g x + 10.可积 二、单选题 ABB三、多选题ACD AB ABD ABC 四、判断题 × √√√ 五、定义题1.答:因为任何无限集均含有可数集,所以可数集是无限集中基数最小的,但无限集没有基数最大的,这是由于任何集合A ,A 的幂集2A 的基数大于A 的基数.2.答: 内点一定是聚点,边界点不一定是聚点,点集的边界点或为孤立点或为聚点.3.答:连续函数一定是可测函数;简单函数一定是可测函数;简单函数可表示成简单函数或连续函数的极限4.答:单调函数是有界变差函数,有界变差函数可表示成两个单调增函数之差.六、解答题1.解:因为0mE =,所以()3,.f x x a e =于[]0,1,于是()[][]30,10,1f x dx x dx =⎰⎰,而3x 在[]0,1上连续,从而黎曼可积,故由黎曼积分与勒贝格积分的关系,[]()41331000,11|44x x dx R x dx ===⎰⎰ 因此()[]0,114f x dx =⎰.2.解:显然()n f x 在[]0,1上可测,另外由()n f x 定义知,()0,.n f x a e =于[]0,1()1n ≥ 所以()[][]0,10,100nf x dx dx ==⎰⎰因此()[]0,1lim0nn f x dx →∞=⎰七、证明题 1.证明(\)()c A B B A B B =U I U ()()()c c A B A B B A B B B A B ===I U I U I U U U2.证明 设F 是[0,1]中的有理数集,则F 是可数集,从而*0m F =,因此F 是可测集,从而c F 可测,又[0,1]\[0,1]cE F F ==I ,故E 是可测集.由于E F =∅I ,所以1[0,1]()0m m E F mE mF mF ===+=+U ,故1mF =3.证明 设{}n r 为全体有理数所成之集,则()11[|()()][|()()][|()][|()]n n n n n E x f x g x E x f x r g x E x f x r E x g x r ∞∞==>=≥>=≥<I U U因为(),()f x g x 是E 上的可测函数,所以[|()]n E x f x r ≥,[|()]n E x g x r <是可测集,1,2,n =L ,于是由可测集性质知[|()()]E x f x g x >是可测集4.证明 因为()f x 在E 上可测,所以|()|f x 在E 上非负可测,由非负可测函数积分性质,[|()|][|()|]|()||()|E x f x a E x f x a Eadx f x dx f x dx ≥≥≤≤⎰⎰⎰而[|()|][|()|]E x f x a adx a mE x f x a ≥=⋅≥⎰,所以1[|()|]|()|E mE x f x a f x dx a≥≤⎰5.证明 因为lim 0n n mE →∞=,所以0,1N δ∀>∃≥,当n N ≥时,n mE δ<,又()f x 在E 上L -可积,所以由积分的绝对连续性,0,0,εδ∀>∃>当,e E me δ⊂<时|()|ef x dx ε<⎰于是当n N ≥时,n mE δ<,因此|()|nE f x dx ε<⎰,即lim ()0nE n f x dx →∞=⎰。
实变函数试题库参考答案

《实变函数》试题库及参考答案(完整版)选择题1,下列对象不能构成集合的是:( )A 、全体自然数B 、0,1 之间的实数全体C 、[0, 1]上的实函数全体D 、全体大个子2、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体整数}C 、{全体小个子}D 、{x :x>1}3、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体整数}C 、{x :x>1}D 、{全体胖子}4、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体整数}C 、{x :x>1}D 、{全体瘦子}5、下列对象不能构成集合的是:( )A 、{全体小孩子}B 、{全体整数}C 、{x :x>1}D 、{全体实数}6、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体大人}C 、{x :x>1}D 、{全体整数}7、设}1:{ααα≤<-=x x A , I 为全体实数, 则ααA I∈⋃= ( ) A 、(-1, 1) B 、(-1, 0) C 、(-∞, +∞) D 、(1,+∞)8、设}1111:{ix i x A i -≤≤+-=, N i ∈, 则i i A ∞=⋃1= ( ) A 、(-1, 1) B 、(-1, 0) C 、[0, 1]D 、[-1, 1]9、设}110:{ix x A i +≤≤=, N i ∈, 则i i A ∞=⋂1= ( ) A 、(0, 1) B 、[0, 1] C 、[0, 1] D 、(0, +∞)10、设}1211:{ix i x A i +<<-=, N i ∈, 则i i A ∞=⋃1= ( ) A 、[1, 2] B 、(1, 2) C 、 (0, 3) D 、(1, 2)11、设}23:{+≤≤=i x i x A i , N i ∈, 则i i A ∞=⋂1= ( ) A 、(-1, 1) B 、[0, 1] C 、Φ D 、{0}12、设}11:{ix i x A i <<-=, N i ∈, 则i i A ∞=⋂1= ( ) A 、(-1, 1) B 、[0, 1] C 、Φ D 、{0}13、设]1212,0[12--=-n A n , ]211,0[2nA n +=, N n ∈,则=∞→n n A lim ( )A 、[0, 2]B 、[0, 2]C 、[0, 1]D 、[0, 1]14、设]1212,0[12--=-n A n , ]211,0[2nA n +=, N n ∈, 则=∞→n n A lim ( ) A 、[0, 2]B 、[0, 2]C 、[0, 1]D 、[0,1]15、设),0(n A n =, N n ∈, 则=∞→n n A lim ( )A 、ΦB 、[0, n]C 、RD 、(0, ∞)16、设)1,0(nA n =, N n ∈, 则=∞→n n A lim ( ) A 、(0, 1)B 、(0, n1) C 、{0} D 、Φ 17、设)1,0(12nA n =-, ),0(2n A n =, N n ∈, 则=∞→n n A lim ( )A 、ΦB 、(0, n1) C 、(0, n) D 、(0, ∞) 18、设)1,0(12nA n =-, ),0(2n A n =, N n ∈, 则=∞→n n A lim ( ) A 、ΦB 、(0, n1) C 、(0, n) D 、(0, ∞) 19、设A 、B 、C 是三个集合, 则A-(A-B)= ( )A 、B B 、AC 、A ⋂BD 、A ⋃B20、设A 、B 、C 是三个集合, 则A-(B ⋃C)= ( )A 、(A-B)⋂(A-C)B 、(A-B)⋃(A-C)C 、A ⋂BD 、A ⋂C21、设A 、B 、C 是三个集合, 则A-(B ⋂C)= ( )A 、(A-B)⋂(A-C)B 、(A-B)⋃(A-C)C 、A ⋂BD 、A ⋂C22、设A 、B 、S 是三个集合, 且S A ⊂, S B ⊂, 则)(B A C s -= ( )A 、BC A C s s ⋃ B 、B C A C s s ⋂ C 、B A C s ⋃D 、B A C s ⋂23、设A 、B 、S 是三个集合, 且S A ⊂, S B ⊂, 则)(B A C s ⋃= ( )A 、BC A C s s ⋃ B 、B C A C s s ⋂ C 、B A C s ⋃D 、B C A s ⋃24、设A 、B 、C 是三个集合, 则A-(B-C) = ( )A 、 A ⋃C-B B 、 A-B-C C 、 (A-B)⋃(A ⋂C)D 、 C-(B-A)25、集合E 的全体内点所成的集合称为E 的 ( )A 、开核B 、边界C 、导集D 、闭包26、集合E 的全体聚点所成的集合称为E 的 ( )A 、开核B 、边界C 、导集D 、闭包27、集合E 的全体边界点和内点所成的集合是E 的 ( )A 、开核B 、边界C 、导集D 、闭包28、E-E '所成的集合是 ( )A 、开核B 、边界C 、外点D 、{E 的全体孤立点}29、E 的全体边界点所成的集合称为E 的 ( )A 、开核B 、边界C 、导集D 、闭包30、设点P 是集合E 的边界点, 则 ( )A 、P 是E 的聚点B 、P 是E 的孤立点C 、P 是E 的内点D 、P 是CE 的边界点31、设)3,2()1,0(⋃=G , 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(21, 1) C 、[0, 1] D 、(0, 2) 32、设)1,0(1=G , )2,21()0,1(2⋃-=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(0, 2)C 、(-1, 21) D 、(-1, 2) 33、设)4,0(1=G , )4,3()1,0(2⋃=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(3, 4)C 、(0, 4)D 、 (1, 4)34、设)1,0(1=G , )4,3()2,1(2⋃=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(0, 3)C 、(0, 4)D 、(1, 4)35、设)2,0(1=G , )4,3()2,1(2⋃=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(0, 2)C 、(1, 2)D 、(1, 4)36、设)2,1()1,0(1⋃=G , )23,21()0,1(2⋃-=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(21, 23) B 、(1, 2) C 、(0, 1) D 、(-1, 0) 37、若B A ⊂ ,则下列命题错误的是: ( )A 、B A ⊂ B 、A '⊂B 'C 、B A ∂⊂∂D 、B A ⊂38、若C B A =⋃, 则下列命题正确的是:( )A 、 CB A =⋃ B 、 A '⋃B '=C ' C 、C B A ∂=∂⋃∂D 、{A 的孤立点}⋃{B 的孤立点}={C 的孤立点}39、若C B A =⋂, 则下列命题错误的是:( )A 、 CB A =⋂ B 、C '⊂ A '⋂B ' C 、C B A =⋂D 、{A 的孤立点}⋂{B 的孤立点}={C 的孤立点}40、设CA 是A 的余集,则下列命题正确的是:( )A 、 )()(CA A C =B 、)(CA A ∂=∂C 、C(A ')=(CA )'D 、CA A C =)(41、设A -B=C, 则下列命题正确的是:( )A 、CB A ∂=∂-∂ B 、C B A =- C 、A '-B '=C 'D 、{A 的孤立点}-{B 的孤立点}={C 的孤立点}42、 (2-4-1-2) 下列命题错误的是:( )A 、A 是闭集B 、A '是闭集C 、A ∂是闭集D 、 A 是闭集43、若A 是闭集,B 是开集,则A -B 是:( )A 、开集B 、闭集C 、既非开集又非闭集D 、无法判断 44、若A 是开集,B 是闭集,则A -B 是:( )A 、开集B 、闭集C 、既非开集又非闭集D 、无法判断 45、若}{n A 是一开集列,则n n A ∞=⋃1是:( )A 、开集B 、闭集C 、既非开集又非闭集D 、无法判断 46、若}{n A 是一开集列,则n n A ∞=⋂1是:( )A 、开集B 、闭集C 、既非开集又非闭集D 、无法判断 47、若}{n A 是一闭集列,则n n A ∞=⋃1是:( )A 、开集B 、闭集C 、既非开集又非闭集D 、无法判断 48、若}{n A 是一闭集列,则n n A ∞=⋂1是:( )A 、开集B 、闭集C 、既非开集又非闭集D 、无法判断 49、若]1,0[ QE =,则=mE ( )A 、0B 、1C 、2D 、350、下述结论( )正确.A 、E m E m **>B 、E m E m *≥*C 、E m E m **<D 、E m E m **≤51、下列说法正确的是( )A 、x x f 1)(=在(0,1)有限B 、xx f 1)(=在)1,21(无界 C 、⎪⎩⎪⎨⎧=∞+∈=0,]1,0(,1)(x x x x f ,在[0,1]有限 D 、⎪⎩⎪⎨⎧=∈=0,1]1,0(,1)(x x x x f ,在[0,1]有界 52、函数列n n x x f =)(在[0,1]上( )于0.A 、a ,e 一致收敛B 、收敛C 、一致收敛D 、基本上一致收敛53、设E 是[0,1]中的不可测集,⎩⎨⎧-∈-∈=Ex E x x f ]1,0[,1,1)( 则下列函数在[0,1]上可测的是( ).A 、)(x fB 、)(x f +C 、|)(|x fD 、)(x f -54、若)(x f 可测,则它必是( ).A 、连续函数B 、单调函数C 、简单函数D 、简单函数列的极限55、若Q E -=]1,0[,则=mE ( )A 、0B 、1C 、2D 、356、下列说法不正确的是( )A 、E 的测度有限,则E 必有界B 、E 的测度无限,则E 必无界C 、有界点集的测度有限D 、n R 的测度无限57、(4-4-2-1)下述论断正确的是( )A 、x x f tg )(=在)4,0(π无界 B 、⎪⎩⎪⎨⎧=∞+∈=2,)2,0[,tg )(ππx x x x f 在]2,0[π有限 C 、⎪⎩⎪⎨⎧=∈=2,1)2,0[,tg )(ππx x x x f 在]2,0[π有界 D 、x x f tg )(=在)2,0(π有限58、函数列n n x x f )21()(=在[0, 2]上( )于0. A 、收敛 B 、一致收敛 C 、基本上一致收敛 D 、a.e.一致收敛59、设⎩⎨⎧-∈-∈=E x x E x x x f ]1,0[,,)(其中E 是[0,1]的不可测集,则下列函数在[0, 1]可测的是( ).A 、|)(|x fB 、)(x fC 、)(x f +D 、)(x f -60、一个函数在其定义域中的( )点处都是连续的.A 、边界点B 、内点C 、聚点D 、孤立点.61、0P 是康托尔(cantor )集,则=0mP ( )A 、0B 、1C 、2D 、362、设A 是B 的真子集,则( )A 、B m A m **< B 、B m A m **≤C 、B m A m **>D 、B m A m **≥63、下列说法正确的是( )A 、x x f ctg )(=在)2,4(ππ无界 B 、⎪⎩⎪⎨⎧=∞+∈=0,]2,0(ctg )(x x x x f π在]2,0[π有限 C 、⎪⎩⎪⎨⎧=∈=0,1]2,0(ctg )(x x xx f π在]2,0[π有界 D 、x x f ctg )(=在)2,0(π有限64、函数列n n n x x f 2)(=在]21,0[上( )于0. A 、收敛 B 、一致收敛、 C 、基本上一致收敛 D 、a. e.一致收敛65、设E 是[0, 1]上的不可测集,⎩⎨⎧-∈-∈=Ex xE x x x f ]1,0[)(22则下列函数在[0, 1]可测的是( ). A 、)(x f B 、)(x f + C 、|)(|x f D 、)(x f -66、设E 为可测集,则下列结论中正确的是( )A 、若)}({x f n 在E 上a , e 收敛于一个a , e 有限的可测函数)(x f ,则)(x f n 一致收敛于)(x fB 、若)}({x f n 在E 上a , e 收敛于一个a , e 有限的可测函数)(x f ,则)(x f n 基本上一致收敛于)(x fC 、若)}({x f n 在E 上a , e 收敛于一个a , e 有限的可测函数)(x f ,则)(x f n ⇒)(x fD 、若)}({x f n 在E 上基本上一致收敛于)(x f ,则)(x f n a , e 收敛于)(x f67、G 表示康托尔(cantor )集在[0,1]中的余集,则mG=( )A 、0B 、1C 、2D 、368、设21,S S 都可测,则21S S ( )A 、可测B 、不可测C 、可能可测也可能不可测D 、以上都不对69、下列说法正确的是( )A 、x x f sec )(=在)4,0(π上无界 B 、x x f sec )(=在)4,0(π上有限C 、⎪⎩⎪⎨⎧=∞+∈=2)2,0[sec )(ππx x x x f 在]2,0[π上有限 D 、⎪⎩⎪⎨⎧=∈=21)2,0[sec )(ππx x x x f 在]2,0[π上有界 70、函数列n n n x x f 3)(=在]31,0[上( )于0 A 、收敛 B 、一致收敛 C 、基本上一致收敛 D 、a. e.一致收敛71、设⎩⎨⎧-∈∈-=Ex x E x x x f ]1,0[,,)(33,其中E 是[0, 1]上的不可测集,则( )在[0, 1]可测.A 、)(x f 、B 、)(x f +C 、)(x f -D 、|)(|x f72、关于连续函数与可测函数,下列论述中正确的是( )A 、它们是同一概念B 、a , e 有限的可测函数是连续函数C 、a , e 有限的可测函数是基本上连续的函数D 、a , e 有限的可测函数是a , e 连续的函数73、()=-)2,1()1,0( m ( )A 、1、B 、2C 、3D 、474、A 可测,B 是A 的真子集,则( )A 、mB mA ≥ B 、B m mA *≥C 、B m mA *=D 、以上都不对75、下列说法正确的是( )A 、21)(x x f =在(0, 1)有限、B 、21)(xx f =在]1,21[无界 C 、⎪⎩⎪⎨⎧=∞+∈=0,]1,0(,1)(2x x x x f 在[0, 1]有限 D 、⎪⎩⎪⎨⎧=∈=1,1]1,0(,1)(2x x x x f 在[0, 1]有界76、函数列x x f n n sin )(=在]2,0[π上( )于0.A 、收敛B 、基本上一致收敛C 、一致收敛D 、a. e.一致收敛77、设⎩⎨⎧-∈∈-=Ex x E x x x f ]1,0[,,)(22其中E 是[0, 1]上的不可测集,则( )在[0, 1]上是可测的.A 、|)(|x fB 、)(x fC 、)(x f +D 、)(x f -78、关于简单函数与可测函数下述结论不正确的是( )A 、简单函数一定是可测函数B 、简单函数列的极限是可测函数C 、简单函数与可测函数是同一概念D 、简单函数列的极限与可测函数是同一概念79、()=-]3,2()1,1[ m ( )A 、1B 、2C 、3D 、480、L 可测集类,对运算( )不封闭.A 、可数和B 、有限交C 、单调集列的极限D 、任意和.81、下列说法正确的是( )A 、31)(x x f =在)1,21(无界B 、31)(xx f =在)1,0(有限C 、⎪⎩⎪⎨⎧=∞+∈=0]1,0(1)(3x x x x f 在[0, 1]有限D 、⎪⎩⎪⎨⎧=∈=01]1,0(1)(3x x x x f 在[0, 1]有界82、函数列x x f n n cos )(=在]2,0[π上( )于0.A 、基本一致收敛B 、收敛C 、一致收敛D 、a. e.一致收敛83、设E 是]2,0[π中的不可测集,⎪⎩⎪⎨⎧-∈-∈=E x x E x x x f ]2,0[,sin ,sin )(π 则下列函数在]2,0[π上可测的是( ).A 、)(x fB 、|)(|x fC 、)(x f +D 、)(x f -84、关于依测度收敛,下列说法中不正确的是( )A 、依测度收敛不一定一致收敛B 、依测度收敛不一定收敛C 、若)}({x f n 在E 上 a.e.收敛于 a.e.有限的可测函数)(x f ,则)()(x f x f n ⇒D 、若)()(x f x f n ⇒,则存在子列)}({x f i n a. e.收敛于)(x f85、设)(x f 是可测集E 上的非负可测函数,则)(x f ( )A 、必可积B 、必几乎处处有限C 、必积分确定D 、不一定积分确定86、设)(x f 在可测集E 上可积,则在E 上( )A 、)(x f +与)(x f -只有一个可积B 、)(x f +与)(x f -皆可积C 、)(x f +与)(x f -不一定可积D 、)(x f +与)(x f -至少有一个不可积87、设0=mE (Φ≠E ),)(x f 是E 上的实函数,则下面叙述正确的是( )A 、)(x f 在E 上不一定可测B 、)(x f 在E 上可测但不一定可积C 、)(x f 在E 上可积且积分值为0D 、)(x f 在E 上不可积88、)(x f 在可测集E 上)(L 可积的必要条件是,)(x f 为( )A 、连续函数B 、几乎处处连续函数C 、单调函数D 、几乎处处有限的可测函数89、设)(x D 为狄立克雷函数,则⎰=10)()(dx x D L ( ) A 、 0 B 、 1 C 、1/2 D 、不存在90、设)(x f 为Cantor 集的特征函数,则⎰=10)()(dx x f L ( ) A 、 0 B 、 1/3 C 、2/3 D 、 1填空题1、设A 为一集合,B 是A 的所有子集构成的集合;若A =n, 则B =2、设A 为一集合,B 是A 的所有子集构成的集合;若A 是一可数集, 则B =3、若c A =, c B =, 则=⋃B A4、若c A =, B 是一可数集, 则=⋃B A5、若c A =, n B =, 则=⋃B A6、若}{n A 是一集合列, 且c A n =, =⋃∞=n n A 1 7、若I A ∈αα}{是任意集族, 其中I 是指标集, 则ααA I∈⋂=8、若I A ∈αα}{是任意集族, 其中I 是指标集, 则ααA I∈⋃= 9、若I A ∈αα}{是任意集族, 其中I 是指标集, S 是一集合, 则)(ααA C IS ∈⋂= 10、若I A ∈αα}{是任意集族, 其中I 是指标集, S 是一集合, 则)(ααA C IS ∈⋃= 11、若}{n A 是任意一个集合列, 则=∞→n n A lim 12、若}{n A 是任意一个集合列, 则=∞→n n A lim13、欧氏空间n R 中, 任意两点),,(21n x x x x =, ),,(21n y y y y =的距离d(x, y)=14、C[a, b]空间中,任意两元素x(t), y(t) 的距离 d(x, y)= 15、2l 空间中, 任意两元素 ),,,(21 n x x x x =, ),,(21 n y y y y =的距离 d(x, y)=16、欧氏空间2R 中, 任意两点),(21x x x =, ),(21y y y =的距离 d(x, y)=17、欧氏空间3R 中, 任意两点),,(321x x x x =, ),,(321y y y y =的距离d(x, y)=18、欧氏空间4R 中, 任意两点),,,(4321x x x x x =, ),,,(4321y y y y y =的距离d(x,y)=19、设2R X =,}1:),{(22<+=y x y x E ,则E =20、设3R X =, }1:),,{(222<++=z y x z y x E , 则E =21、设2R X =,}1:),{(22<+=y x y x E ,则E ∂=22、设2R X =,}1:),{(22<+=y x y x E ,则E '=23、设3R X =, }1:),,{(222<++=z y x z y x E , 则 E ∂=24、设3R X =, }1:),,{(222<++=z y x z y x E , 则E '=25、设A= [0, 1] , B = [3, 4] , 则 d(A, B) =26、设C 是康托完备集, G= [0, 1]-C , 则d (C, G) =27、设C 是康托完备集, 则C 的半径)(C δ=28、两个非空集合A, B 距离的定义为 d (A, B ) =29、一个非空集合A 的直径的定义为)(A δ=30、设A = [0, 1] ⋂Q, 则)(A δ=31、n R E ⊂,对每一列覆盖E 的开区间 ∞=⊃1i i E I ,定义=E m *________。
实变函数试卷及参考答案
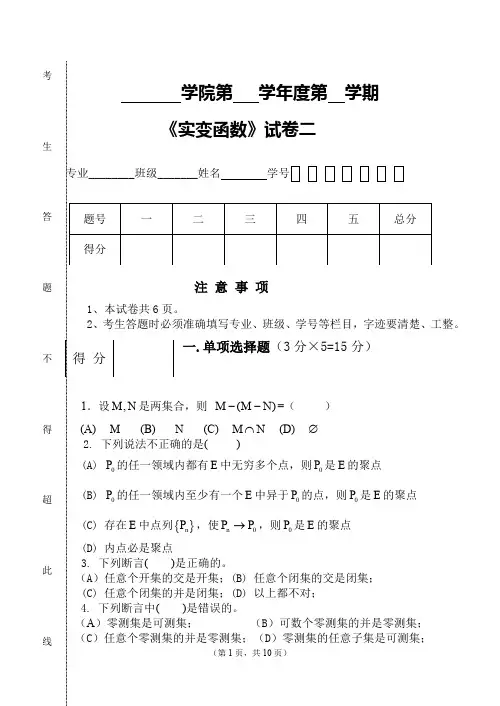
考生答题2不得超此线5. 若()f x 是可测函数,则下列断言( )是正确的 (A) ()f x 在[],a b L -可积|()|f x ⇔在[],a b L -可积; (B) [][](),|()|,f x a b R f x a b R -⇔-在可积在可积 (C) [][](),|()|,f x a b L f x a b R -⇔-在可积在可积; (D) ()()(),()f x a R f x L +∞-⇒∞-在广义可积在a,+可积二. 填空题(3分×5=15分)1、设11[,2],1,2,n A n n n=-= ,则=∞→n n A lim _________。
2、设P 为Cantor 集,则 =P ,mP =_____,oP =________。
3、设{}i S 是一列可测集,则11______i i i i m S mS ∞∞==⎛⎫⋃ ⎪⎝⎭∑4、鲁津定理:_____________________________________________________________________________________________________________________ 5、设()F x 为[],a b 上的有限函数,如果_________________________________ _____________________________________________________________________________________________则称()F x 为[],a b 上的绝对连续函数。
三.下列命题是否成立?若成立,则证明之;若不成立,则说明原因或举出反例.(5分×4=20分)1、由于[](){}0,10,10,1-=,故不存在使()[]0,101和,之间11-对应的映射。
2、可数个零测度集之和集仍为零测度集。
(0195)《实变函数论》网上作业题及答案

[0195]《实变函数论》第一次作业[单选题]1.开集减去闭集是()A:A.开集B:B.闭集C:C.既不是开集也不是闭集参考答案:A[单选题]2.闭集减去开集是()A:开集B:闭集C:既不是开集也不是闭集参考答案:B[单选题]3.可数多个开集的交是()A:开集B:闭集C:可测集参考答案:C[单选题]4.可数多个闭集的并是()A:开集B:闭集C:可测集参考答案:C[单选题]6.可数集与有限集的并是()A:有界集B:可数集C:闭集参考答案:B[判断题]5.任意多个开集的并仍是开集。
参考答案:正确[单选题]8.可数多个有限集的并一定是()A:可数集B:有限集C:以上都不对参考答案:C[单选题]7.设f(x)是定义在[a,b]上的单调函数,则f(x)的间断点集是()A:开集B:闭集C:可数集参考答案:C[单选题]9.设f(x)是定义在R上的连续函数,E=R(f>0),则E是A:开集B:闭集C:有界集参考答案:A[单选题]10.波雷尔集是()A:开集B:闭集C:可测集参考答案:C[判断题]7.可数多个零测集的并仍是零测集合。
参考答案:正确[单选题]1.开集减去闭集是()。
A:A.开集 B.闭集 C.既不是开集也不是闭集参考答案:A[单选题]5.可数多个开集的并是()A:开集B:闭集C:可数集参考答案:A[判断题]8.不可数集合的测度一定大于零。
参考答案:错误[判断题]6.闭集一定是可测集合。
参考答案:正确[判断题]10.开集一定是可测集合。
参考答案:正确[判断题]4.连续函数一定是可测函数。
参考答案:错误[判断题]3.零测度集合或者是可数集合或者是有限集。
参考答案:正确[判断题]2.有界集合的测度一定是实数。
参考答案:正确[判断题]1.可数集合是零测集参考答案:正确[判断题]9.任意多个闭集的并仍是闭集。
参考答案:错误[判断题]9.任意多个闭集的并仍是闭集。
参考答案:错误第二次作业[单选题]4.设E是平面上边长为2的正方形中所有无理点构成的集合,则E的测度是A:0B:2C:4参考答案:C[单选题]3.设E是平面上边长为2的正方形中所有有理点构成的集合,则E的测度是A:0B:2C:4参考答案:A[单选题].2.[0,1] 中的全体有理数构成的集合的测度是()A:0B:1参考答案:A[单选题]1.[0,1] 中的全体无理数构成的集合的测度是()A:0B:1C:2参考答案:B[单选题]5.若E是R的子集,x是一个实数,如果x的任何邻域内均有E中异于x的点,则x是E的()A:内点B:界点C:聚点参考答案:C[判断题]10.简单函数一定是可测函数。
实变函数本科试题及答案
实变函数本科试题及答案一、选择题(每题5分,共20分)1. 实变函数论主要研究的是:A. 数学分析B. 复变函数C. 函数的实值性D. 函数的连续性答案:C2. 以下哪个命题是实变函数论中的基本定理?A. 中值定理B. 泰勒公式C. 勒贝格控制收敛定理D. 柯西-施瓦茨不等式答案:C3. 勒贝格积分与黎曼积分的主要区别在于:A. 定义方式B. 积分值C. 积分对象D. 积分方法答案:A4. 若函数f在区间[a,b]上连续,则以下哪个命题一定成立?A. f在[a,b]上可积B. f在[a,b]上可微C. f在[a,b]上单调D. f在[a,b]上一致连续答案:A二、填空题(每题5分,共20分)1. 若函数f在区间[a,b]上处处有定义,则f在[a,b]上是______的。
答案:有界2. 函数f(x)=x^2在区间[0,1]上的勒贝格积分值为______。
答案:1/33. 勒贝格积分的一个重要性质是______。
答案:可加性4. 若函数f在区间[a,b]上单调增加,则f在[a,b]上是______的。
答案:可积三、简答题(每题10分,共30分)1. 简述实变函数论与复变函数论的主要区别。
答案:实变函数论主要研究实数域上的函数,关注的是函数的实值性质,如连续性、可积性等。
而复变函数论研究的是复数域上的函数,关注的是函数的解析性质,如解析延拓、复积分等。
2. 描述勒贝格积分的定义过程。
答案:勒贝格积分的定义过程首先将积分区间划分为若干子区间,然后选择每个子区间上的样本点,计算函数在这些样本点上的值与子区间长度的乘积之和,最后取这个和的极限,当这个极限存在时,就定义为函数的勒贝格积分。
3. 举例说明实变函数论在数学分析中的应用。
答案:实变函数论在数学分析中的应用非常广泛,例如在研究函数的极限性质、连续性、可微性和可积性等方面都有重要应用。
一个具体的例子是勒贝格控制收敛定理,它在处理函数序列的极限问题时非常有用,特别是在概率论和统计学中,勒贝格积分被用来定义随机变量的期望值。
实变函数(复习资料,带答案)
---《实变函数》试卷一一、单项选择题( 3 分×5=15 分)1、下列各式正确的是()( A) lim A n A k ;(B) lim A nn 1 k n A k ;n n 1 k n n( C) lim A n A k ;( D) lim A nn 1 k A k ;n n 1 k n n n2、设 P 为 Cantor 集,则下列各式不成立的是()(A)P c (B)mP 0(C)P'P(D)P P3、下列说法不正确的是()(A)凡外侧度为零的集合都可测( B)可测集的任何子集都可测(C) 开集和闭集都是波雷耳集(D)波雷耳集都可测4、设f n ( x) 是 E 上的a.e.有限的可测函数列 , 则下面不成立的是()(A)若f n(x) f ( x) ,则f n( x) f ( x)(B)sup f n ( x) 是可测函数(C)inf f n (x) 是可测函数 ; ( D)若n nf n (x) f (x) ,则 f (x) 可测5、设 f(x) 是[ a,b]上有界变差函数,则下面不成立的是()(A) f (x) 在 [ a, b] 上有界(B)f ( x) 在 [ a,b] 上几乎处处存在导数(C)f'( x)在[ a, b]上 L 可积 (D)bf '(x)dx f (b) f (a)a二.填空题 (3 分× 5=15 分 )1、(C s A C s B) ( A ( A B))_________2、设 E 是 0,1 上有理点全体,则oE' =______, E =______, E =______.3、设 E 是 R n中点集,如果对任一点集T 都,则称 E是L可测的4、f ( x)可测的 ________条件是它可以表成一列简单函数的极限函数 . (填“充分”,“必要”,“充要”)5、设f (x)为 a, b 上的有限函数,如果对于a, b 的一切分划,使_____________________________________则,称f ( x)为a, b 上的有界变差函数。
《实变函数》试卷及参考答案
《实变函数》试卷及参考答案《实变函数》试卷一一、单项选择题(3分×5=15分)1、1、下列各式正确的是( ),,,,limAA,,,limAA,,,(A); (B); nknk,,,,nnkn11nknn,,,,,,,,limAA,,,limAA,,,(C); (D); nknk,,,,nnkn1,,nkn1,,n2、设P为Cantor集,则下列各式不成立的是( ),'P,mP,0(A) c (B) (C) (D) P,PP,P3、下列说法不正确的是( ) (A) 凡外侧度为零的集合都可测(B)可测集的任何子集都可测(C) 开集和闭集都是波雷耳集 (D)波雷耳集都可测fx()E是上的有限的可测函数列,则下面不成立的是( ) 4、设ae..,,n sup()fxfxfx()(),fxfx()(),(A)若, 则 (B) 是可测函数 ,,nnnnfxfx()(), (C)是可测函数;(D)若,则可测 inf()fxfx(),,nnn5、设f(x)是上有界变差函数,则下面不成立的是( ) [a,b](A) 在上有界 (B) 在上几乎处处存在导数 f(x)[a,b]f(x)[a,b]b'f'(x)dx,f(b),f(a)f(x)(C)在上L可积 (D) [a,b],a二. 填空题(3分×5=15分)()(())CACBAAB,,,,,1、_________ sso'E0,12、设是上有理点全体,则=______,=______,=______. EEE,, nET3、设是中点集,如果对任一点集都有R1 (第页,共47页)EL_________________________________,则称是可测的、可测的________条件是它可以表成一列简单函数的极限函数. 4f(x)(填“充分”,“必要”,“充要”)ab,ab,5、设为上的有限函数,如果对于的一切分划,使fx(),,,,ab,______________________,则称为上的有界变差函数。
实变函数(复习资料_带答案)资料
集。
0, 开集 G E,使 m* (G E)
,则 E 是可测
(第 7 页,共 19 页)
3. (6 分)在 a, b 上的任一有界变差函数 f ( x) 都可以表示为 两个增函数之差。
5. (8 分)设 f ( x) 在 E a,b 上可积,则对任何 0 ,必存
b
在 E 上的连续函数 ( x) ,使 | f ( x) (x) | dx . a
E
四、解答题 (8 分× 2=16 分) .
1、(8分)设 f (x)
x2, x为无理数 ,则 f ( x) 在 0,1 上是否 R
1, x为有理数
可积,是否 L 可积,若可积,求出积分值。
五、证明题 (6 分× 4+10=34 分) . 1、(6 分)证明 0,1 上的全体无理数作成的集其势为 c
可测集;
二. 填空题 (3 分× 5=15 分)
1、设 An
11 [ , 2 ], n 1,2,
,则 lim An
_________。
nn
n
2、设 P 为 Cantor 集,则 P
o
,mP _____,P =________。
3、设 Si 是一列可测集,则 m i 1 Si ______ mSi i1 4、鲁津定理:
4.(8 分)设函数列 fn (x) ( n 1,2, ) 在有界集 E 上“基本上” 一致收敛于 f ( x) ,证明: fn (x) a.e.收敛于 f ( x) 。
2. x
E , 则存在 E中的互异点列
{
xn },
使 lim n
xn
x ……… .2
分
xn E, f ( xn ) a ………………… .3 分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实变函数论考试试题及答案
证明题:60分
1、证明 1lim =n m n n m n A A ∞
∞
→∞
==UI 。
证明:设lim n n x A →∞
∈,则N ∃,使一切n N >,n x A ∈,所以I
∞
+=∈
1
n m m A x Y I ∞=∞
=⊂1n n
m m A ,
则可知n n A ∞
→lim YI ∞
=∞
=⊂1n n
m m A 。
设YI ∞
=∞
=∈1n n
m m A x ,则有n ,使I ∞
=∈n
m m A x ,所以
n n A x lim ∞
→∈。
因此,n n A lim ∞
→=YI ∞=∞
=1n n
m m A 。
2、若n R E ⊂,对0>∀ε,存在开集G , 使得G E ⊂且满足 *()m G E ε-<, 证明E 是可测集。
证明:对任何正整数n , 由条件存在开集E G n ⊃,使得()1*m G E n
-<。
令I ∞
==1n n G G ,则G 是可测集,又因()()1**n m G E m G E n
-≤-<
, 对一切正整数n 成立,因而)(E G m -*=0,即E G M -=是一零测度集,故可测。
由)(E G G E --=知E 可测。
证毕。
3、设在E 上()()n f x f x ⇒,且1()()n n f x f x +≤几乎处处成立,Λ,3,2,1=n , 则有{()}n f x .收敛于)(x f 。
证明 因为()()n f x f x ⇒,则存在{}{}i n n f f ⊂,使()i n f x 在E 上.收敛到()f x 。
设
0E 是()i n f x 不收敛到()f x 的点集。
1[]n n n E E f f +=>,则00,0n mE mE ==。
因此
()0n n n n m E mE ∞∞==≤=∑U 。
在1
n n E E ∞
=-U 上,()i n f x 收敛到()f x , 且()n f x 是单调的。
因此()n f x 收敛到()f x (单调序列的子列收敛,则序列本身收敛到同一极限)。
即除去一个零集1n n E ∞
=U 外,()n f x 收敛于()f x ,就是()n f x . 收敛到()f x 。
4、设1R E ⊂,()x f 是E 上..e a 有限的可测函数。
证明存在定义于1R 上的一列 连续函数)}({x g n ,使得 )()(lim x f x g n n =∞
→ ..e a 于E 。
证明: 因为)(x f 在E 上可测,由鲁津定理,对任何正整数n ,存在E 的可测子 集n E ,使得()1
n m E E n
-<
,同时存在定义在1R 上的连续函数)(x g n ,使得当 n E x ∈时有)(x g n =)(x f 。
所以对任意的0η>,成立n n E E g f E -⊂≥-][η,
由此可得 ()1
n n mE f g m E E n
η⎡-≥⎤≤-<⎣⎦。
因此 0][lim =≥-∞
→ηn n g f mE ,即)()(x f x g n ⇒,由黎斯定理存在(){}x g n 的
子列
(){}x g k
n ,使得
)()(lim x f x g k n k =∞
→ 于E . 证毕 5、设,mE <∞{}n f 为有限可测函数列,证明:
()
lim 01()n E n n
f x dx f x →∞=+⎰ 的充要条件是()0n f x ⇒。
证明:若⇒)(x f n 0,由于1n n n f E E f f σσ⎡⎤≥⊂⎡≥⎤⎢⎥⎣⎦+⎣⎦
,则01⇒+n n f f 。
又()
011()
n n f x f x ≤
<+,()Λ3,2,1=n ,mE <∞,常函数1在E 上可积分,由
勒贝格控制收敛定理得00)
(1)(lim
==+
⎰⎰∞→E
E
n n n dx dx x f x f 。
反之,若0)
(1)(→+⎰
dx x f x f E
n n (∞→n ),而且
0)
(1)(⇒+x f x f n n ,对0σ∀>,
令n n e E f σ=⎡≥⎤⎣⎦,由于函数x x
y +=1,当1x >-时是严格增加函数,
因此
0)
(1)()
(1)(1→+≤+≤+⎰
⎰
dx x f x f dx x f x f me E
n n e n n n n
σ
σ。
所以[]0lim
=≥σn n
f E ,即0(x )⇒n f
6、设mE <∞,.有限的可测函数列()n f x 和()n g x ,Λ,3,2,1=n ,分别依 测度收敛于)(x f 和)(x g ,证明 ()()()()n n f x g x f x g x +⇒+。
证明:因为()()()()()()()()n n n n f x g x f x g x f x f x g x g x +--≤-+- 于是0δ∀>,成立
[|()()|][||][||]22
n n n n E f g f g E f f E g g δδ
δ+-+≥⊂-≥-≥U ,
所以
[|()()|][||][||]22
n n n n mE f g f g mE f f mE g g δδ
δ+-+≥≤-≥+-≥ lim [|()()|]lim [||]lim [||]022n n n n n n n mE f g f g mE f f mE g g δδ
δ→∞→∞→∞+-+≥≤-≥+-≥=
即n n g f g f +⇒+ 填空题:10分
2、设(){}2
2
2,1E x y x y =
+<。
求2
E 在2
R 内的'2
E ,0
2E ,2
E 。
解:(){}22
2
,1E x y x y '=+≤, (){}22
2
,1E x y x y =+<o
, (){}22
2
,1E x y x y =+<。
计算题:30分
4、试构造一个闭的疏朗的集合[0,1]E ⊂,12
mE =。
解:在[0,1]中去掉一个长度为1
6
的开区间57(,)1212,接下来在剩下的两个闭区间
分别对称挖掉长度为11
63
⨯的两个开区间,以此类推,一般进行到第n 次时,
一共去掉12-n 个各自长度为111
63
n -⨯的开区间,剩下的n 2个闭区间,如此重复
下去,这样就可以得到一个闭的疏朗集,去掉的部分的测度为
11112121663632
n n --+⨯++⨯+=L L 。
所以最后所得集合的测度为11122mE =-=,即1
2
mE =。
8、试求 2
1
211
()(1)n
n x R dx x ∞
-=+∑⎰。
解 令2
2(),[1,1](1)n n
x f x x x =
∈-+,则()n f x 为非负连续函数,从而非负可积。
根据L 积分逐项积分定理,于是,
22
1
221[1,1]112
2[1,1]
1[1,1]
()()(1)(1)()(1)
()12n n n n n n x x R dx L dx x x x L dx x L dx
∞
∞
--==∞
-=-=++=+==∑∑⎰⎰∑⎰⎰。
10、试从
()()
,10,111
32<<+-+-=+x x x x x
Λ求证 111
ln 21234
=-+-+L。
证明:在[0,1]x ∈时,1
0,1,2,3,n
n x x
n +-≥=L ,由L 逐项积分定理,
()()()221
221[0,1]
[0,1]0
01
2210
00()()()1
121221111234
n
n n n n n n n n n L x x
dx L x x dx
R x x dx
n n ∞
∞
++==∞+=∞
=-=-=-⎛⎫=- ⎪
++⎝
⎭=-+-+∑∑⎰
⎰
∑⎰∑L
另一方面
1[0,1]01
1()()211L dx R dx ln x x
==++⎰⎰
因此可得:
111
ln 21234
=-+-+L。
