电路的频率响应36页PPT
合集下载
课件:频率响应概述

最大误差 3 dB
φ
0 0.1fL -20
fL 10fL
900
f 450
最大误差 5.710
-40
0 20dB /十倍频
0.1fL fL 10fL f
上一页 返 回 下一页
低通电路波特图
20lg Au 20lg 1 f fH 2 arctg f fH
20lg|Au |/dB 最大误差 3 dB
f
|Au |
1 0.707
Au
1
1 fL / f 2
φ
900
arg tg fL f
450
00
fL
f
fL
f
上一页 返 回 下一页
三、低通电路
1
R
A u
R
jC
1
1
1 jRC
+
+
jC
Ui
C Uo
时τH
=
1 2π RC
A u
1
1
j H
1
j
1 f
fH
RC低通电路
5.1 频率响应概述
基本概念
波特图
高通电路
低通电路
一、频率响应的概念
A Au ( f )( f )
A u f 幅频特性
|Au | Aum
0.707Aum
f 相频特性
fL :称为下限频率 fH :称为上限频率 fbw :称为通频带
fbw fH fL
O fL
φ
00 900 1800
-2700
fbw
fH
f
f
返 回 下一页
• 频率失真
动画
二、高通电路
Au = R+
《模拟电子技术》课件第5章放大电路的频率响应
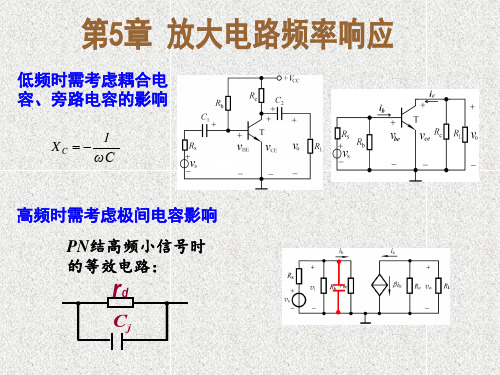
中频增益或通 带源电压增益
f
H
1 2πRC
上限频率
②高频响应和上限频率
共射放大电路
A VSH A VSM 1
1 j( f
/
fH )
RC低通电路
A VH
1
1 j( f
/
fH )
频率响应曲线变化趋势相同
幅频响应
20l g|A VSH | 20l g|A VSM |
20lg
1
1 ( f / fH )2
最大误差 -3dB
1 fH 2 πRC
fH称转折频率,上限截止 频率(上限频率),AVH(s) 的极点频率。
10
2. 低频特性
---- RC高通电路
RC高通电路
RC电路的电压增益:
AVH
Vo Vi
R
R
1
j ωC
1
1 1
j 2 πfR C
令
fL
1 2 πR
C
AVH
Vo Vi
1
1 j(fL /
f)
gmV b'e rce—c-e间的动态电阻(约100kΩ)
Cbe --发射结电容
互导
gm
iC vBE
VCE
iC vBE
VCE
2.混合等效电路中各元件的讨论: 简化模型 rce RL 略去rce
rbc
1 jω Cbc
略 去rbc
混合型高频小信号模型
晶体管的混合Π型等效电路
3.混合型等效电路的获得 低频时,混合模型与H参数模型等价
β0
1 ( f / fβ )2
的相频响应 arctg f
fβ fβ ——共发射极截止频率
第6章 电路频率响应图文

对于(b)图情况,若以 相量,则N的网络函数
U 2 为响应
西 若以 I2为响应相量,则N的网络函数
安
H2 H3 j H4 j
j I2 S单位
IUI2s2Us无Ω单单位位
Is
(6.1-3) (6.1-4) (6.1-5)
电 观察式(6.1-2)~(6.1-5),显而易见:
子
科 技 大
(1)若网络N的结构、元件值一定,当选定激励端与响应端时,H1(jω)~H4(jω) 只是频率的函数。
西 安
大它只输是出最电大压输U2=出U1功,率所的以一最半大,输因出此功3率分正贝比频于率U点12又,称当为ω半=功ω率c时频,U率2 点U。1
2,
电
子 科
说明:(1)3分贝频率点或半功率频率点即是前述的截止频率点,它只是人为
技 定义出来的一个相对标准。
大 学
(2)按 1
2 关系来定义通频带边界频率即截止频率的实际背景与“历史”原
>ωc时,输出信号是减小了,但不是零,并没有明显截止的“界限”。
第 6-9 页
前一页
下一页
回本章目录
6.2 常用一阶电路的频率响应
网络的截止角频率是个重要概念,在滤波网络中经常用到。那么,截止 角频率的电路含义是什么,如何确定它的数值呢?
实际低通网络的截止角频率是指网络函数的幅值 H( j)下降到 H ( j0) 值 0.707即 1 2 倍时所对应的角频率,记为ωc。
H
j
响应相量 激励相量
(6.1-1)
(4)可以是同一对端钮上 的相量,也可以是非同一
对端钮上的相量。
第 6-2 页
前一页
下一页 回本章目录
6.1 网络函数与频率响应
电路课件 电路11 电路的频率响应精品文档

S S(j0)R2(Ij0)U S 2(R j0)P (j0)
• Q也可根据谐振时L或C无功和R消耗有功比值定: Q R 0L 2(2 I(jI j 0)0)Q P L ((jj 0 0 ))Q P C ((jj 0 0 ))
第十一章 正弦稳态电路的分析 11-2 串联电路的谐振
RZ(j)
lim Z(j)
0
第十一章 正弦稳态电路的分析 11-2 串联电路的谐振
2019/10/15
4
ω =ω 0串联谐振-1
• 串联电路感抗和容抗有相互抵消作用,ω =ω 0
时,出现X(jω 0)=0,重要特征:
(1态) 称(j谐 0 ) 振 0 ,I R(Lj C0 串)、 联U S ( 电j 路0 )同发相生,,工称程串上联将谐特振殊。状
接收,利用谐振过电压获得较大输入信号。
第十一章 正弦稳态电路的分析 11-2 串联电路的谐振
2019/10/15
7
ω =ω 0串联谐振-4
• 可测定谐振时L或C电压得Q : • 谐振时QRU U 端C S((电jj 压00)):U USL((jj 00))
U R(j0)U S(j0)
路发生谐振与否。R是控制、调节谐振峰的唯
一元件。
• 图11-4两种R时
电流幅频特性。
第十一章 正弦稳态电路的分析 11-2 串联电路的谐振
2019/10/15
6
ω =ω 0串联谐振-3
(3U )X X((jj ω0) 0)j=( 00 :L 1 0 C )I (j 0)j R 0 L U S(j 0)j 0 1 CU S R (j 0) • L、C串 联U 相L (j当0) 于 U 短C 路(j,0)但 0U L(j0)、 U C (j0)0
• Q也可根据谐振时L或C无功和R消耗有功比值定: Q R 0L 2(2 I(jI j 0)0)Q P L ((jj 0 0 ))Q P C ((jj 0 0 ))
第十一章 正弦稳态电路的分析 11-2 串联电路的谐振
RZ(j)
lim Z(j)
0
第十一章 正弦稳态电路的分析 11-2 串联电路的谐振
2019/10/15
4
ω =ω 0串联谐振-1
• 串联电路感抗和容抗有相互抵消作用,ω =ω 0
时,出现X(jω 0)=0,重要特征:
(1态) 称(j谐 0 ) 振 0 ,I R(Lj C0 串)、 联U S ( 电j 路0 )同发相生,,工称程串上联将谐特振殊。状
接收,利用谐振过电压获得较大输入信号。
第十一章 正弦稳态电路的分析 11-2 串联电路的谐振
2019/10/15
7
ω =ω 0串联谐振-4
• 可测定谐振时L或C电压得Q : • 谐振时QRU U 端C S((电jj 压00)):U USL((jj 00))
U R(j0)U S(j0)
路发生谐振与否。R是控制、调节谐振峰的唯
一元件。
• 图11-4两种R时
电流幅频特性。
第十一章 正弦稳态电路的分析 11-2 串联电路的谐振
2019/10/15
6
ω =ω 0串联谐振-3
(3U )X X((jj ω0) 0)j=( 00 :L 1 0 C )I (j 0)j R 0 L U S(j 0)j 0 1 CU S R (j 0) • L、C串 联U 相L (j当0) 于 U 短C 路(j,0)但 0U L(j0)、 U C (j0)0
2020年电路第11章电路的频率响应

UL
UC
j0 LI j0 L
j I
0 C
j0
U R L
U R
j QU jQU
U L UC QU
特性阻抗
品质因数
Q 0L 1 L
R RC R
(3) 谐振时出现过电压
当 =0L=1/(0C )>>R 时,Q>>1
QC
1 ω0C
I
2 0
0 LI02
注意 电 源 不 向 电 路 输 送
L
C
无功。电感中的无功与电 +
Q
容中的无功大小相等,互 _ 相补偿,彼此进行能量交
R P
换。
返回 上页 下页
(5) 谐振时的能量关系
设 u Um
uC
Im
0C
sin 0t
sin(0t
则 i
90o )
Um R
(2 j)I1 2I2 US
2I1 (4 j)I2 0
I2
4
2US
(j)2
j6
I2
/US
4
2
2
j6
UL
/US
4
j 2 2
j6
转移电压比
返回 上页 下页
注意 ①以网络函数中jω的最高次方的次数定义网络
函数的阶数。 ②由网络函数能求得网络在任意正弦输入时
1. G、C、L 并联电路
Y
G
j(ωC
1 ωL
)
谐振角频率
ω0
1 LC
电路第五版课件-第十一章电路的频率响应-PPT

f
1 2 LC
可知调谐的方法有:
(1) L、C 不变,改变电源 ( f )。可用于L或C的测量
(2) 电源频率 ( f )不变,改变L 或 C (常改变 C )。
用于选择信号。
14
3. 串联谐振电路的特点
(1)电路端口电压与电流同相位,电路呈纯电阻性 ;
(2) |Z|R 最小,电路中的电流达到最大; I US R
U(j)
4
(2) 转移函数(传递函 数) ①激励是电压源
. H(j) U. 2(j)
U1(j)
(响应与激励不在同一端口)
.
I1(j)
.
I2(j)
.
U1(j)
无源 线性 网络
.
U2(j) ZL
为转移电压比; ②激励是电流源
. H(j) I. 2(j)
U1(j) 为转移导纳。
. H(j) I.2(j) 为转移电流比。
为便于比较不同参数的RLC串联电路的频率响应之间在性
能上的差异,纵、横坐标都采用相对于谐振点的比值作为
绘制频率特性的坐标系。即
横坐标: 0
纵坐标:U ( jω) US ( jω0 )
这样所有的RLC电路都在同一个相对尺度下来比较相
互频率特性的差异(偏谐程度)。这样绘制的频率响应
曲线称为通用曲线。
17
例:某收音机的输入回路如图,L=0.3mH;R=10, 为收到中央电台560kHz信号,求调谐电容C值;若 输入电压为1.5V,求谐振电流和此时的电容电压。
解:由串联谐振的条件: C 1 269pF (2f0)2L
I0
U R
1.5 10
0.15A
UC
I0
1
简单RC低通和高通电路的频率响应ppt课件
高通和低通滤波电路的 组成、分析、结论 会有何异同?
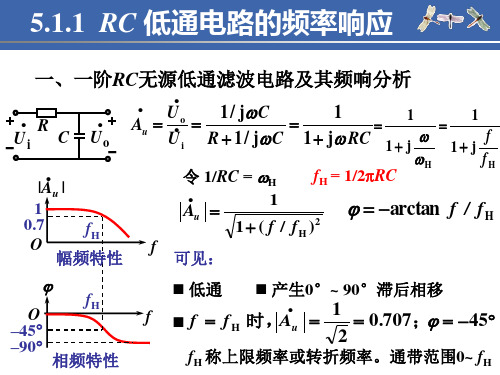
5.1.2 RC 高通电路的频率响应
一、一阶RC无源高通滤波电路及其频响分析
•
Au
U•o U•i
R
R 1 / j C
1
1 1/j RC
1
1
1 j L
1 j
fL
f
令 1/RC = L
fL = 1/2RC
A u
1 1 ( fL / f )2
H
fH
fH = 1/2RC
.
Au
1-
1
jL
1 1- j fL
f
fL = 1/2RC
讨论小结: 渐近波特图
一阶无源低通
一阶无源高通
幅频波特图特点:以截止频率为界,通带内是一条0dB水平线, 通带外是一条斜率为 20dB/十倍频的斜线。
相频波特图特点:在大于10倍截止频率和小于0.1倍截止频率时 是一条 0 或 90 的水平线,在(0.1~10)倍截止频率范 围内为斜率为 45°/ 十倍频的斜线,且在截止频率处相移 45°。
O 幅频特性 f 可见:
O
fH
–45
–90 相频特性
低通 产生0°~ 90°滞后相移
f
f
f H 时,A•u
1Hale Waihona Puke 0.707; 452fH 称上限频率或转折频率。通带范围0~ fH
二、一阶RC无源低通滤波电路的渐近波特图
何谓波特图?为何采用波特图表示? 何谓近似波特图(也称渐近波特图、理想波特图)?
|A•u |
1
0.7
fH
O 幅频特性 f
fH
O
f
–45
–90 相频特性
5.1.2 RC 高通电路的频率响应
一、一阶RC无源高通滤波电路及其频响分析
•
Au
U•o U•i
R
R 1 / j C
1
1 1/j RC
1
1
1 j L
1 j
fL
f
令 1/RC = L
fL = 1/2RC
A u
1 1 ( fL / f )2
H
fH
fH = 1/2RC
.
Au
1-
1
jL
1 1- j fL
f
fL = 1/2RC
讨论小结: 渐近波特图
一阶无源低通
一阶无源高通
幅频波特图特点:以截止频率为界,通带内是一条0dB水平线, 通带外是一条斜率为 20dB/十倍频的斜线。
相频波特图特点:在大于10倍截止频率和小于0.1倍截止频率时 是一条 0 或 90 的水平线,在(0.1~10)倍截止频率范 围内为斜率为 45°/ 十倍频的斜线,且在截止频率处相移 45°。
O 幅频特性 f 可见:
O
fH
–45
–90 相频特性
低通 产生0°~ 90°滞后相移
f
f
f H 时,A•u
1Hale Waihona Puke 0.707; 452fH 称上限频率或转折频率。通带范围0~ fH
二、一阶RC无源低通滤波电路的渐近波特图
何谓波特图?为何采用波特图表示? 何谓近似波特图(也称渐近波特图、理想波特图)?
|A•u |
1
0.7
fH
O 幅频特性 f
fH
O
f
–45
–90 相频特性
模拟电子技术基础 第五章 频率响应PPT课件

第5章 频率响应
UCRUCRUCRsississisCrCrRbCrRbbRbebsebseesee((rr(RCrrbRbCrrbRbCbbSbeMbSeMbSeMrrrrbbrrbCbbeCbbCebebb)Ub)Ub)Ueeesss((1(1R1RRssrgsrbgrbgbmemermeRrbrRbRebeLeLUL)U)UC)CsCsbsbbeee
U1 -
Z1
Z
N
A(jω) =
U2 U1
(a)
I2 +
U2 -
Z2
图5–7 (a)原电路;
(b)等效后的电路
I1 +
U1 -
N
Z1
A(jω) =
U2 U1
第5章 频率响应
I2 +
Z2
U2
-
(b)
图5–7 (a)原电路;
(b)等效后的电路
第5章 频率响应
Z1Z1ZU11IU1I1 11UUII1111 UU 1U1UUZZ1U11ZU1UUZ1U12U2221111ZUUZ2ZZUU2UU12U2U2121212 111Z1ZAZAuZAu Au u
(5–1) (5–2a) (5–2b)
第5章 频率响应
图5–2给出了不产生线性失真的振幅频率响应和相 位频率响应,称之为理想频率响应。
|Au(jω)|
(jω)
K
0
0
ω
ω
∞ω
(a)
(b)
图5–2 (a)理想振幅频率响应;(b)理想相位频率响应
第5章 频率响应
5–1–2实际的频率特性及通频带定义 实际的振幅频率特性一般如图5–3所示。在低频和
三、高频增益表达式及上限频率
第5章 频率响应
