学而思奥数四年级暑期课程经典题型
学而思入学必备题型奥数题答案及解析

小学四年级奥数题及解析第1题:计算:123456789101120082009201020112012_____L--++--++--+++--+=A:0B:4C:8B:2012答案:A 解题思路:本题考查学生的观察能力以及对加法交换律的灵活应用:在式子的尾端加上2013再减去2013,让整个算式更有规律性。
解题思路:1-2-3+4+5-6-7+8+9-10-11+…+2008+2009-2010-2011+2012+2013-2013=1+(4-2)+(5-3)+(8-6)+(9-7)+…+(2012-2010)+(2013-2011)-2013=(2013-1)÷2×2+1-2013=0⨯第2题:下面是一个乘法算式,问当乘积最大时,所填的四个数字的和是______。
5A:27B:24C:20D:22答案:B 解题思路:我们从题中知道两位数乘以5等于两位数,积最大时就是用最小的三位数100-5=95;因此可知道积是95,那么一个乘数就是19,因此1+9+9+5=24。
第3题:算式2357111317⨯⨯⨯⨯⨯⨯最后得到的乘积中,所有数位上的数字和是______。
A:12B:24C:15D:18答案:A 解题思路:2×3×5×7×11×13×17=(7×13×11)×(3×17)×(2×5)=1001×51×10=510510 结果是12第4题:如图所示的表中有55个数,那么它们的和加上______才等于2011。
A:30B:96C:330D:196答案:D 解题思路:第一列:1+2+3+4+5=15第二列: 7+8+9+10+11=(6+1)+(6+2)+(6+3)+(6+4)+(6+5)=6×5×1+15第三列:13+14+15+16+17=(12+1)+(12+2)+(12+3)+(12+4)+(12+5)=12×5+15=6×5×2+15第四列:19+20+21+22+23=(18+1)+(18+2)+(18+3)+(18+4)+(18+5)=18×5+15=6×5×3+15第五列:25+26+27+28+29=(24+1)+(24+2)+(24+3)+(24+4)+(24+5)=24×5+15=6×5×4+15……第十列:55+56+57+58+59=(54+1)+(54+2)+(54+3)+(54+4)+(54+5)=54×5+15=6×5×9+15第十一列:61+62+63+64+65=(60+1)+(60+2)+(60+3)+(60+4)+(60+5)=60×5+15=6×5×10+15 看出规律了吗?55个数和如下:15×11+6×5×(1+2+3+4+5+6+7+8+9+10)=165+30×55=18152011-1815=196第5题:用数字1,2,3可以组成6个没有重复数字的三位数,这6个数的和是______。
学而思四年级第11讲.最值问题(基础-提高-尖子班)

349876第十一讲 最值问题(一)例1(2008年日本小学算术奥林匹克大赛初赛)【分析】 答案:247.要使两个五位数的差最小,这两个五位数首位上的数应该尽力接近,且较大数的后四位应尽可能小,较小数的后四位应尽可能大。
较大的五位数的后四位最小为0123,较小的五位数的后四位最大为9876,还剩下4和5两个数,所以较大的数是50123,较小的数是49876,差为5012247−=.例2 (2008年数学解题能力展示)【分析】 答案:50.一共20张牌,点数之和是固定的:2110(123...10)×++++=.由于每轮的点数差做为两人的得分,那么两人的总分之和就是10轮的点数差之和,即10轮中较大数之和-10轮中较小数之和(令它们分别是A 和B,则总分之和=A-B)又因为A+B=110所以A-B 的最大值即110-2B 的最大值,转换成求出B 的最小值即可。
令B 最小,既最小的十张牌之和:1,2,3,4,5,1,2,3,4,5.所以B 最小为30 ,总分之和最大=110-2B=50例3 (第十三届华杯赛)【分析】 极端分析法—答案:2005.通过找规律解决问题,要得到最小值,即让每次划去最多,应该从大往小擦数,最终得到2。
要得到最大值,即让每次划去最少,应该从小往大擦数,最终得到2007,从而最大与最小的差为220052007−=.例4 (2008年日本小学算术奥林匹克大赛初赛)【分析】 极端分析法—答案:155.最倒霉原则:“保证”=“最倒霉”+1. 最倒霉的情况是:取出了两种颜色的全部和其他颜色各9个依然不满足条件,即个,从而1550296154×+×=41155+=1×+556一定能保证满足条件.例5 (2008年日本小学算术奥林匹克大赛初赛)【分析】 极端分析法—答案:92.总表面积固定,当蓝色面积最大时,白色面积最小.因此,让蓝色木块优先占据特殊位置.分析发现,染色后8个角上的正方体3个面有颜色,扣去两角后的每条棱上的3个正方体有2个面。
小学四年级数学奥数题100题附答案(完整版)

小学四年级数学奥数题100题附答案(完整版)题目1有一个数列:1,3,5,7,9,11,13,15,17,19。
求这个数列的和。
答案:这是一个等差数列,首项为1,末项为19,公差为2,项数为10。
根据等差数列求和公式:总和= (首项+ 末项)×项数÷2即:(1 + 19)×10 ÷2 = 100题目2小明从一楼走到三楼需要2 分钟,那么他从一楼走到六楼需要几分钟?答案:从一楼到三楼,实际上走了 2 层楼梯,用了2 分钟,所以走一层楼梯需要1 分钟。
从一楼到六楼需要走5 层楼梯,所以需要5 分钟。
题目3在一个减法算式里,被减数、减数与差的和等于240,而减数是差的5 倍,差是多少?答案:因为被减数= 减数+ 差,被减数+ 减数+ 差= 240,所以被减数= 240÷2 = 120。
又因为减数是差的5 倍,设差为x,则减数为5x,所以x + 5x = 120,解得x = 20,即差是20。
题目4两个数相除,商是8,余数是20,如果被除数和除数同时扩大10 倍,商是多少?余数是多少?答案:被除数和除数同时扩大相同的倍数,商不变,余数扩大相同的倍数。
所以商还是8,余数是20×10 = 200。
题目5鸡兔同笼,共有头100 个,脚316 只,鸡兔各有多少只?答案:假设全是鸡,那么脚有100×2 = 200 只,比实际少316 - 200 = 116 只。
每把一只鸡换成一只兔,脚就多4 - 2 = 2 只。
所以兔有116÷2 = 58 只,鸡有100 - 58 = 42 只。
题目6一块长方形草地,长18 米,宽12 米,中间有一条宽2 米的小路,求草地(阴影部分)的面积。
答案:方法一:整个长方形的面积为18×12 = 216 平方米。
小路的面积为18×2 + 12×2 - 2×2 = 56 平方米。
小学四年级奥数题练习及答案解析-学而思入学必备

四年级奥数题:统筹规划(一)【试题】1、烧水沏茶时,洗水壶要用1分钟,烧开水要用10分钟,洗茶壶要用2分钟,洗茶杯用2分钟,拿茶叶要用1分钟,如何安排才能尽早喝上茶。
【分析】:先洗水壶然后烧开水,在烧水的时候去洗茶壶、洗茶杯、拿茶叶。
共需要1+10=11分钟。
【试题】2、有137吨货物要从甲地运往乙地,大卡车的载重量是5吨,小卡车的载重量是2吨,大卡车与小卡车每车次的耗油量分别是10公升和5公升,问如何选派车辆才能使运输耗油量最少?这时共需耗油多少升?【分析】:依题意,大卡车每吨耗油量为10÷5=2(公升);小卡车每吨耗油量为5÷2=2.5(公升)。
为了节省汽油应尽量选派大卡车运货,又由于137=5×27+2,因此,最优调运方案是:选派27车次大卡车及1车次小卡车即可将货物全部运完,且这时耗油量最少,只需用油10×27+5×1=275(公升)【试题】3、用一只平底锅烙饼,锅上只能放两个饼,烙熟饼的一面需要2分钟,两面共需4分钟,现在需要烙熟三个饼,最少需要几分钟?【分析】:一般的做法是先同时烙两张饼,需要4分钟,之后再烙第三张饼,还要用4分钟,共需8分钟,但我们注意到,在单独烙第三张饼的时候,另外一个烙饼的位置是空的,这说明可能浪费了时间,怎么解决这个问题呢?我们可以先烙第一、二两张饼的第一面,2分钟后,拿下第一张饼,放上第三张饼,并给第二张饼翻面,再过两分钟,第二张饼烙好了,这时取下第二张饼,并将第三张饼翻过来,同时把第一张饼未烙的一面放上。
两分钟后,第一张和第三张饼也烙好了,整个过程用了6分钟。
四年级奥数题:统筹规划问题(二)【试题】4、甲、乙、丙、丁四人同时到一个小水龙头处用水,甲洗拖布需要3分钟,乙洗抹布需要2分钟,丙用桶接水需要1分钟,丁洗衣服需要10分钟,怎样安排四人的用水顺序,才能使他们所花的总时间最少,并求出这个总时间。
【分析】:所花的总时间是指这四人各自所用时间与等待时间的总和,由于各自用水时间是固定的,所以只能想办法减少等待的时间,即应该安排用水时间少的人先用。
四年级数学竞赛奥数讲义,例题

计算:999999999×111111111计算:66666×133332求算式200982009920096999888666⨯÷个个个的计算结果的各位数字之和。
计算:222010120108888111-个个计算:22222×99999+33333×33334第一讲:多位数计算(★★★)(★★★★)(★★★★)(★★★★)(★★★)计算1009100910099999991999⨯+个个个结果末尾有多少个零?201032010420102201053335556444222⨯+⨯⨯个个个个【你还记得吗】 (★★★)计算:2010×20112011-2011×20102010计算:333×332332333-332×333333332(★★★★)(★★★★★) (★★★★)测试题1.计算222222×999999A .222222217880B .222222788888C .222221777778D .2222221777882.计算6666×13332A .88871112B .88881112C .88872222D .888822223.计算:3001300229931111222233334 个个个A .3013333个3B .2003333个3C .3003333个3D .3063333个34.计算100×100-99×99+98×98-97×97+…+2×2-1×1A .4950B .5050C .5150D .52505.计算 99999×26+33333×24A .3996366B .6933669C .3399966D .36699666.计算:899×899+1799A .819000B .810000C .900000D .9810007.计算111111×777777+444444×555555A .333332666667B .333333666667C .333332777777D .3333337777778.计算2009×20072008-2007×20092008A .2B .4016C .4017D .0网校老师共50人报名参加了羽毛球或乒乓球的训练,其中参加羽毛球训练的有30人,参加乒乓球训练的有35人,请问:两个项目都参加的有多少人?一个班30人,完成作业的情况有三种:一种是完成语文作业没完成数学作业;一种是完成数学作业没完成语文作业;一种是语文、数学作业都完成了。
学而思奥数四年级暑期课程经典题型

暑期课程典型题型总结【题型一】一个等腰三角形的两条边长分别为和,这个三角形的周长是?分析:此类型的题虽然简单,但孩子往往以为轻视就会犯错,具体表现为一下两个方面错误一:考虑不周全,分数砍半。
例如,等腰三角形的两条边长分别为4和5,那么三角形周长是多少?答案有两种可能:4+4+5=13 , 4+4=8>5 成立; 5+5+4=14 , 4+5=9>5成立,如下图示但孩子们往往会忽略掉其中的一种,而丢掉一半分,不应该。
错误二:忽视细节,酿成大错。
例如,等腰三角形的两条边长分别为4和9,那么三角形周长是多少?答案只有一种情况:4+9+9=22 , 4+9=13>9成立,如下图所示但部分孩子会做成:4+4+9=17(4+4=8<9,不能构成三角形), 4+9+9=22,往往不做判断,忽视了三角形的三边关系,导致在细节考虑不周而酿成大错。
【题型二】已知三角形ABC中,边长为,高为,又已知边长为(或已知高为),求高为多少(或求边为多少)?分析:首先,让孩子知道三角形的面积计算公是怎么来的,脑海中清楚的有一个三角形的面积计算公式的推理过程;其次,此类题一定要让孩子们明确的搞清楚高于边的对应关系,即每一条边都有一条固定的高与之对应,这样一来,即使图中没有画出高线,也要根据题中已知明确这条高是那条边上的高,那这类题就没问题了。
BC边上的高是A D,AB边上的高是C F,AC边上的高是B E。
【题型三】已知三角形ABC的面积是800,DEF分别是BC、AC、AD上的中点,求三角形DEF的面积?分析:此类题就是对一半模型的应用,应该教会孩子们以下几点首先,要让孩子们搞清楚中点的作用,就是把线段等分成两段;其次,要让孩子明白怎样的线才能把三角形等分成面积相等的两个三角形(利用三角形的面积计算公式推理),即中线的作用;最后要让孩子们学会两种思想既“隔离的思想”、“还原的思想”在解题中的应用。
【题型四】在等差数列中,孩子们一定要在熟悉三个公式的推理过程的的基础上,将求和作为一个重点学习,以为如果考求和,则会直接涉及到所学的三个公式中的两个,下面来举两个具体的例子。
学而思2011年暑假新四年级超常123班难题汇总
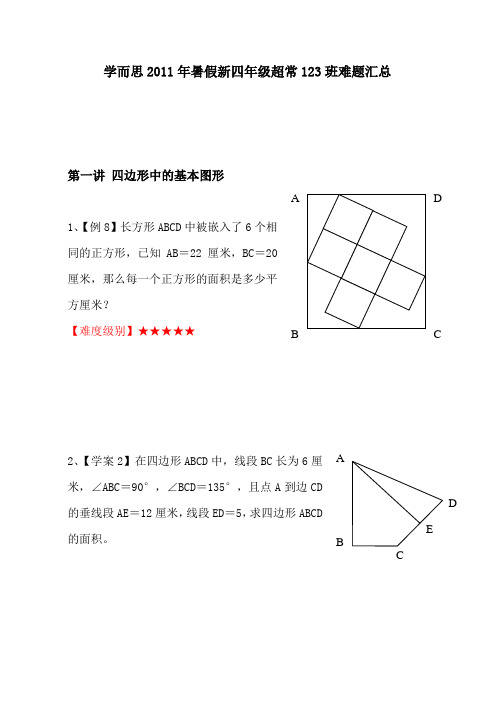
学而思2011年暑假新四年级超常123班难题汇总第一讲四边形中的基本图形1、【例8】长方形ABCD中被嵌入了6个相同的正方形,已知AB=22厘米,BC=20厘米,那么每一个正方形的面积是多少平方厘米?【难度级别】★★★★★2、【学案2】在四边形ABCD中,线段BC长为6厘米,∠ABC=90°,∠BCD=135°,且点A到边CD 的垂线段AE=12厘米,线段ED=5,求四边形ABCD 的面积。
D C3、【学案3】等腰梯形ABCD 中,交于O 点的两条对角线互相垂直,三角形ECB 是直角三角形,OC 比AO长20厘米。
已知三角形ADE 的面积是250平方厘米,则梯形ABCD 的面积是多少平方厘米?4、【学案4】一块边长为180厘米的正方形铁片,四角各被截去一个边长为40厘米的小正方形铁片,现在要从剩下的铁片中剪出一块完整的正方形铁片来,剪出的正方形面积最大为多少平方厘米?5、【作业5】请仅用刻度尺画一个面积是5平方厘米的正方形,保留必要的作图痕迹。
O B C D EA第二讲乘法原理6、【例7】1到1999的自然数中,有多少个与5678相加时,至少发生一次进位?7、【例8】有______个四位数满足下列条件:它的各位数字都是奇数,它的各位数字互不相同,它的每个数字都能整除它本身。
8、【学案1】计算机上编程序打印出前10000个正整数:1,2,3,……,10000时,不幸打印机有毛病,每次打印数字3时,它都打印出x,问其中被错误打印的共有多少个数?9、【学案4】有9张同样大小的圆形纸片,其中标有数码“1”的有1张,标有数码“2”的有2张,标有数码“3”的有3张,标有数码“4”的有3张,把这9张圆形纸片如图所示放置在一起,但标有相同数码的纸片不许挨在一起。
(1)如果M处放标有数码“3”的纸片,一共有多少种不同的放置方法?(2)如果M处放标有数码“2”的纸片,一共有多少种不同的放置方法?10、【越玩越聪明】在例6的后面。
学而思杯数学解析 级

16. 有 12 张卡牌,分别写着 1~12,不同卡牌上的数互不相同.甲、乙、丙分别抓取其中的四张牌,
进行游戏.规则如下:
比赛分 4 轮,每轮三人各出一张牌(出过的牌不能再出),并计算三张牌的和,如果和比中间
牌的 3 倍小,则出最小牌的人获胜,反之,则出最大牌的人获胜.如果和等于中间牌的 3 倍,则
无人获胜.(例如:甲、乙、丙分别出的是 2、4、1,则乙获胜).已知:
① 四轮都有人获胜;
② 甲四轮出牌顺序依次是 3、4、8、1,结果只有前 3 轮获胜;
③ 乙第一次出了他手中四张牌中最小的牌;
④ 乙、丙两人手中四张牌的和相等.
那么,乙所拥有的四张牌的乘积是
.
【考点】逻辑推理
【难度】☆☆☆☆☆
【答案】3150 【分析】①剩余 8 张牌的和是 (1+ 2 +⋯ +12) - 3- 4 - 8-1= 62 ,所以乙、丙的和都是 31;
获胜,剩余的 1 个数一定是 3、4,但 3、4 都已出现,所以 2 也不能在第 3 轮,所以 2 一定是丙第
4 轮由丙出; ④ 如果丙还有 5,那么丙的 4 个数最大,是 2 + 5 +11+12 = 30 < 31,所以 5 一定在乙手上,
那么 5 就是乙最小的牌,5 是在第一轮出的,如果甲的 3 想要获胜,丙只能出 6; ⑤ 丙已经由 2 和 6,丙的 4 个数最大是 2 + 6 +11+12 = 31 ,刚好,所以 11 和 12 只能是丙,
分卡上共出现了
位老师.
【考点】容斥原理
【难度】☆
【答案】550 【分析】 300 + 400 -150 = 550
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
暑期课程典型题型总结
【题型一】
一个等腰三角形的两条边长分别为和,这个三角形的周长是?
分析:
此类型的题虽然简单,但孩子往往以为轻视就会犯错,具体表现为一下两个方面
错误一:考虑不周全,分数砍半。
例如,等腰三角形的两条边长分别为4和5,那么三角形周长是多少?
答案有两种可能:4+4+5=13 , 4+4=8>5 成立; 5+5+4=14 , 4+5=9>5成立,如下图示
但孩子们往往会忽略掉其中的一种,而丢掉一半分,不应该。
错误二:忽视细节,酿成大错。
例如,等腰三角形的两条边长分别为4和9,那么三角形周长是多少?
答案只有一种情况:4+9+9=22 , 4+9=13>9成立,如下图所示
但部分孩子会做成:4+4+9=17(4+4=8<9,不能构成三角形), 4+9+9=22,往往不做判断,忽视了三角形的三边关系,导致在细节考虑不周而酿成大错。
【题型二】
已知三角形ABC中,边长为,高为,又已知边长为(或已知高为),求高为多少(或求边为多少)?
分析:
首先,让孩子知道三角形的面积计算公是怎么来的,脑海中清楚的有一个三角形的面积计算公式的推理过程;
其次,此类题一定要让孩子们明确的搞清楚高于边的对应关系,即每一条边都有一条固定的高与之对应,这样一来,即使图中没有画出高线,也要根据题中已知明确这条高是那条边上的高,那这类题就没问题了。
BC边上的高是A D,AB边上的高是C F,AC边上的高是B E。
【题型三】
已知三角形ABC的面积是800,DEF分别是BC、AC、AD上的中点,求三角形DEF的面积?分析:
此类题就是对一半模型的应用,应该教会孩子们以下几点
首先,要让孩子们搞清楚中点的作用,就是把线段等分成两段;其次,要让孩子明白怎样的线才能把三角形等分成面积相等的两个三角形(利用三角形的面积计算公式推理),即中线的作用;最后要让孩子们学会两种思想既“隔离的思想”、“还原的思想”在解题中的应用。
【题型四】
在等差数列中,孩子们一定要在熟悉三个公式的推理过程的的基础上,将求和作为一个重点学习,以为如果考求和,则会直接涉及到所学的三个公式中的两个,下面来举两个具体的例子。
(1)已知等差数列4、7、10、13、……,问:这个数列的前20项的和是多少?
(2)求4+7+10+13+……+55+58的和是多少?
根据求和公式:和=(首相+末项)·项数÷2
在第一道题中已知首相、项数,并没有末项,所以我们又得结合求某一项公式:
某一项=首相+(项数-1)·公差,而题中的首相、项数、以及公差都已知,将末项求出之后再代回到求和公式中就可以求出这个数列的和了。
在第二道题中已知首相、末项,但却又不知道项数,所以我们又得结合求项数公式:
项数=1+(末项-首相)÷公差,而题中的末项、首相以及公差又是已知的,所以将项数求出之后再代回到求和公式中就可以求出这个数列的和了。
【题型五】
从四年级六个班中评选出学习、体育、卫生先进集体各一个班级,如果要求同一个班级体只能获得一个先进集体(那也可能变成“如果要求同一个班级体可以获得多个先进集体”),那么一共有多少种评选方法?
分析:
此题就是一个乘法原理的应用,在讲这道题的时候一定要让孩子们明白一下几点:第一:清楚主动和被动。
即是“先进”选“班集体”还是“班集体”选“先进”,也就是确定哪个是主动方哪个是被动方,本题明显是将“先进”发给“班集体”,所以“先进”是主动方;
第二:确定要分几步。
有“三个先进”要发给“六个班集体”,为了要让孩子们清楚知道分几步,就可给孩子们假设一种场景:假设你是发奖人,站在讲台上,有六个孩子站在你前面等着发奖,那你该怎么办?那肯定你得一个一个先进的发,因为有三个先进,所以你就得分三次发,也就是说干完这件事得分三步;
第三:确定每一步有几种选择。
假设先发“学习先进”那么你前面的六个孩子都有可能获得,即“学习先进”有六种选择,假设你发给了二班后面你就得注意了,如果题中说同一个班集体可获得多个先进,那么二班在得到“学习先进”之后并没有离开,他会仍然站在你前面等你发另外的两个先进,所以“体育先进”也会有六个人可以选,“卫生先进”也是有六个人可以选,那么结果应该是:6·6·6=216(种);如果题中说同一个班集体只能获得一个先进,那么二班在得到“学习先进”之后就会离开,发“体育先进”时就有五个人可以选,发“卫生先进”时就只有四个人可以选,所以结果就会是:6·5·4=120(种)。
在加乘原理这一讲中,乘法原理是一个重点,而在乘法原理的应用中常见的三种题型有:线路问题,染色问题、组数问题,这三种题型一般都会用乘法原理解题,下面列举三个典型题,孩子们思考一下
线路问题:邮递员投递邮件由A存去B村的路有3条,有B村去C村的道路有2条,那么邮递员从A村经B村去C村,共有多少种不同的走法?
染色问题:“数学”这个词的英文单词是“MATH”。
用红、黄、蓝、绿、紫五种颜色去分别给字母染色,每个字母染的颜色都不一样,这些颜色一共可以染出多少种不同的搭配方式?
组数问题:用1、2、3、4、5、6这六个数,能组成多少个没有重复数字的数?
【题型六】
宫保和艾迪同时从两地相向而行,宫保每分钟行60米,艾迪每分钟行80米,两人在距两地中点50米处相遇,求两地距离是多少?
分析:此题是一道经典的相遇加追击的问题,希望孩子们自己好好思考琢磨。
画图如下。
○1由题中已知可得,两人是“同时出发,相向而行”直到两人相遇,所以相遇路程S就是A、B两地之间距离,所有我们就将题可理解为:宫保和艾迪的相遇路程是多少?由相遇问题可知:s相遇=v和·t相遇,题中已知两人的速度,那么速度和就可以求出60+80=140(米
/分钟),而相遇时间是个未知,所以,此题的关键就落在了求相遇时间的问题上,那如何求相遇时间呢?
○2画图的时候我们要先让孩子们清楚相遇点应该在AB两地中点的左边,这样一来孩子们
就会清楚的知道,艾迪比宫保的速度要快,所以,艾迪比宫保走的多,到底多多少,这块要给孩子好好的分析,最好是画图说明,如下图。
所以,艾迪比宫保多跑了50+50=100米,两个人同时出发同时停止的时间(相遇时间)就是产生这100米的时间,而这段时间正好就是相遇时间。
那孩子们就会想:为什么艾迪比宫保多跑100米,是因为艾迪的速度大,那么两人同时出发艾迪比宫保多跑这100米要多久呢?艾迪每分钟比宫保多走80-60=20,所以100÷(80-60)=5分钟就可以比宫保多走100米,所以艾迪比宫保多走100需要5分钟,即相遇时间为5分钟,算出相遇时间后代入得:
s相遇=v和·t相遇=(60+80)·(100÷20)=700(米)。
即A、B两地之间的距离是700米。
【题型七】
甲对乙说:“当我的岁数是你现在岁数的时候,你才5岁。
”乙对甲说:“当我的岁数是你现在岁数的时候,你讲将50岁。
”问:甲、乙两人现在各多少岁?
分析:
年龄问题中最主要的“一个原则”——年龄差不变原则;再就是要会画线段图,原则是——从小到大,从过去到将来。
此题画数轴图可以,当然也可以画线段图,下面我们用数轴图来看一下,
在图中我们很清楚的看到“乙的现在”是“甲的过去”,“甲的现在”是“乙的将来”,时间关系一定在年龄问题中要分清楚,由于两个人肯定是同增同减的,而且增减的值也是一样的,所以可以发现,“乙的过去”和“甲的将来”就差三个“年龄差”,所以,年龄差=(50-5)÷3=15岁,所以,乙的现在是5+15=20岁,甲的现在是5+15+15=35岁,此题就被轻而易举的解决了。
