坡度、坡角课件

九下数学课件坡度和坡角有关的问题(课件)

C． 1: 2 D． 1: 3
【变式 2】如图，河坝横断面迎水坡 AB 的坡比为 1： 2 （坡
比是坡面的铅直高度 BC 与水平宽度 AC 之比），坝高 BC＝
．
4m，则坡面 AB 的长度是
_____m
题型一一个坡度问题
75m
【变式 4】如图，在平地上种植树木时，要求株距（相邻两棵
树之间的水平距离）为 10m，若在坡度为 i=1:2.5 的山坡上种
题型三坡度修改问题
【变式 1】自开展“全民健身运动”以来，喜欢户外步行健身的人越来越多．为方便群众
步行健身，某地政府决定对一段如图 1 所示的坡路进行改造．如图 2 所示，改造前的斜
坡 AB=200 米，坡度为 1: 3 ；将斜坡 AB 的高度 AE 降低 AC=20 米后，斜坡 AB 改造为
【例 3】为了学生的安全，某校决定将一段如图所示的步梯路段进
行改造．已知四边形 ABCD 为矩形，DE＝10 m，其坡度为 i1＝1∶ 3，
将步梯 DE 改造为斜坡 AF，其坡度为 i2＝1∶4，则斜坡 AF 的长是
20.62mຫໍສະໝຸດ ________．(结果精确到 0.01 m，参考数据： 3≈1.732， 17≈4.123)
计算判断：
3
当 sin α＝，木箱底部顶点 C 与坡面底部点 A 重合时，
5
木箱上部顶点 E 会不会触碰到汽车货厢顶部？
题型四坡度安全问题
又∵∠EKF＝∠AHB＝90°，∴△EFK∽△ABH.
∴
EF EK
1.6 EK
＝，∴ ＝ .
AB AH
1 0.8
解得 EK＝1.28.
∴BJ＋EK＝0.6＋1.28＝1.88.

坡度和坡角

D
4.2米 A
32 °
12.51米
C
28 ° B
9
D
12.51米
C
4.2米 A
32 ° E
∟
∟
28 °
F
B
解：作DE AB,CF AB,垂足分别为E、F .由题意可知
DE CF 4.（2 米），CD EF 12.5（1 米）.
在Rt△ADE中， i DE 4.2 tan 32 , AE AE
α
A
EF
D
=184′，AD=132.5 m，AB=23 10 m
3
问题探究
4
如图，坡面的铅锤高度（ h）和水平长度（ l）的比叫做坡面坡度（或坡比）,记作 i ,即 i h .
l 坡度通常写成 1 : m 的形式，如 i 1 : 6
坡面与水平面的夹角叫做坡角，记作 .
i h:l h
l
5
7
④堤坝横断面是等腰梯形，（如图所示）
若AB=10,CD=4,高h=4,则坡度i=__43___,AD=
____5___;
若AB=10，CD=4，i= 1
5
3
,则h=___5___.
D
C
h
i
∟
∟
AE
F
B
8
例1：如图，一段路基的横断面是梯形，高为4.2 米，上底的宽是12.51米，路基的坡面与地面的倾角分别是32°和28°.求路基下底的宽.（精确到0.1米）
完成该工程需要多少土方？
ED C
α FA
B
11
解：作DG AB于G,作EH AB于H . CD∥AB, EH DG 5米.
ED C
DG 1 , AG 6米. AG 1.2

坡度与坡角PPT课件

（3）斜坡AB的长度以及斜坡CD的坡角的问题实质上
就是解Rt△ ABE和Rt△ CDF。 .
7
应用练习
1、斜坡的坡度是 1 : 3，则坡角α=______度。 2、斜坡的坡角是450 ，则坡度是 _______。 3、斜坡长是12米,坡高6米,则坡度是_______。
h
α
L.
8
应用练习
4、小明沿着坡角为20°的斜坡向上前进80m, 则他上升的高度是( ).
A
D
BE
C
.
10
一段路基的横断面是梯形，高为4米，上底的宽是12米，路基的坡面与地面的倾角分别是 45°和30°，求路基下底的宽．（精确到0.1 米 2 1.414 3 1.732 ）
D 12米
C
4米
45°
A
E
30°
F
B
.
11
效果检测
.
12
A. 80 m cos 20
B. 80 m sin 20
C .80sin20m
D .80cos20m
.
9
应用练习
5、如图是一个拦水大坝的横断面图,AD∥BC, (1)如果斜坡AB=10m,大坝高为8m,则斜坡AB的坡度 iAB ____. (2)如果坡度 iAB 1: 3,则坡角 B____. (3)如果坡度 iAB1:2,AB8m,则大坝高度为___.
导入当我们要测量如图所示大坝的高度h时只要测出仰角a和大坝的坡面长度l就能算出hlsina但是当我们要测量如图所示的山高h时问题就不那么简单了这是由于不能很方便地得到仰角a和山坡长度l与测坝高相比测山高的困难在于
华师大版数学九年级上册
直角三角形的应用第二课时

初三上数学课件(华东师大)-坡度与坡角

h
坡度 (或坡比)，记作 i，即 i＝ l .坡度一般写成 1∶m 的形式．坡面
与水平面的夹角叫做坡角，记作 α，有 i＝hl ＝ tanα α 就越大，坡面就越陡．
.坡度越大，坡角
1．下列对坡度的描述正确的是( B )
A．坡度是指斜坡与水平线夹角的度数
B．坡度是指斜坡的铅垂高度与水平宽度的比
解：(1)∵FD∥CG，∴∠BDF＝∠BAC＝45°，∵斜坡 AB 长 60 2米，D 是 AB 的中点，∴BD＝30 2米，∴DF＝BD·cos∠BDF＝30 2× 22＝30(米)， BF＝DF＝30 米．∵斜坡 BE 的坡比为 3∶1，∴BEFF＝ 13，∴EF＝10 3米， ∴DE＝DF－EF＝(30－10 3)米，∴休闲平台 DE 的长是(30－10 3)米； (2)设 GH＝x 米，则 MH＝GH－GM＝(x－30)米，DM＝AG＋AP＝33＋30 ＝63(米)，在 Rt△DMH 中，tan30°＝MDMH，即x－6330＝ 33，解得 x＝30＋21 3， ∴建筑物 GH 的高为(30＋21 3)米．
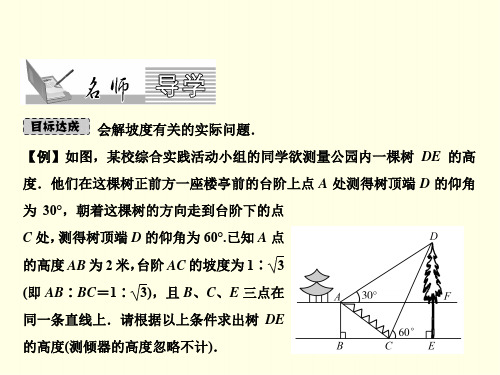
11．为邓小平诞辰 110 周年献礼，广安市政府对城市建设进行了整改．如图，斜坡 AB 长 60 2 米，坡角(即∠BAC)为 45°，BC⊥AC，现计划在斜坡中点 D 处挖去部分斜坡，修建一个平行于水平线 CA 的休闲平台 DE 和一条新的斜坡 BE(下面两个小题结果都保留根号)． (1)若修建的斜坡 BE 的坡比为 3∶1，求休闲平台 DE 的长； (2)一座建筑物 GH 距离 A 点 33 米远(即 AG＝33 米)，小亮在 D 点测得建筑物顶部 H 的仰角(即∠HDM)为 30°.点 B、C、A、G、H 在同一个平面内，点 C、A、G 在同一条直线上，且 HG⊥CG，问建筑物 GH 高为多少米？

24.4.3坡度、坡角问题课件

4.得到实际问题的答案.
课堂小结
3.
4.
P.121 12.； P123页13
人有了知识，就会具备各种分析能力，明辨是非的能力。所以我们要勤恳读书，广泛阅读，古人说“书中自有黄金屋。 ”通过阅读科技书籍，我们能丰富知识，培养逻辑思维能力；通过阅读文学作品，我们能提高文学鉴赏水平，培养文学情趣；通过阅读报刊，我们能增长见识，扩大自己的知识面。有许多书籍还能培养我们的道德情操，给我们巨大的精神力量，鼓舞我们前进。
D
12.51
C
28⁰
【分析】
4.2 A
32⁰
E 12.51 F
B
（1）对于梯形问题通常怎么做辅助线？把它转化成什么问题？（2）要求下底AB的长，可以分别求哪些线段的长？（3）怎么求AE，BF？
变式训练：
如图，某地计划在河流的上游修建一条拦水大坝。大坝的横断面ABCD是梯形，坝顶宽BC=6米，坝高25m，迎水坡AB的坡度 i=1：，背水坡CD的坡角为450 求（1）求坡角α ; （2）求拦水大坝的底面AD的宽.
——坡度、坡角
裴营一初中余超
学习目标
1、知道坡度、坡角的意义。 2、能将h、L、i各量的计算问题转化为解直角三角形的问题，这些量中若已知两个量，可求其他量. 3、会运用解直角三角形有关知识解决与坡度、坡角有关的实际问题。 4、在有些实际问题中没有直角三角形，学会添加辅助线构造直角三角形.
知识回顾
解直角三角形的依据
(1)三边之间的关系:a2＋b2＝c2（勾股定理）；； (2)两锐角之间的关系:∠ A＋ ∠ B＝ 90º (3)边角之间的关系: sinA＝ a b cosA＝ c a tanA＝ b ＡＢ

坡度与坡角

C
i=1:2.5
α
23
EF D
（2）垂线BE、CF将梯形分割成Rt△ABE，Rt△CFD和矩形BEFC，则AD=AE+EF+FD， EF=BC=6m，AE、DF可结合坡度,通过解Rt△ABE和Rt△C的坡角的问题实质上就是解Rt△ ABE和Rt△ CDF。
6
i 1 : 3B
C
i=1:2.5
A
α
23
EF D
例1.水库大坝的横断面是梯形，坝顶宽6m，坝高 23m，斜坡AB的坡度i=1∶3，斜坡CD的坡度 i=1∶2.5，求：坝底AD与斜坡AB的长度。（精确
到0.1m ）
分析：（1）由坡度i会想到产
生铅直高度，即分别过点B、
C作AD的垂线。
A
6
i 1 : 3B
的比叫做坡面的坡度（或坡比）,记作i, 即 i=—h—
l
坡度通常写成1∶m的形式，如i=1∶6.
3、坡度与坡角的关系
i

h l

tan
坡度等于坡角的正切值
显然，坡度越大，坡角就越大，坡面就越陡.
例1.水库大坝的横断面是梯形，坝顶宽6m，坝高23m，斜坡AB的坡度i=1∶3，斜坡CD的坡度i=1∶2.5，求：坝底AD与斜坡AB的长度。（精确到0.1m ）
C.80sin 20m
D.80cos 20m
5、如图是一个拦水大坝的横断面图,AD∥BC, (1)如果斜坡AB=10m,大坝高为8m,则斜坡AB的坡度 iAB ____ . (2)如果坡度 iAB 1: 3,则坡角B ____ .
(3)如果坡度 iAB 1: 2, AB 8m,则大坝高度为___.
直角三角形的应用第3课时

人教版九年级下册数学课件：28.2解直角三角形坡度与坡角

l
h
α
l
h
α
与测坝高相比，测山高的困难在于；坝坡是“直” 的，而山坡是“曲”的，怎样解决这样的问题呢？
我们设法“化曲为直，以直代曲”．我们可以把山坡“化整为零”地划分为一些小段，图表示其中一部分小段，划分小段时，注意使每一小段上的山坡近似是“直”的，可以量出这段坡长l1，测出相应的仰角a1，这样就可以算出这段山坡的高度h1=l1sina1l. h
α
在每小段上，我们都构造出直角三角形，利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,然后我们再 “积零为整”，把h1,h2,…,hn相加，于是得到山高h.
以上解决问题中所用的“化整为零，积零为整”“化曲为直，以直代曲”的做法，就是高等数学中微积分的基本思想，它在数学中有重要地位，在今后的学习中，你会更多地了解这方面的内容．
化整为零，积零为整，化曲为直，
以直代曲的解决问题的策略
解直角三角形有广泛的应用，解决问题时，要根据实际情况灵活运用相关知识，例如，当我们要测量如图所示大坝的高度h时，只要测出仰角a和大坝的坡面长度l，就能算出h=lsina，但是，当我们要测量如图所示的山高h时，问题就不那么简单了，这是由于不能很方便地得到仰角a和山坡长度l
解直角三角形（3）
坡度与坡角如图 28-2-4，坡面的铅垂高度(h)与水平长度(l)的比叫做坡
h l 面的坡度(或坡比)，记作 i，即 i＝________；而坡面与水平面
的夹角叫做__坡__角____，记作α，即 i＝_t_a_n_α____.
显然，坡度越大，坡角a就越大，坡面就越陡.
铅垂 h
分析： 1．引导学生将实际问题
转化为数学问题． 2．要求S等腰梯形ABCD，

解直角三角形(坡度和坡角)讲义

解直角三角形（坡度和坡角）一、知识点讲解1、坡角：坡面与水平面的夹角叫做坡角，记作α。

2、坡度（或坡比）：坡面的铅垂高度（h ）和水平长度（l ）的比叫做坡面的坡度（或坡比），记作i ，即 lh i =，坡度通常写成1∶m 的形式。

3、坡度与坡角的关系： αtan ==lh i 坡度等于坡角的正切值二、典例分析题型一：利用解直角三角形解决坡度、坡角问题例1 水库大坝的横断面是梯形，坝顶宽6m ，坝高23m ，斜坡AB 的坡度i =1∶3，斜坡CD 的坡度i =1∶2.5，求：（1）坝底AD 与斜坡AB 的长度（精确到0.1m ）；（2）斜坡CD 的坡角α（精确到 1°）。

变式练习：1、如图，一人滑雪沿坡度为1：2斜坡滑下，下滑了距离s =100米，则此人下降的高度为（）A 、50米B 、350米C 、520米D 、550米第1题第2题第3题2、如图是人民广场到重百地下通道的手扶电梯示意图，其中AB 、CD 分别表示地下通道、人发广场电梯口处地面的水平线，已知∠ABC =135°，BC 的长约为25m ，则乘电梯从点B 到点C 上升的高度h 是。

3、如图，某拦河坝截面的原设计方案为：AH ∥BC ，坡角∠ABC ＝74°，坝顶到坝脚的距离AB ＝6 m ．为了提高拦河坝的安全性，现将坡角改为55°，由此，点A 需向右平移至点D ，请你计算AD 的长(精确到0.1 m )．题型二：利用解直角三角形解决其它例2 如图所示，我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度．小宇同学在A处观测对岸C点，测得∠CAD=45°，小英同学在距A处50米远的B处测得∠CBD=30°，请你根据这些数据算出河宽．（精确到0.01米，参考数据≈1.414，≈1.732）变式练习：1、如图1是小志同学书桌上的一个电子相框，将其侧面抽象为如图2所示的几何图形，已知BC=BD=15cm，∠CBD=40°，则点B到CD的距离为cm（参考数据sin20°≈0.342，cos20°≈0.940，sin40°≈0.643，cos40°≈0.766，结果精确到0.1cm，可用科学计算器）．第1题第2题2、小强和小明去测得一座古塔的高度，如图，他们在离古塔60m处（A）用测角仪测得塔顶的仰角为30°，已知测角仪高AD=1.5m，则古塔的高BE为。