统计模式识别简介
统计模式识别 统计分类方法

统计模式识别统计分类方法
统计模式识别是一种常见的机器学习算法,用于对未知模式和统
计模式进行学习。
它可以使用模式的历史记录和观察结果来预测未来
模式的行为。
该技术也被称为统计分类,用于解决分类和分组问题,
其目的是根据现有的统计数据来评估一个特定的类别的可能性。
统计模式识别基于概率统计理论,可对数据进行分析并扩展到传
统模式识别范围之外,以解决复杂问题。
它可以用于分类多维数据,
识别新类别或模式,并帮助训练机器学习模型,使用有效的特征提取
和结构学习算法。
它提供一种新的方法,通过有效的表示和分类模型,来表示实体和相关的对象。
与其他分类算法相比,统计模式识别的有点是它'数据挖掘'的概念,在这种类型的模式识别中,模式数据是根据观察数据一直进行改
变的,没有预先定义模式及其功能,它根据具有可利用自学能力的方
法逐渐改善。
统计模式识别非常重要,因为它可以帮助我们找到自动化解决方
案来实现更多基于数据的智能分析和决策,从而增强分析模型的能力,例如,可以使用该技术识别股票市场及其他金融市场的模式变化,以
便于能够更高效地进行投资决定。
它也可以应用于诊断和分析少量样
本事件,进而对学习和决策进行调节和优化。
模式识别(国家级精品课程讲义).ppt

为若干子集, m类就有m个子集,然后根据择近原 则分类。
29
1.1 概述-模式识别的基本方法
理论基础:模糊数学 主要方法:模糊统计法、二元对比排序法、推理法、
模糊集运算规则、模糊矩阵 主要优点:
由于隶属度函数作为样本与模板间相似程度的度量, 故往往能反映整体的与主体的特征,从而允许样本有 相当程度的干扰与畸变。 主要缺点: 准确合理的隶属度函数往往难以建立,故限制了它的 应用。
式中,p(xi )是 X 的第 i 个分量的 边缘
密度。随机矢量 X 的均值矢量 的各
分量是相应的各随机分量的均值。
47
1.3 随机矢量的描述
(二)随机矢量的数字特征:
⑵ 条件期望
在模式识别中,经常 以类别 i 作为条件,在这
种情况下随机矢量 X 的条件期望矢量定义为
i E[ X | i ] X n xp(x | i )dx
34
1.1 概述-模式识别的发展简史
1929年 G. Tauschek发明阅读机 ,能够阅 读0-9的数字。
30年代 Fisher提出统计分类理论,奠定了 统计模式识别的基础。
50年代 Noam Chemsky 提出形式语言理论— —傅京荪提出句法/结构模式识别。
60年代 L.A.Zadeh提出了模糊集理论,模糊 模式识别方法得以发展和应用。
模式(Pattern):对客体(研究对象)特征的描 述(定量的或结构的描述),是取自客观世界 的某一样本的测量值的集合(或综合)。
概念
特征(Features):能描述模式特性的量(测
量值)。在统计模式识别方法中,通常用一
个矢量
x
模式识别详细PPT

无监督学习在模式识别中的应用
无监督学习是一种从无标签数据中提取有用信息的机器学习方法,在模式识别中主要用于聚类和降维 等任务。
无监督学习在模式识别中可以帮助发现数据中的内在结构和规律,例如在图像识别中可以通过聚类算 法将相似的图像分组,或者通过降维算法将高维图像数据降维到低维空间,便于后续的分类和识别。
通过专家知识和经验,手 动选择与目标任务相关的 特征。
自动特征选择
利用算法自动筛选出对目 标任务最相关的特征,提 高模型的泛化能力。
交互式特征选择
结合手动和自动特征选择 的优势,先通过自动方法 筛选出一组候选特征,再 由专家进行筛选和优化。
特征提取算法
主成分分析(PCA)
通过线性变换将原始特征转换为新的特征, 保留主要方差,降低数据维度。
将分类或离散型特征进行编码 ,如独热编码、标签编码等。
特征选择与降维
通过特征选择算法或矩阵分解 等技术,降低特征维度,提高 模型效率和泛化能力。
特征生成与转换
通过生成新的特征或对现有特 征进行组合、转换,丰富特征
表达,提高模型性能。
04
分类器设计
分类器选择
线性分类器
基于线性判别分析,适用于特征线性可 分的情况,如感知器、逻辑回归等。
结构模式识别
总结词
基于结构分析和语法理论的模式识别方法,通过分析输入数据的结构和语法进行分类和 识别。
详细描述
结构模式识别主要关注输入数据的结构和语法,通过分析数据中的结构和语法规则,将 输入数据归类到相应的类别中。这种方法在自然语言处理、化学分子结构解析等领域有
统计模式识别-线性分类器h

训练样本
x1 1 0 1 1 x2 0 1 1 1 x3 1 1 0 1 x4 0 1 0 1
x1 1 0 1 1 x2 0 1 1 1 x3 1 1 0 1 x4 0 1 0 1
x1 1 0 1 1 x2 0 1 1 1 x3 1 1 0 1 x4 0 1 0 1
x1 1 0 1 1 x2 0 1 1 1 x3 1 1 0 1 x4 0 1 0 1
1、线性分类器设计的思路:
两类分类问题:
g(x)=WTX
其中 X= (X1, X2…Xn)
n维特征向量
W= (W1, W2 … Wn , Wn+1) n维权向量
分类准则:
x 1, g(x) 0
x
2
,
g(
x)
0
二、线性分类器的设计
要成功地用判别函数来进行模式分类,依 赖于两个因素:
Wk+1= Wk- D-1▽J —牛顿法的迭代公式 讨论:牛顿法比梯度法收敛的更快,但是D的计算量大并
且要计算D-1。当D为奇异时,无法用牛顿法。
四 感知器法
美国学者F.Rosenblatt在1957年提出了 感知器的模型。
感知器(perceptron)是一个具有单层 计算单元的人工神经网络。感知器训练 算法就是由这种神经网络演变来的。
x1=(1,0,1,1)
x2=(0,1,1,1)
x3=(1,1,0,1)
x4=(0,1,0,1)
假设初始权向量 w1=(1,1,1,1) ρk=1
四、感知器法
第一次迭代: w1Tx1=(1,1,1,1) (1,0,1,1)T=3>0 所以不修正 w1Tx2=(1,1,1,1) (0,1,1,1)T=3>0 所以不修正 w1Tx3=(1,1,1,1) (1,1,0,1)T=3>0 所以修正w1 w2=w1-x3=(0,0,1,0) w2Tx4=(0,0,1,0)T (0,1,0,1) =0 所以修正w2 w3=w2-x4=(0,-1,1,-1) 第一次迭代后,权向量w3=(0,-1,1,-1),再进行第2,3,… 次迭代,如下表
模式识别综述

模式识别综述摘要:介绍了模式识别系统的组成及各组成部分包含的内容。
就统计模式识别、结构模式识别、模糊模式识别、神经网络模式识别等模式识别的基本方法进行简单介绍,并分析了其优缺点。
最后列举了模式识别在各领域的应用,针对其应用前景作了相应分析。
关键字:模式识别系统、统计模式识别、结构模式识别、模糊模式识别、神经网络模式识别背景随着现代科学技术的发展,特别是计算机技术的发展,对事物认识的要求越来越高,根据实际需求,形成了一种模拟人的各种识别能力(主要是视觉和听觉)和认识方法的学科,这个就是模式识别,它是属于一种自动判别和分类的理论。
这一理论孕育于20世纪60年代,随着科学技术的发展,特别是20世纪70年代遥感技术的发展和地球资源卫星的发射,人们通过遥感从卫星取得的巨量信息,需要进行空前规模的处理、识别和应用,在此推动下,模式识别技术便得以迅速发展[1]。
发展到现在,应用领域已经非常广阔,包括文本分类、语音识别、视频识别、信息检索和数据挖掘等。
模式识别技术在生物医学、航空航天、工业生产、交通安全等许多领域发挥着重要的作用[2]。
基本概念什么是模式呢?广义地说,存在于时间和空间中可观察的事物,如果可以区别它们是否相同或是否相似,都可以称之为模式。
但模式所指的不是事物本身,而是我们从事物获取的信息。
因此模式往往表现为具有时间或空间分布的信息[3]。
人们在观察各种事物的时候,一般是从一些具体的个别事物或者很小一部分开始的,然后经过长期的积累,随着对观察到的事物或者现象的数量不断增加,就开始在人的大脑中形成一些概念,而这些概念是反映事物或者现象之间的不同或者相似之处,这些特征或者属性使人们对事物自然而然的进行分类。
从而窥豹一斑,对于一些事物或者现象,不需要了解全过程,只需要根据事物或者现象的一些特征就能对事物进行认识。
人脑的这种思维能力视为“模式”的概念。
模式识别就是识别出特定事物,然后得出这些事物的特征。
识别能力是人类和其他生物的一种基本属性,根据被识别的客体的性质可以将识别活动分为具体的客体与抽象的客体两类。
统计模式识别

分类器
01
Fisher分 类器
02
线性鉴别函 数LDA
03
SVM
04
K-means
06
Adboosti ng
05
Boosting
Fisher分类器
Fisher线性判别分析的基本思想:通过寻找一个投影方向(线性变换,线性组合)将高维问题降低到一维 问题来解决,并且要求变换后的一维数据具有如下性质:同类样本尽可能聚集在一起,不同类的样本尽可能地远。
指纹识别是最成熟的一项生物信息识别技术。目前,各种类型的指纹识别系统已在公安、海关、公司门禁、 PC机设锁等多种场合得到应用,成为展现图像识别技术实用价值的标志。指纹识别系统既有应用于公司、家庭或 个人计算机的嵌入式系统一指纹锁,也有用于刑侦、护照通关、络身份认证等领域的大型系统。嵌入式系统存储 的指纹(特征)数较少(一般在100枚以内),可用简单的算法实现高精度识别,所要解决的主要问题是如何用简单、 小巧、廉价的设备实现指纹的正确采集和识别。大型系统往往需要储存上百万的指纹,因此如何提高指纹的比对 速度便成为关键。为了能够进行快速处理,需要对指纹进行很好的组织和采用高速算法。
K-means
K-means分类器K-Means算法是以距离作为相似度的评价指标,用样本点到类别中心的误差平方和作为聚类 好坏的评价指标,通过迭代的方法使总体分类的误差平方和函数达到最小的聚类方法。
(1)从 n个数据对象任意选择 k个对象作为初始聚类中心; (2)循环(3)到(4)直到每个聚类不再发生变化为止 (3)根据每个聚类对象的均值(中心对象),计算每个对象与这些中心对象的距离;并根据最小距离重新 对相应对象进行划分; (4)重新计算每个(有变化)聚类的均值(中心对象)
第六讲 统计模式识别(三)
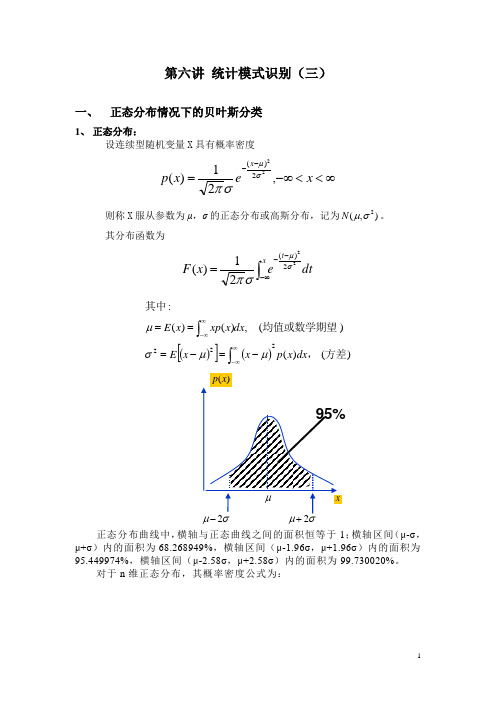
第六讲 统计模式识别(三)一、 正态分布情况下的贝叶斯分类1、 正态分布:设连续型随机变量X 具有概率密度∞<<-∞=--x ex p x ,21)(222)(σμσπ则称X 服从参数为μ,σ的正态分布或高斯分布,记为),(2σμN 。
其分布函数为dt ex F xt ⎰∞---=22)(21)(σμσπ()[]())()()(,)()(:222方差,均值或数学期望其中dx x p x x E dx x xp x E ⎰⎰∞∞-∞∞--=-===μμσμ正态分布曲线中,横轴与正态曲线之间的面积恒等于1;横轴区间(μ-σ,μ+σ)内的面积为68.268949%,横轴区间(μ-1.96σ,μ+1.96σ)内的面积为95.449974%,横轴区间(μ-2.58σ,μ+2.58σ)内的面积为99.730020%。
对于n 维正态分布,其概率密度公式为:()()()()∑∑∑∑∑--∑⨯==⎥⎦⎤⎢⎣⎡---∑=的行列式为的逆阵,为维协方差矩阵,为维均值向量,维特征向量其中121211212),...,,(,,...,,:21exp ||21)(d d d d x x x x p Td Td Tdμμμπμx μx μx均值向量μ的分量μi 为:i i i i i dx x p x x E ⎰∞∞-==)()(μ协方差矩阵为:()()[]()()()()[]()()()()()()()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--------=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=--=∑d d d d d dd d d d d d Tx x x x x x x x E x x x x E E μμμμμμμμμμμμ,...,......,...,,...,......111111111111μx μx()()[]()()[]()()[]()()[]⎪⎪⎭⎫ ⎝⎛≠=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--------=是协方差,非对角线是方差对角线j i j i x x E x x E x x E x x E ij ij dd d d d d d d d d d d d 22222212121221111111111,,..............................σσσσσσσσμμμμμμμμ 多维正态分布具有以下性质:μ与∑对分布起决定作用, μ由d 分量组成,∑由d(d+1)/2个元素组成,所以多维正态分布由d+d(d+1)/2个参数组成。
统计模式识别的原理与方法

统计模式识别的原理与⽅法1统计模式识别的原理与⽅法简介 1.1 模式识别 什么是模式和模式识别?⼴义地说,存在于时间和空间中可观察的事物,如果可以区别它们是否相同或相似,都可以称之为模式;狭义地说,模式是通过对具体的个别事物进⾏观测所得到的具有时间和空间分布的信息;把模式所属的类别或同⼀类中模式的总体称为模式类(或简称为类)]。
⽽“模式识别”则是在某些⼀定量度或观测基础上把待识模式划分到各⾃的模式类中去。
模式识别的研究主要集中在两⽅⾯,即研究⽣物体(包括⼈)是如何感知对象的,以及在给定的任务下,如何⽤计算机实现模式识别的理论和⽅法。
前者是⽣理学家、⼼理学家、⽣物学家、神经⽣理学家的研究内容,属于认知科学的范畴;后者通过数学家、信息学专家和计算机科学⼯作者近⼏⼗年来的努⼒,已经取得了系统的研究成果。
⼀个计算机模式识别系统基本上是由三个相互关联⽽⼜有明显区别的过程组成的,即数据⽣成、模式分析和模式分类。
数据⽣成是将输⼊模式的原始信息转换为向量,成为计算机易于处理的形式。
模式分析是对数据进⾏加⼯,包括特征选择、特征提取、数据维数压缩和决定可能存在的类别等。
模式分类则是利⽤模式分析所获得的信息,对计算机进⾏训练,从⽽制定判别标准,以期对待识模式进⾏分类。
有两种基本的模式识别⽅法,即统计模式识别⽅法和结构(句法)模式识别⽅法。
统计模式识别是对模式的统计分类⽅法,即结合统计概率论的贝叶斯决策系统进⾏模式识别的技术,⼜称为决策理论识别⽅法。
利⽤模式与⼦模式分层结构的树状信息所完成的模式识别⼯作,就是结构模式识别或句法模式识别。
模式识别已经在天⽓预报、卫星航空图⽚解释、⼯业产品检测、字符识别、语⾳识别、指纹识别、医学图像分析等许多⽅⾯得到了成功的应⽤。
所有这些应⽤都是和问题的性质密不可分的,⾄今还没有发展成统⼀的有效的可应⽤于所有的模式识别的理论。
1.2 统计模式识别 统计模式识别的基本原理是:有相似性的样本在模式空间中互相接近,并形成“集团”,即“物以类聚”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性判别函数
• 基于线性判别函数的模式分类器称为线性 分类器。设计线性分类器的主要步骤是: 首先已知一组有类别的样本训练集。第二, 选择一个准则函数,该函数既与样本集X与 W有函数关系,又能反映分类器性能。第三, 用最优化技术求出准则函数的极值解W*, 从而得到线性判别函数优化解。
监督参数统计法
统计模式识别模型
• 该模型主要包括两种操作模型:训练和分类 , 其中训练主要利用已有样本完成对决策边 界的划分 ,并采取了一定的学习机制以保证 基于样本的划分是最优的;而分类主要对输 入的模式利用其特征和训练得来的决策函 数而把模式划分到相应模式类中。
基本原理
• 统计模式识别(statistic pattern recognition) 的基本原理是:有相似性的样本在模式空 间中互相接近,并形成“集团”,即“物以类 聚”。其分析方法是根据模式所测得的特征 向量Xi=(xi1,xi2,…,xid)T(i=1,2,…,N),将一个 给定的模式归入C个类ω1,ω2,…, ωc中,然后 根据模式之间的距离函数来判别分类。其 中,T表示转置;N为样本点数;d为样本特 征数。
非监督参数统计法
• 基于概率密度函数估计的直接方法 • 于样本空间相似性度量的间接聚类方法
聚类分析法
• 在没有训练集的情况下,对一批没有类别的被识别 样本进行自动分类,要按照样本之间的相似程度分 类,即俗语讲的“物以类聚,人以群分”,这种分 类方法称为聚类分析,它是一种无教师的非监督的 分类方法。
• 当被识对象用n随机向量X表示,二我们已 知分类的先验概率的条件概率密度函数, 便可根据贝叶斯公式,求解后验概率并 按后验概率的大小来判别分类,这就是贝 叶斯决策方法。下面介绍三种判别准则:
• (1)最小错误概率贝叶斯判别准则 (2)最小风险贝叶斯判别
• (3)聂曼-皮尔逊判别准则准则
(1)最小错误概率贝叶斯判别准则
• 统计模式识别的方法有: • 贝叶斯决策方法 • (1)最小错误概率贝叶斯判别准则 • (2)最小风险贝叶斯判别 • (3)聂曼-皮尔逊判别准则准则 • 判别函数法 • (1)线性可分的几何分类法 • (2)非线性可分的几何分类法
• 监督参数统计法 • (1)KNN法(K最近邻法) • (2)Fisher判别分析法 • 非监督参数统计法 • (1)基于概率密度函数估计的直接方法 • (2)与样本空间相似性度量的间接聚类方法 • 聚类分析法 • 近邻函数法 • (1)基于最邻近规范的试探法 • (2)最大最小距离法
统计模式识别
统计模式识别方法就是用给定的有限 数量样本集,在已知研究对象统计模型 或已知判别函数类条件下根据一定的准 则通过学习算法把d 维特征空间划分为c 个区域,每一个区域与每一类别相对应。
• 属于同一类别的各个模式之间的差异,部分是 由环境噪声和传感器的性质所引起的,部分是
模式本身所具有的随机性质。前者如纸的质量、 墨水、污点对书写字符的影响;后者表现为同
一个人书写同一字符时,虽形状相似,但不可
能完全一样。因此当用特征向量来表示这些在 形状上稍有差异的字符时,同这些特征向量
对应的特征空间中的点便不同一,而是分布在
特征空间的某个区域中。这个区域就可以用来 表示该随机向量实现的集合。
• 假使在特征空间中规定某种距离度量,从直观 上看,两点之间的距离越小,它们所对应的模 式就越相似。在理想的情况下,不同类的两个 模式之间的距离要大于同一类的两个模式之间 的距离,同一类的两点间连接线上各点所对应 的模式应属于同一类。一个畸变不大的模式所 对应的点应紧邻没有畸变时该模式所对应的点。 在这些条件下,可以准确地把特征空间划分为 同各个类别相对应的区域。在不满足上述条件 时,可以对每个特征向量估计其属于某一类的 概率,而把有最大概率值的那一类作为该点所 属的类别。
• 若有未知类别的n个样本,要把它们分到C类中,可 以有不同的聚类方法,如何评价聚类的好坏,需要 决定一个聚类准则。聚类准则的确定有两种方法, 一是凭经验,根据分类问题,选择一种准则(例如 以距离函数作相似性度量),用不断修改阀值,来 达到某种最佳分类。另一种方法是确定一种函数, 当该函数取最小值时,仍未达到最佳分类。
主要方法
• 贝叶斯决策法 • 线性判别函数 • 邻近法分类(KNN) • 最小距离分类 • 聚类分析法
贝叶斯决策方法
• 运用统计决策理论设计的分类系统又称为 分类器。
• 贝叶斯决策是一种统计模式识别决策法, 它有如下基本假定: 1.各类别总体的概率分布是已知的 2.被决策的分类数是一定的 3.被识别的事物或对象有多个特征观测值
最大最小距离法
• 这种方法以欧氏距离为度量,先选择相距最远的两点为中心,分别计算各种 本到这两中心的距离Di1和Di2,i=1,2, …,n。对每个i点取两个距离Di1和Di2中的 最小:min(Di1,Di2),检测全部min(Di1,Di2)中的最大者是否大于|Z1Z2|/2来判决聚类。故称最大最小距离法。以下图十点为例,具体步骤如下: 第一步:任意取X1为第一个聚类中心,即X1=Z1。 第二步:确定离X1最远的标本,令X6=Z2。 第三步:逐个计算各样本X1,X2, …,Xn与Z1及Z2的距离Di1,Di2。 Di1=|X i-Z1|,Di2=|X i-Z2| 若存在max{ min(Di1,Di2),i=1,2, …,n}>|Z 1-Z2|/2,则令X i=Z3(X 7= Z3),转下一步。否则,转最后一步。 第四步:计算Di1,Di2,Di3若存在max{ min(Di1,Di2,Di3),i=1,2, …,n}>| Z 1-Z2|/2,则令Xi=Z4,转下一步。否则,转最后一步。 …… 最后一步:将全部样本按最小距离分别到最近的聚类中心。本例为三个中心, 得分类结果: {X1X3X4}为第一类,Z 1=X 1 {X2X6}为第二类,Z 2=X 6 {X5X7X8X9X10}为第三类,Z 3=X 7
设有R类样本,分别为w1,w2,…wR, 已知每类的先验概率为P(wi), 其中 i=1,2, …,R。对于待识别的随机向量X,已知每类的条件概率密度为 P(X|wi),则根据贝叶斯公式有后验概率: P(wi|X)=(P(X| wi)*P(wi))/(∑P(X∣wi)*P(wi)) (1) 根据计算得出得后验概率,取最大得后验概率P(wi|X)所属的wi类,判 决X属于wi类。表示为: P(wi|X)>P(wj|X)则X属于wi 其中i,j=1,2, …,R,且存在j≠i,这就是贝叶斯判别准则。 若按统计理论定义“似然比”为: l(X) = P(X| wi)/ P(x| wi) 取判别阀值: θji= P(wj)/ P(wi) 则有贝叶斯判别准则的似然比表示形式: l(X) > P(wj)/ P(wi) 则X属于wi 对于两类模式集(w1,w2)的分类,贝叶斯判别准则简单表示为: 若 P(w1|X)>P(w2|X)则X属于w1 若 P(w2|X)>P(w1|X)则X属于w2 贝叶斯判别准则实质上是最小错误概率的贝叶斯判别准则。
几何分类法(判别函数法)
•
一个模式经某种数学变换后,映射为一特
征向量,并表示为特征空间的一个点。同一类
的点构成点集,表示一类ωi。不同类的点集
(ωi ,i=1,2, …,n)总是互相有不同程度的分离。
若能几何的方法,找出一种不依赖于条件概率
密度的分离函数,把特征空间划分为对应于不
同类别的子空间,便可实现模式分类。因此,
最小风险贝叶斯判别准则
• 在实际工作中,有时仅考•虑错误率最小是 不够的。要引入比错误率更广泛的概念— 风险、损失。
• 如果在采取每一决策时,其条件风险都最 小,则对所有的x作决策时,其平均(期望 风险)也最小。称为最小风险的贝叶斯决 策。
• 在决策理论中,称所采取的决定为决策或
行动。每个决策或行动都会带来一定的损 失。该损失用λ表示,它是与本该属于wi但 采取的决策为αj所造成的损失有关。由此定 义损失函数为λ(αj| wi)=λij(i,j=1,2, …,R)。 对样本X属于wi,有贝叶斯公式已知后验概率 为P(wi|X)
• 模式识别系统在进行工作时只要判断被识 别的对象落入哪一个区域,就能确定出它 所属的类别。由噪声和传感器所引起的变 异性,可通过预处理而部分消除;而模式 本身固有的变异性则可通过特征抽取和特 征选择得到控制,尽可能地使模式在该特 征空间中的分布满足上述理想条件。因此 一个统计模式识别系统应包含预处理、特 征抽取、分类器等部分(见图)。
近邻函数法
• 基于最邻近规范的试探法 • 最大最小距离法
基于最邻近规范的试探法
• 设有n个样本:X1,X2, ……,Xn。取任一样本(例如取X1) 为聚类中心Z1,则有X1=Z1。选取一非负的阀值T1。然 后计算X2到Z1的距离D21,距离函数可以选择上述任一种, 通常选用欧氏距离。计算距离结果,如果D21<T1,则认 为X2在Z1为中心的域内,即X2与X1同类。若D21>T1,则 建立一个新的聚类中心Z2,且X2=Z2。 下一步,取第三个样本X3,分别按距离函数计算X3到Z1、 Z2的距离D31、D32。若D31<T1,则X3与下1同类。若 D31>T1且D32>T1,则X3与X1、X2都不同类。并需建立 第三个聚类中心Z3=X3。 用上述方法对全部样本计算距离,比较阀值,决定聚类。 这种方法计算简单。当具有一些模式分布先验知识,以 指导阀值选取及初始点选择,便可较快获得结果。
统计模式识别的研究进展
• 类条件概率分布的估计 线性判别法 贝叶斯分类器 误差界
类条件概率分布的估计
• 考虑将待识样本X∈Rd判别为C个不同类ω1,ω2,…, ωc中的某一类。由贝叶
斯定理,X应判为具最大后验概率的那一类。由于类条件概率分布未知,故通 常假定分布为某一带参数的模型如多维正态分布(当多维正态分布中均值向量 和协方差矩阵已知时,由此分布得到的二次判别函数是最优的),而表示分 布的参数则由训练样本进行估计。当训练样本不充足时,分布参数包含估计 误差影响识别精度。
