大学物理上-练习册-第4章《振动》答案
湖南大学大学物理练习册答案(一、二两册全)

大学物理(一)练习册 参考解答第1章 质点运动学一、选择题1(D),2(D),3(B),4(D),5(D),6(D),7(D),8(D ),9(B),10(B), 二、填空题(1). sin 2t A ωω,()π+1221n (n = 0,1,… ),(2). 8 m ,10 m. (3). 23 m/s.(4). 16Rt 2 ,4 rad /s 2(5). 4t 3-3t 2 (rad/s),12t 2-6t (m/s 2). (6).331ct ,2ct ,c 2t 4/R .(7). 2.24 m/s 2,104o(8). )5cos 5sin (50j t i t+-m/s ,0,圆. (9). h 1v /(h 1-h 2) (10). 0321=++v v v三、计算题1. 有一质点沿x 轴作直线运动,t 时刻的坐标为x = 4.5 t 2 – 2 t 3 (SI) .试求:(1) 第2秒内的平均速度; (2) 第2秒末的瞬时速度;(3) 第2秒内的路程.解:(1) 5.0/-==∆∆t x v m/s(2) v = d x /d t = 9t - 6t 2, v (2) =-6 m/s. (3) S = |x (1.5)-x (1)| + |x (2)-x (1.5)| = 2.25 m.2. 一质点沿x 轴运动,其加速度为a = 4t (SI),已知t = 0时,质点位于x 0=10 m 处,初速度v 0 = 0.试求其位置和时间的关系式.解: =a d v /d t 4=t , d v 4=t d t⎰⎰=vv 0d 4d tt t v = 2t 2v d =x /d t 2=t 2t t x txx d 2d 02⎰⎰=x 2= t 3 /3+x 0 (SI)3. 质点沿x 轴运动,其加速度a 与位置坐标x 的关系为 a =2+6 x 2(SI),如果质点在原点处的速度为零,试求其在任意位置处的速度.解:设质点在x 处的速度为v ,62d d d d d d 2x tx xta +=⋅==v v()x x xd 62d 02⎰⎰+=v v v() 2 213 x x +=v4. 一物体悬挂在弹簧上作竖直振动,其加速度为-=a ky ,式中k 为常量,y 是以平衡位置为原点所测得的坐标. 假定振动的物体在坐标y 0处的速度为v 0,试求速度v 与坐标y 的函数关系式.解: yt yy t a d d d d d d d d vvv v===又 -=a ky ∴ -k =y v d v / d y⎰⎰+=-=-C kyy ky 222121, d d vv v已知 =y y 0 ,=v v 0 则 20202121ky C --=v)(220202y y k -+=v v5. 一质点沿半径为R 的圆周运动.质点所经过的弧长与时间的关系为221ct bt S += 其中b 、c 是大于零的常量,求从0=t 开始到切向加速度与法向加速度大小相等时所经历的时间.解: ct b t S +==d /d v c t a t ==d /d v ()R ct b a n /2+=根据题意: a t = a n 即 ()R ct b c /2+=解得 cb cR t -=6. 如图所示,质点P 在水平面内沿一半径为R =2 m 的圆轨道转动.转动的角速度ω与时间t 的函数关系为2kt =ω (k 为常量).已知s t 2=时,质点P 的速度值为32 m/s .试求1=t s 时,质点P 的速度与加速度的大小.解:根据已知条件确定常量k()222/rad 4//sRttk ===v ω24t =ω, 24Rt R ==ωvs t 1=时, v = 4Rt 2= 8 m/s2s /168/m Rt dt d a t ===v 22s /32/m R a n ==v()8.352/122=+=n t a a a m/s 27. (1)对于在xy 平面内,以原点O 为圆心作匀速圆周运动的质点,试用半径r 、角速度ω和单位矢量i、j 表示其t 时刻的位置矢量.已知在t = 0时,y = 0, x = r , 角速度ω如图所示;(2)由(1)导出速度 v与加速度 a的矢量表示式; (3)试证加速度指向圆心.解:(1) j t r i t r j y i x rs i n c o s ωω+=+=(2) j t r i t r t rc o s s i nd d ωωωω+-==v j t r i t r tas i n c o s d d 22ωωωω--==v (3) ()r j t r i t r a s i n c o s 22ωωωω-=+-=这说明 a 与 r 方向相反,即a指向圆心8. 一飞机驾驶员想往正北方向航行,而风以60 km/h 的速度由东向西刮来,如果飞机的航速(在静止空气中的速率)为 180 km/h ,试问驾驶员应取什么航向?飞机相对于地面的速率为多少?试用矢量图说明.解:设下标A 指飞机,F 指空气,E 指地面,由题可知:v FE =60 km/h 正西方向 v AF =180 km/h 方向未知v AE 大小未知, 正北方向由相对速度关系有: FE AF AE v v v +=AE v 、 AF v 、EE v 构成直角三角形,可得 ()()k m /h 17022v v v =-=FEAFAE() 4.19/tg1==-AEFEv v θ(飞机应取向北偏东19.4︒的航向).西北θFEv vAF v vAEvv四 研讨题1. 在下列各图中质点M 作曲线运动,指出哪些运动是不可能的?参考解答:(1)、(3)、(4)是不可能的.(1) 曲线运动有法向加速度,加速度不可能为零;(3) 曲线运动法向加速度要指向曲率圆心; (4) 曲线运动法向加速度不可能为零.2. 设质点的运动方程为)(t x x =,)(t y y =在计算质点的速度和加速度时: 第一种方法是,先求出22yx r +=,然后根据 td d r =v 及 22d d tr a =而求得结果;第二种方法是,先计算速度和加速度的分量,再合成求得结果,即 22)d d ()d d (ty t x +=v 和 222222)d d ()d d (ty tx a +=.你认为两种方法中哪种方法正确?参考解答:第二种方法是正确的。
大学物理学振动与波动习题答案

大学物理学振动与波动习题答案word完美格式大学物理学(上)第四,第五章习题答案第4章振动p174.4.1一物体沿x轴搞四极振动,振幅a=0.12m,周期t=2s.当t=0时,物体的加速度x=0.06m,且向x轴正向运动.谋:(1)此简谐振动的表达式;(2)t=t/4时物体的边线、速度和加速度;(3)物体从x=-0.06m,向x轴负方向运动第一次回到平衡位置所需的时间.[答疑](1)设立物体的四极振动方程为x=acos(ωt+φ),其中a=0.12m,角频率ω=2π/t=π.当t=0时,x=0.06m,所以cosφ=0.5,因此φ=±π/3.物体的速度为v=dx/dt=-ωasin(ωt+φ).当t=0时,v=-ωasinφ,由于v>0,所以sinφ<0,因此φ=-π/3.四极振动的表达式为x=0.12cos(πtcπ/3).(2)当t=t/4时物体的位置为x=0.12cos(π/2cπ/3)=0.12cosπ/6=0.104(m).速度为v=-πasin(π/2cπ/3)=-0.12πsinπ/6=-0.188(ms-1).加速度为a=dv/dt=-ω2acos(ωt+φ)=-π2acos(πt-π/3)=-0.12π2cosπ/6=-1.03(ms-2).(3)方法一:求时间差.当x=-0.06m时,可得精心整理自学泰迪cos(πt1-π/3)=-0.5,因此πt1-π/3=±2π/3.由于物体向x轴正数方向运动,即v<0,所以sin(πt1-π/3)>0,因此πt1-π/3=2π/3,得t1=1s.当物体从x=-0.06m处第一次回到平衡位置时,x=0,v>0,因此cos(πt2-π/3)=0,可得πt2-π/3=-π/2或3π/2等.由于t2>0,所以πt2-π/3=3π/2,只须t2=11/6=1.83(s).所需要的时间为δt=t2-t1=0.83(s).方法二:反向运动.物体从x=-0.06m,向x轴正数方向运动第一次返回平衡位置所需的时间就是它从x=0.06m,即为从起点向x轴正方向运动第一次返回平衡位置所需的时间.在平衡位置时,x=0,v<0,因此cos(πt-π/3)=0,可以得πt-π/3=π/2,Champsaurt=5/6=0.83(s).[注意]根据振动方程x=acos(ωt+φ),当t=0时,可得φ=±arccos(x0/a),(-π<φqπ),初位相的值域由速度同意.由于v=dx/dt=-ωasin(ωt+φ),当t=0时,v=-ωasinφ,当v>0时,sinφ<0,因此φ=-arccos(x0/a);当v<0时,sinφ>0,因此word轻松格式φ=arccos(x0/a).可知:当速度大于零时,初位相取负值;当速度大于零时,初位相取正值.如果速度等于零,当初边线x0=a时,φ=0;当初边线x0=-a时,φ=π.4.2已知一简谐振子的振动曲线如图所示,试由图求:(1)a,b,c,d,e各点的位相,及抵达这些状态的时刻t各就是多少?未知周期为t;(2)振x动表达式;aa(3)画a/2b出旋转矢量oc图.dt[答疑]e方法一:由图6.2十一位说媒时间.(1)设曲线方程为x=acosφ,其中a表示振幅,φ=ωt+φ表示相位.由于xa=a,所以cosφa=1,因此φa=0.由于xb=a/2,所以因此φb=±π/3;由于位相φ随时间t增加,b点位相就应该大于a点的位相,因此φb=π/3.由于xc=0,所以cosφc=0,又由于c点位二者大于b位相,因此φc=π/2.同理可以得其他两点位灵府φd=2π/3,φe=π.c点和a点的增益之高为π/2,时间之高为t/4,而b点和a点的增益之高为π/3,时间之差必须为t/6.因为b点的加速度值与o时刻的加速度值相同,所以抵达a点的时刻为ta=t/6.精心整理自学泰迪到达b点的时刻为tb=2ta=t/3.到达c点的时刻为tc=ta+t/4=5t/12.到达d点的时刻为td=tc+t/12=t/2.到达e点的时刻为te=ta+t/2=2t/3.(2)设立振动表达式为x=acos(ωt+φ),当t=0时,x=a/2时,所以cosφ=0.5,因此φ=±π/3;由于零时刻的位相大于a点的位相,所以因此振动表达式为x?acos(2?tt??3).另外,在o时刻的曲线上作一切线,由于速度是位置对时间的变化率,所以切线代表速度的方向;由于其斜率大于dc零,所以速度小b于零,因此初位ea相取负值,从而oφx可得运动方程.a(3)例如图转动矢量图右图.方法二:由时间x求位二者.将aa曲线反方a/2bf向延长与toc轴相交于fdt点,由于exf=0,根据运动方程,可以得cos(2?tt??3)?0所以2?tft??32.word完美格式似乎f点的速度大于零,所以挑负值,Champsaurtf=-t/12.从f点抵达a点经过的时间为t/4,所以抵达a点的时刻为ta=t/4+tf=t/6,其位灵府taa2t30.由图可以确认其他点的时刻,同理只须各点的位相.4.3如图所示,质量为10g的子弹以速度v=103ms-1水平射入木块,并陷入木块中,使弹簧压缩而作简谐mvmk振动.设弹簧的高傲系数k图4.3=8×103nm-1,木块的质量为4.99kg,数等桌面摩擦,试求:(1)振动的振幅;(2)振动方程.[答疑](1)子弹射入木块时,由于时间很短,木块还顾不上运动,弹簧没被放大,它们的动量动量,即为mv=(m+m)v0.Champsaur子弹射入后的速度为v0=mv/(m+m)=2(ms-1),这也就是它们振动的初速度.子弹和木块压缩弹簧的过程机械能守恒,可得(m+m)v220/2=ka/2,所以振幅为a?vm?m0k=5×10-2(m).(2)振动的圆频率为km?m=40(rads-1).取木块静止的位置为原点、向右的方向为位移x的正方向,振动方程可设为x=acos(ωt+φ).当t=0时,x=0,可得精心整理自学泰迪φ=±π/2;由于速度为也已,所以取负的初位二者,因此振动方程为x=5×10-2cos(40t-π/2)(m).4.4如图所示,在倔强系数为k的弹簧下,摆一质量为km的托盘.质量为mx1x2的物体由距盘底高moh处自由下落与盘h发生完全非弹性碰m撞到,而使其并作珍谐振动,设两物体碰后瞬x时为t=0时刻,谋图4.4振动方程.[答疑]物体落后、相撞前的速度为v?2gh,物体与纸盒搞全然非弹簧相撞后,根据动量守恒定律可以得它们的共同速度为vm0?m?mv?mm?m2gh,这也就是它们振动的初速度.设立振动方程为x=acos(ωt+φ),其中圆频率为km?m.物体没落之前,纸盒均衡时弹簧弯曲为x1,则x1=mg/k.物体与纸盒相撞之后,在代莱平衡位置,弹簧弯曲为x2,则x2=(m+m)g/k.挑代莱平衡位置为原点,价值观念下的方向为也已,则它们振动的初加速度为x0=x1-x2=-mg/k.因此振幅为a?x2?v20mg22ghm20?2?(k)?k(m?m)word轻松格式mgk12kh(mm)g;初位相为arctan?v0?x?2kh.0(m?m)g4.5重量为p的物体用两根弹簧竖直悬挂,如图所示,各弹簧的倔强系数标明在图上.试求在图示两种情况下,系统沿竖直方向振动的固有频率.[答疑](1)可以证明:当两根弹簧串联时,总高傲系数为k=k1k2/(k1+k2),因此固有频率为k1kk2πk2?1k2πm(a)(b)图4.51k1k2g2(k1k2)p.(2)因为当两根弹簧并联时,总倔强系数等于两个弹簧的倔强系数之和,因此固有频率为12k2kg2π?2?m?12?p.4.6一匀质细圆环质量为m,半径为r,绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动,求摆动的周期.[答疑]方法一:用旋转定理.通过质心横向环面存有一个轴,环绕着此轴的转动惯量为ori=mr2c.θc根据平行轴定理,环绕过o精心整理学习帮手mg点的平行轴的转动惯量为i=ic+mr2=2mr2.当环偏离平衡位置时,重力的力矩为m=-mgrsinθ,方向与角度θ增加的方向相反.根据旋转定理得iβ=m,即id2?dt2?mgrsin??0,由于环做小幅度摆动,所以sinθ≈θ,可得微分方程d2?dt2?mgri??0.转动的圆频率为mgri,周期为t?2π??2?i2rmgr?2?.g方法二:用机械能守恒定律.取环的质心在最底点为重力势能零点,当环心转过角度θ时,重力势能为ep=mg(r-rcosθ),拖o点的旋转动能为e1k?2i?2,总机械能为e?12i?2?mg(r?rcos?).环路在旋转时机械能动量,即e为常量,将上式对时间微分,利用ω=dθ/dt,β=dω/dt,得0=iωβ+mgr(sinθ)ω,由于ω≠0,当θ不大存有sinθ≈θ,可以得振动的微分方程d2?dt2?mgri??0,从而可求角频率和周期.[特别注意]角速度和圆频率采用同一字母ω,不要将两者混为一谈.word完美格式(4)图画出来这振动的转动矢量图,并4.7横截面均匀的光在图上指明t为1,2,10s等各时刻的矢滑的u型管中有适量液量位置.yy体如图所示,液体的总[答疑](1)比较四极振动的标准方0y长度为l,求液面上下程y微小曲折的民主自由振动的频率。
大学物理上-练习册-第4章《振动》答案

大学物理上-练习册-第4章《振动》答案第4章 振动一、选择题1(C),2(B),3(C),4(E),5(C),6(D),7(B),8(D),9(B),10(C)二、填空题(1). π - π /2分、π/3. (2). k m /22π、k m 2/2π (3). )21cos(04.0π+π=t x (4). )214cos(04.0π-πt (5).)212/5cos(1022π-⨯=-t x(6). 0.05 m ,-0.205π(或-36.9°) (7). 3/4,gl /2∆π(8). 291 Hz 或309 Hz(9). 4×10-2m ,12π (10). )212cos(π-t A ω三、计算题1. 一质点在x 轴上作简谐振动,选取该质点向右运动通过A 点时作为计时起点( t = 0 ),经过2秒后质点第一次经过B 点,再经过2秒后质点第二次经过B 点,若已知该质点在A 、B 两点具有相同的速率,且AB = 10 cm 求:A B v ρ x(1) 质点的振动方程;(2) 质点在A 点处的速率.解:由旋转矢量图和 |v A | = |v B | 可知 T /2 = 4秒,∴ T = 8 s , ν = (1/8) s -1,ω = 2πν = (π /4) s -1(1) 以AB 的中点为坐标原点,x 轴指向右方. t = 0时, 5-=x cm φcos A = t = 2 s 时, 5=x cm φφωsin )2cos(A A -=+=由上二式解得 tg φ = 1 因为在A 点质点的速度大于零,所以φ = -3π/4或5π/4(如图)25cos /==φx A cm∴ 振动方程)434cos(10252π-π⨯=-t x (SI)(2) 速率 )434sin(41025d d 2π-π⨯π-==-t t x v (SI) 当t = 0 时,质点在A 点 221093.3)43sin(10425d d --⨯=π-⨯π-==t x v m/s2.如图1所示,一定滑轮的半径为R ,v Bx A B O t = 0t = 2 st = 4 sφωv AvBm转动惯量为J ,其上挂一轻绳,绳的一端系一质量为m 的物体,另一端与一固定的轻弹簧相连,如图所示.设弹簧的劲度系数为k ,绳与滑轮间无滑动,且忽略轴的摩擦力及空气阻力.现将物体m 从平衡位置拉下一微小距离后放手,证明物体作简谐振动,并求出其角频率.解:取如图x 坐标,平衡位置为原点O ,向下为正,m 在平衡位置时弹簧已伸长x 0kx mg = ① 设m 在x 位置,分析受力, 这时弹簧伸长0x x + )(02x x k T += ② 由牛顿第二定律和转动定律列方程: ma T mg =-1③ βJ R T R T =-21 ④ βR a = ⑤联立解得 mR J kxa +-=)/(2由于x 系数为一负常数,故物体做简谐振动,其角频率为222)/(mRJ kRm R J k +=+=ωm T1T 2T1N xO xmg3.质量m = 10g 的小球与轻弹簧组成的振动系统,按)318cos(5.0π+π=t x 的规律作自由振动,式中t 以秒作单位,x 以厘米为单位,求(1) 振动的角频率、周期、振幅和初相; (2) 振动的速度、加速度的数值表达式; (3) 振动的能量E ; (4) 平均动能和平均势能.解:(1) A = 0.5 cm ;ω = 8π s -1;T = 2π/ω = (1/4) s ;φ = π/3(2) )318sin(1042π+π⨯π-==-t x&v (SI) )318cos(103222π+π⨯π-==-t x a && (SI)(3)2222121A m kA E E E P K ω==+==7.90×10-5J(4) 平均动能⎰=T K tm T E 02d 21)/1(v⎰π+π⨯π-=-Tt t m T 0222d )318(sin )104(21)/1( = 3.95×10-5J = E 21同理EE P 21== 3.95×10-5J4.一质量m = 0.25 kg 的物体,在弹簧的力作用下沿x 轴运动,平衡位置在原点. 弹簧的劲度系数k = 25 N ·m -1.(1) 求振动的周期T 和角频率ω.(2) 如果振幅A =15 cm ,t = 0时物体位于x = 7.5 cm 处,且物体沿x 轴反向运动,求初速v 0及初相φ. (3) 写出振动的数值表达式.解:(1) 1s 10/-==m k ω63.0/2=π=ωT s(2) A = 15 cm ,在 t = 0时,x 0 = 7.5 cm ,v0 < 0由 22)/(ωv +=x A得 3.1202-=--=x A ωv m/s π=-=-31)/(tg 001x ωφv 或 4π/3 ∵ x 0 > 0 ,∴ π=31φ (3) )3110cos(10152π+⨯=-t x (SI)5.如图5所示,有一水平弹簧振子,弹簧的劲度系数k = 24 N/m ,重物的质量m = 6 kg ,重物静止在平衡位置上.设以一水平恒力F = 10 N向左作用于物体(不计摩擦),使之由平衡位置向左运动了0.05 m 时撤去力F .当重物运动到左方最远位置时开始计时,求物体的运动方程.O Fx m图5解:设物体的运动方程为 )cos(φω+=t A x . 恒外力所做的功即为弹簧振子的能量: F ×0.05 = 0.5 J .当物体运动到左方最远位置时,弹簧的最大弹性势能为0.5 J ,即: 5.0212=kA J , ∴ A = 0.204 m .A 即振幅. 4/2==m k ω (rad/s)2 ω = 2 rad/s . 按题目所述时刻计时,初相为φ = π.∴物体运动方程为 )2cos(204.0π+=t x (SI).四 研讨题1. 简谐振动的初相是不是一定指它开始振动时刻的位相?参考解答:对于一个振幅和周期已定的简谐振动,用数学公式表示时,由于选作原点的时刻不同,ϕ值就不同。
大学物理第四版课后习题答案

大学物理第四版课后习题答案大学物理第四版课后习题答案大学物理是一门广受学生喜爱的学科,它涵盖了众多的知识点和概念,需要学生付出大量的努力来掌握。
而课后习题则是检验学生对所学知识的理解和掌握程度的重要方式之一。
然而,对于大多数学生来说,完成课后习题往往是一项具有挑战性的任务。
因此,有一本完整的课后习题答案对学生来说无疑是非常有帮助的。
在大学物理第四版中,课后习题是根据每一章节的内容设计的。
这些习题旨在帮助学生巩固所学的知识,并提供一些实际应用的练习。
然而,由于习题的难度和复杂性不同,学生在解答时可能会遇到一些困难。
因此,拥有一本详细的习题答案可以帮助他们更好地理解和解决问题。
对于大学物理第四版的课后习题,以下是一些可能的答案和解决方法:1. 机械振动和波动习题:一个质点以振幅为0.2m的简谐运动在频率为5Hz的弹簧上进行,求其最大速度和最大加速度。
答案:根据简谐运动的公式,最大速度v_max = Aω,其中A为振幅,ω为角频率。
最大加速度a_max = Aω²。
代入数据,可得到v_max = 0.2m × 2π × 5Hz ≈ 6.28m/s,a_max = 0.2m × (2π × 5Hz)² ≈ 62.8m/s²。
2. 电磁场和电磁波习题:一个半径为0.1m的圆形线圈中通有电流,求该线圈在中心处产生的磁场强度。
答案:根据安培环路定理,磁场强度B = μ₀I/(2πr),其中μ₀为真空中的磁导率,I为电流,r为距离。
代入数据,可得到B = (4π × 10⁻⁷T·m/A) × I/(2π × 0.1m) ≈ 2 × 10⁻⁵T。
3. 热力学习题:一个理想气体从初始状态(P₁,V₁,T₁)经历了一个等温过程,最终达到状态(P₂,V₂,T₁),求气体对外做功。
答案:由于等温过程中气体的温度保持不变,根据理想气体状态方程PV = nRT,可得到P₁V₁ = P₂V₂。
大学物理(第四版)课后习题及答案 机械振动

13 机械振动解答13-1 有一弹簧振子,振幅A=×10-2m ,周期T=,初相=3π/4。
试写出它的运动方程,并做出x--t 图、v--t 图和a--t 图。
13-1分析 弹簧振子的振动是简谐运动。
振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A 、ϕ已知外,ω可通过关系式Tπω2=确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
解 因Tπω2=,则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ,求:(1)振幅、频率、角频率、周期和初相;(2)t=2s 时的位移、速度和加速度。
13-2分析 可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较,即可求得各特征量。
运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t 值后,即可求得结果。
解 (l )将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得:振幅A= 0.10 m ,角频率120-=s πω,初相πϕ25.0=,则周期 s T 1.0/2==ωπ,频率Hz T 10/1==ν。
(2)t= 2s 时的位移、速度、加速度分别为m m x 21007.7)25.040cos()10.0(-⨯=+=ππ )25.040sin()2(/1πππ+⋅-==-s m dt dx v)25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体,密度ρ×103kgm -3。
大学物理简谐振动知识点及试题带答案

简谐振动一、基本要求1、掌握简谐振动的定义,描述简谐振动的各物理量及其相互关系,会根据定义来判断一各物体的运动是不是简谐振动。
2、掌握简谐振动的旋转矢量表示法。
3、掌握简谐振动的基本特征,能根据一定的初始条件写出简谐振动的运动方程。
4、掌握同方向频率的两个简谐振动的合成,了解相互垂直同频率的简谐振动的合成。
二、主要内容1、简谐振动的表达式(运动方程) cos()x A t ωϕ=+三个特征量:振幅A ,决定与振动的能量;角频率ω,决定于振动系统的固有属性; 初相位ϕ,决定于振动系统初始时刻的状态。
简谐运动可以用旋转矢量来表示。
2、振动的相位:()t ωϕ+两个振动的相差:同相2k ϕπ∆=,反相(21)k ϕπ∆=+3、简谐振动的运动微粉方程:2220d x x dtω+=4、简谐振动的实例弹簧振子:220,2d x k x T dt m π+==单摆小角度振动:220,2d g T dt l θθ+==LC振荡:2210,2d q q T dt LCπ+== 5、简谐振动的能量:222111()222k P dx E E E m kx kA dt =+=+= 6、两个简谐振动的能量(1)同方向同频率的简谐振动的合成合振动是简谐振动,合振动的振幅和初相位由下式决定A =11221122sin sin tan cos cos A A A A ϕϕϕϕϕ+=+(2)相互垂直的两个同频率的简谐振动的合成合运动的轨迹一般为椭圆,其具体形状决定于两个分振动的相差和振幅。
当2k ϕπ∆=或(21)k π+时,合运动的轨迹为直线,这时质点在做简谐振动。
三、习题与解答1、两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为)cos(1ϕω+=t A x 。
某时刻当第一个质点正在平衡位置向负方向运动时,第二个质点正在最大位移处。
则第二个质点的振动方程为:( B )(A ))2cos(2πϕω++=t A x (B ))2cos(2πϕω-+=t A x(C ))23cos(2πϕω-+=t A x (D ))cos(2πϕω++=t A x 2、一物体做简谐振动,振幅为A ,在起始时刻质点的位移为2A-且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为:( D )3、一质点作简谐振动,振动方程)cos(ϕω+=t A x ,当时间 t =T/4 时,质点的速度为:( C )(A ) ϕωsin A - (B) ϕωsin A (C )ϕωcos A - (D )ϕωcos A4、一质点作谐振动,周期为T ,当它由平衡位置向 x 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的时间为( A )(A )T /6(B )T /12 (C)T /4 (D )T /85、有两个沿x 轴做简谐运动的质点,其频率、振幅皆相同,当第一个质点自平衡位置向负方向运动时,第二个质点在处(A 为振幅)也向负方向运动,则两者的相位差(12ϕϕ-)为:( C )2Ax -=(A )2π (B )32π (C )6π (D )65π6、质量为10×10-3 kg 的小球与轻弹簧组成的系统,按20.1cos(8)3x t ππ=+(SI)的规律做谐振动,求:(1)振动的周期、振幅、初位相及速度与加速度的最大值;(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等? (3)t 2=5 s 与t 1=1 s 两个时刻的位相差. 解:(1)设谐振动的标准方程为)cos(0φω+=t A x ,则知:3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m -⋅ 51.2=1s m -⋅2.632==A a m ω2s m -⋅(2) N 63.0==ma F mJ 1016.32122-⨯==m mv E J 1058.1212-⨯===E E E k p当p k E E =时,有p E E 2=, 即)21(212122kA kx ⋅= ∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=-=-=∆t t7、一个沿x 轴做简谐振动的弹簧振子,振幅为A ,周期为T ,其振动方程用余弦函数表出.如果t =0时质点的状态分别是:(1)x 0=-A ;(2)过平衡位置向正向运动;(3)过2Ax =处向负向运动; (4)过x =处向正向运动.试求出相应的初位相,并写出振动方程.解:因为 ⎩⎨⎧-==000sin cos ϕωϕA v A x将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有)2cos(1πππϕ+==t T A x)232cos(232πππϕ+==t T A x)32cos(33πππϕ+==t T A x)452cos(454πππϕ+==t T A x8、一质量为10×10-3 kg 的物体做谐振动,振幅为24 cm ,周期为4.0 s ,当t =0时位移为+24 cm.求:(1)t =0.5 s 时,物体所在的位置及此时所受力的大小和方向; (2)由起始位置运动到x =12 cm 处所需的最短时间; (3)在x =12 cm 处物体的总能量. 解:由题已知 s 0.4,m 10242=⨯=-T A ∴ 1s rad 5.02-⋅==ππωT又,0=t 时,0,00=∴+=ϕA x 故振动方程为m )5.0cos(10242t x π-⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=-t x πN102.417.0)2(10103232--⨯-=⨯⨯⨯-=-=-=πωxm ma F方向指向坐标原点,即沿x 轴负向. (2)由题知,0=t 时,00=ϕ,t t =时 3,0,20πϕ=<+=t v A x 故且 ∴ s 322/3==∆=ππωϕt (3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为J101.7)24.0()2(10102121214223222--⨯=⨯⨯⨯===πωA m kA E9、有一轻弹簧,下面悬挂质量为1.0 g 的物体时,伸长为4.9 cm.用这个弹簧和一个质量为8.0 g 的小球构成弹簧振子,将小球由平衡位置向下拉开1.0 cm 后,给予向上的初速度v 0=5.0 cm·s -1,求振动周期和振动表达式. 解:由题知12311m N 2.0109.48.9100.1---⋅=⨯⨯⨯==x g m k 而0=t 时,-12020s m 100.5m,100.1⋅⨯=⨯-=--v x ( 设向上为正)又 s 26.12,51082.03===⨯==-ωπωT m k 即 m102)5100.5()100.1()(22222220---⨯=⨯+⨯=+=∴ωv x A45,15100.1100.5tan 022000πφωϕ==⨯⨯⨯=-=--即x v ∴ m )455cos(1022π+⨯=-t x10、图为两个谐振动的x -t 曲线,试分别写出其谐振动方程.题10图解:由题10图(a),∵0=t 时,s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即 1s rad 2-⋅==ππωT故 m )23cos(1.0ππ+=t x a 由题10图(b)∵0=t 时,35,0,2000πϕ=∴>=v A x 01=t 时,35,0,2000πϕ=∴>=v A x又 ππωϕ253511=+⨯=∴ πω65=故 m t x b )3565cos(1.0ππ+=11、有两个同方向、同频率的简谐振动,其合成振动的振幅为0.20 m ,位相与第一振动的位相差为6π,已知第一振动的振幅为0.173 m ,求第二个振动的振幅以及第一、第二两振动的位相差.解:由题意可做出旋转矢量图如下. 由图知01.02/32.0173.02)2.0()173.0(30cos 222122122=⨯⨯⨯-+=︒-+=A A A A A ∴ m 1.02=A 设角θ为O AA 1,则θcos 22122212A A A A A -+=即 01.0173.02)02.0()1.0()173.0(2cos 2222122221=⨯⨯-+=-+=A A A A A θ 即2πθ=,这说明,1A 与2A 间夹角为2π,即二振动的位相差为2π.12、试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅:(1)125cos(3),375cos(3);3x t cm x t cm ππ⎧=+⎪⎪⎨⎪=+⎪⎩(2)125cos(3),345cos(3).3x t cm x t cm ππ⎧=+⎪⎪⎨⎪=+⎪⎩解: (1)∵ ,233712πππϕϕϕ=-=-=∆ ∴合振幅 cm 1021=+=A A A (2)∵ ,334πππϕ=-=∆∴合振幅 0=A13、一质点同时参与两个在同一直线上的简谐振动,振动方程为120.4cos(2),650.3cos(2).6x t m x t m ππ⎧=+⎪⎪⎨⎪=-⎪⎩试分别用旋转矢量法和振动合成法求合振动的振幅和初相,并写出谐振动方程. 解:∵ πππϕ=--=∆)65(6 ∴ m 1.021=-=A A A 合3365cos 3.06cos 4.065sin3.06sin4.0cos cos sin sin tan 22122211=+-⨯=++=ππππϕϕϕϕφA A A A ∴ 6πϕ=其振动方程为m )62cos(1.0π+=t x14、若简谐运动方程为0.10cos(200.25)()x t m ππ=+,求:(1)振幅、频率、角频率、周期和初相;(2)2t s =时的位移、速度和加速度。
大学物理(第四版)课后习题与答案_机械振动
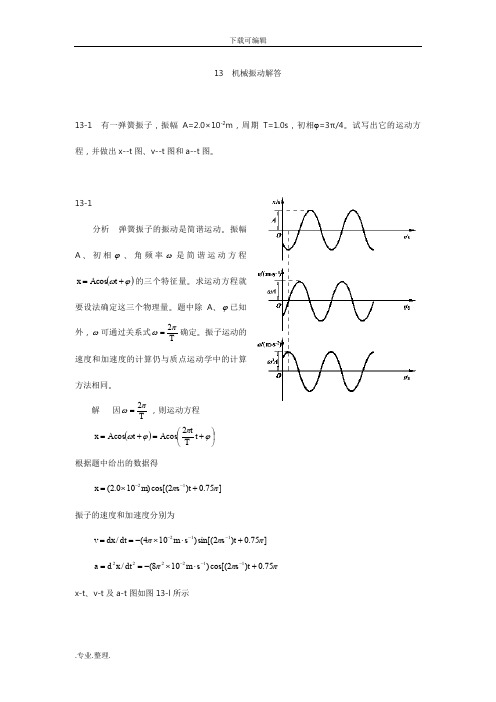
13 机械振动解答13-1 有一弹簧振子,振幅A=2.0×10-2m ,周期T=1.0s ,初相ϕ=3π/4。
试写出它的运动方程,并做出x--t 图、v--t 图和a--t 图。
13-1分析 弹簧振子的振动是简谐运动。
振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A 、ϕ已知外,ω可通过关系式Tπω2=确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
解 因Tπω2=,则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ,求:(1)振幅、频率、角频率、周期和初相;(2)t=2s 时的位移、速度和加速度。
13-2分析 可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较,即可求得各特征量。
运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t 值后,即可求得结果。
解 (l )将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得:振幅A= 0.10 m ,角频率120-=s πω,初相πϕ25.0=,则周期 s T 1.0/2==ωπ,频率Hz T 10/1==ν。
(2)t= 2s 时的位移、速度、加速度分别为m m x 21007.7)25.040cos()10.0(-⨯=+=ππ )25.040sin()2(/1πππ+⋅-==-s m dt dx v )25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体,密度ρ5.5×103kg •m -3。
大学物理学课后习题4第四章答案
[答案:D]
4.2 填空题 (1)一质点在 X 轴上作简谐振动,振幅 A=4cm,周期 T=2s,其平衡位置
取作坐标原点。若 t=0 时质点第一次通过 x=-2cm 处且向 x 轴负方向运动,则 质点第二次通过 x=-2cm 处的时刻为__ __s。
(3) t2 5s 与 t1 1s 两个时刻的位相差;
解:(1)设谐振动的标准方程为 x Acos(t 0 ) ,相比较厚则有:
A 0.1m,
8 ,T
2
1 4
s,
0
2
/3
又
vm A 0.8 m s1 2.51 m s1
am 2 A 63.2 m s2
(2)
Fm mam 0.63N
(1) x0 A ;
(2)过平衡位置向正向运动; (3)过 x A 处向负向运动;
2
(4)过 x A 处向正向运动. 2
试求出相应的初位相,并写出振动方程.
解:因为
v
x0 A cos0 0 Asin
0
将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有
1
x Acos( 2 t ) T
103
(
)2
0.17
4.2
103
N
2
方向指向坐标原点,即沿 x 轴负向.
(2)由题知, t 0 时,0 0 ,
t t时
x0
A ,且v 2
0, 故 t
3
∴
t
3
/
2
2s 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章 振动一、选择题1(C),2(B),3(C),4(E),5(C),6(D),7(B),8(D),9(B),10(C) 二、填空题 (1). 、-/2分、.(2). k m /22π、k m 2/2π (3). )21cos(04.0π+π=t x(4). )214cos(04.0π-πt(5). )212/5cos(1022π-⨯=-t x(6). 0.05 m ,-0.205π(或-36.9°) (7). 3/4,g l /2∆π(8). 291 Hz 或309 Hz(9). 4×10-2m ,12π(10). )212cos(π-t A ω三、计算题1. 一质点在x 轴上作简谐振动,选取该质点向右运动通过A 点时作为计时起点( t = 0 ),经过2秒后质点第一次经过B 点,再经过2秒后质点第二次经过B点,若已知该质点在A 、B 两点具有相同的速率,且AB = 10 cm求:(1) 质点的振动方程; (2) 质点在A 点处的速率.解:由旋转矢量图和 |v A | = |v B | 可知 T /2 = 4秒,∴ T = 8 s , = (1/8) s -1,s -1(1) 以AB 的中点为坐标原点,x 轴指向右方. t = 0时, 5-=x cm φcos A =t = 2 s 时, 5=x cm φφωsin )2cos(A A -=+=由上二式解得 tg = 1 因为在A 点质点的速度大于零,所以 = -3/4或5/4(如图) 25cos /==φx A cm ∴ 振动方程 )434cos(10252π-π⨯=-t x (SI)(2) 速率 )434sin(41025d d 2π-π⨯π-==-t t x v (SI) 当t = 0 时,质点在A 点v Bx A BO t = 0t = 2 st = 4 sφωv A v BA B v x221093.3)43sin(10425d d --⨯=π-⨯π-==tx v m/s2.如图1所示,一定滑轮的半径为R ,转动惯量为J ,其上挂一轻绳,绳的一端系一质量为m 的物体,另一端与一固定的轻弹簧相连,如图所示.设弹簧的劲度系数为k ,绳与滑轮间无滑动,且忽略轴的摩擦力及空气阻力.现将物体m 从平衡位置拉下一微小距离后放手,证明物体作简谐振动,并求出其角频率.解:取如图x 坐标,平衡位置为原点O ,向下为正,m 在平衡位置时弹簧已伸长x 00kx mg = ①设m 在x 位置,分析受力, 这时弹簧伸长0x x + )(02x x k T += ②由牛顿第二定律和转动定律列方程: ma T mg =-1 ③ βJ R T R T =-21 ④ βR a = ⑤ 联立解得mR J kxa +-=)/(2由于x 系数为一负常数,故物体做简谐振动,其角频率为222)/(mR J kR mR J k+=+=ω3.质量m = 10g 的小球与轻弹簧组成的振动系统,按)318cos(5.0π+π=t x 的规律作自由振动,式中t 以秒作单位,x 以厘米为单位,求(1) 振动的角频率、周期、振幅和初相; (2) 振动的速度、加速度的数值表达式; (3) 振动的能量E ; (4) 平均动能和平均势能.解:(1) A = 0.5 cm ;= 8 s -1;T = 2/= (1/4) s ; = /3(2) )318sin(1042π+π⨯π-==-t xv (SI))318cos(103222π+π⨯π-==-t xa (SI) (3) 2222121A m kA E E E P K ω==+==7.90×10-5 J(4) 平均动能 ⎰=T K t m T E 02d 21)/1(vm T 1T 2T 1NMg xx 0mgm图1⎰π+π⨯π-=-Tt t m T 0222d )318(sin )104(21)/1( = 3.95×10-5J = E 21同理E E P 21== 3.95×10-5J4.一质量m = 0.25 kg 的物体,在弹簧的力作用下沿x 轴运动,平衡位置在原点. 弹簧的劲度系数k = 25 N ·m -1. (1) 求振动的周期T 和角频率.(2) 如果振幅A =15 cm ,t = 0时物体位于x = 7.5 cm 处,且物体沿x 轴反向运动,求初速v 0及初相.(3) 写出振动的数值表达式. 解:(1) 1s 10/-==m k ω63.0/2=π=ωT s(2) A = 15 cm ,在 t = 0时,x 0 = 7.5 cm ,v0 < 0 由 2020)/(ωv +=x A得 3.12020-=--=x A ωv m/s π=-=-31)/(tg 001x ωφv 或 4/3 ∵ x 0 > 0 ,∴ π=31φ (3) )3110cos(10152π+⨯=-t x (SI)5.如图5所示,有一水平弹簧振子,弹簧的劲度系数k = 24 N/m ,重物的质量m = 6 kg ,重物静止在平衡位置上.设以一水平恒力F =10 N 向左作用于物体(不计摩擦),使之由平衡位置向左运动了0.05 m 时撤去力F .当重物运动到左方最远位置时开始计时,求物体的运动方程.解:设物体的运动方程为 )cos(φω+=t A x .恒外力所做的功即为弹簧振子的能量: F ×0.05 = 0.5 J .当物体运动到左方最远位置时,弹簧的最大弹性势能为0.5 J ,即:5.0212=kA J , ∴ A = 0.204 m . A 即振幅.4/2==m k ω (rad/s)2= 2 rad/s . 按题目所述时刻计时,初相为 = .∴物体运动方程为 )2cos(204.0π+=t x (SI).OFx m 图5四 研讨题1. 简谐振动的初相是不是一定指它开始振动时刻的位相?参考解答:对于一个振幅和周期已定的简谐振动,用数学公式表示时,由于选作原点的时刻不同,ϕ值就不同。
例如,选物体到达正向极大位移的时刻为时间原点,则ϕ值等于零;如果选物体到达负向极大位移的时刻为时间原点,则ϕ等于π。
由于ϕ是由对时间原点的选择所决定的,所以把它叫做振动的初相。
简谐振动的初相不是一定指它开始振动时刻的位相。
思考题:任何一个实际的弹簧都是有质量的,如果考虑弹簧的质量,弹簧振子的振动周期将变大还是变小?2. 任何一个实际的弹簧都是有质量的,如果考虑弹簧的质量,弹簧振子的振动周期将变大还是变小?参考解答:因为弹簧振子的周期决定于系统的惯性和弹性,惯性越大则周期越大。
因此可以定性地说,在考虑了弹簧的质量之后,弹簧振子的周期肯定会变大。
若振子的质量为M ,弹簧的质量为m ,弹簧的劲度系数为k ,可以计算出,在考虑了弹 簧的质量之后,弹簧振子的振动周期为km M T 3/2+=π例:劲度系数为k 、质量为m 的均匀弹簧,一端固定,另一端系一质量为M 的物体,在光滑水平面作直线运动。
求解弹簧振子的振动周期( m <M )。
解:平衡时0 点为坐标原点。
物体运动到x 处时,速度为v .设此时弹簧的长度为L ,取弹簧元d l 分析:质量l L m m d d =,位移为x Ll(前提: 弹簧各等长小段变形相同,位移是线性规律),速度为:v.Llt x L l =d d弹簧、物体的动能分别为:202161)d (21v v m L l l L m E L k =⎪⎭⎫⎝⎛=⎰,2221v M E k =.系统弹性势能为:22kx E P =.系统机械能守恒,有:=++222216121kx m M v v 常数即 =++2221)3(21kx m M v 常数将上式对时间求导,整理后可得:0d d )3(=++kx tm M v即 03d d 22=++x m M k tx 令 32m M k+=ω比较简谐振动微分方程,知 km M T 3/22+==πωπ.3. 弹簧振子的无阻尼自由振动是简谐运动,同一弹簧振子在简谐驱动力持续作用下的稳态受迫振动也是简谐运动,这两种简谐运动有什么不同?参考解答:这两种振动虽都是简谐振动,其振动的表达式)cos(ϕω+=t A x 形式也相同,但两种运动有很多的不同,这可从振动的运动学特点和动力学特点两个方面来说明。
从运动学来说,两种振动的频率、振幅、初相、速度、加速度的情况都各不相同;从动力学来说,两种振动的受力情况、振动方程(动力学方程)以及振动的能量特点都各有不同。
无阻尼自由振动:谐振过程中221kA E =为定值,不受外界影响,周期为振子的固有周期, 稳态受迫振动:谐振过程中需不停地受外力作用,补充能量才能保证获得稳态受迫振动,周期为策动力的周期.。
