Excel规划求解使用说明
EXCEL规划求解功能操作说明

Excel规划求解功能操作说明以Microsoft Excel2003为例,说明使用Excel的求解线性规划问题功能的使用方法。
一、加载规划求解功能1.点击【工具】按钮,在下拉菜单中选择【加载宏】功能。
2.在弹出的【可加载宏】选项卡中勾选【规划求解】,点击确定按钮。
此时,【工具】下拉菜单中增加规划求解功能,表示加载成功。
二、构造表格Excel表格并填入各项数据以教材18页【例题2-8】为例,构造表格如下:1.录入约束条件系数约束条件(1)为5x1+x2-x3+x4=3,则在约束系数的第一行的x1,x2,x3,x4,x5,限制条件,常数b列下分别录入5,1,-1,1,0,=,3如下图所示。
约束系数区的第二行录入约束条件(2)的系数、限制符号及常数b,即-10,6,2,0,1,=,2;约束系数区的第三行录入约束条件(3)(x1≥0)的系数、限制符号及常数b,即1,0,0,0,0,≥,0;约束系数区的第四行录入约束条件(4)(x2≥0)的系数、限制符号及常数b,即0,1,0,0,0,≥,0;约束系数区的第五行录入约束条件(5)(x3≥0)的系数、限制符号及常数b,即0,0,1,0,0,≥,0;约束系数区的第六行录入约束条件(6)(x4≥0)的系数、限制符号及常数b,即0,0,0,1,0,≥,0;约束系数区的第七行录入约束条件(7)(x5≥0)的系数、限制符号及常数b,即0,0,0,0,1,≥,0。
如下图所示。
2.录入目标函数系数目标函数为maxZ=4x1-2x2-x3,则在目标函数的x1,x2,x3,x4,x5列下分别录入4,-2,-1,0,0,如下图所示。
3. 录入约束条件的计算公式双击约束条件(1)行的“总和”单元格,录入以下内容:“=B3*B12+C3*C12+D3*D12+E3*E12+F3*F12”说明:录入的内容即是约束条件(1)的计算公式,其中“B3*B12”代表5x 1; “C3*C12”代表1x 2;“D3*D12”代表-1x 3;“E3*E12”代表1x 4;“F3*F12”代表0x 5。
用EXCEL求解线性规划

用EXCEL求解线性规划
要用EXCEL求解线性规划问题,需要遵循以下步骤:
1. 给定问题中的约束条件和目标函数。
2. 打开EXCEL,建立一个新的工作表。
3. 在工作表中输入问题的约束条件和目标函数。
在输入目标函数时,需要将所有项移动到等号左侧,使它成为一个线性方程。
需要注意将不等式约束条件转化为等式约束条件,可以通过添加松弛变量来实现。
4. 使用EXCEL的“规划”工具,在工具栏中点击“数据”-“分
析”-“规划器”,打开“规划器”。
5. 在“规划器”中,选择需要优化的目标单元格,在“约束条件”
中输入所有约束条件所在的单元格,设置变量单元格的范围。
6. 可以在“选项”中添加其他约束条件。
例如,可以设定变量的整数或二元特性等。
7. 单击“求解”按钮,EXCEL将自动求解最优解,并输出最优
值和变量值。
需要注意的是,线性规划问题求解的结果是一个数值,而不是图形。
因此,需要谨慎分析问题以确保从数值结果中得到了正确的结论。
EXCEL规划求解功能操作说明

EXCEL规划求解功能操作说明Excel规划求解功能是Excel内置的解决最优化问题的工具,可用于线性规划、整数规划、非线性规划等诸多领域。
该功能十分便捷灵活,可以帮助用户快速找到问题的最优解。
一、添加求解功能1.打开Excel表格,点击“文件”>“选项”>“加载项”。
2.在弹出的窗口中选择“Excel加载项”>“转到”>“excel加载项”>“管理”。
在“可用的加载项”中勾选“求解器”并关闭窗口。
3.返回Excel表格,在数据选项卡中选择“分析”>“求解”,弹出求解对话框。
二、建立规划模型1.确定目标:需要确定最终要达到的目标或绩效指标,例如最大化利润、最小化成本等。
2.确定决策变量:需要确定影响目标的变量,例如销售量、成本等。
3.建立约束:需要确定影响决策变量的条件,例如材料成本、生产时间等。
注意约束需要用等式、不等式等数学形式表示。
例如,在一个玩具生产厂家的例子中,有以下规划问题:在有限的资源下,最大化玩具的利润。
目标:最大化利润。
决策变量:生产每种玩具的数量。
三、设置求解参数1.目标单元格:选择Excel表格中目标单元格,该单元格包含要优化的方程式。
4.变量单元格必须满足约束:勾选此项,保证变量单元格满足约束条件。
5.求解方法:选择要使用的求解算法,包括线性规划、非线性规划和整数规划等。
1.点击“求解”按钮,系统会自动寻找目标单元格、变量单元格和约束单元格区域。
2.系统执行计算,找到最优解并将其展示在新的单元格区域中。
3.若求解成功,单击“继续”将结果保存在Excel表中。
总之,利用Excel规划求解功能,用户可以通过建立规划模型,设置求解参数和运行求解功能轻轻松松地优化各种最优化问题。
EXCEL表格规划求解使用方法

if(jj[2]<=0)
{
ShowMessage(String("3?′í?úμú")+j1+"DD£?è±éùêy?Y,?T·¨????????!!");
return;
}
while(1)
{
j2++;
if(j2>hangcount)
break;
temp1=String(Sh1.PG("Cells",j2,Cjl).PG("Value"));
if(temp1.ToInt()==2)
规划求解方法如下:
在A1到A76 中找到若干个数据,让它们的和等于某固定值
假设你的数据在A1:A76
将B1:B76标成黄色底纹.
在B77输入=SUMPRODUCT(A1:A76,B1:B76)
进入规划求解对话框.
目标单元格引用B77
选"值为",在后面输入你的定值.
然后可变单元格引用B1:B76
{
if(temp1.ToInt()==2)
{
temp2=String(Sh1.PG("Cells",j2,Djl).PG("Value"));
if(temp2.Length()<1)
{
jj[3]=0;
ShowMessage("ERROR");
然后添加三个约束条件
B1:B76=二进制
பைடு நூலகம்
最后按"求解"
注意:这个二进制是选择BIN后自动填进去的
excelsolver(规划求解)的用法及例子

excelsolver(规划求解)的⽤法及例⼦Solve Linear Programming ProblemsCheck that Solver is installedOpen ExcelClick on the ‘tools’ menuIf Solver is listed, then go to Formulation.Otherwise, Solver needs to be installed, as follows:Again under ‘tools’ click ‘Add-ins..’.The window that appears lists the available add-ins,Click the box next to Solver so that it contains a tick, click ok.Solver should now appear under the ‘tools’ menuFormulationWhenever we formulate a worksheet model of a linear program, we perform the following steps (Par. problem as an example, see appendix):Step 1: Enter the data in the worksheetCells B7:C10 show the production requirements per unit for each product.Cells B5:C5 show the profit contributions per unit for the two products.Cells F7:F10 show the number of hours available in each department.Step 2: Specify cell locations for the decision variablesCells B4:C4.Step 3: Select a cell and enter a formulation for computing the objective value function.Cell D5: =B4*B5+C4*C5 or SUMPRODUCT($B$4:$C$4,$B5:$C5)Step 4: Select a cell and enter a formulation for computing the left-hand side of each constraint.Cell D7:=B4*B7+C4*C7 or SUMPRODUCT($B$4:$C$4,$B7:$C7) (copy from Cell D5)Cell D8:=B4*B8+C4*C8 or SUMPRODUCT($B$4:$C$4,$B8:$C8) (copy from Cell D5)Cell D9:=B4*B9+C4*C9 or SUMPRODUCT($B$4:$C$4,$B9:$C9) (copy from Cell D5)Cell D10:=B4*B10+C4*C10 or SUMPRODUCT($B$4:$C$4,$B10:$C10) (copy from Cell D5)Tips:(1)SUMPRODUCT function requires specifying two cell ranges of equal size, separated by a comma, such as SUMPRODUCT($B$4:$C$4,$B5:$C5). The SUMPRODUCT function computes the products of the first entries in each range, second entries in each range, and so on. It then sums these products.(2) The $ symbol in the cells keeps that cell reference fixed when we copy the formula. This is especially convenient since the formula for calculating the sum of the left-hand-side value for each constrain also follows the same structure as the objective function.Excel SolutionThe following steps show how Solver can be used to obtain the optimal solution to the Par, Inc., problem. Step 1: Select the Tools pull-down menu.Step 2: Select the Solver option.Step 3: When the Solver Parameters dialog box appears.Enter D5 into the Set Cell boxSelect the Equal to: Max optionEnter B4:C4 into the By Changing Variable Cells box.Select Add.Step 4: When the Add Constraint dialog box appears:Enter D7:D10 in the Cell Reference boxSelect <=Enter F7:F10 into the Constraint boxClick OKStep 5: When the Solver Parameters dialog box reappears:Choose Options.Step 6: When the Solver Options dialog box appears,Select Assume Linear Models and Assume Non-negativeClick OK.Step 7: When the Solver Parameters dialog box reappears:Choose Solve.Step 8: When the Solver Results dialog box appears:Select Keep Solver Solution, and choose Answer and Sensitivity from Reports box. The following table shows Excel layout for the Par. problem.The answer report for the Par. problem is:Answer the following questions:1.a.Which constraints are binding? Which are not binding?b.What is the range of optimality for the objective function coefficient associated with standard bags?c.What is the range of optimality for the objective function coefficient associated with deluxe bags?d.After the production, how many hours remain in finishing, and inspection and packaging department?e.What would be the impact on the production plan and profit if the objective function coefficientassociated with standard bags were to change to 12?f.What would be the impact on the production plan and profit if the number of sewing department were to decrease to 500?g.What would be the impact on the production plan and profit if the objective function coefficient associated with standard bags were to change to 9 while at the same time the objective function coefficient associated with deluxe bag were to change to 8?2. Solve M&D Problem. (Answer: Obj=800)3. Solve PM Problem. (Answer: Obj=216,300)4. Solve MSA Problem. (Answer: Obj=15,166)5. Solve Whole Wood Problem. (Answer: Obj=0.05)。
excel规划求解的使用教程详细图文步骤

excel规划求解的使用教程详细图文步骤
规划求解使用步骤2:创建表格,如下。
单击“数据“工具栏,选择”规划求解“,随即弹出【规划求解参数】对话框,在【设置目标单元格】中输入“$B$12”;在【可变单元格】中输入“$C$3:$C$5”,单击“添加”按钮,弹出【添加约束】对话框,在【单元格引用位置】输入“$B$10”,在其右侧的下拉列表中选择【<=】,在【约束值】中输入“$B$7”。
规划求解使用步骤3:单击“添加”按钮,继续添加约束条件。
使用相同方式,再添加4个约束条件。
规划求解使用步骤4:约束条件添加完毕,单击“确定”按钮,返回【规划求解参数】对话框,此时可发现在【约束】列表中显示出了添加的所有约束条件,然后单击“选项”按钮。
随即弹出【规划求解选项】对话框,选中“采用线性模型”和“假定非负”,其余保持默认设定,单击“确定”。
返回【规划求解参数】对话框,单击“求解”按钮。
Excel规划求解功能的使用教程

本文整理于网络,仅供阅读参考
Excel规划求解功能的使用教程
excel规划求解功能的使用教程:
规划求解使用步骤1:安装规划求解:规划求解是excel的一个插件,需要安装。
打开新建文档左上角office按钮——excel 选项——自定义——从下列位置选择命令(所有命令)——加载宏——添加——确定。
点击“加载宏”工具,弹出【加载宏】对话框,勾选“分析工具库“和”规划求解加载项“,点击”确定“。
随即弹出microsoft office excel对话框,点击”是“。
开始安装。
规划求解使用步骤2:创建表格,如下。
单击“数据“工具栏,选择”规划求解“,随即弹出【规划求解参数】对话框,在【设置目标单元格】中输入“$b$12”;在【可变单元格】中输入“$c$3:$c$5”,单击“添加”按钮,弹出【添加约束】对话框,在【单元格引用位置】输入“$b$10”,在其右侧的下拉列表中选择【看了excel规划求解功能的使用教程。
Excel的规划求解
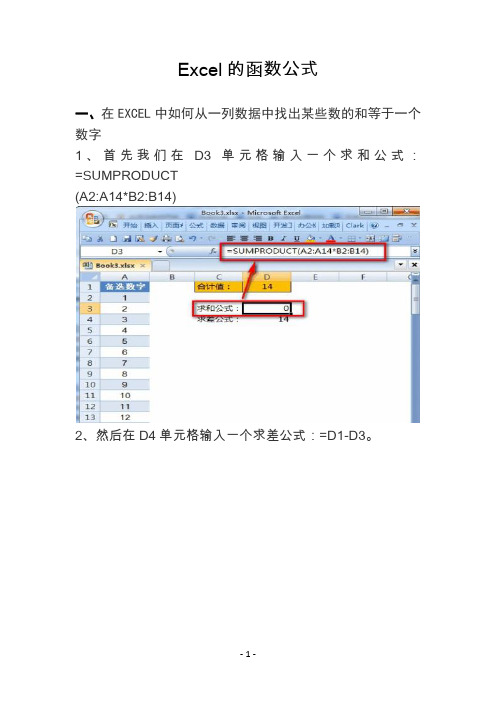
Excel的函数公式一、在EXCEL中如何从一列数据中找出某些数的和等于一个数字1、首先我们在D3单元格输入一个求和公式:=SUMPRODUCT(A2:A14*B2:B14)2、然后在D4单元格输入一个求差公式:=D1-D3。
3、然后,选择【数据】-【规划求解】。
4、选择【目标单元格】为D4,选择【值】处输入0。
5、点击选择按钮选择【可变单元格】6、区域为B2:B14(即A列数据对应B列区域)。
7、点击【添加】【约束条件】8、具体按下图设置。
9、点击【求解】按钮开始计算求解。
10、运算结束后弹出如下对话框,选择【保存规划求解结果】11、这时B列数值为1对应A列数据之和就等于14。
方法二:规划求解可以用规划求解,以下图中的A1:A20数据为例。
假设要在A1:A20中找出某些数的和等于200,操作步骤如下:步骤1:在C1单元格输入公式=SUMPRODUCT(A1:A20,B1:B20)如下图步骤2:选定C1单元格,数据>>>规划求解,“设置目标”会自动设置为C1单元格,到:选择“目标值”,并在右侧文本框中输入固定的数字200,鼠标放在”通过更改可变单元格“框中,并选择B1:B20,Excel将自动输入单元格地址,再单击“遵守约束”右侧的“添加”按钮,如下图:步骤3:在”单元格引用“用鼠标选择B1:B20单元格,中间的下拉框中选择”bin“,右侧框中将自动显示”十进制“,再单击”确定“按钮,如下图步骤4:通过上步操作后,”遵守约束“列表框中就增加了一个约束”$B$1:$B$20 = 二进制“,单击”求解“按钮,如下图步骤5:单击”确定“按钮,结果如下图所示,B列结果为1的表示对应A列的数字相加的和为C1的值200。
知识扩展:1、如果数据菜单没有”规划求解“命令,开发工具>>>加载项,勾选”规划求解加载项“,再单击”确定“按钮,如下图:2、如果连”开发工具“菜单都没有,操作如下:文件>>>Excel选项>>>自定义功能区>>>勾选”开发工具“,再单击”确定“按钮,如下图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在生产管理和经营决策过程中,经常会遇到一些规划问题。例如生产的组织安排,产品 的运输调度,作物的合理布局以及原料的恰当搭配等问题,其共同点就是如何合理地利用有 限的人力、物力、财力等资源,得到最佳的经济效果,即达到产量最高、利润最大、成本最 小、资源消耗最少等目标。这些问题中通常要涉及到众多的关联因素,复杂的数量关系,只 凭经验进行简单估算显然是不行的。而线性规划、非线性规划和动态规划等方法正是研究和 求解该类问题的有效数学方法。但是这些方法的求解大多十分繁琐复杂,常令人望而却步。 而利用 Excel 2000 的规划求解工具,可以方便快捷地帮助我们得到各种规划问题的最佳解。
6.1.关于单元格和区域引用...................................................................................................19 6.1.1.单元格和单元格区域引用样式 ............................................................................ 19 6.1.2.绝对引用与相对引用的区别 ................................................................................ 20
规划求解使用说明..............................................................................................................2 1.1.规划问题.............................................................................................................................2 1.3.利用规划求解解决现实问题的步骤 ................................................................................. 3
Max z = C T X
⎧ AX = b
s .t .⎨ ⎩
X
≥0
X 为决策变量向量 其中: C 为价值向量
b 为资源向量 A 为技术矩阵
这些都是经济生产中所具有的现实意义。
1.3.利用规划求解解决现实问题的步骤
z 建立对应的规划模型 z 在 Excel 表中输入已知数据(如线性规划模型的 A、b、C),以及指定规划模型三
6.2.数组公式...........................................................................................................................21
1-21
规划求解使用说明
1.规划问题以及规划模型
这组决策变量的一组确定值就代表一个具体的规划方案。 2.约束条件:对于规划问题的决策变量通常都有一定的限制条件,称作约束条件。约束
条件可以用与决策变量有关的不等式或等式来表示。 3. 目标:每个问题都有一个明确的目标,如利润最大或成本最小。目标通常可用与决
策变量有关的函数表示。 如果约束条件和目标函数都是线性函数,则称作线性规划;否则为非线性规划。如果要
1.2.规划模型
虽然规划问题种类繁多,但是其所要解决的问题可以分成两类:一类是确定了某个任 务,研究如何使用最少的人力、物力和财力去完成它;另一类是已经有了一定数量的人力、 物力和财力,研究如何使它们获得最大的收益。而从数学角度来看,规划问题都有下述共同 特征(三要素):
1.决策变量:每个规划问题都有一组需要求解的未知数( x1, x2 ,..., x3 ),称作决策变量。
求决策变量的值为整数,则称为整数规划。规划求解问题的首要问题是将实际问题数学化、 模型化。即将实际问题通过一组决策变量、一组用不等式或等式表示的约束条件以及目标函 数来表示。这是求解规划问题的关键。然后即可应用Excel 2000 的规划求解工具求解。
规划模型的线性规划标准型式为:
2-21
规划求解使用说明
5.规划求解小结..............................................................................................................................19 6.Excel补注 ....................................................................................................................................19
3.产销不平衡的运输模型..............................................................................................................13 3.1.问题...................................................................................................................................13 3.2.模型分析...........................................................................................................................14 3.3.模型建立...........................................................................................................................14 3.4.规划求解...........................................................................................................................15 3.5.模型结果...........................................................................................................................16
2.线性规划问题................................................................................................................................3 2.1.在Excel中输入已知数据,并指定三要素到对应单元格。 ............................................4 2.2.赋予约束条件、目标函数的表述形式。 ......................................................................... 4 2.3.规划求解.............................................................................................................................6 2.3.1.安装和加载“规划求解” ..........................................................................................6 2.3.2.规划求解..................................................................................................................7 2.3.3.分析求解结果........................................................................................................10
要素(决策变量、约束条件、目标函数)到相应的单元格,并赋予约束条件、目 标函数的表述形式(关于决策变量的函数)。 z 利用规划求解进行运算,分析结果 下面我们将举三个例子来说明利用 Excel 规划求解的应用,例子从易到难。从上面 三步骤可看出,第一步为建立模型,第二步建立 Excel 表,第三步利用规划求解。三个 例子各有偏重,主要通过第一个例子说明规划求解的应用。 要想高效简洁地运行规划求解,需对 Excel 相关操作比较熟悉。现将 Excel 中要用 到的知识技巧罗列在第六节,会的人可以直接跳过,不熟悉的人推荐先看。更详细信息, 请参考 Excel 帮助。
4.人员安排模型..............................................................................................................................16 4.1.Excel关于规划求解自带的系统示例文件......................................................................16 4.2.问题描述...........................................................................................................................17 4.3.模型分析、建立...............................................................................................................17 4.4.规划求解...........................................................................................................................18
