Excel规划求解
规划求解 excel

规划求解 excelExcel是一款功能强大的电子表格软件,被广泛应用于数据处理、计算和分析。
对于规划求解来说,Excel提供了丰富的函数和工具,可以帮助用户进行各种数学模型求解,优化和决策问题。
在Excel中,可以使用Solver插件进行规划求解。
Solver是一种用于优化问题求解的工具,可以通过调整特定的变量,使得某个目标函数达到最大或最小值。
用户可以根据具体的问题设定目标函数和约束条件,Solver将自动调整变量的取值,找到最优解。
使用Solver进行规划求解的步骤如下:1. 打开Excel,选择需要进行规划求解的工作簿。
2. 在“数据”选项卡中,点击“求解器”,如果没有该选项,可以先点击“文件”-“选项”-“附加组件”-“Excel加载项”,找到“求解器插件”并勾选上。
3. 在“目标单元格”中输入需要求解的目标函数,这通常是一个要最大化或最小化的数值。
4. 在“调整单元格”中输入需要调整的变量,这些变量可以是某些单元格中的数值或者是公式。
5. 在“约束条件”中添加问题的约束条件,例如不等式约束、线性约束或整数约束等。
6. 在“选项”中设置求解选项,如最大迭代次数、允许的精度等。
7. 点击“求解”,Excel将自动调整变量的取值,找到最优解,并将结果显示在相应的单元格中。
除了Solver插件外,Excel还提供了其他一些函数和工具,可以用于常见的规划求解问题,如线性规划、整数规划、非线性规划等。
用户可以通过编写公式、使用数据分析工具包或者自定义宏等方式,实现相关问题的求解。
总而言之,Excel作为一款功能丰富的电子表格软件,提供了多种方法和工具,可以帮助用户进行各种规划求解问题的处理。
无论是简单的线性规划还是复杂的非线性优化,Excel都可以发挥其优势,提供高效、简便的求解方法。
EXCEL规划求解功能操作说明

EXCEL规划求解功能操作说明Excel规划求解功能是Excel内置的解决最优化问题的工具,可用于线性规划、整数规划、非线性规划等诸多领域。
该功能十分便捷灵活,可以帮助用户快速找到问题的最优解。
一、添加求解功能1.打开Excel表格,点击“文件”>“选项”>“加载项”。
2.在弹出的窗口中选择“Excel加载项”>“转到”>“excel加载项”>“管理”。
在“可用的加载项”中勾选“求解器”并关闭窗口。
3.返回Excel表格,在数据选项卡中选择“分析”>“求解”,弹出求解对话框。
二、建立规划模型1.确定目标:需要确定最终要达到的目标或绩效指标,例如最大化利润、最小化成本等。
2.确定决策变量:需要确定影响目标的变量,例如销售量、成本等。
3.建立约束:需要确定影响决策变量的条件,例如材料成本、生产时间等。
注意约束需要用等式、不等式等数学形式表示。
例如,在一个玩具生产厂家的例子中,有以下规划问题:在有限的资源下,最大化玩具的利润。
目标:最大化利润。
决策变量:生产每种玩具的数量。
三、设置求解参数1.目标单元格:选择Excel表格中目标单元格,该单元格包含要优化的方程式。
4.变量单元格必须满足约束:勾选此项,保证变量单元格满足约束条件。
5.求解方法:选择要使用的求解算法,包括线性规划、非线性规划和整数规划等。
1.点击“求解”按钮,系统会自动寻找目标单元格、变量单元格和约束单元格区域。
2.系统执行计算,找到最优解并将其展示在新的单元格区域中。
3.若求解成功,单击“继续”将结果保存在Excel表中。
总之,利用Excel规划求解功能,用户可以通过建立规划模型,设置求解参数和运行求解功能轻轻松松地优化各种最优化问题。
EXCEL规划求解功能操作说明

E X C E L规划求解功能操作说明集团标准化办公室:[VV986T-J682P28-JP266L8-68PNN]Excel规划求解功能操作说明以Microsoft Excel2003为例,说明使用Excel的求解线性规划问题功能的使用方法。
一、加载规划求解功能1.点击【工具】按钮,在下拉菜单中选择【加载宏】功能。
2.在弹出的【可加载宏】选项卡中勾选【规划求解】,点击确定按钮。
此时,【工具】下拉菜单中增加规划求解功能,表示加载成功。
二、构造表格Excel表格并填入各项数据以教材18页【例题2-8】为例,构造表格如下:标题栏约束条件区目标函数区计算结果显示区1.录入约束条件系数约束条件(1)为5x 1+x 2-x 3+x 4=3,则在约束系数的第一行的x 1,x 2,x 3,x 4,x 5,限制条件,常数b 列下分别录入5,1,-1,1,0,=,3如下图所示。
约束系数区的第二行录入约束条件(2)的系数、限制符号及常数b ,即-10,6,2,0,1,=,2;约束系数区的第三行录入约束条件(3)(x1≥0)的系数、限制符号及常数b,即1,0,0,0,0,≥,0;约束系数区的第四行录入约束条件(4)(x2≥0)的系数、限制符号及常数b,即0,1,0,0,0,≥,0;约束系数区的第五行录入约束条件(5)(x3≥0)的系数、限制符号及常数b,即0,0,1,0,0,≥,0;约束系数区的第六行录入约束条件(6)(x4≥0)的系数、限制符号及常数b,即0,0,0,1,0,≥,0;约束系数区的第七行录入约束条件(7)(x5≥0)的系数、限制符号及常数b,即0,0,0,0,1,≥,0。
如下图所示。
2.录入目标函数系数目标函数为maxZ=4x1-2x2-x3,则在目标函数的x1,x2,x3,x4,x5列下分别录入4,-2,-1,0,0,如下图所示。
3. 录入约束条件的计算公式双击约束条件(1)行的“总和”单元格,录入以下内容:“=B3*B12+C3*C12+D3*D12+E3*E12+F3*F12”说明:录入的内容即是约束条件(1)的计算公式,其中“B3*B12”代表5x1; “C3*C12”代表1x2;“D3*D12”代表-1x3;“E3*E12”代表1x4;“F3*F12”代表0x5。
如何使用Excel的“规划求解”功能进行优化

如何使用Excel的“规划求解”功能进行优化在日常工作和生活中,我们经常会遇到需要优化的问题,比如如何在有限的资源条件下实现最大的效益,或者如何找到满足多个条件的最优方案。
这时候,Excel 的“规划求解”功能就可以派上用场了。
“规划求解”是 Excel 中一个强大的工具,它可以帮助我们通过建立数学模型来找到最优解。
接下来,让我们详细了解一下如何使用这个功能。
首先,确保您的 Excel 中已经加载了“规划求解”功能。
如果没有,可以通过以下步骤进行加载:点击“文件”选项卡,选择“选项”,在弹出的“Excel 选项”对话框中,选择“加载项”,然后在“管理”下拉菜单中选择“Excel 加载项”,点击“转到”按钮,在弹出的“加载宏”对话框中勾选“规划求解加载项”,点击“确定”即可。
在使用“规划求解”之前,我们需要明确问题的目标和约束条件,并将其转化为数学模型。
例如,假设我们有一个生产问题,需要决定生产两种产品 A 和 B 的数量,已知产品 A 的单位利润为 10 元,产品 B 的单位利润为 15 元,我们拥有的原材料限制为 100 单位,生产产品 A 每单位需要消耗 2 单位原材料,生产产品 B 每单位需要消耗 3 单位原材料。
我们的目标是最大化总利润。
接下来,我们在 Excel 中建立表格来表示这个问题。
在第一列中输入产品名称(A 和 B),第二列输入生产数量(假设初始值为 10),第三列输入单位利润(分别为 10 和 15),第四列计算每种产品的利润(数量乘以单位利润),第五列输入每种产品消耗的原材料数量(分别为 2 和 3),第六列计算总的原材料消耗(数量乘以消耗的原材料数量)。
然后,我们设置目标单元格。
在这个例子中,目标是最大化总利润,所以我们选择计算总利润的单元格作为目标单元格。
接下来,设置变量单元格,即生产数量所在的单元格。
再然后,添加约束条件。
在这个例子中,约束条件是总的原材料消耗不能超过 100 单位,所以我们添加这个约束条件。
excel 规划求解

excel 规划求解Excel是一款功能强大的电子表格软件,可以用于数据分析、数据处理、数据可视化以及进行规划求解等多种任务。
在Excel中进行规划求解可以帮助我们优化问题的解决方案,提高效率和准确性。
下面我将介绍一下在Excel中进行规划求解的基本步骤和方法。
首先,我们需要确定需求或者问题,明确目标。
比如我们要求解一个优化问题,如如何在预算有限的情况下,获得最大的利润。
接下来,我们需要在Excel中建立一个模型,将问题转化为一个数学模型。
对于优化问题,我们需要确定决策变量、约束条件和目标函数。
决策变量是我们要优化的变量,是我们需要调整的参数。
在上述问题中,我们可以考虑不同的投资方案和预算分配方式作为决策变量。
约束条件是我们需要满足的条件,它们限制了决策变量的取值范围。
在上述问题中,预算是一个约束条件,我们不能超出预算。
目标函数是我们要最大化或最小化的函数。
在上述问题中,我们的目标是最大化利润,所以利润就是我们的目标函数。
然后,我们可以使用Excel中的规划求解工具来求解问题。
在Excel中,我们可以使用“规划求解”工具来实现。
首先,我们需要将问题转化为Excel能够理解的形式,比如将决策变量和目标函数写入Excel表格的某一列或一行,将约束条件写入Excel表格的某一区域。
然后,我们可以打开Excel中的“数据”选项卡,点击“规划求解”按钮,选择求解目标和约束条件,然后点击“求解”按钮。
Excel会自动寻找最优解,并将结果显示在对应的单元格中。
最后,我们需要分析求解结果,并根据需要进行调整和优化。
如果求解结果不符合需求,我们可以根据结果进行适当的调整,重新运行规划求解工具,直到达到满意的结果为止。
总而言之,Excel提供了方便实用的规划求解工具,可以帮助我们解决各种优化问题。
通过正确使用Excel中的规划求解功能,我们可以提高问题求解的效率和准确性,实现更好的决策和结果。
希望本文能对大家在Excel中进行规划求解提供一些帮助。
EXCEL求解线性规划问题

约束右端值降低15时,目旳函数值旳变化量。
解:(1)最优解为x1=0, x2=12.4, x3=9.5
(2) x1旳目旳系数降低5,占允许降低旳百分比=5/∞=0%,x2 旳目旳系数增长4,占允许增长旳百分比=4/7.8=51.2%。
变化旳百分比和为51.2%,没有超出100%,所以最优解不变。
(3)第一资源约束右端值增长30,占允许增长旳30 /∞=0%, 第二资源约束右端值增长4 ,占允许增长旳4/15=26.7%,
•初值和终值分别指 单元格在此次求解 前旳数值和求解后 旳数值。
敏感性分析报告(1)
可变单元格中 • “单元格”指决策变量所在单元格旳地址 • “名字”是决策变量旳名称 • “终值”是决策变量旳终值,即最优值 • “递减成本”指最优解中档于0旳变量,相应旳目旳函数中旳系数
增长或降低多少,最优解不再为0 • “目旳式系数”目旳函数中旳系数,为已知条件 • “允许旳增量”与“允许旳减量”表达目旳函数中旳系数在增量
(1)引用旳类型
三种类型 :
相对引用、 绝对引用、混合引用
(2) 相对引用
格式: A3 、B6
使用相对引用后,系统将会记住建立公式旳单元格和被 引用旳单元格旳相对位置,在复制这个公式时,新旳公式单 元和被引用旳单元依然保持这种相对位置。
(3)绝对引用 格式:$a$3 $d$5
绝对引用是指被引用旳单元与引用旳公式单元旳位置 关系是绝正确,不论将这个公式复制到任何单元,公式所 引用旳还是原来单元格旳数据。
2) 在弹出旳对话框中旳“可用加载宏”列表框 中,选定待添加旳加载宏“规划求解”选项旁 旳复选框,然后单击“拟定”.单击“拟定” 后,“工具”菜单下就会出现一项“规划求解”
3. “规划求解”各参数设置
使用EXCEL的目标求解与规划求解功能

使用EXCEL的目标求解与规划求解功能在Excel这个功能强大的电子表格软件中,目标求解与规划求解功能是许多用户常常忽略但却非常实用的功能之一。
通过这些功能,用户可以轻松地解决复杂的问题,优化决策方案,提高工作效率。
接下来我们将深入探讨这些功能的使用方法和优势。
目标求解功能Excel的目标求解功能可以帮助用户找到最优解以实现特定目标。
无论是制定最佳的销售策略、优化生产计划,还是进行财务分析,目标求解功能都能提供有力支持。
使用步骤打开Excel并载入你的数据表。
选择“数据”选项卡,点击“求解”。
在“目标单元格”中输入你要优化的单元格。
设置约束条件,如变量的取值范围。
点击“确定”并等待Excel计算出最优解。
优势高效优化:通过目标求解功能,可以快速找到最优解,节省大量时间。
灵活性:用户可以根据实际需求设置不同的约束条件,满足多样化的问题求解。
规划求解功能规划求解功能是Excel中另一个强大的工具,可用于解决复杂的规划和调度问题。
无论是资源分配、项目排程,还是路径优化,规划求解功能都能帮助用户找到最佳方案。
使用方法打开Excel并载入你的数据表。
选择“数据”选项卡,点击“规划求解”。
设置目标单元格和约束条件。
点击“求解”并等待Excel计算出最佳规划方案。
优势多功能性:规划求解功能适用于各种规划和调度问题,帮助用户优化决策。
可视化结果:Excel会清晰地展示最佳方案,让用户一目了然。
Excel的目标求解与规划求解功能为用户提供了强大的问题求解工具,帮助他们更高效地处理复杂的任务,优化决策方案,提升工作效率。
掌握并善用Excel的目标求解与规划求解功能,将为您的工作带来便利和效率提升。
立即尝试这些功能,发现它们为您带来的惊喜吧!。
Excel的规划求解
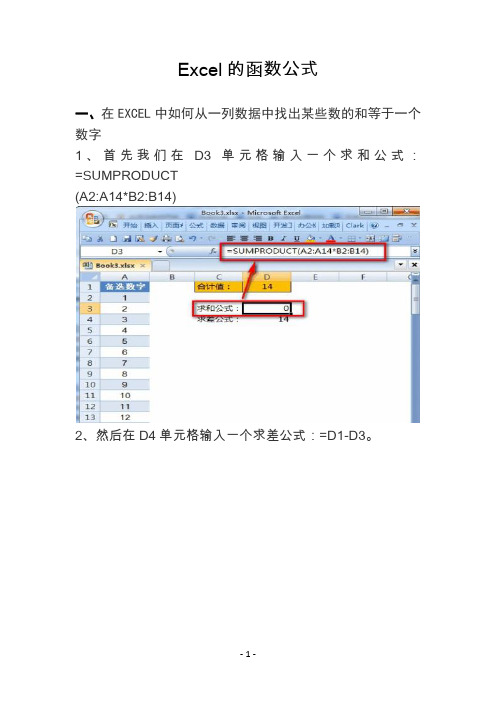
Excel的函数公式一、在EXCEL中如何从一列数据中找出某些数的和等于一个数字1、首先我们在D3单元格输入一个求和公式:=SUMPRODUCT(A2:A14*B2:B14)2、然后在D4单元格输入一个求差公式:=D1-D3。
3、然后,选择【数据】-【规划求解】。
4、选择【目标单元格】为D4,选择【值】处输入0。
5、点击选择按钮选择【可变单元格】6、区域为B2:B14(即A列数据对应B列区域)。
7、点击【添加】【约束条件】8、具体按下图设置。
9、点击【求解】按钮开始计算求解。
10、运算结束后弹出如下对话框,选择【保存规划求解结果】11、这时B列数值为1对应A列数据之和就等于14。
方法二:规划求解可以用规划求解,以下图中的A1:A20数据为例。
假设要在A1:A20中找出某些数的和等于200,操作步骤如下:步骤1:在C1单元格输入公式=SUMPRODUCT(A1:A20,B1:B20)如下图步骤2:选定C1单元格,数据>>>规划求解,“设置目标”会自动设置为C1单元格,到:选择“目标值”,并在右侧文本框中输入固定的数字200,鼠标放在”通过更改可变单元格“框中,并选择B1:B20,Excel将自动输入单元格地址,再单击“遵守约束”右侧的“添加”按钮,如下图:步骤3:在”单元格引用“用鼠标选择B1:B20单元格,中间的下拉框中选择”bin“,右侧框中将自动显示”十进制“,再单击”确定“按钮,如下图步骤4:通过上步操作后,”遵守约束“列表框中就增加了一个约束”$B$1:$B$20 = 二进制“,单击”求解“按钮,如下图步骤5:单击”确定“按钮,结果如下图所示,B列结果为1的表示对应A列的数字相加的和为C1的值200。
知识扩展:1、如果数据菜单没有”规划求解“命令,开发工具>>>加载项,勾选”规划求解加载项“,再单击”确定“按钮,如下图:2、如果连”开发工具“菜单都没有,操作如下:文件>>>Excel选项>>>自定义功能区>>>勾选”开发工具“,再单击”确定“按钮,如下图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
□财会月刊·
全国优秀经济期刊□·110·2014.8下
在传统财务运营管理中,营运决策包括确定最佳现金持有量、最优订货批量,或者只是考虑单个市场的生产与销售决策。
企业集团全球运营管理涉及生产、运输、销售等环节,需要在实现集团利润最大化的同时,解决生产什么产品、在哪里生产、生产多少、运到哪个市场等诸多问题。
显然,采用传统的运营管理方法会比较棘手。
而Ex⁃cel 提供的规划求解工具,不但能非常迅速地求出多种营运决策模型的最优解,还可以给出敏感性分析报告,满足财务全球化运营管理的需求,有效提高公司决策效率,同时也能促进财务人员更多地参与到公司管理决策中。
一、问题描述
某跨国集团在中国和其他地区设立了四个工厂,分别为A 、B 、C 、D 厂,产品主要面向国际市场销售,分别销往北京、香港、纽约、东京四个城市。
各个工厂的单位产品成本、固定成本、产能,各个市场的销售价格和需求量,以及各个工厂到每个市场的运输成本见图1。
在每个工厂产能允许同时最大限度满足市场需求的情况下,集团管理层希望财务部给出能够实现集团利润
最大化目标的年生产和运输预算的决策方案。
二、建立线性数学模型
1.定义决策变量。
下文中,i (i=1,2,3,4)表示工厂,j 表示市场(j=1,2,3,4);决策问题可以用图2表示。
所以定义决策变量为X ij :即在i 工厂生产的产品投放到j 市场。
2.确定目标函数。
最大利润=收入-产品变动成本-其他成本最大利润=55500(X 11+X 21+X 31+X 41)+61100(X 12+X 22+X 32+X 42)+57800(X 13+X 23+X 33+X 43)+62650(X 14+X 24+X 34+X 44)-34900(X 11+X 12+X 13+X 14)-32200(X 21+X 22+X 23+X 24)-38350(X 31+X 32+X 33+X 34)-23400(X 41+X 42+X 43+X 44)-(500X 11+12225X 12+9075X 13+21450X 14+4500X 21+……+15150X 43+5925X 44)。
3.列出约束条件。
(1)产能约束:X 11+X 12+X 13+X 14≤101;X 21+X 22+X 23+X 24≤201;X 31+X 32+X 33+X 34≤121;X 41+X 42+X 43+X 44≤250。
(2)需求约束:X 11+X 21+X 31+X 41≤150;X 12+X 22+X 32+X 42≤75;X 13+X 23+X 33+X 43≤200;X 14+X 24+X 34+X 44≤100。
(3)非负约束:X ij ≥0。
4.最优解:最大利润时的X ij 。
三、数据及公式准备
1.数据输入:把图1集团公司的决策数据输入新建的Excel 表中,如图3所示。
耿海利
(江西财经大学会计学院南昌330013)
【摘要】随着全球经济一体化的深入,企业运营管理方式发生了很大变化。
本文通过一个实例,来探讨企业集团拥有多个生产子公司、多个产品市场并且各个产品市场价格不同的情况下,企业如何使用Excel 规划求解工具进行产品生产、运输和分配决策,以实现集团利润最大化。
【关键词】规划求解
企业集团全球运营决策敏感性分析
Excel 规划求解:
企业全球运营管理工具
图1
集团基本运营决策数据
图2决策问题
全国中文核心期刊·
财会月刊□2014.8下·111·□
2.选择区域B9∶E12为决策变量的决策结果区,用“X11,X12,…,X43,X44”表示。
3.约束条件的公式准备:生产量要小于产能,选择F9单元格,输入公式“=SUM (B9∶E9)”,由于公式单元格是相对引用,把该公式复制到F10、F11、F12单元格即可;同理市场销售量要小于市场总的需求量,在B13单元格输入求和公式“=SUM (B9∶B12)”,然后把该公式复制到C13、D13、E13单元格中。
4.使用Excel 中SUMPRODUCT 函数计算收入、成本。
计算总收入,选择B16单元格,输入公式“=SUM⁃
PRODUCT (B2∶E2,B13∶E13)”;计算变动成本,选择B17单元格,输入公式“=SUMPRODUCT (F4∶F7,F9∶F12)”;计算运输成本,在B18单元格输入公式“=SUMPRODUCT (B4∶E7,B9∶E12)”。
SUMPRODUCT (数组1,数组2)函数,可以用来计算长度相等的行、列或者区域对应元素乘积的和,是模型中重要的函数,在计算多个数据乘法时会非常简便。
5.计算总利润。
选择
B19单元格,输入公式“=B16-B17-B8”;在固定成本
所在单元格输入公式“=SUM (G4∶G7)”;计算净利润,选中B21单元格,输入公式“=B19-B20”。
四、规划求解
使用Excel 规划求解工具,要求安装Excel 时选择“完全安装”,“工具”菜单下才有“规划求解”子菜单。
如果安装Excel 时没有安装规划求解功能,需要加载“规划求解”功能,点击Excel 左上方图标,选择“Excel 选项”,出现Ex⁃cel 选项对话框,选择左侧“加载项”→“规划求解加载项”→“确定”,然后默认安装即可使用规划求解功能。
1.选中目标函数所在单元格B19,然后选择“工具”菜单栏下的“规划求解”,会出现规划求解参数对话框,如图4所示,默认即为求目标函数最大值。
2.设置可变单元格:可变单元格一般是决策变量所在区域,在求解时会不断调整,直到满足目标函数最大化。
把光标移动到可变单元格下的选择框内,然后选中“B9∶E12”区域,松开鼠标即可完成设置。
3.添加约束条件:选择“添加”按钮,出现添加约束条件对话框,见图5,选中“B9∶B12”区域,下拉框选择“>=”,约束值填“0”,即完成决策变量非负性的添加。
同理可以添加另外两个约束条件,最后点击“确定”。
4.选择规划求解参数对话框内的“求解”按钮,会出现“规划求解结果”对话框,选择保存“保持规划求解结果”,单击“确定”,会出现如图6所示的最优结果。
最优运营决策为:A 工厂为北京、香港市场生产97单位和4单位产品;B 工厂仅为北京市场生产53单位产品;C 工厂仅为纽约市场生产121单位产品;D 工厂分别为香港、纽约和东京市场生产71单位、79单位和100单位产品。
集团可实现最大利润为11508900,最大净利润为11500300。
图3
数据准备相关公式
图4
规划求解参数设置
图5添加约束条件设置
□财会月刊·
全国优秀经济期刊该运营决策模型建立后,如果国外产品市场价格、需求,以及各个分厂成本、产能数据发生变化,公司只需把变化部分从模型中替换下来,重新求解,即可更新为最新条件下的最优解,这大大提高了集团运营决策的效率。
五、规划求解敏感性报告分析使用Excel 规划求解工具,不仅可以高效快捷地求出方案最优解,而且还提供了运营结果报告、敏感性报告、极限值报告用于运营决策,这里仅对最重要的敏感性报告进行分析。
在“规划求解结果”对话框内,选择保存“保持规划求解结果”的同时,选择报告下的“敏感性报告”,单击“确定”,会出现图7所示的运营决策敏感性分析报告。
这个报告有两种版本,本例选用“规划求解参数设置”对话框中,“采用线性模型”得出的敏感性报告进行分析。
1.对可变单元格(决策变量)的
敏感性分析,以A 工厂向北京市场供货(单元格B9)为例:“终值”是该决策变量的最优解;“递减成本”为该决策变量再增加一单位时,目标函数(总利润)的增加量;“目标式系数”为该决策变量和目标函数的相对关系;“允许的增量”和“允许的减量”构成该决策变量的最优域,即当变量系数(20100)增加275和减少1300的范围内变化,最优解(97)保持不变。
2.通过对约束条件的分析可以回答下列问题。
哪个工厂增加一个单位的产能将会带来最大的回报,哪个市场增加一个单位的需求可以带来最大的收益。
以A 工厂的产能约束为例:“终值”是A 厂最优的生产量;“阴影价格”表示当约束限制值增加一个单位时总利润的变化量;“约束限制值”即为指定的条件约束值;允许的增量、允许的减量表示当A 工厂的产能约束在增加53个单位和减少97个单位的范围内变化,阴影价格保持不变。
主要参考文献
1.顾维筠.Excel 规划求解的两类应用.计算机应用与软件,2005;1
2.张君.中国企业需要在全球化战略和运营两个层面痛下功夫.中国经贸,2010;12
3.李文锋.全球供应链运营模式对提升我国外贸核心竞争力的启示及思考.国际贸易,2011;
11
图6
规划求解最优结果
图7敏感性分析报告
□·112·2014.8下。
