空间向量及立体几何练习试题和答案解析
高中数学-空间向量和立体几何练习试题[附答案及解析]
![高中数学-空间向量和立体几何练习试题[附答案及解析]](https://img.taocdn.com/s3/m/1a58087426d3240c844769eae009581b6bd9bd6e.png)
空间向量练习题1. 如下图,四棱锥P -ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°,E 是CD的中点,P A ⊥底面ABCD ,P A =2. 〔Ⅰ〕证明:平面PBE ⊥平面P AB ;〔Ⅱ〕求平面P AD 和平面PBE 所成二面角〔锐角〕的大小.如下图,以A 为原点,建立空间直角坐标系.那么相关各点的 坐标分别是A 〔0,0,0〕,B 〔1,0,0〕,33(2C 13(2D P 〔0,0,2〕,3E 〔Ⅰ〕证明 因为3BE =, 平面P AB 的一个法向量是0(0,1,0)n =, 所以0BE n 和共线.从而BE ⊥平面P AB . 又因为BE ⊂平面PBE , 故平面PBE ⊥平面P AB .(Ⅱ)解 易知3(1,0,2),(0,02PB BE =-=), 13(0,0,2),(,22PA AD =-= 设1111(,,)n x y z =是平面PBE 的一个法向量,那么由110,n PB n BE ⎧=⎪⎨=⎪⎩得111122020,3000.2x y z x y z +⨯-=⎧⎪⎨⨯++⨯=⎪⎩所以11110,2.(2,0,1).y x z n ===故可取 设2222(,,)n x y z =是平面PAD 的一个法向量,那么由220,0n PA n AD ⎧=⎪⎨=⎪⎩得2222220020,1300.22x y z x y z ⨯+⨯-=⎧⎪⎨++⨯=⎪⎩所以2220,3.z x ==-故可取2(3,1,0).n =-于是,1212122315cos ,52n n n n n n <>===⨯故平面PAD 和平面PBE 所成二面角〔锐角〕的大小是152. 如图,正三棱柱ABC -A 1B 1C 1的所有 棱长都为2,D 为CC 1中点。
〔Ⅰ〕求证:AB 1⊥面A 1BD ;〔Ⅱ〕求二面角A -A 1D -B 的大小; 〔Ⅲ〕求点C 到平面A 1BD 的距离;〔Ⅰ〕证明 取BC 中点O ,连结AO . ABC △为正三角形,AO BC ∴⊥.在正三棱柱111ABC A B C -中,平面ABC ⊥平面11BCC B ,AD ∴⊥平面11BCC B .取11B C 中点1O ,以O 为原点,OB ,1OO ,OA 的方向为x y z ,,轴的正方向建立空间直角坐标系,那么(100)B ,,,(110)D -,,,1(023)A ,,,(003)A ,,,1(120)B ,,, 1(123)AB ∴=-,,,(210)BD =-,,,1(123)BA =-,,.12200AB BD =-++=,111430AB BA =-+-=, 1AB BD ∴⊥,11AB BA ⊥.1AB ∴⊥平面1A BD .〔Ⅱ〕解 设平面1A AD 的法向量为()x y z =,,n .(113)AD =--,,,1(020)AA =,,.AD ⊥n ,1AA ⊥n ,100AD AA ⎧=⎪∴⎨=⎪⎩,,n n 3020x y z y ⎧-+-=⎪∴⎨=⎪⎩,,03y x z =⎧⎪∴⎨=-⎪⎩,.令1z =得(301)=-,,n 为平面1A AD 的一个法向量. 由〔Ⅰ〕知1AB ⊥平面1A BD ,1AB ∴为平面1A BD 的法向量.cos <n ,1113364222AB AB AB -->===-n n .∴二面角1A A D B --的大小为6arccos4. xzAB CD1A1C1BO F y〔Ⅲ〕解 由〔Ⅱ〕,1AB 为平面1A BD 法向量,1(200)(12BC AB =-=,,,,.∴点C 到平面1A BD的距离1122BC AB d AB -===. 3.如图,在四面体ABCD 中,O 、E 分别是BD 、BC 的中点,2,CA CB CD BD AB AD ======〔1〕求证:AO ⊥平面BCD ;〔2〕求异面直线AB 与CD 所成角的余弦值; 〔3〕求点E 到平面ACD 的距离.⑴ 证明 连结OC,,.BO DO AB AD AO BD ==∴⊥ ,BO DO BC CD ==,CO BD ⊥.在AOC ∆中,由可得1,AO CO == 而2AC =, 222,AO CO AC ∴+=90,o AOC ∴∠=即.AO OC ⊥,BD OC O = ∴AO ⊥平面BCD .(2)解 以O为原点,如图建立空间直角坐标系, 那么(1,0,0),(1,0,0),B D -1(0,0,1),((1,0,1),(1,2C A E BA CD =-=-2cos ,4BA CD BA CD BA CD⋅∴<>==⋅ ∴ 异面直线AB 与CD 所成角的余弦值为4. ⑶解 设平面ACD 的法向量为(,,),n x y z =那么(,,)(1,0,1)0(,,)(0,3,1)0n AD x y z n AC x y z ⎧⋅=⋅--=⎪⎨⋅=⋅-=⎪⎩, ∴030x z y z +=⎧⎪⎨-=⎪⎩,令1,y =得(3,1,3)n =-是平面ACD 的一个法向量. 又13(,,0),22EC =- ∴点E 到平面ACD 的距离 32177EC n h n⋅===. 4.三棱锥P -ABC 中,PA ⊥ABC ,AB ⊥AC ,PA=AC=½AB ,N 为AB 上一点,AB=4AN,M,S分别为PB,BC 的中点.〔Ⅰ〕证明:CM ⊥SN ;〔Ⅱ〕求SN 与平面CMN 所成角的大小.证明:设PA=1,以A 为原点,射线AB ,AC ,AP 分别为x ,y ,z 轴正向建立空间直角坐标系如图。
空间向量与立体几何练习题(带答案)

空间向量与立体几何练习题(带答案)一、选择题1.若空间向量a与b不相等,则a与b一定()A.有不同的方向B.有不相等的模C.不可能是平行向量D.不可能都是零向量【解析】若a=0,b=0,则a=b,这与已知矛盾,故选D.【答案】D图2-1-72.如图2-1-7所示,已知平行六面体ABCD-A1B1C1D1,在下列选项中,CD→的相反向量是()A.BA→B.A1C1→C.A1B1→D.AA1→【解析】由相反向量的定义可知,A1B1→是CD→的相反向量.【答案】C图2-1-83.在如图2-1-8所示的正三棱柱中,与〈AB→,AC→〉相等的是() A.〈AB→,BC→〉B.〈BC→,CA→〉C.〈C1B1→,AC→〉D.〈BC→,B1A1→〉【解析】∵B1A1→=BA→,∴〈BA→,BC→〉=〈AB→,AC→〉=〈BC→,B1A1→〉=60°,故选D.【答案】D4.在正三棱锥A-BCD中,E、F分别为棱AB,CD的中点,设〈EF→,AC→〉=α,〈EF→,BD→〉=β,则α+β等于()A.π6B.π4C.π3D.π2【解析】如图,取BC的中点G,连接EG、FG,则EG∥AC,FG∥BD,故∠FEG=α,∠EFG=β.∵A-BCD是正三棱锥,∴AC⊥BD.∴EG⊥FG,即∠EGF=π2.∴α+β=∠FEG+∠EFG=π2.【答案】D5.如图2-1-9所示,正方体ABCD-A1B1C1D1中,以顶点为向量端点的所有向量中,直线AB的方向向量有()图2-1-9A.8个B.7个C.6个D.5个【解析】与向量AB→平行的向量就是直线AB的方向向量,有AB→,BA→,A1B1→,B1A1→,C1D1→,D1C1→,CD→,DC→,共8个,故选A.【答案】A二、填空题6.在正方体ABCD-A1B1C1D1中,若E为A1C1的中点,则向量CE→和BD→的夹角为________.【解析】∵BD→为平面ACC1A1的法向量,而CE在平面ACC1A1中,∴BD→⊥CE→.∴〈BD→,CE→〉=90°.【答案】90°7.下列命题正确的序号是________.①若a∥b,〈b,c〉=π4,则〈a,c〉=π4.②若a,b是同一个平面的两个法向量,则a=B.③若空间向量a,b,c满足a∥b,b∥c,则a∥c.【解析】①〈a,c〉=π4或3π4,①错;②a∥b;②错;③当c=0时,推不出a∥c,③错;④由于异面直线既不平行也不重合,所以它们的方向向量不共线,④对.【答案】④8.在棱长为1的正方体中,S表示所有顶点的集合,向量的集合P={a|a =P1P2→,P1,P2∈S},则在集合P中模为3的向量的个数为________.【解析】由棱长为1的正方体的四条体对角线长均为3知:在集合P 中模为3的向量的个数为8.【答案】8三、解答题图2-1-109.如图2-1-10所示,在长、宽、高分别为AB=3、AD=2、AA1=1的长方体ABCD-A1B1C1D1的八个顶点的两点为始点和终点的向量中,(1)单位向量共有多少个?(2)试写出模为5的所有向量;(3)试写出与AB→相等的所有向量.【解】(1)由于长方体的高为1,所以长方体4条高所对应的AA1→,A1A→,BB1→,B1B→,CC1→,C1C→,DD1→,D1D→这8个向量都是单位向量,而其他向量的模均不为1,故单位向量共8个.(2)由于这个长方体的左右两侧的对角线长均为5,故模为5的向量有AD1→,D1A→,A1D→,DA1→,BC1→,C1B→,B1C→,CB1→共8个.(3)与向量AB→相等的所有向量(除它自身之外)共有A1B1→,DC→及D1C1→3个.图2-1-1110.如图2-1-11所示,正四棱锥S-ABCD中,O为底面中心,求平面SBD的法向量与AD→的夹角.【解】∵正四棱锥底面为正方形,∴BD⊥AC,SO⊥AC又∵BD∩SO=O∴AC⊥平面SBD.∴AC→为平面SBD的一个法向量.∴〈AC→,AD→〉=45°.图2-1-1211.如图2-1-12,四棱锥P—ABCD中,PD⊥平面ABCD,底面ABCD 为正方形且PD=AD,E、F分别是PC、PB的中点.(1)试以F为起点作直线DE的一个方向向量;(2)试以F为起点作平面PBC的一个法向量.【解】(1)取AD的中点M,连接MF,连接EF,∵E、F分别是PC、PB的中点,∴EF綊12BC,又BC綊AD,∴EF綊12AD,则由EF綊DM知四边形DEFM是平行四边形,∴MF∥DE,∴FM→就是直线DE的一个方向向量.(2)∵PD⊥平面ABCD,∴PD⊥BC,又BC⊥CD,∴BC⊥平面PCD,∵平面PCD,∴DE⊥BC,又PD=CD,E为PC中点,∴DE⊥PC,从而DE⊥平面PBC,∴DE→是平面PBC的一个法向量,由(1)可知FM→=ED→,∴FM→就是平面PBC的一个法向量.。
高二数学空间向量与立体几何试题答案及解析

高二数学空间向量与立体几何试题答案及解析1.长方体中,,,,则与所成角的余弦值为.【答案】【解析】以D为空间原点,DA为x轴,D为z轴,DC为y轴,建立空间直角坐标系则=(-1,2,0),=(-1,-2,3)||=,|'|=,·=-3cos<,>==,即为所求。
【考点】本题主要考查空间向量的应用,向量的数量积,向量的坐标运算。
点评:简单题,通过建立空间直角坐标系,将求异面直线的夹角余弦问题,转化成向量的坐标运算。
2.正方体的棱长为1,是底面的中心,则到平面的距离为.【答案】【解析】因为O是A1C1的中点,求O到平面ABC1D1的距离,就是A1到平面ABC1D1的距离的一半,就是A1到AD1的距离的一半.所以,连接A1D与AD1的交点为P,则A1P的距离是:O到平面ABC1D1的距离的2倍O到平面ABC1D1的距离【考点】本题主要考查空间距离的计算。
点评:本题也可以通过建立空间直角坐标系,将求角、求距离问题,转化成向量的坐标运算,是高考典型题目。
3.已知={-4,3,0},则与垂直的单位向量为= .【答案】(,,0)【解析】设与垂直的向量与垂直的向量=(x,y,0),则-4x+3y=0,,解得x= ,y=,所以=(,,0)。
【考点】本题主要考查向量的坐标运算、向量垂直的充要条件、单位向量的概念。
点评:利用向量垂直的充要条件及单位向量的概念。
4.已知向量与向量平行,则()A.B.C.D.【答案】C【解析】因为向量与向量平行,所以,,故选C。
【考点】本题主要考查平行向量及向量的坐标运算。
点评:简单题,按向量平行的充要条件计算。
5.已知点,为线段上一点,且,则的坐标为()A.B.C.D.【答案】C【解析】设C的坐标为(x,y,z)则向量=(x-4,y-1,z-3)向量=(-2,-6,-2),而即=所以x-4=-,y-1=-2,Z-3=-所以x=,y=-1,z=,C的坐标为,选C。
高中数学立体几何与空间向量真题(解析版)

高中数学专题16立体几何与空间向量真题1.如图,正方体的一个截面经过顶点A,C及棱EF上一点K,且将正方体分成体积比为3:1的两部分,则的值为.【答案】【解析】设.截面与FG交于J.,解得(舍去)故.2.设点P到平面的距离为3,点Q在平面上,使得直线PQ与所成角不小于30°且不大于60°,则这样的点Q所构成的区域的面积为.【答案】【解析】设点P在平面上的射影为O.由条件知,.即OQ∈[1,3],故所求的区域面积为.3.在正三棱锥中,,过AB的平面将其体积平分.则棱与平面所成角的余弦值为_____________。
【答案】【解析】设的中点分別为,则易证平面A BM即为平面由平行四边形的性质知,所以,又直线P C在平面上的射影为直线MK,由得因此,棱P C与平面所成角的余弦值为.故答案为:4.设P为一圆锥的顶点,A、B、C为其底面圆周上的三点,满足∠ABC=90°,M为AP的中点.若AB =1,AC=2,AP=,则二面角M-BC-A的大小为________.【答案】【解析】由,知AC为底面圆的直径.如图所示,设底面中心为O.于是,平面ABC.故.设H为M在底面上的射影.则H为AO的中点.在底面中作于点K.由三垂线定理知.从而,为二面角M-BC-A的平面角.由,结合得:.故二面角M-BC-A的大小为.5.四棱锥P-ABCD中,已知侧面是边长为1的正三角形,M、N分别为边AB、BC的中点.则异面直线MN与PC之间的距离为___________.【答案】【解析】如图,设底面对角线AC与BD交于点O,过点C作直线MN的垂线,与MN交于点H.由于PO为底面的垂线,故PO⊥CH.又AC⊥CH,于是,CH与平面POC垂直.从而,CH⊥PC.因此,CH为直线MN与PC的公垂线段.注意到,.故异面直线MN与PC之间的距离为.6.已知正三棱锥底面边长为1,高为.则其内切球半径为______.【答案】【解析】如图,设球心在平面与平面内的射影分别为,边的中点为,内切球半径为.则分别三点共线,,且.故.解得.7.设同底的两个正三棱锥内接于同一个球.若正三棱锥的侧面与底面所成的角为,则正三棱锥的侧面与底面所成角的正切值是______.【答案】4【解析】如图6,联结.则,垂足为正的中心,且过球心.联结并延长与交于点.则为边的中点,且.易知,分别为正三棱锥、正三棱锥的侧面与底面所成二面角的平面角. 则.由.故.8.在四面体中,已知.则四面体的外接球的半径为______.【答案】【解析】易知,为正三角形,且CA=CB.如图,设P、M分别为AB、CD的中点,联结PD、PC.则平面平面PDC.设的外心为N,四面体ABCD的外接球的球心为O.则.可求得由题意知.在中,由余弦定理得又因为D、M、O、N四点在以DO为直径的圆上所以故外接球的体积.9.已知正三棱柱的9条棱长都相等,是边的中点,二面角.则________.【答案】【解析】解法1 如图,以所在直线为轴、线段的中点为原点、所在直线为轴建立空间直角坐标系.设正三棱柱的棱长为2.则.故.设分别与平面、平面垂直的向量为.则由此可设.所以,,即.因此,.解法2如图..设交于点.则平面.又,则平面.过点在平面上作,垂足为,联结.则为二面角的平面角.设.易求得.在中,.又,则.故.1.四面体P-ABC,,则该四面体外接球的半径为________. 【答案】【解析】将四面体还原到一个长方体中,设该长方体的长、宽、高分别为a,b,c,则,所以四面体外接球的半径为.2.四面体ABCD中,有一条棱长为3,其余五条棱长皆为2,则其外接球的半径为____.【答案】【解析】解:设BC=3,AB=AC=AD=BD=CD=2,E,F分别是BC,AD的中点,D在面ABC上的射影H应是△ABC的外心,由于DH上的任一点到A,B,C等距,则外接球心O在DH上,因,所以AE=DE,于是ED为AD的中垂线是,顒球心O是DH,EF的交点,且是等腰△EAD的垂心,记球半径为r,由△DOF~△EAF,得.而,所以.3.如图,在四棱锥P-ABCD中,P A⊥平面ABCD,底面ABCD为正方形,P A=AB.E、F分别为PD、BC的中点,则二面角E-FD-A的正切值为________.【答案】【解析】如图,作EH⊥AD于H,连HF.由P A⊥面ABCD,知P A⊥AD,EH∥P A,EH⊥ABCD.作HG⊥DF于G,连EG,则EG⊥FD,∠EGH为二面角E-FD-A的平面角.∵ABCD为正方形,E、F分别为PD、BC的中点,∴H为AD中点,FH⊥AD.设P A=AB=2,则,FH=2,HD=4,.∴.∴二面角E-FD-A的正切值为.4.已知正四面体内切球的半径是1,则该正四面体的体积为________.【答案】【解析】设正四面体的棱长为.则该正四面体的体积为,全面积为,所以,解得.从而正四面体的体积为.故答案为:5.正方体AC1棱长是1,点E、F是线段DD1,BC1上的动点,则三棱锥E一AA1F体积为___.【答案】【解析】因为F是BC1上的动点,所以在正方体中有,利用等体积转化有.故答案为.6.顶点为P的圆锥的轴截面是等腰直角三角形,A是底面圆周上的点,B是底面圆内的点,O为底面圆圆心,AB⊥OB,垂足为B,OH⊥HB,垂足为H,且P A=4,C为P A的中点,则当三棱锥O-HPC的体积最大时,OB的长为________.【答案】【解析】法一:AB⊥OB,PB⊥AB,AB⊥面POB,面P AB⊥面POB.OH⊥PB,OH⊥面P AB,OH⊥HC,OH⊥PC,又,PC⊥OC,PC⊥面OCH.PC是三棱锥P-OCH的高.PC=OC=2.而△OCH的面积在时取得最大值(斜边=2的直角三角形).当时,由,知∠OPB=30°,.法二:由C为P A中点,故,而.记则,.∴令,得,.故答案为:7.如图,在正三棱柱中,AB=2,,D、F分别是棱AB、的中点,E为棱AC 上的动点,则△DEF周长的最小值为__________.【答案】【解析】由正三棱锥可得底面ABC,所以AB,AC.在Rt△ADF中,.如图①,把底面ABC与侧面在同一个平面内展开,展开图中只有当D、E、F三点在同一条直线上时,DE+EF取得最小值.如图②,在△ADF中,,由余弦定理可得.所以△DEF周长的最小值为.8.在边长为1的长方体内部有一小球,该小球与正方体的对角线段相切,则小球半径的最大值=___________.【答案】【解析】当半径最大时,小球与正方体的三个面相切.不妨设小球与过点的三个面相切.以为原点,分别为x、y、z轴正方向,建立空间直角坐标系.设A(0,1,1),(1,0,0),小球圆心P(r,r,r),则P到的距离.再由,得.故答案为:9.正方体中,E为AB的中点,F为的中点.异面直线EF与所成角的余弦值是_____. 【答案】【解析】设正方体棱长为1,以DA为x轴,DC为y轴,为z轴建立空间直角坐标系,则.故有.所以.故答案为:10.在半径为R的球内作内接圆柱,则内接圆柱全面积的最大值是_____.【答案】【解析】设内接圆柱底面半径为,则高位,那么全面积为.其中,等号成立的条件是.故最大值为.故答案为:11.已知空间四点满足,且是三棱锥的外接球上的一个动点,则点到平面的最大距离是______.【答案】【解析】将三棱锥补全为正方体,则两者的外接球相同.球心就是正方体的中心,记为,半径为正方体对角线的一半,即为.在正方体里,可求得点到平面的距离为,则点到平面的最大距离是.12.在正四核锥中,已知二面角的正弦值为,则异面直线所成的角为______.【答案】【解析】如图,设的交点为上的射影为,则.又因为,因此,所以,则.因此即为二面角的平面角,从而.设,则.在中,.由此得,因此,解得.从而四棱锥各侧面均为正三角形,则异面直线所成的角为.13.半径分别为6、6、6、7的四个球两两外切.它们都内切于一个大球,则大球的半径是________【答案】14【解析】设四个球的球心分别为A、B、C、D,则AB=BC=CA=12,DA=DB=DC=13,即A、B、C、D两两连结可构成正三棱锥.设待求的球心为X,半径为r.,则由对称性可知DX平面ABC.也就是说,X在平面ABC上的射影是正三角形ABC的中心O.易知.设OX=x,则由于球A内切于球X,所以AX=r-6即①又DX=OD-OX=11-x,且由球D内切于球X可知DX=r-7于是②从①②两式可解得即大球的半径为14.故答案为:1414.一个棱长为6的正四面体纸盒内放一个小正四面体,若小正四面体可以在纸盒内任意转动,则小正四面体棱长的最大值为______.【答案】2【解析】因为小正四面体可以在纸盒内任意转动,所以小正四面体的棱长最大时,为大正四面体内切球的内接正四面体.记大正四面体的外接球半径为,小正四面体的外接球(大正四面体的内切球)半径为,易知,故小正四面体棱长的最大值为.15.已知棱长的正方体内部有一圆柱,此圆柱恰好以直线为轴,则该圆柱体积的最大值为_____.【答案】【解析】由题意知只需考虑圆柱的底面与正方体的表面相切的情况.由图形的对称性可知,圆柱的上底面必与过A点的三个面相切,且切点分别在、AC、上.设线段上的切点为E,圆柱上底面中心为,半径.由,则圆柱的高为,由导数法或均值不等式得.。
空间向量与立体几何-答案解析

,
AB 则{
1
⋅
n
=0
− 即{
3x − y + 3z = 0 , 取z = 1,则x =
3,得 n = ( 3, 0, 1),
B1C1 ⋅ n = 0 2y = 0
∵ cos⟨BB1 ,
n⟩ =
BB1 ⋅ n ∣∣∣BB1 ∣∣∣ ∣∣∣ n ∣∣∣
=
3 3×2
=
1 ,
2
1 ∴ BB1与平面AB1C1所成的角的正弦值为 2 ,
3,
2 2
).
故cos ⟨AE, CF ⟩ =
AE ⋅ CF ∣∣∣AE∣∣∣ ∣∣∣CF ∣∣∣
=−
3. 3
3 所以直线AE与直线CF 所成角的余弦值为 3 .
例题4
1
【答案】 3 3
【解析】在矩形ACC1A1中,∵ AC1⊥平面A1BD,∴ AC1⊥A1D,可知△A1AD ∼ △ACC1,
AC 则
可得AC1 = (−2, 2, 2),A1E = (−2, 2, −1).
由题意可知AC 1 即为平面A1 B D 的一个法向量, 设A1 E与平面A1 B D 所成的角为θ ,
则sin θ
=
∣∣cos⟨AC ∣
1
,
A1
E⟩∣∣ ∣
=
AC1 ⋅ A1E ∣∣∣AC1∣∣∣ ⋅ ∣∣∣A1E∣∣∣
=
2
可得A (0, − 3, 0),C (0, 3, 0),
由BE⊥平面ABCD,AB = BC,可知AE = EC.
又AE⊥EC,所以EG = 3,且EG⊥AC.
在Rt△EBG中,可得BE =
2,故DF =
2. 2
所以E (1, 0, 2),F (−1, 0, 2 ), 2
高中数学空间向量与立体几何练习题附答案
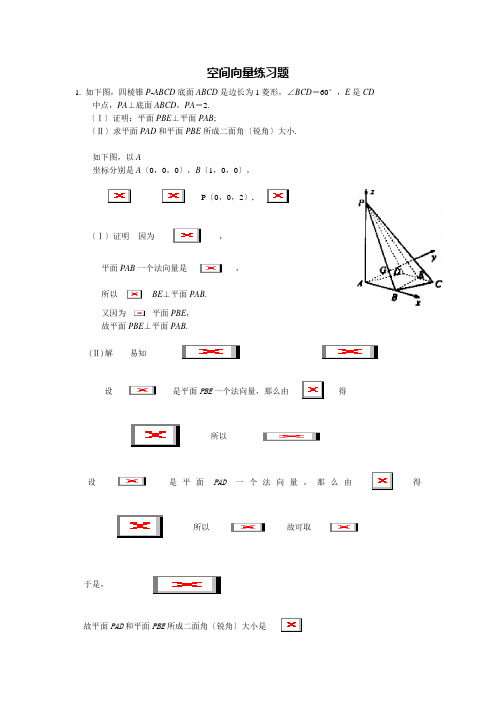
空间向量练习题1. 如下图,四棱锥P-ABCD底面ABCD是边长为1菱形,∠BCD=60°,E是CD中点,PA⊥底面ABCD,PA=2.〔Ⅰ〕证明:平面PBE⊥平面PAB;〔Ⅱ〕求平面PAD和平面PBE所成二面角〔锐角〕大小.如下图,以A坐标分别是A〔0,0,0〕,B〔1,0,0〕,P〔0,0,2〕,〔Ⅰ〕证明因为,平面PAB一个法向量是,所以BE⊥平面PAB.又因为平面PBE,故平面PBE⊥平面PAB.(Ⅱ)解易知设是平面PBE一个法向量,那么由得所以设是平面PAD一个法向量,那么由得所以故可取于是,故平面PAD和平面PBE所成二面角〔锐角〕大小是2. 如图,正三棱柱ABC-A1B1C1全部棱长都为2,D为CC1中点。
〔Ⅰ〕求证:AB1⊥面A1BD;〔Ⅱ〕求二面角A-A1D-B大小;〔Ⅲ〕求点C到平面A1BD间隔;〔Ⅰ〕证明取中点,连结.为正三角形,.在正三棱柱中,平面平面,平面.取中点,以为原点,,,方向为轴正方向建立空间直角坐标系,那么,,,,,,,.,,,.平面.〔Ⅱ〕解设平面法向量为.,.,,令得为平面一个法向量.由〔Ⅰ〕知平面,为平面法向量.,.二面角大小为.xzABCDOFy〔Ⅲ〕解由〔Ⅱ〕,为平面法向量,.点到平面间隔.3.如图,在四面体ABCD中,O、E分别是BD、BC中点,〔1〕求证:平面BCD;〔2〕求异面直线AB与CD所成角余弦值;〔3〕求点E到平面ACD间隔.⑴证明连结OC,.在中,由可得而,即∴平面.(2)解以O为原点,如图建立空间直角坐标系,那么,∴异面直线AB与CD 所成角余弦值为.⑶解设平面ACD 法向量为那么ACDOBEzxACDOBEzx,∴,令得是平面ACD一个法向量.又∴点E到平面ACD间隔.4.三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别为PB,BC中点.〔Ⅰ〕证明:CM⊥SN;〔Ⅱ〕求SN与平面CMN所成角大小.证明:设PA=1,以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图。
《第一章 空间向量与立体几何》单元检测试卷与答案解析(共三套)
《第一章 空间向量与立体几何》单元检测试卷(一)第I 卷(选择题)一、单选题(每题只有一个正确的选项,5分/题,共40分)1.在正四面体P ABC -中,棱长为2,且E 是棱AB 中点,则PE BC ⋅的值为( )A .1-B .1CD .732.已知PA =(2,1,﹣3),PB =(﹣1,2,3),PC =(7,6,λ),若P ,A ,B ,C 四点共面,则λ=( ) A .9B .﹣9C .﹣3D .33.下列说法正确的是( )A .任何三个不共线的向量可构成空间向量的一个基底B .空间的基底有且仅有一个C .两两垂直的三个非零向量可构成空间的一个基底D .基底{}a b c ,,中基向量与基底{}e f g ,,基向量对应相等4.若直线l 的方向向量为(1,2,3)a =-,平面α的法向量为(3,6,9)n =--,则( ) A .l α⊂B .//l αC .l α⊥D .l 与α相交5.在正方体1111ABCD A B C D -中,M N ,分别为AD ,11C D 的中点,O 为侧面11BCC B 的中心,则异面直线MN 与1OD 所成角的余弦值为( ) A .16B .14C .16-D .14-6.已知正四棱柱1111ABCD A B C D -中,12AA AB =,则CD 与平面1BDC 所成角的正弦值等于( )A .23B .3C .3D .137.在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别为棱1AA 、1BB 的中点,M 为棱11A B 上的一点,且1(02)A M λλ=<<,设点N 为ME 的中点,则点N 到平面1D EF 的距离为( )AB .2C D 8.已知空间直角坐标系O xyz -中,()1,2,3OA =,()2,1,2OB =,()1,1,2OP =,点Q 在直线OP 上运动,则当QA QB ⋅取得最小值时,点Q 的坐标为( )A .131,,243⎛⎫ ⎪⎝⎭B .133,,224⎛⎫ ⎪⎝⎭C .448,,333⎛⎫ ⎪⎝⎭D .447,,333⎛⎫ ⎪⎝⎭二、多选题(每题不止一个正确的选项,5分/题,共20分)9.若长方体1111ABCD A B C D -的底面是边长为2的正方形,高为4,E 是1DD 的中点,则( )A .11B E A B ⊥ B .平面1//B CE 平面1A BDC .三棱锥11C B CE -的体积为83D .三棱锥111C B CD -的外接球的表面积为24π 10.正方体1111ABCD A B C D -中,E 、F 、G 、H 分别为1CC 、BC 、CD 、BB 、1BB 的中点,则下列结论正确的是( )A .1B G BC ⊥ B .平面AEF 平面111AAD D AD =C .1//A H 面AEFD .二面角E AF C --的大小为4π 11.设a ,b ,c 是空间一个基底,则( ) A .若a ⊥b ,b ⊥c ,则a ⊥cB .则a ,b ,c 两两共面,但a ,b ,c 不可能共面C .对空间任一向量p ,总存在有序实数组(x ,y ,z),使p xa yb zc =++D .则a +b ,b +c ,c +a 一定能构成空间的一个基底12.(多选题)如图,在菱形ABCD 中,2AB =,60BAD ∠=,将ABD △沿对角线BD 翻折到PBD △位置,连结PC ,则在翻折过程中,下列说法正确的是( )A .PC 与平面BCD 所成的最大角为45B .存在某个位置,使得PB CD ⊥C .当二面角P BD C --的大小为90时,PC =D .存在某个位置,使得B 到平面PDC第II 卷(非选择题)三、填空题(每题5分,共20分)13.若(2, 3, 1)a =-,(2, 0, 3)b =,(3, 4, 2)c =,则()a b c +=___________.14.已知平面α的一个法向量10,,2n ⎛=- ⎝,A α∈,P α∉,且122PA ⎛=- ⎝,则直线PA 与平面α所成的角为______.15.二面角的棱上有A ,B 两点,直线AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB .已知4AB =,6AC =,8BD =,CD =________.16.如图,棱长为3的正方体的顶点A 在平面α上,三条棱,,AB AC AD 都在平面α的同侧,若顶点,B C 到平面α,则顶点D 到平面α的距离是_____.四、解答题(17题10分,其余题目12分每题,共70分)17.如图,2BC =,原点O 是BC 的中点,点A 的坐标为(2,12,0),点D 在平面yOz 上,且90BDC ∠=︒,30DCB ∠=︒.(1)求向量CD 的坐标.(2)求AD 与BC 的夹角的余弦值.18.如图,三棱柱111ABC A B C -中,底面边长和侧棱长都等于1,1160BAA CAA ︒∠=∠=.(1)设1AA a =,AB b =,AC c =,用向量a ,b ,c 表示1BC ,并求出1BC 的长度; (2)求异面直线1AB 与1BC 所成角的余弦值.19.如图所示,在长方体1111ABCD A B C D -中,1AD =,12AB AA ==,N 、M 分别是AB 、1C D 的中点.(1)求证:NM ∥平面11A ADD ; (2)求证:NM ⊥平面11A B M .20.如图,在直棱柱1111ABCD A B C D -中,//AD BC ,90BAD ∠=︒,AC BD ⊥,1BC =,14A D A A ==.(1)证明:面1ACD ⊥面1BB D ; (2)求二面角11B AC D --的余弦值.21.如图,在四棱锥P ABCD -中,AB ⊥平面PAD ,//AB DC ,E 为线段PD 的中点,已知2PA AB AD CD ====,120PAD ∠=︒.(1)证明:直线//PB 平面ACE ;(2)求直线PB 与平面PCD 所成角的正弦值.22.如图,已知梯形ABCD 中,//AD BC ,90DAB ∠=︒,22AB BC AD ===,四边形EDCF 为矩形,2DE =,平面EDCF ⊥平面ABCD . (1)求证://DF 平面ABE ;(2)求平面ABE 与平面BEF 所成二面角的正弦值;(3)若点P 在线段EF 上,且直线AP 与平面BEF ,求线段AP 的长.答案解析第I 卷(选择题)一、单选题(每题只有一个正确的选项,5分/题,共40分)1.在正四面体P ABC -中,棱长为2,且E 是棱AB 中点,则PE BC ⋅的值为( )A .1-B .1CD .73【答案】A 【解析】如图所示由正四面体的性质可得:PA BC ⊥ 可得:0PA BC ⋅=E 是棱AB 中点12PEPA PB 111122cos12012222PE BC PA PB BCPA BC PB BC 故选:A【点睛】本题考查空间向量的线性运算,考查立体几何中的垂直关系,考查转化与化归思想,属于中等题型.2.已知PA =(2,1,﹣3),PB =(﹣1,2,3),PC =(7,6,λ),若P ,A ,B ,C 四点共面,则λ=( ) A .9 B .﹣9C .﹣3D .3【答案】B【解析】由P ,A ,B ,C 四点共面,可得,,PA PB PC 共面,(2,2,33)(7,6,)xPA yPB x y x y C y P x λ∴=+=-+-+=,272633x y x y x y λ-=⎧⎪+=⎨⎪-+=⎩,解得419x y λ=⎧⎪=⎨⎪=-⎩. 故选:B.3.下列说法正确的是( )A .任何三个不共线的向量可构成空间向量的一个基底B .空间的基底有且仅有一个C .两两垂直的三个非零向量可构成空间的一个基底D .基底{}a b c ,,中基向量与基底{}e f g ,,基向量对应相等 【答案】C【解析】A 项中应是不共面的三个向量构成空间向量的基底, 所以A 错.B 项,空间基底有无数个, 所以B 错.D 项中因为基底不唯一,所以D 错.故选C .4.若直线l 的方向向量为(1,2,3)a =-,平面α的法向量为(3,6,9)n =--,则( ) A .l α⊂ B .//l αC .l α⊥D .l 与α相交【答案】C【解析】∵直线l 的方向向量为()1,2,3a =-, 平面α的法向量为()3,6,9n =--,∴13a n =-,∴a n , ∴l α⊥. 故选C .5.在正方体1111ABCD A B C D -中,M N ,分别为AD ,11C D 的中点,O 为侧面11BCC B 的中心,则异面直线MN 与1OD 所成角的余弦值为( ) A .16B .14C .16-D .14-【答案】A【解析】如图,以D 为坐标原点,分别以1,,DA DC DD 所在直线为,,x y z 轴建立空间直角坐标系. 设正方体的棱长为2,则()()()()1100,012,121,002M N O D ,,,,,,,,, ∴()()11,1,2,1,2,1MN OD =-=--. 则1111cos ,66MN OD MN OD MN OD ⋅===. ∴异面直线MN 与1OD 所成角的余弦值为16,故选A .6.已知正四棱柱1111ABCD A B C D -中,12AAAB =,则CD 与平面1BDC 所成角的正弦值等于() A .23B C.3D .13【答案】A【解析】设1AB =11BD BCDC ∴===,1BDC ∆面积为3211C BDC C BCD V V --=131********d d ∴⨯⨯=⨯⨯∴=2sin 3d CD θ∴== 7.在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别为棱1AA 、1BB 的中点,M 为棱11A B 上的一点,且1(02)A M λλ=<<,设点N 为ME 的中点,则点N 到平面1D EF 的距离为( )AB.2CD【答案】D【解析】以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系, 则M (2,λ,2),D 1(0,0,2),E (2,0,1),F (2,2,1), 1ED =(﹣2,0,1),EF =(0,2,0),EM =(0,λ,1), 设平面D 1EF 的法向量n =(x ,y ,z ),则12020n ED x z n EF y ⎧⋅=-+=⎪⎨⋅==⎪⎩ ,取x =1,得n =(1,0,2),∴点M 到平面D 1EF 的距离为:d=||2||5EM n n ⋅==,N 为EM 中点,所以N到该面的故选:D .8.已知空间直角坐标系O xyz -中,()1,2,3OA =,()2,1,2OB =,()1,1,2OP =,点Q 在直线OP 上运动,则当QA QB ⋅取得最小值时,点Q 的坐标为( )A .131,,243⎛⎫⎪⎝⎭B .133,,224⎛⎫⎪⎝⎭C .448,,333⎛⎫⎪⎝⎭D .447,,333⎛⎫⎪⎝⎭【答案】C【解析】设(,,)Q x y z ,由点Q 在直线OP 上,可得存在实数λ使得OQ OP λ=, 即(,,)(1,1,2)x y z λ=,可得(,,2)Q λλλ,所以(1,2,32),(2,1,22)QA QB λλλλλλ=---=---,则2(1)(2)(2)(1)(32)(22)2(385)QA QB λλλλλλλλ⋅=--+--+--=-+, 根据二次函数的性质,可得当43λ=时,取得最小值23-,此时448(,,)333Q . 故选:C.二、多选题(每题不止一个正确的选项,5分/题,共20分)9.若长方体1111ABCD A B C D -的底面是边长为2的正方形,高为4,E 是1DD 的中点,则( )A .11B E A B ⊥B .平面1//B CE 平面1A BDC .三棱锥11C B CE -的体积为83D .三棱锥111C B CD -的外接球的表面积为24π【答案】CD【解析】以1{,,}AB AD AA 为正交基底建立如图所示的空间直角坐标系,则 (0,0,0)A ,(2,0,0)B ,(2,2,0)C ,(0,2,0)D ,1(0,0,4)A ,1(2,0,4)B ,(0,2,2)E ,所以1(2,2,2)B E =--,1(2,0,4)A B =-, 因为1140840B E A B ⋅=-++=≠,所以1B E 与1A B 不垂直,故A 错误; 1(0,2,4)CB =-,(2,0,2)CE =-设平面1B CE 的一个法向量为111(,,)n x y z =,则 由100n CB n CE ⎧⋅=⎨⋅=⎩,得1111240220y z x z -+=⎧⎨-+=⎩,所以11112y z x z =⎧⎨=⎩,不妨取11z =,则11x =,12y = 所以(1,2,1)n =,同理可得设平面1A BD 的一个法向量为(2,2,1)m =,故不存在实数λ使得n λm =,故平面1B CE 与平面1A BD 不平行,故B 错误; 在长方体1111ABCD A B C D -中,11B C ⊥平面11CDD C ,故11B C 是三棱锥11B CEC -的高, 所以111111111184223323三棱锥三棱锥CEC C B CE CEC B V V S B C --==⋅=⨯⨯⨯⨯=△, 故C 正确;三棱锥111C B CD -的外接球即为长方体1111ABCD A B C D -的外接球,故外接球的半径2R ==所以三棱锥111C B CD -的外接球的表面积2424S R ππ==,故D 正确. 故选:CD.10.正方体1111ABCD A B C D -中,E 、F 、G 、H 分别为1CC 、BC 、CD 、BB 、1BB 的中点,则下列结论正确的是( )A .1B G BC ⊥ B .平面AEF 平面111AAD D AD =C .1//A H 面AEFD .二面角E AF C --的大小为4π 【答案】BC【解析】由题可知,1B G 在底面上的射影为BG ,而BC 不垂直BG , 则1B G 不垂直于BC ,则选项A 不正确;连接1AD 和1BC ,E 、F 、G 、H 分别为1CC 、BC 、CD 、BB 、1BB 的中点, 可知11////EF BC AD ,所以AEF ∆⊂平面1AD EF , 则平面AEF平面111AA D D AD =,所以选项B 正确;由题知,可设正方体的棱长为2,以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴, 则各点坐标如下:()()()()()()12,0,0,0,2,0,0,2,1,2,0,2,2,2,1,1,2,0A C E A H F ()()()()110,2,1,1,2,0,1,0,1,0,0,2A H AF EF AA =-=-=-=,设平面AEF 的法向量为(),,n x y z =,则00n AF n EF ⎧⋅=⎨⋅=⎩,即20x y x z -+=⎧⎨-=⎩,令1y =,得2,2x z ==,得平面AEF 的法向量为()2,1,2n =,所以10A H n ⋅=,所以1//A H 平面AEF ,则C 选项正确; 由图可知,1AA ⊥平面AFC ,所以1AA 是平面AFC 的法向量, 则1112cos ,3AA n AA n AA n⋅<>===⋅. 得知二面角E AF C --的大小不是4π,所以D 不正确. 故选:BC.11.设a ,b ,c 是空间一个基底,则( ) A .若a ⊥b ,b ⊥c ,则a ⊥cB .则a ,b ,c 两两共面,但a ,b ,c 不可能共面C .对空间任一向量p ,总存在有序实数组(x ,y ,z),使p xa yb zc =++D .则a +b ,b +c ,c +a 一定能构成空间的一个基底 【答案】BCD【解析】对于A 选项,b 与,a c 都垂直,,a c 夹角不一定是π2,所以A 选项错误. 对于B选项,根据基底的概念可知a ,b ,c 两两共面,但a ,b ,c 不可能共面.对于C 选项,根据空间向量的基本定理可知,C 选项正确.对于D 选项,由于a ,b ,c 是空间一个基底,所以a ,b ,c 不共面.假设a +b ,b +c ,c +a 共面,设()()()1a b x b c x c a +=++-+,化简得()1x a x b c ⋅=-+,即()1c x a x b =⋅+-,所以a ,b ,c 共面,这与已知矛盾,所以a +b ,b +c ,c +a 不共面,可以作为基底.所以D 选项正确. 故选:BCD12.(多选题)如图,在菱形ABCD 中,2AB =,60BAD ∠=,将ABD △沿对角线BD 翻折到PBD △位置,连结PC ,则在翻折过程中,下列说法正确的是( )A .PC 与平面BCD 所成的最大角为45B .存在某个位置,使得PB CD ⊥C .当二面角P BD C --的大小为90时,PC =D .存在某个位置,使得B 到平面PDC 【答案】BC【解析】如图所示:A 项:取BD 的中点O ,连结OP 、OC , 因为四边形ABCD 是菱形,O 是线段BD 的中点, 所以,,OP BD OC BD OPOC O ⊥⊥=,BD ⊥平面POC ,BD ⊂平面BCD ,所以POC ⊥平面BCD ,所以POC 平面BCDOC ,所以PC 在平面BCD 的射影为OC ,PCO ∠即PC 与平面BCD 所成角,PO OC ,三角形POC 是等腰三角形,当60POC ∠=时,PC 与平面BCD 所成角为60,故A 错误; B 项:当PD PC =时,取CD 的中点N ,可得CD PN ⊥,CD BN ⊥,故CD ⊥平面PBN ,PB CD ⊥,故B 正确; C 项:因为四边形ABCD 是菱形,O 是线段BD 的中点, 所以PO BD ⊥,CO BD ⊥,因为BD 是平面PBD 与平面CBD 的交线, 所以POC ∠即平面PBD 与平面CBD 所成角,因为二面角P BD C --的大小为90,所以90POC ∠=,因为PO OC ==PC =C 正确;D 项:因为BN =B 到平面PDC则BN ⊥平面PCD ,2PB =,BN =1PN =,1DN =,则PD =D 错误,故选:BC.第II 卷(非选择题)三、填空题(每题5分,共20分)13.若(2, 3, 1)a =-,(2, 0, 3)b =,(3, 4, 2)c =,则()a b c +=________. 【答案】3.【解析】因为(2, 3, 1)a =-,(2, 0, 3)b =,(3, 4, 2)c =所以()5,4,5b c += 所以()()2534153a b c +=⨯+-⨯+⨯=故答案为:314.已知平面α的一个法向量10,,2n ⎛=- ⎝,A α∈,P α∉,且122PA ⎛=- ⎝,则直线PA 与平面α所成的角为______. 【答案】π3【解析】设直线PA 与平面α所成的角为θ,则s 0in cos n PA n PAθθ===⋅=⋅, ∴直线PA 与平面α所成的角为π3.故答案为:π3.15.二面角的棱上有A ,B 两点,直线AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB .已知4AB =,6AC =,8BD =,CD =________. 【答案】60︒【解析】由条件,知0CA AB ⋅=,0AB BD ⋅=,CD CA AB BD =++.2222222CD CA AB BD CAAB AB BD CA BD=+++⋅+⋅+⋅(2222648268cos ,CA BD =+++⨯⨯=.∴1cos ,2CA BD =-,又∵0,180CA BD ︒≤≤︒,∴,120CABD =︒,∴二面角的大小为60︒. 故答案为:60︒.16.如图,棱长为3的正方体的顶点A 在平面α上,三条棱,,AB AC AD 都在平面α的同侧,若顶点,B C 到平面α,则顶点D 到平面α的距离是______.【解析】如图,以O 为坐标原点,建立空间直角坐标系, 则(0,0,0),(3,0,0),(0,3,0),(3,3,0),(3,3,3)O C B A D , 所以(3,0,0),(0,3,0),(0,0,3)BA CA AD ===, 设平面α的一个法向量为(,,)n x y z =, 则点B 到平面α距离为12||||BA n d n x ⋅===点C 到平面α距离为12||||CA n d n x ⋅===由①②可得||||,|||y x zx==, 所以D 到平面α的距离为2|||||AD n n x x ⋅===故答案为四、解答题(17题10分,其余题目12分每题,共70分) 17.如图,2BC =,原点O 是BC的中点,点A 的坐标为(2,12,0),点D 在平面yOz 上,且90BDC ∠=︒,30DCB ∠=︒.(1)求向量CD 的坐标.(2)求AD 与BC 的夹角的余弦值.【答案】(1)3(0,2-;(2).【解析】(1)过D 作DE BC ⊥于E ,则sin302DE CD =⋅︒=,11cos60122OE OB BD =-︒=-=,所以D 的坐标为1(0,2D -,又因为(0,1,0)C ,所以3(0,2CD =-.(2)依题设有A 点坐标为1,0)2A ,所以(2AD =--,(0,2,0)BC =,则AD 与BC 的夹角的余弦值为·cos ,·AD BC AD BC AD BC==-.18.如图,三棱柱111ABC A B C -中,底面边长和侧棱长都等于1,1160BAA CAA ︒∠=∠=.(1)设1AA a =,AB b =,AC c =,用向量a ,b ,c 表示1BC ,并求出1BC 的长度; (2)求异面直线1AB 与1BC 所成角的余弦值. 【答案】(1)1BC a c b =+-;12BC =(2【解析】(1)1111111111BC BB BC BB AC A B AA AC AB a c b =+=+-=+-=+-, 因为11||||cos 11cos602a b a b BAA ︒⋅=⋅∠=⨯⨯=,同理可得12a cbc ⋅=⋅=,所以22221()2221111BC a c b a c b a c a b c b =+-=+++⋅-⋅-⋅=+++-=.(2)因为1AB a b =+,所以2221()2111AB a b a b a b =+=++⋅=++=因为2211()1111111222)2(AB BC a b a c b a a ca b b a c b b ⋅=+⋅+-=+⋅+-⋅+⋅+⋅=+-+=--,所以111111cos ,62AB BC AB BC AB BC ⋅<>===所以异面直线1AB 与1BC 所成角的余弦值为619.如图所示,在长方体1111ABCD A B C D -中,1AD =,12AB AA ==,N 、M 分别是AB 、1C D 的中点.(1)求证:NM ∥平面11A ADD ; (2)求证:NM ⊥平面11A B M .【答案】(1)证明见解析;(2)证明见解析.【解析】证明:(1)以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,在长方体1111ABCD A B C D -中,1AD =,12AB AA ==,N 、M 分别是AB 、1C D 的中点,(0M ∴,1,1),(1N ,1,0),(1=MN ,0,1)-,平面11A ADD 的法向量可设为(0n =,1,0),∴0=MN n ,MN ⊂/平面11A ADD ,MN ∴平面11A ADD .(2)1(1A ,0,2),1(1B ,2,2),11(0A B =,2,0),1(1A M =-,1,1)-, 11·0MN AB ∴=,1·0MN AM =, 11MN A B ∴⊥,1MN A M ⊥, 1111A B A M A ⋂=,NM ∴⊥平面11A B M .20.如图,在直棱柱1111ABCD A B C D -中,//AD BC ,90BAD ∠=︒,AC BD ⊥,1BC =,14A D A A ==.(1)证明:面1ACD ⊥面1BB D ; (2)求二面角11B AC D --的余弦值.【答案】(1)证明见解析;(2)63. 【解析】(1)证明:1BB ⊥平面ABCD ,AC ⊂平面ABCD ,∴1AC BB ⊥. 又∵AC BD ⊥,且1BB BD B ⋂=,1,BD BB ⊂平面1BB D , ∴AC ⊥平面1BB D . 又∵AC ⊂平面1ACD , ∴面1ACD ⊥面1BB D .(2)易知AB 、AD 、1AA 两两垂直,以A 为坐标原点,AB 、AD 、1AA 所在直线分别为x 轴、y 轴、z 轴建立如图的空间直角坐标系,设AB t =,则相关各点的坐标为()0,0,0A ,(),0,0B t ,()1,0,4B t ,(),1,0C t , ()1,1,4C t ,()0,4,0D ,()10,4,4D .从而(),1,0AC t =,(),4,0BD t =-. ∵AC BD ⊥,∴2400AC BD t ⋅=-++= 解之得2t =或2t =-(舍去).()10,4,4AD =,()2,1,0AC =设()1,,n x y z =是平面1ACD 的一个法向量, 则11100n AC n AD ⎧⋅=⎪⎨⋅=⎪⎩,即20440x y y z +=⎧⎨+=⎩令1x =,则()11,2,2n =-.同理可求面1ACB 的法向量为()22,4,1n =-.∴12122cos 63||||3n n n n θ⋅-===⋅.又∵二面角11B AC D --是锐二面角, ∴二面角11B AC D --21.如图,在四棱锥P ABCD -中,AB ⊥平面PAD ,//AB DC ,E 为线段PD 的中点,已知2PA AB AD CD ====,120PAD ∠=︒.(1)证明:直线//PB 平面ACE ;(2)求直线PB 与平面PCD 所成角的正弦值.【答案】(1)证明见解析;(2【解析】(1)证明:连接BD 交AC 于点H ,连接HE//AB DC ,AB CD =,四边形ABCD 是平行四边形,H ∴是AC 中点,又E 为线段PD 的中点,//B HE P ,又HE ⊂平面ACE ,PB ⊄平面ACE∴ 直线//PB 平面ACE(2)AB ⊥平面PAD ,作Ax AP ⊥,建立如图所示空间直角坐标系A xyz -由已知2PA AB AD CD ====,120PAD ∠=︒ 得(0,0,2)B ,(0,2,0)P,1,0)D -,1,2)C -(0,2,2)PB =-- , (3,3,0)PD =- (0,0,2)CD =-设平面PCD 的法向量(,,)n x y z =·0·0n CD n PD ⎧=⎨=⎩ , 200Z y -=⎧⎪-=,不妨取(1,3,0)n =2cos ,422PB n PBn PB n-∴<>===⨯所以直线PB 与平面PCD 所成角的正弦值为422.如图,已知梯形ABCD 中,//AD BC ,90DAB ∠=︒,22AB BC AD ===,四边形EDCF 为矩形,2DE =,平面EDCF ⊥平面ABCD . (1)求证://DF 平面ABE ;(2)求平面ABE与平面BEF 所成二面角的正弦值;(3)若点P 在线段EF 上,且直线AP 与平面BEF ,求线段AP 的长.【答案】(1)证明见解析;(2;(3)3【解析】(1)证明:四边形EDCF 为矩形,DE CD ∴⊥,又平面EDCF ⊥平面ABCD ,平面EDCF⋂平面ABCD CD =,ED ∴⊥平面ABCD .取D 为原点,DA 所在直线为x 轴,DE 所在直线为z 轴建立空间直角坐标系, 如图,则(1A ,0,0),(1B ,2,0),(1C -,2,0),(0E ,0,2),(1F -,2,2), 设平面ABE 的法向量(,,)m x y z =,(1,2,2)BE =--,(0,2,0)AB =,由·220·20m BE x y z m AB y ⎧=--+=⎨==⎩,取1z =,得(2,0,1)m =,又(1,2,2)DF =-,∴2020DF m =-++=,则DF m ⊥, 又DF ⊂/平面ABE ,//DF ∴平面ABE ;(2)解:设平面BEF 的法向量111(,,)n x y z =,(1,2,2)BE =--,(1,2,0)EF =-,由11111·220·20n BE x y z n EF x y ⎧=--+=⎪⎨=-+=⎪⎩,取11y =,可得(2,1,2)n =,42cos ,||||35m n m n m n +∴<>===,5sin ,5m n ∴<>=, 即平面ABE 与平面BEF ;(3)解:点P 在线段EF 上,设EP EF λ=,[0λ∈,1],∴(1AP AE EF λ=+=-,0,2)(1λ+-,2,0)(1λ=--,2λ,2),又平面BEF 的法向量(2,1,2)n =,设直线AP 与平面BEF 所成角为θ,∴|||2(1sin |cos ,|||||3(AP n AP n AP n θλ-=<>===-,24518110λλ∴+-=,即(31)(1511)0λλ-+=,[0λ∈,1],∴13λ=.∴4(3AP =-,23,2),则||(AP =-,AP ∴.《第一章 空间向量与立体几何》单元检测试卷(二)一、选择题1.在四面体ABCD 中,点F 在AD 上,且2AF FD =,E 为BC 中点,则EF 等于( )323向量()()(,1,1,b 1,,1,c 2,4,2a x y ===-且,//c a c b ⊥,则b a +=( )3.在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别为棱1AA 、1BB 的中点,M 为棱11A B 上的一点,且1(02)A M λλ=<<,设点N 为ME 的中点,则点N 到平面1D EF 的距离为( )4.空间线段AC AB ⊥,BD AB ⊥,且::1:3:1AC AB BD =,设CD 与AB 所成的角为α,CD 与面ABC 所成的角为β,二面角C AB D --的平面角为γ,则( )5.(多选题)在四面体P ABC -中,以上说法正确的有( ).若1233AD AC AB =+,则可知3BC BD = 的重心,则111333PQ PA PB PC =++C .若0PA BC ⋅=,0PC AB ⋅=,则0PB AC ⋅=1MN = 6.(多选题)如图,在菱形ABCD 中,2AB =,60BAD ∠=︒,将ABD △沿对角线BD 翻折到PBD △位置,连结PC ,则在翻折过程中,下列说法正确的是( )A .PC 与平面BCD 所成的最大角为45︒B .存在某个位置,使得PB CD ⊥二、填空题7.在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动,则直线1D E 与1A D 所成角的大小是__________,若1D E EC ⊥,则AE =__________.8.已知四棱柱1111ABCD A B C D -的底面是边长为2的正方形,侧棱与底面垂直.若点C 到9.在正方体1111ABCD A B C D -中,E ,F 分别为线段11A B ,AB 的中点,O 为四棱锥11E C D DC -的外接球的球心,点M ,N 分别是直线1DD ,EF 上的动点,记直线OC 与MN 所成的角为θ,则当θ最小时,tan θ=__________.10.如图,四棱锥P ABCD -中,ABCD 是矩形,PA ⊥平面ABCD ,1==PA AB ,2BC =,四棱锥外接球的球心为O ,点E 是棱AD 上的一个动点.给出如下命题:①直线PB 与直线CE 所成的角中最小的角为45;②BE 与PC 一定不垂直;③三棱锥E BCO -的体积为定题序号都填上)三、解答题, ,为的中点,为的中点,以A 为原点,建立适当的空间坐标系,利用空间向量解答以下问题: (1)证明:直线;(2)求异面直线AB 与MD 所成角的大小; (3)求点B 到平面OCD 的距离.为AC 的中点.(1)求直线AB 与DE 所成角的余弦值;答案解析一、选择题1.在四面体ABCD 中,点F 在AD 上,且2AF FD =,E 为BC 中点,则EF 等于( )A .1223EF AC AB AD →→→→=+-B .112223EF AC AB AD →→→→=--+OA ABCD ⊥底面2OA =M OA N BC MN OCD平面‖C .112223EF AC AB AD →→→→=-+D .112223EF AC AB AD →→→→=-+-【答案】B【解析】在四面体ABCD 中,点F 在AD 上,且2AF FD =,E 为BC 中点,所以EF EB BA AF →→→→=++1223AB AC AB AD →→→→⎛⎫=--+ ⎪⎝⎭112223AC AB AD →→→=--+,即112223EF AC AB AD →→→→=--+.故选:B.2.设,x y R ∈,向量()()(),1,1,b 1,,1,c 2,4,2,a x y ===-且,//c a c b ⊥,则b a +=( )A .BC .3D .4【答案】D 【解析】(),241,2,1,21b c y y b ∴=-⨯∴=-∴=-,,,a b ⊥()214+20,a b x ∴⋅=+⋅-=1x ∴=,()()1,112,1,2a a b ∴=∴+=-,(223a b ∴+=+=,故选C. 3.在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别为棱1AA 、1BB 的中点,M 为棱11A B 上的一点,且1(02)A M λλ=<<,设点N 为ME 的中点,则点N 到平面1D EF 的距离为( )A B .2C .3λ D 【答案】D【解析】以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,则M (2,λ,2),D 1(0,0,2),E (2,0,1),F (2,2,1), 1ED =(﹣2,0,1),EF =(0,2,0),EM =(0,λ,1), 设平面D 1EF 的法向量n =(x ,y ,z ),则1·20·20n ED x z n EF y ⎧=-+=⎨==⎩,取x =1,得n =(1,0,2),∴点M 到平面D 1EF 的距离为:d=255EM nn==,N 为EM 中点,所以N 到该面的距,选D .4.空间线段AC AB ⊥,BD AB ⊥,且::1:3:1AC AB BD =,设CD 与AB 所成的角为α,CD 与面ABC 所成的角为β,二面角C AB D --的平面角为γ,则( ) A .2γβα≤≤B .2γβα≤≤ C .2γαβ≤≤D .2γαβ≤≤【答案】A【解析】因为空间线段AC AB ⊥,BD AB ⊥,所以可将其放在矩形中进行研究,如图,绘出一个矩形,并以A 点为原点构建空间直角坐标系:因为::1:3:1AC AB BD =,所以可设AC x =,3AB x =,BD x =,则()0,0,0A ,0,3,0B x ,0,0,C x ,,3,0D x x ,,3,CD x x x ,0,3,0AB x ,0,3,CBx x ,故CD 与AB 所成的角α的余弦值229311cos α11113CD AB x CD ABx x, 因为根据矩形的性质易知平面ABD ⊥平面ABC ,BD ⊥平面ABC ,所以二面角C ABD --的平面角为γ90,γ452,γ2cos22,所以BCD ∠即CD 与面ABC 所成的角β,故110cos β11CD CB CD CB,因为311211112,所以2γβα≤≤,故选:A.5.(多选题)在四面体P ABC -中,以上说法正确的有( )A .若1233AD AC AB =+,则可知3BC BD = B .若Q 为ABC ∆的重心,则111333PQ PA PB PC =++C .若0PA BC ⋅=,0PC AB ⋅=,则0PB AC ⋅=D .若四面体P ABC -各棱长都为2,M ,N 分别为PA ,BC 的中点,则1MN = 【答案】ABC【解析】对于A ,1233AD AC AB =+,32AD AC AB ∴=+,22AD AB AC AD ∴-=- ,2BD DC ∴=,3BD BD DC ∴=+即3BD BC =,故A 正确;对于B ,若Q 为ABC ∆的重心,则0QA QB QC ++=,33PQ QA QB QC PQ ∴+++=,3PQ PA PB PC ∴=++即111333PQ PA PB PC =++,故B 正确;对于C ,若0PA BC ⋅=,0PC AB ⋅=,则PA BC PC AB ⋅=⋅,0PA BC PC AB ∴⋅+⋅=,()0PA BC PC AC CB ∴⋅+⋅+= 0PA BC PC AC PC CB ∴⋅+⋅+⋅=,0PA BC PC AC PC BC ∴⋅+⋅-⋅=()0PA PC BC PC AC ∴-⋅+⋅=,0CA BC PC AC ∴⋅+⋅=0AC CB PC AC ∴⋅+⋅=,()0AC CB PC ∴⋅+=0AC PB ∴⋅=故C 正确;对于D ,()()111222MN PN PM PB PC PA PB PC PA =-=+-=+-12MN PA PB PC ∴=--,222222PA PB PC PA PB PC PA PB PA PC PB PC --=++-⋅-⋅+⋅===2MN ∴=,故D 错误.故选:ABC6.(多选题)如图,在菱形ABCD 中,2AB =,60BAD ∠=︒,将ABD △沿对角线BD 翻折到PBD △位置,连结PC ,则在翻折过程中,下列说法正确的是( )A .PC 与平面BCD 所成的最大角为45︒B .存在某个位置,使得PB CD ⊥C .当二面角P BD C --的大小为90︒时,PC =D .存在某个位置,使得B 到平面PDC 【答案】BC 【解析】如图所示:对A ,取BD 的中点O ,连结OP ,OC ,则当60POC ∠=时,PC 与平面BCD 所成的最大角为60︒,故A 错误;对B ,当PD PC =时,取CD 的中点N ,可得,,CD PN CD BN ⊥⊥所以CD ⊥平面PBN ,所以PB CD ⊥,故B 正确;对C ,当二面角P BD C --的大小为90时,所以90∠=POC ,所以PO OC ==所以PC =故C 正确;对D ,因为BN =所以如果B 到平面PDC ,则BN ⊥平面PCD ,则2,1,1PB BN PN DN ====,所以PD =D 错误;故选:BC.二、填空题7.在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动,则直线1D E 与1A D 所成角的大小是__________,若1D E EC ⊥,则AE =__________.【答案】90; 1【解析】长方体ABCD ﹣A 1B 1C 1D 1中以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,又11AD AA ==,2AB =,点E 在棱AB 上移动则D (0,0,0),D 1(0,0,1),A (1,0,0),A 1(1,0,1),C (0,2,0), 设E (1,m ,0),0≤m≤2,则1D E =(1,m ,﹣1),1A D =(﹣1,0,﹣1), ∴1D E •1A D =﹣1+0+1=0,∴直线D 1E 与A 1D 所成角的大小是90°. ∵1D E =(1,m ,﹣1),EC =(﹣1,2﹣m ,0),D 1E ⊥EC ,∴1D EEC =﹣1+m (2﹣m )+0=0,解得m=1,∴AE=1.故答案为900,1.8.已知四棱柱1111ABCD A B C D -的底面是边长为2的正方形,侧棱与底面垂直.若点C 到平面11AB D,则直线1B D 与平面11AB D 所成角的余弦值为______.【解析】如图,连接11A C 交11B D 于O 点,过点C 作CH AO ⊥于H ,则CH ⊥平面11AB D ,则CH =,设1AA a =,则AO CO ==AC =得1122AOC S AO CH AC ∆=⨯⨯=⨯a =以1A 为坐标原点,建立如图所示的空间直角坐标系1A xyz -.则(A ,()12,0,0B ,()10,2,0D,(D ,(10,2,AD =-,(12,0,AB =-,(1B D =-,设平面11AB D 的法向量为(),,n x y z =,则1100n AD n AB ⎧⋅=⎪⎨⋅=⎪⎩,即20220y x ⎧-=⎪⎨-=⎪⎩,令x,得()2,2,1n =.11110cos ,10B D n B D n B D n⋅==1B D 与平面1111D C B A所成的角的余弦值为.9.在正方体1111ABCD A B C D -中,E ,F 分别为线段11A B ,AB 的中点,O 为四棱锥11E C D DC -的外接球的球心,点M ,N 分别是直线1DD ,EF 上的动点,记直线OC 与MN 所成的角为θ,则当θ最小时,tan θ=__________. 【答案】42【解析】如图,设,P Q 分别为棱CD 和11C D 的中点,则四棱锥11E C D DC -的外接球即为三棱柱11DFC D EC -的外接球,因为三棱柱11DFC D EC -为直三棱柱,所以其外接球球心O 为上、下底面三角形外心G 和H 连线的中点,由题意,MN 是平面1DD EF 内的一条动直线,所以θ最小是直线OC 与平面1DD EF 所成角,即问题转化为求直线OC 与平面1DD EF 所成角的正切值,不妨设正方体的棱长为2,2EQ =,1ED =,因为11EC D △为等腰三角形,所以11EC D △外接圆的直径为11152sin 2ED GE EC D ===∠,则54GE =,从而53244GQ PH =-==,如图,以D 为原点,以1,,DA DC DD 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系D xyz -,则()0,0,0D ,()10,0,2D ,()0,2,0C ,()2,1,0F ,3,1,14O ⎛⎫⎪⎝⎭,()10,0,2DD ∴=,()2,1,0DF =,设平面1DD EF 的一个法向量为(),,n x y z =,则12020n DD z n DF x y ⎧⋅==⎨⋅=+=⎩,令1x =,则()1,2,0n =-,因为3,1,14OC ⎛⎫=-- ⎪⎝⎭,所以sin cos ,n OC θ===10.如图,四棱锥P ABCD -中,ABCD 是矩形,PA ⊥平面ABCD ,1==PA AB ,2BC =,四棱锥外接球的球心为O ,点E 是棱AD 上的一个动点.给出如下命题:①直线PB 与直线CE 所成的角中最小的角为45;②BE 与PC 一定不垂直;③三棱锥E BCO -的体积为定值;④CE PE +的最小值为其中正确命题的序号是__________.(将你认为正确的命题序号都填上)【答案】①③④【解析】如图所示:以,,AB AD AP 为,,x y z 轴建立空间直角坐标系,则()0,0,1P ,()1,0,0B ,()1,2,0C ,()0,,0E y ,则()1,0,1BP =-,()1,2,0CE y =--,cos ,2BP CE BP CE BP CE⋅==≤⋅2y =时等号成立, 此时,4BP CE π=,故直线PB 与直线CE 所成的角中最小的角为45,①正确;()()1,,01,2,121BE PC y y ⋅=-⋅-=-,当12y =时,BE PC ⊥,②错误; 将四棱锥放入对应的长方体中,则球心为体对角线交点,1111112323226BCE E BCO OBCE AP V V S --==⨯⨯=⨯⨯⨯⨯=△,③正确;如图所示:将平面ABCD 以AD 为轴旋转到平面PAD 内形成平面''AB C D , 则''CE PE C E PE PC +=+≥=='PEC 共线时等号成立,④正确.故答案为:①③④.三、解答题11.如图,在四棱锥中,底面是边长为1的菱形,,, ,为的中点,为的中点,以A 为原点,建立适当的空间坐标系,利用空间向量解答以下问题: (1)证明:直线;(2)求异面直线AB 与MD 所成角的大小;O ABCD -ABCD 4ABC π∠=OA ABCD ⊥底面2OA =M OA N BC MN OCD平面‖(3)求点B 到平面OCD 的距离.【解析】作于点P,如图,分别以AB,AP,AO 所在直线为轴建立坐标系, (1)设平面OCD 的法向量为,则即 取解得(2)设与所成的角为, , 与所成角的大小为(3)设点B 到平面OCD 的距离为,则为在向量上的投影的绝对值,AP CD ⊥,,x yz (0,0,0),(1,0,0),(0,((0,0,2),(0,0,1),(122244A B P D O M N -2222(1,,1),(0,,2),(2)44222MN OP OD =--=-=--(,,)n x y z =0,0n OP n OD ==2022022y z x y z -=⎪⎪⎨⎪-+-=⎪⎩z =(0,4,2)n =22(1,,1)(0,4,2)044MN n =--=∵MN OCD ∴平面‖AB MD θ(1,0,0),(1)2AB MD ==--∵1cos ,23AB MDAB MD πθθ===⋅∴∴AB MD 3πd d OB (0,4,2)n =由 , 得.所以点B 到平面OCD 的距离为12.在三棱锥A —BCD 中,已知,BD=2,O 为BD 的中点,AO ⊥平面BCD ,AO=2,E 为AC 的中点.(1)求直线AB 与DE 所成角的余弦值; (2)若点F 在BC 上,满足BF=14BC ,设二面角F —DE —C 的大小为θ,求sinθ的值. 【解析】(1)连,CO BC CD BO OD CO BD ==∴⊥以,,OB OC OA 为,,x y z 轴建立空间直角坐标系,则(0,0,2),(1,0,0),(0,2,0),(1,0,0)(0,1,1)A B C D E -∴(1,0,2),(1,1,1)cos ,15AB DE AB DE ∴=-=∴<>==- 从而直线AB 与DE 所成角的余弦值为15(2)设平面DEC 一个法向量为1(,,),n x y z =(1,0,2)OB =-23OB n d n⋅==2311200(1,2,0),00x y n DC DC x y z n DE ⎧+=⋅=⎧⎪=∴⎨⎨++=⋅=⎪⎩⎩令112,1(2,1,1)y x z n =∴=-=∴=- 设平面DEF 一个法向量为2111(,,),n x y z =11221117100171(,,0),4244200x y n DF DF DB BF DB BC n DE x y z ⎧⎧+=⋅=⎪⎪=+=+=∴⎨⎨⋅=⎪⎩⎪++=⎩令111272,5(2,7,5)yx z n =-∴==∴=-12cos ,n n ∴<>==,因此sin 13θ==.《第一章 空间向量与立体几何》单元检测试卷(三)一、单选题1.空间直角坐标中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB 与CD 的位置关系是( ) A .平行 B .垂直 C .相交但不垂直D .无法确定2.如图,在平行六面体中,为与的交点若,,,则下列向量中与相等的向量是( )111ABCD A B C D -M AC BD 11A B a =11A D b =1A A c =1B MA .B .C .D . 3.已知向量,.若向量与向量平行,则实数的值是( ) A .2B .C .10D .4.如图,已知正方体ABCD ﹣A'B'C'D'中,E 是CC'的中点,,,,x y z ,则( )A .x =1,y =2,z =3B .x ,y =1,z =1C .x =1,y =2,z =2D .x ,y =1,z5.正方体不在同一侧面上的两顶点,,则正方体外接球体积是( ) A .B .C .D .6.已知,若点D 是AC 中点,则( ) A .2B .C .-3D .67.平行六面体中,,则实数x ,y ,z 的值分别为( ) A . B .C .D .8.三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为( )1122a b c -++1122a b c ++1122a b c -+1122a b c --+()0,1,1a =()1,2,1b =-a b +()2,,4c m =--m2-10-1'2a AA =12b AB =13c AD =AE =a +b +c 12=12=32=(1,2,1)A--(1,0,1)B323π4π(1,2,3),OA =(2,2,1),OB =-(1,1,2)OC =BC OD ⋅=32-1111ABCD A B C D -12,AM MC =1AM xAB yAD zAA =++1,32,3232,31,3232,32,3132,31,223111ABC A B C -1160BAA CAA ︒∠=∠=1AB 1BCABCD .9.如图,在三棱柱中,底面,,,则与平面所成角的大小为A .B .C .D .10.在一直角坐标系中,已知,现沿轴将坐标平面折成的二面角,则折叠后两点间的距离为( )A .BCD .二、多选题11.已知点P 是平行四边形ABCD 所在的平面外一点,如果,,,下列结论正确的有( )A .B .C .是平面ABCD 的一个法向量D .12.在正方体中,,分别是和的中点,则下列结论正确的是( )6111ABC A B C -1AA ⊥ABC 13AA =2AB AC BC ===1AA 11AB C 3045︒60︒90︒(1,6),(3,8)A B --x 60︒,A B ()2,4,1AB =--()4,2,0AD =()1,2,1AP =--AP AB ⊥⊥AP AD AP //AP BD 1111ABCD A B C D -E F 11A D 11C DA .平面B .平面C .D .点与点到平面的距离相等 13.在正三棱柱中,所有棱长为1,又与交于点,则( )A .=B .C .三棱锥的体积为D .与平面BB′C′C 所成的角为三、填空题14.已知向量2,,x ,,且,则x 的值为______. 15.若向量,,且与的夹角为钝角,则实数的取值范围为________.16.如图所示,在正方体中,M 为棱的中点,则异面线与AM 所成角的余弦值为________.17.如图,四边形和均为正方形,它们所在的平面互相垂直,分别为的中点,则直线与平面所成角的正切值为________;异面直线与所成角的余弦值是________.11//A C CEF 1B D ⊥CEF 112DA DD C DC E =+-D 1B CEF ABC A B C '''-BC 'B C 'O AO 111222AB AC AA '++AO B C '⊥A BB O '-24AO π6(3,a =-5)(1,b =1)-8a b ⋅=(2,1,2)a =-(4,2,)b m =-a b m 1111ABCD A B C D -1CC 1BD ABCD ADPQ ,,M E F ,,PQ AB BC ME ABCD EMAF四、解答题18.如图,已知三棱锥的侧棱两两垂直,且,,是的中点.(1)求异面直线与所成角的余弦值; (2)求直线AE 和平面OBC 的所成角.19.如图,在长方体中,,,点、分别为、的中点.(1)证明:平面; (2)求二面角的余弦值.20.如下图所示,在四棱锥中,底面四边形,四边形是直角梯形,且,,点是棱的中点,是上的点,且.O ABC -OA OB OC ,,1OA =2OB OC ==EOC BEAC S OABC -SO ⊥OABC OABC 90COA OAB ∠=∠=︒1,4OA OS AB OC ====M SB N OC :1:3ON NC =(1)求异面直线与所成的角的余弦值; (2)求与平面所成的角的正弦值.21.如图,在正方体中,分别是的中点。
最新人教版高中数学选修一第一单元《空间向量与立体几何》测试题(含答案解析)
一、选择题1.在棱长为1的正方体1111ABCD A B C D -中,,M N 分别为111,BD B C 的中点,点P 在正方体的表面上运动,且满足MP CN ⊥,则下列说法正确的是( )A .点P 可以是棱1BB 的中点 B .线段MP 的最大值为32C .点P 的轨迹是正方形D .点P 轨迹的长度为2+52.如图,在三棱锥O ABC -中,点D 是棱AC 的中点,若OA a =,OB b =,OC c =,则BD 等于( )A .1122a b c -+ B .a b c +- C .a b c -+D .1122a b c -+- 3.在空间直角坐标系中,已知()1,2,3A ,()1,0,4B ,()3,0,5C ,()4,1,3D -,则直线AD 与BC 的位置关系是( ) A .平行B .垂直C .相交但不垂直D .无法判定4.如图,在四面体O ABC -中,1G 是ABC 的重心,G 是1OG 上的一点,且12OG GG =,若OG xOA yOB zOC =++,则(,,)x y z 为( )A .111(,, )222B .222(, , )333C .111(, , )333D .222(,, )9995.已知(),(3,0,1),(131,2,3,1),55a b c =-==--给出下列等式:①a b c a b c ++=--;②()()a b c a b c +⋅=⋅+;③2222()a b c b c a =++++ ④()()a b c a b c ⋅⋅=⋅⋅.其中正确的个数是 A .1个B .2个C .3个D .4个6.在底面为锐角三角形的直三棱柱111ABC A B C -中,D 是棱BC 的中点,记直线1B D 与直线AC 所成角为1θ,直线1B D 与平面111A B C 所成角为2θ,二面角111C A B D --的平面角为3θ,则( ) A .2123,θθθθ<<B .2123 ,θθθθ><C .2123 ,θθθθD .2123 ,θθθθ>>7.已知1e ,2e 是夹角为60的两个单位向量,则12a e e =+与122b e e =-的夹角是( ) A .60B .120C .30D .908.如图,平行六面体中1111ABCD A B C D -中,各条棱长均为1,共顶点A 的三条棱两两所成的角为60°,则对角线1BD 的长为( )A .1B .2C .3D .29.在空间直角坐标系O xyz -中,(0,0,0),(22,0,0),(0,22,0)O E F ,B 为EF 的中点,C 为空间一点且满足||||3CO CB ==,若1cos ,6EF BC <>=,,则OC OF ⋅=( ) A .9B .7C .5D .310.棱长为1的正四面体ABCD 中,点E ,F 分别是线段BC ,AD 上的点,且满足13BE BC =,14AF AD =,则AE CF ⋅=( )A .1324-B .12-C .12D .132411.如图所示,直三棱柱111ABC A B C -的侧棱长为3,底面边长11111A C B C ==,且11190A C B ∠=,D 点在棱1AA 上且12AD DA =,P 点在棱1C C 上,则1PD PB ⋅的最小值为( )A .52B .14-C .14D .52-12.已知在四面体ABCD 中,点M 是棱BC 上的点,且3BM MC =,点N 是棱AD 的中点,若MN x AB y AC z AD =++其中,,x y z 为实数,则x y z ++的值是( )A .12B .12-C .-2D .213.以下四个命题中正确的是( )A .空间的任何一个向量都可用其他三个向量表示B .若{},,a b c 为空间向量的一组基底,则{},,a b b c c a +++构成空间向量的另一组基底 C .ABC ∆为直角三角形的充要条件是0AB AC ⋅= D .任何三个不共线的向量都可构成空间向量的一个基底二、填空题14.三棱锥O ABC -中,OA 、OB 、OC 两两垂直,且OA OB OC ==.给出下列四个命题:①()()223OA OB OCOA ++=;②()0BC CA CO ⋅-=;③()OA OB +和CA 的夹角为60;④三棱锥O ABC -的体积为()16AB AC BC ⋅. 其中所有正确命题的序号为______________.15.在长方体1111ABCD A B C D -中,2AB =,11BC AA ==,则11D C 与平面11A BC 所成角的正弦值为______________.16.在空间直角坐标系中, ()()()2,1,1,3,4,,2,7,1,A B C AB CB 若λ-⊥,则λ=____ 17.ABC ∆的三个顶点分别是(1,1,2)A -,(5,6,2)B -,(1,3,1)C -,则AC 边上的高BD 长为__________.18.在空间直角坐标系O xyz -中,已知(1,0,2)A -,(0,1,1)B -,点,C D 分别在x 轴,y 轴上,且AD BC ⊥,那么CD →的最小值是______.19.已知向量()2,1,3a =-,31,,2b k ⎛⎫=-- ⎪⎝⎭,若向量a 、b 的夹角为钝角,则实数k 的取值范围是__________.20.如图,在空间四边形OABC 中,M ,N 分别为OA 、BC 的中点,点G 在线段MN 上,且3MG GN =,用向量OA 、OB 、OC 表示向量OG ,设OG x OA y OB z OC =⋅+⋅+⋅,则x 、y 、z 的和为______.21.若平面α,β的法向量分别为(4,0,3)u =,(1,1,0)v =-,则这两个平面所成的锐角的二面角的余弦值为________.22.已知(2,1,3)a →=-,(4,2,)b x →=-,(1,,2)c x →=-,若a b c →→→⎛⎫+⊥ ⎪⎝⎭,是x =________.23.如图,在平行六面体1111ABCD A B C D -中,以顶点A 为顶点的三条棱的长均为2,且两两所成角均为60°,则1||AC =__________.24.如图,在正四棱锥V ABCD -中,二面角V BC D --为60°,E 为BC 的中点.已知F 为直线VA 上一点,且F 与A 不重合,若异面直线BF 与VE 所成角为60°,则VFVA=_____________.25.如图,在三棱柱111ABC A B C -中,AB ,AC ,1AA 两两互相垂直,122AA AB AC ==,M ,N 是线段1BB ,1CC 上的点,平面AMN 与平面ABC 所成(锐)二面角为3π,当1B M 最小时,AMB ∠=__________.26.已知四棱柱111ABCD A BC D -的底面ABCD 是矩形,5AB =,3AD =,14AA =,1160BAA DAA ∠=∠=︒,则1AC =________.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】在正方体1111ABCD A B C D -中,以点D 为坐标原点,分别以DA 、DC 、1DD 方向为x 轴、y 轴、z 轴正方向,建立空间直角坐标系,根据MP CN ⊥,确定点P 的轨迹,在逐项判断,即可得出结果. 【详解】在正方体1111ABCD A B C D -中,以点D 为坐标原点,分别以DA 、DC 、1DD 方向为x 轴、y 轴、z 轴正方向,建立空间直角坐标系, 因为该正方体的棱长为1,,M N 分别为111,BD B C 的中点, 则()0,0,0D ,111,,222M ⎛⎫ ⎪⎝⎭,1,1,12N ⎛⎫⎪⎝⎭,()0,1,0C , 所以1,0,12CN ⎛⎫= ⎪⎝⎭,设(),,P x y z ,则111,,222MP x y z ⎛⎫=--- ⎪⎝⎭,因为MP CN ⊥, 所以1110222x z ⎛⎫-+-= ⎪⎝⎭,2430x z +-=,当1x =时,14z =;当0x =时,34z =; 取11,0,4E ⎛⎫ ⎪⎝⎭,11,1,4F ⎛⎫ ⎪⎝⎭,30,1,4G ⎛⎫ ⎪⎝⎭,30,0,4H ⎛⎫ ⎪⎝⎭,连接EF ,FG ,GH ,HE ,则()0,1,0EF GH ==,11,0,2EH FG ⎛⎫==- ⎪⎝⎭, 所以四边形EFGH 为矩形,则0EF CN ⋅=,0EH CN ⋅=,即EF CN ⊥,EH CN ⊥, 又EFEH E =,且EF ⊂平面EFGH ,EH ⊂平面EFGH ,所以CN ⊥平面EFGH , 又111,,224EM ⎛⎫=-⎪⎝⎭,111,,224MG ⎛⎫=- ⎪⎝⎭,所以M 为EG 中点,则M ∈平面EFGH ,所以,为使MP CN ⊥,必有点P ∈平面EFGH ,又点P 在正方体的表面上运动, 所以点P 的轨迹为四边形EFGH , 因此点P 不可能是棱1BB 的中点,即A 错; 又1EF GH ==,5EH FG ==,所以EF EH ≠,则点P 的轨迹不是正方形;且矩形EFGH 的周长为2222+⨯=+C 错,D 正确; 因为点M 为EG 中点,则点M 为矩形EFGH 的对角线交点,所以点M 到点E 和点G的距离相等,且最大,所以线段MP ,故B 错. 故选:D. 【点睛】关键点点睛:求解本题的关键在于建立适当的空间直角坐标系,利用空间向量的方法,由MP CN ⊥,求出动点轨迹图形,即可求解.2.A解析:A 【分析】利用空间向量的加法和减法法则可得出BD 关于a 、b 、c 的表达式. 【详解】()11112222OD OA AD OA AC OA OC OA OA OC =+=+=+-=+, 因此,11112222BD OD OB OA OB OC a b c =-=-+=-+. 故选:A. 【点睛】本题考查利用基底表示空间向量,考查计算能力,属于中等题.3.B解析:B 【分析】根据题意,求得向量AD 和BC 的坐标,再结合空间向量的数量积的运算,即可得到两直线的位置关系,得到答案. 【详解】由题意,点()1,2,3A ,()1,0,4B ,()3,0,5C ,()4,1,3D -, 可得()3,1,6AD =--,()2,0,1BC =, 又由()()2310610AD BC ⋅=⨯+-⨯+-⨯=, 所以AD BC ⊥,所以直线AD 与BC 垂直. 故选:B . 【点睛】本题主要考查了空间向量的数量积的运算及其应用,其中解答中熟记空间向量的坐标运算,以及空间向量的数量积的运算是解答本题的关键,着重考查了推理与运算能力,属于基础题.4.D解析:D 【分析】根据空间向量线性运算进行计算,用,,OA OB OC 表示出OG . 【详解】因为E 是BC 中点,所以1()2OE OB OC =+, 1G 是ABC 的重心,则123AG AE =, 所以122()33AG AE OE OA ==-, 因为12OG GG = 所以112224()()3339OG OG OA AG OA OE OA ==+=+-2422222()9999999OA OE OA OB OC OA OB OC =+=++=++, 若OG xOA yOB zOC =++,则29x y z ===. 故选:D . 【点睛】本题考查空间的向量的线性运算,掌握向量线性运算的运算法则是解题关键.5.D解析:D 【详解】由题设可得197(,3,)55a b c ++=,则63525a b c ++== 923(,1,)55a b c --=-,63525a b c --=,则①正确;因1346()(4,2,2)(,1,)205555a b c +⋅=⋅--=-+-=, 1481424()(1,2,3)(,1,)205555a b c ⋅+=⋅-=+-=,故②正确;又因2635127()255a b c ++==,而22235714,10,255a b c ====, 所以22271272455a b c ++=+=,即③正确; 又3030a b ⋅=+-=,则()0a b c ⋅⋅=,而330055b c ⋅=-++=,故()0a b c ⋅⋅=,也即④正确. 故选:D .6.A解析:A 【分析】以A 为坐标原点,建立空间直角坐标系,写出点的坐标,分别求出直线的方向向量以及平面的法向量,通过向量法即可求得各个角度的余弦值,再结合余弦函数的单调性即可判断. 【详解】由题可知,直三棱柱111ABC A B C -的底面为锐角三角形,D 是棱BC 的中点, 设三棱柱111ABC A B C -是棱长为2的正三棱柱,以A 为原点,在平面ABC 中,过A 作AC 的垂线为x 轴,AC 为y 轴,1AA 为z 轴,建立空间直角坐标系,则1(0,0,2)A ,1(3,1,2)B ,(0,2,0)C ,33,02D ⎫⎪⎪⎝⎭,(0,0,0)A , (0,2,0)AC =,131,22B D ⎛⎫=- ⎪ ⎪⎝⎭,11(3,1,0)A B =,因为直线1B D 与直线AC 所成的角为1θ,10,2πθ⎛⎤∈ ⎥⎝⎦,111||cos ||||25θ⋅∴==⋅B D AC B D AC ,因为直线1B D 与平面111A B C 所成的角为2θ,20,2πθ⎡⎤∈⎢⎥⎣⎦, 平面111A B C 的法向量()0,0,1n =,121||sin ||5∣θ⋅∴==⋅B D n B D n ,222cos 155θ⎛⎫∴=-= ⎪⎝⎭,设平面11A B D 的法向量(,,)m a b c =,则11130312022m A Ba b m B D a b c ⎧⋅=+=⎪⎨⋅=-+-=⎪⎩, 取a =33,3,2m ⎛⎫=--⎪⎝⎭, 因为二面角111C A B D --的平面角为3θ, 由图可知,其为锐角,33||2cos ||57m n m n θ⋅∴===⋅∣,231cos cos cos θθθ>>, 由于cos y θ=在区间(0,)π上单调递减,故231θθθ<<, 则2123,θθθθ<<. 故选:A . 【点睛】本题考查利用向量法研究空间中的线面角以及二面角,属综合基础题.7.B解析:B 【分析】利用平面向量的数量积公式先求解a b ⋅,再计算a 与b ,根据数量积夹角公式,即可求解. 【详解】由题意得:()()12122a b e e e e ⋅=+⋅-221122132111222e e e e =-⋅-=-⨯⨯-=-,2222121122()21a e e e e e e a ==+=++==⋅2222112122(2)4?41b b e e e e e e ==-=+-=-=设,a b 夹角为312,cos ,018032a b a bθθθ-⋅===-︒≤≤︒⋅,∴120θ=.故选:B. 【点睛】本题考查利用平面向量的数量积计算向量的夹角问题,难度一般,准确运用向量的数量积公式即可.8.B解析:B 【分析】在平行六面体中1111ABCD A B C D -中,利用空间向量的加法运算得到11BD BA BB BC =++,再根据模的求法,结合各条棱长均为1,共顶点A 的三条棱两两所成的角为60°,由()()2211BD BA BB BC=++222111222BA BB BC BA BB BC BA BB BC =+++⋅+⋅+⋅求解.【详解】在平行六面体中1111ABCD A B C D -中,因为各条棱长均为1,共顶点A 的三条棱两两所成的角为60°,所以111111cos120,11cos6022BA BB BA BC BC BB ⋅=⋅=⨯⨯=-⋅=⨯⨯=, 所以11BD BA BB BC =++, 所以()()2211BD BA BB BC =++,222111222BA BB BC BA BB BC BA BB BC =+++⋅+⋅+⋅,113+22+2222⎛⎫=⨯-⨯⨯= ⎪⎝⎭,所以12BD =故选:B 【点睛】本题主要考查空间向量的运算以及向量模的求法,还考查了运算求解的能力,属于中档题.9.D解析:D 【分析】利用中点坐标公式可得点B 的坐标,设(,,)C x y z ,利用||||3CO CB ==,1cos ,6EF BC <>=可解出点C 的纵坐标,最后利用数量积的坐标运算可得OC OF ⋅的值. 【详解】设(,,)C x y z ,(2,2,0)B ,(,,)OC x y z =,()BC x y z =,(EF =-,由(()1cos ,436EF BC x y z EF BC EF BC⋅-⋅-===⋅⋅,整理可得:2x y -=-,由||||3CO CB ==化简得x y +=以上方程组联立得x y =,则()(,,)3OC OF x y z =⋅==. 故选:D. 【点睛】本题主要考查了空间直角坐标系下向量数量积的运算,解题关键是掌握向量数量积运算的基础知识,考查了分析能力和计算能力,属于中档题.10.A解析:A 【分析】设AB a =,AC b =,AD c =,以这3个向量为空间中的基底,将AE CF ⋅转化为基底的数量积运算,即可得答案. 【详解】设AB a =,AC b =,AD c =, 由题意可得121()333AE AB BE a b a a b =+=+-=+,14CF c b =-, 则211334AE CF a b c b ⎛⎫⎛⎫⋅=+⋅- ⎪ ⎪⎝⎭⎝⎭2121163123a c a b b c b =⋅-⋅+⋅- 11211111316232122324=⨯-⨯+⨯-⨯=-. 故选:A. 【点睛】本题考查空间向量基本定理的运用、数量积运算,考查空间想象能力和运算求解能力,求解时注意基底思想的运用.11.B解析:B 【分析】由题易知1,,AC BC CC 两两垂直,以C 为坐标原点,建立如图所示的空间直角坐标系,设()03PC a a =≤≤,可知()0,0,P a ,进而可得1,PD PB 的坐标,然后求得1PD PB ⋅的表达式,求出最小值即可.由题意可知,1,,AC BC CC 两两垂直,以C 为坐标原点,建立如图所示的空间直角坐标系,则()10,1,3B ,()1,0,2D ,设()03PC a a =≤≤,则()0,0,P a , 所以()1,0,2P a D =-,()10,1,3a PB =-,则()()2151002324a a a PD PB ⎛⎫=++--=-- ⎪⎝⋅⎭, 当52a =时,1PD PB ⋅取得最小值14-. 故选:B.【点睛】本题考查两个向量的数量积的应用,考查向量的坐标运算,考查学生的计算求解能力,属于中档题.12.B解析:B 【分析】利用向量运算得到131442MN AB AC AD =--+得到答案. 【详解】()3113142442MN MB BA AN AB AC AB AD AB AC AD =++=--+=--+ 故12x y z ++=- 故选:B 【点睛】本题考查了空间向量的运算,意在考查学生的计算能力.13.B解析:B根据空间向量基底的定义:任何三个不共面的向量都可构成空间向量的一组基底,逐一分析A ,B ,D 可判断这三个结论的正误;根据向量垂直的充要条件,及直角三角形的几何特征,可判断C 的真假. 【详解】对A ,空间的任何一个向量都可用其他三个不共面的向量表示,A 中忽略三个基底不共面的限制,故A 错误;对B ,若{},,a b c 为空间向量的一组基底,则,,a b c 三个向量互不共面;则,,a b b c c a +++,也互不共面,故{,,}a b b c c a +++可又构成空间向量的一组基底,故B 正确;对C ,0AB AC ABC ⋅=⇔∆的A ∠为直角ABC ⇒∆为直角三角形,但ABC ∆为直角三角形时,A ∠可能为锐角,此时0AB AC ⋅>,故C 错误;对D ,任何三个不共面的向量都可构成空间向量的一组基底,三个向量不共线时可能共面,故D 错误; 故选:B . 【点睛】本题以命题的真假判断为载体考查空间向量的基底概念、向量垂直的充要条件,考查对概念的理解与应用,属基础题.二、填空题14.①②③【分析】设以点为坐标原点所在直线分别为轴建立空间直角坐标系利用空间向量数量积的坐标运算可判断①②③④的正误【详解】设由于两两垂直以点为坐标原点所在直线分别为轴建立空间直角坐标系如下图所示:则对解析:①②③ 【分析】设OA OB OC a ===,以点O 为坐标原点,OA 、OB 、OC 所在直线分别为x 、y 、z 轴建立空间直角坐标系,利用空间向量数量积的坐标运算可判断①②③④的正误.【详解】设OA OB OC a ===,由于OA 、OB 、OC 两两垂直,以点O 为坐标原点,OA 、OB 、OC 所在直线分别为x 、y 、z 轴建立空间直角坐标系, 如下图所示:则()0,0,0O、(),0,0A a 、()0,,0B a 、()0,0,C a .对于①,(),,OA OB OC a a a ++=,所以,()()22233OA OB OC a OA ++==,①正确;对于②,(),0,0CA CO OA a -==,()0,,BC a a =-,则()0BC CA CO ⋅-=,②正确;对于③,(),,0OA OB a a +=,(),0,CA a a =-,()()221cos ,22OA OB CA a OA OB CA OA OB CAa+⋅<+>===+⋅, 0,180OA OB CA ≤<+>≤,所以,()OA OB +和CA 的夹角为60,③正确;对于④,(),,0AB a a =-,(),0,AC a a =-,()0,,BC a a =-,则2AB AC a ⋅=,所以,()223122666a a AB AC BC BC a ⋅===,而三棱锥O ABC -的体积为3111326V OA OB OC a =⨯⋅⋅=,④错误. 故答案为:①②③. 【点睛】关键点点睛:在立体几何中计算空间向量的相关问题,可以选择合适的点与直线建立空间直角坐标系,利用空间向量的坐标运算即可.15.【详解】如图建立空间直角坐标系则所以设平面的一个法向量为由题可得令可得设与平面所成角为则故直线与平面所成角的正弦值为故答案为:解析:13【详解】如图,建立空间直角坐标系D xyz -,则1(0,0,1)D ,1(0,2,1)C ,1(1,0,1)A ,(1,2,0)B ,所以11(0,2,0)DC =,设平面11A BC 的一个法向量为(,,)n x y z =, 由题可得111(,,)(1,2,0)20(,,)(0,2,1)20n AC x y z x y n A B x y z y z ⎧⋅=⋅-=-+=⎪⎨⋅=⋅-=-=⎪⎩,令1y =,可得(2,1,2)n =, 设11D C 与平面11A BC 所成角为θ, 则11111121sin cos ,233D C n D C n D C nθ⋅====⨯⋅, 故直线11D C 与平面11A BC 所成角的正弦值为13. 故答案为:13.16.【分析】利用空间向量的结论将垂直的问题转化为向量数量积等于零的问题然后利用向量的数量积坐标运算计算的值即可【详解】又即解得故答案为【点睛】本题主要考查空间向量的应用向量垂直的充分必要条件等知识意在考 解析:3±【分析】利用空间向量的结论将垂直的问题转化为向量数量积等于零的问题,然后利用向量的数量积坐标运算计算λ的值即可. 【详解】()()()2,1,1,3,4,,2,7,1A B C λ-, ∴AB ()1,3,1,λ=+CB ()1,3,1λ=--,又,AB CB ⊥0AB CB ∴⋅=,即()()()1133110λλ⨯+⨯-++-=,解得3λ=±, 故答案为3±. 【点睛】本题主要考查空间向量的应用,向量垂直的充分必要条件等知识,意在考查学生的转化能力和计算求解能力.17.5【解析】分析:设则的坐标利用求得即可得到即可求解的长度详解:设则所以因为所以解得所以所以点睛:(1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加减或数乘运算(2)解析:5 【解析】分析:设AD AC λ=,则,OD BD 的坐标,利用BD AC ⊥,求得45λ=-,即可得到 912(4,,)55BD =-,即可求解BD 的长度. 详解:设AD λAC =,则()()()OD OA λAC 1,1,2λ0,4,31,14λ,23λ=+=-+-=-+-,所以()BD OD OB 4,54λ,3λ=-=-+-,因为BD AC ⊥, 所以()BD AC 0454λ9λ0⋅=+++=,解得4λ5=-, 所以912BD 4,,55⎛⎫=- ⎪⎝⎭,所以(22912BD 5⎫⎛⎫=-=.点睛:(1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算.(2)用向量基本定理解决问题的一般思路是:先选择一组基底,并运用该基底将条件和结论表示成向量的形式,再通过向量的运算来解决.18.【分析】设0则由知所以由此能求出其最小值【详解】设001-即(当时取最小值)故答案为:【点睛】方法点睛:求最值常用的方法有:(1)函数法;(2)数形结合法;(3)导数法;(4)基本不等式法要根据已知【分析】设(C x ,0,0),(0D ,y ,0),则(1,,2)AD y →=-,(,1,1)BC x →=-,由20AD BC x y →→=--=,知2x y =+.所以||CD →【详解】设(C x ,0,0),(0D ,y ,0), (1A -,0,2),(0B ,1,-1),∴(1,,2)AD y →=-,(,1,1)BC x →=-,AD BC ⊥,∴20AD BC x y →→=--=,即2x y =+.(,,0)CD x y →=-,∴||CD →=2.(当1y =-时取最小值)【点睛】方法点睛:求最值常用的方法有:(1)函数法;(2)数形结合法;(3)导数法;(4)基本不等式法.要根据已知条件灵活选择方法求解.19.【分析】根据向量夹角为钝角可知且解不等式可求得结果【详解】由题意可知:且解得:且即本题正确结果:【点睛】本题考查向量夹角的相关问题的求解易错点是忽略夹角为的情况造成出现增根解析:1311,,222⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭【分析】根据向量夹角为钝角,可知cos ,0a b <><且cos ,1a b <>≠-,解不等式可求得结果. 【详解】 由题意可知:132cos ,014k a b a b a b--⋅<>==<⋅且13cos ,1ka b --<>=≠-解得:132k >-且12k ≠,即1311,,222k ⎛⎫⎛⎫∈-+∞ ⎪ ⎪⎝⎭⎝⎭本题正确结果:1311,,222⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭【点睛】本题考查向量夹角的相关问题的求解,易错点是忽略夹角为π的情况,造成出现增根.20.【分析】利用向量的加法公式得出再由得出的值即可得出的和【详解】即故答案为:【点睛】本题主要考查了用空间基底表示向量属于中档题解析:78【分析】利用向量的加法公式得出111222MN OA OB OC =-++,再由1324OG OM MG OA MN =+=+,得出,,x y z 的值,即可得出,,x y z 的和.【详解】MN MA AB BN =++11111()22222OA OB OA OC OB OA OB OC =+-+-=-++ 13131112424222OG OM MG OA MN OA OA OB OC ⎛⎫∴=+=+=+-++ ⎪⎝⎭813388OA OB OC =++ 133,,888x y z ∴===即78x y z ++= 故答案为:78【点睛】本题主要考查了用空间基底表示向量,属于中档题.21.【分析】直接利用空间向量的数量积求解两个平面的二面角的大小即可【详解】解:两个平面的法向量分别为则这两个平面所成的锐二面角的大小是这两个平面所成的锐二面角的余弦值为故答案为:【点睛】本题考查空间二面【分析】直接利用空间向量的数量积求解两个平面的二面角的大小即可. 【详解】解:两个平面α,β的法向量分别为(4,0,3)u →=,(1,1,0)v →=-, 则这两个平面所成的锐二面角的大小是θ,2cos a ba bθ→→→→===这两个平面所成的锐二面角的余弦值为5.故答案为:5. 【点睛】本题考查空间二面角的求法,空间向量的数量积的应用,考查计算能力.22.-4【分析】由题可知可得运用向量数量积的坐标运算即可求出【详解】解:根据题意得解得:故答案为:【点睛】本题考查空间向量垂直的数量积关系运用空间向量数量积的坐标运算考查计算能力解析:-4【分析】由题可知,a b c →→→⎛⎫+⊥ ⎪⎝⎭,可得0a b c →→→⎛⎫+= ⎪⎝⎭,运用向量数量积的坐标运算,即可求出x . 【详解】解:根据题意得, ()2,1,3a b x →→+=-+ a b c →→→⎛⎫+⊥ ⎪⎝⎭, ∴22(3)0a b c x x →→→⎛⎫+=--++= ⎪⎝⎭, 解得:4x =-.故答案为:4-.【点睛】本题考查空间向量垂直的数量积关系,运用空间向量数量积的坐标运算,考查计算能力. 23.【分析】设且利用数量积运算即得解【详解】设故答案为:【点睛】本题考查了空间向量的模长数量积运算考查了学生空间想象数学运算能力属于中档题 解析:【分析】设1,,AB a AD b AA c===,且1|||++|AC a b c =,利用数量积运算即得解. 【详解】设1,,||||||2,,,60o AB a AD b AA c a b c a b a c c b ===∴===<>=<>=<>=, 222221|||++|||||||22224AC a b c a b c a b a c c b ==+++⋅+⋅+⋅=||26AC ∴=故答案为:【点睛】本题考查了空间向量的模长,数量积运算,考查了学生空间想象,数学运算能力,属于中档题.24.11【分析】由题意建立空间直角坐标系由二面角的定义得出从而写出的坐标由向量共线的性质设利用向量的加法得出由异面直线与所成角利用向量法得出的值从而得出的值【详解】取的中点G 与的交点为以O 为坐标原点分别 解析:11【分析】由题意建立空间直角坐标系,由二面角的定义得出60OEV ∠=︒,从而写出,,,V E B A 的坐标,由向量共线的性质设(1)VF VA λλ=≠,利用向量的加法得出BF ,由异面直线BF 与VE 所成角,利用向量法得出λ的值,从而得出VF VA 的值. 【详解】 取AB 的中点G ,AC 与DB 的交点为O ,以O 为坐标原点,分别以,,OG OE OV 为,,x y z 轴的正方向,建立空间直角坐标系O xyz -,设2AB =因为二面角V BC D --为60°,所以60OEV ∠=︒则()()()()0,0,3,0,1,0,1,1,0,1,1,0V E B A -()()()1,1,3,1,1,3,0,1,3VA VB VE =--=-=-.设(1)VF VA λλ=≠,则()1,1,33BF VF VB λλλ=-=----+从而22||cos ,cos 60||||24(1)(1)BF VE BF VE BF VE λλ⋅===︒-++ 整理得210110λλ+-=,解得1λ=(舍),11λ=-故11VF VA=. 故答案为:11【点睛】本题主要考查了已知面面角,线线角求参数,属于中档题.25.【分析】根据题意建立空间直角坐标系设出的长写出各个点的坐标求得平面与平面的法向量利用法向量及二面角大小求得的等量关系即可判断当取最小时各自的长即可求得的正切值进而求得的大小【详解】因为三棱柱中两两互 解析:6π【分析】根据题意,建立空间直角坐标系,设出,CN BM 的长,写出各个点的坐标,求得平面AMN 与平面ABC 的法向量,利用法向量及二面角大小,求得,CN BM 的等量关系.即可判断当1B M 取最小时,CN BM 各自的长.即可求得AMB ∠的正切值,进而求得AMB ∠的大小.【详解】因为三棱柱111ABC A B C -中,AB ,AC ,1AA 两两互相垂直,建立如下图所示的空间直角坐标系:122AA AB AC ==,M ,N 是线段1BB ,1CC 上的点可设,,1BM a CN b AB ===,则12,1AA AB ==所以()()0,0,0,1,0,0A B ,()()1,0,,0,1,M a N b则()()1,0,,0,1,AM a AN b ==设平面AMN 的法向量为(),,m x y z =则00AM m AN m ⎧⋅=⎨⋅=⎩,代入可得00x az y bz +=⎧⎨+=⎩,令1z =代入解得x a y b =-⎧⎨=-⎩ 所以(),,1m a b =--平面ABC 的法向量()0,0,1n =由题意可知平面AMN 与平面ABC 所成(锐)二面角为3π 则由平面向量数量积定义可知22cos31m n m n a b π⋅==⋅++ 化简可得223a b += 1B M 最小值,即a 取得最大值,当0b =时,a 取得最大值为3a = 所以3tan 3AB AMB MB ∠=== 所以6AMB π∠=故答案为:6π 【点睛】本题考查了空间向量在立体几何中的应用,由法向量法结合二面角求值,属于中档题. 26.【分析】根据两边平方化简得到得到答案【详解】故故故答案为:【点睛】本题考查了空间向量的运算意在考查学生的计算能力【分析】根据11AC AB AD AA =++,两边平方化简得到182AC =.【详解】11AC AB AD AA =++ 故2222211111222AC AB AD AA AB AD AA AB AD AB AA AD AA =++=+++⋅+⋅+⋅ 222113452432458222=+++⨯⨯⨯+⨯⨯⨯=,故182AC =【点睛】本题考查了空间向量的运算,意在考查学生的计算能力.。
多选题009(立体几何与空间向量30道题+详细解析)
第9模块:立体几何与空间向量多选题(每题5分,选不全得3分,总计100分;建议完成后统计自己的正答率)1.如图,正方体1111ABCD A B C D -的棱长为1,则下列四个命题正确的是( )A .直线BC 与平面11ABC D 所成的角等于4πB .点C 到面11ABCD 的距离为22C .两条异面直线1D C 和1BC 所成的角为4π D .三棱柱1111AA D BB C -外接球半径为322.已知菱形ABCD 中,∠BAD =60°,AC 与BD 相交于点O .将△ABD 沿BD 折起,使顶点A 至点M ,在折起的过程中,下列结论正确的是( )A .BD ⊥CMB .存在一个位置,使△CDM 为等边三角形C .DM 与BC 不可能垂直D .直线DM 与平面BCD 所成的角的最大值为60°3.三棱锥P−ABC 的各顶点都在同一球面上,PC ⊥底面ABC ,若1PC AC ==,2AB =,且60BAC ∠=︒,则下列说法正确的是( )A .PAB ∆是钝角三角形B .此球的表面积等于5πC .BC ⊥平面P ACD .三棱锥A−PBC 的体积为324.沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm ,细沙全部在上部时,其高度为圆锥高度的23(细管长度忽略不计).假设该沙漏每秒钟漏下30.02cm 的沙,且细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.以下结论正确的是( )A .沙漏中的细沙体积为3102481cm π B .沙漏的体积是3128cm πC .细沙全部漏入下部后此锥形沙堆的高度约为2.4cmD .该沙漏的一个沙时大约是1985秒( 3.14π≈)5.如图,正方体1111ABCD A B C D -的棱长为1,动点E 在线段11A C 上,F 、M 分别是AD 、CD 的中点,则下列结论中正确的是( )A .11//FM ACB .BM ⊥平面1CC FC .存在点E ,使得平面//BEF 平面11CCD D D .三棱锥B CEF -的体积为定值6.在棱长为1的正方体1111ABCD A B C D -中,点M 在棱1CC 上,则下列结论正确的是( )A .直线BM 与平面11ADD A 平行B .平面1BMD 截正方体所得的截面为三角形C .异面直线1AD 与11A C 所成的角为3π D .1MB MD +的最小值为5 7.如图,在棱长均相等的四棱锥P ABCD -中, O 为底面正方形的中心, M ,N 分别为侧棱PA ,PB 的中点,有下列结论正确的有:( )A .PD ∥平面OMNB .平面PCD ∥平面OMNC .直线PD 与直线MN 所成角的大小为90 D .ON PB ⊥8.在正方体1111ABCD A B C D -中,N 为底面ABCD 的中心,P 为线段11A D 上的动点(不包括两个端点),M 为线段AP 的中点,则( )A .CM 与PN 是异面直线B .CM PN >C .平面PAN ⊥平面11BDD B D .过P ,A ,C 三点的正方体的截面一定是等腰梯形9.等腰直角三角形直角边长为1 ,现将该三角形绕其某一边旋转一周 ,则所形成的几何体的表面积可以为( )A .2πB .()12π+C .22πD .()22π+ 10.若将正方形ABCD 沿对角线BD 折成直二面角,则下列结论中正确的是( )A .异面直线AB 与CD 所成的角为60︒B .AC BD ⊥ C .ACD ∆是等边三角形 D .二面角A BC D --的平面角正切值是211.已知A ,B ,C 三点不共线,O 为平面ABC 外的任一点,则“点M 与点A ,B ,C 共面”的充分条件的是( )A .2OM OA OB OC =--B .OM OA OB OC =+- C .1123OM OA OB OC =++D .111236OM OA OB OC =++ 12.已知菱形ABCD 中,60BAD ∠=︒,AC 与BD 相交于点O ,将ABD △沿BD 折起,使顶点A 至点M ,在折起的过程中,下列结论正确的是( )A .BD CM ⊥B .存在一个位置,使CDM 为等边三角形C .DM 与BC 不可能垂直D .直线DM 与平面BCD 所成的角的最大值为60︒13.如图,一个结晶体的形状为平行六面体1111ABCD A B C D -,其中,以顶点A 为端点的三条棱长都相等,且它们彼此的夹角都是60°,下列说法中正确的是( )A .()()2212AA AB AD AC ++= B .()10AC AB AD ⋅-=C .向量1B C 与1AA 的夹角是60°D .1BD 与AC 所成角的余弦值为6 14.如图,正方形ABCD 中,EF 、分别是AB BC 、的中点将,,ADE CDF BEF ∆分别沿DE DF EF 、、折起,使、、A B C 重合于点P .则下列结论正确的是( )A .PD EF ⊥B .平面PDE PDF ⊥平面C .二面角P EFD --的余弦值为13 D .点P 在平面DEF 上的投影是DEF ∆的外心15.如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点,E F ,且12EF =,则下列结论中错误的是( )A .AC AF ⊥B .//EF 平面ABCDC .三棱锥A BEF -的体积为定值D .AEF ∆的面积与BEF 的面积相等16.下列命题中正确的是( ) A .,,,A B M N 是空间中的四点,若,,BA BM BN 不能构成空间基底,则,,,A B M N 共面B .已知{},,a b c 为空间的一个基底,若m a c =+,则{},,a b m 也是空间的基底C .若直线l 的方向向量为(1,0,3)e =,平面α的法向量为2(2,0,)3n =-,则直线//l αD .若直线l 的方向向量为(1,0,3)e =,平面α的法向量为(2,0,2)n =-,则直线l 与平面α所成角的正弦值为55 17.如图,在正方体1111ABCD A B C D -中,点P 在线段1B C 上运动,则 ( )A .直线1BD ⊥平面11AC DB .三棱锥11P ACD -的体积为定值C .异面直线AP 与1AD 所成角范围是[]45,90︒︒ D .直线1C P 与平面11AC D 所成角的正弦最大值为63 18.下列选项正确的为( )A .已知直线1l :()()2110a x a y ++--=,2l :()()12320a x a y -+++=,则12l l ⊥的充分不必要条件是1a =B .命题“若数列{}2n a 为等比数列,则数列{}n a 为等比数列”是假命题 C .棱长为a 正方体1111ABCD A B C D -中,平面11AC D 与平面1ACB 距离为33a D .已知P 为抛物线22y px =上任意一点且(),0M m ,若PM OM ≥恒成立,则(],m p ∈-∞19.在四面体P ABC -中,以上说法正确的有( )A .若1233AD AC AB =+,则可知3BC BD = B .若Q 为ABC ∆的重心,则111333PQ PA PB PC =++ C .若0PA BC ⋅=,0PC AB ⋅=,则0PB AC ⋅=D .若四面体P ABC -各棱长都为2,M ,N 分别为PA ,BC 的中点,则1MN =20.给出下列命题,其中正确命题有( )A .空间任意三个不共面的向量都可以作为一个基底B .已知向量//a b ,则,a b 与任何向量都不能构成空间的一个基底C .,,,A B M N 是空间四点,若,,BA BM BN 不能构成空间的一个基底,那么,,,A B M N 共面D .已知向量{},,a b c 组是空间的一个基底,若m a c =+,则{},,a b m 也是空间的一个基底21.正方体1111ABCD A B C D -的棱长为2,,,E F G 分别为11,,BC CC BB 的中点,则( )A .直线1D D 与直线AF 垂直B .直线1A G 与平面AEF 平行C .平面AEF 截正方体所得的截面面积为92D .点C 与点G 到平面AEF 的距离相等22.正方体1111ABCD A B C D -的棱长为1,,,E F G 分别为11,,BC CC BB 的中点.则( )A .直线1D D 与直线AF 垂直B .直线1A G 与平面AEF 平行C .平面AEF 截正方体所得的截面面积为98D .点C 和点G 到平面AEF 的距离相等 23.如图,梯形ABCD 中,//AD BC ,1AD AB ==,AD AB ⊥,45BCD ∠=︒,将ABD ∆沿对角线BD 折起.设折起后点A 的位置为A ',并且平面A BD '⊥平面BCD .给出下面四个命题正确的:()A .A D BC '⊥B .三棱锥A BCD '-的体积为22C .CD ⊥平面A BD ' D .平面A BC '⊥平面A DC ' 24.如图,PA 垂直于以AB 为直径的圆所在的平面,点C 是圆周上异于A ,B 的任一点,则下列结论中正确..的是( )A .PB AC ⊥ B .PC BC ⊥ C .AC ⊥平面PBCD .平面PAB ⊥平面PBC E.平面PAC ⊥平面PBC25.如图,矩形ABCD 中,M 为BC 的中点,将ABM 沿直线AM 翻折成1AB M ,连结1B D ,N 为1B D 的中点,则在翻折过程中,下列说法中所有正确的是( )A .存在某个位置,使得CN AB ⊥ B .翻折过程中,CN 的长是定值C .若AB BM =,则1AM BD ⊥D .若1AB BM ==,当三棱锥1B AMD -的体积最大时,三棱锥1B AMD -的外接球的表面积是4π 26.已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱11AA =,P 为上底面1111D C B A 上的动点,给出下列四个结论中正确结论为( )A .若3PD =,则满足条件的P 点有且只有一个B .若3PD =,则点P 的轨迹是一段圆弧C .若PD ∥平面1ACB ,则DP 长的最小值为2D .若PD ∥平面1ACB ,且3PD =,则平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π 27.如图,矩形ABCD ,M 为BC 的中点,将ABM ∆沿直线AM 翻折成1AB M ∆,连接1B D ,N 为1B D 的中点,则在翻折过程中,下列说法中所有正确的是( )A .存在某个位置,使得1CN AB ⊥;B .翻折过程中,CN 的长是定值;C .若AB BM =,则1AM BD ⊥;D .若1AB BM ==,当三棱锥1B AMD -的体积最大时,三棱锥1B AMD -的外接球的表面积是4π. 28.已知四棱锥P ABCD -,底面ABCD 为矩形,侧面PCD ⊥平面ABCD ,23BC =26CD PC PD ===.若点M 为PC 的中点,则下列说法正确的为( )A .BM ⊥平面PCDB .//PA 面MBDC .四棱锥M ABCD -外接球的表面积为36π D .四棱锥M ABCD -的体积为629.正方体1111ABCD A B C D -的棱长为2,已知平面1AC α⊥,则关于α截此正方体所得截面的判断正确的是( )A .截面形状可能为正三角形B .截面形状可能为正方形C .截面形状可能为正六访形D .截面面积最大值为3330.如图1,点E 为正方形ABCD 边BC 上异于点,B C 的动点,将ABE ∆沿AE 翻折,得到如图2所示-,且平面BAE⊥平面AECD,点F为线段BD上异于点,B D的动点,则在四棱锥的四棱锥B AECD-中,下列说法正确的有( )B AECDA.直线BE与直线CF必不在同一平面上B.存在点E使得直线BE⊥平面DCEC.存在点F使得直线CF与平面BAE平行D.存在点E使得直线BE与直线CD垂直第9模块:立体几何与空间向量 参考答案1.ABD 【解析】根据线面角的定义及求法,点面距的定义,异面直线所成角的定义及求法,三棱柱的外接球的半径求法,即可判断各选项的真假.【详解】正方体1111ABCD A B C D -的棱长为1,对于A ,直线BC 与平面11ABC D 所成的角为14CBC π∠=,故选项A 正确;对于B ,因为1B C ⊥面11ABC D ,点C 到面11ABC D 的距离为1B C 长度的一半,即22h =,故选项B 正确;对于C ,因为11//BC AD ,所以异面直线1D C 和1BC 所成的角为1AD C ∠,而1AD C 为等边三角形,故两条异面直线1D C 和1BC 所成的角为3π,故选项C 错误;对于D ,因为11111,,A A A B A D 两两垂直,所以三棱柱1111AA D BB C -外接球也是正方体1111ABCD A B C D -的外接球,故222111322r ++==,故选项D 正确.故选:ABD .【点睛】本题主要考查线面角的定义以及求法,点面距的定义以及求法,异面直线所成角的定义以及求法,三棱柱的外接球的半径求法的应用,属于基础题.2.ABD 【解析】【分析】画出图形,利用直线与直线的位置关系,直线与平面的位置关系判断选项的正误即可.【详解】对A ,菱形ABCD 中,60BAD ∠=︒,AC 与BD 相交于点O .将ABD ∆沿BD 折起,使顶点A 至点M ,如图:取BD 的中点E ,连接ME ,EC ,可知ME BD ⊥,EC BD ⊥,所以BD ⊥平面MCE ,可知MC BD ⊥,故A 正确;对B ,由题意可知AB BC CD DA BD ====,三棱锥是正四面体时,CDM ∆为等边三角形,故B 正确; 对C ,三棱锥是正四面体时,DM 与BC 垂直,故C 不正确;对D ,平面BDM 与平面BDC 垂直时,直线DM 与平面BCD 所成的角的最大值为60︒,故D 正确. 故选:ABD .【点睛】本题考查空间几何体的直线与直线、直线与平面的位置关系的综合判断、命题的真假的判断,考查转化与化归思想,考查空间想象能力.3.BC 【解析】【分析】根据余弦定理可得底面为直角三角形,计算出三棱锥的棱长即可判断A ,找到外接球的球心求出半径即可判断B ,根据线面垂直判定定理可判断C ,根据椎体的体积计算公式可判断D .【详解】如图,在底面三角形ABC 中,由1AC =,2AB =,60BAC ∠=︒,利用余弦定理可得:2211221232BC =+-⨯⨯⨯=∴222AC BC AB +=,即AC BC ⊥,由于PC ⊥底面ABC ,∴PC AC ⊥,PC BC ⊥,∵PC AC C =,∴BC ⊥平面P AC ,故C 正确;∴222PB PC BC AB =+==,由于2220PB AB PA +->,即PBA ∠为锐角,∴PAB ∆是顶角为锐角的等腰三角形,故A 错误;取D 为AB 中点,则D 为BAC 的外心,可得三角形ABC 外接圆的半径为1,设三棱锥P ABC -的外接球的球心为O ,连接OP ,则215122OP ⎛⎫=+= ⎪⎝⎭, 即三棱锥P ABC -的外接球的半径为52R =,∴三棱锥球的外接球的表面积等于2545ππ⨯=⎝⎭,故B 正确;11313132P ABC V -=⨯⨯=,故D 错误;故选:BC .【点睛】 本题主要考查了线面垂直的判定,椎体的体积计算以及三棱锥外接球体积的计算等等,属于中档题.4.ACD 【解析】【分析】A .根据圆锥的体积公式直接计算出细沙的体积;B .根据圆锥的体积公式直接计算出沙漏的体积;C .根据等体积法计算出沙堆的高度;D .根据细沙体积以及沙时定义计算出沙时.【详解】A .根据圆锥的截面图可知:细沙在上部时,细沙的底面半径与圆锥的底面半径之比等于细沙的高与圆锥的高之比,所以细沙的底面半径28433r cm =⨯=,所以体积23121641610243339381h V r cm πππ=⋅⋅=⋅⋅=; B .沙漏的体积2231125622483233h V h cm πππ⎛⎫=⨯⨯⨯⨯=⨯⨯⨯⨯= ⎪⎝⎭; C .设细沙流入下部后的高度为1h ,根据细沙体积不变可知:21102418132h h ππ⎛⎫⎛⎫=⨯⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭, 所以1102416813h ππ=,所以1 2.4h cm ≈;D .因为细沙的体积为3102481cm π,沙漏每秒钟漏下30.02cm 的沙, 所以一个沙时为:10241024 3.14815019850.0281π⨯=⨯≈秒.故选:ACD.【点睛】本题考查圆锥体积有关的计算,涉及到新定义的问题,难度一般.解题的关键是对于圆锥这个几何体要有清晰的认识,同时要熟练掌握圆锥体积有关的计算公式. 5.ABD 【解析】【分析】对A,根据中位线的性质判定即可.对B,利用平面几何方法证明BM CF ⊥再证明BM ⊥平面1CC F 即可.对C,根据BF 与平面11CC D D 有交点判定即可.对D,根据三棱锥B CEF -以BCF 为底,且同底高不变,故体积不变判定即可.【详解】在A 中,因为,F M 分别是,AD CD 的中点,所以11////FM AC AC ,故A 正确;在B 中,因为tan 2BC BMC CM ∠==,tan 2CD CFD FD∠==,故BMC CFD ∠=∠, 故2BMC DCF CFD DCF π∠+∠=∠+∠=.故BM CF ⊥,又有1BM C C ⊥,所以BM ⊥平面1CC F ,故B 正确;在C 中,BF 与平面11CC D D 有交点,所以不存在点E ,使得平面//BEF 平面11CC D D ,故C 错误.在D 中,三棱锥B CEF -以面BCF 为底,则高是定值,所以三棱锥B CEF -的体积为定值,故D 正确.故选:ABD. 【点睛】本题主要考查了线面垂直平行的证明与判定,同时也考查了锥体体积等问题.属于中档题.6.ACD 【解析】【分析】根据线面平行,异面直线夹角,截面图形,线段最值的计算依次判断每个选项得到答案.【详解】如图所示:易知平面11//BCC B 平面11ADD A ,BM ⊂平面11BCC B ,故直线BM 与平面11ADD A 平行,A 正确;平面1BMD 截正方体所得的截面为1BMD N 为四边形,故B 错误;连接1BC ,1A B ,易知11//AD BC ,故异面直线1AD 与11A C 所成的角为11AC B ∠,1111A B AC BC ==,故113AC B π∠=,故C 正确;延长DC 到'B 使'1CB =,易知'BM B M =,故11'5MB MD D B +≥=,当M 为1CC 中点时等号成立,故D 正确;故选:ACD .【点睛】本题考查了异面直线夹角,截面图形,线面平行,最短距离,意在考查学生的空间想象能力和计算能力.7.ABD 【解析】【分析】选项A,利用线面平行的判定定理即可证明;选项B,先利用线面平行的判定定理证明CD ∥平面OMN ,再利用面面平行的判定定理即可证明;选项C ,平移直线,找到线面角,再计算;选项D,因为ON ∥PD ,所以只需证明PD ⊥PB ,利用勾股定理证明即可.【详解】选项A,连接BD ,显然O 为BD 的中点,又N 为PB 的中点,所以PD ∥ON,由线面平行的判定定理可得,PD ∥平面OMN ;选项B, 由M ,N 分别为侧棱PA ,PB 的中点,得MN ∥AB,又底面为正方形,所以MN ∥CD ,由线面平行的判定定理可得,CD ∥平面OMN,又选项A 得PD ∥平面OMN ,由面面平行的判定定理可得,平面PCD ∥平面OMN ;选项C,因为MN ∥CD ,所以∠ PDC 为直线PD 与直线MN 所成的角,又因为所有棱长都相等,所以∠ PDC=60,故直线PD 与直线MN 所成角的大小为60;选项D ,因底面为正方形,所以222AB AD BD +=,又所有棱长都相等,所以222PB PD BD +=,故PB PD ⊥,又PD ∥ON ,所以ON PB ⊥,故ABD 均正确.【点睛】解决平行关系基本问题的3个注意点(1)注意判定定理与性质定理中易忽视的条件,如线面平行的条件中线在面外易忽视.(2)结合题意构造或绘制图形,结合图形作出判断.(3)会举反例或用反证法推断命题是否正确.8.BCD 【解析】【分析】由,CN PM 交于点A 得共面,可判断A ,利用余弦定理把,CM PN 都用,AC AP 表示后可比较大小,证明AN 与平面11BDD B 后可得面面垂直,可判断C ,作出过P ,A ,C 三点的截面后可判断D .【详解】,,C N A 共线,即,CN PM 交于点A ,共面,因此,CM PN 共面,A 错误;记PAC θ∠=,则2222212cos cos 4PN AP AN AP AN AP AC AP AC θθ=+-⋅=+-⋅, 2222212cos cos 4CM AC AM AC AM AC AP AP AC θθ=+-⋅=+-⋅,又AP AC <, 22223()04CM PN AC AP -=->,22CM PN >,即CM PN >.B 正确; 由于正方体中,AN BD ⊥,1BB ⊥平面ABCD ,则1BB AN ⊥,1BB BD B ⋂=,可得AN ⊥平面11BB D D ,AN ⊂平面PAN ,从而可得平面PAN ⊥平面11BDD B ,C 正确;取11C D 中点K ,连接11,,KP KC AC ,易知11//PK A C ,又正方体中,11//AC AC ,∴//PK AC ,,PK AC 共面,PKCA 就是过P ,A ,C 三点的正方体的截面,它是等腰梯形.D 正确.故选:BCD.【点睛】本题考查共面,面面垂直,正方体的截面等问题,需根据各个知识点进行推理证明判断.难度较大.9.AB 【解析】【分析】分2种情况,一种是绕直角边,一种是绕斜边,分别求形成几何体的表面积.【详解】如果是绕直角边旋转,形成圆锥,圆锥底面半径为1,高为12, 所以所形成的几何体的表面积是)2212121S rl r πππππ=+=⨯⨯=.2,两个圆锥的母线都是直角三角形的直角边,母线长是1,所以写成的几何体的表面积222122S rl πππ=⨯=⨯⨯⨯=.综上可知形成几何体的表面积是()21π+或2π.故选:AB 【点睛】本题考查旋转体的表面积,意在考查空间想象能力和计算能力,属于基础题型. 10.ABCD 【解析】【分析】作出正方形ABCD 翻折后的立体几图形,再对选项进行逐个分析.【详解】如图所示,设正方形的边长为2,对A ,设三角形A 运动到'A ,连接AC 交BD 于O ,连'AA ,因为2'2'2AA AO AO =+=,所以'AA B ∆为正三角形,所以 异面直线AB 与CD 所成的角为60︒,故A 正确; 对B ,因为,,BD AO BD CO AO BO O ⊥⊥⋂=,所以BD ⊥平面AOC ,AC ⊂平面AOC ,所以AC BD ⊥,故B 正确;对C ,由A 选项的证明,同理可得2AC AD CD ===,所以可推理得ACD ∆是等边三角形,故C 正确;对D ,取BC 的中点M ,连接AM ,OM ,AB AD =,O 为BD 的中点,AO BD ∴⊥, 平面ABD ⊥平面BCD ,平面ABD ⋂平面BCD BD =,AO ⊂平面ABD ,AO ∴⊥平面BCD ,BC ⊂平面BCD ,AO BC ∴⊥,OM BC ⊥,AO OM O =,BC ∴⊥平面AOM ,AM ⊂平面AOM ,AM BC ∴⊥,所以AMO ∠为二面角A BC D --的平面角,所以2tan 21AO AMO OM ∠===,故D 正确;故选:ABCD .【点睛】本题考查空间中图形的翻折问题、线面、面面位置关系、异面直线所成角、二面角等知识,考查转化与化归思想,考查空间想象能力和运算求解能力,求解时注意翻折前后的不变量.11.BD 【解析】【分析】根据“OM xOA yOB zOC =++时,若1x y z ++=则点M 与点,,A B C 共面”,分别判断各选项是否为充分条件.【详解】当MA mMB nMC =+时,可知点M 与点,,A B C 共面,所以()()MO OA m MO OB n MO OC +=+++,所以()1x y OM OA xOB yOC +-=-++,所以11111OA mOB nOC m n OM OA OB OC m n m n m n m n -++==-+++-+-+-+-, 不妨令11x m n -=+-,1m y m n =+-,1n z m n =+-,且此时1x y z ++=, 因为()()21101+-+-=≠,()1111++-=,111111236++=≠,1111236++=,由上可知:BD 满足要求. 故选:BD.【点睛】本题考查利用空间向量证明空间中的四点共面,难度一般.常见的证明空间中四点,,,M A B C 共面的方法有:(1)证明MA xMB yMC =+;(2)对于空间中任意一点O ,证明OM OA xMB yMC =++;(3) 对于空间中任意一点O ,证明()1OM xOA yOB zOC x y z =++++=. 12.ABD 【解析】【分析】根据线面垂直的判定定理与性质可判断A 选项;设菱形ABCD 的边长为2,根据题意,当CDM 为等边三角形时,求得二面角M BD C --存在,即可判断B 选项;用向量的方法计算DM BC ⋅,判定其能否为0,即可判断C 选项;根据线面角的概念,找到线面角的最大值,即可判断D 选项.【详解】A 选项,因为菱形ABCD 中,AC 与BD 相交于点O ,所以AO BD ⊥,CO BD ⊥;将ABD △沿BD 折起,使顶点A 至点M ,折起过程中,AO 始终与BD 垂直,因此MO BD ⊥,又MO CO ,由线面垂直的判定定理,可得:BD ⊥平面CMO ,因此BD CM ⊥,故A 正确;B 选项,因为折起的过程中,AD 边长度不变,因此MD CD =;若CDM 为等边三角形,则CM CD =;设菱形ABCD 的边长为2,因为60BAD ∠=︒,则sin 603AO AB =⋅=,即3AO MO ==,又2CM CD ==,所以3341cos 233MOC +-∠==⨯,即二面角M BD C --的余弦值为13时,CDM 为等边三角形;故B 正确; C 选项,DM OM OD =-,BC OC OB =-,由A 选项知,MO BD ⊥,CO BD ⊥,所以0OM OB OD OC ⋅=⋅=,因此()()+DM BC OM OD OC OB OM OC OD OB ⋅=-⋅-=⋅⋅,同B 选项,设菱形ABCD 的边长为2,易得3OC OM ==,1OB OD ==,所以3cos 1DM BC MOC ⋅=∠+,显然当1cos 3MOC ∠=-时,0DM BC ⋅=,即DM BC ⊥;故C 错误; D 选项,同BC 选项,设菱形ABCD 的边长为2,则3OM =,1OD =,2MD =,由几何体直观图可知,当OM ⊥平面BCD ,直线DM 与平面BCD 所成的角最大,为MDO ∠,易知60MDO ∠=︒.故选:ABD. 【点睛】本题主要考查立体几何的综合应用,熟记线面垂直的判定定理,线面角的概念,灵活运用向量的方法判定即可,属于常考题型.13.AB 【解析】【分析】直接用空间向量的基本定理,向量的运算对每一个选项进行逐一判断.【详解】以顶点A 为端点的三条棱长都相等, 它们彼此的夹角都是60°,可设棱长为1,则11111cos602AA AB AA AD AD AB ⋅=⋅=⋅=⨯⨯︒=()22221111=+2+2+2AA AB AD AA AB AD AA AB AB AD AA AD ++++⋅⋅⋅ 11113262=+++⨯⨯= 而()()()22222222AC AB AD AB AD AB AD =+=++⋅ 121122362⎛⎫=++⨯=⨯= ⎪⎝⎭, 所以A 正确.()()()11AC AB AD AA AB AD AB AD ⋅-⋅=++- 2211AA AB AA AD AB AB AD AD AB AD =⋅-⋅+-⋅+⋅- =0,所以B 正确.向量11B C A D =,显然1AA D △ 为等边三角形,则160AA D ∠=︒.所以向量1A D 与1AA 的夹角是120︒ ,向量1B C 与1AA 的夹角是120︒,则C 不正确又11=AD AA BD AB +-,AC AB AD =+ 则()211||=2AD AA A B B D =+-,()2||=3AC AB AD =+()()111AD AA AB BD AC AB AD ⋅=+-=+⋅ 所以11116cos ===6||||23BD AC BD AC BD AC ⋅⋅⨯,,所以D 不正确.故选:AB 【点睛】本题考查空间向量的运算,用向量求夹角等,属于中档题.14.ABC 【解析】【分析】对于A 选项,只需取EF 中点H ,证明EF ⊥平面PDH ;对于B 选项,知,,PE PF PD 三线两两垂直,可知正确;对于C 选项,通过余弦定理计算可判断;对于D 选项,由于PE PF PD =≠,可判断正误.【详解】对于A 选项,作出图形,取EF 中点H ,连接PH ,DH ,又原图知BEF ∆和DEF ∆为等腰三角形,故PH EF ⊥,DH EF ⊥,所以EF ⊥平面PDH ,所以PD EF ⊥,故A 正确;根据折起前后,可知,,PE PF PD 三线两两垂直,于是可证平面PDE PDF ⊥平面,故B 正确;根据A 选项可知 PHD ∠为二面角P EF D --的平面角,设正方形边长为2,因此1PE PF ==,22PH =,2322222DH =-=,222PD DF PF =-=,由余弦定理得:2221cos 23PH HD PD PHD PH HD +-∠==⋅,故C 正确;由于PE PF PD =≠,故点P 在平面DEF 上的投影不是DEF ∆的外心,即D 错误;故答案为ABC.【点睛】本题主要考查异面直线垂直,面面垂直,二面角的计算,投影等相关概念,综合性强,意在考查学生的分析能力,计算能力及空间想象能力,难度较大.15.AD 【解析】【分析】通过特殊化,点F 与点1B 重合可判定A 错误;正方体1111ABCD A B C D -的两个底面平行,判定B 正确,三角形BEF 的面积是定值,A 点到面11DD B B 距离是定值,可判定C 正确,△AEF 的面积与△BEF 的面积相等不正确,可判定D 错误.【详解】A .由题意及图形知,当点F 与点1B 重合时,160o CAB ∠=故选项A 错误;B .//EF 平面ABCD ,由正方体1111ABCD A B C D -的两个底面平行,EF ⊂平面1111D C B A ,故有//EF 平面ABCD ,此命题正确,不是正确选项;C .三棱锥A-BEF 的体积为定值,由几何体的性质及图形知,三角形BEF 的面积是定值,A 点到面11DD B B 距离是定值,故可得三棱锥A-BEF 的体积为定值,此命题正确,不是正确选项;D .由图形可以看出,B 到线段EF 的距离与A 到EF 的距离不相等,故△AEF 的面积与△BEF 的面积相等不正确,故D 是错误的.故选:AD 【点睛】本题考查直线与平面平行、垂直的判定、棱锥的体积,考查空间想象能力与运算求解能力,属于中档题.16.ABD 【解析】【分析】不共面的三个非零向量可以构成空间向量的一个基底,由此可判断A 、B ,若直线的方向向量与平面α的法向量垂直,则线面平行,可判断C ,直线的方向向量与平面的法向量夹角的余弦值的绝对值与该直线与此平面所成角的正弦值相等,由此可判断D .【详解】对于A ,,,,A B M N 是空间中的四点,若,,BA BM BN 不能构成空间基底,则,,BA BM BN 共面,则,,,A B M N 共面,故A 对;对于B ,已知{},,a b c 为空间的一个基底,则,,a b c 不共面,若m a c =+,则,,a b m 也不共面,则{},,a b m 也是空间的基底,故B 对;对于C ,因为21(2)+00+3=03e n ⋅=⨯-⨯⨯,则e n ⊥,若l α⊄,则//l α,但选项中没有条件l α⊄,有可能会出现l α⊂,故C 错;对于D ,∵cos ,e n e n e n ===,则则直线l 与平面α,故D 对;故选:ABD . 【点睛】本题主要考查命题的真假,考查空间基底的定义,考查空间向量在立体几何中的应用,属于中档题.17.ABD 【解析】【分析】利用线面垂直的性质判定可判定选项A,对三棱锥11P AC D -转化顶点可判定选项B,找到异面成角的最小值的情况即可判断选项C,转化直线1C P 与平面11AC D 所成角的正弦值的最大值为直线1C P 与直线1BD 所成角的余弦值最大,进而判断选项D 【详解】对于选项A,连接11B D ,由正方体可得1111AC B D ⊥,且1BB ⊥平面1111D C B A ,则111BB A C ⊥,所以11A C ⊥平面11BD B ,故111AC BD ⊥;同理,连接1AD ,易证得11A D BD ⊥,则1BD ⊥平面11AC D ,故A 正确;对于选项B,1111P A C DC A PD V V --=,因为点P 在线段1B C 上运动,所以1112A DP S A D AB =⋅,面积为定值,且1C 到平面11A PD 的距离即为1C 到平面11A B CD 的距离,也为定值,故体积为定值,故B 正确;对于选项C,当点P 与线段1B C 的端点重合时,AP 与1A D 所成角取得最小值为60︒,故C 错误;对于选项D,因为直线1BD ⊥平面11AC D ,所以若直线1C P 与平面11AC D 所成角的正弦值最大,则直线1C P 与直线1BD 所成角的余弦值最大,则P 运动到1B C 中点处,即所成角为11C BD ∠,设棱长为1,在11Rt D C B中,111126cos 33C B C BD BD ∠===,故D 正确故选:ABD 【点睛】本题考查线面垂直的判定,考查异面成角,线面成角,考查棱锥体积,考查转化思想和空间想象能力18.ABCD 【解析】【分析】A .分析“1a =”与“12l l ⊥”的互相推出情况,由此确定是否为充分不必要条件;B .分析特殊情况:121,2,2a a n =-=≥时,2112,4n n n n a a a a ++==,由此判断命题真假;C .将面面距离转化为点到面的距离,从而可求出面面距离并判断对错;D .根据线段长度之间的关系列出不等式,从而可求解出m 的取值范围.【详解】A .当1a =时,11:3l x =,22:5l y =-,显然12l l ⊥; 当12l l ⊥时,()()()()211230a a a a +-+-+=,解得1a =±,所以12l l ⊥的充分不必要条件是1a =正确;B .当121,2,2a a n =-=≥时,2112,4n n n n a a a a ++==,所以此时{}2n a 为等比数列, 但{}n a 不是等比数列,所以命题是假命题,故正确;C .如图所示:由图可知:111111111//,//,,AC AC B C A D AC B C C AC A D A ==,所以平面1//AB C 平面11AC D ,所以平面11AC D 与平面1ACB 距离即为1B 到平面11AC D 的距离,记为h , 由等体积可知:)21312332a a a h a ⎫⨯⨯=⨯⨯⎪⎪⎝⎭,所以3h =,故正确;D .设()00,P x y ,因为PM OM ≥,所以()2200x m y m -+≥,所以()22200x m y m -+≥且2002y px =,所以200022x px mx +≥, 当00x =时显然符合,当00x >时02x m p ≤+,所以m p ≤,综上可知:(],m p ∈-∞.故正确.故选:ABCD. 【点睛】本题考查命题真假的判断,难度一般.(1)判断命题p 是命题q 的何种条件时,注意从两方面入手:充分性、必要性;(2)立体几何中求解点到平面的距离,采用等体积法较易.19.ABC 【解析】【分析】根据向量的线性运算与数量积一一判断即可.【详解】解:对于A ,1233AD AC AB =+,32AD AC AB ∴=+,22AD AB AC AD ∴-=- ,2BD DC ∴=,3BD BD DC ∴=+即3BD BC =,故A 正确;对于B ,若Q 为ABC ∆的重心,则0QA QB QC ++=,33PQ QA QB QC PQ ∴+++=3PQ PA PB PC ∴=++即111333PQ PA PB PC =++,故B 正确;对于C ,若0PA BC ⋅=,0PC AB ⋅=,则PA BC PC AB ⋅=⋅0PA BC PC AB ∴⋅+⋅=()0PA BC PC AC CB ∴⋅+⋅+=0PA BC PC AC PC CB ∴⋅+⋅+⋅=0PA BC PC AC PC BC ∴⋅+⋅-⋅=()0PA PC BC PC AC ∴-⋅+⋅= 0CA BC PC AC ∴⋅+⋅=0AC CB PC AC ∴⋅+⋅=()0AC CB PC ∴⋅+=0AC PB ∴⋅= 故C 正确; 对于D ,()()111222MN PN PM PB PC PA PB PC PA =-=+-=+- 12MN PA PB PC ∴=--222222PA PB PC PA PB PC PA PB PA PC PB PC --=++-⋅-⋅+⋅==4=2MN ∴=故D 错误.故选:ABC 【点睛】本题考查向量的线性运算,向量的数量积及利用向量的数量积求向量的模,属于中档题.20.ABCD 【解析】【分析】根据空间基底的概念,结合向量的共面定量,逐项判定,即可求解,得到答案.【详解】选项A 中,根据空间基底的概念,可得任意三个不共面的向量都可以作为一个空间基底,所以A 正确;选项B 中,根据空间基底的概念,可得B 正确;选项C 中,由,,BA BM BN 不能构成空间的一个基底,可得,,BA BM BN 共面,又由,,BA BM BN 过相同点B ,可得,,,A B M N 四点共面,所以C 正确;选项D 中:由{},,a b c 是空间的一个基底,则基向量,a b 与向量m a c =+一定不共面,所以可以构成空间另一个基底,所以D 正确.故选:ABCD.【点睛】本题主要考查了空间基底的概念及其判定,其中解答中熟记空间基底的概念,合理利用共面向量定量进行判定是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.21.BC 【解析】【分析】A .利用线面垂直的定义进行分析;B .作出辅助线利用面面平行判断;C .作出截面然后根据线段长度计算出截面的面积;D .通过等体积法进行判断.【详解】A .若1D D AF ⊥,又因为1D D AE⊥且AE AF A ⋂=,所以1DD ⊥平面AEF ,所以1DD EF ⊥,所以1CC EF ⊥,显然不成立,故结论错误; B .如图所示,取11B C 的中点Q ,连接1,A Q GQ ,。
人教版高二数学空间向量与立体几何练习(含答案)
人教版高二数学空间向量与立体几何练习(含答案)1.空间直角坐标系中,已知(1,2,3)A -,(3,2,5)B -,则线段AB 的中点坐标为( ) A.(1,2,4)--B.(2,0,1)-C.(2,0,2)-D.(2,0,1)-2.若向量(1,,0)λ=a ,(2,1,2)=-b ,且a 与b 的夹角的余弦值为23,则实数λ等于( ). A.0B.43-C.0或43-D.0或433.已知棱长为1的正方体1111ABCD A B C D -的上底面1111A B C D 的中心为1O ,则11AO AC ⋅的值为( ).A.-1B.0C.1D.24.已知(1,0,0)A ,(0,1,0)B ,(0,0,1)C ,则下列向量是平面ABC 的一个法向量的是( ) A.(1,1,1)- B.(1,1,1)- C.333,,333⎛⎫--- ⎪ ⎪⎝⎭D.333,,333⎛⎫- ⎪⎪⎝⎭5.如图,在三棱锥P ABC -中,ABC 为等边三角形,PAC 为等腰直角三角形,4PA PC ==,平面PAC ⊥平面ABC ,D 为AB 的中点,则异面直线AC 与PD 所成角的余弦值为( )A.142 3 D.126.如图,点P 为矩形ABCD 所在平面外一点,PA ⊥平面,ABCD Q 为线段AP 的中点,3,4,2AB BC PA ===,则点P 到平面BQD 的距离为( )A.513B.1213C.135D.13127.(多选)已知向量(1,1,)m =-a ,(2,1,2)m =--b ,则下列结论中正确的是( ) A.若||2=a ,则2m = B.若⊥a b ,则1m =- C.不存在实数λ,使得=a b D.若1⋅=-a b ,则(1,2,2)+=---a b8.(多选)已知正方体1111ABCD A B C D -的棱长为1,点E 、O 分别是11A B 、11A C 的中点,P 在正方体内部且满足1312423AP AB AD AA =++,则下列说法正确的是( ) A.点A 到直线BE 5 B.点O 到平面11ABC D 2 C.平面1A BD 与平面11B CD 3 D.点P 到直线AB 的距离为25369.已知(1,52) AB =-,,(3,1,)BC z =,若AB BC ⊥,(1,,3)BP x y =--,且BP ⊥平面ABC ,则x y +=___________.10.如图,在正四棱锥P ABCD -中,PA AB =,点M 为PA 的中点,BD BN λ=.若MN AD ⊥,则实数λ=__________.11.在棱长为2的正方体1111ABCD A B C D -中,M ,N 分别是111,A D CD 的中点,则直线MN 与平面ABCD 所成的角的余弦值为__________.12.如图,ABC △和BCD △都是边长为2的正三角形,且它们所在平面互相垂直.DE ⊥平面BCD ,且6AE =.(1)设P 是DE 的中点,求证://AP 平面BCD . (2)求二面角B AE C --的正弦值.答案以及解析1.答案:D解析:设中点坐标为(,,)x y z ,根据中点坐标公式得1322x +==,2202y -+==,3512z -==-.故选D. 2.答案:C解析:由题意得2202cos ,||31414λλ⋅-+〈〉===+⋅++a b a b a b ,解得0λ=或43λ=-.故选C. 3.答案:D解析:建立如图所示的空间直角坐标系,则(1,0,0)A ,111,,122O ⎛⎫⎪⎝⎭,1(0,1,1)C ,111,,122AO ⎛⎫=- ⎪⎝⎭,1(1,1,1)AC =-,121111,,1(1,1,1)122222AO AC ⎛⎫∴⋅=-⋅-=++= ⎪⎝⎭.故选D.4.答案:C解析:易得(1,1,0)AB =-,(1,0,1)AC =-, 设(,,)x y z =n 为平面ABC 的一个法向量,则0,0,AB AC ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0,x y x z -+=⎧⎨-+=⎩x y z ∴==,故选C.5.答案:B解析:取AC 的中点O ,连接OP ,OB ,PA PC =,AC OP ∴⊥,平面PAC ⊥平面ABC ,平面PAC ⋂平面ABC AC = ,OP ∴⊥平面ABC ,又AB BC =,AC OB ∴⊥,以O 为坐标原点,建立如图所示的空间直角坐标系,PAC 是等腰直角三角形,4PA PC ==,ABC 为等边三角形,(22,0,0)A ∴,(2,0,0)C -,2)P ,(2,6,0)D , (42,0,0)AC ∴=-,(2,6,2)PD =-,2cos ,424||||AC PD AC PD AC PD ⋅∴〈〉===⨯∴异面直线AC 与PD 所成角的余弦值为24. 故选B. 6.答案:B解析:如图,以A 为原点,分别以,,AB AD AP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,则(3,0,0),(0,4,0),(0,0,2),(0,0,1)B D P Q ,(3,0,1),(3,4,0),(0,0,1)QB BD QP =-=-=.设平面BQD 的一个法向量为(,,)x y z =n ,则0,0,BD QB ⎧⋅=⎪⎨⋅=⎪⎩n n 即340,30.x y x z -+=⎧⎨-=⎩ 令4x =,则12,3,(4,3,12)z y ==∴=n .∴点P到平面BQD 的距离||12||13QP d ⋅==n n . 7.答案:AC解析:由||2=a 2221(1)2m +-+, 解得2m =±,故A 选项正确;由⊥a b得2120m m --++=,解得1m =,故B 选项错误; 若存在实数λ,使得λ=a b ,则12λ=-,1(1)m λ-=-,2m λ=,显然λ无解,即不存在实数λ使得λ=a b ,故C 选项正确; 若1⋅=-a b ,则2121m m --++=-,解得0m =, 于是(1,2,2)+=--a b ,故D 选项错误. 8.答案:BC解析:如图,建立空间直角坐标系,则(0,0,0)A ,(1,0,0)B ,(0,1,0)D ,1(0,0,1)A ,1(1,1,1)C ,1(0,1,1)D ,1,0,12E ⎛⎫ ⎪⎝⎭,所以(1,0,0)BA =-,1,0,12BE ⎛⎫=- ⎪⎝⎭.设ABE θ∠=,则||5cos 5||||BA BE BA BE θ⋅==,225sin 1cos θθ-. 故A 到直线BE 的距离12525||sin 1d BA θ===A 错. 易知111111,,0222C O C A ⎛⎫==-- ⎪⎝⎭, 平面11ABC D 的一个法向量1(0,1,1)DA =-,则点O 到平面11ABC D 的距离11211222DA C O d DA ⋅===,故B 对. 1(1,0,1)A B =-,1(0,1,1)A D =-,11(0,1,0)A D =.设平面1A BD 的法向量为(,,)x y z =n ,则110,0,A B A D ⎧⋅=⎪⎨⋅=⎪⎩n n 所以0,0,x z y z -=⎧⎨-=⎩令1z =,得1y =,1x =, 所以(1,1,1)=n .所以点1D 到平面1A BD 的距离1133||3A D d ⋅=n n . 因为易证得平面1//A BD 平面11B CD ,所以平面1A BD 与平面11B CD 间的距离等于点1D 到平面1A BD 的距离,所以平面1A BD 与平面11B CD 3,故C 对.因为1312423AP AB AD AA =++,所以312,,423AP ⎛⎫= ⎪⎝⎭,又(1,0,0)AB =,则34||AP AB AB ⋅=,所以点P 到AB 的距离2218195||144166||AP AB d AP AB ⋅=-=-=,故D 错. 9.答案:257解析:已知AB BC ⊥,由题意,可得BP AB ⊥,BP BC ⊥.利用向量数量积的运算公式,可得352015603(1)30z x y x y z +-=⎧⎪-++=⎨⎪-+-=⎩,,,解得4071574,x y z ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩,,401525777x y ∴+=-=. 10.答案:4解析:连接AC ,交BD 于点O ,连接OP ,以O 为原点,OA 所在直线为x 轴,OB 所在直线为y 轴,OP 所在直线为z 轴,建立空间直角坐标系,设2PA AB ==,则(2,0,0)A ,(0,2,0)D -,22M ⎝⎭,2,0)B ,(0,2,0)BD ∴=-,(2,2,0)AD =-,设(0,,0)N b ,则(0,2,0)BN b =-.BD BN λ=,22(2)b λ∴-=,222b λ-∴=222N λ⎛⎫-∴ ⎪ ⎪⎝⎭,22222,,22MN λλ⎛⎫-∴=-- ⎪ ⎪⎝⎭, MN AD ⊥,2410MN AD λλ-∴⋅=-=,解得4λ=.11.答案:63解析:建立如图所示的空间直角坐标系,则1(0,0,0),(0,0,2),(1,0,2),,(0,1,1)D D M N ,所以(1,1,1)MN =--,平面ABCD 的一个法向量为1(0,0,2)DD =,所以1113cos ,3||MN DD MN DD MN DD ⋅〈==-MN 与平面ABCD 所成的角为θ,则3sin θ,所以6cos θ=. 12.答案:(1)见解析 26解析:(1)证明:取BC 的中点O ,连接,,AO DO AD .ABC ∴△是正三角形, OA BC ∴⊥.∵平面ABC ⊥平面BCD ,平面ABC 平面BCD BC =,OA ∴⊥平面BCD . OD ⊂平面BCD , AO OD ∴⊥.在Rt AOD △中,2sin 603AO DO ===336∴=+=.AD又6AE=,∴△为等腰三角形.ADE∴⊥.P是DE的中点,AP DEDE⊥平面BCD,∴∴⊥∴.AO DE AP AO AP OD////,,BCD AP⊄平面BCD,OD⊂平面,∴平面BCD.//AP(2)由(1)知,,OA DP AP OD,////∴四边形APDO为平行四边形,∴==,PD OA3∴=.23DE以点O为坐标原点,以,,OD OC OA的方向分别为x轴、y轴、z轴的正方向,建立如图的空间直角坐标系O xyz-,则3),(0,1,0)C E,A B-,(0,1,0),(3,0,23)∴===-.BA AE AC(0,1,3),(3,0,3),(0,1,3)设平面ABE的法向量为(,,)m,x y z=则0,0,BA AE ⎧⋅=⎪⎨⋅=⎪⎩m m即0,0.y ⎧=⎪=令y =1,1x z ==-,1)∴=-m .设平面ACE 的法向量为(,,)a b c =n , 则0,0,AE AC ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0.b ==⎪⎩ 令1a =-,则1b c ==,(∴=-n.1cos ,||||5⋅∴===m n m n m n. sin ,∴=m n ∴二面角B AE C --.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.1.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4.的中点;PB(1)求证:M为的大小;A2)求二面角B﹣PD﹣(所成角的正弦值.BDP(3)求直线MC与平面【分析】(1)设AC∩BD=O,则O为BD的中点,连接OM,利用线面平行的性质证明OM∥PD,再由平行线截线段成比例可得M为PB的中点;(2)取AD中点G,可得PG⊥AD,再由面面垂直的性质可得PG⊥平面ABCD,则PG⊥AD,连接OG,则PG⊥OG,再证明OG⊥AD.以G为坐标原点,分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系,求出平面PBD与平面PAD的一个法向量,由两法向量所成角的大小可得二面角B﹣PD﹣A的大小;(3)求出的坐标,由与平面PBD的法向量所成角的余弦值的绝对值可得直线MC与平面BDP所成角的正弦值.【解答】(1)证明:如图,设AC∩BD=O,∵ABCD为正方形,∴O为BD的中点,连接OM,∵PD∥平面MAC,PD?平面PBD,平面PBD∩平面AMC=OM,∴PD∥OM,则,即M为PB的中点;(2)解:取AD中点G,..∵PA=PD,∴PG⊥AD,∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PG⊥平面ABCD,则PG⊥AD,连接OG,则PG⊥OG,由G是AD的中点,O是AC的中点,可得OG∥DC,则OG⊥AD.以G为坐标原点,分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系,由PA=PD=,AB=4,得D(2,0,0),A(﹣2,0,0),P(0,0,),C(2,4,0),B(﹣2,4,0),M(﹣1,2,),,.,PBD的一个法向量为设平面,得,得,取z=.则由取平面PAD.的一个法向量为∴cos<.>==∴二面角B﹣PD﹣A的大小为60°;(3)解:,平面BDP的一个法向量为.>∴直线MC与平面BDP所成角的正弦值为|cos<|=||=||=...【点评】本题考查线面角与面面角的求法,训练了利用空间向量求空间角,属中档题.2.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.(Ⅰ)求证:MN∥平面BDE;(Ⅱ)求二面角C﹣EM﹣N的正弦值;(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为,求线的长.AH段【分析】(Ⅰ)取AB中点F,连接MF、NF,由已知可证MF∥平面BDE,NF∥平面BDE.得到平面MFN∥平面BDE,则MN∥平面BDE;(Ⅱ)由PA⊥底面ABC,∠BAC=90°.可以A为原点,分别以AB、AC、AP 所在直线为x、y、z轴建立空间直角坐标系.求出平面MEN与平面CME的一个法..向量,由两法向量所成角的余弦值得二面角C﹣EM﹣N的余弦值,进一步求得正弦值;(Ⅲ)设AH=t,则H(0,0,t),求出的坐标,结合直线NH与直线BE列式求得线段AH所成角的余弦值为的长.【解答】(Ⅰ)证明:取AB中点F,连接MF、NF,∵M为AD中点,∴MF∥BD,∵BD?平面BDE,MF?平面BDE,∴MF∥平面BDE.∵N为BC中点,∴NF∥AC,又D、E分别为AP、PC的中点,∴DE∥AC,则NF∥DE.∵DE?平面BDE,NF?平面BDE,∴NF∥平面BDE.又MF∩NF=F.∴平面MFN∥平面BDE,则MN∥平面BDE;(Ⅱ)解:∵PA⊥底面ABC,∠BAC=90°.∴以A为原点,分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系.∵PA=AC=4,AB=2,∴A(0,0,0),B(2,0,0),C(0,4,0),M(0,0,1),N(1,2,0),E(0,2,2),则,,,设平面MEN的一个法向量为由,得.,取z=2,得由图可得平面CME的一个法向量为...∴cos<>=.,则正弦值为;∴二面角C﹣EM﹣N的余弦值为(Ⅲ)解:设AH=t,则H(0.,,0,t),所成角的余弦值为BE∵直线,NH与直线|=||=.|=||cos<>∴.t=t=或解得:的长此时线段AHBENH与直线所成角的余弦值为,∴当H与P重合时直线.为或考本题考查直线与平面平行的判定,考查了利用空间向量求解空间角,【点评】查计算能力,是中档题.边所在AB.如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以3的中点.是得到的,G直线为旋转轴旋转120°的大小;BE,求∠CBPⅠ()设P是⊥上的一点,且AP的大小.﹣CAGEAD=2AB=3Ⅱ()当,时,求二面角﹣..【分析】(Ⅰ)由已知利用线面垂直的判定可得BE⊥平面ABP,得到BE⊥BP,结合∠EBC=120°求得∠CBP=30°;(Ⅱ)法一、取的中点H,连接EH,GH,CH,可得四边形BEGH为菱形,取AG中点M,连接EM,CM,EC,得到EM⊥AG,CM⊥AG,说明∠EMC为所求二面角的平面角.求解三角形得二面角E﹣AG﹣C的大小.法二、以B为坐标原点,分别以BE,BP,BA所在直线为x,y,z轴建立空间直角坐标系.求出A,E,G,C的坐标,进一步求出平面AEG与平面ACG的一个法向量,由两法向量所成角的余弦值可得二面角E﹣AG﹣C的大小.【解答】解:(Ⅰ)∵AP⊥BE,AB⊥BE,且AB,AP?平面ABP,AB∩AP=A,∴BE⊥平面ABP,又BP?平面ABP,∴BE⊥BP,又∠EBC=120°,因此∠CBP=30°;(Ⅱ)解法一、取的中点H,连接EH,GH,CH,∵∠EBC=120°,∴四边形BECH为菱形,∴AE=GE=AC=GC=.取AG中点M,连接EM,CM,EC,则EM⊥AG,CM⊥AG,∴∠EMC为所求二面角的平面角...又AM=1,∴EM=CM=.,中,由于∠EBC=120°在△BEC222﹣2×2×2×由余弦定理得:ECcos120=2°+2=12,∴,因此△EMC为等边三角形,故所求的角为60°.解法二、以B为坐标原点,分别以BE,BP,BA所在直线为x,y,z轴建立空间直角坐标系.由题意得:A(0,0,3),E(2,0,0),G(1,,3),C(﹣1,,0),.故,,的一个法向量,为平面设AEG;,得=2,取,得z由1的一个法向量,为平面设ACG.﹣=z,可得2,得,取由2∴cos<>=.∴二面角E﹣AG﹣C的大小为60°...【点评】本题考查空间角的求法,考查空间想象能力和思维能力,训练了线面角的求法及利用空间向量求二面角的大小,是中档题.4.如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D﹣AF﹣E与二面角C﹣BE﹣F都是60°.(Ⅰ)证明平面ABEF⊥平面EFDC;(Ⅱ)求二面角E﹣BC﹣A的余弦值.【分析】(Ⅰ)证明AF⊥平面EFDC,利用平面与平面垂直的判定定理证明平面ABEF⊥平面EFDC;(Ⅱ)证明四边形EFDC为等腰梯形,以E为原点,建立如图所示的坐标系,求出平面BEC、平面ABC的法向量,代入向量夹角公式可得二面角E﹣BC﹣A的余弦值.【解答】(Ⅰ)证明:∵ABEF为正方形,∴AF⊥EF.∵∠AFD=90°,∴AF⊥DF,∵DF∩EF=F,∴AF⊥平面EFDC,..∵AF?平面ABEF,∴平面ABEF⊥平面EFDC;(Ⅱ)解:由AF⊥DF,AF⊥EF,可得∠DFE为二面角D﹣AF﹣E的平面角;由ABEF为正方形,AF⊥平面EFDC,∵BE⊥EF,∴BE⊥平面EFDC即有CE⊥BE,可得∠CEF为二面角C﹣BE﹣F的平面角.可得∠DFE=∠CEF=60°.∵AB∥EF,AB?平面EFDC,EF?平面EFDC,∴AB∥平面EFDC,∵平面EFDC∩平面ABCD=CD,AB?平面ABCD,∴AB∥CD,∴CD∥EF,∴四边形EFDC为等腰梯形.以E为原点,建立如图所示的坐标系,设FD=a,则E(0,0,0),B(0,2a,0),C(,0,a),A(2a,2a,0),=,=0),(,﹣2aa),(﹣2a,0,0),,(∴=02a,设平面BEC的法向量为=(x,y,z),则111则,取=(,0,﹣1)...设平面ABC的法向量为=(x,y,z),则,222则,取=(0,,4).=cosθA的大小为θ,则设二面角E﹣BC﹣,﹣==的余弦值为﹣﹣AE﹣.BC则二面角建考查用空间向量求平面间的夹角,【点评】本题考查平面与平面垂直的证明,立空间坐标系将二面角问题转化为向量夹角问题是解答的关键.F,,点EO,AB=5,AC=6与5.如图,菱形ABCD的对角线ACBD交于点EFD′沿EF折到△H,EF交于BD于点,将△DEF上,分别在AD,CDAE=CF=.=的位置,OD′;ABCDH⊥平面(Ⅰ)证明:D′的正弦值.C′DA﹣)求二面角(ⅡB﹣,AC∥可得,结合为菱形,可得)由底面(【分析】ⅠABCDAD=CDAE=CFEF..再由ABCD是菱形,得AC⊥BD,进一步得到EF⊥BD,由EF⊥DH,可得EF⊥D′H,然后求解直角三角形得D′H⊥OH,再由线面垂直的判定得D′H⊥平面ABCD;(Ⅱ)以H为坐标原点,建立如图所示空间直角坐标系,由已知求得所用点的坐标,得到的坐标,分别求出平面ABD′与平面AD′C的一个,设二面角二面角B﹣D′法向量A﹣C的平面角为θ,求出|cosθ|.则二面角B﹣D′A﹣C的正弦值可求.【解答】(Ⅰ)证明:∵ABCD是菱形,∴AD=DC,又AE=CF=,∴,则EF∥AC,又由ABCD是菱形,得AC⊥BD,则EF⊥BD,∴EF⊥DH,则EF⊥D′H,∵AC=6,∴AO=3,又AB=5,AO⊥OB,∴OB=4,∴OH==1,则DH=D′H=3,222,则D′H′H|⊥OH∴|OD′|,=|OH|+|D又OH∩EF=H,∴D′H⊥平面ABCD;(Ⅱ)解:以H为坐标原点,建立如图所示空间直角坐标系,∵AB=5,AC=6,∴B(5,0,0),C(1,3,0),D′(0,0,3),A(1,﹣3,0),..,,,′的一个法向量为设平面ABD,取x=3,得y=﹣由,得4,z=5..∴同理可求得平面AD′C的一个法向量,,θ﹣C的平面角为设二面角二面角B﹣D′A.|=则|cosθ.=A﹣C的正弦值为sinθ∴二面角B﹣D′【点评】本题考查线面垂直的判定,考查了二面角的平面角的求法,训练了利用平面的法向量求解二面角问题,体现了数学转化思想方法,是中档题.6.在三棱柱ABC﹣ABC中,CA=CB,侧面ABBA是边长为2的正方形,点E,11111F分别在线段AA、AB上,且AE=,AF=,CE⊥EF.1111(Ⅰ)证明:平面ABBA ⊥平面ABC;11(Ⅱ)若CA⊥CB,求直线AC与平面CEF所成角的正弦值.1..【分析】(I)取AB的中点D,连结CD,DF,DE.计算DE,EF,DF,利用勾股定理的逆定理得出DE⊥EF,由三线合一得CD⊥AB,故而CD⊥平面ABBA,从11而平面ABBA⊥平面ABC;11(II)以C为原点建立空间直角坐标系,求出和平面CEF的法向量,则直>|与平面CEF所成角的正弦值等于|cos<.线AC1【解答】证明:(I)取AB的中点D,连结CD,DF,DE.∵AC=BC,D是AB的中点,∴CD⊥AB.∵侧面ABBA是边长为2的正方形,AE=,AF=.111∴AE=,EF==,DE==,1,DF==222,∴DE⊥EF∴EF,+DE=DF又CE⊥EF,CE∩DE=E,CE?平面CDE,DE?平面CDE,∴EF⊥平面CDE,又CD?平面CDE,∴CD⊥EF,又CD⊥AB,AB?平面ABBA,EF?平面ABBA,AB,EF为相交直线,1111∴CD⊥平面ABBA,又CD?ABC,11∴平面ABBA⊥平面ABC.11..(II)∵平面ABBA⊥平面ABC,11∴三棱柱ABC﹣ABC是直三棱柱,∴CC⊥平面ABC.1111∵CA⊥CB,AB=2,∴AC=BC=.以C为原点,以CA,CB,CC为坐标轴建立空间直角坐标系,如图所示:1则A(,0,0),C(0,0,0),C(0,0,2),E(,0,),F(,,1.)2.,,=(2),),=)2,(﹣∴=0,,(,0设平面CEF的法向量为=(x,,y,z),则∴,令z=4,得=(﹣,﹣9,4).∴=10,||=6,||=..=><∴sin=.∴直线AC与平面CEF所成角的正弦值为1【点评】本题考查了面面垂直的判定,线面角的计算,空间向量的应用,属于中档题...7.如图,在四棱锥中P﹣ABCD,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2,BC=4,PA=2.(1)求证:AB⊥PC;(2)在线段PD上,是否存在一点M,使得二面角M﹣AC﹣D的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.【分析】(1)利用直角梯形的性质求出AB,AC的长,根据勾股定理的逆定理得出AB⊥AC,由PA⊥平面ABCD得出AB⊥PA,故AB⊥平面PAC,于是AB⊥PC;(2)假设存在点M,做出二面角的平面角,根据勾股定理求出M到平面ABCD 的距离从而确定M的位置,利用棱锥的体积求出B到平面MAC的距离h,根据勾股定理计算BM,则即为所求角的正弦值.【解答】解:(1)证明:∵四边形ABCD是直角梯形,AD=CD=2,BC=4,==4,∴AC=4,AB=∴△ABC是等腰直角三角形,即AB⊥AC,∵PA⊥平面ABCD,AB?平面ABCD,∴PA⊥AB,∴AB⊥平面PAC,又PC?平面PAC,..∴AB⊥PC.(2)假设存在符合条件的点M,过点M作MN⊥AD于N,则MN∥PA,∴MN⊥平面ABCD,∴MN⊥AC.过点M作MG⊥AC于G,连接NG,则AC⊥平面MNG,∴AC⊥NG,即∠MGN是二面角M﹣AC﹣D的平面角.若∠MGN=45°,则NG=MN,又AN=NG=MN,的中点.是线段MPD∴MN=1,即.45°使得二面角M﹣AC﹣D的大小为∴存在点M,V=S?=MN=在三棱锥M﹣ABC中,ABC﹣ABC△M,V设点B到平面MAC的距离是h,则=MAC﹣B,=,∴S=2=MN=∵MG=MAC△h=2∴.,解得=BN=∴BAN=135°,∠,,在△ABN中,=,AB=4AN=,BM==3∴.所成角的正弦值为=与平面∴BMMAC属于中本题考查了项目垂直的判定与性质,【点评】空间角与空间距离的计算,档题...8.如图,在各棱长均为2的三棱柱ABC﹣ABC中,侧面AACC⊥底面ABC,11111∠AAC=60°.1(1)求侧棱AA与平面ABC所成角的正弦值的大小;11(2)已知点D满足=+,在直线AA上是否存在点P,使DP∥平面ABC?11若存在,请确定点P的位置,若不存在,请说明理由.【分析】(1)推导出AO⊥平面ABC,BO⊥AC,以O为坐标原点,建立如图所1示的空间直角坐标系O﹣xyz,利用向量法能求出侧棱AA与平面ABC所成角的11正弦值.(2)假设存在点P符合题意,则点P的坐标可设为P(0,y,z),则.利用向量法能求出存在点P,使DP∥平面ABC,其坐标为(0,10,),即恰好为A点.1【解答】解:(1)∵侧面AACC⊥底面ABC,作AO⊥AC于点O,111∴AO⊥平面ABC.1又∠ABC=∠AAC=60°,且各棱长都相等,1∴AO=1,OA=OB=,BO⊥AC.…(2分)1故以O为坐标原点,建立如图所示的空间直角坐标系O﹣xyz,则A(0,﹣1,0),B(,0,0),A(0,0,),C(0,1,0),1..∴=(0,1,),=(),=(0,2,0).…(4分)设平面ABC的法向量为,1.)0,1x=1,得=(1,则,取,θABC所成角的为设侧棱AA与平面11,|=>|=|sinθ=|cos<,则所成角的正弦值为ABC∴侧棱6分)AA与平面.…(11,=,而(,2)∵(﹣.D)(﹣20),又∵B(,∴点∴=,0,0,0,)∴,z),P(0,y则点假设存在点P符合题意,P.的坐标可设为的法向量,ABC0,1)为平面,AB∵DP∥平面C,=(﹣111分)10.…(y=0∴由=λ,得,∴,),00,C,使CDP又?平面AB,故存在点PDP∥平面AB,其坐标为(11分)A 即恰好为点.…12(1考查满足条件的点是否存在的判断与【点评】本题考查线面角的正弦值的求法,求法,是中档题,解题时要认真审题,注意向量法的合理运用...9.在三棱柱ABC﹣ABC中,侧面ABBA为矩形,AB=2,AA=2,D是AA1111111.,且ACO⊥平面ABB的中点,BD与AB交于点O111;BCDABC⊥平面(Ⅰ)证明:平面1所成角的正弦ABCGD与平面Ⅱ)若OC=OA,△ABC的重心为G,求直线(1值.【分析】(Ⅰ)通过证明AB⊥BD,AB⊥CO,推出AB⊥平面BCD,然后证明111平面ABC⊥平面BCD.1(Ⅱ)以O为坐标原点,分别以OD,OB,OC所在直线为x,y,z轴,建立如1图所示的空间直角坐标系O﹣xyz.求出平面ABC的法向量,设直线GD与平面ABC所成角α,利用空间向量的数量积求解直线GD 与平面ABC所成角的正弦值即可.【解答】(本小题满分12分)解:(Ⅰ)∵ABBA为矩形,AB=2,,D是AA的中点,∴∠BAD=90°,111,,,∵,,从而∴∠ABD=∠ABB,…(2分)1..∴,∴,从而AB⊥BD…(4分)1∵CO⊥平面ABBA,AB?平面ABBA,∴AB⊥CO,∵BD∩CO=O,∴AB⊥1111111平面BCD,∵AB?平面ABC,11∴平面ABC⊥平面BCD…(6分)1(Ⅱ)如图,以O为坐标原点,分别以OD,OB,OC所在直线为x,y,z轴,1建立如图所示的空间直角坐标系O﹣xyz.在矩形ABBA中,由于AD∥BB,所以△AOD和△BOB相似,1111从而,∴,,又,,,∴∵G为△AB,C的重心,∴1…,(8分)设平面ABC的法向量为,,由可得,令y=1,则z=﹣1,,所以.…(10分)所成ABC平线设直GD与面角α,则=..,所以直线GD与平面ABC所成角的正弦值为…(12分)【点评】本题考查平面与平面垂直的判定定理的应用,直线与平面所成角的求法,考查空间想象能力以及计算能力.10.在矩形ABCD中,AB=4,AD=2,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.(1)当θ=90°时,求A′C的长;(2)当cosθ=时,求BC与平面A′BD所成角的正弦值.【分析】(1)过A作BD的垂线交BD于E,交DC于F,连接CE,利用勾股定理及余弦定理计算AE,CE,由A′E⊥CE得出A′C;(2)利用余弦定理可得A′F=,从而得出A′F⊥平面ABCD,以F为原点和平面A′BD的法向量,则BC建立坐标系,求出与平面A′BD所成角的>正弦值为|cos|.<..【解答】解:(1)在图1中,过A作BD的垂线交BD于E,交DC于F,连接CE.∵AB=4,AD=2,∴BD==10.=8,∴cos∠CBE==,BE=..在△=2BCE中,由余弦定理得CE=∵θ=90°,∴A′E⊥平面ABCD,∴A′E⊥CE.∴|A′C|==2..)DE==2(2.∠FDE==EF=1,DF=,∴∵tan即cos∠A′EF=当时,.222,∴∠A'FE=90+EF′E°=A′F∴A又BD⊥AE,BD⊥EF,∴BD⊥平面A'EF,∴BD⊥A'F∴A'F⊥平面ABCD.以F为原点,以FC为x轴,以过F的AD的平行线为y轴,以FA′为z轴建立空间直角坐标系如图所示:∴A′(0,0,),D(﹣,0,0),B(3,2,0),C(3,0,0).).,,20)(2,0,0,)=4,=,0,((∴=设平面A,′BD的法向量为=(x,y,z),则∴,令z=1得=(﹣,2,1).∴cos<>===...∴BC与平面A'BD所成角的正弦值为.【点评】本题考查了空间角与空间距离的计算,空间向量的应用,属于中档题.11.如图,由直三棱柱ABC﹣ABC和四棱锥D﹣BBCC构成的几何体中,∠11111.A⊥平面ACCD=CD=D,平面CCBAC=90°,AB=1,BC=BB=2,C11111;DCAC ⊥(Ⅰ)求证:1;DBB的中点,求证:(Ⅱ)若M为DCAM∥平面11?若存Ⅲ)在线段BC上是否存在点P,所成的角为DDP与平面BB使直线(1的值,若不存在,说明理由.在,求.⊥DCCCD,即可证明AC⊥【分析】(Ⅰ)证明ACCC,得到AC⊥平面111,xyz,建立空间直角坐标系A﹣(Ⅱ)易得∠BAC=90°,)100B)0,,,(,,,,(依据已知条件可得A00,B)1,,2(0,1..利用向量求得AM与平面DBB所成角为0,即AM∥平面DBB.11(Ⅲ)利用向量求解【解答】解:(Ⅰ)证明:在直三棱柱ABC﹣ABC中,CC⊥平面ABC,故AC1111⊥CC,1由平面CCD⊥平面ACCA,且平面CCD∩平面ACCA=CC,1111111所以AC⊥平面CCD,1又CD?平面CCD,所以AC⊥DC.111(Ⅱ)证明:在直三棱柱ABC﹣ABC中,AA⊥平面ABC,1111所以AA⊥AB,AA⊥AC,11又∠BAC=90°,所以,如图建立空间直角坐标系A﹣xyz,依据已知条件可得A(0,0,0),,,B(0,0,1),,),1,B(2,01,,所以设平面DBB,的法向量为1即由,,于是,则x=0,令y=1中点,所以DCM为,,所以因为1由,,可得,所成角为0所以AM与平面DBB1.DBB即AM∥平面1.DBB的法向量为)可知平面)解:由((ⅢⅡ1..设,λ∈[0,1],,则.角直为,平面DBB成则线DP与若1,解得,故不存在这样的点.【点评】本题考查了空间线线垂直、线面平行的判定,向量法求二面角.属于中档题12.如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB=EA=ED,EF∥BD(I)证明:AE⊥CD(II)在棱ED上是否存在点M,使得直线AM与平面EFBD所成角的正弦值为?若存在,确定点M的位置;若不存在,请说明理由...【分析】(I)利用面面垂直的性质得出CD⊥平面AED,故而AE⊥CD;(II)取AD的中点O,连接EO,以O为原点建立坐标系,设,求出平面,根据方程的解得出结论.>|=的法向量,令|cos<BDEF【解答】(I)证明:∵四边形ABCD是正方形,∴CD⊥AD,又平面AED⊥平面ABCD,平面AED∩平面ABCD=AD,CD?平面ABCD,∴CD⊥平面AED,∵AE?平面AED,∴AE⊥CD.(II)解:取AD的中点O,过O作ON∥AB交BC于N,连接EO,∵EA=ED,∴OE⊥AD,又平面AED⊥平面ABCD,平面AED∩平面ABCD=AD,OE?平面AED,∴OE⊥平面ABCD,以O为原点建立空间直角坐标系O﹣xyz,如图所示:设正方形ACD的边长为2,,则A(1,0,0),B(1,2,0),D(﹣1,0,0),E(0,0,1),M(﹣λ,0,1﹣λ)∴=(﹣λ﹣1,0,1﹣λ),=(1,0,1),=(2,2,0),设平面BDEF的法向量为=(x,y,z),则,即,令x=1得=(1,﹣1,﹣1),..∴cos<>==,令||=,解得λ=0,.∴当M与点E重合时,直线AM与平面EFBD所成角的正弦值为【点评】本题考查了线面垂直的判定,空间向量与线面角的计算,属于中档题.13.如图,在四棱锥P﹣ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.(1)设点E为PD的中点,求证:CE∥平面PAB;(2)线段PD上是否存在一点N,使得直线CN与平面PAC所成的角θ的正弦值为?若存在,试确定点N的位置,若不存在,请说明理由.【分析】(1)取AD中点M,利用三角形的中位线证明EM∥平面PAB,利用同位角相等证明MC∥AB,得到平面EMC∥平面PAB,证得EC∥平面PAB;(2)建立坐标系,求出平面PAC的法向量,利用直线CN与平面PAC所成的角θ的正弦值为,可得结论...【解答】(1)证明:取AD中点M,连EM,CM,则EM∥PA.∵EM?平面PAB,PA?平面PAB,∴EM∥平面PAB.在Rt△ACD中,∠CAD=60°,AC=AM=2,∴∠ACM=60°.而∠BAC=60°,∴MC∥AB.∵MC?平面PAB,AB?平面PAB,∴MC∥平面PAB.∵EM∩MC=M,∴平面EMC∥平面PAB.∵EC?平面EMC,∴EC∥平面PAB.(2)解:过A作AF⊥AD,交BC于F,建立如图所示的坐标系,则A(0,0,0),B(,﹣,0),C(,1,0),D(0,4,0),P(0,0,2),设平面PAC的法向量为=(x,y,z),则,取=(,﹣3,0),=(0,4λ,﹣2λ),=(﹣λ﹣1,2﹣2λ))≤≤(=设λ0λ1,则,,∴,=∴>|=|cos<,∴N为PD的中点,使得直线CN与平面.PAC所成的角θ的正弦值为【点评】本题考查线面平行的判定,考查线面角,考查向量知识的运用,考查学..生分析解决问题的能力,属于中档题.14.如图,四棱锥P﹣ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°,点E是线段PA上靠近点A的三等分点.(Ⅰ)求证:AB⊥PC;(Ⅱ)若△PAB是边长为2的等边三角形,求直线DE与平面PBC所成角的正弦值.【分析】(Ⅰ)作PO⊥AB于O,连接OC,可得PO⊥面ABCD.由△POB≌△POC,∠ABC=45°,得OC⊥AB,即得AB⊥面POC,可证得AB⊥PC.(Ⅱ)以O为原点建立空间坐标系,,利用向量求解.【解答】解:(Ⅰ)作PO⊥AB于O…①,连接OC,∵平面PAB⊥平面ABCD,且面PAB∩面ABCD=AB,∴PO⊥面ABCD.…(2。
