应用回归分析-第8章课后习题参考答案
《应用回归分析》部分课后习题答案-何晓群版

《应用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
应用回归分析课后习题

使用其中的一个。
2.12* 如果把自变量观测值都乘以 2,回归参数的最小二乘估计 ˆ0 和 ˆ1 会发生什么变化?
#;
.
如果把自变量观测值都加上 2,回归参数的最小二乘估计 ˆ0 和 ˆ1 会发生什么变化?
2.13 如果回归方程 yˆ ˆ0 ˆ1x 相应的相关系数 r 很大,则用它预测时,预测误差一定较小。
#;
.
第三章 习题
3.1 写出多元线性回归模型的矩阵表示形式,并给出多元线性回归模型的基本假设。 3.2 讨论样本量 n 与自变量个数 p 的关系,它们对模型的参数估计有何影响?
3.3 证明ˆ 2 1 SSE 是误差项方差 2 的无偏估计。 n p 1
3.4 一个回归方程的复相关系数 R=0.99,样本决定系数 R2 0.9801 ,我们能判断这个回归
2.15 一家保险公司十分关心其总公司营业部加班的程度,决定认真调查一下现状。经过 10
周时间,收集了每周加班工作时间的数据和签发的新保单数目,x 为每周签发的新保单数目,
y 为每周加班工作时间(小时)。见表
周序 1
2
3
4
5
6
7
8
9
10
号
X
825 215 1070 550 480 920 1350 325 670 1215
《应用回归分析》课后习题部分答案-何晓群版

第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=(5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2||(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()ni i nii y y r y y ∧-=-=-==≈-∑∑(7)由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。
课后习题答案--第8章组织变革

课后习题答案--第8章组织变革第8章组织变革与组织创新【同步测试】一、单项选择题1.组织变革按照_____C___可以分为主动性变革和被动性变革。
A.工作的对象不同B.变革的程度与速度不同C.组织所处的经营环境状况不同2.___B_____指组织需要根据环境的变化适时对组织的结构进行变革,并重新在组织中进行权力和责任的分配,使组织变得更为柔性灵活、易于合作。
A.战略性变革B.结构性变革C.流程主导性变革D.以人为中心的变革3.关于组织冲突的避免,说法不正确的是___D_____。
A.对于非正式组织来讲,首先要认识到非正式组织存在的必要性和客观性B.对于直线与参谋应该首先明确必要的职权关系C.对于委员会,应注意委员会人选的理论和实践背景D.冲突是组织内部的事,信息反馈会浪费时间4.对人员的变革,叙述正确的是___C_____。
A.指员工在态度,技能、期望、认知和行为上的改变B.变革的主要任务是组织成员之间在权力和利益等资源方面的重新分配C.必须注重员工的参与D.注重改善人际关系并提高实际沟通的质量5.关于组织变革,下列____A____是正确的。
A.组织冲突是不可避免的B.应当反对组织冲突C.组织变革中存在压力是不利的二、多项选择题1.战略性变革是指_ACD_____。
A.组织需要根据环境的变化适时对组织的结构进行的变革B.组织对员工的培训、教育等引导C.充分应用现代信息技术对业务流程进行重新构造D.组织对其长期发展战略或使命所做的变革2.组织变革的目标应该是__ABC______。
A.使组织更具环境适应性B.使管理者更具环境适应性C.使员工更具环境适应性D.使董事会更具环境适应性3.消除组织变革阻力的管理对策有_BCD______。
A.加强流程改造B.创新组织文化C.创新策略方法和手段D.客观分析变革的推力和阻力的强弱4.下列组织冲突中,最典型的三种是_ABC_______。
A.正式组织与非正式组织之间的冲突B.直线与参谋之间的冲突C.委员会内部之间的冲突D.个体内部的心理冲突5.组织变革的步骤包括___ABCD____。
应用回归分析第四版课后习题答案-全-何晓群-刘文卿

实用回归分析第四版 第一章 回归分析概述1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y 与x1,x2…..xp 的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp 是非随机的,观测值xi1.xi2…..xip 是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.第二章 一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答: 假设1、解释变量X 是确定性变量,Y 是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性: E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关: Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
证明:其中:∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ01ˆˆˆˆi i i i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂即: ∑e i =0 ,∑e i X i =02.5 证明0ˆβ是β0的无偏估计。
实验设计与数据处理第八章例题及课后习题答案doc资料
0
428
0 1.162084
492
0 1.162084
512
0
0
509
0
0
Signific ance F
7.93E-05
Lower Upper 下限 上限
95%
95% 95.0% 95.0%
465.4405 471.5595 465.4405 471.5595
5.242078 12.93644 5.242078 12.93644
0.002795085 2.593838854 0.122018
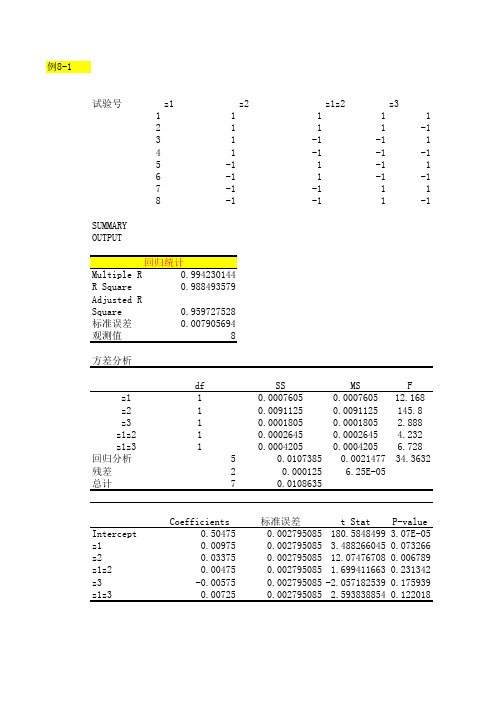
例8-2
回归方程: 由该回归方程 中偏回归系数 绝对值的大 小,可以得到 各因素和交互 作用的主次顺 序为:
y=0.50475+0.00 975z1+0.03375z 2+0.00475z1z20.00575z3+0.00 725z1z3
0 0 -41.73590203
y=468.5+9.09z1 -26.56z2+z3
标准误差
t Stat P-value
1.10193312 425.1619191 1.84E-10
1.385649972 6.55956341 0.002794
1.385649972 -19.17042163 4.36E-05
SS 0.0091125
0.001626 0.0108635
MS
F
0.0091125 33.62546
0.000271
试验号
z1 1 2 3 4 5 6 7 8 9 10 11
z2 1 1 1 1 -1 -1 -1 -1 0 0 0
z3 1 1 -1 -1 1 1 -1 -1 0 0 0
第八章-相关与回归分析练习题

第八章-相关与回归分析练习题第八章相关与回归分析一、单选题1.相关分析研究的是()A、变量间相互关系的密切程度B、变量之间因果关系C、变量之间严格的相依关系D、变量之间的线性关系2.若变量X的值增加时,变量Y的值也增加,那么变量X和变量Y之间存在着()。
A、正相关关系 B、负相关关系 C、直线相关关系 D、曲线相关关系3.若变量X的值增加时,变量Y的值随之下降,那么变量X和变量Y之间存在着()。
A、正相关关系 B、负相关关系 C、直线相关关系 D、曲线相关关系4.相关系数等于零表明两变量()。
A.是严格的函数关系B.不存在相关关系C.不存在线性相关关系D.存在曲线线性相关关系5.相关关系的主要特征是()。
A、某一现象的标志与另外的标志之间的关系是不确定的B、某一现象的标志与另外的标志之间存在着一定的依存关系,但它们不是确定的关系C、某一现象的标志与另外的标志之间存在着严格的依存关系D、某一现象的标志与另外的标志之间存在着不确定的直线关系 6.时间数列自身相关是指()。
A、两变量在不同时间上的依存关系 B、两变量静态的依存关系C、一个变量随时间不同其前后期变量值之间的依存关系D、一个变量的数值与时间之间的依存关系7.如果变量X和变量Y之间的相关系数为负1,说明两个变量之间()。
A、不存在相关关系 B、相关程度很低 C、相关程度很高 D、完全负相关8.若物价上涨,商品的需求量愈小,则物价与商品需求量之间()。
A、无相关 B、存在正相关 C、存在负相关 D、无法判断是否相关 9.相关分析对资料的要求是()。
A.两变量均为随机的 B.两变量均不是随机的 C、自变量是随机的,因变量不是随机的 D、自变量不是随机的,因变量是随机的 10.回归分析中简单回归是指()。
A.时间数列自身回归 B.两个变量之间的回归 C.变量之间的线性回归 D.两个变量之间的线性回归11.已知某工厂甲产品产量和生产成本有直线关系,在这条直线上,当产量为1000时,其生产成本为30000元,其中不随产量变化的成本为6000元,则成本总额对产量的回归方程为()A. y=6000+24xB. y=6+0.24xC. y=24000+6xD. y=24+6000x12.直线回归方程中,若回归系数为负,则() A.表明现象正相关 B.表明现象负相关C.表明相关程度很弱D.不能说明相关方向和程度二、多项选择题1.下列属于相关关系的有()。
第八章 相关分析与回归分析习题答案

第八章 相关分析与回归分析习题参考答案一、名词解释函数关系:函数关系亦称确定性关系,是指变量(现象)之间存在的严格确定的依存关系。
在这种关系中,当一个或几个相互联系的变量取一定的数值时,必定有另一个且只有一个变量有确定的值与之对应。
相关关系:是指变量(现象)之间存在着非严格、不确定的依存关系。
在这种关系中,当一个或几个相互联系的变量取一定的数值时,可以有另一变量的若干数值与之相对应。
这种关系不能用完全确定的函数来表示。
相关分析:相关分析主要是研究两个或者两个以上随机变量之间相互依存关系的方向和密切程度的方法,直线相关用相关系数表示,曲线相关用相关指数表示,多元相关用复相关系数表示。
回归分析:回归分析是研究某一随机变量关于另一个(或多个)非随机变量之间数量关系变动趋势的方法。
其目的在于根据已知非随机变量来估计和预测随机变量的总体均值。
单相关:单相关是指仅涉及两个变量的相关关系。
复相关:复相关是指一个变量对两个或者两个以上其他变量的相关关系。
正相关:正相关是指两个变量的变化方向是一致的,当一个变量的值增加(或减少)时,另一变量的值也随之增加(或减少)。
负相关:负相关是指两个变量的变化方向相反,即当一个变量的值增加(或减少)时,另一个变量的值会随之减少(或增加)。
线性相关:如果相关的两个变量对应值在直角坐标系中的散点图近似呈一条直线,则称为线性相关。
非线性相关:如果相关的两个变量对应值在直角坐标系中的散点图近似呈现出某种曲线形式,则为非线性相关。
相关系数:相关系数是衡量变量之间线性相关密切程度及相关方向的统计分析指标。
取值在-1到1之间。
两个变量之间的简单样本相关系数的计算公式为:()()niix x y y r --∑二、单项选择1.B;2.D;3.D;4.C;5.A;6.D 。
三、判断题(正确的打“√”,错误的打“×”) 1.×; 2.×; 3.√; 4.×; 5.×; 6.×; 7.×; 8.√. 四、简答题1、什么是相关关系?相关关系与函数关系有什么区别?答:相关关系,是指变量(现象)之间存在着非严格、不确定的依存关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8章 非线性回归思考与练习参考答案8.1 在非线性回归线性化时,对因变量作变换应注意什么问题?答:在对非线性回归模型线性化时,对因变量作变换时不仅要注意回归函数的形式, 还要注意误差项的形式。
如:(1)乘性误差项,模型形式为e y AK L αβε=, (2)加性误差项,模型形式为y AK L αβε=+。
对乘法误差项模型(1)可通过两边取对数转化成线性模型,(2)不能线性化。
一般总是假定非线性模型误差项的形式就是能够使回归模型线性化的形式,为了方便通常省去误差项,仅考虑回归函数的形式。
8.2为了研究生产率与废料率之间的关系,记录了如表8.15所示的数据,请画出散点图,根据散点图的趋势拟合适当的回归模型。
表8.15生产率x (单位/周)1000 2000 3000 3500 4000 4500 5000废品率y (%)5.26.56.88.110.210.313.0解:先画出散点图如下图:从散点图大致可以判断出x和y之间呈抛物线或指数曲线,由此采用二次方程式和指数函数进行曲线回归。
(1)二次曲线SPSS输出结果如下:从上表可以得到回归方程为:72ˆ 5.8430.087 4.4710yx x -=-+⨯ 由x 的系数检验P 值大于0.05,得到x 的系数未通过显著性检验。
由x 2的系数检验P 值小于0.05,得到x 2的系数通过了显著性检验。
(2)指数曲线从上表可以得到回归方程为:0.0002t ˆ 4.003ye = 由参数检验P 值≈0<0.05,得到回归方程的参数都非常显著。
从R2值,σ的估计值和模型检验统计量F值、t值及拟合图综合考虑,指数拟合效果更好一些。
8.3 已知变量x与y的样本数据如表8.16,画出散点图,试用αeβ/x来拟合回归模型,假设:(1)乘性误差项,模型形式为y=αeβ/x eε(2)加性误差项,模型形式为y=αeβ/x+ε。
表8.16序号x y 序号x y 序号x y1 4.20 0.086 6 3.20 0.150 11 2.20 0.3502 4.06 0.090 7 3.00 0.170 12 2.00 0.4403 3.80 0.100 8 2.80 0.190 13 1.80 0.6204 3.60 0.120 9 2.60 0.220 14 1.60 0.9405 3.40 0.130 10 2.40 0.240 15 1.40 1.620解:散点图:(1) 乘性误差项,模型形式为y=αe β/x e ε线性化:lny=ln α+β/x +ε 令y1=lny, a=ln α,x1=1/x . 做y1与x1的线性回归,SPSS 输出结果如下:Model Summ aryb.999a .997.997.04783Model 1RR SquareAdjusted R SquareStd. E rror of the EstimateP redictors: (Constant), x1a. Dependent Variable: y1b. ANOVA b10.930110.9304778.305.000a.03013.00210.96014Regression Residual TotalModel 1Sum of Squares dfMean SquareF Sig.P redictors: (Constant), x1a. Dependent Variable: y1b.Coe fficientsa -3.856.037-103.830.0006.080.088.99969.125.000(Constant)x1Model1B Std. E rror Unstandardized Coefficients BetaStandardizedCoefficientstSig.Dependent Variable: y1a.从以上结果可以得到回归方程为:y1=-3.856+6.08x1F 检验和t 检验的P 值≈0<0.05,得到回归方程及其参数都非常显著。
回代为原方程为:y=0.021e 6.08/x (2)加性误差项,模型形式为y=αeβ/x+ε不能线性化,直接非线性拟合。
给初值α=0.021,β=6.08(线性化结果),NLS 结果如下:Parameter E stimates.021.001.020.0236.061.0445.9656.157P arametera b E stimateStd. E rrorLow er Bound Upper Bound95% Confidence I ntervalANOVA a4.4582 2.229.00113.0004.459152.46714Source Regression ResidualUncorrected Total Corrected TotalSum of SquaresdfMean SquaresDependent variable: yR squared = 1 - (Residual Sum of Squares) /(Corrected Sum of Squares) = 1.000.a.从以上结果可以得到回归方程为: y=0.021e 6.061/x根据R 2≈1,参数的区间估计不包括零点且较短,可知回归方程拟合非常好,且其参数都显著。
8.4 Logistic 函数常用于拟合某种消费品的拥有率,表8.17(书上239页,此处略)是北京市每百户家庭平均拥有的照相机数,试针对以下两种情况拟合Logistic 回归函数。
(1)已知100u =,用线性化方法拟合, (2)u 未知,用非线性最小二乘法拟合。
解:(1),100u =时,的线性拟合。
对0111t y b b u=+函数线性化得到:11ln() 1.8510.264100y -=--0111ln()ln ln 100b t b y -=+,令311ln()100y y =-,作3y 关于t 的线性回归分析,SPSS 输出结果如下:由表Model Summary 得到,0.994R =趋于1,回归方程的拟合优度好,由表ANOVA 得到回归方程显著,由Coefficients 表得到,回归系数都是显著的,得到方程:11ln() 1.8510.264100y -=--,进一步计算得到:00.157b =,10.768b =(100u =)回代变量得到最终方程形式为: 1ˆ0.010.1570.768ty=+⨯ 最后看拟合效果,通过sequence 画图:由图可知回归效果比较令人满意。
(2)非线性最小二乘拟合,取初值100u =,00.157b =,10.768b =: 一共循环迭代8次,得到回归分析结果为:Parameter E stimates91.062 2.03586.74795.377.211.028.152.271.727.012.701.753P arameteru b c E stimate Std. E rrorLow er Bound Upper Bound95% Confidence I ntervalANOVA a60774.331320258.11085.36916 5.33660859.7001915690.38618Source Regression Residual Uncorrected Total Corrected Total Sum ofSquares df MeanSquaresDependent variable: yR squared = 1 - (Residual Sum of Squares) /(Corrected Sum of Squares) = .995.a.0.995R =>0.994,得到回归效果比线性拟合要好,且:91.062u =,00.211b =,10.727b =,回归方程为:110.211*0.72791.062ty =+。
最后看拟合效果,由sequence 画图:得到回归效果很好,而且较优于线性回归。
8.5表8.18(书上240页,此处略)数据中GDP 和投资额K 都是用定基居民消费价格指数(CPI )缩减后的,以1978年的价格指数为100。
(1) 用线性化乘性误差项模型拟合C-D 生产函数;(2) 用非线性最小二乘拟合加性误差项模型的C-D 生产函数; (3) 对线性化检验自相关,如果存在自相关则用自回归方法改进; (4) 对线性化检验多重共线性,如果存在多重共线性则用岭回归方法改进; (5) 用线性化的乘法误差项模型拟合C-D 生产函数;解:(1)对乘法误差项模型可通过两边取对数转化成线性模型。
ln y =ln A + α ln K + β ln L令y ′=ln y ,β0=ln A ,x 1=ln K ,x 2=ln L ,则转化为线性回归方程:y ′=β0+ α x 1+ βx 2+ εSPSS 输出结果如下:模型综述表Model Summ aryb.997a .994.993.04836Model 1RR SquareAdjusted R SquareStd. E rror of the EstimateP redictors: (Constant), lnL, lnK a. Dependent Variable: lnYb.从模型综述表中可以看到,调整后的为0.993,说明C-D 生产函数拟合效果很好,也说明GDP 的增长是一个指数模型。
方差分析表ANOVA b8.4462 4.2231805.601.000a.05122.0028.49724Regression Residual TotalModel 1Sum of SquaresdfMean SquareF Sig.P redictors: (Constant), lnL, lnKa. Dependent Variable: lnYb.从方差分析表中可以看到,F 值很大,P 值为零,说明模型通过了检验,这与上述分析结果一致。
系数表Coe fficients a-1.785 1.438-1.241.228.801.056.86114.370.000.402.171.141 2.354.028 (Constant)lnKlnLModel1B Std. E rrorUnstandardizedCoefficientsBetaStandardizedCoefficientst Sig.Dependent Variable: lnYa.根据系数表显示,回归方程为:尽管模型通过了检验,但是也可以看到,常数项没有通过检验,但在这个模型里,当lnK和lnL都为零时,lnY为-1.785,即当K和L都为1时,GDP为0.168,也就是说当投入资本和劳动力都为1个单位时,GDP将增加0.168个单位,这种解释在我们的承受范围内,可以认为模型可以用。
