复变函数论课后题答案(第三版钟玉泉)
复变函数论第三版课后习题答案[1]
![复变函数论第三版课后习题答案[1]](https://uimg.taocdn.com/03de2b78a26925c52cc5bf62.webp)
第一章习题解答(一)1.设z ,求z 及Arcz 。
解:由于3iz e π-==所以1z =,2,0,1,3Arcz k k ππ=-+=±。
2.设121z z =,试用指数形式表示12z z 及12z z 。
解:由于6412,2i i z e z i e ππ-==== 所以()64641212222i i iiz z e eee πππππ--===54()146122611222ii i i z e e e z e πππππ+-===。
3.解二项方程440,(0)z a a +=>。
解:12444(),0,1,2,3k ii za e aek πππ+====。
4.证明2221212122()z z z z z z ++-=+,并说明其几何意义。
证明:由于2221212122Re()z z z z z z +=++2221212122Re()z z z z z z -=+-所以2221212122()z z z z z z ++-=+其几何意义是:平行四边形对角线长平方和等于于两边长的和的平方。
5.设z 1,z 2,z 3三点适合条件:0321=++z z z ,1321===z z z 。
证明z 1,z 2,z 3是内接于单位圆1=z 的一个正三角形的顶点。
证 由于1321===z z z,知321z z z ∆的三个顶点均在单位圆上。
因为33331z z z ==()[]()[]212322112121z z z z z z z z z z z z +++=+-+-=21212z z z z ++=所以, 12121-=+z z z z ,又)())((122122112121221z z z z z z z z z z z z z z +-+=--=-()322121=+-=z z z z故 321=-z z ,同理33231=-=-z z z z ,知321z z z ∆是内接于单位圆1=z 的一个正三角形。
第二章 复变函数钟玉泉版习题解答提示

第二章 习题解答提示(一)1.(定理)设连续曲线[]βα,),(:∈=t t z z C ,有[]),(0)(00βα∈≠'t t z ,则(试证)曲线C 在点)(0t z 有切线。
分析 1)在)(0t z 的某去心领域内能联结割线()(10t z t z ; 2)割线的极限位置就是切线。
证1),0>∃δ使}{\),(0001t t t t δδ+-∈∀,有)()(01t z t z ≠,即C 在)(0t z 的 对应去心领域内无重点,即能够连接割线()(10t z t z ,否则就存在数列{},01t t n →使)()(01t z t z n =。
于是0)()(lim )(0101001=--='→t t t z t z t z n n t t n ,这与假设矛盾。
2)01001),(t t t t t >⇒+∈δ,[],)()(arg )()(arg010101t z t z t t t z t z -=--[])()(arg lim 010t z t z t t -∴→(对)(0t z 割线)()(10t z t z 倾角的极限)⎥⎦⎤⎢⎣⎡--=--=→→01010101)()(lim arg )()(arglim 0101t t t z t z t t t z t z t t t t )(a r g0t z '=。
因此,割线确实有极限位置,即曲线C 在点)(0t z 的切线存在,其 倾角为)(arg 0t z '.3. 设 ⎪⎩⎪⎨⎧=≠+==+++-.0,0;0,)(223333)(z iy x z z f y x y x i y x试证)(z f 在原点满足..R C -条件,但却不可微. 证 1) 有公式(2.5)及(2.6)有;1)0()(lim0i z f z f iv u x y x x +=-=+→=.1)0()(lim0+=-=+-→=i zf z f v iu y x y y2) 但z 当沿直线0)0(→≠=m mx y 时,zf z f z )0()(lim-→随m 而变.4. 试证下列函数在z 平面上任何点都不解析: (1) z ; (2) y x +; (3) z Re ; (4)z1. 分析 由于孤立的可微点不是解析点,故只须证明各函数 个别点外处处不满足解析的必要条件:..R C -条件.证 (1) 当0≠z 时,即y x ,至少有一0≠时,或有,y x v u ≠ 或有.x x v u -≠故z 至多在原点可微;(2) 在上处处不满足..R C -条件;(3) 的结论同(2); (4),122y x iy x zz z z ++==除原点外,..R C -条件处处不成立. 5. 判断下列函数的可微性和解析性: (1) ;)(22y ix xy z f += (2) ;22iy x +(3) ;32)(33iy x z f += (4) ).3(33223y xy i xy x -+- 分析 如只在孤立点或只在直线上可微,都未形成由可微点构成的圆邻域,故都在其上不解析;利用推论2.3考查可微性,然后应用解析的定义.解 (1) .),(,),(22y x y x v xy y x u == 仅当0==y x 时,22,22xy v u xy x v u y x y y x -=-=====且此四偏导数在原点连续,故)(z f 只在原点可微,且.0)2()()0()0,0(2)0,0(===+='xyi x iv u f x x6. 若函数)(z f 在区域D 内解析,且满足下列条件之一,试 证)(z f 在D 内必为常数.(1) 在D 内;0)(='z f (2))(z f 在D 内解析; (3) )(z f 在D 内为常数;(4) )(Re z f 或)(Im z f 在D 内为常数. 分析 分别由各题设条件及..R C -条件得:在D 内,0====y x y x v v u u 从而v u ,在D 内为常数.引理* 在区域D 内0====y x y x v v u u(A)⇒在D 内v u ,为常数.事实上,1) 设000iy x z +=为D 内一定点.)(00y y i x x iy x z ∆++∆+=+=是D 内任一点.若这两点能用全含于D 内的直线段z z 0来联结, 则有:),(),(0000y x u y y x x u u -∆+∆+=∆ x y y x x u x ∆∆+∆+=),(00θθ).10(),(00<<∆∆+∆++θθθy y y x x u y )(B这是因为,”若令),10(,00≤≤∆+=∆+=t y t y y x t x x 则有),,()(00y t y x t x u t F ∆+∆+= x y t y x t x u t F x ∆∆+∆+='),()(00 .),(00y y t y x t x u y ∆∆+∆++而.,y dtdy x dt dx ∆=∆= 由数学分析中的微分中值定理得)()01)(()0()1(θθF F F F '=-'=-).10(<<θ于是)(B 式成立.”从而由)(A 知,0=∆u 即),(),(00y x u y x u =.即在D 内u 为常数.同理,在D 内v 为常数.2) 若联结两点0z 与z 的直线段不全含于D 内,由区域的连通性知,可用全含在D 内的折线段将0z 与z 连接.若111iy x z +=是折线上0z 后面的一个顶点,则在)1段中u ∆的表达式)(B 中, 令,1010,y y y x x x =∆+=∆+立即得).,(),(0011y x u y x u =如此逐步推算,由一顶点至另一顶点,最后可得()().,,00y x u y x u =即在D 内u 为常数. 同理,在D 内v 为常数.引理*证毕. 证(1)...)(0,y y x x iu v R C iv u z f D iy x z --+='=∈+=∀(2) 由题设条件iv u +及iv u -在D 内解析,再由..R C -条件可推得0====y x y x v v u u 最后有引理*可得证.(3) 由题设,在D 内=)(z f 常数C . 1) .0)(0≡⇒=z f C 2) .0)(0≠⇒≠z f C证一 )()()(2z f C z f C z f =⇒=在D 内解析,于是由题(2)得知D z f 在)(内为常数.证二 ,0222≠=+C v u 分别对y x ,微分,再应用..R C - 条件,讨论解二元一次方程组,即得在D 内.0====y x y x v v u u(4) 由..R C -条件推得,在D 内.0====y x y x v v u u 8. 试证下列函数在z 平面上解析,并分别求出其导函数. (1) ;33)(3223i y xy yi x x z f --+=(2) );sin cos ()sin cos ()(y x y y ie y y y x e z f xx ++-= (3) ;cos sin )(xshy i xchy z f += (4) ;sin cos )(xshy i xchy z f -= 证 应用定理2.5及求导公式(2.7).),2cos(2sin 21sin )cos()cos(cos nb a b bn nb a b a a ++=+++++ (1)及).2sin(2sin 21sin )sin()sin(sin nb a b bn nb a b a a ++=+++++ (2)证一 分别证明(1)和(2).按定义将正,余弦函数表成指数函数,再等比级数求和的公式简化.注 由于a 和b 是复数,不能从(1)+i (2)着手化简后,再比较实,虚部. 证二 先将(1)和(2)式两端各乘2sin b去分母后,再应用三角函数中积化和差的公式,代入左端化简.16. 试证:(1)ishz iz =)sin(;(2)chz iz =)cos(;(3)z i iz sh sin )(=;(4)z iz ch cos )(=; (5)ithz iz tg =)(;(6)itgz iz th =)(.证 (1)、(2)应用定义2.5及2.7;(3)由(1);(4)由(2);(5)、(6)由定义2.6、及2.7及(1)、(2). 17. 试证:(1)122=-z sh z ch ;(2)1sec 22=+z th z h ;(3)212121)(shz shz chz chz z z ch +=+.证 (1)由16题(1)、(2);(2)由本题(1);(3)由16题(1)、(2). 18. 若,iy x z +=试证:(1)xshy i xchy z cos sin sin +=; (2)xshy i chy z sin cos cos -=;(3)y sh x z 222sin sin +=; (4)y sh x z222cos cos +=.证 (1)、(2)应用16题(1)、(2);(3)、(4)分别应用本题(1)、(2)及17题(1). 20. 试解方程:(4)0sin cos =+z z ;(5)i tgz 21+=. 解 (4).0)sin 21cos 21(2=+z zππk z +-=4(k 为整数).(5)Arc z =)21(1)21(121)21(i i i i Lni i tg +-++=+=+-=5221i Ln i⎥⎦⎤⎢⎣⎡-+=21)12(21arctg k z π +).,1,0(5ln 4±=k i21. 设θi re z =,试证[])cos 21ln(21)1ln(Re 2θr r z -+=-. 证 设ϕρi e z =-1,则[]ρln )1ln(Re =-z .22. 设3z w =确定在从原点0=z 起沿正实轴割破了的z 平面上,并且i i w -=)(,试求)(i w -之值.解一 32)(3)()(πθk z ik ez r z w +=,(G z ∈:πθ2)(0<<z ;2,1,0=k )1) 利用i i w -=)(定)2;2,=k k 求)(2i w -. 解二 作图2.0.13)(z z f =3arg 31)(arg π=∆=∆⇒z z f c c .再由公式(2.25)计算).)((6i ei f π-=-23. 设3z w =确定在从原点0=z 起沿负实轴割破了的z 平面上,并且32)2(-=-w (这是边界上岸点对应的函数值),试求)(i w 之值.解一 .,222ππii e i e ==-由32)2(-=-w 定,1,=k k 从而.)(651i ei w π=解二 作图2.0.2.3)(z z f =,而[].arg )2(arg 3π=-=-z f又∆ .6arg 31)(arg ,2arg ππ-=∆=∆-=z z f z c c 再应用公式(2.25)计算))((65i e i f π=.24. 已知1)(4+=z z f 在ox 轴上A 点(1>=R OA )的初值为14++R ,令z 由A 起沿正向再以原点为中心的圆周上走41圆周而至oy 轴的B 点,问)(z f 在B 点的终值为何?分析 题设的函数1)(4+=z z f 是具有四个有限支点的二值函数,讨论起来比较繁难,而经过变数代换4z w =后,就简化成具有单有限支点-1的二值函数1+=w w .解 z 在z 平面上沿以0=z 为心,1>R 为半径的圆周c 从A 走到B ,经过变换4z w =,其象点w 在w 平面上w=0为心,14>R 为半径的象圆周Γ从'A 走到B ',刚好绕1+=w w 的交点-1转一整周.故它在B '的值为1+-w .因此1|)(|)(4+-=-=R z f z f A B . 25. 试证:在将z 平面适当割开后,函数32)1()(z z z f -=能分出三个单值解析分支.并求出在点2=z 取负值的那个分支在i z =的值.分析 仿例2.3.14,2.3.15及2.3.16解之.证 )(z f 的支点是,1,0=z 在沿]1,0[割开的z 平面的区域D 内,)(z f 能分出三个单值解析分支.证一 令11r z =-1θi e ,2r z = 2θi e当2=z 时,2,1,0,2121====r r θπθ.由已知π)(arg z f k 定1,=k k .然后计算i ei f 127612)(π-=32232121)]()[()(πθθk ik ez r z r z f ++=证二 作图2.0.4.由2到i ,取路线1C .,127)(arg 1π=∆z f c 再按公式(2.25)计算)(i f 证三 作图2.0.4.由2到I ,取路线2C ,π1217)(arg 2-=∆z f c .再按(2.25)计算)(i f .(二)1.设21)(z z z f -=,试证().1,0)()(Re <>⎥⎦⎤⎢⎣⎡'z z f z f z证2224221I m (2111)()(zz i z z z z f z f z -=-=-+='.2.设zzz f -=1)(,试证 ().1,0)()(1Re <>⎥⎦⎤⎢⎣⎡'''+z z f z f z 证3.若函数在上半平面内解析,试证函数在下半平面内解析. 证一设z z 、0分别为下半z 平面内的定点及动点,可证)()()(lim0000z f z z z f z f z z '=--→.由0z 的任意性及解析的定义得证.证二),(),()(y x iv y x u z f +=在上半平面)0(>y 内解析⇒1)),(),,(y x v y x u 在0>y 可微,且2)yy x v x y x u ∂∂=∂∂),(),(, )0(),(),(>∂∂-=∂∂y xy x v y y x u ()* 考查)0)(,(),()(<--=y y x iv y x u z f ,则可证:1)),(),,(y x v y x u ---在0<y 内可微,且由()*式有 2)[][]yy x v x y x u y ∂--∂*∂-∂>-),()(,)0(, [][]xy x v y y x u ∂--∂-=∂-∂),()(,. 4.(形式导数)(1)设二元函数),(y x u 有偏导数.此函数可以写成iy x z +=及z 的函数).2,2(izz z z u u -+= 试证(形式地)⎪⎪⎭⎫⎝⎛∂∂+∂∂=∂∂⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=∂∂y u i x u z u y u i x u z u 21,21 (2)设复变函数),(),()(y x iv y x u z f +=,且),(y x u 和),(y x v 都有偏导数.试证(形式地):对于)(z f ,柯西—黎曼(Cauchy-Riemann)条件可以写成0=∂∂+∂∂=∂∂zvi z u z f (由此可见,解析函数是以条件0=∂∂zf为其特征的.因此,我们不妨说,一个解析函数与z 无关,而是z 一数的函数.)证 (形式地)(1)由于)(21),(21z z iy z z x -=+=. 这里视z z ,为两个独立变量.根据复合函数求偏导的法则,即可形式地得证。
复变函数答案 钟玉泉 第五章习题全解
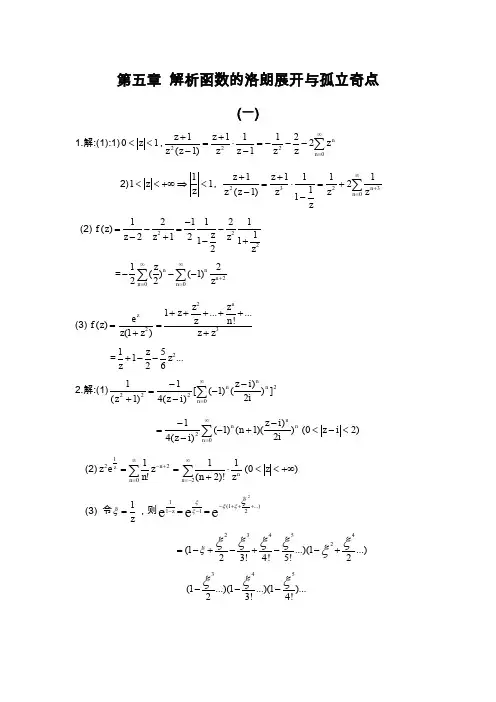
(z 2 1)2 4(z i)2 n0
2i
1 4(z i)2
(1)n (n 1)( z i)n )n
n0
2i
(0
z i
2)
1
(2) z 2e z
1 z n2
1 1 (0 z )
n0 n!
n2(n 2)! z n
e e e (3) 令 1 ,则 z
1
1z
1
2
(1 ...) 2
f (z) w0 解 析 , 即 为整函数 . 又 因 f (z) 非 常 数 , 所 以 g(z) 非常 数 , 其值全 含于一圆
g(z) 1 之内,与刘维尔定理矛盾. 0
11.证明:由题意, f (z) 在 z0 的去心邻域内的洛朗展开式可设为
f (z)
c1 z z0
cn (z z0 )n
(a)
0
6.证明:令 g(z) (z a)k f (z) 。由题设, g(z) 在 k {a}: 0 | z a | R 内有界。由
定理 5.3(3),a 为 g(z) 的可去奇点,则 a 为 g(z) 的解析点。又由定理 5.4(2),
若
a
为
f
(z) 的
m
级极点,则在点
a
的某去心邻域内能表成
正好是以 1 为中心的无穷远点的去心领域。所以根据题中的洛朗展式,只能判
定 z 是 f (z) 的可去奇点。
3.证明:由孤立奇点的定义,又有 f (z) 在点 a 解析,故知 a 为 g(z) 的孤立奇点,
且 lim g(z) lim f (z) f (a) f (a) g(a) ,故 a 为 g(z) 的可去奇点。故在 a 业
(充分性) 若
复变函数论第三版课后习题答案

第一章习题解答(一)1.设z ,求z 及Arcz 。
解:由于3i z e π-== 所以1z =,2,0,1,3Arcz k k ππ=-+=±。
2.设121z z =,试用指数形式表示12z z 及12z z 。
解:由于6412,2i i z e z i e ππ-==== 所以()64641212222i i iiz z e eee πππππ--===54()146122611222ii i i z e e e z e πππππ+-===。
3.解二项方程440,(0)z a a +=>。
解:12444(),0,1,2,3k ii za e aek πππ+====。
4.证明2221212122()z z z z z z ++-=+,并说明其几何意义。
证明:由于2221212122Re()z z z z z z +=++2221212122Re()z z z z z z -=+-所以2221212122()z z z z z z ++-=+其几何意义是:平行四边形对角线长平方和等于于两边长的和的平方。
5.设z 1,z 2,z 3三点适合条件:0321=++z z z ,1321===z z z 。
证明z 1,z 2,z 3是内接于单位圆1=z 的一个正三角形的顶点。
证 由于1321===z z z,知321z z z ∆的三个顶点均在单位圆上。
因为33331z z z ==()[]()[]212322112121z z z z z z z z z z z z +++=+-+-=21212z z z z ++=所以, 12121-=+z z z z ,又)())((122122112121221z z z z z z z z z z z z z z +-+=--=-()322121=+-=z z z z故 321=-z z ,同理33231=-=-z z z z ,知321z z z ∆是内接于单位圆1=z 的一个正三角形。
复变函数答案 钟玉泉 第三章习题全解

14.证明:由上题知 C 和 Γ 均为光滑曲线,因 Φ(w) 沿 Γ 连续以及 f (z), f ′′(z) 在包 含 C 的区域 D内解析,因此 Φ[ f (z)] f ′(z) 也连续,故公式中的两端积分存在.则
|z| =1 z + 2
设 z = eiθ , dz = ieiθ dθ ⇒
2π i iθdθ 2π (i cosθ − sinθ )[(cosθ + 2) − i sinθ ]
e 0 = ∫ e ∫ 0
iθ + 2 = 0
dθ (cos θ + 2)2 +sin2 θ
∫= 2π −2 sinθ + i(1+ 2 cosθ )dθ
∂2 ( ∂x2
+
∂2 ∂y2 )
f(Biblioteka )2=4(ux 2
+
vx2 ) +
2u (ux2
+
uy2
)+
2v (vx2
+
vy2
)
=4( ux2 + vx2 )=4 f ′(z ) 2
18.证明: f (z)在 D 内解析,则 f ′(z) 在 D 内也解析.已知 f ′(z) ≠ 0,则 ln f ′(z)在
π
(3)下半圆周方程为 z = eiθ ,π ≤ θ ≤ 2π ,则
∫ ∫ ∫ z dz = 2π deiθ = i 0ie iθ dθ = 2
C
π
π
3.证明:(1) C : x = 0,−1 ≤ y ≤ 1
复变函数论第三版课后习题答案

第一章习题解答〔一〕1.设z =z 及Arcz 。
解:由于3i z e π-== 所以1z =,2,0,1,3Arcz k k ππ=-+=±。
2.设121z z =,试用指数形式表示12z z 及12z z 。
解:由于6412,2i i z e z i e ππ-==== 所以()64641212222i i iiz z e eee πππππ--===54()146122611222ii i i z e e e z e πππππ+-===。
3.解二项方程440,(0)z a a +=>。
解:12444(),0,1,2,3k ii z a e aek πππ+====。
4.证明2221212122()z z z z z z ++-=+,并说明其几何意义。
证明:由于2221212122Re()z z z z z z +=++2221212122Re()z z z z z z -=+-所以2221212122()z z z z z z ++-=+其几何意义是:平行四边形对角线长平方和等于于两边长的和的平方。
5.设z 1,z 2,z 3三点适合条件:0321=++z z z ,1321===z z z 。
证明z 1,z 2,z 3是内接于单位圆1=z 的一个正三角形的顶点。
证 由于1321===z z z,知321z z z ∆的三个顶点均在单位圆上。
因为33331z z z ==()[]()[]212322112121z z z z z z z z z z z z +++=+-+-=21212z z z z ++=所以, 12121-=+z z z z ,又)())((122122112121221z z z z z z z z z z z z z z +-+=--=-()322121=+-=z z z z故 321=-z z ,同理33231=-=-z z z z ,知321z z z ∆是内接于单位圆1=z 的一个正三角形。
复变函数答案 钟玉泉 第六章习题全解
Re s
z
(6) Re s
z 1
ez ez e ( z 1) 2 | z 1 2 z 1 z 1 2
Re s
z 1
ez ez e 1 ez ez e ( z 1 ) | Re s ( z 1 ) | z 1 z 1 2 2 2 2 z 1 z 1 2 z 1 z 1 z 1 2 ez e 1 e ( Re s f ( z ) Re s f ( z )) z 1 z 1 z 2 1 2
第六章 留数理论及其应用
(一)
1.解:(1)z=1 是一级极点,故由推论 6.3 知
Re s f ( z ) ( z 1)
z 1
1 1 | 2 z 1 ( z 1)( z 1) 4
Z=-1 是二级极点,同前由推论 6.4 知
Re s f ( z ) [( z 1) 2
Re s f ( z ) C1
z 0
4 3
z z 0
又由 z=0 是唯一有限奇点,故 Re s f ( z ) Re s f ( z ) (4)由 e z 1 1
1
4 3
1 1 所以 Re s f ( z ) 1 z 1 z 1 2!z 12
由儒歇定理,f(z)与
而 f(z)=-z 在 C 内只有一个零点,所以
f ( z) g ( z) ( z) z
只有一个零点,记为 z ,使得 ( z ) z C 或 ( z ) z 0 0 0 0 0
Re s f ( z )
z n
1 的 sin z
1 | z (1) n (sin z )
1 e2 z 1 (2 z ) 2 (2 z ) 3 2 2 4 (3)由 4 4 2z 3 2 所以 z z 2! 3! z z 3z
复变函数论第三版钟玉泉第五章
(3)
(1).
因主要部分的系数
cn
1
2i
f
a n1
d
其中 : a , 可任意小,故
cn
1
2
f
a n1
d
1
2
M
n1
2
M n
cn 0 n 1,2,
13
2020/7/9
复变函数
华中科技大学数学与统计学院
3. 施瓦茨(Schwarz)引理
Schwarz引理 如果函数f(z)在单位圆|z|<1内解析, 并且满足条件 f(0)=0,|f(z)|<1(|z|<1),则在单位圆 |z|<1内恒有|f(z)|≤|z|,且有 | f (0) |1. 如果上式等号成立,或在圆|z|<1内一点z0≠0 处前一式等号成立,则(当且仅当)
12
2020/7/9
复变函数
华中科技大学数学与统计学院
证 (1) (2). 由(1)有
f z c0 c1z a c2z a2 0 z a R
因此 lim za
(2) (3).
f
z
因
c0
lim
f z
b
则
0,
za
0, z
:0
|
z
a
| ,有 |
f
(z) b |
,
于是,有 | f (z) || b | ,即f (z)在a的去心邻域内有界。
ez z3
展开成洛朗级数.
例2 求函数
f
z
sinh z2
z
在 0 z
内的洛朗级数。
例3 试问函数 f 洛朗级数?
z
tan
《复变函数》第二章习题全解钟玉泉版
《复变函数》第二章习题全解钟玉泉版第二章解析函数(一)1.证明:0>?δ,使{}0001/),(t t t t δδ+-∈?,有)()(01t z t z ≠,即C 在)(0t z 的对应去心邻域内无重点,即能够联结割线)()(10t z t z ,是否就存在数列{}01t t n →,使)()(01t z t z n =,于是有0)()(lim )(0101001=--='→t t t z t z t z n n t t n此与假设矛盾.01001),(t t t t t >?+∈δ 因为 [])()(arg )()(arg010101t z t z t t t z t z -=--所以 []])()(lim arg[)()(arglim )()(arg lim 0101010101010101t t t z t z t t t z t z t z t z t t t t t t --=--=-→→→因此,割线确实有其极限位置,即曲线C 在点)(0t z 的切线存在,其倾角为)(arg 0t z '.2.证明:因)(),(z g z f 在0z 点解析,则)(),(00z g z f ''均存在.所以 )()()()()()(lim )()()()(lim )()(lim 00000000000z g z f z z z g z g z z z f z f z g z g z f z f z g z f z z z z z z ''=----=--=→→→ 3.证明:()()()()()3322,0,0,,0,00x y x y u x y x y x y ≠?-?=+??=?()()()()()3322,0,0,,0,00x y x y v x y x y x y ≠?+?=+??=?于是()()()00,00,00,0limlim 1x x x u x u xu xx →→-===,从而在原点()f z 满足C R -条件,但在原点,()()()()()'0,00,0x x u iv u iv f f z z z+-+-=()()()()()()333311i x y i zx y z ??+--+??=+??当z 沿0y x =→时,有()()()'212f f z i z x --+= 故()f z 在原点不可微.4.证明:(1)当0≠z 时,即y x ,至少有一个不等于0时,或有y x u u ≠,,或有y x u u ≠-,故z 至多在原点可微.(2)在C 上处处不满足C R -条件. (3)在C 上处处不满足C R -条件.(4)221yx yix z z z z ++==,除原点外, 在C 上处处不满足C R -条件. 5.解:(1) y x y x v xy y x u 22),(,),(==,此时仅当0==y x 时有 xy v xy u x v y u x y y x 22,22-=-===== 且这四个偏导数在原点连续,故)(z f 只在原点可微. (2) 22),(,),(y y x v x y x u ==,此时仅当y x =这条直线上时有00,22=-=====x y y x v u y v x u且在y x =这四个偏导数连续,故)(z f 只在y x =可微但不解析. (3) 333),(,2),(y y x v x y x u ==,且00,9622=-=====x y y x v u y v x u 故只在曲线0212312=-x y 上可微但不解析.(4) 32233),(,3),(y y x y x v xy x y x u -=-=在全平面上有xy v xy u y x v y x u x y y x 66,33332222-=-=-=-==-= 且在全平面上这四个偏导数连续,故可微且解析. 6.证明:(1)y y x x iu v iv u z fD yi x z -=+='=∈+=?)(0,(2)设().f z u iv =+则()f z u iv =-,由()f z 与()f z 均在D 内解析知,,x y y x u v u v ==-,,x y y x u v u v =-=结合此两式得0x y x y u u v v ====,故,u v 均为常数,故)(z f 亦为常数. (3)若0)(=≡C z f ,则显然0)(≡z f ,若0)(≠≡C z f ,则此时有0)(≠z f ,且2)()(C z f z f ≡,即)()(2z f C z f ≡也时解析函数,由(2)知)(z f 为常数.(4)设().f z u iv =+,若C y x u ≡),(,则0,0≡≡y x u u ,由C R -条件得0,0≡=≡-=x y y x u v u v 因此v u ,为常数, 则)(z f 亦为常数.7.证明:设,f u iv g i f p iQ =+==+则,,f u iv g v iu =-=-由 ()f z 在D 内解析知,x y y x u v u v ==-从而 ,x x y v y y x p v u Q p v u Qx ==-====- 因而()g z 亦D 内解析.8.解:(1)由32233),(,3),(y y x y x v xy x y x u -=-=,则有222233,6,6,33y x v xy v xy u y x u y x y x -==-=-=故y x y x v v u u ,,,为连续的,且满足C R -条件,所以()z f 在z 平面上解析,且 22236)33()(z xyi y x i v u z f x x =+-=+='(2) ()()()(),cos sin ,cos sin x x u x y e x y y y v x y e y y x y =-?=- ()cos sin cos x x y u e x y y y y v =-+= ()sin sin cos x y x u e x y y y y v =--+=-故()f z 在z 平面上解析,且()()()'cos 1sin sin 1cos x xf z e y x y y ie y x y y =?+-+?+-(3)由xshy y x v xchy y x u cos ),(,sin ),(==,则有xchy v xshy v xshy u xchy u y x y x cos ,sin ,sin ,cos =-===故y x y x v v u u ,,,为连续的,且满足C R -条件,所以()z f 在z 平面上解析,且 z xshyi xchy i v u z f x x cos sin cos )(=-=+=' (4)由xshy y x v xchy y x u sin ),(,cos ),(-==,则有xchy v xshy v xshy u xchy u y x y x sin ,cos ,cos ,sin -=-==-= 故y x y x v v u u ,,,为连续的,且满足C R -条件,所以()z f 在z 平面上解析,且 z xshyi xchy i v u z f x x sin cos sin )(-=--=+=' 9.证明:设,i z x yi re θ=+=则cos ,sin ,x r y r θθ== 从而cos sin ,sin cos r x y x y u u u u u r u r θθθθθ=+=-+cos sin ,sin cos ,r x y x y v u v v v r v r θθθθθ=+=-+再由11,r r u v v u r rθθ==-,可得,x y y x u v u v ==-,因此可得()f z 在点z 可微且()()()'11cos sin sin cos x y r r f z u iu r u u i r u u r r θθθθθθ=-=--+ ()()1cos sin sin cos r i u i u r θθθθθ=--+()()cos sin sin cos r r i u i v θθθθ=-++ ()()cos sin r r i u iv θθ=-+ ()()1cos sin r r r r ru iv u iv i zθθ=+=++10.解:(1)x y i x z i e e e 2)21(22--+--== (2)222222y zxyiy zz e e e -+-==(3) 22222211x yi xy ix iyx yx yx y ze eeee--++++===?所以22221Re cos x yx y x y ze e ++??=11.证明:(1)因为)sin (cos y i y e e e e e x yi x yi z z +=?==+ 因此 )sin (cos y i y e e x z -=而)sin (cos y i y e e e e e x yi x yi z z -=?==--,得证.(2)因为 ie e z iziz 2sin --=所以 z ie e i e e z iziz z i z i sin 22sin =+=-=--- (3)因为2cos iziz e e z -+=所以z e e e e z iziz z i z i cos 22cos =+=+=-- 12.证明:分别就m 为正整数,零,负整数的情形证明,仅以正整数为例当1=m 时,等式自然成立. 假设当1-=k m 时,等式成立.那么当k m =时,kz z k z k z e e e e =?=-1)()(,等式任成立. 故结论正确.13.解:(1) )1sin 1(cos 333i e e e e i i +=?=+(2) ()()()11cos 12i i i i e e i ---+-=()112i i i e e -+++=cos11sin1122e i e e e=++- ? ?????14.证明:(1)由于z z g z z f ==)(,sin )(在点0=z 解析且01)0(,0)0()0(≠='==g g f 因此 11cos sin lim0===→z z zz z(2)由于0)(,1)(=-=z g e z f z 在点0=z 解析,且01)0(,0)0()0(≠='==g g f因此 11lim0==-=→z z z z e ze(3)由于z z z g z z z z f sin )(,cos )(-=-=在点0=z 解析, 且1)0(,0)0()0(,0)0()0(,0)0()0(='''=''=''='='==g g f g f g f 因此3cos 1sin cos 1lim sin cos lim00=-+-=--→→zzz z z z z z z z z 15.证明:2cos iziz e e z -+=)cos()cos(cos nb a b a a +++-+=222)()()()(nb a i nb a i b a i b a i ia ia e e e e e e +-++-+-++++++ =??--?+--?+-+ib bn i ia ib b n i ia e e e e e e 111121)1()1(=)2cos(2sin 21sinnb a b bn ++=右边同理证明(2).16.证明:(1) z i e e i i e e i e e iz zz z z iz i iz i sinh 222)sin()()(=-?=-=-=--- (2) z e e e e iz z z iz i iz i cosh 22)cos()()(=+=+=-- (3) z i ie e i e e iz iziz iz iz sin 22)sinh(=-?=-=-- (4) z z iz i iz cos )cos()cos()cosh(=-=?=(5) z i zzi iz iz iz tanh cosh sinh )cos()sin()tan(===(6) z i zzi iz iz iz tan cos sin )cosh()sinh()tanh(===17.证明:(1) 1)(sin )(cos )(222222=+=+=-iz iz ishz z ch z sh z ch(2) 111sec 222222=+=+=+zch zsh z ch z sh z ch z th z h (3) )sin()sin()cos()cos()cos()(21212121iz iz iz iz iz iz z z ch -=+=+ 2121shz shz chz chz +=18.证明:(1) xshy i xchy iy x yi x yi x z cos sin )sin(cos )cos(sin )sin(sin +=+=+= (2) xshy i xchy iy x yi x yi x z sin cos )sin(sin )cos(cos )cos(cos +=-=+= (3) y x y xsh y xch xshy i xchy z 22222222sinh sin cos sin cos sin sin +=+=+= (4) y x y xsh y xch xshy i xchy z 22222222sinh cos sin cos sin cos cos +=+=-=19.证明: chz e e e e shz zz z z =+='-='--2)2()( shz e e e e chz zz z z =-='+='--2)2()( 20.解:(1) )31arg(31ln )31ln(i i i i z +++=+= )23(2ln ππk i ++= ),1,0( ±=k(2)由于2ln iz π=,则有i i e z i=+==2sin2cosππ(3)由于)2(1ππk e e i z +=-=,故)2(ππk i z += (4)z z sin cos -=,即1tan -=z ,所以ππk i i i z +-=+-=411ln 21 (5) 设,z x iy =+由12tgz i =+得()()sin 122cos iz iz iz iz zi e e i e e z--=+→-=-+2255iz i e →=-+22cos 25y e x -→=-,1sin 25x =41ln 5,54y e y -→==且1112,222tg x x arctg π=-=-+11ln 5224z arctg i π→=-++21.证明:因)1arg(1ln )1ln()1ln(-+-=-=-θθθi i i re i re re z ,所以)cos 21ln(21)sin ()1(ln 1ln )]1Re[ln(222θθθθr r r re re z i i -+=+-=-=- 22.解: 32)(3)()(πθk z ik ez r z w +=,)2,1,0;2)(0;(=<<∈k z G z πθ利用i i w -=)(定2,=k k ,再计算)(2i w -23.解: 2,22ππii e i e ==-,由32)2(-=-w 定1,=k k ,再计算i ei w π451)(=24.解: )24(2ln )]2)1(arg(1[ln )1ln()1(πππk i k i i i i i i ieeei +-+++++===+)24(2lnππk i ee +-?= ),2,1,0( ±±=kππk i k i i i i e e e e 23ln )]23(arg 3[ln 3ln 3-++?=== ),2,1,0( ±±=k25.解:z 在z 平面上沿0=z 为圆心,1>R 为半径的圆周C 从A 走到B ,经过变换4z w =,其象点w 在w 平面上沿以0=w 为心,14>R 为半径的象圆周从A '走到B ',刚好绕1+=w w 的支点-1转一整周,故它在B '的值为B w '+1.因此1)()(4+-=-=R z f z f AB.26.证明:()f z =可能的支点为0,1,∞由于 3|12+,故()f z 的支点为0,1z =,因此在将z 平面沿实轴从0到期割开后,就可保证变点z 不会单绕0或者说转一周,于是在这样割开后的z 平面上()f z 就可以分出三个单值解析分支. 另由已知 ()arg f z π=得()()arg c i f zi f i e π?=()2arg 1arg 3c c i z z e-+??=32342i ππ??+=712i eπ=.(二)1.证明:由()21z f z z =-得()()2'2211z f z z +=-,从而于是()f z 在D 必常数()()()()()()22'2222111111z zf z z z f z z z z+-+?==---()4242121Re m z I z i z z -+=+- 所以 ()()4'421Re 12Re z f z z f z z z ??-?= ? ?+-??由于1z <,因此410,z ->且()24422212Re 1210z z z z z+-≥+-=->故()()'Re 0f z z f z ??> ? ???.2.证明:同第一题221Im 2111)()(1zzi z z z z f z f z -+-=-+='''+. 3.证明:题目等价域以下命题:设1,E E 为关于实轴对称的区域,则函数在E 内解析)(z f ?在1E 内解析.设)(z f 在E 内解析,对任意的10E z ∈,当1E z ∈时,有E z E z ∈∈,0,所以)()()(lim )()(lim0000000z f z z z f z f z z z f z f z z z z '=--=--→→ 这是因为)(z f 在E 内解析,从而有)()()(lim 0000z f z z z f z f z z '=--→,由0z 的任意性可知, )(z f 在1E 内解析. 4.证明:(1)由于)(21),(21z z iy z z x -=+=,根据复合函数求偏导数的法则,即可得证. (2))(21)(21x vy u i y v x u z v i z u z f ??+??+??-??=??+??=??所以x v y u y v x u ??-==??,,得 0=??zf5.证明: x y sh y sh x y xch yi x z 222222sin )sin 1(sin )sin(sin +=-+=+= 所以z x y sh shy sin sin 22=+≤ 而z y shy Im =≥ ,故左边成立.右边证明可应用z sin 的定义及三角不等式来证明. 6.证明:有 R ch y ch y sh y sh x z 2222221sin sin ≤=+≤+= 即chR t ≤sin又有 R ch y ch y sh y x z 2222221sinh cos cos ≤=+≤+= 7.证明:据定义,任两相异点21,z z 为单位圆1<="" bdsfid="432" p="">212221212121)32()32()()(z z z z z z z z z f z f -++-++=--0112222121=-->--≥++=z z z z 故函数)(z f 在1<="">8.证明:因为)(z f 有支点-1,1,取其割线[-1,1],有(1) 10182)(,8)(arg ie c ei f z f ππ-=-=?(2) i c c e i f z f i z f 852)(,85)(arg ,811)(arg 32πππ=--=?-=?9.解: 因为)(z f 有支点∞±,,1i ,此时支割线可取为:沿虚轴割开],[i i -,沿实轴割开],1[+∞,线路未穿过支割线,记线路为C ,)]arg())(arg()1arg([21)(arg i z i z z z f c c c c ??+--?+-?=?2]0[21ππ-=-=故 i z f 5)(-=.10.证明:因为()f z =的可能支点为0,1,z =∞,由题知()f z 的支点为0,1,z =于是在割去线段0Re 1≤≤的平面上变点就不可能性单绕0或1转一周,故此时可出两二个单值解析分支,由于当z 从支割线上岸一点出发,连续变动到1z =-时,只z 的幅角共增加2π,由已知所取分支在支割线上岸取正值,于是可认为该分支在上岸之幅角为0,因而此分支在1z =-的幅角为2π,故()21i f e π-==,i f 162)1(-=-''.。
复变函数论第三版钟玉泉第二章
如果函数 f (z)在区域 D内每一点解析, 则称 f (z)在区域 D内解析. 或称 f (z)是 区域 D内的一 个解析函数(全纯函数或正则函数).
2. 奇点的定义
若函数 f (z )在点 z 0不解析,但在 z 0 的任一邻域内总 有f (z )的解析点,则称 z 0 为函数f (z ) 的奇点.
dw f (z0 ) z f (z0 ) dz, 即
f
( z0
)
dw dz
z z0
函数w f (z)在 z0 可导与在 z0 可微是等价的.
如果函数 f (z)在区域 D内处处可微, 则称
8 f (z)在区域 D内可微.
复变函数论
广西教育学院
二、解析函数的概念
1. 解析函数的定义 如果函数 f (z) 在 z0 及 z0 的某邻域内处处可导 ,
若 f (z ) = u (x, y ) + iv (x, y ) 在一点z = x + iy,可微,设
lim f (z + D z ) - f (z ) = f ' (z )
Dz? 0
Dz
(1)
设 Vz =Vx + iVy, f (z + Vz )- f (z ) = Vu + i Vv,
Vu = u (x + Vx, y + Vy )- u (x, y )
z
z
x iy
y , x iy
当点沿平行于实轴的方向(y 0)而使z 0时,
lim f lim f (z z) f (z) lim y 0,
z0 z z0
z
x0 x iy
y0
当点沿平行于虚轴的方向(x 0)而使z 0时,
