玩转九宫格 填数游戏 一年级
9宫格填数字技巧

9宫格填数字技巧一、引言在9宫格填数字游戏中,我们需要在一个3x3的方格中填入1~9的数字,使得每一行、每一列和每一个小九宫格内的数字都不重复。
这需要一定的思考和技巧才能够解决。
本文将介绍一些在9宫格填数字游戏中常用的技巧,帮助大家更好地完成游戏任务。
二、技巧分享1. 找出已有数字在开始填数字之前,我们首先需要观察已经给出的数字。
通过观察可以找出已经确定的数字,并将其标记在相应的位置上。
这样可以有针对性地进行填数字的操作,减少犯错的可能性。
2. 寻找唯一数字在某些情况下,我们可以通过排除法找到某一格子中唯一可能的数字。
例如,如果某一行或某一列已经有了1、2、3这三个数字,那么该行或该列的剩余格子中就只能填入4~9这些数字。
通过类似的推理,我们可以找到一些唯一数字,从而简化填数字的过程。
3. 利用候选数字在填数字的过程中,我们可以在每一个格子中列出候选数字。
候选数字是指某一格子可以填入的数字的可能集合。
通过列出候选数字,我们可以更好地进行推理和判断。
当某一格子的候选数字只有一个时,我们可以确定该格子的数字。
4. 利用区块判断在9宫格填数字游戏中,我们可以利用区块判断的技巧来推理。
区块判断是指通过观察小九宫格的数字分布情况,来判断某一行或某一列中的数字。
例如,如果在某一个小九宫格中已经有了1、2、3这三个数字,那么该小九宫格的剩余格子中就只能填入4~9这些数字。
通过区块判断,我们可以进一步缩小候选数字的范围,从而更准确地填入数字。
5. 尝试与回溯当我们遇到一些复杂的情况时,可以尝试不同的数字组合,并通过回溯的方式找到正确的解法。
回溯是指在填数字的过程中,当发现填入某个数字后导致矛盾出现时,我们需要回到上一步,尝试其他数字。
通过不断尝试与回溯,我们可以找到正确的数字组合。
6. 综合运用各种技巧在实际填数字的过程中,我们往往需要综合运用各种技巧。
通过观察、推理和判断,我们可以逐步填入数字,并最终完成游戏任务。
九宫格的填数
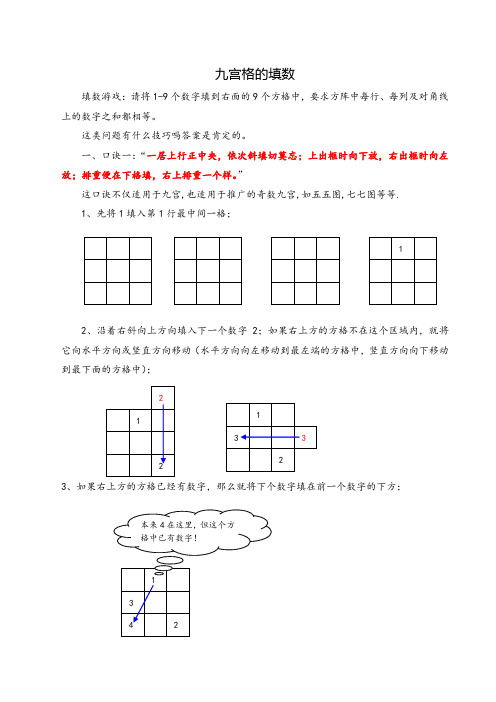
九宫格的填数填数游戏:请将1-9个数字填到右面的9个方格中,要求方阵中每行、每列及对角线上的数字之和都相等。
这类问题有什么技巧吗答案是肯定的。
一、口诀一:“一居上行正中央,依次斜填切莫忘;上出框时向下放,右出框时向左放;排重便在下格填,右上排重一个样。
”这口诀不仅适用于九宫,也适用于推广的奇数九宫,如五五图,七七图等等. 1、先将1填入第1行最中间一格;2、沿着右斜向上方向填入下一个数字2;如果右上方的方格不在这个区域内,就将它向水平方向或竖直方向移动(水平方向向左移动到最左端的方格中,竖直方向向下移动到最下面的方格中);3、如果右上方的方格已经有数字,那么就将下个数字填在前一个数字的下方;4、如果右上方的方格向左或向右移动都不在区域内,仍然将它填在前一个数字的下方;5、继续以上步骤,就可以完成所有方格数字的填写。
特别注意的是,这种方法不但可以填3×3的方阵,还可以填所有奇数×奇数方阵。
如7×7,9×9方阵等。
二、在《射雕英雄传》中黄蓉曾破解九宫格,口诀:戴九履一,左七右三,二四有肩,六八为足,五居中央。
但是“二四有肩,六八为足“只是提示答案的快捷方法,并不是具体的解法。
三、九宫格填数的决窍(三阶幻方) 活动要求:1、熟练100以内的加法口算。
2、知道两个单数或两个双数相加的和一定是双数,一个单数和一个双数相加的和是单数。
例1: 把1、2、3、4、5、6、7、8、9九个数分别填入右边的九宫格里,使横行、竖行、斜行三个数的和都相等。
1、要解决这个问题,关键是什么先要求出“和”是多少怎么求呢方法是先把所有数的和求出来:1+2+3+4+5+6+7+8+9=45然后因为三行和都相等,所以45/ 3=15 所以各行各列的和是15。
(写在格子旁) 师:接下来再考虑什么2、中间数是几是53、然后将凑成10的四对数填在四周,这四对数的填法也很有讲究。
因为“15”是单数,根据: 单数+单数=双数 单数+双数=单数 双数+双数=双数只能把两对双数(2、4、6、8)填在四个角上,并且对角线的和=15,四角可以旋转。
1年级数学北师大版下册教案第5单元《数学 好玩——填数 游戏》

北师大版一年级数学下册《数学好玩——填数游戏》教学设计教材分析:《填数游戏》是北师大版一年级下册数学第五章加与减(二)“数学好玩”中的第二个实践活动。
本课是根据数独游戏改编的填数游戏,“数独”的意思是“单独的数字”或“只出现一次的数字”。
概括来说,它就是一种填数字游戏,它是18世纪的瑞士数学家欧拉发明的。
数独的游戏规则很简单,9×9个格子里,已有若干数字,其他格子空白,玩家需要自己按照规则在空格里填上数字,使得每一行每一列都有1-9的数字,每个小九宫格(按3×3排列的9个方格)里也有1-9的数字,并且一个数字在每个行列及每个小九宫格里都只能出现一次。
本课主要内容是通过填数游戏积累推理的经验,提高推理能力。
教科书主要涉及了三个活动。
1.合作闯关。
呈现按3×3排列的简单的填数问题和游戏规则。
首先帮助学生读懂游戏规则,并用自己的话解释游戏规则,然后引导学生学习如何交流学习中的困难,寻找解决问题的办法。
最后让学生尝试做一做,并解释自己的想法。
目的是让学生初步经历一次解决问题的过程。
2.更上一层。
提高游戏的难度,呈现按5×5排列的稍微难一点的填数问题和游戏规则。
帮助学生学习简单的推理,能够根据两行中缺的数和现有的数判断该填的数。
3.数字迷宫。
这是另一个游戏,目的是让学生在游戏中学会简单的推理。
学情分析:一年级的孩子,他们大都活泼好动天真烂漫,对身边的新鲜事物充满好奇,大多数人思维活跃,学习的兴趣较浓,善于展现自己,对动手践操作很感兴趣,但认知能力相对比较弱,缺乏分析问题、解决问题以及灵活运用知识的能力,在理解和接受能力上也存在着一定的差异。
数学学习最好的办法是让孩子们在玩中感知数学,领悟数学知识,让孩子们在玩数学游戏的过程中,重在参与,让孩子们亲历知识的形成过程,在操作和实践的过程中领悟数学游戏的乐趣。
教学目标:知识目标:经历填数游戏的活动,通过游戏积累推理的经验,初步提高学生的分析推理能力。
数字游戏题九宫格

数字游戏题九宫格引言数字游戏题是一种常见而受欢迎的智力游戏,它既能锻炼我们的思维能力,又能带来乐趣。
在数字游戏题中,九宫格是一种常见的题型。
九宫格是由3×3的格子组成的方阵,其中每个格子内都填有一个数字,我们需要根据一定的规则或条件来完成九宫格的数字填充。
本文将介绍几种常见的数字游戏题九宫格的解法策略。
数字游戏题九宫格的规则在数字游戏题九宫格中,通常会给出一些已知的数字,我们需要根据已知数字以及一定的规则来填充九宫格的其余空格,使每行、每列和每个小方块内的数字都满足特定的条件。
以下是九宫格填充的规则:1.每个格子内的数字必须是1到9中的一个数字;2.每行中的数字不能重复;3.每列中的数字不能重复;4.每个小方块内的数字不能重复。
解法策略穷举法穷举法是一种最直接的解法,它通过尝试所有可能的数字组合来填充九宫格。
穷举法的基本思路是从左上角的格子开始,按照行序依次填充数字,然后逐个格子向右移动。
当一个格子的数字填完后,再尝试填充下一个格子。
如果在填充的过程中发现某个格子无法找到合适的数字填充,就需要回溯到前一个格子重新选择数字。
穷举法的优势是能够找到九宫格的所有解,但缺点是计算量较大,时间复杂度较高。
对于大规模的九宫格,穷举法可能需要很长的时间才能找到解。
以下是使用穷举法解决数字游戏题九宫格的示例代码:def solve_sudoku(board):for i in range(9):for j in range(9):if board[i][j] ==0:for num in range(1, 10):if is_valid(board, i, j, num):board[i][j] = numif solve_sudoku(board):return Trueboard[i][j] =0return Falsereturn Truedef is_valid(board, row, col, num):for i in range(9):if board[row][i] == num or board[i][col] == num or board[(row// 3)*3+i//3][(col//3)*3+i%3] == num:return Falsereturn True约束编程约束编程是一种更高效的解法,它利用数学规划的方法来解决九宫格问题。
数独游戏九宫格怎么玩

数独游戏九宫格怎么玩数独其实就是九宫格。
玩法:用1至9之间的数字填满空格,每个格子只能填一个数字,每个数字在每一行,每一列和每一九宫格区域只能出现一次。
1.游戏规则数独是一种运用纸、笔进行演算的逻辑游戏。
玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫内的数字均含1-9,不重复。
每一道合格的数独谜题都有且仅有唯一答案,推理方法也以此为基础,任何无解或多解的题目都是不合格的。
2.唯一数法如果我们发现某个格子中只有一个可用候选数,那么这个格子必然是这个数字,这就是唯一数法如下面例子,H5格子中只有唯一候选数3。
3.隐含唯一数法如果我们发现某一行某一列或某个九宫有一个候选数只出现在一个格子里面,那么这个格子必然是这个数字,这就是隐含唯一数法,如下面例子,第3列候选数4只出现在格子I3中。
4.数对法如果我们发现某一行某一列或某个九宫有两个格子只使用了两个候选数,那么这两个格子必然正好是这两个数字,那么在这个单元(行,列,或九宫)中,其它格子不会出现这两个候选数,这就是数对法,如下面例子,第一列中B1和G1的候选数都是7,8;那么D1,H1中的候选数7,8可以删除。
5.三链数法如果我们发现某一行某一列或某个九宫有三个格子只使用了三个候选数,那么这三个格子必然正好是这三个数字,那么在这个单元(行,列,或九宫)中,其它格子不会出现这三个候选数,这就是三链数法,如下面例子,最下面中间的九宫中格子H4,H5,I5三个格子都只使用候选数2,8,6;所以G4,G6,I6中出现的8,6都可以删除。
6.四链数法如果我们发现某一行某一列或某个九宫有四个格子只使用了四个候选数,那么这四个格子必然正好是这四个数字,那么在这个单元(行,列,或九宫)中,其它格子不会出现这四个候选数,这就是四链数法;如下面例子中上面中间的九宫中四个格子A5,B5,C4,C5都只使用了数字1,2,3,4;所以另外4个格子A4,A6,B4,C6中出现的数字1,2,3,4可以删除。
完整版九宫格的填数

九宫格的填数填数游戏:请将1-9个数字填到右面的9个方格中,要求方阵中每行、每列及对角线上的数字之和都相等。
这类问题有什么技巧吗?答案是肯定的。
一、口诀一:“一居上行正中央,依次斜填切莫忘;上出框时向下放,右出框时向左 放;排重便在下格填,右上排重一个样。
”这口诀不仅适用于九宫,也适用于推广的奇数九宫,如五五图,七七图等等•到最下面的方格中);3、如果右上方的方格已经有数字,那么就将下个数字填在前一个数字的下方;1、先将1填入第1行最中间一格;12、沿着右斜向上方向填入下一个数字2;如果右上方的方格不在这个区域内,就将它向水平方向或竖直方向移动 (水平方向向左移动到最左端的方格中, 竖直方向向下移动 133 f24、如果右上方的方格向左或向右移动都不在区域内,仍然将它填在前一个数字的下方;5、继续以上步骤,就可以完成所有方格数字的填写。
特别注意的是,这种方法不但可以填3X3的方阵,还可以填所有奇数X奇数方阵。
女口7X 7,9X 9方阵等。
二、在《射雕英雄传》中黄蓉曾破解九宫格,口诀:戴九履一,左七右三,二四有肩,六八为足,五居中央。
294753618上图按顺时针转动一周,可得到以下三个变化图:67215983417241815 2357141646132022 101219213 11182529816 357 4928 1 6 3 5 7 4 9 24 389 5 1 276但是“二四有肩,六八为足“只是提示答案的快捷方法,并不是具体的解法三、九宫格填数的决窍(三阶幻方) 活动要求:1熟练100以内的加法口算2、知道两个单数或两个双数相加的和一定是双数,一个单数和一个双数 相加的和是单数。
例1: 把1、2、3、4、5、6 7、8、9九个数分别填入右边的九宫格里, 使横行、竖行、斜行三个数的和都相等。
1、要解决这个问题,关键是什么?先要求出“和”是多少?怎么求呢? 方法是先把所有数的和求出来:1+2+3+4+5+6+7+8+9=45然后因为三行和都相 等,所以45/ 3=15所以各行各列的和是15。
小学数学一年级下册数学好玩《填数游戏》教学设计
《填数游戏》教学设计教学内容:北师大版数学一年级下册第66-67页。
教学目标:1、经历填数游戏活动,培养学生初步的分析推理能力。
2、激发学生的学习兴趣,培养学生合作意识和主动探索的精神。
3、培养学生观察、语言表达、动手和初步运用已有生活经验解决问题的能力。
教学重、难点:合理使用“唯一法”或“排除法”探索填数的方法。
教学准备:课件、题纸。
教学过程:一、情境引入师:同学们,今天老师将带大家一起到数字王国去和我们的数字宝宝玩游戏,大家愿意吗?(愿意)好,这个游戏的名字叫做“填数游戏”。
(板书:填数游戏)二、填数游戏1、游戏一师:在玩游戏之前,老师要给大家介绍一位朋友给大家认识,它叫“九宫格”,(课件出示“九宫格”图)九宫格一共有9个一样大小的格子,它有3个横行和3个竖行,(师可以用手比划)我们把横行分别叫第一横行、第二横行和第三横行,竖行呢?生:第一竖行、第二竖行、第三竖行。
师:认识了这位“九宫格”朋友,我们现在就可以和数字宝宝玩一个关于“九宫格”的填数游戏。
(课件出示游戏一)要玩这个填数游戏,我们首先要知道这个游戏的规则,来我们一起来看看这个游戏的规则。
(课件出示游戏规则)大家一起齐读一遍,(学生齐读游戏规则)刚才我们大家一起读了这个游戏规则,你想告诉大家,我们在玩这个游戏时应注意什么呢?生1:空格中只能填 1、2、3,不能填别的数。
生2:每一横行和每一竖行的数字不能重复。
(勾画重点)师:好了,看来我们大家对这个游戏的规则已经熟知了,现在可以开始这个游戏了,看着这么多的空格,你想先从哪一格开始填?为什么要从这一格开始填?请你仔细想想。
想好了就翻开我们的数学书66页,按照你的想法,完成书上最上面的表格。
(在你先填的那个格子的旁边画一个五角星)学生动手操作。
师:填完了就用行动来告诉老师。
看来孩子们都填完了,哪位同学愿意上台来给大家讲讲你是怎么填的?为了讲述的更清楚,先说你看的哪一行,再说你填是几,为什么这样填。
一年级数学九宫格题目
一年级数学九宫格题目一、题目。
1. 在下面的九宫格中填上1 - 9这九个数字,使每行、每列以及对角线上的三个数字之和都相等。
- 解析:1+2+3+4+5+6+7+8 + 9=(1 + 9)×9÷2 = 45。
因为每行、每列、对角线上三个数字之和相等,所以这个和是45÷3 = 15。
然后可以先确定中间数是5(因为中间数在计算每行、每列、对角线和时会用到4次,1 - 9这几个数中5处于中间位置且4个5相加为20,再加上其他两个数凑15比较容易)。
接着可以尝试填写其他数字,例如1、9在一条对角线,2、8在一条对角线等。
2. 九宫格中,已知左上角数字为1,右上角数字为3,请把1 - 9这九个数字填完整,使每行、每列以及对角线上的三个数字之和都相等。
- 解析:因为每行、每列、对角线上三个数字之和相等,设这个和为S。
左上角为1,右上角为3,那么中间数可以通过计算得到。
先算出1 - 9的总和为45,三条线(行或列或对角线)的总和为3S,中间数在三条线的总和计算中被加了3次,其他数字都加了1次,设中间数为x,则3S=45 + 2x。
又因为左上角1和右上角3所在对角线的和为S,即1 + x+3 = S,联立方程可求出中间数和S的值,再根据和为S来填写其他数字。
3. 在九宫格中填上合适的数字(数字范围1 - 9),使第一行三个数字之和为12,且每行、每列以及对角线上的三个数字之和都相等。
- 解析:设每行、每列、对角线上三个数字之和为S。
已知第一行和为12,因为总和为45,中间数在计算总和时用到3次,设中间数为x,可得3S = 45+2x。
又因为第一行和为12,设第一行另外两个数为a和b,则a + b=11。
根据这些关系逐步确定其他数字。
4. 九宫格中,中间数字是5,把1 - 9这九个数字填完整,使每行、每列以及对角线上的三个数字之和都相等。
为15(前面已解释计算方法)。
那么与5在一条直线上的两个数之和为10。
一年级下册数学开学第一课 奇妙的填数游戏 数独游戏
设计意图转眼到了一年级下学期,学生已经在学校度过了一个学期。
他们由原来刚入学时的懵懵懂懂到现在对新知识和新事物的逐渐渴望。
但是由于年龄比较小,在教学中仍然要以启发式教学为主。
作为数学学科,更应结合所学的知识,引导并激发学生对数学学习的兴趣,寓教于乐。
从而保持学生学习数学的持久动力。
开学第一课让学生由填字游戏开始,然后逐步过渡到风靡世界的数独游戏。
数独重对学生思维的培养,开发学生的智力,培养注通过意力,提高做题速度。
从一年级开始培养数学思维和数感,为以后的数学学习做铺垫。
教学目标知识与技能1 通过填数游戏活动,学生初步掌握填数游戏规则2 在游戏过程中,学生正确理解填数游戏规则,并能进行分析推理。
3 在初步掌握分析推理之后,能够完成简单的数独游戏。
情感态度与价值观1 在操作、探索、发现中,是学生感受数学在日常生活中的重要性。
2 在教学情境中,培养学生合作意识和主动探索的精神。
3 在探索、尝试、交流活动中体会填数游戏的乐趣,激发学生学习数学的兴趣。
教学重点在填数游戏中掌握游戏规则,学习简单的推理方法,分析并解决问题。
教学难点在填数游戏中学习简单的推理方法。
教学准备教师:多媒体 PPT 数独小卡片及相应的数学练习题表扬用的小粘贴教学过程同学们,新年新气象。
老师从你们端正的坐姿就能看出你们长大了一岁。
老师希望你们在新的学期里课堂行习惯表现棒棒的,学习也棒棒的。
接下来老师讲个故事,大家一定要认真听啊,因为故事里有些小动物需要你们的帮忙哦!同学们,最近“羊羊乐园”发生了一件大事,起因是这样的:灰太狼每次来抓羊的时候,都不成功,所以灰太狼叫着他的爸爸黑太狼和他的亲戚--七大恶狼一起帮忙,想着一举把“羊羊乐园”里的所有羊都抓回去,来个全羊宴。
灰太狼一想起全羊宴就心里乐开了花。
但是没有不透风的墙,在灰太狼他们商议的时候,被暖暖(暖羊羊的宠物)听到了,暖暖赶紧回去报信。
到底该怎么办呢?“羊羊乐园”里一片恐慌。
这时慢羊羊(村长)站出来说“我们在西域草原还有一批老祖宗留下的宝藏,我们要是把宝藏找到,就能去买武器对付灰太狼他们了”,慢羊羊的这番话让“羊羊乐园”又燃起了希望,那还等什么,立马行动起来吧。
一年级数学下册课件数学好玩填数游戏4北师大版17张
63 84 87 88 89 90 91 94 99 60 83 82 81 80 81 92 93 98
59 60 61 64 79 94 93 96 97
58 69 62 79 78 77 94 95 94
57 56 63 64 65 76 77 96 95
57 55 54 55 66 75 74 93 96
4、完成的小组快速坐好。
按照从51到100的顺序走走看,遇到★要填一个数才能通过。
1、四人一组合作走迷宫。
按照从51到100的顺序走走看,遇到★要填一个数才能通过。
每一横行、每一竖行的数字不能重复。
2、用彩笔画出走过的路线。
2、每个小的九宫格内也都包含数字1~9,也不能重复。
1、四人一组合作走迷宫。
九宫图
游戏规则: ·将1-9这9个数字填入空格内。 ·每一横行,每一竖行,以及对角线上3个数的和都是15。
1在每个小方格内填上数字19使得每行和每列的9个格子都包含数字19但不重复
填数游戏
游戏规则: 每个空格中只能填1、2、3中的一个。
··每一横行、每一竖行的数字不能重复。
3 1
43 1
1
52 2 1 2
1 1 21
游戏规则: 按照从51到100的顺序走走看,遇到★要填一个数才能通过。
2、用彩笔画出走过的路线。 1、在每个小方格内填上数字1~9,使得每行和每列的9个格子都包含数字1~9,但不重复。 4、完成的小组快速坐好。
74 93 96
开始 51 52 53 68 67 69 73 98 97
52 54 54 69 70 71 72 99 98
比赛要求:
1、四人一组合作走迷宫。 2、用彩笔画出走过的路线。 3、推选代表全班汇报。 4、完成的小组快速坐好。
