人教版 第26章《二次函数》小结与复习(2)
第26章小结二次函数的复习课件

2、抛物线 y = 3x 2 + 2 的开口向
坐标为
.
, 顶点
3、抛物线 y =2( x +1)2 - 4 的顶点坐标为
对称轴为
.
4、当a 为最高点.
时,抛物线 y =(a +2)x 2 的顶点
5、抛物线 y = ( x - 2) 2 + 3 的开口向 ,对称
轴为
,在对称轴左侧,y 随 x 的增大而
2
1
A
-8 -7 -6 -5 -4 -3 -2 -1
1
-1
D B
2 3 4 56 7
8x
1、本课主要复习了哪些内容? 2、通过复习,你有什么体会或收获呢?
二次函数 y x2 2x 3
1)用配方法求其顶点D的坐标; 2)求其与y轴的交点C的坐标、与x轴交点A、B (且点A在点B的左边)的坐标。
y x2 2x 1
y
9
8 y=x2-2x+3
7
6
y x2 4x 3
5
4
3
2
1
-8 -7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7 8x
-1
知识点回顾四:
二次函数一般式与顶点式的转化
一般式
y ax2 bx c
配方
顶点式
y ax m2 k
y ax2 bx c
(
大 a >0 致 图 象 a<0
函 数
a >0
变 化 a<0
在对称轴左侧,y 随 x 的增大而减小. 在对称轴右侧,y 随 x 的增大而增大. 在对称轴左侧,y 随 x 的增大而增大. 在对称轴右侧,y 随 x 的增大而减小.
由a、b、c
数学知识点人教版数学九下《第26章二次函数》word总结提升-总结

第26章 二次函数全章总结提升◆本章总结归纳(一)知识框架(二)重点难点突破1.函数图象的理解与应用易错点:函数图象的意义认识不表,它的性质、特征与函数图象联系不上,不能达到数形互助;突破点:加强对函数图象中点的坐标的意义认识,分析各点的坐标,理解y 随x 的变化情况,从而达到能直接根据图象说出二次函数的有关性质。
(如:增减性、极值、对称轴等)理解,,a b c 的值对抛物线2y ax bx c =++的影响,提高解题效率 2.抛物线2y ax bx c =++的特征与,,a b c 符号:,,a b c 决定开口方向0,0,a a >⎧⎨<⎩开口向上;开口向下.,,a b c 与b 决定对称轴位置,,a b a b ⎧⎨⎩同号,在轴左侧;异号,在轴右侧.c 决定抛物线与y 轴交点的位置0,0,0,c c c >⎧⎪=⎨⎪<⎩交点在y 轴的正半轴上;交点在原点;交点在y 轴的负半轴上. 易错点:以上关系不清楚,导致做题盲目,出错。
突破点:数形结合,变式训练,特别是,,a b c 与b 一走决定对称轴位置的理解与判定。
3.解析式之间的转化与解析式的求法。
易错点:①将2y ax bx c =++化成顶点式224()24b ac b y a x a a -=++ ②用待定系数法求解时,不能根据不同条件恰当地选取解析式。
突破点:①强调配方的步骤、配方的规律,注意恒等变形与检验。
②比较不同形式的解析式的优劣,应用的环境,加强对顶点式、交点式的理解,并能正确运用。
4.抛物线的平移规律,表达式的变化。
易错点:抛物线的移动,对解析式变化理解不透,不同方向的移动,到底是加还是减判断不清。
突破点:抓住顶点坐标的变化,熟记平移规律,左加右减,上加下减。
5.抛物线与x 轴交点情况。
易错点:此类题综合性较大,对应关系不很明确,隐含条件较多,极易出错。
突破点:抛物线与x 轴交点横坐标就是相应一元二次方程的两根,把交点的个数转化为方程。
人教版数学九年级上册 第二十二章《二次函数》章节知识点归纳复习总结

人教版数学九年级上学期《二次函数》章节知识点归纳总结一、二次函数概念:1.二次函数的概念:(1)一般地,形如2y ax bx c =++(a b c ,,是常数,a ≠0)的函数,叫做二次函数。
(2)这里需要强调:和一元二次方程类似,二次项系数a ≠0,而b c ,可以为零.二次函数的定义域(x)是全体实数.2. 二次函数 2y ax bx c =++ 的结构特征:(1)等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. (2)a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项.3. 二次函数解析式的几种形式(1)一般式:y=ax 2+bx+c (a ,b ,c 为常数,a ≠0) (2)顶点式:y=a(x-h)2+k [抛物线的顶点P ( h ,k )](3)交点式:y=a(x-x 1)(x-x 2)[仅限于与x 轴有交点A (x 1,0)和 B (x 2,0)的抛物线]其中x 1,x 2是抛物线与x 轴的交点的横坐标,即一元二次方程ax 2+bx+c =0的两个根,a ≠0. x 1,x 2 = (-b ±ac 4b 2-)/2a在三种形式的互相转化中,有如下关系:h= -b / 2a ; k=(4ac-b 2) / 4a ; x 1,x 2 = (-b ±ac 4b 2-) / 2a说明:(1)任何一个二次函数通过配方都可以化为顶点式y=a(x-h)2+k,抛物线的顶点坐标是(h,k);(2) 当h=0时,抛物线y=ax2+k的顶点在y轴上;当k=0时,抛物线a(x-h)2的顶点在x轴上;当h=0且k=0时,抛物线y=ax2的顶点在原点;(3) 如果图像经过原点,并且对称轴是y轴,则设y=ax2;如果对称轴是y轴,但不过原点,则设y=ax2+k4.抛物线的性质(1).抛物线是轴对称图形。
对称轴为直线 x = -b/2a。
对称轴与抛物线唯一的交点为抛物线的顶点P。
人教版七年级下册数学26二次函数(复习与小结)
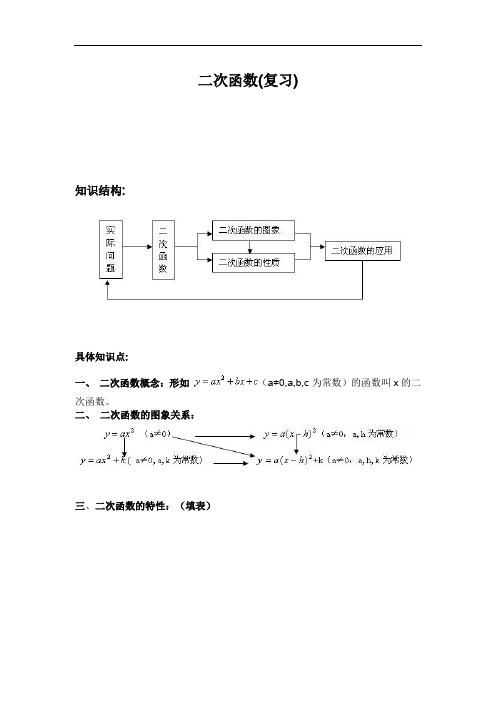
二次函数(复习)知识结构:具体知识点:一、二次函数概念:形如(a≠0,a,b,c为常数)的函数叫x的二次函数。
二、二次函数的图象关系:三、二次函数的特性:(填表)巩固练习:一、基础练习:①二次函数的定义:⑴.下列函数中,二次函数的是()⑵.当k= 时,函数为二次函数。
②二次函数的图像与性质:二次函数y=-x2+6x+3的图象开口方向顶点坐标为_________对称轴为_________当x= 时函数有值,为。
当x 时,y的值随x的增大而增大。
它是由y=-x2向平移个单位得到的,再向平移个单位得到的.③抛物线与x轴的交点个数:抛物线与x轴的交点有个,抛物线与x轴的交点有个,抛物线y=x2+2x+1与x轴的交点有个。
总结:抛物线与x轴的交点个数由决定。
④抛物线的图象与a、b、c及b2-4ac的关系。
⑴如图是y=ax2+bx+c的图象,则a______0 b______0 c______0 b2-4ac________0⑵.二次函数与一次函数在同一直角坐标系中图象大致是()总结:抛物线的图象与a、b、c及b2-4ac的关系是:a:开口方向;b:结合a看对称轴;c:与y轴交点坐标;b2-4ac:与x轴的交点个数。
⑤求函数解析式:⑴.根据下列条件,分别求出对应的二次函数的关系式.A、已知二次函数的图象经过点A(0,-1)、B(1,0)、C(-1,2);B、已知抛物线的顶点为(1,-3),且与y轴交于点(0,1);C、已知抛物线过点(—2,5),(4,5),且有最小值为y=3,求此函数关系式。
总结:(1)一般式:,给出三点坐标可利用此式来求.(2)顶点式:,给出两点,且其中一点为顶点时可利用此式来求.。
26章二次函数知识点归纳1

人教版九年级数学下二次函数知识点总结✧ 相关概念及定义二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2.⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. ✧ 二次函数各种形式之间的变换二次函数c bx ax y ++=2用配方法可化成:()k h x a y +-=2的形式,其中ab ac k a b h 4422-=-=,.二次函数由特殊到一般,可分为以下几种形式:①2ax y =;②k ax y +=2;③()2h x a y -=;④()k h x a y +-=2;⑤c bx ax y ++=2.✧ 二次函数解析式的表示方法一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). ✧ 二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.几种特殊的二次函数的图像特征如下:抛物线c bx ax y ++=2中,c b a ,,与函数图像的关系a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小.a越大开口越小在a 确定的前提下,b 决定了抛物线对称轴的位置. (1)a,b 同号在左,异号在右(2)当对称轴为x=1时2a+b=0当对称轴为x=-1的时候2a-b=0 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置. 注意当x=1的时候y=a+b+c 当x=-1的时候y=a-b+c 总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的. ✧ 求抛物线的顶点、对称轴的方法公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,∴顶点是),(a b ac a b 4422--,对称轴是直线ab x 2-=.配方法:运用配方的方法,将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.用待定系数法求二次函数的解析式一般式:c bx ax y ++=2.已知图像上三点或三对x 、y 的值,通常选择一般式. 顶点式:()k h x a y +-=2.已知图像的顶点或对称轴,通常选择顶点式.交点式:已知图像与x 轴的交点坐标1x 、2x ,通常选用交点式:()()21x x x x a y --=.✧ 直线与抛物线的交点y 轴与抛物线c bx ax y ++=2得交点为(0, c ).抛物线与x 轴的交点:二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ,是对应一元二次方程02=++c bx ax 的两个实数根.抛物线与x 轴的交点情况可以由对应的一元二次方程的根的判别式判定:①有两个交点⇔0>∆⇔抛物线与x 轴相交;②有一个交点(顶点在x 轴上)⇔0=∆⇔抛物线与x 轴相切; ③没有交点⇔0<∆⇔抛物线与x 轴相离.一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G 的交点,由方程组 2y kx n y ax bx c=+⎧⎨=++⎩的解的数目来确定:①方程组有两组不同的解时⇔l 与G 有两个交点; ②方程组只有一组解时⇔l 与G 只有一个交点;③方程组无解时⇔l 与G 没有交点.抛物线与x 轴两交点之间的距离:若抛物线c bx ax y ++=2与x 轴两交点为()()0021,,,x B x A ,由于1x 、2x 是方程02=++c bx ax 的两个根,故acx x a b x x =⋅-=+2121,二次函数图象的对称:二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达关于x 轴对称2y a x b x c =++关于x 轴对称后,得到的解析式是2y ax bx c =---; ()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;关于原点对称 2y a x b x c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 关于顶点对称2y a x b x c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-; ()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.总结:根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.✧ 二次函数图象的平移平移步骤:将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; 在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”.✧ 根据条件确定二次函数表达式的几种基本思路。
九年级数学下册 第26章 二次函数小结与复习教学课件

值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1
的左侧而抛物线y=-x2+2bx+c的对称轴 故选择D .
x ,b 即b≤b1, 2(1)
第十五页,共二十六页。
考点四 抛物线的几何变换
例4 将抛物线y=x2-6x+5向上(xiàngshàng)平移 2个单位长
度,再向右平移1个单位长度后,得到的抛物线表达式是
3.若已知二次函数图象与x轴的交点坐标为 (x1,0)、(x2,0)
时,可设交点式求表达式,最后化为一般式.
第十九页,共二十六页。
针对训练
5.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在 直线x=1上,且顶点到x轴的距离为5,请写出满足(mǎnzú)此条件的抛物线
的表达式.
y最大=
4ac b2 4a
在对称轴左边, x ↗y↘ ;在对称轴右边, x ↗ y ↗
在对称轴左边, x ↗y ↗ ;在对称轴右边, x ↗ y ↘
第四页,共二十六页。
6.二次函数(hánshù)与一元二次方程及一元二次不等式的关系:
判别式△=b2-4ac
△>0
△=0
△<0
二次函数y=ax2+bx+c (a>0) 的图象
方法总结 抛物线平移的规律可总结如下(rúxià)口诀:左加右减 自变量,上加下减常数项.
第十六页,共二十六页。
针对训练
4.若抛物线 y=-7(x+4)2-1平移(pínɡ yí)得到 y=-7x2,则必须( )B A.先向左平移4个单位,再向下平移1个单位 B.先向右平移4个单位,再向上平移1个单位 C.先向左平移1个单位,再向下平移4个单位 D.先向右平移1个单位,再向下平移4个单位
人教版九年级数学下册第二十六章二次函数复习小结学案三

人教版数学第26章《二次函数》小结与复习(3)教学目标:1.使学生掌握二次函数模型的建立,并能运用二次函数的知识解决实际问题。
2.能够分析和表示不同背景下实际问题中变量之间的二次函数关系,获得用数学方法解决实际问题的经验,感受数学模型、思想在实际问题中的应用价值。
重点难点:重点:利用二次函数的知识解决实际问题,并对解决问题的策略进行反思。
难点:将实际问题转化为函数问题,并利用函数的性质进行决策。
教学过程:一、例题精析,引导学法,指导建模1.何时获得最大利润问题。
例:重庆市某区地理环境偏僻,严重制约经济发展,丰富的花木产品只能在本地销售,区政府对该花木产品每投资x万元,所获利润为P=-150(x-30)2+10万元,为了响应我国西部大开发的宏伟决策,区政府在制定经济发展的10年规划时,拟开发此花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元,若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路,且5年修通,公路修通后,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每投资x万元可获利润Q=-4950(50-x)2+1945(50-x)+308万元。
(1)若不进行开发,求10年所获利润最大值是多少?(2)若按此规划开发,求10年所获利润的最大值是多少?(3)根据(1)、(2)计算的结果,请你用一句话谈谈你的想法。
学生活动:投影给出题目后,让学生先自主分析,小组进行讨论。
教师活动:在学生分析、讨论过程中,对学生进行学法引导,引导学生先了解二次函数的基本性质,并学会从实际问题中抽象出二次函数的模型,借助二次函数的性质来解决这类实际应用题。
教师精析:(1)若不开发此产品,按原来的投资方式,由P=-150(x-30)2+10知道,只需从50万元专款中拿出30万元投资,每年即可获最大利润10万元,则10年的最大利润为M1=10×10=100万元。
人教版数学九年级下册教案:第26章 《二次函数》小结与复习(2)

第26章 《二次函数》小结与复习(2)教学目标:会用待定系数法求二次函数的解析式,能结合二次函数的图象掌握二次函数的性质,能较熟练地利用函数的性质解决函数与圆、三角形、四边形以及方程等知识相结合的综合题。
重点难点:重点;用待定系数法求函数的解析式、运用配方法确定二次函数的特征。
难点:会运用二次函数知识解决有关综合问题。
教学过程:一、例题精析,强化练习,剖析知识点用待定系数法确定二次函数解析式.例:根据下列条件,求出二次函数的解析式。
(1)抛物线y =ax2+bx +c 经过点(0,1),(1,3),(-1,1)三点。
(2)抛物线顶点P(-1,-8),且过点A(0,-6)。
(3)已知二次函数y =ax2+bx +c 的图象过(3,0),(2,-3)两点,并且以x =1为对称轴。
(4)已知二次函数y =ax2+bx +c 的图象经过一次函数y =-3/2x +3的图象与x 轴、y 轴的交点;且过(1,1),求这个二次函数解析式,并把它化为y =a(x -h)2+k 的形式。
教师归纳:二次函数解析式常用的有三种形式:(1)一般式:y =ax2+bx +c (a ≠0)(2)顶点式:y =a(x -h)2+k (a ≠0)(3)两根式:y =a(x -x1)(x -x2) (a ≠0)当已知抛物线上任意三点时,通常设为一般式y =ax2+bx +c 形式。
当已知抛物线的顶点与抛物线上另一点时,通常设为顶点式y =a(x -h)2+k 形式。
当已知抛物线与x 轴的交点或交点横坐标时,通常设为两根式y =a(x -x1)(x -x2) 强化练习:已知二次函数的图象过点A(1,0)和B(2,1),且与y 轴交点纵坐标为m 。
(1)若m 为定值,求此二次函数的解析式;(2)若二次函数的图象与x 轴还有异于点A 的另一个交点,求m 的取值范围。
二、知识点串联,综合应用例:如图,抛物线y =ax2+bx +c 过点A(-1,0),且经过直线y =x -3与坐标轴的两个交点B 、C 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第26章《二次函数》小结与复习(2)
教学目标:
会用待定系数法求二次函数的解析式,能结合二次函数的图象掌握二次函数的性质,能较熟练地利用函数的性质解决函数与圆、三角形、四边形以及方程等知识相结合的综合题。
重点难点:
重点;用待定系数法求函数的解析式、运用配方法确定二次函数的特征。
难点:会运用二次函数知识解决有关综合问题。
教学过程:
一、例题精析,强化练习,剖析知识点
用待定系数法确定二次函数解析式.
例:根据下列条件,求出二次函数的解析式。
(1)抛物线y=ax2+bx+c经过点(0,1),(1,3),(-1,1)三点。
(2)抛物线顶点P(-1,-8),且过点A(0,-6)。
(3)已知二次函数y=ax2+bx+c的图象过(3,0),(2,-3)两点,并且以x=1为对称轴。
(4)已知二次函数y=ax2+bx+c的图象经过一次函数y=-3/2x+3的图象与x轴、y 轴的交点;且过(1,1),求这个二次函数解析式,并把它化为y=a(x-h)2+k的形式。
学生活动:学生小组讨论,题目中的四个小题应选择什么样的函数解析式?并让学生阐述解题方法。
教师归纳:二次函数解析式常用的有三种形式:(1)一般式:y=ax2+bx+c (a≠0)
(2)顶点式:y=a(x-h)2+k (a≠0) (3)两根式:y=a(x-x1)(x-x2) (a≠0)
当已知抛物线上任意三点时,通常设为一般式y=ax2+bx+c形式。
当已知抛物线的顶点与抛物线上另一点时,通常设为顶点式y=a(x-h)2+k形式。
当已知抛物线与x轴的交点或交点横坐标时,通常设为两根式y=a(x-x1)(x-x2)
强化练习:已知二次函数的图象过点A(1,0)和B(2,1),且与y 轴交点纵坐标为m 。
(1)若m 为定值,求此二次函数的解析式;
(2)若二次函数的图象与x 轴还有异于点A 的另一个交点,求m 的取值范围。
二、知识点串联,综合应用
例:如图,抛物线y =ax 2+bx +c 过点A(-1,0),
且经过直线y =x -3与坐标轴的两个交点B 、C 。
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标,
(3)若点M 在第四象限内的抛物线上,且OM ⊥BC ,
垂足为D ,求点M 的坐标。
学生活动:学生先自主分析,然后小组讨论交流。
教师归纳:
(1)求抛物线解析式,只要求出A 、B ,C 三点坐标即可,设y =x 2-2x -3。
(2)抛物线的顶点可用配方法求出,顶点为(1,-4)。
(3)由|0B|=|OC|=3 又OM ⊥BC 。
所以,OM 平分∠BOC
设M(x ,-x)代入y =x 2-2x -3 解得x =1±132
因为M 在第四象限:∴M(1+132,1-132
) 题后反思:此题为二次函数与一次函数的交叉问题,涉及到了用待定系数法求函数 解析式,用配方法求抛物线的顶点坐标;等腰三角形三线合一等性质应用,求M 点坐标 时应考虑M 点所在象限的符号特征,抓住点M 在抛物线上,从而可求M 的求标。
强化练习;已知二次函数y =2x 2-(m +1)x +m -1。
(1)求证不论m 为何值,函数图象与x 轴总有交点,并指出m 为何值时,只有一个交点。
(2)当m 为何值时,函数图象过原点,并指出此时函数图象与x 轴的另一个交点。
(3)若函数图象的顶点在第四象限,求m 的取值范围。
三、课堂小结
1.投影:让学生完成下表:
2.归纳二次函数三种解析式的实际应用。
3.强调二次函数与方程、圆、三角形,三角函数等知识综合的综合题解题思路。
四、作业:
课后反思:本节课重点是用待定系数法求函数解析式,应注意根据不同的条件选择合适的解析式形式;要让学生熟练掌握配方法,并由此确定二次函数的顶点、对称轴,并能结合图象分析二次函数的有关性质。
对于二次函数与其他知识的综合应用,关键要让学生掌握解题思路,把握题型,能利用数形结合思想进行分析,从而把握解题的突破口。
课时作业优化设计一、填空。
1. 如果一条抛物线的形状与y=-1
3x2+2的形状相同,且顶点坐标是(4,-2),则它
的解析式是_____。
2.开口向上的抛物线y=a(x+2)(x-8)与x轴交于A、B两点,与y轴交于C点,若∠ACB=90°,则a=_____。
3.已知抛物线y=ax2+bx+c的对称轴为x=2,且过(3,0),则a+b+c=______。
二、选择。
1.如图(1),二次函数y=ax2+bx+c图象如图所示,则下列结论成立的是( ) A.a>0,bc>0 B. a<0,bc<0 C. a>O,bc<O D. a<0,bc>0
2.已知二次函数y=ax2+bx+c图象如图(2)所示,那么函数解析式为( )
A.y=-x2+2x+3 B. y=x2-2x-3
C.y=-x2-2x+3 D. y=-x2-2x-3
3.若二次函数y=ax2+c,当x取x1、x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为( )
A.a+c B. a-c C.-c D. c
4.已知二次函数y=ax2+bx+c图象如图(3)所示,下列结论中:①abc>0,②b=2a;
③a+b+c<0,④a-b+c>0,正确的个数是( )
A.4个B.3个 C. 2个D.1个
三、解答题。
已知抛物线y=x2-(2m-1)x+m2-m-2。
(1)证明抛物线与x轴有两个不相同的交点,
(2)分别求出抛物线与x轴交点A、B的横坐标x A、x B,以及与y轴的交点的纵坐标yc(用含m的代数式表示)
(3)设△ABC的面积为6,且A、B两点在y轴的同侧,求抛物线的解析式。
