小学数学典型应用题类型分析与解题思路
小学数学典型应用题归类总结(30种)

小学数学典型应题归类总结(30种)1、归一问题【含义】在解题时,先求出一份是多少(即单一量),然后以单一量为标准求出所要求的数量。
这类应用题叫做归一问题。
【数量关系】总量÷份数=1份数量1份数量×所占份数=所求几份的数量总量÷(总量÷份数)=所求份数【解题思路和方法】先求出单一量,以单一量为标准,求出所要求的数量。
例1、买5支铅笔要0.6元钱,买同样的铅笔16支,需要多少钱?解(1)买1支铅笔多少钱?0.6÷5=0.12(元)(2)买16支铅笔需要多少钱?0.12×16=1.92(元)列成综合算式0.6÷5×16=0.12×16=1.92(元)答:需要1.92元。
例2、 3台拖拉机3天耕地90公顷,照这样计算,5台拖拉机6 天耕地多少公顷?解(1)1台拖拉机1天耕地多少公顷?90÷3÷3=10(公顷)(2)5台拖拉机6天耕地多少公顷?10×5×6=300(公顷)列成综合算式90÷3÷3×5×6=10×30=300(公顷)答:5台拖拉机6 天耕地300公顷。
例3 5辆汽车4次可以运送100吨钢材,如果用同样的7辆汽车运送10吨钢材,需要运几次?解(1)1辆汽车1次能运多少吨钢材?100÷5÷4=5(吨)(2)7辆汽车1次能运多少吨钢材?5×7=35(吨)(3)105吨钢材7辆汽车需要运几次?105÷35=3(次)列成综合算式105÷(100÷5÷4×7)=3(次)答:需要运3次。
2 、归总问题【含义】解题时,常常先找出“总数量”,然后再根据其它条件算出所求的问题,叫归总问题。
所谓“总数量”是指货物的总价、几小时(几天)的总工作量、几公亩地上的总产量、几小时行的总路程等。
小学数学应用题21种类型总结(附例题、解题思路)

小学数学应用题21种类型总结(附例题、解题思路)1、归一问题【含义】在解题时,先求出一份是多少(即单一量),然后以单一量为标准,求出所要求的数量。
这类应用题叫做归一问题。
【数量关系】总量÷份数=1份数量1份数量×所占份数=所求几份的数量另一总量÷(总量÷份数)=所求份数【解题思路和方法】先求出单一量,以单一量为标准,求出所要求的数量。
例1买5支铅笔要0.6元钱,买同样的铅笔16支,需要多少钱?解(1)买1支铅笔多少钱?0.6÷5=0.12(元)(2)买16支铅笔需要多少钱?0.12×16=1.92(元)列成综合算式0.6÷5×16=0.12×16=1.92(元)答:需要1.92元。
例23台拖拉机3天耕地90公顷,照这样计算,5台拖拉机6天耕地多少公顷?解(1)1台拖拉机1天耕地多少公顷?90÷3÷3=10(公顷)(2)5台拖拉机6天耕地多少公顷?10×5×6=300(公顷)列成综合算式90÷3÷3×5×6=10×30=300(公顷)答:5台拖拉机6天耕地300公顷。
例35辆汽车4次可以运送100吨钢材,如果用同样的7辆汽车运送105吨钢材,需要运几次?解(1)1辆汽车1次能运多少吨钢材?100÷5÷4=5(吨)(2)7辆汽车1次能运多少吨钢材?5×7=35(吨)(3)105吨钢材7辆汽车需要运几次?105÷35=3(次)列成综合算式105÷(100÷5÷4×7)=3(次)答:需要运3次。
2、归总问题【含义】解题时,常常先找出“总数量”,然后再根据其它条件算出所求的问题,叫归总问题。
所谓“总数量”是指货物的总价、几小时(几天)的总工作量、几公亩地上的总产量、几小时行的总路程等。
小学数学常考的10种应用题类型_考前必看

小学数学常考的10种应用题类型_考前必看今天小编给大家带来小学数学常考的10种应用题类型,希望可以帮助到大家。
一、归一问题1.含义在解题时,先求出一份是多少(即单一量),然后以单一量为标准,求出所要求的数量。
这类应用题叫做归一问题。
2.数量关系总量÷份数=1份数量1份数量×所占份数=所求几份的数量另一总量÷(总量÷份数)=所求份数3.解题思路和方法先求出单一量,以单一量为标准,求出所要求的数量。
例1买5支铅笔要0.6元钱,买同样的铅笔16支,需要多少钱?解:(1)买1支铅笔多少钱?0.6÷5=0.12(元)(2)买16支铅笔需要多少钱?0.12×16=1.92(元)列成综合算式0.6÷5×16=0.12×16=1.92(元)答:需要1.92元。
例23台拖拉机3天耕地90公顷,照这样计算,5台拖拉机6天耕地多少公顷?解:(1)1台拖拉机1天耕地多少公顷?90÷3÷3=10(公顷)(2)5台拖拉机6天耕地多少公顷?10×5×6=300(公顷)列成综合算式90÷3÷3×5×6=10×30=300(公顷)答:5台拖拉机6天耕地300公顷。
例35辆汽车4次可以运送100吨钢材,如果用同样的7辆汽车运送105吨钢材,需要运几次?解(1)1辆汽车1次能运多少吨钢材?100÷5÷4=5(吨)(2)7辆汽车1次能运多少吨钢材?5×7=35(吨)(3)105吨钢材7辆汽车需要运几次?105÷35=3(次)列成综合算式105÷(100÷5÷4×7)=3(次)答:需要运3次。
二、归总问题1.含义解题时,常常先找出“总数量”,然后再根据其它条件算出所求的问题,叫归总问题。
小学数学必考应用题思路解析(附例题)

小学数学必考应用题思路解析(附例题)(1)平均数问题:平均数是等分除法的发展。
解题关键:在于确定总数量和与之相对应的总份数。
算术平均数:已知几个不相等的同类量和与之相对应的份数,求平均每份是多少。
数量关系式:数量之和÷数量的个数=算术平均数。
加权平均数:已知两个以上若干份的平均数,求总平均数是多少。
数量关系式(部分平均数×权数)的总和÷(权数的和)=加权平均数。
差额平均数:是把各个大于或小于标准数的部分之和被总份数均分,求的是标准数与各数相差之和的平均数。
数量关系式:(大数-小数)÷2=小数应得数最大数与各数之差的和÷总份数=最大数应给数最大数与个数之差的和÷总份数=最小数应得数。
例1. 一辆汽车以每小时100 千米的速度从甲地开往乙地,又以每小时60 千米的速度从乙地开往甲地。
求这辆车的平均速度。
分析:求汽车的平均速度同样可以利用公式。
此题可以把甲地到乙地的路程设为“1 ”,则汽车行驶的总路程为“2 ”,从甲地到乙地的速度为100 ,所用的时间为,汽车从乙地到甲地速度为60 千米,所用的时间是,汽车共行的时间为+ = , 汽车的平均速度为2 ÷=75 (千米)(2)归一问题:已知相互关联的两个量,其中一种量改变,另一种量也随之而改变,其变化的规律是相同的,这种问题称之为归一问题。
根据求“单一量”的步骤的多少,归一问题可以分为一次归一问题,两次归一问题。
根据球痴单一量之后,解题采用乘法还是除法,归一问题可以分为正归一问题,反归一问题。
一次归一问题,用一步运算就能求出“单一量”的归一问题。
又称“单归一。
”两次归一问题,用两步运算就能求出“单一量”的归一问题。
又称“双归一。
”正归一问题:用等分除法求出“单一量”之后,再用乘法计算结果的归一问题。
反归一问题:用等分除法求出“单一量”之后,再用除法计算结果的归一问题。
解题关键:从已知的一组对应量中用等分除法求出一份的数量(单一量),然后以它为标准,根据题目的要求算出结果。
小学数学典型应用题类型解题思路.doc

实用标准文档小学数学应用题复习小学数学应用题是教学的重点,又是教学的难点。
每次毕业考试所占比例较大 ,因此在总复习中它至关重要。
应用题的系统复习有助于学生理解概念,掌握数量关系,培养和提高分析问题、解决问题的能力。
现对应用题的复习教学谈谈我自己的看法:小学的应用题主要分为以下两种:1 、简单应用题 :(1)简单应用题的含义:只含有一种基本数量关系,或用一步运算解答的应用题 .2、复合应用题:(1)复合应用题:有两个或两个以上的基本数量关系组成的,用两步或两步以上运算解答的应用题 .(2)主要类型:(1)含有三个已知条件的两步计算的应用题。
(2)含有两个已知条件的两步计算的应用题。
文案大全实用标准文档(3)解答连乘连除应用题。
(4)解答三步计算的应用题。
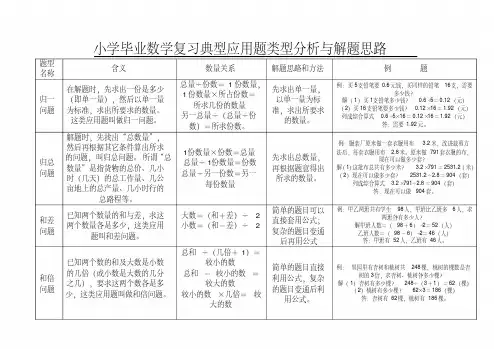
(5)解答小数计算的应用题:3.复合应用题中典型应用题:题型数量关系解题思路题含义例名和方法称总量÷份数= 1在解题时,先求出一份数量, 1 份数先求出单归份是多少(即单一量×所占份数一量,以单一量),然后以单一量=所求几份的一量为标问为标准,求出所要求数量准,求出所题的数量。
这类应用题另一总量÷(总要求的数叫做归一问题。
量÷份数)=所量。
求份数。
例:买 5 支铅笔要 0.6 元钱,买同样的铅笔16 支,需要多少钱?解( 1)买 1 支铅笔多少钱? 0.6÷5= 0.12 (元)( 2)买 16 支铅笔要多少钱? 0.12 ×16 =1.92(元)列成综合算式0.6 ÷5 ×16 =0.12 ×16 =1.92 (元)答:需要 1.92 元。
归解题时,先找出“总 1 份数量×份数先求出总例:服装厂原来做一套衣总数量”,然后再根据=总量数量,再根服用布 3.2米,改进裁剪方文案大全问其它条件算出所求总量÷1份数量据题意得法后,每套衣服用布 2.8 题的问题,叫归总问=份数出所求的米。
小学数学典型应用题类型分析和解题思路.doc
这是与列车行驶有关的一些问 题,解答时要注意列车车身的 长度。
火车过桥:过桥时间=(车长+ 桥长)÷车速 火车追及: 追及时间=(甲车 长+乙车长+距离) ÷(甲车速-乙车速) 火车相遇: 相遇时间=(甲车 长+乙车长+距离) ÷(甲车速+乙车速)
大多数情况可以 直接利用数量关 系的公式。
例: 南京到上海的水路长 392 千米, 同时从两港各开 出一艘轮船相对而行,从南京开出的船每小时行 28
千米, 从上海开出的船每小时行 21千米, 经过几小时
两船相遇?
解 :392÷(28 + 21 )= 8(小时)
答:经过 8 小时两船相遇。
例: 好马每天走 120 千米, 劣马每天走 75 千米, 劣马 先走 12 天,好马几天能追上劣马? 解( 1 )劣马先走 12 天能走多少千米? 75×12 =900 (千米) ( 2)好马几天追上劣马? 900÷(120 -75 )= 20 (天) 列成综合算式 75×12÷( 120 - 75 )= 900÷45 =20 (天) 答:好马 20 天能追上劣马。
(顺水速度+逆水速 度)÷ 2=船速 (顺水速度-逆水速 度)÷ 2=水速 顺水速=船速× 2-逆 水速=逆水速+水速× 2 逆水速=船速× 2-顺 水速=顺水速-水速× 2
大多数情况可以 直接利用数量关 系的公式
例: 一只船顺水行 320 千米需用 8小时,水流速度为
每小时 15千米, 这只船逆水行这段路程需用几小时?
分针的速度是时针的 12
倍, 二者的速度差为 11/12 。 通常按追及问题来对 待,也可以按差倍问题 来计算。
一般地说,在两次分配中,如果 一次盈,一次亏,则有: 参加分配总人数=(盈+亏)÷ 分配差 如果两次都盈或都亏,则有: 参加分配总人数=(大盈-小 盈)÷分配差 参加分配总人数=(大亏-小 亏)÷分配差
(完整版)小学数学30种典型应用题分类讲解附带例题和解题过程
小学数学30种典型应用题讲解应用题可分为一般应用题与典型应用题。
没有特定的解答规律的两步以上运算的应用题,叫做一般应用题。
题目中有特殊的数量关系,可以用特定的步骤和方法来解答的应用题,叫做典型应用题.以下主要研究30类典型应用题:1 归一问题【含义】在解题时,先求出一份是多少(即单一量),然后以单一量为标准,求出所要求的数量。
这类应用题叫做归一问题。
【数量关系】总量÷份数=1份数量1份数量×所占份数=所求几份的数量另一总量÷(总量÷份数)=所求份数【解题思路和方法】先求出单一量,以单一量为标准,求出所要求的数量。
例1 买5支铅笔要0.6元钱,买同样的铅笔16支,需要多少钱?解(1)买1支铅笔多少钱? 0.6÷5=0.12(元)(2)买16支铅笔需要多少钱?0.12×16=1.92(元)列成综合算式 0.6÷5×16=0.12×16=1.92(元)答:需要1.92元。
例2 3台拖拉机3天耕地90公顷,照这样计算,5台拖拉机6 天耕地多少公顷?解(1)1台拖拉机1天耕地多少公顷? 90÷3÷3=10(公顷)(2)5台拖拉机6天耕地多少公顷? 10×5×6=300(公顷)列成综合算式 90÷3÷3×5×6=10×30=300(公顷)答:5台拖拉机6 天耕地300公顷。
例3 5辆汽车4次可以运送100吨钢材,如果用同样的7辆汽车运送105吨钢材,需要运几次?解(1)1辆汽车1次能运多少吨钢材? 100÷5÷4=5(吨)(2)7辆汽车1次能运多少吨钢材? 5×7=35(吨)(3)105吨钢材7辆汽车需要运几次? 105÷35=3(次)列成综合算式 105÷(100÷5÷4×7)=3(次)答:需要运3次。
小学数学应用题解题思路及方法
小学数学应用题解题思路及方法小学数学应用题是指将数学知识应用于实际生活问题的题目。
这类题目要求学生能够理解问题背景,运用数学知识解决问题,并在解题过程中培养学生的逻辑思维能力和实际问题解决能力。
本文将介绍一些常见的小学数学应用题解题思路及方法。
一、读懂题目解决任何问题的第一步是仔细阅读题目,确保完全理解题意。
特别是对于应用题而言,理解问题的背景和条件非常重要。
掌握题目的关键信息有助于建立正确的解题思路。
二、确定解题过程每个数学应用题都有一个解题过程,学生需要明确解题的步骤。
例如,一些问题需要先确定未知数,然后建立方程式,最后解方程式求解未知数。
而对于另一些问题,学生需要根据条件进行分类、比较或计算。
明确解题过程有助于学生把握整个解题过程的思路和步骤。
三、分析问题在解决数学应用题时,学生需要对问题进行细致的分析。
这包括提取关键信息、确定数学关系、寻找规律等。
通过分析问题,学生可以建立正确的数学模型,并能够准确地运用数学知识解决问题。
四、运用适当的数学方法在解决数学应用题时,学生需要选择并运用适当的数学方法。
这需要学生掌握一定的数学基础知识,并能够灵活运用它们。
常见的数学方法包括四则运算、比例、百分数、图形的面积和体积计算等。
根据问题的要求,选择适当的方法能够更快、更准确地解决问题。
五、试错和检查解决数学应用题时,学生应通过试错和检查来验证解题过程和答案的正确性。
试错和检查是解题过程中重要的环节,能够帮助学生发现和纠正错误,并提高解决问题的准确性。
六、练习和实践解决数学应用题需要不断的练习和实践。
通过反复做题,学生可以熟悉各种题型,积累解题经验,并逐渐提高解题效率和准确率。
此外,学生还可以尝试解决一些实际生活中的问题,如购物计算问题、时间计算问题等,这样可以培养学生用数学解决实际问题的能力。
七、合理利用辅助工具在解决一些复杂的数学应用题时,学生可以合理利用辅助工具。
例如,绘制图表、图形,使用计算器等。
小学数学常用的解题思路+详细分析+例子说明
小学数学常用的11种解题思路+详细分析+例子说明一、直接思路"直接思路〞是解题中的常规思路。
它一般是通过分析、综合、归纳等方法,直接找到解题的途径。
【顺向综合思路】从条件出发,根据数量关系先选择两个数量,提出可以解决的问题;然后把所求出的数量作为新的条件,与其他的条件搭配,再提出可以解决的问题;这样逐步推导,直到求出所要求的解为止。
这就是顺向综合思路,运用这种思路解题的方法叫"综合法〞。
例1 兄弟俩骑车出外郊游,弟弟先出发,速度为每分钟200米,弟弟出发5分钟后,哥哥带一条狗出发,以每分钟250米的速度追赶弟弟,而狗以每分钟300米的速度向弟弟追去,追上弟弟后,立即返回,见到哥哥后又立即向弟弟追去,直到哥哥追上弟弟,这时狗跑了多少千米?分析〔按顺向综合思路探索〕:〔1〕根据弟弟速度为每分钟200米,出发5分钟的条件,可以求什么?可以求出弟弟走了多少米,也就是哥哥追赶弟弟的距离。
〔2〕根据弟弟速度为每分钟200米,哥哥速度为每分钟250米,可以求什么?可以求出哥哥每分钟能追上弟弟多少米。
〔3〕通过计算后可以知道哥哥追赶弟弟的距离为1000米,每分钟可追上的距离为50米,根据这两个条件,可以求什么?可以求出哥哥赶上弟弟所需的时间。
〔4〕狗在哥哥与弟弟之间来回不断奔跑,看起来很复杂,仔细想一想,狗跑的时间与谁用的时间是一样的?狗跑的时间与哥哥追上弟弟所用的时间是一样的。
〔5〕狗以每分钟300米的速度,在哥哥与弟弟之间来回奔跑,直到哥哥追上弟弟为止,和哥哥追上弟弟所需的时间,可以求什么?可以求出这时狗总共跑了多少距离?这个分析思路可以用下列图〔图2.1〕表示。
例2 下面图形〔图2.2〕中有多少条线段?分析〔仍可用综合思路考虑〕:我们知道,直线上两点间的一段叫做线段,如果我们把上面任意相邻两点间的线段叫做根本线段,则就可以这样来计数。
〔1〕左端点是A的线段有哪些?有AB AC AD AE AF AG共6条。
小学数学典型应用题分类型分析与解题思路
两个运动物体在不同地点 同时出发(或者在同一地 点而不同时出发,或者在 不同地点又不是同时出 追及 发)作同向运动,在后面 问题 的,行进速度要快些,在 前面的,行进速度较慢 些,在一定时间内,后面 的追上前面的物体。这类 应用题就叫做追及问题。
按相等的距离植树,在距 植树 离、棵距、棵数三个量之 问题 间,已知其中的两个量,
答:杏树有62棵,桃树有186棵。
小学数学典型应用题类型分析与解题思路
题型 名称
含义
有两个已知的同类量,其
倍比 问题
中一个量是另一个量的若 干倍,解题时先求出这个 倍数,再用倍比的方法算
出要求的数。
数量关系
总量÷一个数量=倍数 另一个数量×倍数=另一总量
解题思路和方法
例题
例:100千克油菜籽可以榨油40千克,现在有油菜籽3700千克,可以榨油
要求第三个量。
相遇时间=总路程÷(甲速+乙速) 总路程=(甲速+乙速)×相遇时间
例:南京到上海的水路长392千米,同时从两港各开出一艘轮船相对而 简单的题目直接利用 行,从南京开出的船每小时行28千米,从上海开出的船每小时行21千米, 公式,复杂的题目变 经过几小时两船相遇? 通后利用公式。 解:392÷(28+21)=8(小时)
公式。
答:一共要栽69棵垂柳。
题型 名称
含义
这类问题是根据题目的内
年龄 问题
容而得名,它的主要特点 是两人的年龄差不变,但 是,两人年龄之间的倍数
关系随着年龄的增长在发
行船问题也就是与航行有
关的问题。解答这类问题
要弄清楚船速与水速,船
速是船只本身行的速度,
行船 也就是船只在静水中航行
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关键是把工作总量看作“1”,这样,工作效率 例1 一项工程,甲队单独做需要10天完成,乙队单独做需要15天 就是工作时间的倒数(它表示单位时间内完 完成,现在两队合作,需要几天完成? 成工作总量的几分之几),进而就可以根据 解:由于没有给出这项工程的具体数量,因此,把此项工程看作 工作量、工作效率、工作时间三者之间的关 变通后可以利用上述数 单位1。甲队独做需10天完成,那么每天完成这项工程的1/10;乙 系列出算式。 队单独做需15天完成,每天完成这项工程的1/15;两队合做,每 量关系的公式。 工作量=工作效率× 工作时间 天可以完成这项工程的(1/10+1/15)。即: 工作时间=工作量÷ 工作效率 1÷ (1/10+1/15)=1÷ 1/6=6(天) 工作时间=总工作量÷ (甲工作效率+乙工作 答:两队合做需要6天完成。 效率)
小学数学典型应用题类型分析与解题思路
题型名 称 含义 数量关系 解题思路和方法 例题 例:买5支铅笔要0.6元钱,买同样的铅笔16支,需要多少钱? 解:(1)买1支铅笔多少钱? 0.6÷ 5=0.12(元) 先求出单一量,以单一 ( 2 )买 16支铅笔要多少钱? 量为标准,求出所要求 0.12× 16=1.92(元) 的数量。 列成综合算式0.6÷ 5× 16=0.12× 16=1.92(元) 答:需要1.92元。 例:服装厂原来做一套衣服用布3.2米,改进裁剪方法后,每套衣 服用布2.8米。原来做791套衣服的布, 现在可以做多少套? 先求出总数量,再根据 解:(1)这批布总共有多少米? 3.2× 791=2531.2(米) 题意得出所求的数量。 (2)现在可以做多少套? 2531.2÷ 2.8=904(套) 列成综合算式 3.2× 791÷ 2.8=904(套) 答:现在可以做904套。 例:甲乙两班共有学生98人,甲班比乙班多6人,求 两班各有多 简单的题目可以 直接套 少人? 用公式; 复杂的题目变 解:甲班人数=(98+6)÷ 2=52(人) 乙班人数=(98-6)÷ 2=46(人) 通 后再用公式 。 答:甲班有52人,乙班有46人。 例: 果园里有杏树和桃树共248棵,桃树的棵数是杏 树的3倍,求 简单的题目直接 利用公 杏树、桃树各多少棵? 式,复杂 的题目变通后 解:(1)杏树有多少棵? 248÷ (3+1)=62(棵) (2)桃树有多少棵? 62× 3=186(棵) 利 用公式。 答:杏树有62棵,桃树有186棵。 例: 果园里桃树的棵数是杏树的3倍,而且桃树比杏树多124棵。 简单的题目直接利用公 求杏树、桃树各多少棵? 式,复杂的题目变通后 解:(1)杏树有多少棵? 124÷ (3-1)=62(棵) 利用公式。 (2)桃树有多少棵? 62× 3=186(棵) 答:果园里杏树是62棵,桃树是186棵。 例: 100千克油菜籽可以榨油40千克,现在有油菜籽3700千克, 可以榨油多少? 先求出倍数,再用倍比 解:(1)3700千克是100千克的多少倍? 3700÷ 100=37(倍) (2)可以榨油多少千克? 40× 37=1480(千克) 关系求出要求的数。 列成综合算式 40× (3700÷ 100)=1480(千克) 答:可以榨油1480千克。
小学数学典型应用题类型分析与解题思路
题型名 称 含义 数量关系 解题思路和方法 例题 例: 一座大桥长2400米,一列火车以每分钟900米的速度通过大 桥,从车头开上桥到车尾离开桥共需要3 分钟。这列火车长多少 火车过桥:过桥时间=(车长+桥长)÷ 车速 米? 火车追及: 追及时间=(甲车长+乙车长+ 这是与列车行驶有关的一些问 列车问 大多数情况可以直接利 解:火车3分钟所行的路程,就是桥长与火车车身长度的和。 题,解答时要注意列车车身的长 距离) ÷ (甲车速-乙车速) 题 用数量关系的公式。 (1)火车3分钟行多少米? 900× 3=2700(米) 度。 火车相遇: 相遇时间=(甲车长+乙车长+ (2)这列火车长多少米? 2700-2400=300(米) 距离) ÷ (甲车速+乙车速) 列成综合算式 900× 3-2400=300(米) 答:这列火车长300米。 就是研究钟面上时针与分针关系 的问题,如两针重合、两针垂直 分针的速度是时针的12倍, 二者的速度差为 时钟问 变通为“追及问 题”后可 、两针成一线、两针夹角为60度 11/12。 通常按追及问题来对待,也可以按 题 以直接 利用公式。 等。时钟问题可与追及问题相类 差倍问题来计算。 比。 例: 从时针指向4点开始,再经过多少分钟时针正好与分针重合? 解:钟面的一周分为60格,分针每分钟走一格,每小时走60格; 时针每小时走5格,每分钟走5/60=1/12 格。每分钟分针比时针 多走(1-1/12)=11/12格。4点整,时针在前,分针在后,两针 相距20格。所以分针追上时针的时间为 20÷ (1-1/12)≈ 22 (分) 答:再经过22分钟时针正好与分针重合。
已知两个数的和及大数是小数的 总和 ÷ (几倍+1)= 较小的数 和倍问 几倍(或小数是大数的几分之 总和 - 较小的数 = 较大的数 几),要求这两个数各是多 少, 题 较小的数 × 几倍= 较大的数 这类应用题叫做和倍问题。 已知两个数的差及大数是小数的 两个数的差÷ (几倍-1)=较小的数 差倍问 几倍(或小数是大数的几分之 几),要求这两个数各是多 少, 较小的数× 几倍=较大的数 题 这类应用题叫做差倍问题。 有两个已知的同类量,其中一个 量是另一个量的若干倍,解题时 总量÷ 一个数量=倍数 倍比问 先求出这个倍数,再用倍比 的 题 另一个数量× 倍数 =另一总量 方法算出要求的数,这类应用题 叫做倍比问题。
根据一定的人数,分配一定的物 品,在两次分配中,一次有余 盈亏问 (盈),一次不足(亏), 或 题 两次都有余,或两次都不足,求 人数或物品数,这类应用题叫做 盈亏问题。 工程问题主要研究工作量、工作 效率和工作时间三者之间的关系 。这类问题在已知条件中, 常 工程问 常不给出工作量的具体数 量, 只提出“一项工程”、“一块土地” 题 、“一条水渠”、“一件工作”等, 在解题时,常常用单位“1”表示工 作总量。
可以利用“差倍问题”的 解题思路和方法
例: 一只船顺水行320千米需用8小时,水流速度为每小时15千 米,这只船逆水行这段路程需用几小时? 解:由条件知,顺水速=船速+水速=320÷ 8,而水速为每小时 大多数情况可以直接利 15千米,所以,船速为每小时 320÷ 8-15 =25(千米) 用数量关系的公式 船的逆水速为 25-15=10(千米) 船逆水行这段路程的时间为 320÷ 10=32(小时) 答:这只船逆水行这段路程需用32小时。
一般地说,在两次分配中,如果一次盈,一 次亏,则有: 参加分配总人数=(盈+亏)÷ 分配差 如果两次都盈或都亏,则有: 参加分配总人数=(大盈-小盈)÷ 分配差 参加分配总人数=(大亏-小亏)÷ 分配差
例: 给幼儿园小朋友分苹果,若每人分3个就余11个;若每人分4 个就少1个。问有多少小朋友?有多少 个苹果? 大多数情况可以直接利 解:按照“参加分配的总人数=(盈+亏)÷ 分配差”的数量关系: 用数量关系的公式。 (1)有小朋友多少人?(11+1)÷ (4-3)=12(人) (2)有多少个苹果? 3× 12+11=47(个) 答:有小朋友12人,有47个苹果。
小学数学典型应用题类型分析与解题思路
题型名 称 含义 数量关系 相遇时间=总路程÷ (甲速+乙速) 总路程=(甲速+乙速)× 相遇时间 解题思路和方法 例题 例: 南京到上海的水路长392千米,同时从两港各开出一艘轮船 简单的题目可直接利用 相对而行,从南京开出的船每小时行28 千米,从上海开出的船每 公式,复杂的题目变通 小时行21千米,经过几小时两船相遇? 后再利用公式。 解 :392÷ (28+21)=8(小时) 答:经过8小时两船相遇。 例: 好马每天走120千米,劣马每天走75千米,劣马先走12天, 好马几天能追上劣马? 简单的题目直接利用公 解:(1)劣马先走12天能走多少千米? 75× 12=900(千米) 式,复杂的题目变通后 (2)好马几天追上劣马? 900÷ (120-75)=20(天) 利用公式。 列成综合算式 75× 12÷ (120-75)=900÷ 45=20(天) 答:好马20天能追上劣马。 例: 一条河堤136米,每隔2米栽一棵垂柳,头尾都栽,一共要栽 先弄清楚植树问题的类 多少棵垂柳? 型,然后可以利用公式 解: 136÷ 2+1=68+1=69(棵) 。 答:一共要栽69棵垂柳。 例1 爸爸今年35岁,亮亮今年5岁,今年爸爸的年龄是亮亮的几 倍?明年呢? 解: 35÷ 5=7(倍) (35+1)÷ (5+1)=6(倍) 答:今年爸爸的年龄是亮亮的7倍, 明年爸爸的年龄是亮亮的6倍 。
两个运动的物体同时由两地出 相遇问 发相向而行,在途中相遇动物体在不同地点同时出 发(或者在同一地点而不是同时 出发,或者在不同地点又不 是 追及问 同时出发)作同向运动,在后面 追及时间=追及路程÷ (快速-慢速) 题 追及路程=(快速-慢速)× 追及时间 的,行进速度要快些,在前面 的,行进速度较慢些,在一定时 间之内,后面的追上前面的物体 。这类应用题就叫做追及问题。 线形植树: 棵数=距离÷ 棵距+1 按相等的距离植树,在距离、棵 环形植树:棵数=距离÷ 棵距 植树问 距、棵数这三个量之间,已知其 方形植树:棵数=距离÷ 棵 距-4 中的两个量,要求第三个 量, 题 三角形植树:棵数=距离÷ 棵距-3 这类应用题叫做植树问题。 面积植树:棵数=面积÷ (棵距× 行距) 这类问题是根据题目的内容而得 名,它的主要特点是两人的 年龄 年龄问题往往与和差、和倍、差倍问题有着 年龄问 差不变,但是,两人年龄之间的 密切联系,尤其与差倍问题的解题思路是一 题 倍数关系随着年龄的增长在发生 致的,要紧紧抓住“年龄差不变”这个特点。 变化。 行船问题也就是与航行有关的 问 题。解答这类问题要弄清船 速与 水速,船速是船只本身行 的速 (顺水速度+逆水速 度)÷ 2=船速 行船问 度,也就是船只在静水中 航行的 (顺水速度-逆水速 度)÷ 2=水速 题 速度;水速是水流的速 度,船只 顺水速=船速× 2-逆水速=逆水速+水速× 2 顺水航行的速度是船 速与水速之 逆水速=船速× 2-顺水速=顺水速-水速× 2 和;船只逆水航行 的速度是船速 与水速之差。
