山东大学威海分校 试卷分析表
山大威海考试试题库
山大威海考试试题库一、试题库简介山大威海考试试题库是山东大学威海分校为提高教学质量、加强学生自主学习能力而开发的一套在线学习系统。
试题库包含各个学科的历年考试真题、模拟试题以及练习题，覆盖了从基础课程到专业课程的广泛领域。
二、试题库特点1. 全面性：试题库覆盖了文、理、工、商等多个学科，满足不同专业学生的需求。
2. 系统性：试题按照学科、课程、年份等进行分类，便于学生快速定位所需内容。
3. 实时更新：定期更新试题库内容，确保学生能够接触到最新的考试信息和题型。
4. 互动性：学生可以通过在线讨论区与教师和其他学生交流，共同探讨问题。
三、试题库使用指南1. 注册与登录：学生需要使用学号和密码进行注册和登录。
2. 选择学科：登录后，学生可以根据自己的专业选择相应的学科。
3. 浏览试题：学生可以浏览不同年份的试题，进行自我测试。
4. 在线练习：试题库提供在线练习功能，学生可以即时检查自己的答案。
5. 反馈与讨论：学生可以在讨论区提出疑问，获取教师和同学的帮助。
四、部分试题示例[数学]1. 选择题：若函数f(x) = x^2 - 4x + 3，求f(x)的最小值。
A. 0B. 1C. 3D. 42. 计算题：求下列不定积分的解。
∫(2x + 1)dx[物理]1. 选择题：根据牛顿第二定律，下列哪个选项描述正确？A. F = maB. F = mvC. F = m/aD. F = a/m2. 实验题：描述如何使用弹簧秤测量物体的重力。
[化学]1. 选择题：下列哪个化合物是酸？A. NaClB. HClC. CaCO3D. H2O2. 简答题：解释什么是化学平衡，并给出一个例子。
五、结语山大威海考试试题库是学生学习的重要辅助工具，它不仅提供了丰富的学习资源，还促进了学生的自主学习和批判性思维能力的发展。
我们鼓励所有学生充分利用这一资源，提高自己的学术水平。
请注意，以上内容仅为示例，实际的试题库内容会根据学校的教学大纲和课程设置有所不同。
山大威海考试试题库
山大威海考试试题库一、选择题（每题2分，共20分）1. 山东大学威海校区成立于哪一年？A. 1984年B. 1990年C. 2000年D. 2005年2. 山东大学威海校区位于哪个城市？A. 青岛B. 济南C. 威海D. 烟台3. 山东大学威海校区的校训是什么？A. 厚德、博学、求是、创新B. 厚德、博学、笃行、创新C. 厚德、博学、明辨、笃行D. 厚德、博学、明辨、创新4. 山东大学威海校区的校园面积大约是多少？A. 1000亩B. 2000亩C. 3000亩D. 4000亩5. 山东大学威海校区的图书馆藏书量大约是多少？A. 50万册C. 150万册D. 200万册6. 山东大学威海校区的校徽中包含哪些元素？A. 书、火炬、地球B. 书、火炬、山峰C. 书、火炬、帆船D. 书、火炬、海浪7. 山东大学威海校区的校园内有多少个学院？A. 10个B. 15个C. 20个D. 25个8. 山东大学威海校区的校园内有多少个研究所？A. 5个B. 10个C. 15个D. 20个9. 山东大学威海校区的校园内有多少个学生社团？A. 50个B. 100个C. 150个D. 200个10. 山东大学威海校区的校园内有多少个运动场馆？A. 5个B. 10个D. 20个二、填空题（每空1分，共10分）11. 山东大学威海校区的校风是“_________、_________、_________”。
12. 山东大学威海校区的校园内有_________个食堂，能够满足不同学生的餐饮需求。
13. 山东大学威海校区的校园内有_________个运动场，包括足球场、篮球场等。
14. 山东大学威海校区的校园内有_________个实验室，涵盖了多个学科领域。
15. 山东大学威海校区的校园内有_________个教学楼，为学生提供了良好的学习环境。
三、简答题（每题5分，共20分）16. 请简述山东大学威海校区的办学理念。
17. 请简述山东大学威海校区的校园文化特点。
山东大学威海分校马克思主义基本原理试卷a(含答案)
32、马克思的两个伟大理论发现是 A.辩证唯物主义和历史唯物主义 C.唯物史观和剩余价值学说 33、唯心主义的认识论根源是（
50. 有人认为只有写到书本上的理论才是真实可靠的，便不顾实际情况，生搬硬套书本上的理论。这犯 A.唯心主义先验论的错误 C.教条主义的错误 B.直观被动反映论的错误 D.经验主义的错误
学院（系）
专业
级
班
学号
姓名
第 1 页共 3 页
山东大学
…………………………密…………………………封………………………线………………………… 密 封 线
A.机械唯物主义的观点 C.辩证唯物主义的观点 21、发展的实质是 ( ) B.量变和质变的相互转化 A.前进性和曲折性的统一 C.运动和静止的相对统一 22、 “拔苗助长”的事例是 A.重视可能性的表现 C.违反事物发展规律的表现 A.客观实在性的观点 B.唯心主义的观点 D.庸俗唯物主义的观点
学期
20、否认意识形式的主观性，把意识看成是人脑的分泌物，这是(
35、加快资本周转可以提高年剩余价值量和年剩余价值率，根本原因是（
36、社会资本再生产的核心问题是（ D.新事物的产生和旧事物的灭亡 ( ) B.忽视可能性的表现 D.发挥主观能动性的表现 ( ) D.实践的观点
姓名
37、在资本主义条件下，部门之间的竞争形成了（ B、商品的市场价格 D、平均利润率 ） 。 C、资本转移
） D.辩证唯物主义 D.制订周密计划 D.共同的形式
B、具体劳动和私人劳动的矛盾 D、生产力与生产关系的矛盾 ） 。 B、劳动力在一定条件下可以转化为商品 D、劳动力价值受历史道德因素影响 ） 。 B、劳动过程和价值增殖过程的统一 D、价值形成过程与价值增殖过程的统一 ） 。 B、能够发生价值增殖 D、借助抽象劳动而再生产出来 ） 。
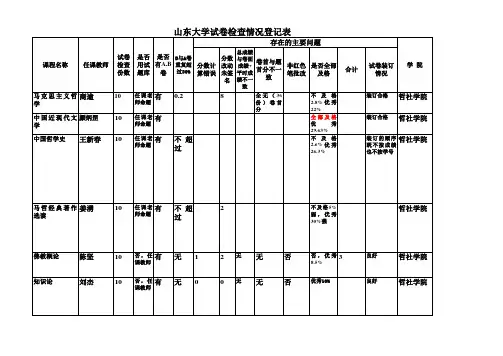
山东大学试卷检查情况登记表
不及格 6.96% ，优 秀3.48%
不及格 5.26% ，优 秀4.91%
不及格 4.94% ，优 秀4.10%
无
否，优秀 0
5%
无
否，优秀 0
2%
好 ， 试 卷 和 政治学院
总成绩单排 列顺序一致
装 订 整 齐 规 政治学院
范
装 订 整 齐 规 政治学院
范
装订规范 军理部
装订规范 军理部
装订规范 军理部
塑造工艺原理
师命题
过30%
不及格 2% ， 优 秀 50.8%
装订规范 信息学院
不及格 12.5% ，优 秀25%
装订规范 信息学院
不及格 2.326%, 优 秀32.558%
好
信息学院
电 磁 场 与 电 磁 雷虹
波
10 任 课 教 有 不 超 1
师命题
过
高频电子线路 陈延湖 10 题库 有 不 超 过
不及格3人 1.62% ，优 秀3.24%
良好
马列学院
装订整齐 马列学院
装订整齐 马列学院
自 然 认 证 法 概 范杰敏 10 校 内 统 有 不 超
论
一命题
过
气 动 与 液 压 控 刘延俊 10 校 内 统 是 否
制
一命题
画 法 几 何 与 机 刘素萍 10 校 内 统 是 否
械制图
一命题
计 算 机 技 术 基 查黎敏
军事理论
陈军升 20 校 内 统 有 不 超
一命题
过
军事理论
李传道 20 校 内 统 有 不 超
一命题
过
军事理论 军事理论
赵学武 10 校 内 统 有 否 无
山东威海市届高三下学期第二次高考模拟数学理试题word含解析
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页．考试时间120分钟．满分150分．答题前，考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、考号填写在答题纸规定的位置．第Ⅰ卷（选择题 共50分）注意事项：每小题选出答案后，用铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．一、选择题:本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知复数z 满足2(2)1i z -⋅=，则z 的虚部为( ) （A ）325i （B ）325 （C ）425i （D ）425【答案】D 【解析】试题分析：由213434(2)1(34)134(34)(34)2525i i z i z z i i i i +-⋅=⇒-=⇒===+--+，所以复数z 的虚部为425，故答案选D . 考点：1.复数的计算；2.复数的定义.2. 已知集合2{|},{1,0,1}A x x a B ===-，则1a =是A B ⊆的( ) （A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分也不必要条件 【答案】A 【解析】试题分析：由A B ⊆得集合A 是空集或者非空集合， 当集合A 是空集时，0a <，当集合A 是非空集合时，1x =-或1或0，此时1a =或0， 故答案选A .考点：1.集合之间的关系；2.命题的充分必要性.3. 设单位向量12,e e 的夹角为120，122a e e =-，则 ||a =( )（A ）3 （B （C ）7 （D 【答案】D考点：1.向量的模；2.数量积.4. 已知等差数列{}n a 满足61020a a +=，则下列选项错误的是( ) （A ）15150S = （B ）810a = （C ）1620a =（D ）41220a a += 【答案】C 【解析】试题分析：因为{}n a 是等差数列，所以6108220a a a +==，得810a =，11515815()151502a a S a +===；4128220a a a +==故答案选C .考点：等差数列的性质.5. 双曲线22124x y -=的顶点到其渐近线的距离为( )（A （B （C （D【答案】B 【解析】试题分析：由双曲线22124x y -=，得其顶点坐标，(，渐近线方程y =，点到y =的距离为3d ==，由双曲线的性质得双曲线22124x y -=B .考点：双曲线的性质.6. 已知,x y 满足约束条件224220220x y x y x y ⎧+≤⎪--≤⎨⎪-+≥⎩，则2z x y =+的最大值为( )（A ）2 （B（C ）4 （D）【答案】D 【解析】试题分析：如图所示阴影部分为不等式组224220220x y x y x y ⎧+≤⎪--≤⎨⎪-+≥⎩表示的可行域，由图可知，当直线20x y z +-=与圆224x y +=相切时，z 取得最大值，2z =⇒=±max z =D .考点：1.线性规划；2.直线与圆的位置关系.7. 周期为4的奇函数()f x 在[0,2]上的解析式为22,01()log 1,12x x f x x x ⎧≤≤=⎨+<≤⎩，则(2014)+(2015)f f =( )（A ）0 （B ）1 （C ）2 （D ）3 【答案】B 【解析】试题分析：因为函数()f x 是周期为4的奇函数，所以2(2014)(50342)(2)log 212f f f =⨯+==+=，2(2015)(50441)(1)(1)11f f f f =⨯-=-=-=-=-，(2014)+(2015)1f f =，故答案选B .考点：1.函数求值；2.函数的周期性和奇偶性.8. 已知,,m n l 是不同的直线，,αβ是不同的平面，以下命题正确的是( )①若m ∥n ，,m n αβ⊂⊂，则α∥β；②若,m n αβ⊂⊂，α∥l m β⊥，，则l n ⊥；③若,,m n αβα⊥⊥∥β，则m ∥n ；④若αβ⊥，m ∥α，n ∥β，则m n ⊥； （A ）②③ （B ）③ （C ）②④ （D ）③④ 【答案】B 【解析】试题分析：如图所示，在正方体1111ABCD A BC D -中，11//AD B C ,AD ⊂平面ABCD ,11B C ⊂平面11BB C C ,但平面ABCD 与平面11BB C C 相交于BC ，故选项①错误；平面//ABCD 平面1111A B C D ，AD ⊂平面ABCD ,11D C ⊂平面11BB C C ，CD AD ⊥,但CD 与11D C 不垂直，，故选项②错误；选项③是线面垂直的一个性质定理，故选项③是正确的；平面ABCD ⊥平面11BB C C ，11//B C 平面ABCD ，//AD 平面11BB C C ，但11//B C AD ，故选项④错误.故答案选B考点：点、线、面的位置关系.9. 在ABC ∆中，内角C B A 、、的对边分别是c b a 、、，若22()6c a b =-+，ABC ∆的面积为2，则C =( ) 3π23π6π56π（A ） （B ） （C ） （D ） 【答案】A考点：解三角形.10. 设()f x '为函数()f x 的导函数，已知21()()ln ,()x f x xf x x f e e'+==，则下列结论正确的是 ( )（A ）()f x 在(0,)+∞单调递增 （B ）()f x 在(0,)+∞单调递减 （C ）()f x 在(0,)+∞上有极大值 （D ）()f x 在(0,)+∞上有极小值 【答案】D 【解析】 试题分析：22ln ln 1()()ln ()()[()]()(ln )2x x x f x xf x x xf x f x xf x xf x x c x x '''+=⇒+=⇒=⇒=+ 所以2ln ()2x c f x x x =+，又1()f e e =，得12c =，即2ln 1()22x f x x x=+所以222222ln ln 1(ln 1)()0222x x x f x x x x---'=-=≤，所以()f x 在(0,)+∞单调递减 故答案选D考点：1.导数的应用；2.构造函数.第Ⅱ卷（非选择题 共100分）1． 请用0.5毫米的黑色签字笔将每题的答案填写在答题纸的指定位置．书写的答案如需改动，要先划掉原来的答案，然后再写上新答案．2． 不在指定答题位置答题或超出答题区域书写的答案无效．在试题卷上答题无效． 二、填空题:本大题共5小题，每小题5分，共25分.11. 用分层抽样的方式对某品牌同一批次两种型号的产品进行抽查，已知样本容量为80，其中有50件甲型号产品，乙型号产品总数为1800，则该批次产品总数为________. 【答案】4800 【解析】试题分析：由题知乙型号产品所占比例为80503808-=，所以该批次产品总数为3180048008÷=考点：分层抽样.12. 右面的程序框图输出的S 的值为_____________.【答案】2512【解析】试题分析：1n =时，1011s =+=；2n =时，13122s =+=；3n =时，3111236s =+=；4n =时，111256412s =+=；5n =时,输出2512s =. 考点：程序框图的识别.13. 已知0,0x y >>且2x y +=，则22111x y xy++的最小值为______.【解析】试题分析：2222222221111111()()[4()3()]24x y y x y xx y xy x y xy x y x y+++=++=++++11[423(426)344y x x y ≥+⋅⋅+⋅=++=，当且仅当""x y =时，等号成立.考点：基本不等式.14. 若1()()f x f x dx x +=⎰， 则1()f x dx =⎰_________.【答案】14【解析】试题分析：因为1()f x dx ⎰是一常数，即可设1()f x dx m =⎰，所以()f x x m =-()f x 的原函数2(1()2g x x m c x c =-+为常数）所以1()(1)(0)f x dx g g =-⎰，即得12m m =- 解得14m =，即11()4f x dx =⎰考点：1.定积分. 15. 函数213()|2|122f x x x x =-+-+的零点个数为___________. 【答案】2 【解析】试题分析：令()0f x =，即213|2|122x x x -+=- 则函数21()|2|2h x x x =-+和函数3()12g x x =-的交点个数即为函数()f x 的零点个数，如上图所示，()h x 与()g x 有两个交点，所以函数()f x 的零点个数为2. 考点：1.函数的零点；2.数形结合.三、解答题:本大题共６小题，共75分．解答应写出文字说明，证明过程或演算步骤． 16. （本小题满分12分）已知向量)2,cos (sin ),1,cos 2(x x x ωωω-=-=)0(>ω， 函数3)(+⋅=n m x f ，若函数)(x f 的图象的两个相邻对称中心的距离为2π. （Ⅰ）求函数)(x f 的单调增区间；（Ⅱ）若将函数)(x f 的图象先向左平移4π个单位，然后纵坐标不变，横坐标缩短为原来的21倍，得到函数)(x g 的图象，当]2,6[ππ∈x 时，求函数)(x g 的值域.【答案】（Ⅰ）Z k k k ∈+-],83,8[ππππ；（Ⅱ）[.【解析】试题分析：（Ⅰ）利用向量的数量积公式以及三角函数的恒等变换得())4f x x πω=-，由函数)(x f 的图象的两个相邻对称中心的距离为2π，所以函数)(x f 的周期为π，利用周期公式即可求得1ω=，即())4f x x π=-，令Z k k x k ∈+≤-≤-,224222πππππ，解之即可求出函数)(x f 的单调增区间；（Ⅱ）由三角函数图像变换得)44sin(2)(π+=x x g ，因为]2,6[ππ∈x ，即得1194[,]4124x πππ+∈，根据三角函数的性质得22)44sin(1≤+≤-πx ，最后求得函数)(x g 在]2,6[ππ∈x 的值域.试题解析：（Ⅰ）32)cos (sin cos 23)(+--=+⋅=x x x x f ωωω2sin 22cos 1sin 2cos 2)4x x x xx ωωωωπω=-+=-=-，由题意知，πωπ==22T ，1=∴ω， )42sin(2)(π-=∴x x f .由Z k k x k ∈+≤-≤-,224222πππππ，解得：Z k k x k ∈+≤≤-,838ππππ,∴)(x f 的单调增区间为Z k k k ∈+-],83,8[ππππ.（Ⅱ）由题意，若)(x f 的图像向左平移4π个单位，得到)4y x π=+，再纵坐标不变，横坐标缩短为原来的21倍，得到)44sin(2)(π+=x x g ，]2,6[ππ∈x ，]49,1211[44πππ∈+∴x ， ∴22)44sin(1≤+≤-πx ， ∴函数()g x的值域为[.考点：1.三角函数的性质；2.三角函数图像；3.三角函数的值域.17. （本小题满分12分）一汽车4S 店新进A ,B ,C 三类轿车,每类轿车的数量如下表:同一类轿车完全相同，现准备提取一部分车去参加车展.（Ⅰ）从店中一次随机提取2辆车，求提取的两辆车为同一类型车的概率;（Ⅱ）若一次性提取4辆车，其中A ,B ,C 三种型号的车辆数分别记为,,a b c ，记ξ为,,a b c 的最大值，求ξ的分布列和数学期望. 【答案】（Ⅰ）518; （Ⅱ）分布列略，209.∴其分布列为数学期望为23414631269E ξ=⨯+⨯+⨯= 考点：古典概型的分布列及期望.18. （本小题满分12分）已知 {}n a 是各项都为正数的数列，其前 n 项和为 n S ，且n S 为n a 与1na 的等差中项. （Ⅰ）求证：数列2{}n S 为等差数列； （Ⅱ）求数列{}n a 的通项公式；（Ⅲ）设(1),nn nb a -=求{}n b 的前n 项和n T .【答案】（Ⅰ）证明略；（Ⅱ）n a ；（Ⅲ）(1)n T =-【解析】试题分析：（Ⅰ）由题意知12n n nS a a =+，即221n n n S a a -=，当1n =时，可得11S =;又2n ≥时,有1n n n a S S -=-，得2112()()1n n n n n S S S S S -----=，整理得2211,(2)n n S S n --=≥，2{}n S 是首项为1，公差为1的等差数列.（Ⅱ）由（Ⅰ）可得211n S n n =+-=，{}n a 是各项都为正数，n S =1n n n a S S -=-=2n ≥），又111a S ==,∴n a =；（Ⅲ）由（Ⅱ）得(1)(1),n n nn n b a -===-当n 为奇数时，n T =当n 为偶数时，n T ={}n b 的前n 项和(1)n T =-试题解析：（Ⅰ）由题意知12n n nS a a =+，即221n n n S a a -=，① 当1n =时，由①式可得11S =;又2n ≥时,有1n n n a S S -=-，代入①式得2112()()1n n n n n S S S S S -----=整理得2211,(2)n n S S n --=≥． ∴ 2{}n S 是首项为1，公差为1的等差数列. （Ⅱ） 由（Ⅰ）可得211n S n n =+-=，∵{}n a 是各项都为正数，∴n S∴1n n n a S S -=-=2n ≥），又111a S ==,∴n a（Ⅲ）(1)(1),n n nn n b a -===-当n 为奇数时，11)(1n T n =-+-++--=当n 为偶数时，11)(1n T n =-+-+--+=∴{}n b 的前n 项和(1)n T =-考点：1.等差数列的判定；2.通项公式的求法；3.数列求和.19. （本小题满分12分）如图：BCD 是直径为O 为圆心，C 是BD 上一 点，且2BC CD =.DF CD ⊥，且2DF =，BF =，E 为FD 的中点，Q 为BE 的中点，R 为FC 上一点,且3FR RC =.(Ⅰ) 求证：QR ∥平面BCD ；（Ⅱ）求平面BCF 与平面BDF 所成二面角的余弦值.【答案】(Ⅰ)证明略；. 【解析】试题分析：(Ⅰ) 连接OQ ，在面CFD 内过R 做RM CD ⊥,则OQ //DF ,且12OQ DE =，又DF CD ⊥，所以//RM FD ，又3F R R C =,则14RM CR DF CF ==,所以14RM DF =，因为E 为FD 的中点，所以12RM DE =，故OQ //RM ,且OQ RM =，即得OQRM 为平行四边形，得RQ //OM ，即证QR //平面BCD ；（Ⅱ）可证得DF ⊥平面BCD ，以O 为原点，OD 为y 轴建立如图空间直角坐标系求平面BCF 与平面BDF 所成二面角的余弦值.BED试题解析：(Ⅰ) 连接OQ ，在面CFD 内过R 做RM CD ⊥ ∵,O Q 为中点，∴OQ //DF ,且12OQ DE = ∵DF CD ⊥ ∴//RM FD又3FR RC =,∴14RM CR DF CF ==,∴14RM DF = ∵E 为FD 的中点，∴12RM DE =.∴OQ //RM ,且OQ RM = ∴OQRM 为平行四边形，∵RQ //OM又RQ ⊄平面BCD , OM ⊂平面BCD , ∴QR //平面BCD .（Ⅱ）∵2DF =,BF =BD =∴222BF BD DF =+,∴BD DF ⊥,又DF CD ⊥,∴DF ⊥平面BCD . 以O 为原点，OD 为y 轴建立如图空间直角坐标系B考点：1.线面平行的判定；2.二面角的求法. 20. （本小题满分13分）已知函数(),ln xf x ax x=+1x >. （Ⅰ）若()f x 在()1,+∞上单调递减，求实数a 的取值范围； （Ⅱ）若2a =，求函数()f x 的极小值；（Ⅲ）若存在实数a 使()f x 在区间1(,)(,n ne e n N *∈且1)n >上有两个不同的极值点，求n 的最小值.【答案】（Ⅰ）14a ≤-;（Ⅱ）()f x 的极小值为1122()4f e e =;（Ⅲ）3.【解析】试题分析：（Ⅰ）2ln 1()ln x f x a x-'=+,由题意可得()0f x '≤在()1,x ∈+∞上恒成立；2111()ln 24a x ≤--， 即2min 111[()]ln 24a x ≤--，求得函数2111()ln 24y x =--在()1,+∞的最小值即可； （Ⅱ）当2a =时，()2ln x f x x x =+，求得222ln 1ln 12ln ()2ln ln x x xf x x x--+'=+=令()0f x '=，解得1ln 2x =或ln 1x =-（舍），即12x e =，当121x e <<时，()0f x '<，当12x e >时，()0f x '>，()f x 的极小值为1122()4f e e =；（Ⅲ）原题等价于()0f x '=在1(,),(,n ne e n N *∈且1)n >上有两个不等的实数根；由题意可知22ln 1ln ()ln x a x f x x-+'=，即2l n l n 10a x x +-=在1(,)n ne e 上有两个不等实根，令1ln ,()x u u n n =<<，2()1g u au u =+-在1(,)n n上有两个不等实根，根据二次函数根的分别列出不等式组，即可求出n 的最小值.试题解析：（Ⅰ）2ln 1()ln x f x a x-'=+,由题意可得()0f x '≤在()1,x ∈+∞上恒成立； ∴2211111()ln ln ln 24a x x x ≤-=--， ∵()1,x ∈+∞，∴()ln 0,x ∈+∞，∴110ln 2x -=时函数t =2111()ln 24x --的最小值为14-， ∴14a ≤-(Ⅱ) 当2a =时，()2ln xf x x x=+ 222ln 1ln 12ln ()2ln ln x x xf x x x--+'=+=令()0f x '=得22ln ln 10x x +-=，解得1ln 2x =或ln 1x =-（舍），即12x e =当121x e <<时，()0f x '<，当12x e >时，()0f x '>∴()f x 的极小值为11112222()242e f e e e =+= （Ⅲ）原题等价于()0f x '=在1(,),(,n ne e n N *∈且1)n >上有两个不等的实数根；由题意可知222ln 1ln 1ln ()ln ln x x a xf x a x x--+'=+= 即2ln ln 10a x x +-=在1(,)nne e 上有两个不等实根.令1ln ,()x u u n n=<<，2()1g u au u =+- ∵(0)10g =-<，根据图象可知：1401121()0()0a a n n a g n g n ⎧⎪<⎪∆=+>⎪⎪⎪<-<⎨⎪⎪<⎪⎪<⎪⎩，整理得2210412211a n a n a n n a n n ⎧-<<⎪⎪⎪-<<-⎪⎨⎪<-⎪⎪<-⎪⎩ - 即2min 21111{,,}24n n n n n --->-，解得2n >， ∴n 的最小值为3. 考点：1.导函数的应用；2.函数的极值；3.二次函数根的分布.21. （本小题满分14分）如图，过原点O 的直线12,l l 分别与x 轴，y 轴成30︒的角，点(,)P m n 在1l 上运动，点(,)Q p q 在2l上运动，且||PQ =（Ⅰ）求动点(,)M m p 的轨迹C 的方程；（Ⅱ）设,A B 是轨迹C 上不同两点，且13OA OB k k ⋅=-， （ⅰ）求OA OB ⋅的取值范围；(ⅱ)判断OAB ∆的面积是否为定值？若是,求出该定值，不是请说明理由.【答案】（Ⅰ）22162m p +=；（Ⅱ）（ⅰ）22OA OB -≤⋅< ；(ⅱ【解析】试题分析：（Ⅰ）由题意知12:,:,3l y x l y ==可得(),(,)3P m m Q p p，由||PQ =22()()83m p -+=，整理得22162p m +=，所以动点M 的轨迹C 的方程22162m p +=；（Ⅱ）（ⅰ）设1122(,),(,)A x y B x y 所在直线为l ，当l 斜率不存在时，1111(,),(,),A x y B x y -则1111,OA OB y yk k x x ==- 由22211121133OA OBy k k x y x ⋅=-=-⇒=，又2211162x y +=，211y =，21212122OA OB x x y y y ⋅=+==， 当l 斜率存在时，设l 方程y kx m =+，联立2236y kx mx y =+⎧⎨+=⎩，得222(13)6360k x kmx m +++-=2222223612(31)(2)12(62)0.........()k m k m k m a ∴∆=-+-=-+>且2121222636,.3131km m x x x x k k --+==++由121213OA OB y y k k x x ⋅==-，整理得2213................()m k b =+，又1212242OA OB x x y y m⋅=+=-由(),()a b 得22131m k =+≥，可得22OA OB -≤⋅<；(ⅱ) 由（i ）知，l 斜率不存在时，2111||OAB S x y ∆== 当l斜率存在时，1||2OABS AB d ∆== 将2213m k =+带入整理得OAB S ∆=，所以OAB ∆试题解析：（Ⅰ）由题意知12:,:,l y x l y ==∴(),(,)P m m Q p，由||PQ =22()()83m p -+=，整理得22162p m += 所以动点M 的轨迹C 的方程22162m p +=. （Ⅱ）（ⅰ）设1122(,),(,)A x y B x y 所在直线为l ， 当l 斜率不存在时，则11111111(,),(,),,OA OB y yA x yB x y k k x x -∴==- 由22211121133OA OBy k k x y x ⋅=-=-⇒=，又2211162x y +=，211y ∴= 21212122OA OB x x y y y ∴⋅=+==当l 斜率存在时，设l 方程y kx m =+，联立2236y kx m x y =+⎧⎨+=⎩，得222(13)6360k x kmx m +++-= 2222223612(31)(2)12(62)0.........()k m k m k m a ∴∆=-+-=-+>且2121222636,.3131km m x x x x k k --+==++ 由1212121212133()()3OA OB y y k k x x y y kx m kx m x x ⋅==-⇒=-=-++ 221212(13)3()30k x x km x x m ⇒++++=整理得2213................()m k b =+221212122222242442313m m OA OB x x y y x x k m m --∴⋅=+====-+由(),()a b 得2224131,04m k m=+≥∴<≤，22OA OB ∴-≤⋅< 综上：22OA OB -≤⋅≤.(ⅱ)由（i ）知，l 斜率不存在时，2111||OAB S x y ∆==当l斜率存在时，121||2OABS AB d x x ∆==-=将2213m k =+带入整理得OAB S ∆=所以OAB ∆考点：1.椭圆的标准方程；2.向量在圆锥曲线中的应用；3.圆锥曲线中的定值问题.。
09A1-1942207-山东大学威海分校-陈双廷,王文思,郝建坤_教研组
全国第六届研究生数学建模竞赛题目我国城镇登记失业率的数学模型摘要：本文讨论了我国城镇登记失业率的影响因素问题，我们对与失业率相关因素的数据进行处理，利用相关性分析，主成分分析，回归分析等统计方法，得出影响我国失业率的主要因素有上一年的失业率、产业结构变化指标、城乡收入差距指数、第一产业GDP所占比例，而经济增长的影响是比较微弱的结论。
我们对上述主要因素建立了合理的失业率的多元线性回归模型。
在第三问中，我们以上海和甘肃为例分地区讨论了我国的地区失业率的影响因素，使失业率的模型更加精确。
利用该模型我们预测了我国2009年和2010年上半年的失业率分别为4.46%和4.446%，根据模型结论，我们给予了一些合理性建议。
关键字失业率影响因素相关分析主成分分析回归分析一、问题重述失业、经济增长和通货膨胀为宏观经济中特别重要的三个指标，就业（或者失业）是社会、国民经济中极其重要的问题。
从经济学的角度，影响就业（或者失业）的因素很多。
从宏观层面上，消费、投资、政府购买和进出口都是重要的因素；而从中观层面，不同地区、不同产业也会表现出不同的特征。
当然，中央政府调整宏观经济政策（包括财政政策和货币政策），以及对不同地区和不同产业实行不同的扶持政策都会对就业产生巨大的影响。
2008年我国经济社会经受了历史罕见的考验，GDP依然保持9%以上平稳较快增长，城镇新增就业1113万人，城镇登记失业率为4.2%。
2009年我国就业面临更大的挑战，一是国际金融危机导致国际市场需求难以在短期内复苏；二是今年我国经济增速下滑；三是国内消费需求乏力；四是一些行业产能过剩与市场预期不确定导致企业投资不足，所以就业形势十分严峻。
下面我们参考就业问题的研究成果，利用近年来我国有关的统计数据并结合一年多来我国国民经济的运行数据，就我国就业人数或城镇登记失业率研究如下问题：1．对有关统计数据进行分析，寻找出影响就业的主要因素或指标。
2．建立城镇就业人数或城镇登记失业率与上述主要因素或指标之间联系的数学模型。
2011年山东大学威海分校电子设计大赛试题
[A]温度测量仪表指导教师：杜清府一、基本要求1、测量范围：0~300℃，温度分辨率0.2℃以上。
[12bit ADC isrequired]2、能调整零点和满量程：在零点附近，如实际温度10℃，仪表显示温度12℃，可以通过调节零点参数，使仪表显示温度正确温度；同样，在满量程附近，如实际温度290℃，仪表显示温度288℃，通过调整满量程参数，使仪表显示正确温度。
3、测量速度达到1个读数/秒二、扩展要求1、能与计算机进行通讯，将仪表温度在计算机上显示出来。
[RS232/USB History Curve]2、仪表低功耗，普通3节1号电池（串联成4.5V）供电3个月以上。
[5Ah/3*30*24=2mA for average work current include active modeand sleep mode]3、引线电阻10Ω不影响测量结果。
三、所用主要元件（参考）1、单片机、LCD显示【LED is OK】2、铂电阻PT1003、双积分型AD转换器[Msp430f2003from Texas Instruments is a perfect selection for this project]16bit Sigma-DeltaUltralow-Power ConsumptionActive Mode220uA@1MHz2.2VStandby Mode0.5uAOff Mode0.1uA16Bit RISC Architecture with SPI and I2C10GPIOPackage:14PDIP&14TSSOP[B]电子台历的制作指导教师：郑亚民一、基本要求1、可实现公历、农历、节气、节日、天气、温度、湿度等信息2、具有闹钟和定时关机功能3、内置电源，接驳220V交流[Design a linear power supply with78xx Series regulator]二、扩展要求1、有时间提醒功能，提醒重要的日期或者时间2、有通讯录功能，可以添加、查阅联系人信息，包括、地址、电话、电子邮箱等[How to input these contacts]3、设计并制作适合电子台历外壳三、所用主要元件（参考）1、单片机2、LCM3、PS/2键盘or数字键盘0-9T9*在本题目中可能涉及220V交流电，请务必注意涉及安全[C]一、基本要求1、实现ARM 处理器读写Micro SD 卡的功能2、文件格式为FAT 或FAT32或NTFS 3、支持USB2.04、ARM 处理器可以通过USB 接口与计算机通信，交换数据信息二、具备的知识1、USB2.02、ARM 芯片相关3、FAT 文件系统三、所用主要元件（参考）1、LM3S8962[ARM Processor with Cortex M3core from TI]基于ARM 处理器的SD 卡读卡器指导教师：王小利[D]单管半导体收音机的设计与制作指导教师：王怡俊一、设计任务：设计并制作一个单管半导体收音机用来收听当地和附近城市的中波调幅无线电广播.二、基本要求：1、频率范围:535KHZ~1605KHZ2、灵敏度小于6mV/m(此项不测试,以能收听到附近城市的电台的个数和声音质量为考核项目)3、用两节5号电池供电4、用小型耳塞机收听三、主要材料:单联(或双联)可变电容器,型号:CBM-223,12-260pf可调2元天线磁棒1元晶体管90182个2元二极管2AP92个1元小型耳塞机及插1个2元塑料盒式1个5元其它(如扼流圈,天线线圈等)5元合计18元[E]5一、设计任务：设计并制作一个双路直流稳压电源.二、基本要求：1、能同时输出二路直流电压,输出电压范围:±2V~±30V ，连续可调,最大输出电流可达0.5A.2、纹波电压<15mV3、电压调整率<20mV4、有输出电压显示5、有简单的过流保护功能三、主要材料:30W,220V/双30V 变压器,LM317,LM337等约需90元*在本题目中涉及220V 交流电，请务必注意涉及安全直流稳压电源的设计与制作指导教师：王怡俊[F]6一、设计任务：用湿度传感器，设计一个湿度检测电路二、基本要求：1、湿度测量范围：5%RH ∽95%RH ，2、测量精度：±2%RH3、数字显示湿度测量值4、具有超限报警功能5、9V 电池供电三、主要材料：电容式湿度传感器HS1101约10.00元LM331约5.00元CMOS 555定时器1片、运放CF7413片、ADC 1片、若干电阻、电容、数码管等四、参考资料：数字电子技术、模拟电子技术、HS1101型湿度传感器的原理及使用方法湿度测量电路指导教师：李素梅湿度传感器电容/频率变换频率/电压变换A/D 转换数字显示[G]7流水线产品统计电路的设计指导教师：李素梅一、设计任务：设计并制作一个流水线上的产品数量统计电路。
山大党课试卷分析
四、论述题：（30—37分）
2-3道大题，每题10—20分
另、辨析题：（2009年以来没有此类题型）
（共12分，每题3分；先回答正误，再说明现由。）
4道题。
① 只判断对或错，没有任何分析或分析完全错误者不得分。
试卷构成、分数分布及评卷要求
一、填空题：（共22-28分，每空0.5分）
12—16道题，共46-56个填空；完全正确得分。
二、选择题：（共10分，每题1分）
10道不定项选择题；完全正确得分。
三、简答题：（共21-31分）
4—5道题，每题4—8分。
①每错、漏一句扣一分，扣完本题分为止；错别字两个扣一分。 ②必须正确地答出所有八条才得满分。基本意思正确，每答出其
②判断正确，理由分析不完全正确即要害把握不准者，可得2分。 ③理由分析完全正确，没有判断或判断模糊，可得3分。
一、 填空题：
2010-2011学年第一学期入党积极分子培训考试试题
1． 中国共产党是 中国工人阶级 的先锋队，同时是 中国人民和中华民族 的先锋队。
2． 科学发展观，是立足 社会主义初级阶段基本国情 、总结 我国发展实践 、借鉴 国外发展经验 、适应 新的发展要求 提出来的。
3． 社会主义初级阶段，我国社会的主要矛盾是 人民日益增长的物质文化需求 与 落后的社会生产 的矛盾。
威海高三物理试题解读
2010年2月威海高三物理试题解读第Ⅰ卷（选择题共32分）理科2320人一、选择题：本题共8个小题，每小题4分，共32分．在每个小题给出的四个选项中，至少有一个是正确的．每小题全选对的得4分；选对但不全的得2分；有选错或不答的得0分．1．2008年1月10日开始的低温雨雪冰冻造成我国部分地区严重灾害，其中高压输电线因结冰而损毁严重．为消除高压输电线上的凌冰，事后有人设计了利用电流的热效应除冰的融冰思路．若在正常供电时，高压线上送电电压为U，电流为I，热耗功率为ΔP；除冰时，在输电功率、用户的输入电压和输电线电阻不变的情况下，通过自动调节高压输电变压器的变压比，使输电线上的热耗功率变为16ΔP，则除冰时A．输电电流为4I B．输电电流为16I C．输电电压为4U D．输电电压为16U/2．我国2007年建成的国家大剧院外部呈椭球型．为了简化，将国家大剧院的屋顶近似为半球形，某警卫人员在执行特殊任务时，必须在屋顶上向上缓慢爬行，他在爬行的过程中屋顶对他的A ．支持力不变B ．支持力变小C ．摩擦力变小D ．摩擦力变大3．如图甲所示，在线圈1l 中通入电流1i 后，在2l 上产生的感应电流随时间变化的规律如图乙所示，1l、2l 中电流的正方向如甲图中的箭头所示．则通入线圈1l 中的电流1i 随时间变化的图线是下图中的i i i i i4．如图所示，A 、B 两物体的质量分别为m 、2m ，中间用轻杆相连，放在光滑的斜面上．现将它们从静止释放，在下滑的过程中 A ．两物体下滑的加速度相同 B ．轻杆对A 做正功，对B 做负功 C ．系统的机械能守恒D ．任意时刻两物体重力的功率相同5．如图所示，一个绝缘圆环，当它的1/4均匀带电且电荷量为q 时，圆心O 处的电场强度大小为E ．现使半圆ABC 均匀带电2q ；而另一半圆ADC 均匀带电–2q ．则圆心O 处的场强的大小和方向为A ．E 22，方向由O 指向DB ．4E ，方向由O 指向DC ．E 22，方向由O 指向BD ．0C6．设月亮和地球同步通讯卫星都绕地球做匀速圆周运动，其轨道半径分别为r 1、r 2；向心加速度大小分别为a 1、a 2；环绕速度大小分别为v 1、v 2.．下列关系式正确的是A ．r 1> r 2B ．a 1> a 2C ．1221r r v v = D ．222211r a r a =7．电子在电场中仅受电场力作用运动时，由a 点运动到b 点的轨迹如图中虚线所示．图中一组平行等距实线可能是电场线，也可能是等势线．下列说法正确的是 A ．若a 点的电势比b 点低，图中实线是等势线B ．不论图中实线是电场线还是等势线，电子在a 点的电势能都比b 点小aC．若电子在a点动能较小，则图中实线是电场线D．如果图中实线是等势线，则电子在b点电势能较大8．如图所示，在一个直立的光滑圆管内放置一根轻质弹簧，弹簧的上端O 与管口A 的距离为2o x ，一个质量为m 的小球从管口由静止开始下落，将弹簧压缩至最低点B ，压缩量为o x ，设小球运动到O 点时的速度大小为0v ，不计空气阻力，则在这一过程中 A ．小球运动的最大速度大于0v B ．小球运动的最大速度等于0v C ．弹簧的劲度系数为x m gD ．弹簧的最大弹性势能为03mgx7.（2009·广州模拟）如图14所示，在绝缘水平面上固定两个等量同种电荷A 、B ，在AB 连线上的P 点由静止释放一带电滑块，则滑块会由静止开始一直向右运动到AB 连线上的一点M 而停下.则以下判断正确的是A.滑块一定带的是与A、B异种的电荷B.滑块的电势能一定是先减小后增大C.滑块的动能与电势能之和一定减小D.AP间距一定小于BM间距解析由于物块没有做往复运动，而是最后停下，说明P与地面间有摩擦，所以滑块的动能与电势能之和减小，C正确；且AP<BM.滑块一定与A、B同种电性所以A错；由于不知道M点位置，若M点在A、B连线中点右侧，则电势能先减小后增大.若在中点左侧则电势能一直在减小，B错.综上所述C、D正确.答案CD第Ⅱ卷（非选择题 共68分）注意事项：只取前60%，共计1369人二、实验题：本题共2个小题，第9题6分，第10题8分，满分14分，把答案直接填在题中的横线上或按要求作图．9．（6分）甲图中螺旋测微器的读数为 mm ．如图乙所示，为用多用电表的“×1”欧姆挡正确操作后测某电阻时指针的位置，其读数为 Ω．9．（6分）0.730（3分），8.0（或8）（3分）10．（8分）热敏电阻是传感电路中常用的电子元件．广泛应用甲乙于室内空调、电冰箱和微波炉等家用电器中的温度传感器，是利用热敏电阻随温度变化而变化的特性工作的．现在用伏安法研究热敏电阻在不同温度下的伏安特性曲线，要求特性曲线尽可能完整．已知常温下待测热敏电阻的阻值约40～50Ω．热敏电阻和温度计插入烧杯中，烧杯内有一定量的冷水，其他备用的仪表和器具有：盛有热水的热水杯、直流电源(电动势15V ，内阻可忽略)、直流电流表(对应不同的量程内阻约为0.2Ω或1Ω)、直流电压表(对应不同的量程内阻约为5kΩ或15kΩ)、滑动变阻器(0～10Ω)、电键、导线若干．①在图（a ）的方框中用给定的器材画出完整的实验电路图，要求测量误差尽可能小．②根据电路图，在实物图上用铅笔线做导线进行连线．热敏电阻10．（8分）（1）如图所示（4分）（2）如图所示（4分）三、计算题（必做部分）：本题共3个小题，满分38分，解答应写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题，答案中必须明确写出数值和单位．11．（10分）如图所示，某放射源A 均匀地向外辐射出平行于y 轴的、速度一定的α粒子（质量为m ，电荷量为+q ）．为测定其飞出的速度大小，先让其经过一个磁感应强度为B 、区域为半圆形的匀强磁场，经该磁场偏转后，它恰好能够沿x 轴进入右侧的平行板电容器，并打到置于N 板上的荧光屏上．调节滑动触头P 位于滑动变阻器的中央位置时，通过显微镜Q 看到屏上的亮点恰好能消失．已知电源电动势为E ，内电阻为0r ，滑动变阻器的总阻值002r R =，试求：（1）α粒子从放射源飞出时速度v 的大小； （2）屏上的亮点恰好能消失时的α粒子，在磁场中运动的总时间t ．（3）半圆形磁场区域的半径R ．11．（10分）解：（1）由闭合电路的欧姆定律，回路中的电流强度0R r EI +=--------------------------------------------------------------------------------- 1分两极板间的电压2/0IR U =----------------------------------------------------------- 1分对某一α粒子，在加速电场中应用动能定理得：2/02mv qU -=----------------------------------------------------------------------- 1分联立解得mqEv 32=-------------------------------------------------------------------- 1分 （2）由题意，α粒子向上射入磁场偏转90°后射出，后来又从O 点返回磁场再偏转90°，最后向上射出磁场．所以α粒子在磁场中运动的总时间24⨯=Tt -----------1分 α粒子在磁场中运动的周期为qBmT π2=-------------------------------------------1分 联立解得qBmt π=---------------------------------------------------------------------------18v x分（3）设α粒子在磁场中运动轨迹的半径为r ，则r mv qvB /2=---------------1分由题意半圆形磁场区域的半径22r r R +=--------------------------------------1分联立解得qmEB R 32=-----------------------------------------------------------------1分★（2010年2月11日，腊月28在家中进行了合理的修订） 12．（14分）某中学生对刚买来的一辆小型遥控车的性能进行研究．他让这辆小车在水平的地面上由静止开始沿直线轨道运动，并将小车运动的全过程通过传感器记录下来，通过数据处理得到如图所示的υ~t 图象．已知小车在0~2s 内做匀加速直线运动，2s ~11s 内小车牵引力的功率保持不变，9s ~11s 内小车做匀速直线运动，在11s 末开始小车失去动力而自由滑行．已知小车质量kg 1=m ，整个过程中小车受到的阻力大小不变，试求：（1）在2s~11s 内小车牵引力的功率P （2）小车在s 2末的速度x v 为多大？（3) 小车在2s~9s 内通过的距离x12．（14分）解：（1）根据题意，在11s 末撤去牵引力后，小车只在阻力f 作用下做匀减速直线运动，设其加速度大小为a ，根据图象可知22m/s =∆∆=ta υ-----------------------1分 根据牛顿第二定律有ma f =----------------------------------------------------------1分解得N 2=f---------------------------------------------------------------------------1分设小车在匀速运动阶段的牵引力为F ，则f F =，m/s 8=m v根据m F P υ=---------------------------------------------------------------------------1分解得W16=P --------------------------------------------------------------------------1分（2）0~2s 的匀加速运动过程中，小车的加速度为2xx v t a =∆∆=υ------------------1分 设小车的牵引力为x F ，根据牛顿第二定律有x x ma f F =-----------------2分根据题意有x x v F P =-------------------------------------------------------------------2分解得m/s 4=x v -----------------------------------------------------------------------1分（3）在2s~9s 内的变加速过程，s 7=∆t ，由动能定理可得2122121υυm m fx t P m -=-∆---------------------------------------------------------2分解得小车通过的距离是m 44=x ---------------------------------------------------1分★（2010年2月11日，腊月28姜进辉在家中进行了合理的修订）13．（14分）边长为L 的正方形闭合金属导线框，其质量为m ，回路电阻为R ．图中M 、N 、P 为磁场区域的边界，且均为水平，上下两部分水平匀强磁场的磁感应强度大小均为B ，方向如图所示．现让线框由图示位置由静止开始下落，线框在穿过M 和P 两界面的过程中均为匀速运动．已知M 、N 之间和N 、P之间的高度差相等，均为442283L B gR m L h +=，下落过程中线框平面始终保持竖直，底边始终保持水平，当地的重力加速度为g ．试求： （1）图示位置线框的底边到M 的高度d ．（2）线框的底边刚通过磁场边界N 时，线框加速度的大小． （3）线框在通过磁场边界N 的过程中，线框中产生的焦耳热．13．（14分）解：（1）根据题意分析可知，导线框在穿过M 和P 的MN P过程中，速度相同，设为1v ，根据自由落体运动的公式有gd v 221= 在导线框穿过M 的过程中，线框中产生的感应电动势1BLv E =-------------------1分线框中产生的感应电流R E I /=-----------------------------------------------------------1分线框受到的安培力BILF =-----------------------------------------------------------------1分 根据物体的平衡条件有F mg =----------------------------------------------------------1分联立解得44222L B gR m d =-----------------------------------------------------------------------1分 （2）设线框的底边刚通过磁场边界N 时，线框的速度大小为2v ，根据题意和运动学公式有)(22122L h g v v -=-----------------------------------------------------1分此时线框中产生的感应电动势22BLv E ='--------------------------------------1分线框中产生的感应电流R E I /'='-------------------------------------------------1分线框受到的安培力L I B F '='2------------------------------------------------------1分根据牛顿第二定律有a m mg F '=-'----------------------------------------------1分解得线框的加速度大小为g a )172(-=---------------------------------------1分 （其中的221L B mgR v =，22227L B mgR v =） （2）根据能的转化和守恒定律，在线框通过磁场边界M 和P 的过程中，产生的焦耳热相同，均为mgL Q =0--------------------------------------------------------------1分在整个运动过程中，线框中产生的焦耳热为)2(L h mg Q +=-------------------------------------------------------------------------2分所以线框通过磁场边界N 的过程中，线框中产生的焦耳热为02Q Q Q x -=-----------------------------------------------------------------------------1分解得：)4/3(4422L B gR m L mg Q x +=---------------------------------------------1分【或设线框的上边刚要通过磁场边界N 时，线框的速度大小为3v ，根据题意和运动学公式有 )(22321L h g v v -=-（解得2232L B mgR v =）-----------------------1分 根据能的转化和守恒定律，线框通过磁场边界N 的过程中，线框中产生的焦耳热为)(212322v v m mgL Q x -+=------------------------------------------------------2分解得)4/3(4422L B gR m L mg Q x +=-----------------------------------------------1分四、计算题（选做部分）：本题共3个小题，每题8分．考生必须从中选择2个题作答，不按规定选做者，阅卷时将根据所选题号的先后顺序只判前面的2个题，其他作答的题目答案无效，考生最多得分16分．填空题的答案直接填在题中的横线上，计算题的解答应写出必要的文字说明、方程式和重要的演算步骤，只写出最后答案的不能得分．有数值计算的题，答案中必须明确写出数值和单位．14．（物理3-3模块，8分） （1）如图所示，在玻璃筒内装入一些塑料小球，这些小球代表气体分子．在小球上面放一个轻质活塞，用电动机带动玻璃筒底部的振动器使小球无规则运动．当电动机启动后，活塞受到小球的撞击，悬浮在一定的高度．增加电动机的转速，活塞高度将 ，保持电动机的转速不变，减少塑料小球的数目，活塞高度将 （填“增大”、“减小”或“不变”）．（2）热水瓶是日常生活中的用品，在使用中会出现许多物理现象．若热水瓶没有倒满水时，经过一夜，再拔软木瓶塞时感觉瓶塞被吸住了．①试根据有关的物理原理分析瓶塞被吸住的原因（设封闭气体的质量和体积不变）．②若拔起瓶塞的瞬间，瓶内气体对外界做功2J ，并向外界释放了4J 的热量．问瓶内原有气体的内能变化了多少？14．（物理3-3模块，8分）（1）增大（1分）．减小（2分）（2）①由于被封气体的体积不变，根据查理定律2211T P T P =-----------------------------1分 可知，当温度降低时，瓶内气体的压强减小----------------------------------------1分小于大气压强所以感觉到瓶塞被吸住了．②根据热力学第一定律J 6-=+=∆Q W E ----------------------------------------------2分减少了 6 J------------------------------------------------------------------------------------1分15．（物理3-4模块，8分）一列简谐横波，在t =0 时的波动图象如图所示，此时波恰好传播到A 点，再经过1.0s ，Q 点正好完成第一次全振动．试求：（1）波速v 的大小．（2）画出第1 s 内质点P 的振动图象（要求标明有关数据）．15．（物理3-4模块，8分）解：（1）由图象可知：波长m 4=λ，对于周期有0.145=T --------------------------1分 解得s 8.0=T --------------------------------------------------------------------------1分所以波速T v λ=-----------------------------------------------------------------------1分联立解得m/s 5=v ----------------------------------------------------------------1分（2）如图（4分，时间轴没有正确数据的扣2分，纵横坐标轴没有标明物理量或单位的不给分）16．（物理3-5模块，8分）用中子打击2311Na 得到一种新的生成物．（1）写出这一反应的核反应方程．（2）设入射的中子速度大小为v ，2311Na 原来处于静止状态，求生成物的速度大小．（3）生成物具有放射性，半衰期为15天，经过45天后，剩下的生成物是原来的多少？（直接写答案）16．（物理3-5模块，8分）解：（1）Na n Na 2411102311→+-------------------------2分（2）设中子的质量为m ，则生成物的质量为m 24．根据动量守恒定律有：/24mv mv =-----------------------------------------------------------------3分解得：v v 241/=------------------------------------------------------------1分 （3）剩下的生成物是原来的8/1-----------------------------------------------2分。
山东大学威海分校综合测评办法
山东大学威海分校学生综合素质测评办法为了全面贯彻党的方针，进一步推进素质教育，充分调动和激发学生自我教育、自我管理、提高素质、努力成才的积极性和主动性，根据《中国普通高等学校教育大纲》、《普通高等学校学生管理规定》和《中共中央国务院关于深化教育改革全面推进素质教育的决定》等有关文件精神，结合我校学生学习生活实际，制定本办法。
一、指导思想（一）综合素质测评是对学生素质发展水平的全面、规范、科学的评价，测评结果是评定优秀学生奖学金和三好学生、推荐参加“第二校园经历”和“海外经历”、评选优秀毕业生和推荐保送研究生的重要依据。
（二）综合素质测评鼓励学生以培养强烈的社会责任感、创造力，过硬的社会竞争力乃至国际竞争力和健全发展的人格与个性为目标，刻苦学习、积极进取、努力实践，在达到大学基本要求的前提下充分发展自己的个性、特长和综合的素质。
（三）综合素质测评采取定量与定性、记实与评价相结合的办法，对学生的素质发展水平进行测评。
（四）综合素质测评分为基础性素质测评和发展性素质测评两个方面。
基础性素质是指学生在学校规定的教学和第二课堂中形成的德、智、体、美等方面的一般性素质。
发展性素质是学生在学校教育过程中形成的体现创造性、实践性和个性发展的素质。
（五）综合素质测评办法是对学生进行综合评定的指导性办法。
具体操作时，各院（系）可根据不同专业、不同年级的实际情况进行适当调整。
但本办法中有明确规定的评定原则、程序和加减分标准等，不得随意改动。
如确需调整，可由院系党总支提出建议，报学生处批准。
二、实施办法（一）基础性素质测评1、操行评定“操行评定”是对学生思想道德修养、身体和心理素质、美育和人文科学素养等方面的综合考评，通过“记实”和“评议”综合得出。
“操行评定”由“记实”分值与“评议”分值组成，满分100分。
（1）“记实”是指对学生在日常学习和生活过程的行为进行记录，并根据此记录得出记实分值。
需“记实”的关键行为有：①学校要求每个学生必须做到的行为；②学校提倡、鼓励学生做到的行为；③学校反对并予以纪律处分的行为。
2021年威海上学期期末考试语文讲评及作文分析
阅读下面这首古诗，完成各题。
咏怀（其六）
阮籍
昔闻东陵瓜①，近在青门外。
连畛距阡陌，子母相钩带。----邵平---乡村生活
五色曜朝日，嘉宾四面会②。
对比
膏火自煎熬，多财为患害。-----萧何----在朝为官
布衣可终身，宠禄岂足赖。-----结论：过布衣生活，为什么？
【注】①东陵瓜：汉初人邵平在秦破后失侯，为布衣，在长安城东种瓜，时谓 Nhomakorabea东陵瓜。
第二句出错的字：交通、二臣
解释下面加红的字 赵良弼，字辅之，多智略，初举进士，教授赵州。世祖在潜簿，召见，占对称旨。会立邢 州安抚司，擢良弼为幕长。邢久不得善吏，且当要冲，使者旁午，民多逃去。良弼区画有 方，事或掣制，则请诸簿邸。再阅岁，凡六往返，所请无不从。己未七月，世祖南征，召
参议元帅事。亲执桴鼓率先士卒五战皆捷禁焚庐舍杀降民所至宣布恩德民皆按堵 闻宪
13. 把文中画横线的句子翻译成现代汉语。
（1）良弼区画有方，事或掣制，则请诸簿邸。
（2）后平李壇乱，得文统与壇交通书，益有疑二臣意，切责良弼， 至欲断其舌。
第一句翻译出错多，掣制、诸、簿邸
（1）良弼规划有方法，事情有时受到牵制，就请示于王府。
（2）后来平定李璮叛乱，（皇帝）得到王文统与李璮来往（暗中 勾结）的书信，更加怀疑这二人有二心，严厉谴责良弼，甚至要割 他的舌头。
宗崩 ，世祖北还，良弼陈时务十二事，言皆有征。庚申，良弼凡五上言劝进，曰：“今中 外皆愿大王早进正宸，以安天下，事势如此，岂容中止，社稷安危，间不容发。”世祖嘉 之。既即位，立陕西四川宣抚司，以廉希宪、商挺为使、副，良弼为参议。良弼先行，谋 诸断事官八春，曰：“今浑都海日夜思北归，纽璘迁延不即行，当先遣使奉上旨促纽璘入 朝，刘太平速还京兆。”八春从其议。纽璘果移营将入泾，刘太平将趋六盘，闻命乃止。 后浑都海果叛北归，良弼与汪惟正、刘黑马二宣抚决议，执浑都海之党元帅诛之。升参议 陕西省事。蜀人费寅以私憾诬廉希宪、商挺在京兆有异志者九事，以良弼为证。帝召良弼 诘问，良弼泣曰：“二臣忠良，保无是心，愿剖臣心以明之。”帝意不释。初挺荐王文统可 大用。后平李擅乱，得文统与擅交通书，益有疑二臣意。切责良弼，至欲断其舌。良弼誓 死不少变，帝意乃解，费寅卒以反诛。后帝将讨日本，三问，良弼言：“臣居日本岁余， 睹其民俗，狠勇嗜杀，不知有父子之亲，上下之礼。其地多山水，无耕桑之利，得其人不 可役，得其地不加富。况舟师渡海，海风无期，海风无期，祸害莫测。是谓以有用之民力， 填无穷之巨壑也，臣谓勿击便。”帝从之。二十三年卒，追封韩国公，谥文正。
山东大学威海学生成绩单
FIRST ACADEMIC YEAR ( 2002-2003)
THIRD ACADEMIC YEAR (2004 -2005)
Computer Interface Technology f8y c#
Computer Language and Program Designing
Computer System Signal and System Television Technology Principles Principle & Application of Database Digital Signal Processing Principle of Communication System MATLAB Scientific English Software Engineering Data Compression
E
72 71
E
72 60
T
54 31
60
T
54 68
June 11,2006
Art Appreciation Physical Education Deng Xiaoping’s Theories Fundamental Theory of Circuit Engineering Mathematics # General Physics Experiment Skill
COURSE
Make-up COURSE
Make-up
ITEMS HOURS MARKS
HOURS MARKS ITEMS
exam
exam
E
90
77
E
72
70
E
36
77
E
72
91
山东大学试卷检查情况登记表
10
任课教师命题
有
不超过
无
无
有平时成绩
无
无
试卷和成绩单排列一致，材料齐全
信息学院
备注：
光纤通信《双语》课程
李桂秋
10
否
有
不超
无
无
无
无
无
装订符合要求
信息学院
备注：1）教考未分离；2）缺平时成绩记录档案。
通信原理
孙健
10
否
有
不超
无
无
无
无
无
装订规范
信息学院
备注：1）教考未分离；2）忘签字（课程负责人）；3）试卷评卷人未签字；
无
无
无
装订规范
外语学院
备注：1）合格率100%，优秀率53.1%；2）A、B试卷重复占63%；3）考试大纲未填写具体内容；
4）成绩中平时成绩占比例未说明。（该任课教师为韩国外籍教师）
高级英语（3）
马文
15
否
有
不超过
无
无
无
无
全部（51份）
装订规范
外语学院
备注：1）封面填写不全；2）大纲中看不出试卷来源；3）全部考试用蓝笔批改；4）合格率100%。
大学物理（2）
刘东红
10
否
有
否
0
无
无
无
√
0
良好
物理学院
备注：1）成绩单未与试卷放在一起；
2）总体阅卷认真，装订整齐。
理论力学
代由勇
10
否
有
否
0
无
无
无
√
0
良好
物理学院
2024年山东省威海市示范名校物理高三上期末调研试题含解析
2024年山东省威海市示范名校物理高三上期末调研试题注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、单项选择题：本题共6小题，每小题4分，共24分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1、如图所示，O1、O2两轮通过皮带传动，两轮半径之比r1：r2=2：1，点A在O1轮边缘上，点B在O2轮边缘上，则A、B两点的向心加速度大小之比a A：a B为（）A．1：1 B．1：2 C．2：1 D．1：4θ>．小球自M点由静止滑下，小球经过O点时无机2、如图所示，同种材料制成的轨道MO和ON底端由对接且a械能损失，以v、s、a、f分别表示小球的速度、位移、加速度和摩擦力四个物理量的大小．下列图象中能正确反映小球自M点到左侧最高点运动过程的是( )A．B．C．D．3、2017年11月24日，国家航天局探月与航天工程中心副主任裴照宇表示，嫦娥五号任务将是我国首次月球表面采样返回任务，这次任务的完成将标志着我国探月工程“三步走”顺利收官。
若已知万有引力常量G，那么在下列给出的各种情景中，能根据测量的数据求出月球密度的是()A．在月球表面使一个小球做自由落体运动，测出落下的高度H和时间tB ．嫦娥五号贴近月球表面做匀速圆周运动，测出运行周期TC ．嫦娥五号在高空绕月球做匀速圆周运动，测出距月球表面的高度H 和运行周期TD ．观察月球绕地球的匀速圆周运动，测出月球的直径D 和运行周期T4、伽利略在研究力和运动的关系的时候，用两个对接的斜面，一个斜面固定，让小球从斜面上滚下，又滚上另一个倾角可以改变的斜面，斜面倾角逐渐改变至零，如图所示．伽利略设计这个实验的目的是为了说明（ ）A ．如果没有摩擦，小球将运动到与释放时相同的高度B ．如果没有摩擦，物体运动过程中机械能守恒C ．维持物体做匀速直线运动并不需要力D ．如果物体不受到力，就不会运动5、如图，长为L 的直棒一端可绕固定轴O 在竖直平面内转动，另一端搁在升降平台上，平台以速度v 匀速上升，当棒与竖直方向的夹角为θ时，棒的角速度为A ．(1)n Tθω=- B ．cos vL θC ．sin v LθD ．sin vL θ6、曲柄连杆结构是发动机实现工作循环，完成能量转换的主要运动零件如图所示，连杆下端连接活塞Q ，上端连接曲轴P 。
2023年山东大学威海分校计算机科学与技术专业算法分析与设计科目期末试卷
2023年山东大学威海分校计算机科学与技术专业算法分析与设计科目期末试卷一、选择题（共15题，每题2分，共计30分）1.在算法分析中，时间复杂度是评估算法所需要的哪种资源？–[ ] A. 内存空间–[ ] B. 执行时间–[ ] C. 输入数据规模–[ ] D. 存储空间2.对于一个具有n个元素的数组进行顺序查找，最坏情况下的时间复杂度是多少？–[ ] A. O(1)–[ ] B. O(log n)–[ ] C. O(n)–[ ] D. O(n^2)3.在算法设计中，分治法属于哪一类算法？–[ ] A. 动态规划算法–[ ] B. 贪心算法–[ ] C. 回溯算法–[ ] D. 分支限界算法4.在快速排序算法中，采用哪种策略选择基准元素？–[ ] A. 随机选择–[ ] B. 中位数选择–[ ] C. 最小元素选择–[ ] D. 最大元素选择5.在动态规划算法中，状态转移方程是用来描述什么？–[ ] A. 子问题的划分规则–[ ] B. 最优子结构–[ ] C. 最优解的大小–[ ] D. 问题的递归解…二、填空题（共5题，每题4分，共计20分）1.Dijkstra算法是一种用于最短路径问题的 ____________ 算法。
2.哈夫曼编码是一种有效的 ____________ 算法，用于数据的压缩和解压缩。
3.在动态规划算法中，最优子结构要求子问题的解能够 ____________ 到原问题的解。
4.拓扑排序是一种对有向无环图进行排序的算法，利用的是图的____________ 特性。
5.基数排序是一种多关键字排序算法，通过对关键字的 ____________ 来进行排序。
…三、简答题（共4题，每题10分，共计40分）1.请简要说明动态规划算法的基本思想，并举一个实际问题的例子进行说明。
2.手写实现插入排序算法，并分析其最好情况和最坏情况下的时间复杂度。
3.请简要描述分治法的基本思想，并给出一个使用分治法解决的问题的例子。
2024届山东省威海市示范名校高三下学期第四次诊断考试语文试题试卷含解析
2024届山东省威海市示范名校高三下学期第四次诊断考试语文试题试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．1、阅读下面的文章，完成各题。
泉州，泉州丁立梅①我到泉州，泉州用雨迎接了我。
②我住在风雅颂书局的民宿里。
民宿在五店市，栖身于一群老建筑中。
③月洞门进去，有一小小院落，红红的院墙上攀着三角梅。
在南方，见多了这花，它一旦开起来就没完没了，用汹涌澎湃来形容一点儿也不过头。
它打扮得既艳丽又妖娆，或一身热烈的红，或一身昂扬的紫，或一身橘色，或一身素白。
它让人误以为它就是风华绝代的，真是聪明得有些狡黠．．了，鬼精灵般的。
其实呢，它的花朵细小得很，乳黄色，藏在艳丽的三枚苞片间。
如它这般懂得包装自己的花，少见。
我每回见它，都要惊诧、惊喜。
④院落的花架上爬着蜜豆花，不见花只见叶，这也是好的。
密匝匝的叶片油亮油亮的，它们倒垂下来，跟耍杂技一般。
花架下安放着一架秋千，秋千没人荡的时候，就荡清风、荡日影、荡星光、荡雨声。
⑤雨声真好，我在听雨!雨嘀嗒嘀嗒，如弹六弦琴。
苏东坡的十六件赏心事里有“微雨竹窗夜话”，又有“雨后登楼看山”。
我轻易就得到了这样的赏心事。
当然，夜话最好不要，我情愿沉默。
在这样的老房子里，实在不宜多话，就听听雨敲竹叶吧，一声声里，敲的都是从前的韵律。
从前的那户人家去了哪里呢?我在那木门上，闻到了面线糊的味道;还有润饼的味道，薄薄的面皮里，包着万般滋味。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2试题总量□偏多■适中□偏少
3考题难易度□偏难■适中□偏易
4考题覆盖面（覆盖大纲要求的）■80%以上□60%-80%□60%以下
5题型结构是否合理■合理□较合理□不合理
6试卷综合分析：■合理□较合理□不合理
其它意见：由于统一试题，缺乏个性，不便于考察学生对补充有难度知识的掌握情况。
教学中存在的问题及改进意见：（包括基本知识、理论、技能及实践能力、分析解决问题反馈能力与创新意识培养等方面）
试卷分析表
院系：商学院专业：经济学类
2005至2006学年第一学期
考试科目
微观经济学
考试班级
2005级3
任课教师
崔宇明
考试日期
2006-01-14
阅卷
方式
集体阅卷
考试
成绩
应考人数
实考人数
平均分
最高分
最高分
最低分
及ቤተ መጻሕፍቲ ባይዱ率
优秀率
个人阅卷
√
64
64
81.4
98
40
96.8%
31.2%
成绩分布情况
90以上
80-89
70-79
60-69
60以下
20
31.2%
21
32.8%
13
20.3%
8
12.5%
2
3.12%
试题试卷定量分（标准差、全距、难度、区分度等统计指标）：
标准差δ=12.1；全距R=57.5；难度P=0.18；区分度D=0.28；信度σ=0.64；中位数84.2；众数83，89，89.5。
试题分析
1试题符合教学目的任务的程度■符合□基本符合□不符合