圆-第10讲圆幂定理圆中比例线段6学
《圆幂定理》课件(15张PPT)
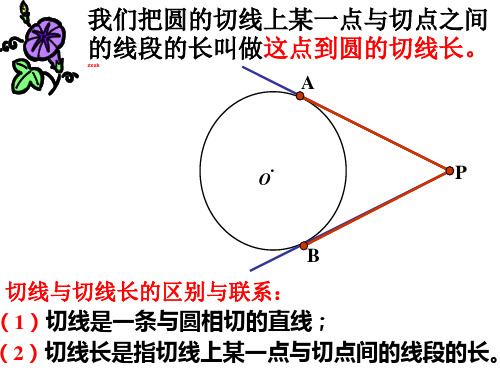
圆幂定理：过一个定点P的任何一条直线 与圆相交，则这点到直线与圆的交点的两 条线段的乘积为定值 OP r .=d （等 于点P到圆心的距离与半径的平方差的绝 对值）
2 2
z.x.x.k
C
PA•PB=PC•PD
统一叙述为：过一点P（无论点P在圆内，还是在圆外） 的两条直线，与圆相交或相切（把切点看成两个重合 的“交点”）于点A、B、C、D，PA•PB=PC•PD 。
zxxk
• 如图，在⊙O中，P是弦AB上一点， OP⊥PC，PC交⊙O于C。 求证：PC2＝PA· PB
C A D P O
。
O
1 2
A
几何语言:
PA、PB分别切⊙O于A、B
PA = PB ∠1=∠2
反思：切线长定理为证明线段相等、角相等
提供了新的方法。
圆幂定理
A
• 相交弦定理 圆内的两条相交 弦，被交点分成的两条线段长 的积相等。
O
C
D
P
B
PA· PB=PC· PD
A
P
C O
D
• 如图，CD是弦，AB是直 径，CD⊥AB，垂足为P。 求证：PC2＝PA· PB
B
PA· PB＝PC· PD
• 切割线定理推论（割线定理） 从圆外一 点引圆的两条割线，这一点到每条割线与圆 的交点的两条线段长的积相等。
运动观点看本质
• • • • 相交弦定理 相交弦定理推论 切割线定理 割线定理
本质一样
圆幂定理
几个定理得统一
相交弦定理 割线定理 切割线定理 切线长定理 A •P B D PA•PB=PC•PD PA²=PC•PD PA=PC
B
学会用半径加减或加减半径
圆（圆幂定理、根轴，托勒密定理、帕斯卡定理、牛顿定理Ⅰ、Ⅱ）
圆（圆幂定理、根轴，托勒密定理、帕斯卡定理、牛顿定理
Ⅰ、Ⅱ）
一、圆幂定理、根轴
1. 圆幂定理：
圆幂定理为以下三个定理的统称，即
相交弦定理（Ⅰ:AP·PB=CP·PD）
割线定理（Ⅱ：PA·PB=PC·PD）
切割线定理（Ⅲ：PA2=PC·PD）
2. 根轴：
到两圆幂相等的点的集合为一条垂直于两圆圆心连线的直线且：若两圆相交则根轴为公共弦所在直线
若两圆相切则根轴为公切线
同心圆无根轴
二、几条重要的定理
1. 托勒密定理
凸四边形 ABCD 中有
AC · BD ≥ AB · CD + AD · BC
等号当且仅当四边形 ABCD 是圆内接四边形时成立
2. 帕斯卡定理
圆内接六边形三组对边所在直线交点共线
3. 牛顿定理Ⅰ
圆外切四边形的对角线交点和以切点为顶点的四边形对角线交点重
合
4. 牛顿定理Ⅱ
圆外切四边形两条对角线中点和该圆圆心，三点共线
本文素材来源网络！。
圆幂定理
圆中的比例线段根轴相交弦定理圆内的两条相交弦被交点分成的两条线段的积相等.切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项割线定理从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等.上述三个定理统称为圆幂定理，它们的发现距今已有两千多年的历史，它们有下面的同一形式：圆幂定理过一定点作两条直线与圆相交，则定点到每条直线与圆的交点的两条线段的积相等，即它们的积为定值.这里切线可以看作割线的特殊情形，切点看作是两个重合的交点.若定点到圆心的距离为d，圆半径为r，则这个定值为|d2-r2|.当定点在圆内时，d2-r2<0，|d2-r2|等于过定点的最小弦的一半的平方；当定点在圆上时，d2-r2=0；当定点在圆外时，d2-r2>0，d2-r2等于从定点向圆所引切线长的平方.特别地，我们把d2-r2称为定点对于圆的幂.一般地我们有如下结论：到两圆等幂的点的轨迹是与此二圆的连心线垂直的一条直线；如果此二圆相交，那么该轨迹是此二圆的公共弦所在直线．这条直线称为两圆的“根轴”．对于根轴我们有如下结论：三个圆两两的根轴如果不互相平行，那么它们交于一点，这一点称为三圆的“根心”．三个圆的根心对于三个圆等幂．当三个圆两两相交时，三条公共弦(就是两两的根轴)所在直线交于一点．练习：1．如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P.若PB＝1，PD＝3，则BCAD的值为________．2．如图，四边形ABCD内接于⊙O，BC是直径，MN与⊙O相切，切点为A，∠MAB＝35°，则∠D＝________.3．如图，AB是⊙O的直径，D是⊙O上一点，E为BD的中点，⊙O 的弦AD与BE的延长线相交于点C，若AB＝18，BC＝12，则AD＝_____4．如图，过点D作圆的切线切于B点，作割线交圆于A，C两点，其中BD＝3，AD＝4，AB＝2，则BC＝________.5如图，半径为2的⊙O 中，∠AOB ＝90°，D 为OB 的中点，AD 的延长线交⊙O 于点E ，则线段DE 的长为________．6.如图所示，P A 为⊙O 的切线，A 为切点，PBC 是过点O 的割线，P A ＝10，PB ＝5，∠BAC 的平分线与BC 和⊙O 分别交于点D 和E ，则AD ·AE 的值为__________．例1. 在ΔABC 中，已知CM 是∠ACB 的平分线，ΔAMC 的外接圆交BC于N ，若AC =12AB ，求证：BN =2AM .例2 ⊙O 与⊙O '外切于点P ，一条外公切线分别切两圆于点A 、B ，AC 为⊙O 的直径，从C 引⊙O '的切线CT ，切点为T ．求证：CT =AB ．例3. AD 是Rt △ABC 斜边BC 上的高,∠B 的平分线交AD于M ,交AC 于N .求证：AB 2－AN 2＝BM ·BN .O AB C M N AP O'O B C T E A N C D BF M 1 2 3 4 5例4. 已知AB 切⊙O 于B ，M 为AB 的中点，过M 作⊙O 的割线MD 交⊙O 于C 、D 两点，连AC 并延长交⊙O 于E ，连AD 交⊙O 于F .求证：EF ∥AB .例5.（I ）已知四边形PQRS 是圆内接四边形，∠PSR ＝90°，过点Q 作PR 、PS 的垂线，垂足分别为点H 、K .(1)求证：Q 、H 、K 、P 四点共圆；(2)求证：QT ＝TS .（II ）如图所示，AB 是⊙O 的直径，G 为AB 延长线上的一点，GCD 是⊙O 的割线，过点G 作AB 的垂线，交AC 的延长线于点E ，交AD 的延长线于点F ，过G 作⊙O 的切线，切点为H .求证：(1)C ，D ，F ，E 四点共圆；(2)GH 2＝CE ·GF .例6. 如图,ABCD 是⊙O 的内接四边形,延长AB 和DC 相交于E ,延长AB 和DC 相交于E ,延长AD 和BC 相交于F ,EP 和FQ 分别切⊙O 于P 、Q .求证：EP 2＋FQ 2＝EF 2.O E F D A B C M A O QP C B G FE D例7. 如图所示，P A 、PB 是⊙O 的两条切线，PEC 是⊙O 的一条割线，D 是AB 与PC 的交点，若PE =2，CD =1，求DE 的长.例8．以O 为圆心的圆通过⊿ABC 的两个顶点A 、C ，且与AB 、BC 两边分别相交于K 、N 两点，⊿ABC 和⊿KBN 的两外接圆交于B 、M 两点．证明：∠OMB 为直角．例9 AB 是⊙O 的弦，M 是其中点，弦CD 、EF 经过点M ，CF 、DE 交AB 于P 、Q ，求证：MP =QM ．P AA B D E FM 1 2 3 4 O P Q1.13 2.125° 3.14 4.325.355 6.(1)利用∠PHQ＝∠PKQ＝90°；(2)先证∠HKS＝∠QSP，TS＝TK，再证TS＝QT.证明(1)∵∠PHQ＝∠PKQ＝90°，∴Q、H、K、P四点共圆．(2)∵Q、H、K、P四点共圆，∴∠HKS＝∠HQP，①∵∠PSR＝90°，∴PR为圆的直径，∴∠PQR＝90°，∠QRH＝∠HQP，②而∠QSP＝∠QRH，③由①②③得，∠QSP＝∠HKS，TS＝TK，又∠SKQ＝90°，∵∠SQK＝∠TKQ，∴QT＝TK，∴QT＝TS. （2）证明(1)如图，连接BC.∵AB是⊙O的直径，∴∠ACB＝90°.∵AG⊥FG，∴∠AGE＝90°.又∠EAG＝∠BAC，∴∠ABC＝∠AEG.又∠FDC＝∠ABC，∴∠FDC＝∠AEG.∴∠FDC＋∠CEF＝180°.∴C，D，F，E四点共圆．(2)∵GH为⊙O的切线，GCD为割线，∴GH2＝GC·GD.由C，D，F，E四点共圆，得∠GCE＝∠AFE，∠GEC＝∠GDF.∴△GCE∽△GFD.∴GCGF＝GEGD，即GC·GD＝GE·GF.∴CH2＝GE·GF.。
和圆有关的比例线段课件
题目4
若圆内接四边形ABCD中，$angle A + angle C = 160^circ$，且$angle A :
angle B : angle C = 3 : 4 : 5$，求$angle D$的度数。
答案及解析
答案
$frac{AB}{AC} = frac{sqrt{3}}{2}$
解析
$frac{AB}{AC} = frac{sqrt{3}}{2}$
详细描述
圆的周长（或称为圆的周界）是围绕圆边界的 长度，其计算公式为C=2πr，其中π是一个数 学常数（约等于3.14159），r是圆的半径。圆 的面积是指圆所占平面的大小，其计算公式为 A=πr²，其中π是一个数学常数（约等于 3.14159），r是圆的半径。
02
和圆有关的比例线段
弦、直径和半径的比例关系
题目2
若圆内接四边形ABCD中，$angle A : angle B : angle C = 2 : 3 : 4$，且$angle B = 100^circ$，求$angle D$的度数。
进阶练习题
题目3
已知圆O的半径为3，点A、B、C、D在圆上 ，且$angle AOB = 90^circ$，$angle BOC = 120^circ$，求$frac{AB}{BC}$的值 。
旋转
将圆绕圆心旋转一定的角 度。
缩放
将圆沿x轴或y轴方向放大 或缩小一定的比例。
圆和其他几何图形的关系
圆和直线的关系：相 交、相切、相离。
圆和三角形的关系： 内切、外切、相交。
圆和圆的关系：相交 、相切、相离。
05
练习题和答案
基础练习题
题目1
已知圆O的半径为5，点A、B、C在圆上，且$angle AOB = 120^circ$，$angle BOC = 135^circ$，求 $frac{AB}{AC}$的值。
圆幂定理浙教版八年级上册
圆幂定理浙教版八年级上册圆幂定理是几何学中一个重要的定理，出现在我国初中数学教材的八年级上册。
它涉及到圆、线段、角度等几何元素，为我们解决实际问题提供了有力的工具。
下面，我们将详细介绍圆幂定理的相关内容。
一、圆幂定理的定义及意义圆幂定理是指：在同一个圆中，相交弦（非直径）的长度乘以其所对的圆心角的正弦值，等于两弦端点与圆心构成的直角三角形的面积的两倍。
用数学公式表示为：AC × sinA = 2 × △ABC的面积。
这个定理在实际应用中具有很大的价值，可以帮助我们快速计算几何图形的面积、周长等参数。
二、圆幂定理的应用1.求解弦心距：已知弦长和弦所对的圆心角，可以利用圆幂定理求解弦心距。
2.求解三角形面积：已知三角形的一条边和对应的角度，可以利用圆幂定理求解三角形面积。
3.求解圆的半径：在已知弦长和弦所对的圆心角的情况下，可以利用圆幂定理求解圆的半径。
4.求解扇形面积：已知扇形的半径和圆心角，可以利用圆幂定理求解扇形面积。
三、圆幂定理的证明证明圆幂定理的方法有很多，这里我们以向量法为例进行证明。
设圆心为O，弦AB的两端点分别为A、B，圆心角为AOB，弦心距为OC。
根据向量加法、减法及数乘运算，我们可以得到以下关系：1.OA × OB = OC × OA + OC × OB2.OC × OA = △AOC的面积× 23.OC × OB = △BOC的面积× 2将上述三个式子相加，可以得到：OA × OB +OC × OA + OC × OB = 2 × (△AOC的面积+ △BOC的面积)根据向量数量积的性质，我们知道：OA × OB = △AOB的面积× R（R为圆的半径）将上式代入前面的等式，可以得到：△AOB的面积× R + OC × OA + OC × OB = 2 × (△AOC的面积+△BOC的面积)整理后，我们可以得到圆幂定理的公式：AC × sinA = 2 × △ABC的面积四、总结与拓展圆幂定理是几何学中的一个基本定理，掌握它有助于我们更好地解决实际问题。
数学圆幂定理
数学圆幂定理圆幂定理，是平面几何中的一个重要定理，它描述了一个点到一个圆或两个圆的幂的关系。
圆幂定理有多种形式和推广，是解决几何问题的有力工具。
圆幂定理的基本形式是：如果一条直线同时切割两个圆，那么这条直线上的任意一点到两个圆的切线段的乘积是一个常数，这个常数叫做这个点到两个圆的幂。
数学上，可以用公式表示为：$$PA \cdot PB = PC \cdot PD$$其中，$P$是直线上的任意一点，$A$和$B$是直线分别与第一个圆的两个交点，$C$和$D$是直线分别与第二个圆的两个交点，如下图所示：!圆幂定理的基本形式圆幂定理的一个特殊情况是：如果一条直线同时切割一个圆，那么这条直线上的任意一点到圆的切线段的平方是一个常数，这个常数叫做这个点到这个圆的幂。
数学上，可以用公式表示为：$$PA^2 = PB^2$$其中，$P$是直线上的任意一点，$A$和$B$是直线与圆的两个切点，如下图所示：!圆幂定理的特殊情况圆幂定理的一个推广是：如果一条直线同时切割两个圆，那么这条直线上的任意一点到两个圆的切线段的比值是一个常数，这个常数叫做这个点到两个圆的幂比。
数学上，可以用公式表示为：$$\frac{PA}{PC} = \frac{PB}{PD}$$其中，$P$是直线上的任意一点，$A$和$B$是直线分别与第一个圆的两个切点，$C$和$D$是直线分别与第二个圆的两个切点，如下图所示：!圆幂定理的推广圆幂定理的一个应用是：如果一个三角形的外接圆和内切圆相切于一点，那么这个点到三角形的三条边的垂线段的乘积是一个常数，这个常数叫做这个三角形的幂积。
数学上，可以用公式表示为：$$PH \cdot PK \cdot PL = rR^2$$其中，$P$是外接圆和内切圆的切点，$H$，$K$，$L$是$P$到三角形的三条边的垂足，$r$是内切圆的半径，$R$是外接圆的半径，如下图所示：!圆幂定理的应用圆幂定理是一个简单而深刻的定理，它揭示了点和圆之间的一种基本的几何关系，它可以用来解决很多关于圆和三角形的几何问题，也可以推导出很多其他的几何定理，是平面几何中的一个重要的基础知识。
圆幂定理
圆幂定理圆幂定理是对、及（切割线定理推论）以及它们推论统一归纳的结果。
=PO^2-R^2（该结论为）所以圆内的点的幂为负数，圆外的点的幂为正数，圆上的点的幂为零。
相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。
切定理：从圆外一点引圆的和割线，是这点到割线与圆交点的两条线段长的。
割线定理：从圆外一点P引两条割线与圆分别交于A、B；C、D，则有PA·PB=PC·PD。
统一归纳：过任意不在圆上的一点P引两条直线L1、L2，L1与圆交于A、B（可重合，即切线），L2与圆交于C、D（可重合），则有PA·PB=PC·PD。
问题1相交弦定理：圆内的两条相交弦,被交点分成的两条线段长的乘积相等。
证明：连结AC，BD，由的推论，得∠A=∠D，∠C=∠B。
∴△PAC∽△PDB∴PA/PD=PC/PB∴PA·PB=PC·PD问题2割线定理：从圆外一点P引两条割线与圆分别交于则有PA·PB=PC·PD，当PA=PB，即直线AB重合，即PA切线时得到切线定理PA^2=PC·PD证明：（令A在P、B之间，C在P、D之间）∵ABCD为∴∠CAB+∠CDB=180°又∠CAB+∠PAC=180°∴∠PAC=∠CDB∵∠APC公共∴△APC∽△DPB∴PA/PD=PC/PB∴PA·PB=PC·PD切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项几何语言：∵PT切⊙O于点T，PBA是⊙O的割线∴PT^2=PA·PB（切割线定理）推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等几何语言：∵PBA、PDC是⊙O的割线∴PD·PC=PA·PB（切割线定理推论）问题3过点P任作直线交定圆于两点A、B，证明PA·PB为定值（圆幂定理）。
圆幂定理（教案）.doc
圆幂定理（教案）教学内容 圆幂定理，圆中的比例线段教学目标 1、帮助学生理清圆中比例线段的基本思考路劲;2、培养学生的线段比的转化能力.教学过程一、知识点梳理处理圆中的比例线段问题，通常用到圆幂定理，相交线定理、切割线定理和割线定理统称圆幂定理.1. 相交线定理如果圆内两条弦AB 和CD 相交于P ，那么PD PC PB PA ⋅=⋅.2. 割线定理，如果从圆外一点P 向圆引割线PAB 和PCD ，那么PD PC PB PA ⋅=⋅.3. 切割线定理如果从圆外一点P 向圆引割线PAB 和切线PC ，那么2PC PB PA =⋅.实际上可以把切割线定理看着割线定理的极限情况，于是上述可以合并为： 如果交点为P 的两条相交直线与圆O 相交于A 、B 与C 、D 那么就有 PD PC PB PA ⋅=⋅二、例题讲解例1 (2003年昆明市中考题)已知,如图,⊙O 及⊙O 外一点C,CA 切⊙O •于点A,CB 切⊙O 于点B,且∠ACB=90°,过点B 作⊙O 的割线交⊙O 于点D,交AC •的延长线于点P,AC=3,PC=4.求⊙O 的弦BD 的长.解： ∵CA 切⊙O 于点A,CB 切⊙O 于点B,∴AC=BC=3,∵∠BCP=90°,PC=4,∴∵PA 2=PB ·PD,PA=7,PB=5,∴5PD=72,∴PD=495(或PD=9.8). ∴DB=PD-PB=495-5=245(或4.8)点评 本题利用切割线定理,使问题得解.例2 (2003年四川省中考题)已知,如图,以正方形ABCD 的AB 边为直径,•在正方形内部作半圆,圆心为O,DF 切半圆于点E,交AB 的延长线于点F,BF=4.求:(1)cos ∠F 的值; (2)BE 的长.解析 (1)连结OE ∵DF 切半圆O 于点E,OE 为半径,∴OE ⊥EF,即∠OEF=90°. ∵ABCD 是正方形,∴AB=AD,∠DAF=90°.∴∠OEF=∠DAF.又∵∠F 为公共角,∴△OEF ∽△DAF. ∴12EF OE OF AF OA DF ===,即AF=2EF. ∵DF 切半圆O 于点E,FBA 为半圆O 的割线,∴由切割线定理有 EF 2=FB ·FA=BF ·2EF. ∴EF=2BF.∵BF=4. ∴EF=2×4=8,AF=2×8=16. ∴AB=AF-BF=16-4=12,FO=12AB+BF=12×12+4=10. ∴在Rt △OEF 中,cos ∠F=84105EF FO == (2)连结AE,∵DF 切半圆O 于点E, ∴∠EAF=∠BEF.∵∠F 为公共角, ∴△BEF ∽△EAF, 81162BE EF EA AF ===.设BE=k,则AE=2k.∵AB 为半圆O 的直径,∴∠AEB=90°.在Rt △AEB 中,由勾股定理,得AE 2+BE 2=AB 2,即(2k)2+k 2=122.∵k>0,∴k=125,∴BE=125点评：本题利用三角形相似,切割线定理,勾股定理等将已知和未知的关系联系起来,•从而使问题得以解决.例3 (2001年TI 杯全国初中数学竞赛)如图,已知点P 是⊙O 外一点,PS,•PT 是⊙O 的两条切线,过点P 作⊙O 的割线PAB,交⊙O 于A 、B 两点,与ST 交于点C. 求证: 1111()2PC PA PB=+. 证明 连PO 交ST 于点D,则PD ⊥ST,连SO,作OE ⊥PB,垂足为E,则E 为AB 中点.于是,PE=2PA PB +. ∵C 、E 、O 、D 四点共圆, ∴PC ·PE=PD ·PO.又∵Rt △SPD ∽Rt △OPS. ∴PS OP PD PS =,即PS 2=PD ·PO. 而由切割线定理知,PS 2=PA ·PB,则PC ·2PA PB +=PA ·PB. 即1111()2PC PA PB=+. 点评：本例利用切线长定理、垂径定理、切割线定理构造图形来解题.例4 (2002年山西太原市初中数学竞赛)如图,AB 为⊙O 的直径,C 为⊙O •上一点,延长BC 至点D,使CD=BC,CE ⊥AD,垂足为点E,BE 交⊙O 于点F,AF 交CE 于点P.求证:PE=PC.证明 延长DA 交⊙O 于点K,连结BK,OC.∵AB 是⊙O 的直径, ∴BK ⊥DA.又∵CE ⊥AD,∴CE ∥BK,故∠1=∠2,又∵A 、K 、B 、F 四点共圆,有∠2=∠3, ∴∠1=∠3.∴△PEF ∽△PAE, 因此,有PE 2=PA ·PF.又∵为△ABD 的中位线,∴OC ∥AD.则CE ⊥OC.可知CE 为⊙O 的切线,故PC 2=PF ·PA,∴PE 2=PC 2,即PE=PC.点评：几何图形中有直径这一条件,常添加辅助线,构成直径上的圆周角是直角,•使其构成直角三角形.三、课后作业1、如图,已知AB 是⊙O 的直径,P 是⊙O 外一点,PD ⊥AB 于D,交⊙O 于E.PA 交⊙O 于C,BC 交PD 于F.求证:DE 2=DF ·DP.2、如图,△ABC 是⊙O 的内接三角形,∠BAC 的平分线交BC 于D,交⊙O 于E.求证:AB ·AC=AD 2+BD ·DC.。
与圆有关的比例线段 课件
3．切线长定理 (1)文字叙述： 从圆外一点引圆的两条切线，它们的 切线长相等 ， 圆心和这一点的连线平分 两条切线 的夹角． (2)图形表示： 如图，⊙O的切线PA，PB， 则PA＝ PB，∠OPA＝ ∠OPB .
切割线定理 [例 2] 如图，AB 是⊙O 的一条切线，切点为 B，ADE， CFD，CGE 都是⊙O 的割线，已知 AC＝AB.
证明：(1)AD·AE＝AC2； (2)FG∥AC. [思路点拨] (1)利用切割线定理； (2)证△ADC∽△ACE.
[证明] (1)∵AB 是⊙O 的一条切线，ADE 是⊙O 的割线， ∴由切割线定理得 AD·AE＝AB2. 又 AC＝AB，∴AD·AE＝AC2. (2)由(1)得AADC＝AACE， 又∠EAC＝∠DAC，∴△ADC∽△ACE. ∴∠ADC＝∠ACE. 又∠ADC＝∠EGF，∴∠EGF＝∠ACE.∴FG∥AC.
切线长定理 [例 3] 如图，AB 是⊙O 的直径，C 是⊙O 上一点，过点 C 的 切线与过 A，B 两点的切线分别交于点 E，F，AF 与 BE 交于点 P. 求证：∠EPC＝∠EBF.
[思路点拨] 切线长定理 → EA＝EC，FC＝FB → EFCC＝EPBP → CP∥FB → 结论
[证明] ∵EA，EF，FB 是⊙O 的切线， ∴EA＝EC，FC＝FB. ∵EA，FB 切⊙O 于 A，B，AB 是直径， ∴EA⊥AB，FB⊥AB. ∴EA∥FB.∴EBAF＝EBPP.∴EFCC＝EPBP. ∴CP∥FB.∴∠EPC＝∠EBF.
和圆有关的比例线段课件
建筑案例
通过分析一座建筑物的பைடு நூலகம்计 和结构，我们可以探索比例 线段在建筑领域中的应用。
• 比例线段的使用方法 • 如何确保建筑物的平
衡和结构 • 实际案例分析
艺术案例
通过研究一幅艺术作品的构 图和比例关系，我们可以深 入理解比例线段在艺术创作 中的应用。
• 艺术作品中的比例线 段运用
• 构图的重要性和原则 • 艺术家的案例分析
艺术构图
在艺术中，比例线段可以帮助我们创造符合审 美标准的平衡和比例感的作品。
地图绘制
在地图绘制中，比例线段可以帮助我们准确地 表示和测量地理距离和尺寸。
工程设计
在工程设计中，比例线段可以帮助我们计算和 绘制精确的图纸和设计图。
案例分析
通过一些案例分析，我们可以深入了解比例线段在实际问题中的应用和重要性。
2
分数比较
将线段的长度表示为分数，可以更方便地计算比例关系。
3
比例计算公式
通过比例计算公式，我们可以准确地计算比例线段的各个部分长度。
比例线段的应用场景
比例线段在许多实际场景中起到重要的作用，帮助我们解决现实生活中的问题。
建筑设计
在建筑设计中，比例线段可以帮助我们计算和 绘制精确的蓝图和设计图纸。
数学应用
通过比例线段的计算和应用，我们可以在数学
比例线段的性质
比例线段具有许多独特的性质和特点，帮助我们理解几何图形中的相对大小和比例关系。
黄金比例
比例线段中的黄金比例是一种特殊比例，广 泛应用于艺术和建筑领域。
相似性
比例线段的性质与几何图形的相似性密切相 关，帮助我们研究和理解这一概念。
比例关系
地理案例
通过研究地图的绘制和比例 尺的使用，我们可以了解比 例线段在地理学中的应用。
【初中数学】圆幂定理
【初中数学】圆幂定理圆幂定理是一个总结性的定理，是对相交弦定理、切割线定理及割线定理（切割线定理推论）以及它们推论的统一与归纳，所以目前书上已经把这个定理删除了，也作为补充知识点介绍。
根据两条与圆有相交关系的线的位置不同，有以下定理：（1）相交弦定理（2）切割线定理（3）割线定理从上述定理可以看出，两条线的位置从内到外，都有着相似的结论。
经过总结和归纳，便得出了圆幂定理。
圆幂定理是几何学中的一条定理，它描述了一个点与一个圆之间的关系。
具体来说，圆幂定理说明了如果有一条直线通过了一个P点，与一个圆相交于点A和点B，那么这个点P到点A、点B的长度的乘积等于点P到圆心O的距离的平方减去圆的平方的绝对值，即可以表示为：PA·PB=|PO²-r²|（r表示圆的半径）.如何证明这个定理呢？就需要分三种情况讨论，点P与圆的位置关系。
我们非常清楚，点与圆的位置关系只有三种：圆外、圆上、圆内。
1、点P在圆外如图，点P在⊙O外部，过点P的直线与⊙O相交于A、B两点，连接OP交⊙O于点C，⊙O的半径为r.证明：如图，延长PO交⊙O与点D.由割线定理可得：PA·PB=PC·PD∵ PC=PO+OC，PD=PO+OD，OC=OD=r∴ PC=PO+r，PD=PO+r∴ PA·PB=（PO+r）（PO-r）∴ PA·PB=PO²-r²=|PO²-r²|2、点P在圆内如图，点P在⊙O内部，过点P的直线与⊙O相交于A、B两点，连接OP交⊙O于点C，⊙O的半径为r.证明：延长PO交⊙O于C、D两点根据相交弦定理，得：PA·PB=PC·PD∵ PC=OC-PO，PD=PO+OD，OD=OC=r∴ PC=r-PO，PD=PO+r∴ PA·PC=（r-OP）（PO+r）∴ PA·PC=r²-PO²=|PO²-r²|3、当点P在圆上通过以上两种情况的证明可得，PA·PB=|PO²-r²|，那么当P点在圆上时，P、A 两点重合，故PA=0，OP=r，所以PA·PB=0，PO²-r²=0，所以也成立。
圆中的重要模型-圆幂定理模型(解析版)
圆中的重要模型--圆幂定理模型圆幂定理是一个总结性的定理，是对相交弦定理、切割线定理、割线定理、弦切角定理、托勒密定理以及它们推论的统一与归纳。
可能是在19世纪由德国数学家施泰纳(Steiner )或者法国数学家普朗克雷(Poncelet )提出的。
圆幂定理的用法：可以利用圆幂定理求解与圆有关的线段比例、角度、面积等问题。
模型1.相交弦模型条件：在圆O 中，弦AB 与弦CD 交于点E ，点E 在圆O 内。
结论：△CAE ∼△BDE ⇒EC EB =EA ED⇒EC ⋅ED =EB ⋅EA 。
1(2023·广东广州·九年级校考期中)如图，两个同心圆，大圆的弦AB 与小圆相切于点P ，大圆的弦CD 经过点P ，且CD =13，PD =4，两圆组成的圆环的面积是．【答案】36π【分析】连接AC ，BD ，OP ，OA ，先根据切线的性质定理和垂径定理证出PA =PB ，再证明△APC ∽△DPB ，得到AP DP =CP BP，代入数据求得AP =BP =6，最后根据圆环的面积公式进行计算即可求解．【详解】解：如图，连接AC ，BD ，OP ，OA ，∵大圆的弦AB 与小圆相切于点P ，∴OP ⊥AB ，∴PA =PB ，OA 2-OP 2=AP 2，∵CD =13，PD =4，∴PC =13-4=9，∵∠BAC =∠BDC ，∠C =∠B ，∴△APC ∽△DPB ，∴AP DP =CP BP ，即AP 4=9BP，解得：AP =BP =6(负值舍去)，∴圆环的面积为：π⋅OA 2-π⋅OP 2=π⋅AP 2=36π，故答案为：36π．【点睛】此题综合运用了切线的性质定理、垂径定理、勾股定理、圆周角定理、圆环的面积公式，分别求出大圆和小圆的半径是解题的关键．2(2023·江西景德镇·九年级校考期末)如图，PT是⊙O的切线，T为切点，PA是割线，交⊙O于A、B两点，与直径CT交于点D．已知CD=2，AD=3，BD=4，那PB=．【答案】20.【分析】连接AC，BT，AT，易证∆CAD~∆BTD，得到TD=6，易证：∆BTP~∆TAP，得：TP2=AP⋅BP，设PB=x，则AP=x+7，TP2=(x+7)⋅x，PD=x+4，根据勾股定理，即可求解.【详解】连接AC，BT，AT，∵∠CAD=∠BTD，∠ADC=∠TDB，∴∆CAD~∆BTD，∴CD BD =ADTD，即：24=3TD∴TD=6，∵PT是⊙O的切线，T为切点，∴∠BTP+∠BTD=90°，∵CT是直径，∴∠CAD+∠TAP=90°∵∠CAD=∠BTD，∴∠BTP=∠TAP，∵∠P=∠P，∴∆BTP~∆TAP，∴TPAP =BPTP，即：TP2=AP⋅BP，设PB=x，则AP=x+7，TP2=(x+7)⋅x，PD=x+4，∵在Rt∆DPT中，DT2+PT2=PD2，∴62+(x+7)x=(x+4)2，解得：x=20，故答案是：20.【点睛】本题主要考查相似三角形的判定和性质定理与圆的性质的综合，根据题意，添加辅助线，构造相似三角形，是解题的关键.3(2023·江苏·九年级专题练习)相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等．(1)为了说明相交弦定理正确性，需要对其进行证明，如下给出了不完整的“已知”“求证”，请补充完整，并写出证明过程．已知：如图①，弦AB，CD交于点P，求证：．(2)如图②，已知AB是⊙O的直径，AB与弦CD交于点P，且AB⊥CD于点P，过D作⊙O的切线，交BA的延长线于E，D为切点，若AP=2，⊙O的半径为5，求AE的长．【答案】(1)PA ⋅PB =PC ⋅PD ，证明见解析(2)103【分析】(1)先证明△ACP ∽△DBP ，再利用相似的性质即可；(2)利用(1)可知PA ⋅PB =PC ⋅PD ，求出PD ，再证明△OPD ∼△DPE ，利用相似的性质求出PE ，求差即可得到AE 的长．【详解】(1)求证：PA ⋅PB =PC ⋅PD ．证明：连接AC 、BD ．如图①．∵∠A =∠D ，∠C =∠B ．∴△ACP ∽△DBP ．∴AP PD =PC BP．∴PA ⋅PB =PC ⋅PD ．(2)解：∵AP =2，OA =5，PB =10-2=8．由(1)可知PA ⋅PB =PC ⋅PD ．∴PC ⋅PD =16．∵AB ⊥CD ，AB 是⊙O 的直径，PC =PD ，PD =4．连接OD ．如图②．∵DE 为切线．∴∠EDO =90°．∵∠1+∠2=90°．∠E +∠2=90°．∴∠1=∠E ．∴△OPD ∼△DPE ．∵OP PD =PD PE，∴OP ⋅PE =PD ⋅PD ．∴16=3PE ，PE =163．又∵AP =2．∴AE =163-2=103．【点睛】本题考查了圆的相关性质，三角形相似的判定与性质，严格的逻辑思维和严密的书写过程是解题的关键．模型2.双割线模型条件：如图，割线CH 与弦CF 交圆O 于点E 和点G 。
圆幂定理及其证明
1 / 1圆幂定理圆幂定理是相交弦定理、切割线定理及割线定理(切割线定理推论)以及他们推论的统称。
图１ 图２图３ 图４一、相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。
（如图，弦AB 和CD 交于O ⊙内一点P ，则PA PB PC PD ⋅=⋅）．1、证 明：如图１，AB 、CD 为圆O 的两条任意弦。
相交于点P ，连接AD 、BC ，则∠D=∠B ， ∠A=∠C 。
所以△APD ∽△BPC 。
所以AP PDAP BP PC PD PC BP=⇒⋅=⋅ 2、练习：如图２，在O ⊙中，弦AB 与CD 相交于点P ，已知3cm 4cm 2cm PA PB PC ===，，，那么PD = cm ．二、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆焦点的两条线段长的比例中项。
（如图，PT 是O 的切线，PB 是O 的割线，则有PT ２＝ＰＡ ＰＢ）1、证明：如图３，PT 为圆切线，PAB 为割线。
连接TA ，TB ，则∠PTA=∠B （弦切角等于同弧圆周角）所以△PTA ∽△PBT ，所以2PT PAPT PA PB PB PT=⇒=⋅ 2、练习 如图４，PC 是半圆的切线，且PB OB =，过B 的切线交PC 与D ，若6PC =，则O ⊙半径长= ，:CD DP =__________．三、割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等。
（从圆外一点P 引两条割线与圆分别交于A.B.C.D 则有 PA·PB=PC·PD ）1、证明：这个证明就比较简单了。
可以过P 做圆的切线，也可以连接CB 和AD 。
证相似。
存在：PA PB PC PD ⋅=⋅2、练习如下图，过点P 作O ⊙的两条割线分别交O ⊙于点A B 、和点C D 、，已知32PA AB PC ===，，则PD 的长是( )A ．3B ．7.5C ．5D ．5.5。
圆幂定理
圆幂定理圆幂定理就是对相交弦定理、切割线定理及割线定理(切割线定理推论)以及它们推论统一归纳的结果。
ﻩﻩﻩﻩ圆幂=PO^2-Ｒ^2(该结论为欧拉公式)所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。
相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
切割线定理:从圆外一点引圆的切线与割线,切线长就是这点到割线与圆交点的两条线段长的比例中项。
割线定理:从圆外一点P引两条割线与圆分别交于Ａ、B;C、D,则有PA·PB=PＣ·PＤ。
线),L2与圆交于C、D(可重合),则有ＰA·PB=PC·PD。
问题１相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的乘积相等。
证明:连结AC,BD,由圆周角定理的推论,得∠A=∠Ｄ,∠C=∠B。
∴△ＰAＣ∽△PDＢ∴ＰＡ/PD=PC/ＰＢ∴PＡ·PB=PC·PＤ问题２割线定理:从圆外一点Ｐ引两条割线与圆分别交于Ａ、B.C、D 则有PA·PB=PC·PD,当ＰA=ＰB,即直线AＢ重合,即ＰA切线时得到切线定理PA^2=PC·PD证明:(令A在P、B之间,Ｃ在P、D之间)∵ＡBCＤ为圆内接四边形∴∠CAB+∠CDB=１80°又∠ＣAB＋∠PAC=180°∴∠PＡC=∠CＤB∵∠APC公共∴△AＰC∽△DPＢ∴PＡ/PD=PC/PB∴PA·PB=ＰC·PＤ切割线定理:从圆外一点引圆的切线与割线,切线长就是这点到割线与圆交点的两条线段长的比例中项几何语言:∵PＴ切⊙O于点T,PBA就是⊙O的割线∴PT＾2=PA·ＰB(切割线定理)推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言:∵PＢA、PDC就是⊙O的割线∴PD·PC=PA·PＢ(切割线定理推论)问题3过点Ｐ任作直线交定圆于两点A、B,证明PA·PB为定值(圆幂定理)。
和圆有关的比例线段
和圆有关的比例线段介绍在几何学中，圆是一个非常重要的图形。
而比例则是数学中常见的一个概念，用来描述两个量之间的关系。
本文将讨论和圆有关的比例线段。
圆的定义圆是平面上离一个固定点距离相等的所有点的集合。
这个固定点被称为圆心，而距离圆心最远的点与圆心的距离被称为半径。
圆可以通过圆心和半径来唯一确定。
比例线段在几何中，线段分为很多种类，比例线段是其中一种。
比例线段指的是线段上一个点将线段分割成两个部分，且两个部分的比例与整个线段的比例相等。
如果一个线段被比例为a:b，那么可以得到以下等式：AB/BC = a/b其中，AB表示线段的一部分，BC表示线段的另一部分。
和圆有关的比例线段和圆有关的比例线段主要涉及到圆的直径、半径和切线。
下面以这些情况分别进行讨论。
圆的直径与半径的关系圆的直径是通过圆心的两个点，并且直径的长度等于半径的两倍。
因此，如果线段AB是圆的直径，那么可以得到以下等式：AB/BC = 2这意味着直径上的任意一点将直径划分成两段，其中一段是整个直径的两倍大小。
圆的半径与切线的关系切线是与圆相切且垂直于半径的直线。
在与圆的一个点A相切并垂直于半径的切线上，连接圆心O与A点的线段称为半径OA。
如果线段AB是切线上的一段，那么可以得到以下等式：AB/BC = 1这意味着切线上的任意一点将切线划分成两段，其中一段的长度等于半径的长度。
应用实例求解比例线段的长度已知圆的半径为r，线段AB分割线段OC，如下图所示：A B|--------|O ----------- C根据比例线段的定义，可以得到以下等式：AB/BC = a/b要求解比例线段的长度，可以应用以下公式：AB = (BC * a) / b其中，BC是已知的线段长度，a和b分别是给定的比例。
求解与切线相交的线段长度已知圆的半径为r，线段AB是与一个切线相交的线段，如下图所示：A|--|-------O | B|根据比例线段的定义，可以得到以下等式：AB/BC = a/b要求解与切线相交的线段的长度，可以应用以下公式：AB = (BC * a) / b其中，BC是切线上的线段长度，a和b分别是给定的比例。
与圆有关的比例线段(圆幂定理精品)
P
O A(B)
切线长定理 PA=PC,∠APO=∠CPO
由上看出，两条线的交点位置从内到外，都有着相似的 结论 .这些等积式会是一个定值吗？
12
C P A
E
B
C D 动到圆外.
O
P
PA PB PE PF OP ROP R 2 2 OP R PA PB PE PF R OP R OP
D
图１
D
图２
A B
A
P O C
B
D
图３
B
P A O C
PA·PB=PC·PD……(3)
P C
O
PA·PB=PC·PD……(1)
PA·PB=PC·PD……(2)
证明:连接AD、BC. 则由圆周角定理的推论可得:∠A＝∠C.
又∵
∠APD= ∠CPB
∴△APD∽△CPB.
综上所述，不论AB 、 CD具有什么样的位置， 都有结论（１）成立！
2
2 2 PA2=PC∙PD OP R
PA PC OP R
13
思考：从这几个定理的结论里大家能发现什么共同点？ 1.结论都为乘积式; 2.几条线段都是从同一点出发; 3.都是通过三角形相似来证明（都隐含着三角形相似）. 4. PA∙PB=PC∙PD=定值= (OP+R)│OP-R│=│OP²-R²│ .
（2）多元素分析图形；
图中有没有特殊点、特殊线段、特殊三角形、特殊四 边形、全等三角形、相似三角形. （3）将以上分析组合，寻找联系.
2
一、下面我们沿用从特殊到一般的思路,讨论与圆有关 的相交弦的问题. 探究1:如图,AB是⊙O的直径,CD⊥AB,AB与CD相交于P,
初三数学第十章圆知识点整理
初三数学第十章圆知识点整理
2019年初三数学第十章圆知识点整理
【编者按】为了丰富同学们的学习生活，查字典数学网初中频道搜集整理了2019年初三数学第十章圆知识点整理，供大家参考，希望对大家有所帮助!
2019年初三数学第十章圆知识点整理
初三数学知识点第十章圆
★重点★①圆的重要性质;②直线与圆、圆与圆的位置关系;③与圆有关的角的定理;④与圆有关的比例线段定理。
☆ 内容提要☆
一、圆的基本性质
1.圆的定义(两种)
2.有关概念：弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。
3.三点定圆定理
4.垂径定理及其推论
5.等对等定理及其推论
5. 与圆有关的角：⑴圆心角定义(等对等定理)
⑵圆周角定义(圆周角定理，与圆心角的关系)
⑶弦切角定义(弦切角定理)
二、直线和圆的位置关系
1.三种位置及判定与性质：
2.切线的性质(重点)
5.弓形面积的计算方法
6.圆柱、圆锥的侧面展开图及相关计算
七、点的轨迹
六条基本轨迹
八、有关作图
1.作三角形的外接圆、内切圆
2.平分已知弧
3.作已知两线段的比例中项
4.等分圆周：4、8;6、3等分
九、基本图形
十、重要辅助线
1.作半径
2.见弦往往作弦心距
3.见直径往往作直径上的圆周角
4.切点圆心莫忘连
5.两圆相切公切线(连心线)
6.两圆相交公共弦。
初三数学第十章圆知识点整理
初三数学第十章圆知识点整理【编者按】为了丰富同学们的学习生活，查字典数学网初中频道搜集整理了2021年初三数学第十章圆知识点整理，供大伙儿参考，期望对大伙儿有所关心!2021年初三数学第十章圆知识点整理初三数学知识点第十章圆★重点★①圆的重要性质;②直线与圆、圆与圆的位置关系;③与圆有关的角的定理;④与圆有关的比例线段定理。
☆内容提要☆一、圆的差不多性质1.圆的定义(两种)2.有关概念：弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。
3.三点定圆定理4.垂径定理及其推论5.等对等定理及其推论5. 与圆有关的角：⑴圆心角定义(等对等定理)⑵圆周角定义(圆周角定理，与圆心角的关系)⑶弦切角定义(弦切角定理)二、直线和圆的位置关系1.三种位置及判定与性质：2.切线的性质(重点)3.切线的判定定理(重点)。
圆的切线的判定有⑴⑵4.切线长定理三、圆换圆的位置关系1.五种位置关系及判定与性质：(重点：相切)2.相切(交)两圆连心线的性质定理3.两圆的公切线：⑴定义⑵性质四、与圆有关的比例线段1.相交弦定理2.切割线定理五、与和正多边形1.圆的内接、外切多边形(三角形、四边形)2.三角形的外接圆、内切圆及性质3.圆的外切四边形、内接四边形的性质4.正多边形及运算中心角：内角的一半：(右图)(解Rt△OAM可求出相关元素, 、等)六、一组运算公式1.圆周长公式2.圆面积公式3.扇形面积公式4.弧长公式5.弓形面积的运算方法6.圆柱、圆锥的侧面展开图及相关运算七、点的轨迹六条差不多轨迹八、有关作图1.作三角形的外接圆、内切圆2.平分已知弧3.作已知两线段的比例中项4.等分圆周：4、8;6、3等分九、差不多图形十、重要辅助线1.作半径2.见弦往往作弦心距3.见直径往往作直径上的圆周角4.切点圆心莫忘连死记硬背是一种传统的教学方式,在我国有悠久的历史。
但随着素养教育的开展,死记硬背被作为一种僵化的、阻碍学生能力进展的教学方式,慢慢为人们所摒弃;而另一方面,老师们又为提高学生的语文素养煞费苦心。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆幕定理是初中平面几何中重要定理之一，在有关计算和证明中应用非常多，尤其是在证明圆中线段 比例式（或等积式）时，能有效地考査学生综合运用相似形和圆的有关知识分析.解决问题的能力，因而 成为全国各省市中考及数学竞赛命题的一个热点，切实加强这方面知识的复习与训练，全面掌握这类问题 的证明思路和方法，对每一个同学都非常重要.
此外，证明圆中线段比例式（或等积式）的基本思路有（1）利用平行线分线段成比例定理；（2）利用相 似三角形给出证明；（3）利用圆幕定理给出证明；（4）利用面积或三角函数给出证明.
一、 基础知识
1、 相交弦定理
如果圆内两条弦AB 和CD 相交于点P,那么PA ・PB=PC ・PD （如下图1）；
2、 割线定理
如果从圆外一点P 向圆引割线PAB 和PCD,那么PA ・PB=PC ・PD （如下图2）；
3、 切割线定理
如果从圆外一点P 向圆引割线PAB 和切线PC,那么PA • PB=PC2 （如下图3）；
上述三个定理统称为圆基定理•实际上，可以把切割线定理看作是割线定理的极限情形，于是上述三 个结论可以合并为：如果交点为P 的两条宜线与圆O 相交于A 、B 与C 、D,那么就有PA ・PB=PC ・PD, 这里P 、A. B 共线及P. C\ D 共线；
二 例题
例 1 （★）已知，如图 AB 是OO 的弦，P 是 AB 上一点,AB=10cm, PA=4cm, OP=5cm,求：OO 的半径•
例2 （★）如图，已知OOi 和002相交于CD 两点.其外公切线AB 分别切OO K OO2于点AB,求证: 直线CD 平分线段AB.
例3 （★）如图，E 是圆内弦AB. CD 的交点，直线EF 〃CB,交AD 的延长线于F, FG 切圆于G,连
第十讲
扇定理, 中比例线段
结EG,求证：ZFEG=ZFGE.
例4 (★★)如图，PA切OO于A, PBC是OO的割线，M是PA的中点，MC交QO于N, PN的延长线交OO于D,连结BD,求证：PA/7BD;
例5 (★★)如图，已知B是线段AC上任一点，在AC同侧分别以AB、AC为直径作两个半圆4〃出、
A H C ,若CD切半圆如于点D, EBXAC, B为垂足，且交半圆MC于E, M是DE的中点，求证:
CM 丄DE.
例6 (★★)如图，a21 ABC中，AB>AC,如果/ABC的内切圆把BC边上的中线AD三等分，求证: BC=2AC；
例7 (★)图中,AB是OO的直径.宜线MN切OO于点C, AD丄MN于D, AD交OO于E, AB的延
长线交MN于点P,求证：AC2=AE • AP；
例8(*)如图，Z1ABC中，ZA的平分线AD交BC于D, 0OJ±点A,且和BC切于点D,和AB. AC分别相交于E、F, AD与EF相交于G,求证：BD - EG=BE - EA；
例9 (★★)如图，已知BC是圆中一条弦，EF切圆于A, AD丄BC于D, BE丄EF于E, CF丄EF于F, 求证：AD2=BE • CF；
例10 (★, 2002年东城区中考)如图，P是OO的直径AB延长线上一点，割线PCD交OO于C. D两点,弦DF 丄AB于H, CF交AB于点E,求证：PA • PB=PO • PE；
例11 (★)如图，已知PA. PB是0O的切线，切点为A. B, PCD是割线，求证:
AC • BD=AD • BC
例12（資）如图，BC是圆的直径，O是圆心，P是BC延长线上一点，PA切半圆于点A, AD丄BC于点D,求证：PD • PO=PC • PB
例14 （★★,托勒密定理）求证：在圆的内接四边形ABCD中，AB・CD+BC・ AD=AC・BD
例15 （★★★, 96年全国初中数学联赛）设凸四边形ABCD的对角线AC和BD交于点M,过M作AD
的平行线分别交AB. CD 于E. F,交BC 的延长线于点O, P 是以O 为圆心.以OM 长为半径的圆上一 点，求证：ZOPF=ZOEP ；
A £ B
三、 练习题
1. (★)如图，PA 为OO 的切线，A 为切点，PBC 是过点O 的割线，PA = 10cm, PB=5cm,求OO 的半径•
2. (★)过OO 外一点P 作OO 的两条切线PA. PB,连结OP 与AB 交于D,与OO 交于C,过C 作
AP 的垂线，垂足为 E,若 PA = 10cm, PC=5cm,则 CE= __________ ；
3. (★★) AB. AC 分别是OO 的切线与割线，若ZC=45° , ZBDA=60° , CD= >?6 ,求切线AB 的 长;
4. (★★)如图A 、B 、C. D 四点在同一个圆周上，且BC=CD=4, AE=6,线段BE 和DE 的长都是 正整数，则BD 的长等于 _________ :
P
5. （★★）在平行四边形ABCD中，过A、B. C三点的圆交AD于点E,且与CD相切，若AB=4,
BE=5,贝ljDE= _________ ；
6. （★★,2003年全国）已知AB是OO的直径,BC是0O的切线,OC平行于弦AD,过点D作DE丄AB
于点E,连结AC与DE交于点P,求证：EP=PD；
7. （★★★, 2001年全国）已知P是OO外一点，PS. PT是OO的两条切线，过点P作OO的割线PAB,交OO于AB两点，与ST交于点C,求证：+
1 C Z 1 A ltj。