Lingo解目标规划1
Lingo解目标规划

B
0.3 0.3 3.2
棉花库存量
300 180
甲绵(kg) 乙绵(kg)
利润(元/km)
若利润指标为1755元,A种棉花要生产650km,问 A,B两种棉纱各应该生产多少?
目标规划模型:
设分别生产A、B两种棉纱x1, x 2km,则: min z p d p2 d
1 1 2
0.5 x1 0.3x 2 300 0.1x1 0.3x 2 180 2.5 x1 3.2 x 2 d1 d1 1755 x1 d 2 d 2 650 x1, x 2, d i 0
整数线性规划的几种类型
纯整数线性规划 混合整数线性规划
0-1型整数线性规划
例:
max z 20x1 10x 2 5 x1 4 x 2 24 2 x1 5 x 2 13 s.t. x1, x 2 0 x1, x 2取整数
不考虑整数约束时求解
Lingo代码:
min=d21; 0.5*x1+0.3*x2<=300; 0.1*x1+0.3*x2<=180; 2.5*x1+3.2*x2+d11-d12=1755; x1+d21-d22=650; d11=0;
例4:已知有三个产地给四个销地供应某种产品,产销 地之间的供需量和单 7 13
Lingo代码
sets: cd/1..3/:a; xd/1..4/:b; links(cd,xd):c,x; px/1..13/:d1,d2; endsets data: a=300 200 400; b=200 100 450 250; c=5 2 6 7 3546 4 5 2 3; enddata min=d2(13); @for(cd(i):@sum(xd(j):x(i,j))=a(i)); @for(xd(j):@sum(cd(i):x(i,j))<=b(j)); x(1,4)+x(2,4)+x(3,4)+d1(4)-d2(4)=250; x(3,1)+d1(5)-d2(5)=100; @for(xd(j):@sum(cd(i):x(i,j))+d1(j+5)-d2(j+5)=b(j)*0.8); @sum(links(i,j):c(i,j)*x(i,j))+d1(10)-d2(10)=2950*1.1; x(2,4)+d1(11)-d2(11)=0; (x(1,1)+x(2,1)+x(3,1))-(200/450)*(x(1,3)+x(2,3)+x(3,3))+d1(12)-d2(12)=0; @sum(links(i,j):c(i,j)*x(i,j))+d1(13)-d2(13)=2950; y=@sum(links(i,j):c(i,j)*x(i,j)); d1(4)=0; d1(5)=0; d1(6)+d1(7)+d1(8)+d1(9)=0; d2(10)=115; d2(11)=0; d1(12)+d2(12)=30; d1(1)+d1(2)+d1(3)+d2(1)+d2(2)+d2(3)=0;
用Lingo求解整数(0-1)规划模型

1、建立数学模型, 2、用lingo循环语句编写程序.
上机作业题 人员安排问题
某城市的巡逻大队要求每天的各个时间段都有一
定数量的警员值班, 以便随时处理突发事件, 每人连续 工作6h, 中间不休息. 如表所示是一天8个班次所需值 班警员的人数情况统计:
班次
时间段
人数 班次
时间段
人数
1
6:00~9:00
例 4 求函数 z x 22 y 22 的最小值.
例 4 求函数 z x 22 y 22 的最小值.
解: 编写Lingo 程序如下:
min=(x+2)^2+(y-2)^2; @free(x); 求得结果: x=-2, y=2
二、Lingo 循环编程语句
(1) 集合的定义 包括如下参数: 1) 集合的名称.
12,8 3,0; enddata
!数据赋值;
max=@sum(bliang(i):a(i)*x(i)); !目标函数;
@for(yshu(j):@sum(bliang(i):x(i)*c(j,i))<=b(j));
!约束条件;
例6:人员选拔问题
队员号码 身高 / m 位置 队员号码 身高 / m 位置
例 2 用Lingo软件求解整数规划问题
min z 2 x1 5 x2 3 x3
4 x1 x2 x3 0
2
x1
4 x2
2 x3
2
x1
x2
x3
2
xi 0 且取整数, i 1, 2, 3
Lingo 程序:
min=2*x1+5*x2+3*x3; -4*x1-x2+x3>=0; -2*x1+4*x2-2*x3>=2; x1-x2+x3>=2; @gin(x1);@gin(x2);@gin(x3);
附1:用LINGO求解线性规划的例子一奶制品加工厂用牛奶生产A1、A2

附1:用LINGO求解线性规划的例子一奶制品加工厂用牛奶生产A1、A2两种奶制品,1桶牛奶可以在设备甲上用12小时加工成3公斤A1,或者在设备乙上用8小时加工成4公斤A2。
根据市场需求,生产的A1、A2能全部售出,且每公斤A1获利24元,每公斤A2获利16元。
现在加工厂每天能得到50桶牛奶的供应,每天正式工人总的劳动时间为480小时,并且设备甲每天至多能加工100公斤A1,设备乙的加工能力没有限制。
试为该厂制定一个生产计划,使每天获利最大,并进一步讨论以下3个附加问题:1)若用35元可以购买到1桶牛奶,应否作这项投资?若投资,每天最多购买多少桶牛奶?2)若可以聘用临时工人以增加劳动时间,付给临时工人的工资最多是每小时几元?3)由于市场需求变化,每公斤A1的获利增加到30元,应否改变生产计划?数学模型:设每天用x1桶牛奶生产A1 ,用x2桶牛奶生产A2目标函数:设每天获利为z元。
x1桶牛奶可生产3x1公斤A1,获利24*3x,x2桶牛奶可生产4*x2公1斤A2,获利16*4x2,故z=72x1+64x2约束条件:原料供应:生产A1、A2的原料(牛奶)总量不超过每天的供应50桶,即x1+x2≤50劳动时间:生产A1、A2的总加工时间不超过每天正式工人总的劳动时间480小时,即12x1+8x2≤480设备能力:A1的产量不得超过设备甲每天的加工能力100小时,即3x1≤100≥0非负约束:x1、x2均不能为负值,即x1≥0,x2综上所述可得max z=72x1+64x2s.t.x1+x2≤5012x1+8x2≤4803x1≤100x1≥0,x2≥0显然,目标函数和约束条件都是线性的,这是一个线性规划(LP),求出的最优解将给出使净利润最大的生产计划,要讨论的问题需要考虑参数的变化对最优解和影响,一般称为敏感性(或灵敏度)分析。
LINGO求解线性规划用LINGO求解线性规划时,首先在LINGO软件的模型窗口输入一个LP模型,模型以MAX或MIN 开始,按线性规划问题的自然形式输入(见下面例子所示)。
线性规划问题的Lingo求解

Lingo中参数设置与调整
01
参数设置
02
调整策略
Lingo允许用户设置求解器的参数, 如求解方法、迭代次数、收敛精度等 。这些参数可以通过`@option`进行 设置。
如果求解过程中遇到问题,如无解、 解不唯一等,可以通过调整参数或修 改模型来尝试解决。常见的调整策略 包括放松约束条件、改变目标函数权 重等。
02
比较不同方案
03
验证求解结果
如果存在多个可行解,需要对不 同方案进行比较,选择最优方案。
可以通过将求解结果代入原问题 进行验证,确保求解结果的正确 性和合理性。
感谢您的观看
THANKS
问题,后面跟随线性表达式。
02 03
约束条件表示
约束条件使用`subject to`或简写为`s.t.`来引入,后面列出所有约束条 件,每个约束条件以线性表达式和关系运算符(如`<=`, `>=`, `=`, `<`, `>`)表示。
非负约束
默认情况下,Lingo中的变量是非负的,如果变量可以为负,需要使用 `@free`进行声明。
问题的解通常出现在约束条件的边界上 。
变量通常是连续的。
特点 目标函数和约束条件都是线性的。
线性规划问题应用场景
生产计划
确定各种产品的最优生产量, 以最大化利润或最小化成本。
资源分配
在有限资源下,如何最优地分 配给不同的项目或任务。
运输问题
如何最低成本地将物品从一个 地点运输到另一个地点。
金融投资
03
求解结果
通过Lingo求解,得到使得总加工时间最短的生产计划安 排。
运输问题优化案例
问题描述
某物流公司需要将一批货物从A地运往B地,可以选择不同的运输方式和路径,每种方式和路径的运输时间和成本不 同。公司需要在满足货物送达时间要求的前提下,选择最优的运输方式和路径,使得总成本最低。
用LINGO软件求解目标规划问题

10 x1 + 15 x2 + d1 d1+ = 40 + x1 + x2 + d 2 d 2 = 10 s.t. d1+ = 0 x1 , x2 , d , d + ≥ 0, j = 1,2 j j
用LINGO求解,得最优解 d = d 具体LINGO程序及输出信息如下:LINGO程序为(参见图 4.4.4):
+ 1
=0, 1
d2 = 6 ,最优值为6.
精品课程《运筹学》
图4.4.4
精品课程《运筹学》
LINGO运算后输出为(参见图4.4.5):
图4.4.5 精品课程《运筹学》
d 对应于第三优先等级,将d1+ =0, 2 = 6 作为约束条件, 建立线性规划问题:
min z = d 3 10 x1 + 15 x2 + d1 d1+ = 40 + x1 + x2 + d 2 d 2 = 10 x2 + d 3 d 3+ = 7 s.t. d1+ = 0, d 2 = 6 + x1 , x2 , d j , d j ≥ 0, j = 1,2,3
10 x1 + 15 x 2 + d 1 d 1+ = 40 + x1 + x 2 + d 2 d 2 = 10 s.t. x 2 + d 3 d 3+ = 7 x1 , x 2 , d , d + ≥ 0, j = 1,2,3 j j
精品课程《运筹学》
解:首先对应于第一优先等级,建立线性规 划问题:
x1 = 4, x2 = 0, d1+ = d1 = 0 , 用LINGO求解,得最优解是
运筹学实例分析及lingo求解讲解

运筹学实例分析及lingo 求解一、线性规划某公司有6个仓库,库存货物总数分别为60、55、51、43、41、52,现有8个客户各要一批货,数量分别为35,37,22,32,41,32,43,38。
各供货仓库到8个客户处的单位货物运输价见表试确定各仓库到各客户处的货物调运数量,使总的运输费用最小。
解:设ijx 表示从第i 个仓库到第j 个客户的货物运量。
ij c表示从第i 个仓库到第j 个客户的单位货物运价,i a 表示第i 个仓库的最大供货量,j d 表示第j 个客户的订货量。
目标函数是使总运输费用最少,约束条件有三个:1、各仓库运出的货物总量不超过其库存数2、各客户收到的货物总量等于其订货数量3、非负约束数学模型为:∑∑===6181)(min i j ijij x c x f⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥===≤∑∑==08,,2,1,6,2,1,,..6181ij j i ij i j ij x j d x i a x t s 编程如下:model : Sets :Wh/w1..w6/:ai; Vd/v1..v8/:dj;links(wh,vd):c,x;endsetsData:ai=60,55,51,43,41,52;dj=35,37,22,32,41,32,43,38;c=6,2,6,7,4,2,5,94,9,5,3,8,5,8,25,2,1,9,7,4,3,37,6,7,3,9,2,7,12,3,9,5,7,2,6,55,5,2,2,8,1,4,3;EnddataMin=@sum(links(i,j):c(i,j)*x(i,j));@for(wh(i):@sum(vd(j):x(i,j))<=ai(i));@for(vd(j):@sum(wh(i):x(i,j))=dj(j));endGlobal optimal solution found.Objective value: 664.0000Total solver iterations: 0Variable Value Reduced Cost AI( W1) 60.00000 0.000000 AI( W2) 55.00000 0.000000 AI( W3) 51.00000 0.000000 AI( W4) 43.00000 0.000000 AI( W5) 41.00000 0.000000 AI( W6) 52.00000 0.000000 DJ( V1) 35.00000 0.000000 DJ( V2) 37.00000 0.000000 DJ( V3) 22.00000 0.000000 DJ( V4) 32.00000 0.000000 DJ( V5) 41.00000 0.000000 DJ( V6) 32.00000 0.000000 DJ( V7) 43.00000 0.000000 DJ( V8) 38.00000 0.000000 C( W1, V1) 6.000000 0.000000 C( W1, V2) 2.000000 0.000000 C( W1, V3) 6.000000 0.000000 C( W1, V4) 7.000000 0.000000 C( W1, V5) 4.000000 0.000000 C( W1, V6) 2.000000 0.000000 C( W1, V7) 5.000000 0.000000C( W2, V1) 4.000000 0.000000 C( W2, V2) 9.000000 0.000000 C( W2, V3) 5.000000 0.000000 C( W2, V4) 3.000000 0.000000 C( W2, V5) 8.000000 0.000000 C( W2, V6) 5.000000 0.000000 C( W2, V7) 8.000000 0.000000 C( W2, V8) 2.000000 0.000000 C( W3, V1) 5.000000 0.000000 C( W3, V2) 2.000000 0.000000 C( W3, V3) 1.000000 0.000000 C( W3, V4) 9.000000 0.000000 C( W3, V5) 7.000000 0.000000 C( W3, V6) 4.000000 0.000000 C( W3, V7) 3.000000 0.000000 C( W3, V8) 3.000000 0.000000 C( W4, V1) 7.000000 0.000000 C( W4, V2) 6.000000 0.000000 C( W4, V3) 7.000000 0.000000 C( W4, V4) 3.000000 0.000000 C( W4, V5) 9.000000 0.000000 C( W4, V6) 2.000000 0.000000 C( W4, V7) 7.000000 0.000000 C( W4, V8) 1.000000 0.000000 C( W5, V1) 2.000000 0.000000 C( W5, V2) 3.000000 0.000000 C( W5, V3) 9.000000 0.000000 C( W5, V4) 5.000000 0.000000 C( W5, V5) 7.000000 0.000000 C( W5, V6) 2.000000 0.000000 C( W5, V7) 6.000000 0.000000 C( W5, V8) 5.000000 0.000000 C( W6, V1) 5.000000 0.000000 C( W6, V2) 5.000000 0.000000 C( W6, V3) 2.000000 0.000000 C( W6, V4) 2.000000 0.000000 C( W6, V5) 8.000000 0.000000 C( W6, V6) 1.000000 0.000000 C( W6, V7) 4.000000 0.000000 C( W6, V8) 3.000000 0.000000 X( W1, V1) 0.000000 5.000000 X( W1, V2) 19.00000 0.000000 X( W1, V3) 0.000000 5.000000X( W1, V5) 41.00000 0.000000 X( W1, V6) 0.000000 2.000000 X( W1, V7) 0.000000 2.000000 X( W1, V8) 0.000000 10.00000 X( W2, V1) 1.000000 0.000000 X( W2, V2) 0.000000 4.000000 X( W2, V3) 0.000000 1.000000 X( W2, V4) 32.00000 0.000000 X( W2, V5) 0.000000 1.000000 X( W2, V6) 0.000000 2.000000 X( W2, V7) 0.000000 2.000000 X( W2, V8) 0.000000 0.000000 X( W3, V1) 0.000000 4.000000 X( W3, V2) 11.00000 0.000000 X( W3, V3) 0.000000 0.000000 X( W3, V4) 0.000000 9.000000 X( W3, V5) 0.000000 3.000000 X( W3, V6) 0.000000 4.000000 X( W3, V7) 40.00000 0.000000 X( W3, V8) 0.000000 4.000000 X( W4, V1) 0.000000 4.000000 X( W4, V2) 0.000000 2.000000 X( W4, V3) 0.000000 4.000000 X( W4, V4) 0.000000 1.000000 X( W4, V5) 0.000000 3.000000 X( W4, V6) 5.000000 0.000000 X( W4, V7) 0.000000 2.000000 X( W4, V8) 38.00000 0.000000 X( W5, V1) 34.00000 0.000000 X( W5, V2) 7.000000 0.000000 X( W5, V3) 0.000000 7.000000 X( W5, V4) 0.000000 4.000000 X( W5, V5) 0.000000 2.000000 X( W5, V6) 0.000000 1.000000 X( W5, V7) 0.000000 2.000000 X( W5, V8) 0.000000 5.000000 X( W6, V1) 0.000000 3.000000 X( W6, V2) 0.000000 2.000000 X( W6, V3) 22.00000 0.000000 X( W6, V4) 0.000000 1.000000 X( W6, V5) 0.000000 3.000000 X( W6, V6) 27.00000 0.000000 X( W6, V7) 3.000000 0.000000Row Slack or Surplus Dual Price 1 664.0000 -1.000000 2 0.000000 3.000000 3 22.00000 0.000000 4 0.000000 3.000000 5 0.000000 1.000000 6 0.000000 2.000000 7 0.000000 2.000000 8 0.000000 -4.000000 9 0.000000 -5.000000 10 0.000000 -4.000000 11 0.000000 -3.000000 12 0.000000 -7.000000 13 0.000000 -3.000000 14 0.000000 -6.000000 15 0.000000 -2.000000由以上结果可以清楚的看到由各仓库到各客户处的货物调运数量,由此得出的符合条件的最佳运货方案,而使运费最低,最低为664。
用lingo求解线性规划问题
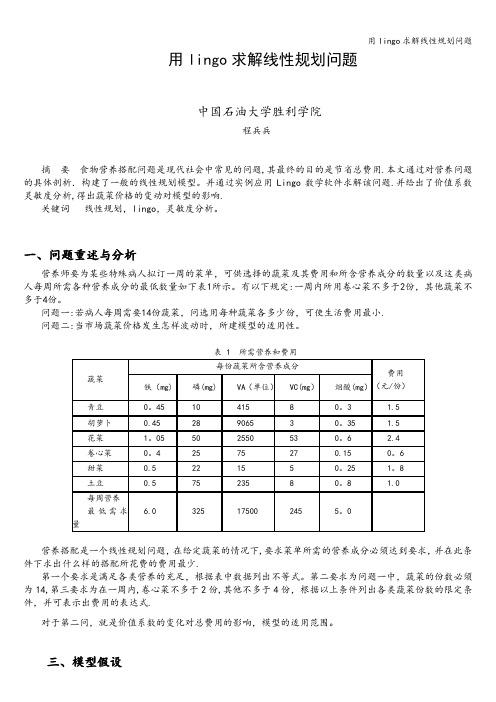
用lingo求解线性规划问题中国石油大学胜利学院程兵兵摘要食物营养搭配问题是现代社会中常见的问题,其最终的目的是节省总费用.本文通过对营养问题的具体剖析.构建了一般的线性规划模型。
并通过实例应用Lingo数学软件求解该问题.并给出了价值系数灵敏度分析,得出蔬菜价格的变动对模型的影响.关键词线性规划,lingo,灵敏度分析。
一、问题重述与分析营养师要为某些特殊病人拟订一周的菜单,可供选择的蔬菜及其费用和所含营养成分的数量以及这类病人每周所需各种营养成分的最低数量如下表1所示。
有以下规定:一周内所用卷心菜不多于2份,其他蔬菜不多于4份。
问题一:若病人每周需要14份蔬菜,问选用每种蔬菜各多少份,可使生活费用最小.问题二:当市场蔬菜价格发生怎样波动时,所建模型的适用性。
表 1 所需营养和费用营养搭配是一个线性规划问题,在给定蔬菜的情况下,要求菜单所需的营养成分必须达到要求,并在此条件下求出什么样的搭配所花费的费用最少.第一个要求是满足各类营养的充足,根据表中数据列出不等式。
第二要求为问题一中,蔬菜的份数必须为14,第三要求为在一周内,卷心菜不多于2份,其他不多于4份,根据以上条件列出各类蔬菜份数的限定条件,并可表示出费用的表达式.对于第二问,就是价值系数的变化对总费用的影响,模型的适用范围。
三、模型假设第一,假设各蔬菜营养成分保持稳定,满足题干要求。
第二,假设各蔬菜价格在一定时间内保持相对稳定。
第三,假设各类蔬菜供应全部到位,满足所需要求量. 第四,假设所求出最优解时不要求一定为整数。
四、符号约定(1)Z 代表目标函数,此题即为费用。
(2)i c 为价值系数,此题即为每份蔬菜的价格。
下标i 代表蔬菜的种类。
(3)i x 为决策变量,表示各种蔬菜的数量。
(4)i b 为最低限定条件,表示蔬菜最低营养需要。
五、模型建立根据以上各种假设和符号约定,建立模型如下。
所求的值就是min,也就是最优化结果.s 。
用Lingo求解整数(0-1)规划模型.

Lingo 程序: max=2*x1+5*x2+3*x3+4*x4;
-4*x1+x2+x3+x4>=0; -2*x1+4*x2+2*x3+4*x4>=1; x1+x2-x3+x4>=1; @bin(x1);@bin(x2);@bin(x3);@bin(x4);
温州大学城市学院
例 2 用Lingo软件求解整数规划问题 min z 2 x1 5 x2 3 x3
温州大学城市学院
注意:
Lingo 默认变量的取值从0到正无穷大,
变量定界函数可以改变默认状态.
@free(x): 取消对变量x的限制(即x可取任意实数值)
例 4 求函数 z x 2 y 2 的最小值.
2 2
温州大学城市学院 例 4 求函数 z x 2 y 2 的最小值.
,8
温州大学城市学院
温州大学城市学院
上机作业题
要求:
1、建立数学模型,
2、用lingo循环语句编写程序.
温州大学城市学院
上机作业题
人员安排问题
某城市的巡逻大队要求每天的各个时间段都有一 定数量的警员值班, 以便随时处理突发事件, 每人连续 工作6h, 中间不休息. 如表所示是一天8个班次所需值 班警员的人数情况统计:
成绩 甲 乙 丙 丁 自由泳 / s 56 63 57 55 蛙泳 / s 74 69 77 76 蝶泳 / s 61 65 63 62 仰泳 / s 63 71 67 62
甲, 乙, 丙, 丁 四名队员各自游什么姿势 , 才最有可能取得好成绩?
温州大学城市学院
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A 0.5 0.1 2.5
B 0.3 0.3 3.2
棉花库存量 300 180
甲绵(kg) 甲绵 乙绵(kg) 乙绵
利润( 利润(元/km) )
若利润指标为1755元,A种棉花要生产650km,问 A,B两种棉纱各应该生产多少?
目标规划模型:
设分别生产A、B两种棉纱x1, x 2km,则: min z = p d + p2 d
+ 5 11
− 12
+ 12
+ 7 13
Lingo代码
sets: cd/1..3/:a; xd/1..4/:b; links(cd,xd):c,x; px/1..13/:d1,d2; endsets data: a=300 200 400; b=200 100 450 250; c=5 2 6 7 3546 4 5 2 3; enddata min=d2(13); @for(cd(i):@sum(xd(j):x(i,j))=a(i)); @for(xd(j):@sum(cd(i):x(i,j))<=b(j)); x(1,4)+x(2,4)+x(3,4)+d1(4)-d2(4)=250; x(3,1)+d1(5)-d2(5)=100; @for(xd(j):@sum(cd(i):x(i,j))+d1(j+5)-d2(j+5)=b(j)*0.8); @sum(links(i,j):c(i,j)*x(i,j))+d1(10)-d2(10)=2950*1.1; x(2,4)+d1(11)-d2(11)=0; (x(1,1)+x(2,1)+x(3,1))-(200/450)*(x(1,3)+x(2,3)+x(3,3))+d1(12)-d2(12)=0; @sum(links(i,j):c(i,j)*x(i,j))+d1(13)-d2(13)=2950; y=@sum(links(i,j):c(i,j)*x(i,j)); d1(4)=0; d1(5)=0; d1(6)+d1(7)+d1(8)+d1(9)=0; d2(10)=115; d2(11)=0; d1(12)+d2(12)=30; d1(1)+d1(2)+d1(3)+d2(1)+d2(2)+d2(3)=0;
考虑目标规划:
供应约束: x11 + x12 + x13 + x14 ≤ 300 x 21 + x 22 + x 23 + x 24 ≤ 200 x31 + x32 + x33 + x34 ≤ 400
需求约束: x11 + x 21 + x31 ≤ 200 x12 + x 22 + x32 ≤ 100 x13 + x 23 + x33 ≤ 450
调运方案的总运费不超过最小费用的10%
− + cij xij +d10 − d10 = 2950 * (1 + 10%) ∑∑ i =1 j =1 3 4
因路段原因,尽量避免将A2的产品往B 4 x 24 + d − d = 0
给B1和B 2的供应率要相同
− + x11 + x 21 + x31 − (200 / 450)( x13 + x 23 + x33) + d12 − d12 = 0
−ij xij + d13 + d13 = 2950 ∑∑ i =1 j =1 3 4
目标函数:
− + min z = P d 4 + P2 d 5− + P3 (d 5− + d 6− + d 7− + d 8− ) + P4 d10 1
+ P d + P6 (d + d ) + P d
B 4的需求量必须全部满足:
− + x14 + x 24 + x34 + d 4 − d 4 = 250
A3向B1提供的产品不少于100 x31 + d 5− − d 5+ = 100
每个销地的供应量不小于其需求量的80%: x11 + x 21 + x31 + d 6− − d 6+ = 200 * 0.8 x12 + x 22 + x32 + d 7− − d 7+ = 100 * 0.8 x13 + x 23 + x33 + d8− − d8+ = 450 * 0.8 x14 + x 24 + x34 + d 9− − d 9+ = 250 * 0.8
不考虑目标,运输问题的数学模型为:
设xij 表示从第i个产地向第j个销地的运量。则: min z = ∑∑ cij xij
i =1 j =1 3 4
∑x
j =1 3
4
ij
= ai , i = 1,2,3 ≤ b j , j = 1,2,3,4
∑x
i =1
ij
xij ≥ 0
Lingo代码:
sets: cd/1..3/:a; xd/1..4/:b; links(cd,xd):c,x; endsets data: a=300 200 400; b=200 100 450 250; c=5 2 6 7 3546 4 5 2 3; enddata min=@sum(links(i,j):c(i,j)*x(i,j)); @for(cd(i):@sum(xd(j):x(i,j))<=a(i)); @for(xd(j):@sum(cd(i):x(i,j))>=b(j));
整数线性规划的几种类型
纯整数线性规划 混合整数线性规划 0-1型整数线性规划
例:
max z = 20 x1 + 10 x 2 5 x1 + 4 x 2 ≤ 24 2 x1 + 5 x 2 ≤ 13 s.t. x1, x 2 ≥ 0 x1, x 2取整数
不考虑整数约束时求解
Lingo解目标规划
方法:按目标的优先级次序,依次用lingo 求解。每次求得的值再作为下一次的约束条 件。
例1:求解下列目标规划
− + min z = p1d1+ + p2 (d 2 + d 2 ) + p3 d 3−
2 x1 + x 2 ≤ 11 x1 − x 2 + d − − d + = 0 1 1 − + s.t. x1 + 2 x 2 + d 2 − d 2 = 10 8 x1 + 10 x 2 + d − − d + = 56 3 3 x1, x 2, d i+ − ≥ 0
max=20*x1+10*x2; 5*x1+4*x4<=24; 2*x1+5*x2<=13; 可以解得: X1=4.8 x2=0 最优解为z=96 X1的取值不是整数?!怎么办???
对x1 化整: 取x1=5,x2=0:无可行解。 取x1=4,x2=0:可行解,z=80; 是最优解吗? x1=4,x2=1:可行解,z=90; 因此简单对决策变量化整是不能解决整数问题 的,有必要讨论整数规划的解决方法。
整数线性规划一般形式: 整数线性规划一般形式:
max(min)
n
z =
∑
n
j =1
c jx
j
L L (a )
L L (b ) ∑ a ij x j ≤ ( = , ≥ ) b i j =1 L L (c ) xj ≥ 0 x , x , L , x 中部分或全部取整数L L ( d ) n 1 2
有关部门在研究调运方案时依次考虑以下七项目标, 并规定其相应的优先等级: P1-B4是重点保证单位,必须全部满足其需求; P2-A3向B1提供的产量不少于100; P3-每个销地供应量不小于其需要的80%; P4-所订调运方案的总运费不超过最小运费的10%; P5-因路段问题,尽量避免安排将A2产品往B4; P6-给B1,B2的供应率要相同; P7-力求总运费最省。 试求满意的调运方案?
注:
关于算法的复杂性问题:P112? 度量方法: 当问题的规模为n时,利用该算法求解此 问题需要做的加减乘除四则运算的次数。
整数规划
1.整数规划的数学模型及解的特点 2.分支定界法、割平面法 3.0-1整数规划 4.指派问题
1.整数规划问题的提出
整数规划数学模型的一般形式 一部分或全部决策变量取整数值的规划问题 ——整数规划 整数规划中不考虑整数条件是对应的规划问题 ——该整数规划的松弛问题 松弛问题为线性规划的整数规划问题 ——整数线性规划
− 1 − 2 + 1 + 2 − 1 1 + 2 − 3 − 4
Lingo代码
min=2*d31+d41; x1+x2+d11-d12=40; x1+x2+d21-d22=50; x1+d31-d32=24; x2+d41-d42=30; d11=0; d22=0;
例3:某棉纺车间用甲乙两种棉花混纺生产A、B两种 棉纱,其相关数据如下表:
Lingo代码
min=d31; 2*x1+x2<=11; x1-x2+d11-d12=0; x1+2*x2+d21-d22=10; 8*x1+10*x2+d31-d32=56; d12=0; d21+d22=0;
