一个使用Lingo求解多目标0-1整数规划问题答案
一个使用Lingo求解多目标0-1整数规划问题答案
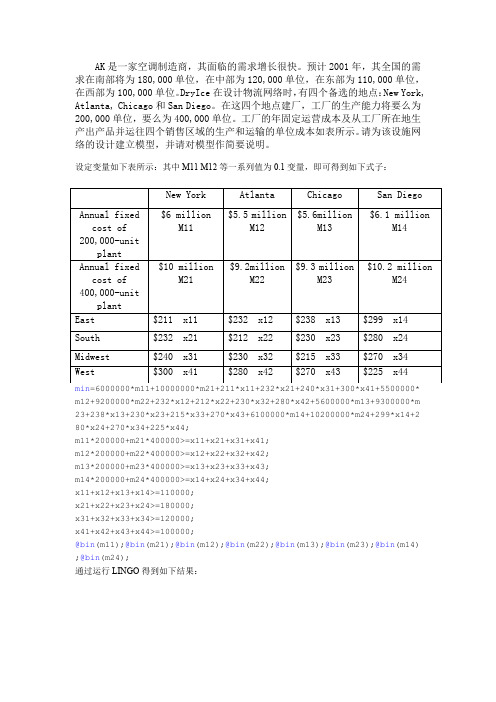
AK是一家空调制造商,其面临的需求增长很快。
预计2001年,其全国的需求在南部将为180,000单位,在中部为120,000单位,在东部为110,000单位,在西部为100,000单位。
DryIce在设计物流网络时,有四个备选的地点:New York, Atlanta, Chicago和San Diego。
在这四个地点建厂,工厂的生产能力将要么为200,000单位,要么为400,000单位。
工厂的年固定运营成本及从工厂所在地生产出产品并运往四个销售区域的生产和运输的单位成本如表所示。
请为该设施网络的设计建立模型,并请对模型作简要说明。
设定变量如下表所示:其中M11 M12等一系列值为0.1变量,即可得到如下式子:m12+9200000*m22+232*x12+212*x22+230*x32+280*x42+5600000*m13+9300000*m 23+238*x13+230*x23+215*x33+270*x43+6100000*m14+10200000*m24+299*x14+2 80*x24+270*x34+225*x44;m11*200000+m21*400000>=x11+x21+x31+x41;m12*200000+m22*400000>=x12+x22+x32+x42;m13*200000+m23*400000>=x13+x23+x33+x43;m14*200000+m24*400000>=x14+x24+x34+x44;x11+x12+x13+x14>=110000;x21+x22+x23+x24>=180000;x31+x32+x33+x34>=120000;x41+x42+x43+x44>=100000;@bin(m11);@bin(m21);@bin(m12);@bin(m22);@bin(m13);@bin(m23);@bin(m14);@bin(m24);通过运行LINGO得到如下结果:Global optimal solution found.Objective value: 0.1294800E+09Extended solver steps: 0Total solver iterations: 131Variable Value Reduced CostM11 0.000000 -6200000.M21 0.000000 -0.1440000E+08 X11 0.000000 0.000000X21 0.000000 41.00000X31 0.000000 31.00000X41 0.000000 136.0000M12 0.000000 -2500000.M22 1.000000 -6800000.X12 110000.0 0.000000X22 180000.0 0.000000X32 110000.0 0.000000X42 0.000000 95.00000M13 0.000000 -5400000.M23 0.000000 -0.1270000E+08 X13 0.000000 21.00000X23 0.000000 33.00000X33 0.000000 0.000000X43 0.000000 100.0000M14 1.000000 6100000.M24 0.000000 0.1020000E+08 X14 0.000000 27.00000X24 0.000000 28.00000X34 10000.00 0.000000X44 100000.0 0.000000Row Slack or Surplus Dual Price1 0.1294800E+09 -1.0000002 0.000000 -61.000003 0.000000 -40.000004 0.000000 -55.000005 90000.00 0.0000006 0.000000 -272.00007 0.000000 -252.00008 0.000000 -270.00009 0.000000 -225.0000如下表:总成本为:$129480000。
0-1规划在各种实际问题中的应用以及lingo求解

势,才最有可能取得好成绩?
姿势 成绩
队员
自由泳
蛙泳
蝶泳
仰泳
A B
56 63
74 69
61 65
63 71
C
D
57
55
77
76
63
62
67
62
• 假设问题的决策变量 1 , 第i名运动员游第j种姿势 xij= 0 , 第i名运动员不游第j种姿势
四名运动员的成绩矩阵aij=
56 63 57 55
74 69 77 76
280 30 200
400 40 300
5 1 4
3 0.5 2
300 300 300
• 三种服装的利润分别为120元、10元、100元.
• 设xi表示生成第i(i=1,2,3)种服装的数量,yi表示是否 生产第i种服装. 生产第 i种 服 装 1, yi i种 服 装 0, 不 生 产 第
即甲完成B任务,乙完成D任务,丙完成E任务,丁完成A任务 总用时105分钟.
• 第(2)题,按照指派模型,可添加一个虚拟完
成人戊.而实际上,戊所完成任务还是由甲乙
丙丁完成的.
• 为了保证时间最少,戊完成各项任务的时间,
就取完成各任务所需时间最短人的时间.
• 若戊完成哪项任务,则那项任务所需时间最
短人来完成.
建立i污水厂 1, yi 0,不建立i污水厂
min z=0.03x1+0.03x2+0.04x3+400y1+300y2+250y3 80x1+50x2+40x3≥80000 60x1+40x2+50x3≥60000 x1≤800y1 s.t. x2≤500y2 x3≤400y3 xi≥0 yi=0或1
用Lingo求解整数(0-1)规划模型

1、建立数学模型, 2、用lingo循环语句编写程序.
上机作业题 人员安排问题
某城市的巡逻大队要求每天的各个时间段都有一
定数量的警员值班, 以便随时处理突发事件, 每人连续 工作6h, 中间不休息. 如表所示是一天8个班次所需值 班警员的人数情况统计:
班次
时间段
人数 班次
时间段
人数
1
6:00~9:00
例 4 求函数 z x 22 y 22 的最小值.
例 4 求函数 z x 22 y 22 的最小值.
解: 编写Lingo 程序如下:
min=(x+2)^2+(y-2)^2; @free(x); 求得结果: x=-2, y=2
二、Lingo 循环编程语句
(1) 集合的定义 包括如下参数: 1) 集合的名称.
12,8 3,0; enddata
!数据赋值;
max=@sum(bliang(i):a(i)*x(i)); !目标函数;
@for(yshu(j):@sum(bliang(i):x(i)*c(j,i))<=b(j));
!约束条件;
例6:人员选拔问题
队员号码 身高 / m 位置 队员号码 身高 / m 位置
例 2 用Lingo软件求解整数规划问题
min z 2 x1 5 x2 3 x3
4 x1 x2 x3 0
2
x1
4 x2
2 x3
2
x1
x2
x3
2
xi 0 且取整数, i 1, 2, 3
Lingo 程序:
min=2*x1+5*x2+3*x3; -4*x1-x2+x3>=0; -2*x1+4*x2-2*x3>=2; x1-x2+x3>=2; @gin(x1);@gin(x2);@gin(x3);
用LINGO求解整数规划

用LINGO求解整数规划在LINGO中,输入总是以model:开始,以end结束;中间的语句之间必须以“;”分开;LINGO不区分字母的大小写;目标函数用MAX=…;或MIN=…;给出(注意有等号“=”)。
在LINDO中所有的函数均以“@”符号开始,如约束中@gin(x1)表示x1为整数,用@bin(x1)表示x1为0-1整数。
在现在的LINDO中,默认设置假定所有变量非负。
函数中变量的界定:@GIN(X):限制X为整数@BIN(X):限定变量X为0 或1。
@FREE(X):取消对x的符号限制(即可取任意实数包括负数)@BND(L,X,U):限制L<= X <= ULINGO提供了大量的标准数学函数:@abs(x) 返回x的绝对值@sin(x) 返回x的正弦值,x采用弧度制@cos(x) 返回x的余弦值@tan(x) 返回x的正切值@exp(x) 返回常数e的x次方@log(x) 返回x的自然对数@lgm(x) 返回x的gamma函数的自然对数@sign(x) 如果x<0返回-1;否则,返回1@smax(x1,x2,…,xn) 返回x1,x2,…,xn中的最大值@smin(x1,x2,…,xn) 返回x1,x2,…,xn中的最小值例1:整数规划模型在LINGO中可以如下输入:model:Max=5*x1+8*x2;!*号不能省略x1+x2<=6;!约束条件和目标函数可以写在model:与end之间的任何位置5*x1<=45-9*x2;@gin(x1);@gin(x2); !和LINDO不同,不能写在end之后end运行后同样得到最优解为x1=0,x2=5,最优值为40。
例2:在线性规划中的应用max Z =5X1+3X2+6X3,s.t.X1 +2 X2 + X3 ≤182 X1 + X2 +3 X3 =16X1 + X2 + X3 =10X1 ,X2 ≥0 , X3 为自由变量应用LINGO 来求解该模型,只需要在 lingo窗口中输入以下信息即可:max=5*x1+3*x2+6*x3;x1+2*x2+x3<=18;2*x1+x2+3*x3=16;x1+x2+x3=10;@free(x3);然后按运行按钮,得到模型最优解,具体如下:Objective value: 46.00000Variable Value Reduced Costx1 14.00000 0.000000x2 0.000000 1.000000x3 -4 .000000 0.000000由此可知,当 x1 =14 , x2 =0 , x3 =-4 时,模型得到最优值,且最优值为 46。
Lingo精选题目及参考答案

Lingo 精选题目及答案答题要求:将Lingo 程序复制到Word 文档中,并且附上最终结果。
1、简单线性规划求解(目标函数)2134maxx x z += s.t.(约束条件)⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0,781022122121x x x x x x x2、整数规划求解219040Max x x z +=⎪⎩⎪⎨⎧≥≤+≤+0,702075679212121x x x x x x 3、0-1规划求解Max 432215.18.04.0x x x x f +++=10106234321≤+++x x x x10,,,4321或=x x x x4、非线性规划求解||4||3||2||min 4321x x x x z +++=s.t. ⎪⎪⎩⎪⎪⎨⎧-=+--=-+-=+--2132130432143214321x x x x x x x x x x x x5、集合综合应用产生一个集合5052--=x x y ,(10,...,2,1=x ),求y 前6个数的和S 1,后6个数的和S 2,第2~8个数中的最小值S 3,最大值S 4。
6、综合题要求列出具体的目标函数和约束条件,然后附上Lingo 程序和最终结果。
6.1 指派问题有四个工人,要指派他们分别完成4项工作,每人做各项工作所消耗的时间如下表:问指派哪个人去完成哪项工作,可使总的消耗时间为最小?6.2 分配问题某两个煤厂A1,A2每月进煤数量分别为60t和100t,联合供应3个居民区B1,B2,B3。
3个居民区每月对煤的需求量依次分别为50t,70t,40t,煤厂A1离3个居民区B1,B2,B3的距离依次分别为10km,5km,6km,煤厂A2离3个居民区B1,B2,B3的距离分别为4km,8km,12km。
问如何分配供煤量使得运输量(即t·km)达到最小?1、model:max=4*x1+3*x2;2*x1+x2<10;x1+x2<8;x2<7;end2、model:max=40*x1+90*x2;9*x1+7*x2<56;7*x1+20*x2<70;@gin(x1);@gin(x2);end3、model:max=x1^2+0.4*x2+0.8*x3+1.5*x4;3*x1+2*x2+6*x3+10*x4<10;@bin(x1); @bin(x2);@bin(x3); @bin(x4);end4、model:max=@abs(x1)+2*@abs(x2)+3*@abs(x3)+4*@abs(x4);x1-x2-x3+x4=0;x1-x2+x3-3*x4=1;x1-x2-2*x3+3*x4=-1/2;end5、model:sets:jihe/1..10/:y;ss/1..4/:S;endsets!由于y和s中部分有负数,所以要先去掉这个约束;@for(jihe:@free(y));@for(ss(i):@free(S));!产生元素;@for (jihe(x):y(x)=x^2-5*x-50); S(1)=@sum (jihe(i)|i#le#6:y(i)); S(2)=@sum (jihe(i)|i#ge#5:y(i));S(3)=@min (jihe(i)|i#ge#2 #and# i#le#8:y(i)); S(4)=@max (jihe(i)|i#ge#2 #and# i#le#8:y(i)); end6.1、设:第i 个工人做第j 项工作用时ij t ,标志变量ij f 定义如下:⎩⎨⎧=其他件工作个工人去做第指派第01j i f ijmin∑∑==⨯4141i j ij ijt fs.t. 141=∑=i ijf()4,3,2,1=j 每份工作都有一人做∑==411j ijf()4,3,2,1=i 每人都只做一项工作model : sets :work/A B C D/;worker/jia yi bing ding/; time(worker,work):t,f; endsets!目标函数可以用[obj]标志出,也可以省略;[obj] min =@sum (time(i,j):t(i,j)*f(i,j)); data :!可以直接复制表格,但是在最后要有分号; t=; e !每份工作都有一人做;@for (work(j):@sum (time(i,j):f(i,j))=1); !每人都只做一项工作;@for (worker(i):@sum (time(i,j):f(i,j))=1); !让f 取0-1值,此条件可以省略;!@for(time(i,j):@bin(f(i,j))); end6.2设:煤厂进煤量i s ,居民区需求量为i d ,煤厂i 距居民区j 的距离为ij L ,煤厂i 供给居民区j 的煤量为ij g那么可以列出如下优化方程式∑∑==⨯=3121min j i ij ij L gs.t ()3,2,121==∑=j d gi jij()2,131=≤∑=i s gj iijmodel : sets :supply/1,2/:s; demand/1,2,3/:d;link(supply,demand):road,sd; endsets data :road=10 5 6 4 8 12; d=50 70 40; s=60 100; enddata[obj] min =@sum (link(i,j):road(i,j)*sd(i,j)); @for (demand(i):@sum (supply(j):sd(j,i))=d(i)); @for (supply(i):@sum (demand(j):sd(i,j))<s(i));end1.线性规划模型。
用Lingo求解整数(0-1)规划模型.

Lingo 程序: max=2*x1+5*x2+3*x3+4*x4;
-4*x1+x2+x3+x4>=0; -2*x1+4*x2+2*x3+4*x4>=1; x1+x2-x3+x4>=1; @bin(x1);@bin(x2);@bin(x3);@bin(x4);
温州大学城市学院
例 2 用Lingo软件求解整数规划问题 min z 2 x1 5 x2 3 x3
温州大学城市学院
注意:
Lingo 默认变量的取值从0到正无穷大,
变量定界函数可以改变默认状态.
@free(x): 取消对变量x的限制(即x可取任意实数值)
例 4 求函数 z x 2 y 2 的最小值.
2 2
温州大学城市学院 例 4 求函数 z x 2 y 2 的最小值.
,8
温州大学城市学院
温州大学城市学院
上机作业题
要求:
1、建立数学模型,
2、用lingo循环语句编写程序.
温州大学城市学院
上机作业题
人员安排问题
某城市的巡逻大队要求每天的各个时间段都有一 定数量的警员值班, 以便随时处理突发事件, 每人连续 工作6h, 中间不休息. 如表所示是一天8个班次所需值 班警员的人数情况统计:
成绩 甲 乙 丙 丁 自由泳 / s 56 63 57 55 蛙泳 / s 74 69 77 76 蝶泳 / s 61 65 63 62 仰泳 / s 63 71 67 62
甲, 乙, 丙, 丁 四名队员各自游什么姿势 , 才最有可能取得好成绩?
温州大学城市学院
用Lingo软件编程求解规划问题

x2桶牛奶生产A2 获利 16×4 x2
Max z 72 x1 64 x2
x1 x2 50
12 x1 8x2 480 3x1 100
x1, x2 0
线性规 划模型 (LP)
例1——加工奶制品的生产计划
x1 x2 50
12
x1 8x2 480 3x1 100
Lingo软件——基本集合元素的列举
一个原始集是由一些最基本的对象组成的。 setname [/member_list/] [: attribute_list];
sets: students/John Jill, Rose Mike/: sex, age;
endsets
集、集成员和集属性
• 集成员无论用何种字符标记,它的索引都是 从1开始连续计数。
ij
8
j 1
N Nij
V
i
i 1, ,6,j 1, ,8, i 1, ,6,
N 6
i1 ij
d
j
j 1, ,8.
结果
Lingo软件
Lingo 是一个可以简洁地阐述、解决和分析复杂问题的简便工具。
其特点是程序执行速度很快,易于输入、修改、求解和分析一个数 学规划问题。
N 6
i1 ij
d
j
j 1, ,8.
corps
需求量 35 37 22 32 41 32 43 38
拥有量
60 55 51 depot 43 41 52
B1 B2 B3 B4 B5 B6 B7 B8
A1
62674259
A2
49538582
Lingo精选题目及答案

Lingo精选题目及答案Lingo 精选题目及答案答题要求:将Lingo 程序复制到Word 文档中,并且附上最终结果。
1、简单线性规划求解(目标函数)2134m axx x z += s.t.(约束条件)≥≤≤+≤+0,781022122121x x x x x x x2、整数规划求解219040Maxx x z +=≥≤+≤+0,702075679212121x x x x x x 3、0-1规划求解Max 432215.18.04.0x x x x f +++=10106234321≤+++x x x x10,,,4321或=x x x x4、非线性规划求解||4||3||2||m in4321x x x x z +++=s.t.-=+--=-+-=+--2132130432143214321x x x x x x x x x x x x5、集合综合应用产生一个集合5052--=x x y ,(10,...,2,1=x ),求y 前6个数的和S 1,后6个数的和S 2,第2~8个数中的最小值S 3,最大值S 4。
6、综合题要求列出具体的目标函数和约束条件,然后附上Lingo 程序和最终结果。
6.1 指派问题问指派哪个人去完成哪项工作,可使总的消耗时间为最小?6.2 分配问题某两个煤厂A1,A2每月进煤数量分别为60t和100t,联合供应3个居民区B1,B2,B3。
3个居民区每月对煤的需求量依次分别为50t,70t,40t,煤厂A1离3个居民区B1,B2,B3的距离依次分别为10km,5km,6km,煤厂A2离3个居民区B1,B2,B3的距离分别为4km,8km,12km。
问如何分配供煤量使得运输量(即t·km)达到最小?1、model:max=4*x1+3*x2;2*x1+x2<10;x1+x2<8;x2<7;end2、model:max=40*x1+90*x2;9*x1+7*x2<56;7*x1+20*x2<70;@gin(x1);@gin(x2);end3、model:max=x1^2+0.4*x2+0.8*x3+1.5*x4;3*x1+2*x2+6*x3+10*x4<10;@bin(x1); @bin(x2);@bin(x3); @bin(x4);end4、model:max=@abs(x1)+2*@abs(x2)+3*@abs(x3)+4*@abs(x4);x1-x2-x3+x4=0;x1-x2+x3-3*x4=1;x1-x2-2*x3+3*x4=-1/2;end5、model:sets:jihe/1..10/:y;ss/1..4/:S;endsets!由于y和s中部分有负数,所以要先去掉这个约束;@for(jihe:@free(y));@for (ss(i):@free (S));!产生元素;@for (jihe(x):y(x)=x^2-5*x-50); S(1)=@sum (jihe(i)|i#le#6:y(i)); S(2)=@sum (jihe(i)|i#ge#5:y(i));S(3)=@min (jihe(i)|i#ge#2 #and# i#le#8:y(i)); S(4)=@max (jihe(i)|i#ge#2 #and# i#le#8:y(i)); end6.1、设:第i 个工人做第j 项工作用时ij t ,标志变量ij f 定义如下:=其他件工作个工人去做第指派第01j i f ijmin∑∑==?4141i j ij ijt fs.t. 141=∑=i ijf()4,3,2,1=j 每份工作都有一人做∑==411j ijf()4,3,2,1=i 每人都只做一项工作model : sets :work/A B C D/;worker/jia yi bing ding/; time(worker,work):t,f; endsets!目标函数可以用[obj]标志出,也可以省略;[obj] min =@sum (time(i,j):t(i,j)*f(i,j)); data :!可以直接复制表格,但是在最后要有分号; t=; e nddata!每份工作都有一人做;@for (work(j):@sum (time(i,j):f(i,j))=1); !每人都只做一项工作;@for (worker(i):@sum (time(i,j):f(i,j))=1); !让f 取0-1值,此条件可以省略;!@for(time(i,j):@bin(f(i,j))); end6.2设:煤厂进煤量i s ,居民区需求量为i d ,煤厂i 距居民区j 的距离为ij L ,煤厂i 供给居民区j 的煤量为ij g那么可以列出如下优化方程式∑∑==?=3121min j i ij ij L gs.t ()3,2,121==∑=j d gi jij()2,131=≤∑=i s gj iijmodel : sets :supply/1,2/:s; demand/1,2,3/:d;link(supply,demand):road,sd; endsets data :road=10 5 6 4 8 12; d=50 70 40; s=60 100; enddata[obj] min =@sum (link(i,j):road(i,j)*sd(i,j)); @for (demand(i):@sum (supply(j):sd(j,i))=d(i)); @for (supply(i):@sum (demand(j):sd(i,j))<s(i));< p="">end1.线性规划模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AK是一家空调制造商,其面临的需求增长很快。
预计2001年,其全国的需求在南部将为180,000单位,在中部为120,000单位,在东部为110,000单位,在西部为100,000单位。
DryIce在设计物流网络时,有四个备选的地点:New York, Atlanta, Chicago和San Diego。
在这四个地点建厂,工厂的生产能力将要么为200,000单位,要么为400,000单位。
工厂的年固定运营成本及从工厂所在地生产出产品并运往四个销售区域的生产和运输的单位成本如表所示。
请为该设施网络的设计建立模型,并请对模型作简要说明。
设定变量如下表所示:其中M11 M12等一系列值为0.1变量,即可得到如下式子:
m12+9200000*m22+232*x12+212*x22+230*x32+280*x42+5600000*m13+9300000*m 23+238*x13+230*x23+215*x33+270*x43+6100000*m14+10200000*m24+299*x14+2 80*x24+270*x34+225*x44;
m11*200000+m21*400000>=x11+x21+x31+x41;
m12*200000+m22*400000>=x12+x22+x32+x42;
m13*200000+m23*400000>=x13+x23+x33+x43;
m14*200000+m24*400000>=x14+x24+x34+x44;
x11+x12+x13+x14>=110000;
x21+x22+x23+x24>=180000;
x31+x32+x33+x34>=120000;
x41+x42+x43+x44>=100000;
@bin(m11);@bin(m21);@bin(m12);@bin(m22);@bin(m13);@bin(m23);@bin(m14)
;@bin(m24);
通过运行LINGO得到如下结果:
Global optimal solution found.
Objective value: 0.1294800E+09
Extended solver steps: 0
Total solver iterations: 131
Variable Value Reduced Cost
M11 0.000000 -6200000.
M21 0.000000 -0.1440000E+08 X11 0.000000 0.000000
X21 0.000000 41.00000
X31 0.000000 31.00000
X41 0.000000 136.0000
M12 0.000000 -2500000.
M22 1.000000 -6800000.
X12 110000.0 0.000000
X22 180000.0 0.000000
X32 110000.0 0.000000
X42 0.000000 95.00000
M13 0.000000 -5400000.
M23 0.000000 -0.1270000E+08 X13 0.000000 21.00000
X23 0.000000 33.00000
X33 0.000000 0.000000
X43 0.000000 100.0000
M14 1.000000 6100000.
M24 0.000000 0.1020000E+08 X14 0.000000 27.00000
X24 0.000000 28.00000
X34 10000.00 0.000000
X44 100000.0 0.000000
Row Slack or Surplus Dual Price
1 0.1294800E+09 -1.000000
2 0.000000 -61.00000
3 0.000000 -40.00000
4 0.000000 -55.00000
5 90000.00 0.000000
6 0.000000 -272.0000
7 0.000000 -252.0000
8 0.000000 -270.0000
9 0.000000 -225.0000
如下表:
总成本为:$129480000。
