数字信号处理教程(第三版)程佩青清华大学出版社(精)
合集下载
《数字信号处理教程》程佩青(第三版)清华大学出版社课后答案
结果 y (n ) 中变量是 n ,
∞
∞
∑ ∑ y (n ) =
x ( m )h (n − m ) =
h(m)x(n − m) ;
m = −∞
m = −∞
②分为四步 （1）翻褶（ -m ），（2）移位（ n ）,（3）相乘，
（4）相加，求得一个 n 的 y(n) 值 ，如此可求得所有 n 值的 y(n) ;
10
T [ax1(n)+ bx2 (n)] =
n
∑
[ax1
(n
)
+
bx2
(n
)]
m = −∞
T[ax1(n) + bx2(n)] = ay1(n) + by2(n)
∴ 系统是线性系统
解：(2) y(n) =
[x(n )] 2
y1(n)
= T [x1(n)] = [x1(n)] 2
y2 (n) = T [x2 (n)] = [x2 (n)] 2
(3) y(n) = δ (n − 2) * 0.5n R3(n) = 0.5n−2 R3(n − 2) (4) x(n) = 2n u(−n −1) h(n) = 0.5n u(n)
当n ≥ 0 当n ≤ −1
∑ y(n) = −1 0.5n−m 2m = 1 ⋅ 2−n
m = −∞
3
y(n) = ∑n 0.5n−m 2m = 4 ⋅ 2n
+ 1)
−
x1 (n
+ 1)]
=
−a n
综上 i) , ii) 可知： y1 (n) = −a nu(−n − 1)
(b) 设 x(n) = δ (n − 1)
i)向 n > 0 处递推 ，
数字信号处理程佩青第三版课件(全套课件)
j0n
M 0, 1, 2
表明复指数序列具有以2为周期的周期性，在 以后的研究中，频率域只考虑一个周期就够了。
7. 周期序列
如果对所有n存在一个最小的正整数N，使下面等
式成立： x(n) x(n N)
则称x(n)为周期序列，最小周期为N。
例：
x(n) sin( n)
4
x(n) sin[ (n 8)],
4
N 8
一般正弦序列的周期性
设 x(n) Asin( 0n )
式中，A为幅度，ω0为数字域频率，为初相。
那么 x(n N ) Asin[ 0 (n N ) ] Asin( 0n 0N )
如果 x(n) x(n N)
则 Asin( 0n ) Asin[ 0 (n N) ]
N (2 /0 )k N，k均取整数
xa(t) 0
xa(nT)
t
2T
0
t
T
这里 n 取整数。对于不同的 n 值，xa(nT) 是 一个有序的数字序列，该数字序列就是离散时间信 号。注意，这里的n取整数，非整数时无定义，另 外，在数值上它等于信号的采样值，即
x(n) xa (nT ), n
离散时间信号的表示方法：公式表示法、图形 表示法、集合符号表示法，如
线性卷积的计算
y(n) x(m)h(n m) x(n) h(n) m
计算它们的卷积的步骤如下： (1)折叠：先在哑变量坐标轴k上画出x(k)和
h(k)，将h(k)以纵坐标为对称轴折叠成 h(-k)。 (2)移位：将h(-k)移位n，得h(n-k)。当n为
正数时，右移n；当n为负数时，左移n。 (3)相乘：将h(n-k)和x(k)的对应取样值相乘。 (4)相加：把所有的乘积累加起来，即得y(n)。
数字信号处理程佩青第三版课件第五章数字滤波器的基本结构
N
M
y(n) aky(nk) bkx(nk)
k1
k0
1、直接 I 型
x(n)
b0
y(n) 结构特点：
1/z b1
a1 1/z
直接实现
1/z b2
a2 1/z
第一个网络实现零点
1/z
1/z
...
1/z bN
aN 1/z
第二个网络实现极点 N+M个时延单元
2、直接II型:典范型
H(z)Y X((zz))H （ 1z） H （ 2 z） H （ 2 z） H （ 1z）
H(z)
k0 N
AkN 1 1
k1 N2
1 akzk
(1ckz1) (1dkz1)(1dk*z1)
k1
k1
k1
A为常数
M M 12M 2
p k 和 c k 分 别 为 实 数 零 、 极 点NN 12N 2
q k , q k * 和 d k , d k * 分 别 为 复 共 轭 零 、 极 点1/z Nhomakorabea11
11
1/z
21
21
特点: 方便调整极点，不便
于调整零点；部分分式展 开计算量大。
1/z
1M
1M
1/z
2M
2M
IIR滤波器结构表示举例
例：用典范型和一阶级联型、并联型实现方程：
y (n ) x (n ) 1 x (n 1 ) 3 y (n 1 ) 1 y (n 2 )
3
4
8
解：正准型、一阶级联和并联的系统函数表示：
结构：将分解为一阶及二阶系统的串联，每级 子系统都用典范型实现。
H ( z ) H 1 ( z ) H 2 ( z ).H .M .( z )
数字信号处理教程 (第三版)程佩青 清华大学出版社dsp-ch5-1
3）存在输出到输入的反馈，递归型结构
X
第
二、有限阶IIR的表达式：
（其中至少有一个 ak≠0）
Y ( z) 系统函数： H ( z ) X ( z)
N
10 页
bk z k 1 ak z k
k 1
M
M
k 0 N
差分方程： y ( n ) ak y ( n k ) bk x (n k )
2、直接Ⅱ型（典范型）
13 页
只需实现N阶滤波器所需的最少的N个延时单元， 故称典范型。（ N M ）
X
第
14 页
直接Ⅰ型与直接Ⅱ型结构比较
1)直接Ⅰ型需要一个相加器，而直接Ⅱ型 需要两个相加器； 2)直接Ⅱ型需要的延迟器比直接Ⅰ型少， 因此所需的存储单元少；
3)从节约存储单元的角度来看，直接Ⅱ型
第
18 页
X
第
19 页
N 1 当M=N时，二阶因子配对方式有 ! 种 2 N 1 各二阶基本节的排列次序有 ! 种 2
X
第
级联型的特点：
20 页
• 调整系数 1k， 2k能单独调整滤波器的第k对零点， 而不影响其它零极点 调整系数1k ， 2k 能单独调整滤波器的第k对极点， 而不影响其它零极点
方框图
流图
z
1
z
1
a
a
X
第 5 页
x(n)
z
-1
x(n-1)
x(n)
z -1
x(n-1)
支路増益
x(n)
x(n)
ax(n)
a x1(n)
a
网络 节点
ax(n)
源节点
X
第
二、有限阶IIR的表达式：
（其中至少有一个 ak≠0）
Y ( z) 系统函数： H ( z ) X ( z)
N
10 页
bk z k 1 ak z k
k 1
M
M
k 0 N
差分方程： y ( n ) ak y ( n k ) bk x (n k )
2、直接Ⅱ型（典范型）
13 页
只需实现N阶滤波器所需的最少的N个延时单元， 故称典范型。（ N M ）
X
第
14 页
直接Ⅰ型与直接Ⅱ型结构比较
1)直接Ⅰ型需要一个相加器，而直接Ⅱ型 需要两个相加器； 2)直接Ⅱ型需要的延迟器比直接Ⅰ型少， 因此所需的存储单元少；
3)从节约存储单元的角度来看，直接Ⅱ型
第
18 页
X
第
19 页
N 1 当M=N时，二阶因子配对方式有 ! 种 2 N 1 各二阶基本节的排列次序有 ! 种 2
X
第
级联型的特点：
20 页
• 调整系数 1k， 2k能单独调整滤波器的第k对零点， 而不影响其它零极点 调整系数1k ， 2k 能单独调整滤波器的第k对极点， 而不影响其它零极点
方框图
流图
z
1
z
1
a
a
X
第 5 页
x(n)
z
-1
x(n-1)
x(n)
z -1
x(n-1)
支路増益
x(n)
x(n)
ax(n)
a x1(n)
a
网络 节点
ax(n)
源节点
数字信号处理程佩青第三版课件第三章离散付氏变换-1
解 法 一 ： 数 值 解
N1
X(k) x(n)WNnk
n0
7
3
x(n)W8nk
W
n 8
k
n0
n0
j2 k j2 2 k j2 3 k
1 e8 e8 e8
X (0 ) 4X ( 1 ) 1 j 2 1X (2 ) 0X (3 ) 1 j 2 1
X (4 ) 0X (5 ) 1 j 2 1X (6 ) 0X (7 ) 1 j 2 1
关于离散傅里叶变换(DFT)：
序列x(n)在时域是有限长的(长度为N)，它的离 散傅里叶变换X(k)也是离散、有限长的(长度也 为N)。
n为时域变量，k为频域变量。 离散傅里叶变换与离散傅里叶级数没有本质区别，
2、序列的移位
D F S [ x ( n m ) ] W N m k X ( k ) e j2 N m k X ( k )
N 1
证 ： D F S [x(n m )] x(n m )W N n k
n 0
令inmN1mx(i)WNk(im)
im
N1
W N m k x(i)W N ki W N m kX(k)
同样，利用对称性
若 y (n ) x 1 (n )x 2 (n )
则
N 1
Y(k)D F S[y(n)] y(n)W N nk
n 0
N 1N l01X1(l)X2(kl)
N 1N l01X2(l)X1(kl)
§3.5 离散傅里叶变换
——有限长序列的离散频域表示
在进行DFS分析时，时域、频域序列都是无限 长的周期序列
x2 m … 5 4 3 2 1 0 5 4 3 2 1 0 … 10 x2 1m … 0 5 4 3 2 1 0 5 4 3 2 1 … 8 x2 2m … 1 0 5 4 3 2 1 0 5 4 3 2 … 6 x2 3m … 2 1 0 5 4 3 2 1 0 5 4 3 … 10 x2 4m … 3 2 1 0 5 4 3 2 1 0 5 4 … 14 x2 5m … 4 3 2 1 0 5 4 3 2 1 0 5 … 12
N1
X(k) x(n)WNnk
n0
7
3
x(n)W8nk
W
n 8
k
n0
n0
j2 k j2 2 k j2 3 k
1 e8 e8 e8
X (0 ) 4X ( 1 ) 1 j 2 1X (2 ) 0X (3 ) 1 j 2 1
X (4 ) 0X (5 ) 1 j 2 1X (6 ) 0X (7 ) 1 j 2 1
关于离散傅里叶变换(DFT)：
序列x(n)在时域是有限长的(长度为N)，它的离 散傅里叶变换X(k)也是离散、有限长的(长度也 为N)。
n为时域变量，k为频域变量。 离散傅里叶变换与离散傅里叶级数没有本质区别，
2、序列的移位
D F S [ x ( n m ) ] W N m k X ( k ) e j2 N m k X ( k )
N 1
证 ： D F S [x(n m )] x(n m )W N n k
n 0
令inmN1mx(i)WNk(im)
im
N1
W N m k x(i)W N ki W N m kX(k)
同样，利用对称性
若 y (n ) x 1 (n )x 2 (n )
则
N 1
Y(k)D F S[y(n)] y(n)W N nk
n 0
N 1N l01X1(l)X2(kl)
N 1N l01X2(l)X1(kl)
§3.5 离散傅里叶变换
——有限长序列的离散频域表示
在进行DFS分析时，时域、频域序列都是无限 长的周期序列
x2 m … 5 4 3 2 1 0 5 4 3 2 1 0 … 10 x2 1m … 0 5 4 3 2 1 0 5 4 3 2 1 … 8 x2 2m … 1 0 5 4 3 2 1 0 5 4 3 2 … 6 x2 3m … 2 1 0 5 4 3 2 1 0 5 4 3 … 10 x2 4m … 3 2 1 0 5 4 3 2 1 0 5 4 … 14 x2 5m … 4 3 2 1 0 5 4 3 2 1 0 5 … 12
程佩青数字信号处理第三版笔记
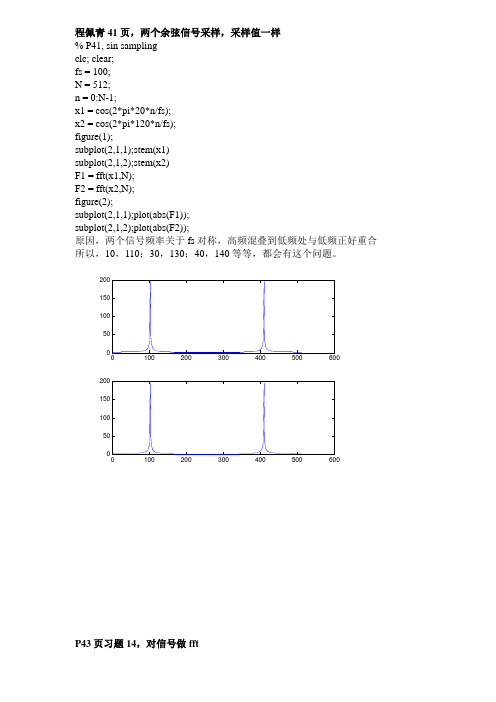
程佩青41页，两个余弦信号采样，采样值一样% P41, sin samplingclc; clear;fs = 100;N = 512;n = 0:N-1;x1 = cos(2*pi*20*n/fs);x2 = cos(2*pi*120*n/fs);figure(1);subplot(2,1,1);stem(x1)subplot(2,1,2);stem(x2)F1 = fft(x1,N);F2 = fft(x2,N);figure(2);subplot(2,1,1);plot(abs(F1));subplot(2,1,2);plot(abs(F2));原因，两个信号频率关于fs对称，高频混叠到低频处与低频正好重合所以，10，110；30，130；40，140等等，都会有这个问题。
01002003004005006000100200300400500600% p43, exercise14clc; clear;fs = 3000;N = 512;n = 0:N-1;x = ( 1+cos(2*pi*100*n/fs) ).*cos(2*pi*600*n/fs);F = fft(x,N);plot(abs(F)); ylabel('|X(k)|'); xlabel('k');010*******400500600020406080100120140160180200|X (k )|k三个峰值分别对应500，600，700Hz ，对应k 值分别为86103120计算方法：采样间隔：Ts = 1/fs;信号持续时间：T = Ts*N频域分辨率为：F = 1/T; 每个k 代表的频率值，K1 = f1/F=K2 = f2/F=K3 = f3/F=Ps ：在使用data cursor 时候，我们会发现，每次只能显示一个点的数据，当需要显示多个点的时候就会觉得很不方便。
告诉大家一个小窍门，当你选择data cursor 工具时，按住alt 键，点左键选择曲线上的点。
程佩青《数字信号处理教程(第三版)》课后习题答案精编版
4
第一章 离散时间信号与系统
1 .直接计算下面两个序列的卷积和 y( n ) = x( n )* h( n )
h (n )
=
⎧an ⎨
⎩0
, 0 ≤ n ≤ N −1 , 其他n
x (n )
=
⎧⎪ β ⎨
n−n 0
⎪⎩ 0
,n0 ≤ n , n < n0
请用公式表示。
分析：
①注意卷积和公式中求和式中是哑变量 m （ n 看作参量），
y (n ) ={1，2，3，3，2，1} ;
②δ (n)* x(n) = x(n) , δ (n − m)* x(n) = x(n − m) ;
③卷积和求解时， n 的分段处理。
6
解：(1) y(n) = x(n) * h(n) = R5(n) (2) y(n) = x(n) * h(n) = {1,2,3,3,2,1}
β α
n +1
β α β =
n +1− N −n0
N−
N
α −β
y(n) = Nα n−n0 ,
(α = β )
, (α ≠ β )
如此题所示，因而要分段求解。
2 .已知线性移不变系统的输入为 x( n ) ,系统的单位抽样响应
为 h( n ) ,试求系统的输出 y( n ) ,并画图。
(1)x(n) = δ (n)
∑ ∑( ) n α m−n0 n−m = β α = β m=n0
nn β
n0
α
n β −n0
− β n0
α
β n +1 α
1
−
β α
α β =
− n +1− n0
第一章 离散时间信号与系统
1 .直接计算下面两个序列的卷积和 y( n ) = x( n )* h( n )
h (n )
=
⎧an ⎨
⎩0
, 0 ≤ n ≤ N −1 , 其他n
x (n )
=
⎧⎪ β ⎨
n−n 0
⎪⎩ 0
,n0 ≤ n , n < n0
请用公式表示。
分析：
①注意卷积和公式中求和式中是哑变量 m （ n 看作参量），
y (n ) ={1，2，3，3，2，1} ;
②δ (n)* x(n) = x(n) , δ (n − m)* x(n) = x(n − m) ;
③卷积和求解时， n 的分段处理。
6
解：(1) y(n) = x(n) * h(n) = R5(n) (2) y(n) = x(n) * h(n) = {1,2,3,3,2,1}
β α
n +1
β α β =
n +1− N −n0
N−
N
α −β
y(n) = Nα n−n0 ,
(α = β )
, (α ≠ β )
如此题所示，因而要分段求解。
2 .已知线性移不变系统的输入为 x( n ) ,系统的单位抽样响应
为 h( n ) ,试求系统的输出 y( n ) ,并画图。
(1)x(n) = δ (n)
∑ ∑( ) n α m−n0 n−m = β α = β m=n0
nn β
n0
α
n β −n0
− β n0
α
β n +1 α
1
−
β α
α β =
− n +1− n0
数字信号处理教程 (第三版)程佩青 清华大学出版社dsp-ch6-4
H a ( p) 1
18 页
(p p )
k 0 k
N 1
式中，s/Ω c=jΩ /Ω c。 令 λ =Ω /Ω c ， λ 称 为 归 一 化 频 率 ； 令 p=jλ =s/Ω c，p称为归一化复变量，这样归一 化巴特沃斯的系统函数为
X
第
• pk为归一化极点，用下式表示：
19 页
pk s k / c e
X
第
5）低通巴特沃斯滤波器的设计步骤
• 确定技术指标： p p s s • 根据技术指标求出滤波器阶数N：
20 页
由 P 20lg H a ( j p )
2N
H a ( j p )
2
1 p 1 c
2N
p /10 得： 1 10 p N /10 c p 10 p 1 2N s s 10 s /10 1 s /10 同理：1 10 c /10 lg ksp s 10 1 则：N 令 sp ksp lg sp 10 /10 1 p
p s
取大于等于N的最小整数
X
第
21 页
求出归一化系统函数：
H a ( p) 1
(p p )
k 0 k
N 1
其中极点： pk e
1 2 k 1 j ( ) 2 2N
k 1,2,..., N
或者由N，直接查表得 H a ( p )
X
第
22 页
去归一化
s H a ( s) H a ( p) H a c
第 1 页
X
第
• 模拟滤波器按幅度特性可分成低通、高通、 带通和带阻滤波器，它们的理想幅度特性如图0 Ω H a (jΩ) 0
18 页
(p p )
k 0 k
N 1
式中，s/Ω c=jΩ /Ω c。 令 λ =Ω /Ω c ， λ 称 为 归 一 化 频 率 ； 令 p=jλ =s/Ω c，p称为归一化复变量，这样归一 化巴特沃斯的系统函数为
X
第
• pk为归一化极点，用下式表示：
19 页
pk s k / c e
X
第
5）低通巴特沃斯滤波器的设计步骤
• 确定技术指标： p p s s • 根据技术指标求出滤波器阶数N：
20 页
由 P 20lg H a ( j p )
2N
H a ( j p )
2
1 p 1 c
2N
p /10 得： 1 10 p N /10 c p 10 p 1 2N s s 10 s /10 1 s /10 同理：1 10 c /10 lg ksp s 10 1 则：N 令 sp ksp lg sp 10 /10 1 p
p s
取大于等于N的最小整数
X
第
21 页
求出归一化系统函数：
H a ( p) 1
(p p )
k 0 k
N 1
其中极点： pk e
1 2 k 1 j ( ) 2 2N
k 1,2,..., N
或者由N，直接查表得 H a ( p )
X
第
22 页
去归一化
s H a ( s) H a ( p) H a c
第 1 页
X
第
• 模拟滤波器按幅度特性可分成低通、高通、 带通和带阻滤波器，它们的理想幅度特性如图0 Ω H a (jΩ) 0